Hostname: page-component-7dd5485656-jtdwj Total loading time: 0 Render date: 2025-10-31T16:41:40.762Z Has data issue: false hasContentIssue false
  • English
  • Français

ON A MEASURE ZERO STABILITY PROBLEM OF A CYCLIC EQUATION

Published online by Cambridge University Press:  27 October 2015

JAEYOUNG CHUNG  and
JOHN MICHAEL RASSIAS
JAEYOUNG CHUNG*
Affiliation:
Department of Mathematics, Kunsan National University, Kunsan 573-701, Republic of Korea email jychung@kunsan.ac.kr
JOHN MICHAEL RASSIAS
Affiliation:
Section of Mathematics and Informatics, Pedagogical Department E. E., National and Kapodistrian University of Athens, Greece email jrassias@primedu.uoa.gr
*
✉jychung@kunsan.ac.kr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 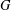$G$ be a commutative group, 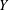$Y$ a real Banach space and 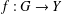$f:G\rightarrow Y$. We prove the Ulam–Hyers stability theorem for the cyclic functional equation

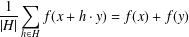$$\begin{eqnarray}\displaystyle \frac{1}{|H|}\mathop{\sum }_{h\in H}f(x+h\cdot y)=f(x)+f(y) & & \displaystyle \nonumber\end{eqnarray}$$
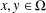for all $x,y\in {\rm\Omega}$, where 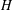$H$ is a finite cyclic subgroup of 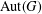$\text{Aut}(G)$ and 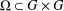${\rm\Omega}\subset G\times G$ satisfies a certain condition. As a consequence, we consider a measure zero stability problem of the functional equation
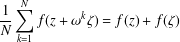$$\begin{eqnarray}\displaystyle \frac{1}{N}\mathop{\sum }_{k=1}^{N}f(z+{\it\omega}^{k}{\it\zeta})=f(z)+f({\it\zeta}) & & \displaystyle \nonumber\end{eqnarray}$$
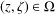 for all $(z,{\it\zeta})\in {\rm\Omega}$, where 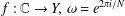$f:\mathbb{C}\rightarrow Y,\,{\it\omega}=e^{2{\it\pi}i/N}$ and 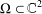${\rm\Omega}\subset \mathbb{C}^{2}$ has four-dimensional Lebesgue measure 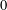$0$.

Keywords

asymptotic behaviourBaire category theoremCauchy functional equationcyclic functional equationfirst categoryLebesgue measurequadratic functional equation

MSC classification

Primary: 39B82: Stability, separation, extension, and related topics
Secondary: 39B52: Equations for functions with more general domains and/or ranges

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 93 , Issue 2 , April 2016 , pp. 272 - 282
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Bahyrycz, A., ‘On solutions of the second generalization of d’Alembert equation on a restricted domain’, Appl. Math. Comput. 223 (2013), 209–215.Google Scholar
Bahyrycz, A. and Brzdȩk, J., ‘On solutions of the d’Alembert equation on a restricted domain’, Aequationes Math. 85 (2013), 169–183.CrossRefGoogle Scholar
Bahyrycz, A. and Piszczek, M., ‘Hyper stability of Jensen functional equation’, Acta Math. Hungar. 142 (2014), 353–365.CrossRefGoogle Scholar
Batko, B., ‘Stability of an alternative functional equation’, J. Math. Anal. Appl. 339 (2008), 303–311.Google Scholar
Bouikhalene, B., Elquorachi, E. and Rassias, J. M., ‘A fixed points approach to stability of the Pexider equation’, Tbil. Math. J. 7(2) (2014), 95–110.Google Scholar
Brzdȩk, J., ‘On a method of proving the Hyers–Ulam stability of functional equations on restricted domains’, Aust. J. Math. Anal. Appl. 6 (2009), 1–10.Google Scholar
Chung, J. and Rassias, J. M., ‘Quadratic functional equations in a set of Lebesgue measure zero’, J. Math. Anal. Appl. 419 (2014), 1065–1075.Google Scholar
Hyers, D. H., ‘On the stability of the linear functional equations’, Proc. Nat. Acad. Sci. USA 27(1941) 222–224.CrossRefGoogle Scholar
Jung, S.-M., ‘On the Hyers–Ulam stability of the functional equations that have the quadratic property’, J. Math. Anal. Appl. 222 (1998), 126–137.Google Scholar
Jung, S.-M., Hyers–Ulam–Rassias Stability of Functional Equations in Nonlinear Analysis (Springer, New York, 2011).CrossRefGoogle Scholar
Kuczma, M., ‘Functional equations on restricted domains’, Aequationes Math. 18 (1978), 1–34.Google Scholar
Oxtoby, J. C., Measure and Category (Springer, New York, 1980).Google Scholar
Rassias, J. M., ‘On the Ulam stability of mixed type mappings on restricted domains’, J. Math. Anal. Appl. 281 (2002), 747–762.CrossRefGoogle Scholar
Sibaha, M. A., Bouikhalene, B. and Elqorachi, E., ‘Hyers–Ulam–Rassias stability of K-quadratic functional equation’, J. Inequal. Pure Appl. Math. 8(3) (2007), 13 pages; Art 89.Google Scholar
Sikorska, J., ‘On two conditional Pexider functinal equations and their stabilities’, Nonlinear Anal. 70 (2009), 2673–2684.Google Scholar
Skof, F., ‘Proprietá locali e approssimazione di operatori’, Rend. Sem. Mat. Fis. Milano 53 (1983), 113–129.Google Scholar