No CrossRef data available.
Article contents
Compactifications of moduli of del Pezzo surfaces via line arrangement and K-stability
Published online by Cambridge University Press: 13 November 2023
Abstract
In this paper, we study compactifications of the moduli of smooth del Pezzo surfaces using K-stability and the line arrangement. We construct K-moduli of log del Pezzo pairs with sum of lines as boundary divisors, and prove that for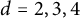 
$d=2,3,4$, these K-moduli of pairs are isomorphic to the K-moduli spaces of del Pezzo surfaces. For 
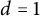$d=1$, we prove that they are different by exhibiting some walls.
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
References
Alper, J., Blum, H., Halpern-Leistner, D., and Chenyang, X., Reductivity of the automorphism group of K-polystable Fano varieties. Invent. Math. 222(2020), no. 3, 995–1032.CrossRefGoogle Scholar
Araujo, C., Castravet, A.-M., Cheltsov, I., Fujita, K., Kaloghiros, A.-S., Martinez-Garcia, J., Shramov, C., and Viswanathan, N., The Calabi problem for Fano threefolds, London Mathematical Society Lecture Note Series, 485, Cambridge University Press, Cambridge, 2021.Google Scholar
Ascher, K., DeVleming, K., and Liu, Y., Wall crossing for K-moduli spaces of plane curves. Preprint, 2019. arXiv:1909.04576Google Scholar
Ascher, K., DeVleming, K., and Liu, Y., K-moduli of curves on a quadric surface and K3 surfaces. J. Inst. Math. Jussieu 22(2023), no. 3, 1251–1291.CrossRefGoogle Scholar
Blum, H. and Chenyang, X., Uniqueness of K-polystable degenerations of Fano varieties. Ann. Math. 190(2019), no. 2, 609–656.CrossRefGoogle Scholar
Blum, H., Halpern-Leistner, D., Liu, Y., and Chenyang, X., On properness of K-moduli spaces and optimal degenerations of Fano varieties. Sel. Math., New Ser. 27(2021), no. 4, 73.CrossRefGoogle Scholar
Blum, H., Liu, Y., and Chenyang, X., Openness of K-semistability for Fano varieties. Duke Math. J. 171(2022), no. 13, 2753–2797.Google Scholar
Caporaso, L. and Sernesi, E., Recovering plane curves from their bitangents. J. Algebraic Geom. 12(2003), 225–244.CrossRefGoogle Scholar
Cayley, A., A memoir on cubic surfaces. Philos. Trans. R. Soc. Lond. 159(1869), 231–326.Google Scholar
Chenyang, X., A minimizing valuation is quasi-monomial. Ann. Math. 191(2020), no. 3, 1003–1030.Google Scholar
Chenyang, X., K-stability of Fano varieties: an algebro-geometric approach. EMS Surv. Math. Sci. 8(2021), no. 1, 265–354.Google Scholar
Chenyang, X. and Zhuang, Z., On positivity of the CM line bundle on K-moduli spaces. Ann. Math. 192(2020), no. 3, 1005–1068.Google Scholar
Codogni, G. and Patakfalvi, Z., Positivity of the CM line bundle for families of K-stable klt Fano varieties. Invent. Math. 223(2021), no. 3, 811–894.CrossRefGoogle Scholar
Dervan, R., On K-stability of finite covers. Bull. Lond. Math. Soc. 48(2016), no. 4, 717–728.CrossRefGoogle Scholar
Fujita, K., Optimal bounds for the volumes of Kähler–Einstein Fano manifolds. Amer. J. Math. 140(2018), no. 2, 391–414.CrossRefGoogle Scholar
Fujita, K., A valuative criterion for uniform K-stability of
$\mathbb{Q}$
-Fano varieties. J. Reine Angew. Math. 2019(2019), no. 751, 309–338.CrossRefGoogle Scholar
$\mathbb{Q}$
-Fano varieties. J. Reine Angew. Math. 2019(2019), no. 751, 309–338.CrossRefGoogle ScholarFujita, T.,
On singular del Pezzo varieties
. In: Algebraic geometry, Springer, Berlin–Heidelberg, 1990, pp. 117–128.CrossRefGoogle Scholar
Gallardo, P., Kerr, M., and Schaffler, L., Geometric interpretation of toroidal compactifications of moduli of points in the line and cubic surfaces. Adv. Math. 381(2021), 107632.CrossRefGoogle Scholar
Hacking, P., Keel, S., and Tevelev, J., Stable pair, tropical, and log canonical compactifications of moduli spaces of del Pezzo surfaces. Invent. Math. 178(2009), no. 1, 173–227.CrossRefGoogle Scholar
Hassett, B., Kresch, A., and Tschinkel, Y.,
On the moduli of degree 4 del Pezzo surfaces
. In: Development of moduli theory (Kyoto, 2013), Advanced Studies in Pure Mathematics, 69, Mathematical Society of Japan, Tokyo, 2013, 349–386.Google Scholar
Hidaka, F. and Watanabe, K.-i., Normal Gorenstein surfaces with ample anti-canonical divisor. Tokyo J. Math. 4(1981), no. 2, 319–330.CrossRefGoogle Scholar
Hilbert, D.,
Über die vollen invariantensysteme
. In: Algebra · Invariantentheorie geometrie, Springer, Berlin–Heidelberg, 1970, pp. 287–344.CrossRefGoogle Scholar
Hyeon, D. and Lee, Y., Log minimal model program for the moduli of stable curves of genus three. Math. Res. Lett. 17(2010), no. 4, 625–636.CrossRefGoogle Scholar
Kollár, J. and Mori, S., Birational geometry of algebraic varieties, Cambridge Tracts in Mathematics, 134, Cambridge University Press, Cambridge, 1998.CrossRefGoogle Scholar
Kollár, J. and Shepherd-Barron, N. I., Threefolds and deformations of surface singularities. Invent. Math. 91(1988), no. 2, 299–338.CrossRefGoogle Scholar
Kulkarni, A., Ren, Y., Namin, M. S., and Sturmfels, B.,
Real space sextics and their tritangents
. In: Proceedings of the 2018 ACM international symposium on symbolic and algebraic computation, Association for Computing Machinery, New York, 2018, pp. 247–254.CrossRefGoogle Scholar
Li, C., K-semistability is equivariant volume minimization. Duke Math. J. 166(2017), no. 16, 3147–3218.CrossRefGoogle Scholar
Li, C. and Liu, Y., Kähler–Einstein metrics and volume minimization. Adv. Math. 341(2019), 440–492.CrossRefGoogle Scholar
Li, C., Wang, X., and Chenyang, X., Algebraicity of the metric tangent cones and equivariant K-stability. J. Amer. Math. Soc. 34(2021), no. 4, 1175–1214.CrossRefGoogle Scholar
Liu, Y., The volume of singular Kähler–Einstein Fano varieties. Compos. Math. 154(2018), no. 6, 1131–1158.CrossRefGoogle Scholar
Liu, Y., Chenyang, X., and Zhuang, Z., Finite generation for valuations computing stability thresholds and applications to K-stability. Ann. Math. 196(2022), no. 2, 507–566.CrossRefGoogle Scholar
Liu, Y. and Zhu, Z., Equivariant K-stability under finite group action. Int. J. Math. 33(2022), no. 1, 2250007.CrossRefGoogle Scholar
Mabuchi, T. and Mukai, S.,
Stability and Einstein–Kähler metric of a quartic del Pezzo surface
. In: Einstein metrics and Yang–Mills connections, CRC Press, Boca Raton, FL, 1993, pp. 133–160.Google Scholar
Mumford, D., Fogarty, J., and Kirwan, F., Geometric invariant theory, Ergebnisse der Mathematik und ihrer Grenzgebiete. 2. Folge, 34, Springer, Berlin–Heidelberg, 1994.CrossRefGoogle Scholar
Odaka, Y., The GIT stability of polarized varieties via discrepancy. Ann. Math. (2013), 645–661.CrossRefGoogle Scholar
Odaka, Y., Spotti, C., and Sun, S., Compact moduli spaces of del Pezzo surfaces and Kähler–Einstein metrics. J. Differ. Geom. 102(2016), no. 1, 127–172.CrossRefGoogle Scholar
Paul, S. T. and Tian, G., CM stability and the generalized Futaki invariant II. Astérisque 328(2009), 339–354.Google Scholar
Spotti, C. and Song, S., Explicit Gromov–Hausdorff compactifications of moduli spaces of Kähler–Einstein Fano manifolds. Pure Appl. Math. Q. 13(2017), no. 3, 477–515.CrossRefGoogle Scholar
Tian, G., On Kähler–Einstein metrics on certain Kähler manifolds with
${c}_1(M)>0$
. Invent. Math. 89(1987), no. 2, 225–246.CrossRefGoogle Scholar
${c}_1(M)>0$
. Invent. Math. 89(1987), no. 2, 225–246.CrossRefGoogle ScholarTu, N. C., On semi-stable, singular cubic surfaces. Singul. Franco-Japonaises 10(2005), 373–389.Google Scholar
Zhao, J., Moduli of genus six curves and K-stability. Preprint, 2023. arXiv:2212.06992
Google Scholar
Zhuang, Z., Optimal destabilizing centers and equivariant K-stability. Invent. Math. 226(2021), no. 1, 195–223.CrossRefGoogle Scholar