No CrossRef data available.
Article contents
Approximation in the Zygmund and Hölder classes on 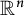 $\mathbb {R}^n$
$\mathbb {R}^n$
Published online by Cambridge University Press: 13 September 2021
Abstract
We determine the distance (up to a multiplicative constant) in the Zygmund class
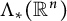 $\Lambda _{\ast }(\mathbb {R}^n)$
to the subspace
$\Lambda _{\ast }(\mathbb {R}^n)$
to the subspace
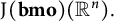 $\mathrm {J}_{}(\mathbf {bmo})(\mathbb {R}^n).$
The latter space is the image under the Bessel potential
$\mathrm {J}_{}(\mathbf {bmo})(\mathbb {R}^n).$
The latter space is the image under the Bessel potential
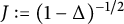 $J := (1-\Delta )^{{-1}/2}$
of the space
$J := (1-\Delta )^{{-1}/2}$
of the space
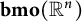 $\mathbf {bmo}(\mathbb {R}^n)$
, which is a nonhomogeneous version of the classical
$\mathbf {bmo}(\mathbb {R}^n)$
, which is a nonhomogeneous version of the classical
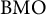 $\mathrm {BMO}$
. Locally,
$\mathrm {BMO}$
. Locally,
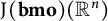 $\mathrm {J}_{}(\mathbf {bmo})(\mathbb {R}^n)$
consists of functions that together with their first derivatives are in
$\mathrm {J}_{}(\mathbf {bmo})(\mathbb {R}^n)$
consists of functions that together with their first derivatives are in
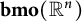 $\mathbf {bmo}(\mathbb {R}^n)$
. More generally, we consider the same question when the Zygmund class is replaced by the Hölder space
$\mathbf {bmo}(\mathbb {R}^n)$
. More generally, we consider the same question when the Zygmund class is replaced by the Hölder space
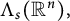 $\Lambda _{s}(\mathbb {R}^n),$
with
$\Lambda _{s}(\mathbb {R}^n),$
with
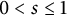 $0 < s \leq 1$
, and the corresponding subspace is
$0 < s \leq 1$
, and the corresponding subspace is
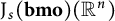 $\mathrm {J}_{s}(\mathbf {bmo})(\mathbb {R}^n)$
, the image under
$\mathrm {J}_{s}(\mathbf {bmo})(\mathbb {R}^n)$
, the image under
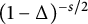 $(1-\Delta )^{{-s}/2}$
of
$(1-\Delta )^{{-s}/2}$
of
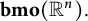 $\mathbf {bmo}(\mathbb {R}^n).$
One should note here that
$\mathbf {bmo}(\mathbb {R}^n).$
One should note here that
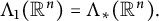 $\Lambda _{1}(\mathbb {R}^n) = \Lambda _{\ast }(\mathbb {R}^n).$
Such results were known earlier only for
$\Lambda _{1}(\mathbb {R}^n) = \Lambda _{\ast }(\mathbb {R}^n).$
Such results were known earlier only for
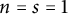 $n = s = 1$
with a proof that does not extend to the general case.
$n = s = 1$
with a proof that does not extend to the general case.
Our results are expressed in terms of second differences. As a by-product of our wavelet-based proof, we also obtain the distance from
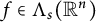 $f \in \Lambda _{s}(\mathbb {R}^n)$
to
$f \in \Lambda _{s}(\mathbb {R}^n)$
to
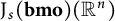 $\mathrm {J}_{s}(\mathbf {bmo})(\mathbb {R}^n)$
in terms of the wavelet coefficients of
$\mathrm {J}_{s}(\mathbf {bmo})(\mathbb {R}^n)$
in terms of the wavelet coefficients of
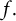 $f.$
We additionally establish a third way to express this distance in terms of the size of the hyperbolic gradient of the harmonic extension of f on the upper half-space
$f.$
We additionally establish a third way to express this distance in terms of the size of the hyperbolic gradient of the harmonic extension of f on the upper half-space
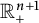 $\mathbb {R}^{n +1}_+$
.
$\mathbb {R}^{n +1}_+$
.
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2021
Footnotes
First author is supported by the Finnish Academy grant 1309940. Second author is supported by the Generalitat de Catalunya grant 2017 SGR 395, the Spanish Ministerio de Ciencia e Innovación projects MTM2014-51824-P and MTM2017-85666-P, and the European Research Council project CHRiSHarMa no. DLV-682402.




