Hostname: page-component-7f64f4797f-m2b9p Total loading time: 0 Render date: 2025-11-03T12:45:02.675Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterization of Parallel Isometric Immersions of Space Forms into Space Forms in the Class of Isotropic Immersions

Published online by Cambridge University Press:  20 November 2018

Sadahiro Maeda  and
Seiichi Udagawa
Sadahiro Maeda
Affiliation:
(Maeda) Department of Mathematics, Shimane University, Matsue 690-8504, Japan Current address: Department of Mathematics, Saga University, 1 Honzyo, Saga 840-8502, Japan, smaeda@ms.saga-u.ac.jp
Seiichi Udagawa
Affiliation:
(Udagawa) Department of Mathematics, School of Medicine, Nihon University, Itabashi, Tokyo 173-0032, Japan, sudagawa@med.nihon-u.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For an isotropic submanifold 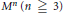${{M}^{n}}(n\underline{\underline{>}}3)$ of a space form 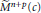${{\tilde{M}}^{n+p}}(c)$ of constant sectional curvature $c$ , we show that if the mean curvature vector of 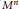${{M}^{n}}$ is parallel and the sectional curvature $K$ of 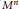${{M}^{n}}$ satisfies some inequality, then the second fundamental form of 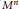${{M}^{n}}$ in 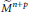${{\tilde{M}}^{n+p}}$ is parallel and our manifold 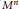${{M}^{n}}$ is a space form.

Keywords

53C4053C42space formsparallel isometric immersionsisotropic immersionstotally umbilicVeronese manifoldssectional curvaturesparallel mean curvature vector

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 3 , 01 June 2009 , pp. 641 - 655
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Bryant, R., Conformal and minimal immersions of compact surfaces into the 4-sphere. J. Differential Geom. 17(1982), no. 3, 455–473.Google Scholar
[2] do, M. Carmo and N.Wallach, Minimal immersions of spheres into spheres. Ann. of Math. 93(1971), 43–62.Google Scholar
[3] Ferus, D., Immersions with parallel second fundamental form. Math. Z. 140(1974), 87–92.Google Scholar
[4] Itoh, T., Addendum to “On Veronese manifolds”. J. Math. Soc. Japa. 30(1978), no. 1, 73–74.Google Scholar
[5] Maeda, S., On some isotropic submanifolds in spheres. Proc. Japan Acad. Ser. A Math. Sci. 77(2001), no. 11, 173–175.Google Scholar
[6] Maeda, S. and Tsukada, K., Isotropic immersions into a real space form. Canad. Math. Bull. 37(1994), no. 2, 245–253.Google Scholar
[7] O’Neill, B., Isotropic and Käehler immersions. Canad. J. Math. 17(1965), 905–915.Google Scholar
[8] Ros, A., A characterization of seven compact Kaehler submanifolds by holomorphic pinching. Ann. of Math. 121(1985), no. 2, 377–382.Google Scholar
[9] Takeuchi, M., Parallel submanifolds of space forms. In: Manifolds and Lie groups, Progr. Math. 14, Birkhäuser, Boston, MA, 1981, pp. 429–447.Google Scholar
[10] Tsukada, K., Isotropic minimal immersions of spheres into spheres. J. Math. Soc. Japa. 35(1983), no. 2, 355–379.Google Scholar