Hostname: page-component-7dd5485656-wjfd9 Total loading time: 0 Render date: 2025-10-31T17:35:05.710Z Has data issue: false hasContentIssue false
  • English
  • Français

Furstenberg Transformations and Approximate Conjugacy

Published online by Cambridge University Press:  20 November 2018

Huaxin Lin
Huaxin Lin*
Affiliation:
Department of Mathematics, East China, Normal University, Shanghai, China and (current) Department of Mathematics, University of Oregon, Eugene, OR 97403-1222, U.S.A. e-mail: hlin@uoregon.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

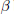Let $\alpha $ and $\beta $ be two Furstenberg transformations on 2-torus associated with irrational numbers 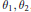${{\theta }_{1}},\,{{\theta }_{2}}$ , integers 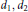${{d}_{1}},\,{{d}_{2}}$ and Lipschitz functions 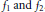${{f}_{1}}\,\text{and}\,{{f}_{2}}$ . It is shown that $\alpha $ and 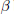$\beta $ are approximately conjugate in ameasure theoretical sense if (and only if) 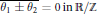$\overline{{{\theta }_{1}}\,\pm \,{{\theta }_{2}}}\,=\,0\,\text{in}\,\mathbb{R}\text{/}\mathbb{Z}$ . Closely related to the classification of simple amenable 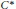${{C}^{*}}$ -algebras, it is shown that $\alpha $ and 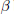$\beta $ are approximately 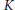$K$ -conjugate if (and only if) 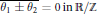$\overline{{{\theta }_{1}}\,\pm \,{{\theta }_{2}}}\,=\,0\,\text{in}\,\mathbb{R}\text{/}\mathbb{Z}$ and 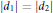$|{{d}_{1}}|\,=\,|{{d}_{2}}|$ . This is also shown to be equivalent to the condition that the associated crossed product 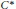${{C}^{*}}$ -algebras are isomorphic.

Keywords

37A55secondary46L35Furstenberg transformationsapproximate conjugacy

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 1 , 01 February 2008 , pp. 189 - 207
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Dadarlat, M. and Eillers, S., On the classification of nuclear C*-algebras, Proc. LondonMath. Soc. 85(2002), no. 1, 168–210.Google Scholar
[2] Elliott, G. A. and Gong, G., On the classification of C*-algebras of real rank zero, II. Ann. of Math. 144(1996), no. 3, 497–610.Google Scholar
[3] Elliott, G. A., Gong, G. and Li, L., On the classification of simple inductive limit C*-algebras. II. The isomorphism theorem. Invent.Math. 168(2007), no. 2, 249–320.Google Scholar
[4] Furstenberg, H., Strict ergodicity and transformation of the torus. Amer. J. Math. 83(1961), 573–601.Google Scholar
[5] Giordano, T., Putnam, I. and Skau, C., Topological orbit equivalence and C*-crossed products. J. Reine Angew.Math. 469(1995), 51–111.Google Scholar
[6] Ji, R., On the Crossed Product C*-algebras Associated with Furstenberg Transformation on tori. Ph. D. Thesis, State University of New York at Stoney Brook, 1986.Google Scholar
[7] Kodaka, K., Tracial states on crossed products associated with Furstenberg transformations on the 2-torus. Studia Math. 115(1995), no. 2, 183–187. Erratum to: “Tracial states on crossed products associated with Furstenberg transformations on the 2-torus”. Studia Math. 119(1996), no. 1, 97–98.Google Scholar
[8] Kodaka, K., Anzai and Furstenberg transformations on the 2-torus and topologically quasi-discrete spectrum. Canad. Math. Bull. 38(1995), no. 1, 87–92.Google Scholar
[9] Lin, H., Classification of simple tracially AF C*-algebras. Canad. J. Math. 53(2001), no. 1, 161–194.Google Scholar
[10] Lin, H., The tracial topological ranks of C*-algebras, Proc. LondonMath. Soc. 83(2001), no. 1, 199–234.Google Scholar
[11] Lin, H., An Introduction to the Classification of Amenable C*-algebras, World Scientific, River Edge, NJ, 2001.Google Scholar
[12] Lin, H., Classification of simple C*-algebras and higher dimensional noncommutative tori. Ann. of Math. 157(2003), no. 2, 521–544.Google Scholar
[13] Lin, H., Classification of simple C*-algebras of tracial topological rank zero. Duke Math. J. 125(2004), no. 1, 91–119.Google Scholar
[14] Lin, H., Classification of homomorphisms and dynamical systems, Trans. Amer.Math. Soc. 359(2007), no. 2, 859–895.Google Scholar
[15] Lin, H. and Matui, H., Minimal dynamical systems and approximate conjugacy. Math. Ann. 332(2005), no. 4, 795–822.Google Scholar
[16] Lin, H. and Matui, H., Minimal dynamical systems on the product of the Cantor set and the circle, Comm. Math. Phys. 257(2005), no. 2, 425–471.Google Scholar
[17] Lin, H. and Matui, H., Minimal dynamical systems on the product of the Cantor set and the circle, II. Selecta Math. 12(2006), no. 2, 199–239.Google Scholar
[18] Lin, H. and Phillips, N. C., Crossed products by minimal homeomorphisms , preprint, math.OA/0408291.Google Scholar
[19] Lin, Q. and Phillips, N. C., Ordered K-theory for C*-algebras of minimal homeomorphisms. In: Operator Algebras and Operator Theory. ContemporaryMathematics 228, American Mathematical Society, Providence, RI, 1998 pp. 289–314.Google Scholar
[20] Matui, H., Approximate conjugacy and full groups of Cantor minimal systems, Publ. Res. Inst.Math. Sci. 41(2005), no. 3, 695–722.Google Scholar
[21] Osaka, H. and Phillips, N. C., Furstenberg transformation on irrational rotation algebras. Ergodic Theory Dynam. Systems 26(2006), no. 5, 1623–1651.Google Scholar
[22] Pedersen, G. K., C*-algebras and their Automorphism Groups, Academic Press, London, 1979.Google Scholar
[23] Phillips, N. C., Cancellation and stable rank for direct limits of recursive subhomogeneous algebras, Trans. Amer.Math. Soc., to appear, (math.OA/0101157).Google Scholar
[24] Rouhani, H., A Furstenberg transformation of the 2-torus without quasi-discrete spectrum. Canad. Math. Bull. 33(1990), no. 3, 316–322.Google Scholar
[25] Tomiyama, J., Topological full groups and structure of normalizers in transformation group C*-algebras. Pacific J. Math. 173(1996), no. 2, 571–583.Google Scholar