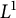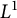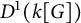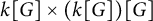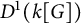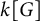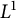1 Introduction
In this paper, we investigate and establish the relation between some extensions of two well-known conjectures in symbolic dynamics and ring theory, namely, Gottschalk’s surjunctivity conjecture and Kaplansky’s stable finiteness conjecture. More specifically, given a group G, a field k, and a finite set A, Kaplansky conjectured [Reference Kaplansky22] that the group ring
![]() $k[G]$
is stably finite, i.e., every one-sided invertible element of the ring of square matrices of size
$k[G]$
is stably finite, i.e., every one-sided invertible element of the ring of square matrices of size
![]() $n \times n$
with coefficients in
$n \times n$
with coefficients in
![]() $k[G]$
must be a two-sided unit, while Gottschalk’s surjunctivity conjecture [Reference Gottschalk and Beck19] states that every injective G-equivariant uniformly continuous self-map
$k[G]$
must be a two-sided unit, while Gottschalk’s surjunctivity conjecture [Reference Gottschalk and Beck19] states that every injective G-equivariant uniformly continuous self-map
![]() must be surjective. It is known that every one-sided unit of
must be surjective. It is known that every one-sided unit of
![]() $\mathbb {C}[G]$
must be a two-sided unit [Reference Kaplansky22]. Moreover, both conjectures are known for the wide class of sofic groups introduced by Gromov (see [Reference Ara, O’Meara and Perera1, Reference Ceccherini-Silberstein and Coornaert4, Reference Elek and Szabó16, Reference Gromov20, Reference Li and Liang23, Reference Phung35, Reference Weiss39]) but they are still open in general. As an application of our main results, we obtain an extension of the known equivalence (cf. [Reference Phung35, Theorem B], [Reference Phung36, Theorem B]) between Kaplansky’s stable finiteness and a weak form of Gottschalk’s surjunctivity conjecture. More precisely, we establish the equivalence between the surjunctivity property of locally disturbed linear cellular automata (CA) and the stable finiteness of some twisted group rings (Theorem B).
$\mathbb {C}[G]$
must be a two-sided unit [Reference Kaplansky22]. Moreover, both conjectures are known for the wide class of sofic groups introduced by Gromov (see [Reference Ara, O’Meara and Perera1, Reference Ceccherini-Silberstein and Coornaert4, Reference Elek and Szabó16, Reference Gromov20, Reference Li and Liang23, Reference Phung35, Reference Weiss39]) but they are still open in general. As an application of our main results, we obtain an extension of the known equivalence (cf. [Reference Phung35, Theorem B], [Reference Phung36, Theorem B]) between Kaplansky’s stable finiteness and a weak form of Gottschalk’s surjunctivity conjecture. More precisely, we establish the equivalence between the surjunctivity property of locally disturbed linear cellular automata (CA) and the stable finiteness of some twisted group rings (Theorem B).
To state the main results, let us recall some notions of symbolic dynamics. Given a discrete set A and a group G, a configuration
![]() $c \in A^G$
is a map
$c \in A^G$
is a map
![]() $c \mathop{\colon} G \to A$
. Two configurations
$c \mathop{\colon} G \to A$
. Two configurations
![]() $x,y \in A^G$
are asymptotic if
$x,y \in A^G$
are asymptotic if
![]() $x\vert _{G \setminus E}=y\vert _{G \setminus E}$
for some finite subset
$x\vert _{G \setminus E}=y\vert _{G \setminus E}$
for some finite subset
![]() $E \subset G$
. The Bernoulli shift action
$E \subset G$
. The Bernoulli shift action
![]() $G \times A^G \to A^G$
is defined by
$G \times A^G \to A^G$
is defined by
![]() $(g,x) \mapsto g x$
, where
$(g,x) \mapsto g x$
, where
![]() $(gx)(h) = x(g^{-1}h)$
for
$(gx)(h) = x(g^{-1}h)$
for
![]() $g,h \in G$
,
$g,h \in G$
,
![]() $x \in A^G$
. We equip the full shift
$x \in A^G$
. We equip the full shift
![]() $A^G$
with the prodiscrete topology. For
$A^G$
with the prodiscrete topology. For
![]() $x \in A^G$
, we define
$x \in A^G$
, we define
![]() $\Sigma (x) = \overline {\{gx \mathop{\colon} g \in G\}} \subset A^G$
as the smallest closed subshift containing x. Following an idea of von Neumann and Ulam [Reference Neumann and Burks27], a CA over the group G (the universe) and the set A (the alphabet) is a self-map
$\Sigma (x) = \overline {\{gx \mathop{\colon} g \in G\}} \subset A^G$
as the smallest closed subshift containing x. Following an idea of von Neumann and Ulam [Reference Neumann and Burks27], a CA over the group G (the universe) and the set A (the alphabet) is a self-map
![]() which is G-equivariant and uniformly continuous (cf. [Reference Ceccherini-Silberstein and Coornaert6, Reference Hedlund21]). One refers to group elements
which is G-equivariant and uniformly continuous (cf. [Reference Ceccherini-Silberstein and Coornaert6, Reference Hedlund21]). One refers to group elements
![]() $g \in G$
as to the cells of the universe. When different cells can evolve according to different local transition maps, we obtain nonuniform CA (NUCA). More precisely, we have (cf. [Reference Dennunzio, Formenti and Provillard14, Reference Dennunzio, Formenti and Provillard15], [Reference Phung33, Definition 1.1]) the following:
$g \in G$
as to the cells of the universe. When different cells can evolve according to different local transition maps, we obtain nonuniform CA (NUCA). More precisely, we have (cf. [Reference Dennunzio, Formenti and Provillard14, Reference Dennunzio, Formenti and Provillard15], [Reference Phung33, Definition 1.1]) the following:
Definition 1.1 Let G be a group, and let A be a set. Let
![]() $M \subset G$
be a subset, and let
$M \subset G$
be a subset, and let
![]() ${S = A^{A^M}}$
be the set of all maps
${S = A^{A^M}}$
be the set of all maps
![]() $A^M \to A$
. Given
$A^M \to A$
. Given
![]() $s \in S^G$
, the NUCA
$s \in S^G$
, the NUCA
![]() $\sigma _s \mathop{\colon} A^G \to A^G$
is defined for all
$\sigma _s \mathop{\colon} A^G \to A^G$
is defined for all
![]() $x \in A^G$
and
$x \in A^G$
and
![]() $g \in G$
by the formula
$g \in G$
by the formula
The set M is called a memory and
![]() $s \in S^G$
the configuration of local defining maps of
$s \in S^G$
the configuration of local defining maps of
![]() $\sigma _s$
. Every CA is thus a NUCA with finite memory and constant configuration of local defining maps. Following [Reference Phung33], we say that
$\sigma _s$
. Every CA is thus a NUCA with finite memory and constant configuration of local defining maps. Following [Reference Phung33], we say that
![]() $\sigma _s$
is invertible if it is bijective and the inverse map
$\sigma _s$
is invertible if it is bijective and the inverse map
![]() $\sigma _s^{-1}$
is a NUCA with finite memory. Moreover,
$\sigma _s^{-1}$
is a NUCA with finite memory. Moreover,
![]() $\sigma _s$
is left-invertible, resp. right-invertible, if
$\sigma _s$
is left-invertible, resp. right-invertible, if
![]() $\tau \circ \sigma _s= \operatorname {\mathrm {Id}}$
, resp.
$\tau \circ \sigma _s= \operatorname {\mathrm {Id}}$
, resp.
![]() $\sigma _s\circ \tau = \operatorname {\mathrm {Id}}$
, for some NUCA
$\sigma _s\circ \tau = \operatorname {\mathrm {Id}}$
, for some NUCA
![]() $\tau \mathop{\colon} A^G \to A^G$
with finite memory. The NUCA
$\tau \mathop{\colon} A^G \to A^G$
with finite memory. The NUCA
![]() $\sigma _s$
is pre-injective if
$\sigma _s$
is pre-injective if
![]() $\sigma _s(x) = \sigma _s(y)$
implies
$\sigma _s(x) = \sigma _s(y)$
implies
![]() $x= y$
whenever
$x= y$
whenever
![]() ${x, y \in A^G}$
are asymptotic, and
${x, y \in A^G}$
are asymptotic, and
![]() $\sigma _s$
is post-surjective if for all
$\sigma _s$
is post-surjective if for all
![]() $x, y \in A^G$
with y asymptotic to
$x, y \in A^G$
with y asymptotic to
![]() $\sigma _s(x)$
, then
$\sigma _s(x)$
, then
![]() $y= \sigma _s(z)$
for some
$y= \sigma _s(z)$
for some
![]() $z \in A^G$
asymptotic to x. We say that
$z \in A^G$
asymptotic to x. We say that
![]() $\sigma _s$
is stably injective if
$\sigma _s$
is stably injective if
![]() $\sigma _p$
is injective for every
$\sigma _p$
is injective for every
![]() $p \in \Sigma (s)$
. Similarly,
$p \in \Sigma (s)$
. Similarly,
![]() $\sigma _s$
is stably post-surjective if
$\sigma _s$
is stably post-surjective if
![]() $\sigma _p$
is post-surjective for every
$\sigma _p$
is post-surjective for every
![]() $p \in \Sigma (s)$
.
$p \in \Sigma (s)$
.
If A is a vector space,
![]() $A^G$
is naturally a vector space with component-wise operations and we call a NUCA
$A^G$
is naturally a vector space with component-wise operations and we call a NUCA
![]() $\tau \mathop{\colon} A^G \to A^G$
linear if it is also a linear map of vector spaces. Clearly,
$\tau \mathop{\colon} A^G \to A^G$
linear if it is also a linear map of vector spaces. Clearly,
![]() $\tau $
is a linear NUCA if and only if its local transition maps are all linear. Such linear NUCA with finite memory are interesting dynamical objects since they satisfy the shadowing property [Reference Phung29, Reference Phung37].
$\tau $
is a linear NUCA if and only if its local transition maps are all linear. Such linear NUCA with finite memory are interesting dynamical objects since they satisfy the shadowing property [Reference Phung29, Reference Phung37].
Definition 1.2 Given a group G and a vector space V, we denote by
![]() $\mathrm {LNUCA}_{c}(G, V)$
the space of all linear NUCA
$\mathrm {LNUCA}_{c}(G, V)$
the space of all linear NUCA
![]() $\tau \mathop{\colon} V^G \to V^G$
with finite memory which admit asymptotically constant configurations of local defining maps, i.e.,
$\tau \mathop{\colon} V^G \to V^G$
with finite memory which admit asymptotically constant configurations of local defining maps, i.e.,
![]() $\tau \in \mathrm {LNUCA}_{c}(G, V)$
if there exist finite subsets
$\tau \in \mathrm {LNUCA}_{c}(G, V)$
if there exist finite subsets
![]() $M, E \subset G$
and
$M, E \subset G$
and
![]() $s \in \mathcal {L}(V^M, V)^G$
such that
$s \in \mathcal {L}(V^M, V)^G$
such that
![]() $\tau =\sigma _s$
and
$\tau =\sigma _s$
and
![]() $s(g)=s(h)$
for all
$s(g)=s(h)$
for all
![]() $g,h \in G \setminus E$
.
$g,h \in G \setminus E$
.
Let G be a group, and let k be a field, it is not hard to deduce from [Reference Phung33, Theorem 6.2] that
![]() $\mathrm {LNUCA}_{c}(G, k^n)$
is a k-algebra whose multiplication is given by the composition of maps and whose addition is component-wise.
$\mathrm {LNUCA}_{c}(G, k^n)$
is a k-algebra whose multiplication is given by the composition of maps and whose addition is component-wise.
In parallel, we can define a generalization of the group ring
![]() $k[G]$
, namely,
$k[G]$
, namely,
![]() $D^1(k[G])$
, which is given as the product
$D^1(k[G])$
, which is given as the product
![]() $D^1(k[G])= k[G] \times (k[G])[G]$
with component-wise addition but where the multiplication is given by
$D^1(k[G])= k[G] \times (k[G])[G]$
with component-wise addition but where the multiplication is given by
Here, the product
![]() $\alpha _1 \alpha _2$
is computed with the multiplication rule in the group ring
$\alpha _1 \alpha _2$
is computed with the multiplication rule in the group ring
![]() $k[G]$
so that
$k[G]$
so that
![]() $k[G]$
is naturally a subring of
$k[G]$
is naturally a subring of
![]() $D^1(k[G])$
via the map
$D^1(k[G])$
via the map
![]() $\alpha \mapsto (\alpha , 0)$
. However,
$\alpha \mapsto (\alpha , 0)$
. However,
![]() $\alpha _1 \beta _2$
,
$\alpha _1 \beta _2$
,
![]() $\beta _1 \alpha _2$
,
$\beta _1 \alpha _2$
,
![]() $\beta _1 \beta _2$
are twisted products (see Definition 5.1) which are different from the products computed with the multiplication rule of the group ring
$\beta _1 \beta _2$
are twisted products (see Definition 5.1) which are different from the products computed with the multiplication rule of the group ring
![]() $(k[G])[G]$
with coefficients in
$(k[G])[G]$
with coefficients in
![]() $k[G]$
.
$k[G]$
.
By [Reference Ceccherini-Silberstein and Coornaert5], there exists a canonical ring isomorphism between
![]() $M_n(k[G])$
and the ring
$M_n(k[G])$
and the ring
![]() $\mathrm {LCA}(G,k^n)$
of all linear CA
$\mathrm {LCA}(G,k^n)$
of all linear CA
![]() $(k^n)^G \to (k^n)^G$
. Extending the above isomorphism, we can also interpret
$(k^n)^G \to (k^n)^G$
. Extending the above isomorphism, we can also interpret
![]() $\mathrm {LNUCA}_c(G,k^n)$
algebraically in terms of the ring
$\mathrm {LNUCA}_c(G,k^n)$
algebraically in terms of the ring
![]() $M_n(D^1(k[G]))$
as follows (see Theorem 6.2 and Proposition 7.1):
$M_n(D^1(k[G]))$
as follows (see Theorem 6.2 and Proposition 7.1):
Theorem A For every field k and every infinite group G, there exists a canonical isomorphism
![]() $ \mathrm {LNUCA}_{c}(G, k^n)\simeq M_n(D^1(k[G]))$
for every
$ \mathrm {LNUCA}_{c}(G, k^n)\simeq M_n(D^1(k[G]))$
for every
![]() $n \geq 1$
.
$n \geq 1$
.
In [Reference Ceccherini-Silberstein and Coornaert5] and [Reference Phung36], respectively, the authors study the L-surjunctivity and the finite L-surjunctivity of a group, namely, a group G is L-surjunctive, resp. finitely L-surjunctive, if for every finite-dimensional vector space V, resp. finite vector space V, every injective
![]() $\tau \in \mathrm {LCA}(G,V)$
is also surjective. It was shown that all sofic groups are L-surjunctive [Reference Ceccherini-Silberstein and Coornaert5, Reference Gromov20]. Notably, we know from [Reference Ceccherini-Silberstein and Coornaert5] that a group G is L-surjunctive if and only if
$\tau \in \mathrm {LCA}(G,V)$
is also surjective. It was shown that all sofic groups are L-surjunctive [Reference Ceccherini-Silberstein and Coornaert5, Reference Gromov20]. Notably, we know from [Reference Ceccherini-Silberstein and Coornaert5] that a group G is L-surjunctive if and only if
![]() $k[G]$
is stably finite for every field k. Moreover, results in [Reference Phung36] show that L-surjunctivity and finite L-surjunctivity are equivalent notions. In this vein, we introduce the following various notions of surjunctivity in the case of linear NUCA.
$k[G]$
is stably finite for every field k. Moreover, results in [Reference Phung36] show that L-surjunctivity and finite L-surjunctivity are equivalent notions. In this vein, we introduce the following various notions of surjunctivity in the case of linear NUCA.
Definition 1.3 Let G be a group. We say that G is
![]() $L^1$
-surjunctive, resp. finitely
$L^1$
-surjunctive, resp. finitely
![]() $L^1$
-surjunctive, if for every finite-dimensional vector space V, resp. for every finite vector space V, every stably injective
$L^1$
-surjunctive, if for every finite-dimensional vector space V, resp. for every finite vector space V, every stably injective
![]() $\tau \in \mathrm {LNUCA}_c(G,V)$
is also surjective.
$\tau \in \mathrm {LNUCA}_c(G,V)$
is also surjective.
In the line of some recent results which establish the multifold interaction between symbolic dynamics, group theory, and ring theory such as [Reference Bartholdi2, Reference Ceccherini-Silberstein, Coornaert and Phung10, Reference Phung31, Reference Phung35, Reference Phung36], etc. our main result is the following:
Theorem B For every infinite group G, the following are equivalent:
-
(i) G is
 $L^1$
-surjunctive;
$L^1$
-surjunctive; -
(ii) G is finitely
 $L^1$
-surjunctive;
$L^1$
-surjunctive; -
(iii) for every field k, the ring
 $D^1(k[G])$
is stably finite;
$D^1(k[G])$
is stably finite; -
(iv) for every finite field k, the ring
 $D^1(k[G])$
is stably finite;
$D^1(k[G])$
is stably finite; -
(v) G is dual
 $L^1$
-surjunctive;
$L^1$
-surjunctive; -
(vi) G is finitely dual
 $L^1$
-surjunctive.
$L^1$
-surjunctive.
Here, a group G is dual
![]() $L^1$
-surjunctive, resp. finitely dual
$L^1$
-surjunctive, resp. finitely dual
![]() $L^1$
-surjunctive, if for every finite-dimensional vector space V, resp. for every finite vector space V, every stably post-surjective
$L^1$
-surjunctive, if for every finite-dimensional vector space V, resp. for every finite vector space V, every stably post-surjective
![]() $\tau \in \mathrm {LNUCA}_c(G,V)$
is pre-injective.
$\tau \in \mathrm {LNUCA}_c(G,V)$
is pre-injective.
The dual surjunctivity is studied in [Reference Capobianco, Kari and Taati3] where it was shown that every post-surjective CA over a sofic universe and a finite alphabet is also pre-injective. See also [Reference Phung32] for some extensions. As an application of Theorem B, we obtain the following result which extends [Reference Phung33, Theorem B] and [Reference Phung37, Theorem D] to cover the case of initially subamenable group universes (see Section 2) and arbitrary finite-dimensional vector space alphabets.
Theorem C All initially subamenable groups and all residually finite groups are
![]() $L^1$
-surjunctive and dual
$L^1$
-surjunctive and dual
![]() $L^1$
-surjunctive.
$L^1$
-surjunctive.
We deduce immediately from Theorems B and C the following result on the stable finiteness of twisted group rings.
Corollary 1.1 Let G be a residually finite group or an initially subamenable group. Then for every field k, the ring
![]() $D^1(k[G])$
is stably finite.
$D^1(k[G])$
is stably finite.
The paper is organized as follows: We recall in Section 2, the definition of initially subamenable groups and residually finite groups. Section 3 collects the construction of various induced local maps of NUCA. Then we establish the equivalence of the left-invertibility and the stable injectivity of elements of the class
![]() $\mathrm {LNUCA}_c(G,V)$
, where V is any finite-dimensional vector space (Theorems 4.2 and 4.3). The construction of the twisted group ring
$\mathrm {LNUCA}_c(G,V)$
, where V is any finite-dimensional vector space (Theorems 4.2 and 4.3). The construction of the twisted group ring
![]() $D^1(k[G])$
is given in Section 4. We then present the proof of Theorem A as a consequence of Theorem 6.2 and Proposition 7.1, respectively, in Sections 5 and 6. The dynamical characterization of the direct finiteness of the ring
$D^1(k[G])$
is given in Section 4. We then present the proof of Theorem A as a consequence of Theorem 6.2 and Proposition 7.1, respectively, in Sections 5 and 6. The dynamical characterization of the direct finiteness of the ring
![]() $M_n(D^1(k[G]))$
in terms of the direct finiteness of
$M_n(D^1(k[G]))$
in terms of the direct finiteness of
![]() $\mathrm {LNUCA}_c(G,k^n)$
. The proof of the main result Theorem B is contained in Section 8. Finally, in Section 9, we prove Theorem C as an application of Theorem B.
$\mathrm {LNUCA}_c(G,k^n)$
. The proof of the main result Theorem B is contained in Section 8. Finally, in Section 9, we prove Theorem C as an application of Theorem B.
2 Initially subamenable groups and residually finite groups
2.1 Amenable groups
Amenable groups were defined by von Neumann [Reference Neumann26]. A group G is amenable if the Følner’s condition [Reference Følner18] is satisfied: for every
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $T \subset G$
finite, there exists
$T \subset G$
finite, there exists
![]() $F \subset G$
finite such that
$F \subset G$
finite such that
![]() $\vert TF \vert \leq (1+\varepsilon )\vert F \vert $
. Finitely generated groups of subexponential growth and solvable groups are amenable. However, all groups containing a subgroup isomorphic to a free group of rank 2 are non-amenable (see, e.g., [Reference Wagon38] for some more details). The celebrated Moore and Myhill Garden of Eden theorem [Reference Moore24, Reference Myhill25] was generalized to characterize amenable groups (cf. [Reference Bartholdi2, Reference Ceccherini-Silberstein, Coornaert and Phung9, Reference Ceccherini-Silberstein, Machì and Scarabotti12, Reference Phung28, Reference Phung32]) and asserts that a CA with finite alphabet over an amenable group universe is surjective if and only if it is pre-injective.
$\vert TF \vert \leq (1+\varepsilon )\vert F \vert $
. Finitely generated groups of subexponential growth and solvable groups are amenable. However, all groups containing a subgroup isomorphic to a free group of rank 2 are non-amenable (see, e.g., [Reference Wagon38] for some more details). The celebrated Moore and Myhill Garden of Eden theorem [Reference Moore24, Reference Myhill25] was generalized to characterize amenable groups (cf. [Reference Bartholdi2, Reference Ceccherini-Silberstein, Coornaert and Phung9, Reference Ceccherini-Silberstein, Machì and Scarabotti12, Reference Phung28, Reference Phung32]) and asserts that a CA with finite alphabet over an amenable group universe is surjective if and only if it is pre-injective.
More generally, we say that a group G is initially subamenable if for every
![]() $E \subset G$
finite, there exist an amenable group H and an injective map
$E \subset G$
finite, there exist an amenable group H and an injective map
![]() $\varphi \mathop{\colon} E \to H$
such that
$\varphi \mathop{\colon} E \to H$
such that
![]() $\varphi (gh)= \varphi (g) \varphi (h)$
for all
$\varphi (gh)= \varphi (g) \varphi (h)$
for all
![]() $g,h \in E$
with
$g,h \in E$
with
![]() $gh \in E$
. Initially subamenable groups are sofic but the converse does not hold [Reference Cornulier13]. Note also that finitely presented initially subamenable groups are residually amenable but there exist initially subamenable groups which are not residually amenable [Reference Elek and Szabó17].
$gh \in E$
. Initially subamenable groups are sofic but the converse does not hold [Reference Cornulier13]. Note also that finitely presented initially subamenable groups are residually amenable but there exist initially subamenable groups which are not residually amenable [Reference Elek and Szabó17].
2.2 Residually finite groups
We say that a group G is residually finite if for every finite subset
![]() $F \subset G$
, there exists a finite group H and a surjective group homomorphism
$F \subset G$
, there exists a finite group H and a surjective group homomorphism
![]() $\varphi \mathop{\colon} G \to H$
such that the restriction
$\varphi \mathop{\colon} G \to H$
such that the restriction
![]() $\varphi \vert _F \mathop{\colon} F \to H$
is injective. All finitely generated abelian groups and, more generally, all finitely generated linear groups are residually finite. Note that free groups are non-amenable but residually finite.
$\varphi \vert _F \mathop{\colon} F \to H$
is injective. All finitely generated abelian groups and, more generally, all finitely generated linear groups are residually finite. Note that free groups are non-amenable but residually finite.
3 Induced local maps of NUCA
To fix the notation, for all sets
![]() $E \subset F$
and
$E \subset F$
and
![]() $\Lambda \subset A^F$
, we denote
$\Lambda \subset A^F$
, we denote
![]() $\Lambda _E=\{ x\vert _{E}\mathop{\colon} x \in \Lambda \} \subset A^E$
. Let G be a group, and let A be a set. For every subset
$\Lambda _E=\{ x\vert _{E}\mathop{\colon} x \in \Lambda \} \subset A^E$
. Let G be a group, and let A be a set. For every subset
![]() $E\subset G$
,
$E\subset G$
,
![]() $g \in G$
, and
$g \in G$
, and
![]() $x \in A^E$
, we define
$x \in A^E$
, we define
![]() $gx \in A^{gE}$
by setting
$gx \in A^{gE}$
by setting
![]() $gx(gh)=x(h)$
for all
$gx(gh)=x(h)$
for all
![]() $h \in E$
. In particular,
$h \in E$
. In particular,
![]() $gA^E= \{gx \mathop{\colon} x \in A^E\}=A^{gE}$
.
$gA^E= \{gx \mathop{\colon} x \in A^E\}=A^{gE}$
.
Let M be a subset of a group G. Let A be a set, and let
![]() $S=A^{A^M}$
. For every finite subset
$S=A^{A^M}$
. For every finite subset
![]() $E \subset G$
and
$E \subset G$
and
![]() $w \in S^{E}$
, we define a map
$w \in S^{E}$
, we define a map
![]() $f_{E,w}^+ \mathop{\colon} A^{E M} \to A^{E}$
by setting
$f_{E,w}^+ \mathop{\colon} A^{E M} \to A^{E}$
by setting
for all
![]() $x \in A^{EM}$
and
$x \in A^{EM}$
and
![]() $g \in E$
(see, e.g., [Reference Ceccherini-Silberstein, Coornaert and Phung9, Lemma 3.2], [Reference Phung28, Proposition 3.5], [Reference Phung30, Section 2.2] for the case of CA).
$g \in E$
(see, e.g., [Reference Ceccherini-Silberstein, Coornaert and Phung9, Lemma 3.2], [Reference Phung28, Proposition 3.5], [Reference Phung30, Section 2.2] for the case of CA).
In the above formula, note that
![]() $g^{-1}x \in A^{g^{-1}EM}$
and
$g^{-1}x \in A^{g^{-1}EM}$
and
![]() $M \subset g^{-1}EM$
since
$M \subset g^{-1}EM$
since
![]() $1_G \in g^{-1}E$
for
$1_G \in g^{-1}E$
for
![]() $g \in E$
. Therefore, the map
$g \in E$
. Therefore, the map
![]() $f_{E,w}^+ \mathop{\colon} A^{E M} \to A^{E}$
is well defined.
$f_{E,w}^+ \mathop{\colon} A^{E M} \to A^{E}$
is well defined.
Consequently, for every
![]() $s \in S^G$
, we have a well-defined induced local map
$s \in S^G$
, we have a well-defined induced local map
![]() $f_{E, s\vert _E}^+ \mathop{\colon} A^{E M} \to A^{E}$
for every finite subset
$f_{E, s\vert _E}^+ \mathop{\colon} A^{E M} \to A^{E}$
for every finite subset
![]() $E \subset G$
which satisfies
$E \subset G$
which satisfies
for all
![]() $x \in A^G$
and
$x \in A^G$
and
![]() $g \in E$
. Equivalently, we have, for all
$g \in E$
. Equivalently, we have, for all
![]() $x \in A^G$
, that
$x \in A^G$
, that
4 Left-invertibility of stably injective linear NUCA
For the proof of the main result of the section Theorem 4.2, we shall need the following useful technical lemma.
Lemma 4.1 Let G be a finitely generated infinite group, and let V be a finite-dimensional vector space. Let
![]() $\tau \in \mathrm {LNUCA}_c(G,V)$
be a stably injective linear NUCA, and let
$\tau \in \mathrm {LNUCA}_c(G,V)$
be a stably injective linear NUCA, and let
![]() . Then there exists a finite subset
. Then there exists a finite subset
![]() $N\subset G$
such that the following condition holds:
$N\subset G$
such that the following condition holds:
-
 $\mathrm {(C)}$
for any
$\mathrm {(C)}$
for any
 $d\in \Gamma $
and
$d\in \Gamma $
and
 $g \in G$
, the element
$g \in G$
, the element
 $\tau ^{-1}(d)(g)\in V$
depends only on the restriction
$\tau ^{-1}(d)(g)\in V$
depends only on the restriction
 $d \vert _{gN}$
.
$d \vert _{gN}$
.
Proof Since
![]() $\tau $
is a linear NUCA with finite memory, there exists a finite subset
$\tau $
is a linear NUCA with finite memory, there exists a finite subset
![]() $M \subset G$
and
$M \subset G$
and
![]() $s \in S^G$
, where
$s \in S^G$
, where
![]() $S= \mathcal {L}(V^M, V)$
such that
$S= \mathcal {L}(V^M, V)$
such that
![]() $\tau = \sigma _s$
. By hypothesis, s is asymptotic to a constant configuration
$\tau = \sigma _s$
. By hypothesis, s is asymptotic to a constant configuration
![]() $c \in S^G$
. Up to enlarging M, we can also suppose that
$c \in S^G$
. Up to enlarging M, we can also suppose that
![]() $s\vert _{G \setminus M}= c\vert _{G \setminus M}$
and that
$s\vert _{G \setminus M}= c\vert _{G \setminus M}$
and that
![]() $1_G \in M$
. Since the group G is finitely generated, thus countable, it admits an increasing sequence of finite subsets
$1_G \in M$
. Since the group G is finitely generated, thus countable, it admits an increasing sequence of finite subsets
![]() $M=E_0 \subset \dots \subset E_n \dots $
such that
$M=E_0 \subset \dots \subset E_n \dots $
such that
![]() $G=\cup _{n\in \mathbb {N}} E_n$
.
$G=\cup _{n\in \mathbb {N}} E_n$
.
Suppose on the contrary that there does not exist a finite subset
![]() $N\subset G$
which satisfies condition
$N\subset G$
which satisfies condition
![]() $\mathrm {(C)}$
. Then, by linearity, there exist, for each
$\mathrm {(C)}$
. Then, by linearity, there exist, for each
![]() $n \in \mathbb {N}$
, a configuration
$n \in \mathbb {N}$
, a configuration
![]() $d_n \in \Gamma $
and an element
$d_n \in \Gamma $
and an element
![]() $g_n \in G$
such that for
$g_n \in G$
such that for
![]() $c_n=\tau ^{-1}(d_n)$
(which is well-defined since
$c_n=\tau ^{-1}(d_n)$
(which is well-defined since
![]() $\tau $
is injective), we have
$\tau $
is injective), we have
Consequently, by letting
![]() $x_n=g_n^{-1}c_n$
and
$x_n=g_n^{-1}c_n$
and
![]() $y_n= g_n^{-1}d_n$
, we infer from [Reference Phung33, Lemma 5.1] that
$y_n= g_n^{-1}d_n$
, we infer from [Reference Phung33, Lemma 5.1] that
![]() $\sigma _{g_n^{-1}s}(x_n)=y_n$
and
$\sigma _{g_n^{-1}s}(x_n)=y_n$
and
Since s is asymptotic to a constant configuration
![]() $c \in S^G$
by hypothesis, the set
$c \in S^G$
by hypothesis, the set
![]() ${T=\{s(g) \mathop{\colon} g \in G\}}$
is actually a finite subset of
${T=\{s(g) \mathop{\colon} g \in G\}}$
is actually a finite subset of
![]() $S= \mathcal {L}(V^M, V)$
. It follows that
$S= \mathcal {L}(V^M, V)$
. It follows that
![]() $\Sigma (s) \subset T^G$
is a compact subspace. Therefore, up to restricting to a subsequence, we can suppose without loss of generality that the sequence
$\Sigma (s) \subset T^G$
is a compact subspace. Therefore, up to restricting to a subsequence, we can suppose without loss of generality that the sequence
![]() $(g_n^{-1}s)_{n \in \mathbb {N}}$
converges to a configuration
$(g_n^{-1}s)_{n \in \mathbb {N}}$
converges to a configuration
![]() $t \in T^G \subset S^G$
with respect to the prodiscrete topology.
$t \in T^G \subset S^G$
with respect to the prodiscrete topology.
By [Reference Phung33, Lemma 8.1], we know that
![]() $\Sigma (s) = \{gs \mathop{\colon} g \in G\} \cup \{c\}$
. Note that if s is constant then the lemma results from [Reference Ceccherini-Silberstein and Coornaert5]. Hence, we can suppose in the sequel that s is not a constant configuration. In particular, T and
$\Sigma (s) = \{gs \mathop{\colon} g \in G\} \cup \{c\}$
. Note that if s is constant then the lemma results from [Reference Ceccherini-Silberstein and Coornaert5]. Hence, we can suppose in the sequel that s is not a constant configuration. In particular, T and
![]() $\Sigma (s)$
are not singletons. We distinguish two cases according to whether
$\Sigma (s)$
are not singletons. We distinguish two cases according to whether
![]() $t = c$
or not.
$t = c$
or not.
Case 1:
![]() $t=gs$
for some
$t=gs$
for some
![]() $g \in G$
. Then, since G is infinite and s is asymptotic but not equal to c, we can, up to restricting to a subsequence again, assume without loss of generality that
$g \in G$
. Then, since G is infinite and s is asymptotic but not equal to c, we can, up to restricting to a subsequence again, assume without loss of generality that
![]() $g_n^{-1}=g$
for all
$g_n^{-1}=g$
for all
![]() $n \in \mathbb {N}$
. Up to replacing s by
$n \in \mathbb {N}$
. Up to replacing s by
![]() $gs$
, we can also suppose that
$gs$
, we can also suppose that
![]() $g=1_G$
so that
$g=1_G$
so that
![]() $\sigma _s(x_n)=y_n$
for all
$\sigma _s(x_n)=y_n$
for all
![]() $n \in \mathbb {N}$
. For each
$n \in \mathbb {N}$
. For each
![]() $n\in \mathbb {N}$
, consider the following linear subspace of
$n\in \mathbb {N}$
, consider the following linear subspace of
![]() $V^{E_nM}$
:
$V^{E_nM}$
:
Observe that
![]() $x_n\vert _{E_nM} \in I_n \setminus \{0^{E_nM} \}$
. Note also that, for all
$x_n\vert _{E_nM} \in I_n \setminus \{0^{E_nM} \}$
. Note also that, for all
![]() $n \leq m \leq k$
, the projection
$n \leq m \leq k$
, the projection
![]() $p_{nm} \mathop{\colon} A^{E_m} \to A^{E_n}$
induces a linear map
$p_{nm} \mathop{\colon} A^{E_m} \to A^{E_n}$
induces a linear map
![]() $\pi _{nm} \mathop{\colon} I_m \to I_n$
and
$\pi _{nm} \mathop{\colon} I_m \to I_n$
and
![]() $\pi _{nk}(I_{k}) \subset \pi _{nm}(I_m)$
. Hence, for each
$\pi _{nk}(I_{k}) \subset \pi _{nm}(I_m)$
. Hence, for each
![]() $n\in \mathbb {N}$
, we obtain a decreasing sequence of linear subspaces
$n\in \mathbb {N}$
, we obtain a decreasing sequence of linear subspaces
![]() $(\pi _{nm}(I_m))_{m \geq n}$
of
$(\pi _{nm}(I_m))_{m \geq n}$
of
![]() $I_n$
. Hence,
$I_n$
. Hence,
![]() $(\pi _{nm}(I_m))_{m \geq n}$
is stationary and there exists a linear subspace
$(\pi _{nm}(I_m))_{m \geq n}$
is stationary and there exists a linear subspace
![]() $J_n \subset I_n\subset A^{E_nM}$
such that
$J_n \subset I_n\subset A^{E_nM}$
such that
![]() $\pi _{nm}(I_m)=J_n$
for all m large enough.
$\pi _{nm}(I_m)=J_n$
for all m large enough.
Observe that
![]() $\pi _{nm}(J_m) \subset J_n$
for all
$\pi _{nm}(J_m) \subset J_n$
for all
![]() $m \geq n$
. We claim that the restriction linear map
$m \geq n$
. We claim that the restriction linear map
![]() $q_{nm} \mathop{\colon} J_m \to J_n$
is surjective for all
$q_{nm} \mathop{\colon} J_m \to J_n$
is surjective for all
![]() $m\geq n$
. Indeed, let
$m\geq n$
. Indeed, let
![]() $y\in J_n$
and let
$y\in J_n$
and let
![]() $k \geq m$
be sufficiently large such that
$k \geq m$
be sufficiently large such that
![]() $q_{n k}(I_k)=J_n$
and
$q_{n k}(I_k)=J_n$
and
![]() $q_{m k}(I_k)=J_m$
. Thus,
$q_{m k}(I_k)=J_m$
. Thus,
![]() $q_{nk}(x)=y$
for some
$q_{nk}(x)=y$
for some
![]() $x\in I_k$
. As
$x\in I_k$
. As
![]() $q_{nk}= q_{nm} \circ q_{mk}$
, we have
$q_{nk}= q_{nm} \circ q_{mk}$
, we have
![]() $q_{nm}(y')=y$
, where
$q_{nm}(y')=y$
, where
![]() $y'=q_{mk}(x) \in J_m$
. The claim is proved.
$y'=q_{mk}(x) \in J_m$
. The claim is proved.
We choose
![]() $k\in \mathbb {N}$
large enough such that
$k\in \mathbb {N}$
large enough such that
![]() $\pi _{0k}(I_k)=J_0$
. Let
$\pi _{0k}(I_k)=J_0$
. Let
![]() $z_0=\pi _{0k}(x_k) \in J_0$
then
$z_0=\pi _{0k}(x_k) \in J_0$
then
![]() $z_0(1_G) \neq 0$
. We define by induction a sequence
$z_0(1_G) \neq 0$
. We define by induction a sequence
![]() $(z_n)_{n \in \mathbb {N}}$
, where
$(z_n)_{n \in \mathbb {N}}$
, where
![]() $z_n \in J_n$
for all
$z_n \in J_n$
for all
![]() $n\in \mathbb {N}$
as follows. Given
$n\in \mathbb {N}$
as follows. Given
![]() $z_n \in J_n$
for some
$z_n \in J_n$
for some
![]() $n\in \mathbb {N}$
, there exists by the surjectivity of the map
$n\in \mathbb {N}$
, there exists by the surjectivity of the map
![]() $q_{n,n+1}$
an element
$q_{n,n+1}$
an element
We thus obtain a configuration
![]() $c \in V^G$
defined by
$c \in V^G$
defined by
![]() $z\vert _{E_nM}=z_n$
for all
$z\vert _{E_nM}=z_n$
for all
![]() $n \in \mathbb {N}$
. Since
$n \in \mathbb {N}$
. Since
![]() $G=\cup _{n \in \mathbb {N}} E_n M$
, the configuration z is well-defined.
$G=\cup _{n \in \mathbb {N}} E_n M$
, the configuration z is well-defined.
By construction, we have for all
![]() $n \in \mathbb {N}$
that
$n \in \mathbb {N}$
that
Therefore,
![]() $\tau (z)= 0^{G}$
but
$\tau (z)= 0^{G}$
but
![]() $z(1_G)\neq 0$
which then contradicts the injectivity of the linear NUCA
$z(1_G)\neq 0$
which then contradicts the injectivity of the linear NUCA
![]() $\tau $
.
$\tau $
.
Case 2:
![]() $t = c$
. Then, since
$t = c$
. Then, since
![]() $\lim _{n \to \infty } g_n^{-1}s=t$
and
$\lim _{n \to \infty } g_n^{-1}s=t$
and
![]() $s \neq c$
, we deduce immediately that
$s \neq c$
, we deduce immediately that
![]() $g_n \to \infty $
when
$g_n \to \infty $
when
![]() $n \to \infty $
, i.e., for every finite subset
$n \to \infty $
, i.e., for every finite subset
![]() $E \subset G$
, there exists
$E \subset G$
, there exists
![]() $N \in \mathbb {N}$
such that
$N \in \mathbb {N}$
such that
![]() $g_n \notin E$
for all
$g_n \notin E$
for all
![]() $n \geq N$
. Consequently, by restricting to a suitable subsequence, we can suppose without loss of generality that
$n \geq N$
. Consequently, by restricting to a suitable subsequence, we can suppose without loss of generality that
![]() $g_nE_nM \cap M = \varnothing $
for all
$g_nE_nM \cap M = \varnothing $
for all
![]() $n \in \mathbb {N}$
. As
$n \in \mathbb {N}$
. As
![]() $s\vert _{G \setminus M}= c\vert _{G \setminus M}$
, it follows that
$s\vert _{G \setminus M}= c\vert _{G \setminus M}$
, it follows that
![]() $(g_n^{-1}s)\vert _{E_nM} = c\vert _{E_nM}$
for all
$(g_n^{-1}s)\vert _{E_nM} = c\vert _{E_nM}$
for all
![]() $ n \in \mathbb {N}$
. Since c is constant, we deduce that
$ n \in \mathbb {N}$
. Since c is constant, we deduce that
![]() $\sigma _c(x_n)\vert _{E_n}=0^{E_n}$
and
$\sigma _c(x_n)\vert _{E_n}=0^{E_n}$
and
![]() $x_n(1_G)\neq 0$
. We infer from the stable injectivity of
$x_n(1_G)\neq 0$
. We infer from the stable injectivity of
![]() $\sigma _s$
that
$\sigma _s$
that
![]() $\sigma _c$
is injective. Therefore, a similar argument as in Case 1 applied for
$\sigma _c$
is injective. Therefore, a similar argument as in Case 1 applied for
![]() $\sigma _c$
and the sequence
$\sigma _c$
and the sequence
![]() $(x_n)_{n \in \mathbb {N}}$
leads to a contradiction.
$(x_n)_{n \in \mathbb {N}}$
leads to a contradiction.
Consequently, there must exist a finite subset
![]() $N \subset G$
which satisfies condition (C) and the proof is thus complete.
$N \subset G$
which satisfies condition (C) and the proof is thus complete.
Our next results Theorems 4.2 and 4.3 extend the results [Reference Phung37, Theorem 10.1] and [Reference Phung33, Theorem 7.1] for NUCA over finite alphabet to the class
![]() $\mathrm {LNUCA}_c$
over an arbitrary finite-dimensional vector space.
$\mathrm {LNUCA}_c$
over an arbitrary finite-dimensional vector space.
Theorem 4.2 Let G be a group, and let V be a finite-dimensional vector space. Let
![]() $\tau \in \mathrm {LNUCA}_c(G,V)$
be a stably injective linear NUCA. Then
$\tau \in \mathrm {LNUCA}_c(G,V)$
be a stably injective linear NUCA. Then
![]() $\tau $
is left-invertible, i.e., there exists
$\tau $
is left-invertible, i.e., there exists
![]() $\sigma \in \mathrm {LNUCA}_c(G,V)$
such that
$\sigma \in \mathrm {LNUCA}_c(G,V)$
such that
![]() $\sigma \circ \tau = \operatorname {\mathrm {Id}}$
.
$\sigma \circ \tau = \operatorname {\mathrm {Id}}$
.
Proof As the linear NUCA
![]() $\tau $
has finite memory, we can find a finite subset
$\tau $
has finite memory, we can find a finite subset
![]() $M \subset G$
and
$M \subset G$
and
![]() $s \in S^G$
where
$s \in S^G$
where
![]() $S= \mathcal {L}(V^M, V)$
such that
$S= \mathcal {L}(V^M, V)$
such that
![]() $\tau = \sigma _s$
. By hypothesis, the configuration s is asymptotic to a constant configuration
$\tau = \sigma _s$
. By hypothesis, the configuration s is asymptotic to a constant configuration
![]() $c \in S^G$
. Hence, we can, up to enlarging M, suppose that
$c \in S^G$
. Hence, we can, up to enlarging M, suppose that
![]() $s\vert _{G \setminus M}= c\vert _{G \setminus M}$
and that
$s\vert _{G \setminus M}= c\vert _{G \setminus M}$
and that
![]() $1_G \in M$
.
$1_G \in M$
.
Assume first that G is a finitely generated infinite group. Then we infer from Lemma 4.1 that there exists a finite subset
![]() $N \subset G$
such that for any
$N \subset G$
such that for any
![]() $d\in \tau (V^G)$
and
$d\in \tau (V^G)$
and
![]() $g \in G$
, the element
$g \in G$
, the element
![]() $\tau ^{-1}(d)(g)\in V$
depends only on the restriction
$\tau ^{-1}(d)(g)\in V$
depends only on the restriction
![]() $d \vert _{gN}$
. Up to enlarging M and N, we can clearly suppose that
$d \vert _{gN}$
. Up to enlarging M and N, we can clearly suppose that
![]() $M=N$
. Consequently, for each
$M=N$
. Consequently, for each
![]() $g \in G$
, we have a well-defined map
$g \in G$
, we have a well-defined map
![]() $\varphi _g\mathop{\colon} \tau (V^G)_{gM} \to V$
given by
$\varphi _g\mathop{\colon} \tau (V^G)_{gM} \to V$
given by
![]() $d\vert _{gM} \mapsto \tau ^{-1}(d)(g)$
for every
$d\vert _{gM} \mapsto \tau ^{-1}(d)(g)$
for every
![]() $d \in V^G$
.
$d \in V^G$
.
Since
![]() $\tau $
is linear and
$\tau $
is linear and
![]() $\tau (V^G)_{gM}$
is a linear subspace of
$\tau (V^G)_{gM}$
is a linear subspace of
![]() $V^{gM}$
, it follows that
$V^{gM}$
, it follows that
![]() $\varphi _g$
is also a linear map and we can extend
$\varphi _g$
is also a linear map and we can extend
![]() $\varphi _g$
to a linear map
$\varphi _g$
to a linear map
![]() $\tilde {\varphi }_g \mathop{\colon} V^{gM} \to V$
which coincides with
$\tilde {\varphi }_g \mathop{\colon} V^{gM} \to V$
which coincides with
![]() $\varphi _g$
on
$\varphi _g$
on
![]() $\tau (V^G)_{gM}$
. Let
$\tau (V^G)_{gM}$
. Let
![]() $\phi _g \mathop{\colon} V^M \to V^{gM}$
be the canonical automorphism induced by the bijection
$\phi _g \mathop{\colon} V^M \to V^{gM}$
be the canonical automorphism induced by the bijection
![]() $M \simeq gM$
,
$M \simeq gM$
,
![]() $h \mapsto gh$
. Let us define an configuration
$h \mapsto gh$
. Let us define an configuration
![]() $t \in S^G$
where
$t \in S^G$
where
![]() $S= \mathcal {L}(V^M, V)$
by setting
$S= \mathcal {L}(V^M, V)$
by setting
![]() $t(g)= \tilde {\varphi }_g \circ \phi _g \mathop{\colon} V^M \to M$
for every
$t(g)= \tilde {\varphi }_g \circ \phi _g \mathop{\colon} V^M \to M$
for every
![]() $g \in G$
. It is immediate from the construction that for every
$g \in G$
. It is immediate from the construction that for every
![]() $c \in V^G$
,
$c \in V^G$
,
![]() $g \in G$
, and
$g \in G$
, and
![]() $d = \tau (c) \in \tau (V^G)$
, we have
$d = \tau (c) \in \tau (V^G)$
, we have
Therefore,
![]() $\sigma _t \circ \sigma _s = \operatorname {\mathrm {Id}}$
and we conclude that
$\sigma _t \circ \sigma _s = \operatorname {\mathrm {Id}}$
and we conclude that
![]() $\tau =\sigma _s$
is left-invertible. In fact, since
$\tau =\sigma _s$
is left-invertible. In fact, since
![]() $s\vert _{G \setminus M}= c\vert _{G \setminus M}$
, the linear spaces
$s\vert _{G \setminus M}= c\vert _{G \setminus M}$
, the linear spaces
![]() $W=\phi _g^{-1}(\tau (V^G)_{gM}) =\phi ^{-1}( f^+{gM,s\vert _{gM}}(V^{gM^2}))$
coincide as linear subspaces of
$W=\phi _g^{-1}(\tau (V^G)_{gM}) =\phi ^{-1}( f^+{gM,s\vert _{gM}}(V^{gM^2}))$
coincide as linear subspaces of
![]() $V^M$
for all
$V^M$
for all
![]() $g \in G \setminus M M^{-1}$
. Let us fix a direct sum decomposition
$g \in G \setminus M M^{-1}$
. Let us fix a direct sum decomposition
![]() $V^M = W \oplus U$
of
$V^M = W \oplus U$
of
![]() $V^M$
. Thus, if we define
$V^M$
. Thus, if we define
![]() $\tilde {\varphi }_g$
by setting
$\tilde {\varphi }_g$
by setting
![]() $\tilde {\varphi }_g(v)=0$
for all
$\tilde {\varphi }_g(v)=0$
for all
![]() $v \in \phi _g(U)$
and
$v \in \phi _g(U)$
and
![]() $\tilde {\varphi }_g(v)=\varphi _g(v)$
if
$\tilde {\varphi }_g(v)=\varphi _g(v)$
if
![]() $v \in \phi _g(W)$
and extend by linearity on the whole space
$v \in \phi _g(W)$
and extend by linearity on the whole space
![]() $V^{gM}$
, then it is clear that t is also asymptotically constant, which completes the proof of the theorem in the case when G is a finitely generated infinite group.
$V^{gM}$
, then it is clear that t is also asymptotically constant, which completes the proof of the theorem in the case when G is a finitely generated infinite group.
The case when G is a finite group is trivial since every injective endomorphism of a finite-dimensional vector space is an automorphism. Let us consider the general case where G is an infinite group. Let H be the subgroup of G generated by M. Let
![]() $G/H=\{gH \mathop{\colon} g \in G\}$
be the set of all right cosets of H in G. By identifying
$G/H=\{gH \mathop{\colon} g \in G\}$
be the set of all right cosets of H in G. By identifying
![]() $x \in A^G$
with
$x \in A^G$
with
![]() $(x\vert _{u})_{u \in G/H}$
, we obtain a factorization
$(x\vert _{u})_{u \in G/H}$
, we obtain a factorization
![]() $A^G = \prod _{u \in G/H} A^u$
. Moreover,
$A^G = \prod _{u \in G/H} A^u$
. Moreover,
![]() $\sigma _s= \prod _{u \in G/H} \sigma _s^u$
, where
$\sigma _s= \prod _{u \in G/H} \sigma _s^u$
, where
![]() $\sigma _s^u\mathop{\colon} A^u \to A^u$
is given by
$\sigma _s^u\mathop{\colon} A^u \to A^u$
is given by
![]() $\sigma _{s}^u (y) = \sigma _s(x)\vert _u$
for all
$\sigma _{s}^u (y) = \sigma _s(x)\vert _u$
for all
![]() $y \in A^u$
and any
$y \in A^u$
and any
![]() $x \in A^G$
extending y. Similarly, we have
$x \in A^G$
extending y. Similarly, we have
![]() $\sigma _c= \prod _{u \in G/H} \sigma _c^u$
.
$\sigma _c= \prod _{u \in G/H} \sigma _c^u$
.
For every coset
![]() $u \in G/H$
, let us choose
$u \in G/H$
, let us choose
![]() $g_u\in G$
such that
$g_u\in G$
such that
![]() $g_H=1_G$
. Then, if
$g_H=1_G$
. Then, if
![]() $u \neq H$
, we have
$u \neq H$
, we have
![]() $s\vert _u =c\vert _u$
and
$s\vert _u =c\vert _u$
and
![]() $\sigma _s^u=\sigma _c^u$
is conjugate to the restriction CA
$\sigma _s^u=\sigma _c^u$
is conjugate to the restriction CA
![]() $ \sigma _{c\vert _H} = \sigma _{c}^H \mathop{\colon} A^H \to A^H$
by the uniform homeomorphism
$ \sigma _{c\vert _H} = \sigma _{c}^H \mathop{\colon} A^H \to A^H$
by the uniform homeomorphism
![]() $\phi _u \mathop{\colon} A^u \to A^H$
given by
$\phi _u \mathop{\colon} A^u \to A^H$
given by
![]() $\phi _u(y)(h)=y(g_uh)$
for all
$\phi _u(y)(h)=y(g_uh)$
for all
![]() $y \in A^u$
and
$y \in A^u$
and
![]() $h \in H$
(cf. the discussion following [Reference Ceccherini-Silberstein, Coornaert and Phung11, Lemma 2.8]). Hence,
$h \in H$
(cf. the discussion following [Reference Ceccherini-Silberstein, Coornaert and Phung11, Lemma 2.8]). Hence,
![]() $\sigma _s$
and
$\sigma _s$
and
![]() $\sigma _c$
are left-invertible (resp. injective) if and only if so are
$\sigma _c$
are left-invertible (resp. injective) if and only if so are
![]() $\sigma _{s\vert _H}$
and
$\sigma _{s\vert _H}$
and
![]() $\sigma _{c \vert _H}$
(see also [Reference Ceccherini-Silberstein and Coornaert7, Theorem 1.2]). Consequently, the general case follows from the case when G is finite or when G is a finitely generated infinite group. The proof is thus complete.
$\sigma _{c \vert _H}$
(see also [Reference Ceccherini-Silberstein and Coornaert7, Theorem 1.2]). Consequently, the general case follows from the case when G is finite or when G is a finitely generated infinite group. The proof is thus complete.
Conversely, we show that left-invertibility implies stable injectivity for linear NUCA with finite memory whose configuration of local defining maps is asymptotically constant.
Theorem 4.3 Let G be a group, and let V be a finite-dimensional vector space. Suppose that
![]() $\tau \in \mathrm {LNUCA}_c(G,V)$
is a left-invertible linear NUCA. Then
$\tau \in \mathrm {LNUCA}_c(G,V)$
is a left-invertible linear NUCA. Then
![]() $\tau $
stably injective.
$\tau $
stably injective.
Proof As in the proof of Theorem 4.2, we can suppose without loss of generality that G is a finitely generated infinite group. Since
![]() $\tau $
is a linear NUCA with finite memory and left-invertible, we can find a finite subset
$\tau $
is a linear NUCA with finite memory and left-invertible, we can find a finite subset
![]() $M\subset G$
and
$M\subset G$
and
![]() $s,t \in S^G$
, where
$s,t \in S^G$
, where
![]() $S= \mathcal {L}(V^M, V)$
such that
$S= \mathcal {L}(V^M, V)$
such that
![]() $\tau =\sigma _s$
and
$\tau =\sigma _s$
and
![]() $\sigma _t \circ \sigma _s= \operatorname {\mathrm {Id}}$
. In particular, we deduce immediately that
$\sigma _t \circ \sigma _s= \operatorname {\mathrm {Id}}$
. In particular, we deduce immediately that
![]() $\sigma _s$
is injective.
$\sigma _s$
is injective.
As s is asymptotically constant, we infer from [Reference Phung33, Lemma 8.1] that
![]() $\Sigma (s)=\{g s \mathop{\colon} g \in G\}\cup \{c\}$
for some constant configuration
$\Sigma (s)=\{g s \mathop{\colon} g \in G\}\cup \{c\}$
for some constant configuration
![]() $c \in S^G$
. Note that by [Reference Phung33, Lemma 5.1], the injectivity of
$c \in S^G$
. Note that by [Reference Phung33, Lemma 5.1], the injectivity of
![]() $\sigma _{gs}$
for all
$\sigma _{gs}$
for all
![]() $g \in G$
follows from the injectivity of
$g \in G$
follows from the injectivity of
![]() $\sigma _s$
. We must show that
$\sigma _s$
. We must show that
![]() $\sigma _c$
is injective. For this, we can suppose, up to enlarging M, that
$\sigma _c$
is injective. For this, we can suppose, up to enlarging M, that
![]() $s\vert _{G \setminus M}= c\vert _{G \setminus M}$
. Since G is infinite, there exists
$s\vert _{G \setminus M}= c\vert _{G \setminus M}$
. Since G is infinite, there exists
![]() $g \in G$
such that
$g \in G$
such that
![]() $g M \cap M= \varnothing $
. It follows that
$g M \cap M= \varnothing $
. It follows that
![]() $s\vert _{gM}=c\vert _{gM}$
. On the other hand, we infer from the identity
$s\vert _{gM}=c\vert _{gM}$
. On the other hand, we infer from the identity
![]() $\sigma _t \circ \sigma _s= \operatorname {\mathrm {Id}}$
that
$\sigma _t \circ \sigma _s= \operatorname {\mathrm {Id}}$
that
where
![]() $\pi _{F,E} \mathop{\colon} V^F \to V^E$
denotes the canonical projection induced by any inclusion of sets
$\pi _{F,E} \mathop{\colon} V^F \to V^E$
denotes the canonical projection induced by any inclusion of sets
![]() $E \subset F$
. Consequently,
$E \subset F$
. Consequently,
![]() $t(g) \circ f^+_{gM, c\vert _{gM}}= \pi _{gM^2, g}$
. Since c is constant, we deduce that
$t(g) \circ f^+_{gM, c\vert _{gM}}= \pi _{gM^2, g}$
. Since c is constant, we deduce that
![]() $\sigma _d \circ \sigma _c= \operatorname {\mathrm {Id}}$
, where
$\sigma _d \circ \sigma _c= \operatorname {\mathrm {Id}}$
, where
![]() $d \in S^G$
is the constant configuration defined by
$d \in S^G$
is the constant configuration defined by
![]() $d(h)=t(g)$
for all
$d(h)=t(g)$
for all
![]() $h \in G$
. In particular,
$h \in G$
. In particular,
![]() $\sigma _c$
is injective and we conclude that
$\sigma _c$
is injective and we conclude that
![]() $\sigma _s$
is stably injective. The proof is thus complete.
$\sigma _s$
is stably injective. The proof is thus complete.
5 The twisted group ring
 $D^1(k[G])$
$D^1(k[G])$
Given a group G and a ring R (with unit), recall that the group ring
![]() $R[G]$
is the R-algebra which admits G as a basis and whose multiplication is defined by the group product on basis elements and the distributive law.
$R[G]$
is the R-algebra which admits G as a basis and whose multiplication is defined by the group product on basis elements and the distributive law.
Definition 5.1 Let k be a ring, and let G be a group. We define
![]() $D^1(k[G])$
as the Cartesian product
$D^1(k[G])$
as the Cartesian product
Elements of
![]() $D^1(k[G])$
are couples
$D^1(k[G])$
are couples
![]() $(\alpha , \beta )$
, where
$(\alpha , \beta )$
, where
![]() $\alpha \in k[G]$
is called the regular part and
$\alpha \in k[G]$
is called the regular part and
![]() $\beta \in (k[G])[G]$
is called the singular part of
$\beta \in (k[G])[G]$
is called the singular part of
![]() $(\alpha , \beta )$
. The addition operation of
$(\alpha , \beta )$
. The addition operation of
![]() $D^1(k[G])$
is component-wise:
$D^1(k[G])$
is component-wise:
The multiplication operation
![]() $*\mathop{\colon} D^1(k[G]) \times D^1(k[G]) \to D^1(k[G])$
is defined as follows:
$*\mathop{\colon} D^1(k[G]) \times D^1(k[G]) \to D^1(k[G])$
is defined as follows:
Here,
![]() $\alpha _1 \alpha _2$
is computed with the multiplication rule in the group ring
$\alpha _1 \alpha _2$
is computed with the multiplication rule in the group ring
![]() $k[G]$
. However, for
$k[G]$
. However, for
![]() $\alpha \in k[G]$
and
$\alpha \in k[G]$
and
![]() $\beta , \gamma \in (k[G])[G]$
, we define, by abuse of notation, the twisted products
$\beta , \gamma \in (k[G])[G]$
, we define, by abuse of notation, the twisted products
![]() $\alpha \beta $
,
$\alpha \beta $
,
![]() $\beta \alpha $
, and
$\beta \alpha $
, and
![]() $\beta \gamma $
as elements of
$\beta \gamma $
as elements of
![]() $(k[G])[G]$
as follows, which should be distinguished from the multiplication rule of the group ring
$(k[G])[G]$
as follows, which should be distinguished from the multiplication rule of the group ring
![]() $(k[G])[G]$
with coefficients in
$(k[G])[G]$
with coefficients in
![]() $k[G]$
. Let
$k[G]$
. Let
![]() $g, h\in G$
, we set:
$g, h\in G$
, we set:
 $$ \begin{align} (\alpha \beta)(g)(h)& = \sum_{t \in G} \alpha(t) \beta(gt)(t^{-1}h),\\ (\beta \alpha)(g)(h)&= \sum_{t \in G} \beta(g)(t) \alpha(t^{-1}h), \nonumber\\ (\beta\gamma)(g)(h)&= \sum_{t \in G} \beta(g)(t) \gamma(gt)(t^{-1}h). \nonumber \end{align} $$
$$ \begin{align} (\alpha \beta)(g)(h)& = \sum_{t \in G} \alpha(t) \beta(gt)(t^{-1}h),\\ (\beta \alpha)(g)(h)&= \sum_{t \in G} \beta(g)(t) \alpha(t^{-1}h), \nonumber\\ (\beta\gamma)(g)(h)&= \sum_{t \in G} \beta(g)(t) \gamma(gt)(t^{-1}h). \nonumber \end{align} $$
It is not hard to check that the above product rule (5.2) is associative and distributive with respect to addition. For example, with the above
![]() $\alpha , \beta , \gamma $
, we have
$\alpha , \beta , \gamma $
, we have
![]() $\alpha (\beta \gamma ) = (\alpha \beta ) \gamma $
since for all
$\alpha (\beta \gamma ) = (\alpha \beta ) \gamma $
since for all
![]() $g,h\in G$
:
$g,h\in G$
:
 $$ \begin{align*} (\alpha (\beta\gamma))(g)(h) &= \sum_{t \in G} \alpha(t) \sum_{q \in G} \beta(gt)(q) \gamma(gtq)(q^{-1}t^{-1}h)\\ & = \sum_{t \in G} \alpha(t) \sum_{r\in G} \beta(gt)(t^{-1}r) \gamma(gr)(r^{-1}h) \qquad (r=tq)\\ & = \sum_{r \in G} \sum_{t \in G}\alpha(t) \beta(gt)(t^{-1}r)\gamma(gr)(r^{-1}h) \\ & = ((\alpha \beta)\gamma)(g)(h). \end{align*} $$
$$ \begin{align*} (\alpha (\beta\gamma))(g)(h) &= \sum_{t \in G} \alpha(t) \sum_{q \in G} \beta(gt)(q) \gamma(gtq)(q^{-1}t^{-1}h)\\ & = \sum_{t \in G} \alpha(t) \sum_{r\in G} \beta(gt)(t^{-1}r) \gamma(gr)(r^{-1}h) \qquad (r=tq)\\ & = \sum_{r \in G} \sum_{t \in G}\alpha(t) \beta(gt)(t^{-1}r)\gamma(gr)(r^{-1}h) \\ & = ((\alpha \beta)\gamma)(g)(h). \end{align*} $$
The following lemma tells us that
![]() $D^1(k[G])$
is indeed a ring with unit.
$D^1(k[G])$
is indeed a ring with unit.
Lemma 5.1 For every group G and every ring k, the set
![]() $D^1(k[G])$
equipped with the addition and multiplication operations as defined in Definition 5.1 is a ring with unit
$D^1(k[G])$
equipped with the addition and multiplication operations as defined in Definition 5.1 is a ring with unit
![]() $(1_G, 0)$
and neutral element
$(1_G, 0)$
and neutral element
![]() $(0,0)$
.
$(0,0)$
.
Proof Since the addition is component-wise and
![]() $k[G]$
and
$k[G]$
and
![]() $(k[G])[G]$
are abelian groups,
$(k[G])[G]$
are abelian groups,
![]() $D^1(k[G])$
is also an abelian group. It is clear that
$D^1(k[G])$
is also an abelian group. It is clear that
![]() $(\alpha , \beta )*(1_G, 0)=(1_G, 0)*(\alpha , \beta )=(\alpha , \beta )$
for all
$(\alpha , \beta )*(1_G, 0)=(1_G, 0)*(\alpha , \beta )=(\alpha , \beta )$
for all
![]() $(\alpha , \beta ) \in D^1(k[G])$
. Moreover, the associativity of the multiplication is satisfied since for all
$(\alpha , \beta ) \in D^1(k[G])$
. Moreover, the associativity of the multiplication is satisfied since for all
![]() $(\alpha _i, \beta _i) \in D^1(k[G])$
(
$(\alpha _i, \beta _i) \in D^1(k[G])$
(
![]() $i=1,2,3$
), we find that
$i=1,2,3$
), we find that
 $$ \begin{align*} & \left( (\alpha_1, \beta_1) * (\alpha_2, \beta_2)\right) * (\alpha_3, \beta_3) = (\alpha_1 \alpha_2, \alpha_1 \beta_2 + \beta_1 \alpha_2 + \beta_1 \beta_2) * (\alpha_3, \beta_3) \\ & = (\alpha_1 \alpha_2 \alpha_3, \alpha_1 \alpha_2 \beta_3+ \alpha_1 \beta_2 \alpha_3 + \beta_1 \alpha_2 \alpha_3+ \beta_1 \beta_2 \alpha_3+ \alpha_1 \beta_2 \beta_3+ \beta_1 \alpha_2\beta_3 + \beta_1 \beta_2\beta_3) \\ &= (\alpha_1 \alpha_2 \alpha_3, \alpha_1 \alpha_2 \beta_3+ \alpha_1 \beta_2 \alpha_3 + \alpha_1 \beta_2 \beta_3+ \beta_1 \alpha_2 \alpha_3+ \beta_1 \alpha_2\beta_3 + \beta_1 \beta_2 \alpha_3+ \beta_1 \beta_2\beta_3)\\ & = (\alpha_1, \beta_1) * (\alpha_2 \alpha_3, \alpha_2 \beta_3 + \beta_2 \alpha_3 + \beta_2 \beta_3)\\ & = (\alpha_1, \beta_1) * \left( (\alpha_2, \beta_2) * (\alpha_3, \beta_3) \right). \end{align*} $$
$$ \begin{align*} & \left( (\alpha_1, \beta_1) * (\alpha_2, \beta_2)\right) * (\alpha_3, \beta_3) = (\alpha_1 \alpha_2, \alpha_1 \beta_2 + \beta_1 \alpha_2 + \beta_1 \beta_2) * (\alpha_3, \beta_3) \\ & = (\alpha_1 \alpha_2 \alpha_3, \alpha_1 \alpha_2 \beta_3+ \alpha_1 \beta_2 \alpha_3 + \beta_1 \alpha_2 \alpha_3+ \beta_1 \beta_2 \alpha_3+ \alpha_1 \beta_2 \beta_3+ \beta_1 \alpha_2\beta_3 + \beta_1 \beta_2\beta_3) \\ &= (\alpha_1 \alpha_2 \alpha_3, \alpha_1 \alpha_2 \beta_3+ \alpha_1 \beta_2 \alpha_3 + \alpha_1 \beta_2 \beta_3+ \beta_1 \alpha_2 \alpha_3+ \beta_1 \alpha_2\beta_3 + \beta_1 \beta_2 \alpha_3+ \beta_1 \beta_2\beta_3)\\ & = (\alpha_1, \beta_1) * (\alpha_2 \alpha_3, \alpha_2 \beta_3 + \beta_2 \alpha_3 + \beta_2 \beta_3)\\ & = (\alpha_1, \beta_1) * \left( (\alpha_2, \beta_2) * (\alpha_3, \beta_3) \right). \end{align*} $$
Finally, we see without difficulty that the distributivity of
![]() $D^1(k[G])$
follows from the distributivity of
$D^1(k[G])$
follows from the distributivity of
![]() $k[G]$
and
$k[G]$
and
![]() $(k[G])[G]$
. Hence, we conclude that
$(k[G])[G]$
. Hence, we conclude that
![]() $D^1(k[G])$
is a ring with unit
$D^1(k[G])$
is a ring with unit
![]() $(1_G, 0)$
and neutral element
$(1_G, 0)$
and neutral element
![]() $(0,0)$
.
$(0,0)$
.
The next lemma says that the generalized group ring
![]() $D^1(k[G])$
contains naturally the group ring
$D^1(k[G])$
contains naturally the group ring
![]() $k[G]$
as the subring of regular elements, i.e., elements whose singular parts are zero.
$k[G]$
as the subring of regular elements, i.e., elements whose singular parts are zero.
Lemma 5.2 Let k be a ring, and let G be a group. Then we have a canonical embedding of rings
![]() $\varphi \mathop{\colon} k[G] \hookrightarrow D^1(k[G])$
given by the formula
$\varphi \mathop{\colon} k[G] \hookrightarrow D^1(k[G])$
given by the formula
![]() $\varphi (\alpha )= (\alpha ,0)$
for all
$\varphi (\alpha )= (\alpha ,0)$
for all
![]() $\alpha \in k[G]$
.
$\alpha \in k[G]$
.
Proof The map
![]() $\varphi $
is trivially injective. Moreover, it is a direct consequence of the definition of the addition of multiplication operations of
$\varphi $
is trivially injective. Moreover, it is a direct consequence of the definition of the addition of multiplication operations of
![]() $D^1(k[G])$
that
$D^1(k[G])$
that
![]() $\varphi (\alpha _1) + \varphi (\alpha _2) = \varphi (\alpha _1+\alpha _2)$
and
$\varphi (\alpha _1) + \varphi (\alpha _2) = \varphi (\alpha _1+\alpha _2)$
and
![]() $\varphi (\alpha _1 \alpha _2) =\varphi (\alpha _1\alpha _2)$
for all
$\varphi (\alpha _1 \alpha _2) =\varphi (\alpha _1\alpha _2)$
for all
![]() $\alpha _1, \alpha _2 \in k[G]$
.
$\alpha _1, \alpha _2 \in k[G]$
.
Observe that the group ring
![]() $k[G]$
is naturally a Hopf k-algebra where the antipodal map is induced by
$k[G]$
is naturally a Hopf k-algebra where the antipodal map is induced by
![]() $g\mapsto g^{-1}$
and the comultiplication map is induced by
$g\mapsto g^{-1}$
and the comultiplication map is induced by
![]() $g \mapsto g\otimes g$
for all
$g \mapsto g\otimes g$
for all
![]() $g \in G$
. In general, our construction of the twisted group ring
$g \in G$
. In general, our construction of the twisted group ring
![]() $D^1(k[G])$
can be suitably extended in various ways where we replace
$D^1(k[G])$
can be suitably extended in various ways where we replace
![]() $k[G]$
by an arbitrary Hopf k-algebra A as follows. We denote the comultiplication map of A by
$k[G]$
by an arbitrary Hopf k-algebra A as follows. We denote the comultiplication map of A by
![]() $\Delta \mathop{\colon} A \to A \otimes A$
. Let us first define
$\Delta \mathop{\colon} A \to A \otimes A$
. Let us first define
![]() $D^1(A)=A\oplus (A\otimes A)$
as a k-module. Suppose that we have defined bilinear product rules
$D^1(A)=A\oplus (A\otimes A)$
as a k-module. Suppose that we have defined bilinear product rules
![]() $\alpha * \beta $
,
$\alpha * \beta $
,
![]() $\beta * \alpha $
,
$\beta * \alpha $
,
![]() $\beta * \gamma \in A \otimes A$
, where
$\beta * \gamma \in A \otimes A$
, where
![]() $\alpha \in A$
and
$\alpha \in A$
and
![]() $\beta , \gamma \in A \otimes A$
, which satisfy the associativity
$\beta , \gamma \in A \otimes A$
, which satisfy the associativity
![]() $(u*v)*w =u*(v*w)$
for all
$(u*v)*w =u*(v*w)$
for all
![]() $u,v,w \in A \cup (A\otimes A)$
where we set
$u,v,w \in A \cup (A\otimes A)$
where we set
![]() if
if
![]() $x,y \in A$
. Then a straightforward application of the proof of Lemma 5.1 shows that the space
$x,y \in A$
. Then a straightforward application of the proof of Lemma 5.1 shows that the space
![]() $D^1(A)$
will become an unital k-algebra via the following multiplication rule defined in a similar fashion as in (5.1):
$D^1(A)$
will become an unital k-algebra via the following multiplication rule defined in a similar fashion as in (5.1):
As an immediate example, let
![]() $\varphi \mathop{\colon} A\otimes A \to A \otimes A$
be a k-algebra homomorphism. For
$\varphi \mathop{\colon} A\otimes A \to A \otimes A$
be a k-algebra homomorphism. For
![]() $\alpha \in A$
and
$\alpha \in A$
and
![]() $\beta , \gamma \in A \otimes A$
, consider the following bilinear product rules:
$\beta , \gamma \in A \otimes A$
, consider the following bilinear product rules:

Then clearly
![]() $(u*v)*w =u*(v*w)$
for all
$(u*v)*w =u*(v*w)$
for all
![]() $u,v,w \in A \cup (A\otimes A)$
and
$u,v,w \in A \cup (A\otimes A)$
and
![]() $D^1(A)$
is thus an unital k-algebra. The rules described by the formula (5.2) provide another nontrivial example of dynamical origin (see Section 6) when A is the group ring
$D^1(A)$
is thus an unital k-algebra. The rules described by the formula (5.2) provide another nontrivial example of dynamical origin (see Section 6) when A is the group ring
![]() $k[G]$
for some group G. We suspect that such constructions may lead to further interesting investigations concerning Hopf algebras.
$k[G]$
for some group G. We suspect that such constructions may lead to further interesting investigations concerning Hopf algebras.
6 Non-uniform linear NUCA
 and
and
 $D^1(M_n(k)[G])$
$D^1(M_n(k)[G])$
Let k be a field, and let G be a group. Let us fix an integer
![]() $n \geq 1$
and denote
$n \geq 1$
and denote
![]() $V= k^n$
. Recall that
$V= k^n$
. Recall that
![]() $\mathrm {LNUCA}_{c}(G, k^n)$
is the k-algebra of all linear NUCA with finite memory
$\mathrm {LNUCA}_{c}(G, k^n)$
is the k-algebra of all linear NUCA with finite memory
![]() $\tau \mathop{\colon} (k^n)^G \to (k^n)^G$
which admit asymptotically constant configurations of local defining maps. The multiplication of
$\tau \mathop{\colon} (k^n)^G \to (k^n)^G$
which admit asymptotically constant configurations of local defining maps. The multiplication of
![]() $\mathrm {LNUCA}_c(G,k^n)$
is given by the composition of maps and whose addition is component-wise.
$\mathrm {LNUCA}_c(G,k^n)$
is given by the composition of maps and whose addition is component-wise.
With every element
![]() $\omega = (\alpha , \beta ) \in D^1(M_n(k)[G])$
, we can associate a map
$\omega = (\alpha , \beta ) \in D^1(M_n(k)[G])$
, we can associate a map
![]() $\tau ^\omega \mathop{\colon} V^G \to V^G$
defined as follows:
$\tau ^\omega \mathop{\colon} V^G \to V^G$
defined as follows:
For every element
![]() $\gamma \in M_n(k)[G]$
, we denote the support of
$\gamma \in M_n(k)[G]$
, we denote the support of
![]() $\gamma $
as the finite subset
$\gamma $
as the finite subset
![]() $\operatorname {\mathrm {supp}}(\gamma ) = \{ g \in G\mathop{\colon} \gamma (g) \neq 0\}$
of G. Given
$\operatorname {\mathrm {supp}}(\gamma ) = \{ g \in G\mathop{\colon} \gamma (g) \neq 0\}$
of G. Given
![]() $\omega = (\alpha , \beta ) \in D^1(M_n(k)[G])$
, we define its support
$\omega = (\alpha , \beta ) \in D^1(M_n(k)[G])$
, we define its support
![]() $\operatorname {\mathrm {supp}} (\omega ) \subset G$
by
$\operatorname {\mathrm {supp}} (\omega ) \subset G$
by
Lemma 6.1 The map
![]() $\tau ^\omega \mathop{\colon} V^G \to V^G$
is a linear NUCA with finite memory. Moreover,
$\tau ^\omega \mathop{\colon} V^G \to V^G$
is a linear NUCA with finite memory. Moreover,
![]() $\tau ^\omega $
admits a configuration of local defining maps which is asymptotic to a constant configuration, i.e.,
$\tau ^\omega $
admits a configuration of local defining maps which is asymptotic to a constant configuration, i.e.,
![]() $\tau ^{\omega } \in \mathrm {LNUCA}_{c}(G, k^n)$
.
$\tau ^{\omega } \in \mathrm {LNUCA}_{c}(G, k^n)$
.
Proof Since
![]() $\alpha (g) , \beta (g)(h) \in M_n(k)$
for all
$\alpha (g) , \beta (g)(h) \in M_n(k)$
for all
![]() $g,h \in G$
, it follows from (6.1) that
$g,h \in G$
, it follows from (6.1) that
![]() $\tau ^\omega $
is a linear map. Let
$\tau ^\omega $
is a linear map. Let
![]() $M = \operatorname {\mathrm {supp}}(\omega ) \subset G$
(see (6.2)).
$M = \operatorname {\mathrm {supp}}(\omega ) \subset G$
(see (6.2)).
We define a configuration of local defining maps
![]() $s \in S^G$
, where
$s \in S^G$
, where
![]() $S= \mathcal {L}(V^G, V)$
as follows. For every
$S= \mathcal {L}(V^G, V)$
as follows. For every
![]() $g \in G$
, let
$g \in G$
, let
![]() $s(g) \in S$
be the linear map determined for all
$s(g) \in S$
be the linear map determined for all
![]() $w \in V^M$
by
$w \in V^M$
by
Let
![]() $x \in V^G$
and
$x \in V^G$
and
![]() $g \in G$
. Then we infer from the definition (6.1) and the choice of M that
$g \in G$
. Then we infer from the definition (6.1) and the choice of M that
 $$ \begin{align*} \sigma_s(x)(g) &= s(g)((g^{-1}x)\vert_M) \\ & = \sum_{h \in M} \alpha(h)x(gh) + \sum_{h \in M} \beta(g)(h)x(gh)\\ & = \sum_{h \in G} \alpha(h)x(gh) + \sum_{h \in G} \beta(g)(h)x(gh)\\ & = \tau^\omega(x)(g). \end{align*} $$
$$ \begin{align*} \sigma_s(x)(g) &= s(g)((g^{-1}x)\vert_M) \\ & = \sum_{h \in M} \alpha(h)x(gh) + \sum_{h \in M} \beta(g)(h)x(gh)\\ & = \sum_{h \in G} \alpha(h)x(gh) + \sum_{h \in G} \beta(g)(h)x(gh)\\ & = \tau^\omega(x)(g). \end{align*} $$
We deduce that
![]() $\tau ^\omega = \sigma _s$
is indeed a linear NUCA with finite memory. On the other hand, if we denote
$\tau ^\omega = \sigma _s$
is indeed a linear NUCA with finite memory. On the other hand, if we denote
![]() $E= \operatorname {\mathrm {supp}} \beta $
then E is a finite subset of G and we have
$E= \operatorname {\mathrm {supp}} \beta $
then E is a finite subset of G and we have
![]() $s(g)= \alpha (g)$
for all
$s(g)= \alpha (g)$
for all
![]() $g \in G \setminus E$
by construction. Consequently, s is asymptotic to the constant configuration
$g \in G \setminus E$
by construction. Consequently, s is asymptotic to the constant configuration
![]() $\alpha ^G$
. Thus,
$\alpha ^G$
. Thus,
![]() $\tau ^\omega \in \mathrm {LNUCA}_c(G, k^n)$
and the proof is complete.
$\tau ^\omega \in \mathrm {LNUCA}_c(G, k^n)$
and the proof is complete.
It turns out that the converse of the above lemma also holds. In other words, every linear NUCA over
![]() $V^G$
with finite memory and asymptotically constant configuration of local defining maps arises uniquely as a map
$V^G$
with finite memory and asymptotically constant configuration of local defining maps arises uniquely as a map
![]() $\tau ^\omega $
described above. More specifically, the following results says that the map
$\tau ^\omega $
described above. More specifically, the following results says that the map
![]() $\omega \mapsto \tau ^{\omega }$
is a ring isomorphism when G is infinite.
$\omega \mapsto \tau ^{\omega }$
is a ring isomorphism when G is infinite.
Theorem 6.2 Let k be a field, and let G be an infinite group. Then for every integer
![]() $n \geq 1$
, the map
$n \geq 1$
, the map
![]() $\Psi \mathop{\colon} D^1(M_n(k)[G]) \to \mathrm {LNUCA}_{c}(G, k^n)$
given by
$\Psi \mathop{\colon} D^1(M_n(k)[G]) \to \mathrm {LNUCA}_{c}(G, k^n)$
given by
![]() $\omega \mapsto \tau ^{\omega }$
is a k-linear ring isomorphism.
$\omega \mapsto \tau ^{\omega }$
is a k-linear ring isomorphism.
Proof Let
![]() $V= k^n$
. We claim that
$V= k^n$
. We claim that
![]() $\Psi $
is injective. Indeed, let
$\Psi $
is injective. Indeed, let
![]() $\omega =(\alpha , \beta ) \in D^1(M_n(k)[G])$
be an element such that
$\omega =(\alpha , \beta ) \in D^1(M_n(k)[G])$
be an element such that
![]() $\tau ^\omega = 0$
as a map from
$\tau ^\omega = 0$
as a map from
![]() $V^G$
to itself. Let
$V^G$
to itself. Let
![]() $M = \operatorname {\mathrm {supp}}(\omega )$
(see (6.2)) then M is a finite subset of G. Since G is infinite, we can choose some
$M = \operatorname {\mathrm {supp}}(\omega )$
(see (6.2)) then M is a finite subset of G. Since G is infinite, we can choose some
![]() $g_0 \in G \setminus M$
. In particular,
$g_0 \in G \setminus M$
. In particular,
![]() $\beta (g_0)=0$
by the choice of M. Then for every
$\beta (g_0)=0$
by the choice of M. Then for every
![]() $x \in V^G$
, we find that
$x \in V^G$
, we find that
![]() $\tau ^\omega (x)(g_0)=0$
and it follows from (6.1) that
$\tau ^\omega (x)(g_0)=0$
and it follows from (6.1) that
Since x is arbitrary, we deduce that
![]() $\alpha (h)=0$
for all
$\alpha (h)=0$
for all
![]() $h \in M$
and thus
$h \in M$
and thus
![]() $\alpha =0$
since
$\alpha =0$
since
![]() $\operatorname {\mathrm {supp}} (\alpha ) \subset \operatorname {\mathrm {supp}}(\omega )=M$
. Consequently, we infer again from (6.1) that for all
$\operatorname {\mathrm {supp}} (\alpha ) \subset \operatorname {\mathrm {supp}}(\omega )=M$
. Consequently, we infer again from (6.1) that for all
![]() $g \in G$
:
$g \in G$
:
Thus,
![]() $\beta (g)(h)=0$
for all
$\beta (g)(h)=0$
for all
![]() $g,h \in G$
. In other words,
$g,h \in G$
. In other words,
![]() $\beta =0$
and we conclude that
$\beta =0$
and we conclude that
![]() $\omega =0$
. Hence,
$\omega =0$
. Hence,
![]() $\Psi $
is indeed injective as claimed.
$\Psi $
is indeed injective as claimed.
To check that
![]() $\Psi $
is surjective, let
$\Psi $
is surjective, let
![]() $\sigma _s \in \mathrm {LNUCA}_c(G, V)$
where
$\sigma _s \in \mathrm {LNUCA}_c(G, V)$
where
![]() $s \in S^G$
for some
$s \in S^G$
for some
![]() $S=\mathcal {L}(V^M, V)$
, where
$S=\mathcal {L}(V^M, V)$
, where
![]() $M \subset G$
is a finite subset, such that s is asymptotic to a constant configuration
$M \subset G$
is a finite subset, such that s is asymptotic to a constant configuration
![]() $c \in S^G$
. Up to enlarging M, we can also suppose that
$c \in S^G$
. Up to enlarging M, we can also suppose that
![]() $s\vert _{G \setminus M} = c\vert _{G \setminus M}$
.
$s\vert _{G \setminus M} = c\vert _{G \setminus M}$
.
Since
![]() $c(1_G) \in \mathcal {L}(V^M, V)$
, there exist
$c(1_G) \in \mathcal {L}(V^M, V)$
, there exist
![]() $\gamma _h \in \mathcal {L}(V,V)= M_n(k)$
for every
$\gamma _h \in \mathcal {L}(V,V)= M_n(k)$
for every
![]() $h \in M$
such that for all
$h \in M$
such that for all
![]() $w \in V^M$
, we have
$w \in V^M$
, we have
![]() $c(1_G)(w) = \sum _{h \in M} \gamma _h w$
. Let us denote
$c(1_G)(w) = \sum _{h \in M} \gamma _h w$
. Let us denote
![]() $\alpha = \sum _{h \in M}\gamma _h h \in M_n(k)[G]$
.
$\alpha = \sum _{h \in M}\gamma _h h \in M_n(k)[G]$
.
For each
![]() $g \in M$
, we define
$g \in M$
, we define
![]() $ \delta _g=s(g) - c(g) \in \mathcal {L}(V^M,V)$
. By linearity, there exists uniquely
$ \delta _g=s(g) - c(g) \in \mathcal {L}(V^M,V)$
. By linearity, there exists uniquely
![]() $\delta _g(h) \in M_n(k)= \mathcal {L}(V,V)$
for
$\delta _g(h) \in M_n(k)= \mathcal {L}(V,V)$
for
![]() $h \in M$
such that for all
$h \in M$
such that for all
![]() $w \in V^M$
, we have
$w \in V^M$
, we have
Hence, we obtain an element
![]() $\mu _g = \sum _{h \in M} \delta _g(h) \in M_n(k)[G]$
for every
$\mu _g = \sum _{h \in M} \delta _g(h) \in M_n(k)[G]$
for every
![]() $g \in M$
. Let us denote
$g \in M$
. Let us denote
![]() $\beta = \sum _{g \in M} \mu _g g \in (M_n(k)[G])[G]$
and
$\beta = \sum _{g \in M} \mu _g g \in (M_n(k)[G])[G]$
and
![]() $\omega =(\alpha , \beta ) \in D^1(M_n(k)[G])$
. We claim that
$\omega =(\alpha , \beta ) \in D^1(M_n(k)[G])$
. We claim that
![]() $\tau ^\omega = \sigma _s$
. Indeed, for every
$\tau ^\omega = \sigma _s$
. Indeed, for every
![]() $x \in V^G$
and
$x \in V^G$
and
![]() $g \in G$
, we find that
$g \in G$
, we find that
 $$ \begin{align*} \tau^\omega(x)(g) & = \sum_{h \in G} \alpha(h) x(gh) + \sum_{h \in G} \beta(g)(h)x(gh) \\ & = \sum_{h \in M} \gamma_h x(gh) + \sum_{h \in M} \mu_g(h)x(gh)\\ &= c(1_G)((g^{-1}x)\vert_M) + \sum_{h \in M} \delta_g(h)x(gh)\\ & = c(g)((g^{-1}x)\vert_M) + \delta_g((g^{-1}x)\vert_M)\\ & = s(g)((g^{-1}x)\vert_M)\\ &=\sigma_s(x)(g). \end{align*} $$
$$ \begin{align*} \tau^\omega(x)(g) & = \sum_{h \in G} \alpha(h) x(gh) + \sum_{h \in G} \beta(g)(h)x(gh) \\ & = \sum_{h \in M} \gamma_h x(gh) + \sum_{h \in M} \mu_g(h)x(gh)\\ &= c(1_G)((g^{-1}x)\vert_M) + \sum_{h \in M} \delta_g(h)x(gh)\\ & = c(g)((g^{-1}x)\vert_M) + \delta_g((g^{-1}x)\vert_M)\\ & = s(g)((g^{-1}x)\vert_M)\\ &=\sigma_s(x)(g). \end{align*} $$
We conclude that
![]() $\sigma _s = \tau ^\omega =\Psi (\omega )$
from which the surjectivity of the map
$\sigma _s = \tau ^\omega =\Psi (\omega )$
from which the surjectivity of the map
![]() $\Psi $
follows. It is immediate from (6.1) that
$\Psi $
follows. It is immediate from (6.1) that
![]() $\Psi $
is a k-linear homomorphism of groups and
$\Psi $
is a k-linear homomorphism of groups and
![]() $\Psi $
sends the unit of
$\Psi $
sends the unit of
![]() $D^1(M_n(k)[G])$
to the unit of
$D^1(M_n(k)[G])$
to the unit of
![]() $\mathrm {LNUCA}_c(G, V)$
.
$\mathrm {LNUCA}_c(G, V)$
.
To finish the proof, we have to check that for all elements
![]() $\omega =(\alpha , \beta )$
and
$\omega =(\alpha , \beta )$
and
![]() $\omega '=(\alpha ', \beta ')$
of
$\omega '=(\alpha ', \beta ')$
of
![]() $D^1(M_n(k)[G])$
, we have
$D^1(M_n(k)[G])$
, we have
![]() $\Psi (\omega * \omega ') = \Psi (\omega ) \circ \Psi (\omega ')$
. Indeed, using the formula
$\Psi (\omega * \omega ') = \Psi (\omega ) \circ \Psi (\omega ')$
. Indeed, using the formula
![]() $\omega * \omega ' = (\alpha \alpha ', \alpha \beta ' + \beta \alpha '+ \beta \beta ')$
and (5.2), we can compute for all
$\omega * \omega ' = (\alpha \alpha ', \alpha \beta ' + \beta \alpha '+ \beta \beta ')$
and (5.2), we can compute for all
![]() $x \in V^G$
,
$x \in V^G$
,
![]() $g \in G$
, and
$g \in G$
, and
![]() $y = \tau ^{\omega '}(x)$
that
$y = \tau ^{\omega '}(x)$
that
 $$ \begin{align*} & \Psi(\omega * \omega') (x)(g) = \sum_{h \in G} \left( \alpha\alpha' + (\alpha \beta' + \beta \alpha'+ \beta \beta')(g)\right)(h) x(gh) \\ &\ \ = \sum_{h, t \in G} \left( \alpha(t) ( \alpha'(t^{-1}h)\kern1.2pt{+}\kern1.2pt \beta'(gt)(t^{-1}h)) \kern1.2pt{+}\kern1.2pt \beta(g)(t) (\alpha'(t^{-1}h) \kern1.2pt{+} \beta'(gt)(t^{-1}h)\right)x(gh) \\ &\ \ = \sum_{t\in G} ( \alpha(t) + \beta(g)(t))\sum_{ r \in G}\left( \alpha'(r) + \beta'(gt)(r) \right) x(gtr) \qquad \qquad (r=t^{-1}h) \\ &\ \ = \sum_{t \in G} \left( \alpha(t) + \beta(g)(t)\right) y(gt) \\ &\ \ = \tau^\omega(y)(g) \\ &\ \ = (\tau^\omega \circ \tau^{\omega'})(x)(g) \\ &\ \ = \left( \Psi(\omega)\circ \Psi(\omega')\right) (x)(g). \end{align*} $$
$$ \begin{align*} & \Psi(\omega * \omega') (x)(g) = \sum_{h \in G} \left( \alpha\alpha' + (\alpha \beta' + \beta \alpha'+ \beta \beta')(g)\right)(h) x(gh) \\ &\ \ = \sum_{h, t \in G} \left( \alpha(t) ( \alpha'(t^{-1}h)\kern1.2pt{+}\kern1.2pt \beta'(gt)(t^{-1}h)) \kern1.2pt{+}\kern1.2pt \beta(g)(t) (\alpha'(t^{-1}h) \kern1.2pt{+} \beta'(gt)(t^{-1}h)\right)x(gh) \\ &\ \ = \sum_{t\in G} ( \alpha(t) + \beta(g)(t))\sum_{ r \in G}\left( \alpha'(r) + \beta'(gt)(r) \right) x(gtr) \qquad \qquad (r=t^{-1}h) \\ &\ \ = \sum_{t \in G} \left( \alpha(t) + \beta(g)(t)\right) y(gt) \\ &\ \ = \tau^\omega(y)(g) \\ &\ \ = (\tau^\omega \circ \tau^{\omega'})(x)(g) \\ &\ \ = \left( \Psi(\omega)\circ \Psi(\omega')\right) (x)(g). \end{align*} $$
It follows that
![]() $\Psi (\omega * \omega ')=\Psi (\omega )\circ \Psi (\omega ')$
. The proof is thus complete.
$\Psi (\omega * \omega ')=\Psi (\omega )\circ \Psi (\omega ')$
. The proof is thus complete.
Observe that Theorem 6.2 does not hold when G is a finite group since the ring morphism
![]() $\Psi $
fails to be injective in this case.
$\Psi $
fails to be injective in this case.
7 Stable finiteness of generalized group rings and stably L-surjunctive groups
The main goal of the present section is to show that the stable finiteness property of the generalized group ring
![]() $D^1(k[G])$
is equivalent to the surjunctivity property of the classes
$D^1(k[G])$
is equivalent to the surjunctivity property of the classes
![]() $\mathrm {LUNCA}_c(G,k^n)$
for every
$\mathrm {LUNCA}_c(G,k^n)$
for every
![]() $n \geq 1$
(Theorem 7.2).
$n \geq 1$
(Theorem 7.2).
We begin with the following isomorphism between the ring
![]() $M_n(D^1(k[G]))$
of square matrices of size
$M_n(D^1(k[G]))$
of square matrices of size
![]() $n \times n$
with coefficients in the generalized group ring
$n \times n$
with coefficients in the generalized group ring
![]() $D^1(k[G])$
and the ring
$D^1(k[G])$
and the ring
![]() $D^1(M_n(k[G]))$
.
$D^1(M_n(k[G]))$
.
Proposition 7.1 Let k be a ring, and let G be a group. Then for every integer
![]() $n \geq 1$
, there exists a canonical ring isomorphism
$n \geq 1$
, there exists a canonical ring isomorphism
Proof By [Reference Phung28, Lemma 9.4], there exists a canonical isomorphism of rings
![]() $ M_n(k)[G] \simeq M_n(k[G])$
given by
$ M_n(k)[G] \simeq M_n(k[G])$
given by
![]() $\sum _{g\in G}A(g) g \mapsto (\sum _{g \in G} A(g)_{ij}g)_{1 \leq i,j \leq n}$
. Consider the map
$\sum _{g\in G}A(g) g \mapsto (\sum _{g \in G} A(g)_{ij}g)_{1 \leq i,j \leq n}$
. Consider the map
![]() $F\mathop{\colon} D^1(M_n(k)[G]) \to M_n(D^1(k[G]))$
defined as follows. For
$F\mathop{\colon} D^1(M_n(k)[G]) \to M_n(D^1(k[G]))$
defined as follows. For
![]() $ x= (\alpha , \beta ) \in D^1(M_n(k)[G])$
, we can write
$ x= (\alpha , \beta ) \in D^1(M_n(k)[G])$
, we can write
![]() $\beta = \sum _{g \in G} \beta (g)g \in (M_n(k)[G])[G]$
where
$\beta = \sum _{g \in G} \beta (g)g \in (M_n(k)[G])[G]$
where
![]() $\beta (g) = (\beta (g)_{ij})_{1 \leq i,j \leq n} \in M_n(k)[G]$
for all
$\beta (g) = (\beta (g)_{ij})_{1 \leq i,j \leq n} \in M_n(k)[G]$
for all
![]() $g \in G$
. Then we define
$g \in G$
. Then we define
![]() $F(x) \in M_n(D^1(k[G]))$
by setting for all
$F(x) \in M_n(D^1(k[G]))$
by setting for all
![]() $1 \leq i,j \leq n$
:
$1 \leq i,j \leq n$
:
It is clear that F is a bijective homomorphism of groups and that
![]() $F((I_n, 0))= J_n$
, where
$F((I_n, 0))= J_n$
, where
![]() $I_n \in M_n(k)[G]$
and
$I_n \in M_n(k)[G]$
and
![]() $J_n \in M_n(D^1(k[G]))$
are identity matrices of
$J_n \in M_n(D^1(k[G]))$
are identity matrices of
![]() $M_n(k)[G]$
and
$M_n(k)[G]$
and
![]() $M_n(D^1(k[G]))$
, respectively.
$M_n(D^1(k[G]))$
, respectively.
Now, let
![]() $x_i=(\alpha _i, \beta _i)\in D^1(M_n(k)[G])$
for
$x_i=(\alpha _i, \beta _i)\in D^1(M_n(k)[G])$
for
![]() $i=1,2$
. Then
$i=1,2$
. Then
![]() $x_1*x_2=(\alpha _1 \alpha _2, \alpha _1 \beta _2+ \beta _1 \alpha _2+\beta _1 \beta _2)$
and thus
$x_1*x_2=(\alpha _1 \alpha _2, \alpha _1 \beta _2+ \beta _1 \alpha _2+\beta _1 \beta _2)$
and thus
On the other hand, we find that
 $$ \begin{align*} (F(x_1)F(x_2))_{ij} = \sum_{r=1}^n F(x_1)_{ir}*F(x_2)_{rj} = \sum_{r=1}^n ((\alpha_1)_{ir}, (\beta_1)_{ir})*((\alpha_2)_{rj}, (\beta_2)_{rj}). \end{align*} $$
$$ \begin{align*} (F(x_1)F(x_2))_{ij} = \sum_{r=1}^n F(x_1)_{ir}*F(x_2)_{rj} = \sum_{r=1}^n ((\alpha_1)_{ir}, (\beta_1)_{ir})*((\alpha_2)_{rj}, (\beta_2)_{rj}). \end{align*} $$
Therefore, if we denote
![]() $(F(x_1)F(x_2))_{ij}= (u,v)$
then
$(F(x_1)F(x_2))_{ij}= (u,v)$
then
 $$ \begin{align} u= \sum_{r=1}^n (\alpha_1)_{ir} (\alpha_2)_{rj} = (\alpha_1\alpha_2)_{ij} \end{align} $$
$$ \begin{align} u= \sum_{r=1}^n (\alpha_1)_{ir} (\alpha_2)_{rj} = (\alpha_1\alpha_2)_{ij} \end{align} $$
by the definition of matrix multiplication. Moreover, we deduce from the definition of the operation
![]() $*$
that
$*$
that
![]() $v= \sum _{g \in G} v(g) g$
, where
$v= \sum _{g \in G} v(g) g$
, where
 $$ \begin{align*} v(g) & = \sum_{r=1}^n ((\alpha_1)_{ir}(\beta_2)_{rj})(g) + ((\beta_1)_{ir}(\alpha_2)_{rj})(g)+ ((\beta_1)_{ir}(\beta_2)_{rj})(g). \end{align*} $$
$$ \begin{align*} v(g) & = \sum_{r=1}^n ((\alpha_1)_{ir}(\beta_2)_{rj})(g) + ((\beta_1)_{ir}(\alpha_2)_{rj})(g)+ ((\beta_1)_{ir}(\beta_2)_{rj})(g). \end{align*} $$
We infer from (5.2) that
 $$ \begin{align*} \sum_{r=1}^n ((\alpha_1)_{ir}(\beta_2)_{rj})(g) & = \sum_{r=1}^n \sum_{h \in G}((\alpha_1)_{ir}(\beta_2)_{rj})(g)(h) h \\ & = \sum_{r=1}^n \sum_{h, t \in G} \alpha_1(t)_{ir} \beta_2(gt)(t^{-1}h)_{rj} h\\ & = \sum_{h\in G} \sum_{t\in G}\sum_{r=1}^n \alpha_1(t)_{ir} \beta_2(gt)(t^{-1}h)_{rj} h\\ & = \sum_{h \in G} (\alpha_1 \beta_2)(g)(h)_{ij} h \\ & = (\alpha_1 \beta_2)(g)_{ij}. \end{align*} $$
$$ \begin{align*} \sum_{r=1}^n ((\alpha_1)_{ir}(\beta_2)_{rj})(g) & = \sum_{r=1}^n \sum_{h \in G}((\alpha_1)_{ir}(\beta_2)_{rj})(g)(h) h \\ & = \sum_{r=1}^n \sum_{h, t \in G} \alpha_1(t)_{ir} \beta_2(gt)(t^{-1}h)_{rj} h\\ & = \sum_{h\in G} \sum_{t\in G}\sum_{r=1}^n \alpha_1(t)_{ir} \beta_2(gt)(t^{-1}h)_{rj} h\\ & = \sum_{h \in G} (\alpha_1 \beta_2)(g)(h)_{ij} h \\ & = (\alpha_1 \beta_2)(g)_{ij}. \end{align*} $$
Similarly, we have the equalities
![]() $ \sum _{r=1}^n ((\beta _1)_{ir}(\alpha _2)_{rj})(g) = (\beta _1 \alpha _2)(g)_{ij}$
and also
$ \sum _{r=1}^n ((\beta _1)_{ir}(\alpha _2)_{rj})(g) = (\beta _1 \alpha _2)(g)_{ij}$
and also
![]() $ \sum _{r=1}^n ((\beta _1)_{ir}(\beta _2)_{rj})(g) = (\beta _1 \beta _2)(g)_{ij}$
. Comparing to (7.2), it follows that v is equal to the singular part of
$ \sum _{r=1}^n ((\beta _1)_{ir}(\beta _2)_{rj})(g) = (\beta _1 \beta _2)(g)_{ij}$
. Comparing to (7.2), it follows that v is equal to the singular part of
![]() $F(x_1*x_2)_{ij}$
. Consequently, we deduce from (7.3) that for all
$F(x_1*x_2)_{ij}$
. Consequently, we deduce from (7.3) that for all
![]() $1 \leq i,j \leq n$
, we have
$1 \leq i,j \leq n$
, we have
Hence,
![]() $F(x_1)F(x_2)= F(x_1*x_2)$
and we can finally conclude that F is a ring isomorphism. The proof is thus complete.
$F(x_1)F(x_2)= F(x_1*x_2)$
and we can finally conclude that F is a ring isomorphism. The proof is thus complete.
The main result of the section is the following dynamical characterization of the direct finiteness of the ring
![]() $M_n(D^1(k[G]))$
.
$M_n(D^1(k[G]))$
.
Theorem 7.2 Let G be an infinite group, and let k be a field. Then for every integer
![]() $n \geq 1$
, the following are equivalent:
$n \geq 1$
, the following are equivalent:
-
(i) Every stably injective
 $\tau \in \mathrm {LNUCA}_c(G,k^{n})$
is surjective.
$\tau \in \mathrm {LNUCA}_c(G,k^{n})$
is surjective. -
(ii) The ring
 $\mathrm {LNUCA}_c(G,k^n)$
is directly finite.
$\mathrm {LNUCA}_c(G,k^n)$
is directly finite. -
(iii) The ring
 $M_n(D^1(k[G]))$
is directly finite.
$M_n(D^1(k[G]))$
is directly finite.
Proof The equivalence between (ii) and (iii) results directly from Proposition 7.1 and Theorem 6.2 which imply that
![]() $\mathrm {LNUCA}_c(G,k^n) \simeq M_n(D^1(k[G]))$
.
$\mathrm {LNUCA}_c(G,k^n) \simeq M_n(D^1(k[G]))$
.
Suppose that (i) holds and let
![]() $\tau , \sigma \in \mathrm {LNUCA}_c(G,k^n)$
be two linear NUCA such that
$\tau , \sigma \in \mathrm {LNUCA}_c(G,k^n)$
be two linear NUCA such that
![]() $\tau \circ \sigma = \operatorname {\mathrm {Id}}$
. Then Theorem 4.3 implies that
$\tau \circ \sigma = \operatorname {\mathrm {Id}}$
. Then Theorem 4.3 implies that
![]() $\sigma $
is stably injective. Consequently, we infer from (i) that
$\sigma $
is stably injective. Consequently, we infer from (i) that
![]() $\sigma $
is surjective. In particular,
$\sigma $
is surjective. In particular,
![]() $\sigma $
is bijective and thus so is
$\sigma $
is bijective and thus so is
![]() $\tau $
. It follows from
$\tau $
. It follows from
![]() $\tau \circ \sigma = \operatorname {\mathrm {Id}}$
that
$\tau \circ \sigma = \operatorname {\mathrm {Id}}$
that
![]() $\sigma \circ \tau = \operatorname {\mathrm {Id}}$
as well. This shows that the ring
$\sigma \circ \tau = \operatorname {\mathrm {Id}}$
as well. This shows that the ring
![]() $\mathrm {LNUCA}_c(G,k^n)$
is directly finite. Therefore, we have shown that (i) implies (ii).
$\mathrm {LNUCA}_c(G,k^n)$
is directly finite. Therefore, we have shown that (i) implies (ii).
Suppose now that (ii) holds and let
![]() $\tau \in \mathrm {LNUCA}_c(G,k^n)$
be a stably injective linear NUCA. Then we deduce from Theorem 4.2 that
$\tau \in \mathrm {LNUCA}_c(G,k^n)$
be a stably injective linear NUCA. Then we deduce from Theorem 4.2 that
![]() $\tau $
is left-invertible, i.e., there exists
$\tau $
is left-invertible, i.e., there exists
![]() $\sigma \in \mathrm {LNUCA}_c(G,k^n)$
such that
$\sigma \in \mathrm {LNUCA}_c(G,k^n)$
such that
![]() $\sigma \circ \tau = \operatorname {\mathrm {Id}}$
. Hence, (ii) implies that
$\sigma \circ \tau = \operatorname {\mathrm {Id}}$
. Hence, (ii) implies that
![]() $\tau \circ \sigma = \operatorname {\mathrm {Id}}$
and it follows at once that
$\tau \circ \sigma = \operatorname {\mathrm {Id}}$
and it follows at once that
![]() $\tau $
is surjective. Therefore, we also have that (ii) implies (i). The proof is thus complete.
$\tau $
is surjective. Therefore, we also have that (ii) implies (i). The proof is thus complete.
Corollary 7.3 Suppose that G is an infinite group. Then the following are equivalent:
-
(a) The group G is
 $L^1$
-surjunctive.
$L^1$
-surjunctive. -
(b) For every field k, the ring
 $D^1(k[G])$
is stably finite.
$D^1(k[G])$
is stably finite.
Proof It is a direct consequence of Theorem 7.2.
8 Stable finiteness of generalized group rings and
 $L^1$
-surjunctive groups
$L^1$
-surjunctive groups
Extending [Reference Phung36, Theorem B], we establish various characterizations of the stable finiteness of the ring
![]() $D^1(k[G])$
(for all field k) notably in terms of the finite
$D^1(k[G])$
(for all field k) notably in terms of the finite
![]() $L^1$
-surjunctivity of the group G. For ease of reading, we recall the statement of Theorem B in the Introduction.
$L^1$
-surjunctivity of the group G. For ease of reading, we recall the statement of Theorem B in the Introduction.
Theorem 8.1 For every infinite group G, the following are equivalent:
-
(i) G is
 $L^1$
-surjunctive;
$L^1$
-surjunctive; -
(ii) G is finitely
 $L^1$
-surjunctive;
$L^1$
-surjunctive; -
(iii) for every field k, the ring
 $D^1(k[G])$
is stably finite;
$D^1(k[G])$
is stably finite; -
(iv) for every finite field k, the ring
 $D^1(k[G])$
is stably finite;
$D^1(k[G])$
is stably finite; -
(v) G is dual
 $L^1$
-surjunctive;
$L^1$
-surjunctive; -
(iv) G is finitely dual
 $L^1$
-surjunctive.
$L^1$
-surjunctive.
Proof Let V be a finite-dimensional vector space, and let
![]() $\tau \in \mathrm {LNUCA}_c(G,V)$
. Then we obtain a dual linear NUCA
$\tau \in \mathrm {LNUCA}_c(G,V)$
. Then we obtain a dual linear NUCA
![]() $\tau ^* \in \mathrm {LNUCA}_c(G,V)$
whose dual is exactly
$\tau ^* \in \mathrm {LNUCA}_c(G,V)$
whose dual is exactly
![]() $\tau $
, that is,
$\tau $
, that is,
![]() $(\tau ^*)^* = \tau $
(see [Reference Phung37]). We infer from [Reference Phung37, Theorem A] that
$(\tau ^*)^* = \tau $
(see [Reference Phung37]). We infer from [Reference Phung37, Theorem A] that
![]() $\tau $
is pre-injective if and only if
$\tau $
is pre-injective if and only if
![]() $\tau ^*$
is surjective and that
$\tau ^*$
is surjective and that
![]() $\tau ^*$
is stably injective if and only if
$\tau ^*$
is stably injective if and only if
![]() $\tau $
is stably post-surjective. Hence, we deduce immediately the equivalences (i)
$\tau $
is stably post-surjective. Hence, we deduce immediately the equivalences (i)
![]() $\iff $
(v) and (ii)
$\iff $
(v) and (ii)
![]() $\iff $
(vi).
$\iff $
(vi).
The equivalence (i)
![]() $\iff $
(ii) is the content of Corollary 7.3. Similarly, the exact same proof of Theorem 7.2 shows that (ii)
$\iff $
(ii) is the content of Corollary 7.3. Similarly, the exact same proof of Theorem 7.2 shows that (ii)
![]() $\iff $
(iv). Finally, the equivalence (i)
$\iff $
(iv). Finally, the equivalence (i)
![]() $\iff $
(ii) results from Theorem 8.2. The proof is thus complete.
$\iff $
(ii) results from Theorem 8.2. The proof is thus complete.
Our next key result extends [Reference Phung36, Theorem A]. The proof follows quite closely the reduction strategy of the proof of [Reference Phung36, Theorem A] and [Reference Phung35, Theorem B] which is less involved in our linear case.
Theorem 8.2 Let G be a group, and let
![]() $n\geq 1$
be an integer. Then the following are equivalent:
$n\geq 1$
be an integer. Then the following are equivalent:
-
(i) For every finite field k, all stably injective
 $\tau \in \mathrm {LNUCA}_c(G,k^n)$
are surjective.
$\tau \in \mathrm {LNUCA}_c(G,k^n)$
are surjective. -
(ii) For every field k, all stably injective
 $\tau \in \mathrm {LNUCA}_c(G,k^n)$
are surjective.
$\tau \in \mathrm {LNUCA}_c(G,k^n)$
are surjective.
Proof Since the case when G is finite is clear and (ii)
![]() $\implies $
(i) trivially, we suppose in the rest of the proof that G is an infinite group which satisfies (i). Let V be a finite-dimensional vector space over a field k (not necessarily finite), and let
$\implies $
(i) trivially, we suppose in the rest of the proof that G is an infinite group which satisfies (i). Let V be a finite-dimensional vector space over a field k (not necessarily finite), and let
![]() $\tau \in \mathrm {LNUCA}_c(G, V)$
. Suppose that
$\tau \in \mathrm {LNUCA}_c(G, V)$
. Suppose that
![]() $\tau $
is stably injective. Then, by definition, we can choose a finite subset
$\tau $
is stably injective. Then, by definition, we can choose a finite subset
![]() $M \subset G$
with
$M \subset G$
with
![]() $1_G \in M=M^{-1}$
and a configuration
$1_G \in M=M^{-1}$
and a configuration
![]() $s \in \mathcal {L}(V^M,V)^G$
which is asymptotic to a constant configuration
$s \in \mathcal {L}(V^M,V)^G$
which is asymptotic to a constant configuration
![]() $c \in \mathcal {L}(V^M,V)^G$
such that
$c \in \mathcal {L}(V^M,V)^G$
such that
![]() $\tau =\sigma _s$
and
$\tau =\sigma _s$
and
![]() $s_{G \setminus M}=c\vert _{G \setminus M}$
. We infer from Theorem 4.2 that
$s_{G \setminus M}=c\vert _{G \setminus M}$
. We infer from Theorem 4.2 that
![]() $\tau $
is left-invertible. Hence, we can find
$\tau $
is left-invertible. Hence, we can find
![]() $\sigma \in \mathrm {LNUCA}_c(G,V)$
such that
$\sigma \in \mathrm {LNUCA}_c(G,V)$
such that
![]() $\sigma \circ \tau =\operatorname {\mathrm {Id}}$
. Moreover, up to enlarging the finite set M, we can find
$\sigma \circ \tau =\operatorname {\mathrm {Id}}$
. Moreover, up to enlarging the finite set M, we can find
![]() $t \in \mathcal {L}(V^M, V)^G$
asymptotic to a constant configuration
$t \in \mathcal {L}(V^M, V)^G$
asymptotic to a constant configuration
![]() $d\in \mathcal {L}(V^M, V)^G$
such that
$d\in \mathcal {L}(V^M, V)^G$
such that
![]() $\sigma = \sigma _t$
and
$\sigma = \sigma _t$
and
![]() $t\vert _{G \setminus M}=d\vert _{G \setminus M}$
.
$t\vert _{G \setminus M}=d\vert _{G \setminus M}$
.
Let us denote
![]() $\Gamma = \tau (V^G)$
. As
$\Gamma = \tau (V^G)$
. As
![]() $\sigma _t \circ \sigma _s= \operatorname {\mathrm {Id}}$
, we deduce for all
$\sigma _t \circ \sigma _s= \operatorname {\mathrm {Id}}$
, we deduce for all
![]() $g \in G$
that
$g \in G$
that
where
![]() $\pi _{F, E} \mathop{\colon} V^F\to V^E$
denotes the canonical projection for all sets
$\pi _{F, E} \mathop{\colon} V^F\to V^E$
denotes the canonical projection for all sets
![]() $E \subset F$
. Consider the similar condition where we switch the role of s and t:
$E \subset F$
. Consider the similar condition where we switch the role of s and t:
Since G is infinite, we can choose a finite subset
![]() $M^*\subset G$
such that
$M^*\subset G$
such that
![]() $M^2 \subsetneq M^*$
. Then observe that
$M^2 \subsetneq M^*$
. Then observe that
![]() $\sigma _t \circ \sigma _s= \operatorname {\mathrm {Id}}$
, resp.
$\sigma _t \circ \sigma _s= \operatorname {\mathrm {Id}}$
, resp.
![]() $\sigma _s \circ \sigma _t= \operatorname {\mathrm {Id}}$
, if and only if (8.1), resp. (8.2), holds for all
$\sigma _s \circ \sigma _t= \operatorname {\mathrm {Id}}$
, if and only if (8.1), resp. (8.2), holds for all
![]() $g \in M^*$
(see [Reference Phung34, Lemma 2.2] for the case of CA). Hence, up to making the base change to
$g \in M^*$
(see [Reference Phung34, Lemma 2.2] for the case of CA). Hence, up to making the base change to
![]() $k'$
(replacing V,
$k'$
(replacing V,
![]() $s(g)$
,
$s(g)$
,
![]() $t(g)$
resp. by
$t(g)$
resp. by
![]() $V \otimes _k k'$
,
$V \otimes _k k'$
,
![]() $s(g) \otimes _k k'$
,
$s(g) \otimes _k k'$
,
![]() $t(g) \otimes _k k'$
etc.), where
$t(g) \otimes _k k'$
etc.), where
![]() $k'$
is an algebraically closed field which contains k, we can suppose without loss of generality that k is algebraically closed.
$k'$
is an algebraically closed field which contains k, we can suppose without loss of generality that k is algebraically closed.
We obtain from [Reference Phung36, Lemma 2.1] a finitely generated
![]() $\mathbb {Z}$
-algebra
$\mathbb {Z}$
-algebra
![]() $R \subset k$
and R-modules of finite type
$R \subset k$
and R-modules of finite type
![]() $V_R$
and
$V_R$
and
such that for some fixed
![]() $g_0 \in M^*\setminus M^2$
,
$g_0 \in M^*\setminus M^2$
,
![]() $s_R(g) = s_R(g_0)$
,
$s_R(g) = s_R(g_0)$
,
![]() $t_R(g)=t_R(g_0)$
for all
$t_R(g)=t_R(g_0)$
for all
![]() $g \in G \setminus M^*$
and the following hold:
$g \in G \setminus M^*$
and the following hold:
-
I.
 $V= V_R \otimes _R k$
,
$V= V_R \otimes _R k$
, -
II.
 $s(g)= s_R(g) \otimes _R k$
and
$s(g)= s_R(g) \otimes _R k$
and
 $t(g)= t_R(g) \otimes _R k$
for all
$t(g)= t_R(g) \otimes _R k$
for all
 $g \in M^*$
,
$g \in M^*$
,
where
![]() $\pi _R \mathop{\colon} (V_R)^{E_n M} \to (V_R)^{\{1_G\}}$
is the canonical projection. Essentially, we can take
$\pi _R \mathop{\colon} (V_R)^{E_n M} \to (V_R)^{\{1_G\}}$
is the canonical projection. Essentially, we can take
![]() $R=\mathbb {Z}[\Omega ]$
, where
$R=\mathbb {Z}[\Omega ]$
, where
![]() $\Omega \subset k$
is a finite subset consisting of the entries of the matrices which represent the linear maps
$\Omega \subset k$
is a finite subset consisting of the entries of the matrices which represent the linear maps
![]() $s(g)$
,
$s(g)$
,
![]() $t(g)$
for all
$t(g)$
for all
![]() $g \in M^*$
.
$g \in M^*$
.
Let us denote
![]() $S=\operatorname {\mathrm {Spec}} R$
which is a
$S=\operatorname {\mathrm {Spec}} R$
which is a
![]() $\mathbb {Z}$
-scheme of finite type. Then we infer from [Reference Phung36, Lemma 2.2] that the set of closed points of
$\mathbb {Z}$
-scheme of finite type. Then we infer from [Reference Phung36, Lemma 2.2] that the set of closed points of
![]() $V_R^{E_n}$
is given by
$V_R^{E_n}$
is given by
![]() $\Delta = \cup _{p \in \mathcal {P}, a \in S_p, d\in \mathbb {N}} H_{p,a,d}^{E_n}$
. Here,
$\Delta = \cup _{p \in \mathcal {P}, a \in S_p, d\in \mathbb {N}} H_{p,a,d}^{E_n}$
. Here,
![]() $\mathcal {P}$
denotes the set of prime numbers. By
$\mathcal {P}$
denotes the set of prime numbers. By
![]() $a \in S_p= S \otimes _{\mathbb {Z}} \mathbb {F}_p$
, we mean a is a closed point of
$a \in S_p= S \otimes _{\mathbb {Z}} \mathbb {F}_p$
, we mean a is a closed point of
![]() $S_p$
. In particular,
$S_p$
. In particular,
![]() $\kappa (a)$
is a finite field. The set
$\kappa (a)$
is a finite field. The set
![]() $H_{p,a, d}$
is defined by
$H_{p,a, d}$
is defined by
which is a finite linear subspace of the finite-dimensional
![]() $\kappa (a)$
-vector space
$\kappa (a)$
-vector space
![]() ${V_a=V_R \otimes _R \kappa (a)}$
.
${V_a=V_R \otimes _R \kappa (a)}$
.
Let us fix
![]() $p \in \mathcal {P}$
,
$p \in \mathcal {P}$
,
![]() $a \in S_p$
,
$a \in S_p$
,
![]() $d \in \mathbb {N}$
and consider the configurations of local defining maps
$d \in \mathbb {N}$
and consider the configurations of local defining maps
![]() $s_a, t_a \in \mathcal {L}(V_a^M, V_a)^G$
where for all element
$s_a, t_a \in \mathcal {L}(V_a^M, V_a)^G$
where for all element
![]() $g \in G$
, we define
$g \in G$
, we define
![]() $s_a(g) = s_R(g)\otimes _R \kappa (a)$
and
$s_a(g) = s_R(g)\otimes _R \kappa (a)$
and
![]() $t_a(g) = t_R(g)\otimes _R \kappa (a)$
. Observe that
$t_a(g) = t_R(g)\otimes _R \kappa (a)$
. Observe that
![]() $s_{a}(g)(H_{p,a,d}^M)$
and
$s_{a}(g)(H_{p,a,d}^M)$
and
![]() $t_{a}(g)(H_{p,a,d}^M)$
are subsets of
$t_{a}(g)(H_{p,a,d}^M)$
are subsets of
![]() $H_{p,a,d}$
for all
$H_{p,a,d}$
for all
![]() $g \in G$
(cf. e.g., [Reference Phung35, Lemma 3.1]). Consequently, we can define
$g \in G$
(cf. e.g., [Reference Phung35, Lemma 3.1]). Consequently, we can define
![]() $s_{p,a,d}, t_{p,a,d} \in \mathcal {L}(H_{p,a,d}^M, H_{p,a,d})$
by setting
$s_{p,a,d}, t_{p,a,d} \in \mathcal {L}(H_{p,a,d}^M, H_{p,a,d})$
by setting
![]() $s_{p,a,d} = s_a\vert _{H_{p,a,d}}$
and
$s_{p,a,d} = s_a\vert _{H_{p,a,d}}$
and
![]() $t_{p,a,d} = t_a\vert _{H_{p,a,d}}$
for all
$t_{p,a,d} = t_a\vert _{H_{p,a,d}}$
for all
![]() $g \in G$
. Thus, we obtain well-defined linear NUCA
$g \in G$
. Thus, we obtain well-defined linear NUCA
![]() $\sigma _{s_{p,a,d}}, \sigma _{t_{p,a,d}} \mathop{\colon} H_{p,a,d}^G \to H_{p,a,d}^G$
.
$\sigma _{s_{p,a,d}}, \sigma _{t_{p,a,d}} \mathop{\colon} H_{p,a,d}^G \to H_{p,a,d}^G$
.
From (8.1), it is clear from our construction that for all
![]() $g \in M^*$
, we have
$g \in M^*$
, we have
where
![]() $\pi ^{p,a,d}_{F, E} \mathop{\colon} H_{p,a,d}^F\to H_{p,a,d}^E$
denotes the canonical projection for all sets
$\pi ^{p,a,d}_{F, E} \mathop{\colon} H_{p,a,d}^F\to H_{p,a,d}^E$
denotes the canonical projection for all sets
![]() $E \subset F$
. It follows that
$E \subset F$
. It follows that
![]() $\sigma _{t_{p,a,d}}\circ \sigma _{s_{p,a,d}}=\operatorname {\mathrm {Id}}$
. In particular,
$\sigma _{t_{p,a,d}}\circ \sigma _{s_{p,a,d}}=\operatorname {\mathrm {Id}}$
. In particular,
![]() $\sigma _{s_{p,a,d}}$
is left-invertible and we deduce from Theorem 4.3 that
$\sigma _{s_{p,a,d}}$
is left-invertible and we deduce from Theorem 4.3 that
![]() $\sigma _{s_{p,a,d}}$
is stably injective. Since (i) holds by hypothesis and
$\sigma _{s_{p,a,d}}$
is stably injective. Since (i) holds by hypothesis and
![]() $H_{p,a,d}$
is a finite
$H_{p,a,d}$
is a finite
![]() $\kappa (a)$
-vector space,
$\kappa (a)$
-vector space,
![]() $\sigma _{s_{p,a,d}}$
is surjective. It follows at once that
$\sigma _{s_{p,a,d}}$
is surjective. It follows at once that
![]() ${\sigma _{s_{p,a,d}}\circ \sigma _{t_{p,a,d}}=\operatorname {\mathrm {Id}}}$
.
${\sigma _{s_{p,a,d}}\circ \sigma _{t_{p,a,d}}=\operatorname {\mathrm {Id}}}$
.
Therefore, we deduce that for every
![]() $g \in M^*$
, the equality
$g \in M^*$
, the equality
where
![]() $\pi ^R_{gM^2, \{g\}} \mathop{\colon} V_R^{gM^2} \to V_R^{\{g\}}$
, holds over the set
$\pi ^R_{gM^2, \{g\}} \mathop{\colon} V_R^{gM^2} \to V_R^{\{g\}}$
, holds over the set
![]() $\Delta = \cup _{p \in \mathcal {P}, s \in S_p, d\in \mathbb {N}} H_{p,s,d}^{gM^2}$
of all closed points of
$\Delta = \cup _{p \in \mathcal {P}, s \in S_p, d\in \mathbb {N}} H_{p,s,d}^{gM^2}$
of all closed points of
![]() $(V_R)^{gM^2}$
. Since
$(V_R)^{gM^2}$
. Since
![]() $V_R$
is a Jacobson scheme (cf., e.g., [Reference Phung35, Section 3]), an argument using the equalizer as in [Reference Ceccherini-Silberstein, Coornaert and Phung8, Lemma 7.2] shows that
$V_R$
is a Jacobson scheme (cf., e.g., [Reference Phung35, Section 3]), an argument using the equalizer as in [Reference Ceccherini-Silberstein, Coornaert and Phung8, Lemma 7.2] shows that
![]() $ f^+_{\{g\}, s_R(g)} \circ f^+_{gM, t_R \vert _{gM}} = \pi ^R_{gM^2, \{g\}} $
as R-morphisms
$ f^+_{\{g\}, s_R(g)} \circ f^+_{gM, t_R \vert _{gM}} = \pi ^R_{gM^2, \{g\}} $
as R-morphisms
![]() $V_R^{gM^2} \to V_R^{\{g\}}$
. Consequently, we obtain the relation (8.2) for all
$V_R^{gM^2} \to V_R^{\{g\}}$
. Consequently, we obtain the relation (8.2) for all
![]() $g \in M^*$
by making the base change (8.5)
$g \in M^*$
by making the base change (8.5)
![]() $\otimes _R k$
. It follows that
$\otimes _R k$
. It follows that
![]() $\sigma _s \circ \sigma _t=\operatorname {\mathrm {Id}}$
and we can finally conclude that
$\sigma _s \circ \sigma _t=\operatorname {\mathrm {Id}}$
and we can finally conclude that
![]() $\tau =\sigma _s$
is surjective. Therefore, we also have (i)
$\tau =\sigma _s$
is surjective. Therefore, we also have (i)
![]() $\implies $
(ii) and the proof is complete.
$\implies $
(ii) and the proof is complete.
9 Applications
For the proof of Theorem C, we first establish the following extension of [Reference Phung33, Theorem B] and [Reference Phung37, Theorem D] to cover the case of initially subamenable group universes and finite vector space alphabets:
Theorem 9.1 Every initially amenable group is finitely
![]() $L^1$
-surjunctive.
$L^1$
-surjunctive.
Proof Let G be an initially subamenable group, and let V be a finite vector space. Suppose that
![]() $\tau \in \mathrm {LNUCA}_c(G,V)$
is stably injective. Then we can infer without difficulty from [Reference Phung33, Theorem A] or [Reference Phung37, Theorem B] that there exist a large enough finite subset
$\tau \in \mathrm {LNUCA}_c(G,V)$
is stably injective. Then we can infer without difficulty from [Reference Phung33, Theorem A] or [Reference Phung37, Theorem B] that there exist a large enough finite subset
![]() $M \subset G$
and two configurations
$M \subset G$
and two configurations
![]() $s,t \in \mathcal {L}(V^M, V)^G$
and another configuration
$s,t \in \mathcal {L}(V^M, V)^G$
and another configuration
![]() ${c \in \mathcal {L}(V^M, V)^G}$
such that
${c \in \mathcal {L}(V^M, V)^G}$
such that
![]() $\tau = \sigma _s$
,
$\tau = \sigma _s$
,
![]() $s\vert _{G \setminus M} = t\vert _{G \setminus M} = c\vert _{G \setminus M}$
, and
$s\vert _{G \setminus M} = t\vert _{G \setminus M} = c\vert _{G \setminus M}$
, and
![]() $\sigma _t \circ \sigma _s= \operatorname {\mathrm {Id}}$
. Up to enlarging M, we can suppose without loss of generality that
$\sigma _t \circ \sigma _s= \operatorname {\mathrm {Id}}$
. Up to enlarging M, we can suppose without loss of generality that
![]() $1_G \in M$
and
$1_G \in M$
and
![]() $M=M^{-1}$
.
$M=M^{-1}$
.
If
![]() $G=M^4$
then G is finite and the theorem is trivial since every injective endomorphism of
$G=M^4$
then G is finite and the theorem is trivial since every injective endomorphism of
![]() $V^G$
is surjective. Consider the case
$V^G$
is surjective. Consider the case
![]() $M^4 \subsetneq G$
. Let
$M^4 \subsetneq G$
. Let
![]() $E \subset G$
be any finite subset which contains strictly
$E \subset G$
be any finite subset which contains strictly
![]() $M^4$
, that is,
$M^4$
, that is,
![]() $M^4 \subsetneq E$
. Since the group G is initially subamenable, we can find an amenable group H and an injective map
$M^4 \subsetneq E$
. Since the group G is initially subamenable, we can find an amenable group H and an injective map
![]() $\varphi \mathop{\colon} E \to H$
such that
$\varphi \mathop{\colon} E \to H$
such that
![]() $\varphi (gh)=\varphi (g) \varphi (h)$
for all
$\varphi (gh)=\varphi (g) \varphi (h)$
for all
![]() $g,h \in E$
such that
$g,h \in E$
such that
![]() $gh \in E$
. In particular,
$gh \in E$
. In particular,
![]() $\varphi (gh)=\varphi (g) \varphi (h)$
for all
$\varphi (gh)=\varphi (g) \varphi (h)$
for all
![]() $g,h \in M$
. Since
$g,h \in M$
. Since
![]() $M=M^{-1}$
and
$M=M^{-1}$
and
![]() $1_G \in M$
, we deduce that
$1_G \in M$
, we deduce that
![]() $1_H \in \varphi (M)$
and
$1_H \in \varphi (M)$
and
![]() $\varphi (M)=\varphi (M)^{-1}$
.
$\varphi (M)=\varphi (M)^{-1}$
.
Up to replacing H by the subgroup generated by
![]() $\varphi (E)$
, we can suppose that H is generated by
$\varphi (E)$
, we can suppose that H is generated by
![]() $\varphi (E)$
. As
$\varphi (E)$
. As
![]() $\sigma _t \circ \sigma _s= \operatorname {\mathrm {Id}}$
, we deduce for all
$\sigma _t \circ \sigma _s= \operatorname {\mathrm {Id}}$
, we deduce for all
![]() $g \in E$
that
$g \in E$
that
where we denote by
![]() $\pi _{F, Q} \mathop{\colon} V^F\to V^Q$
the canonical linear projection for all sets
$\pi _{F, Q} \mathop{\colon} V^F\to V^Q$
the canonical linear projection for all sets
![]() ${Q \subset F}$
. The bijection
${Q \subset F}$
. The bijection
![]() $\varphi \vert _E \mathop{\colon} E \to \varphi (E)$
induces, in particular, an isomorphism
$\varphi \vert _E \mathop{\colon} E \to \varphi (E)$
induces, in particular, an isomorphism
![]() $\phi \mathop{\colon} V^{\varphi (M)} \to V^M$
. Let us fix
$\phi \mathop{\colon} V^{\varphi (M)} \to V^M$
. Let us fix
![]() $g_0 \in E \setminus M$
. The patterns
$g_0 \in E \setminus M$
. The patterns
![]() $s\vert _{E}$
,
$s\vert _{E}$
,
![]() $t\vert _E$
in turn induce the configurations
$t\vert _E$
in turn induce the configurations
![]() $\tilde {s}, \tilde {t}\in \mathcal {L}(V^{\varphi (M)}, V)^H$
defined by
$\tilde {s}, \tilde {t}\in \mathcal {L}(V^{\varphi (M)}, V)^H$
defined by
![]() $\tilde {s}(h) = s(h) \circ \phi $
,
$\tilde {s}(h) = s(h) \circ \phi $
,
![]() $\tilde {t}(h) = t(h) \circ \phi $
for all
$\tilde {t}(h) = t(h) \circ \phi $
for all
![]() $h \in \varphi (E)$
and
$h \in \varphi (E)$
and
![]() $\tilde {s}(h) = s(g_0) \circ \phi $
,
$\tilde {s}(h) = s(g_0) \circ \phi $
,
![]() $\tilde {t}(h) = t(g_0) \circ \phi $
for all
$\tilde {t}(h) = t(g_0) \circ \phi $
for all
![]() $h \in H \setminus \varphi (E)$
.
$h \in H \setminus \varphi (E)$
.
Since
![]() $\varphi $
is injective, it follows from (9.1) that for all
$\varphi $
is injective, it follows from (9.1) that for all
![]() $h \in \varphi (E)$
, we have
$h \in \varphi (E)$
, we have
Consequently, we deduce that
![]() $\sigma _{\tilde {t}}\circ \sigma _{\tilde {s}}=\operatorname {\mathrm {Id}}$
. In particular,
$\sigma _{\tilde {t}}\circ \sigma _{\tilde {s}}=\operatorname {\mathrm {Id}}$
. In particular,
![]() $\sigma _{\tilde {s}}$
is injective. Since H is amenable and
$\sigma _{\tilde {s}}$
is injective. Since H is amenable and
![]() $\tilde {s}$
is asymptotically constant by construction, we infer from [Reference Phung33, Theorem B(i)] that
$\tilde {s}$
is asymptotically constant by construction, we infer from [Reference Phung33, Theorem B(i)] that
![]() $\tilde {s}$
is surjective. Hence, it follows from
$\tilde {s}$
is surjective. Hence, it follows from
![]() $\sigma _{\tilde {t}}\circ \sigma _{\tilde {s}}=\operatorname {\mathrm {Id}}$
that
$\sigma _{\tilde {t}}\circ \sigma _{\tilde {s}}=\operatorname {\mathrm {Id}}$
that
![]() $\sigma _{\tilde {s}}\circ \sigma _{\tilde {t}}=\operatorname {\mathrm {Id}}$
. We deduce that for every
$\sigma _{\tilde {s}}\circ \sigma _{\tilde {t}}=\operatorname {\mathrm {Id}}$
. We deduce that for every
![]() $h \in \varphi (E)$
, we have
$h \in \varphi (E)$
, we have
Therefore, via the injection
![]() $\varphi $
, we obtain for all
$\varphi $
, we obtain for all
![]() $g \in E$
that
$g \in E$
that
By the choice of E and
![]() $\varphi $
, we can thus conclude that
$\varphi $
, we can thus conclude that
![]() $\sigma _s \circ \sigma _t= \operatorname {\mathrm {Id}}$
which implies in particular that
$\sigma _s \circ \sigma _t= \operatorname {\mathrm {Id}}$
which implies in particular that
![]() $\sigma _s$
is surjective. The proof is thus complete.
$\sigma _s$
is surjective. The proof is thus complete.
Observe that by a similar argument, [Reference Phung33, Theorem B(i)] also holds for initially subamenable group universes. As an immediate consequence of Theorems B and 9.1, we obtain the proof of Theorem C in the Introduction as follows:
Proof of Theorem C
Thanks to Theorem B, we infer, respectively, from Theorem 9.1 and [Reference Phung33, Theorem B(ii)] that all initially amenable groups and all residually finite groups are
![]() $L^1$
-surjunctive. We can thus conclude the proof of the theorem since dual
$L^1$
-surjunctive. We can thus conclude the proof of the theorem since dual
![]() $L^1$
-surjunctivity is equivalent to
$L^1$
-surjunctivity is equivalent to
![]() $L^1$
-surjunctivity also by Theorem B.
$L^1$
-surjunctivity also by Theorem B.
Acknowledgment
We would like to express our deep gratitude to the anonymous reviewers for the careful reading of our manuscript and for their numerous insightful comments and suggestions.