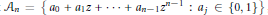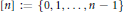Let ${{A}_{n}}\,=\,\{{{a}_{0}}+{{a}_{1}}z+\,.\,.\,.\,+\,{{a}_{n-1}}{{z}^{n-1}}\,:\,{{a}_{j}}\,\in \,\{0,1\}\}$ , whose elements are called zero-one polynomials and correspond naturally to the ${{2}^{n}}$ subsets of $\left[ n \right]\,:=\,\{0,\,1,\,.\,.\,.\,,\,n-1\}$ . We also let 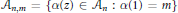${{A}_{n,m\,}}\,=\,\{\alpha \left( z \right)\,\in \,{{A}_{n}}\,:\,\alpha \left( 1 \right)\,=\,m\}$ , whose elements correspond to the 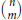$\left( _{m}^{n} \right)$ subsets of $\left[ n \right]$ of size 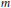$m$ , and let 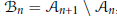${{B}_{n}}\,=\,{{A}_{n+1}}\,\backslash \,{{A}_{n}}$ , whose elements are the zero-one polynomials of degree exactly $n$ .

Many researchers have studied norms of polynomials with restricted coefficients. Using 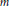$\|\alpha {{\|}_{p}}$ to denote the usual 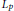${{L}_{p}}$ norm of $\alpha$ on the unit circle, one easily sees that 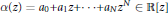$\alpha \left( z \right)\,=\,{{a}_{0}}+{{a}_{1}}z+.\,.\,.+{{a}_{N}}{{z}^{N}}\,\in \,\mathbb{R}\left[ z \right]$ satisfies 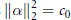$\|\alpha \|_{2}^{2}\,=\,{{c}_{0}}$ and 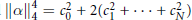$\|\alpha \|_{4}^{4}\,=\,c_{0}^{2}\,+\,2\left( c_{1}^{2}\,+\,.\,.\,.\,+\,c_{N}^{2} \right)$ , where ${{c}_{k}}\,:=\,\sum _{j=0}^{N-k}\,{{a}_{j}}{{a}_{j+k}}\,\text{for}\,\text{0}\le \,\text{k}\,\le N$ .

If 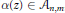$\alpha \left( z \right)\,\in \,{{A}_{n,m}}$ , say $\alpha \left( z \right)\,=\,{{z}^{{{\text{ }\!\!\beta\!\!\text{ }}_{1}}}}\,+\,.\,.\,.\,+\,{{z}^{{{\text{ }\!\!\beta\!\!\text{ }}_{m}}}}$ where 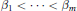${{\beta }_{1}}\,<\,.\,.\,.\,<\,{{\beta }_{m}}$ , then 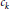${{c}_{k}}$ is the number of times $k$ appears as a difference 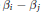${{\beta }_{i}}\,-\,{{\beta }_{j}}$ . The condition that 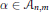$\alpha \,\in \,{{A}_{n,m}}$ satisfies 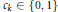${{c}_{k}}\,\in \,\{0,1\}$ for 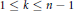$1\,\le \,k\,\le \,n\,-\,1$ is thus equivalent to the condition that 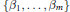$\{{{\beta }_{1}},\,.\,.\,.\,,\,{{\beta }_{m}}\}$ is a Sidon set (meaning all differences of pairs of elements are distinct).

In this paper, we find the average of 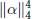$\left\| \alpha\right\|_{4}^{4}$ over 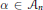$\alpha \,\in \,{{A}_{n}}$ , 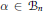$\alpha \,\in \,{{B}_{n}}$ and $\alpha \,\in \,{{A}_{n,m}}$ . We further show that our expression for the average of 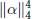$\left\| \alpha\right\|_{4}^{4}$ over 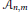${{A}_{n,m}}$ yields a new proof of the known result: if 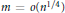$m\,=\,o\left( {{n}^{1/4}} \right)$ and 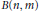$B\left( n,\,m \right)$ denotes the number of Sidon sets of size 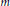$m$ in $\left[ n \right]$ , then almost all subsets of $\left[ n \right]$ of size 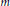$m$ are Sidon, in the sense that 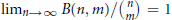${{\lim }_{n\to \infty }}\,B\left( n,\,m \right)/\left( _{m}^{n} \right)\,=\,1$ .