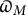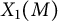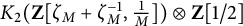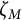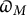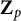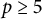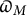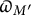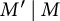1 Introduction and notation
Sharifi [Reference Sharifi8] has constructed a beautiful and explicit map (1.1) between modular symbols and a cyclotomic K-group. This map is conjecturally annihilated by a certain Eisenstein ideal. This conjecture, despite its apparent simplicity, turns out to be highly nontrivial and has led to much work in recent years, in particular by Fukaya and Kato [Reference Fukaya and Kazuya4] and more recently by Sharifi and Venkatesh [Reference Sharifi and Venkatesh9].
This paper is devoted to the study of certain norm relations satisfied by Sharifi’s map. This aspect has been studied before by Fukaya–Kato and Scott [Reference Williams11]. Their results are, however, quite restrictive (cf. Remark 1.5 for a detailed comparison between their results and ours). We use the techniques developed by Sharifi and Venkatesh to remove most of these restrictions.
Our main motivation is to apply the results of the present note to obtain results toward the Birch and Swinnerton–Dyer conjecture in the “Eisenstein” case [Reference Lecouturier and Wang6]. We now set up some notation and describe our results in details.
1.1 Homology of modular curves and Hecke operators
Let
![]() $M\geq 4$
be an integer. Let
$M\geq 4$
be an integer. Let
 $$ \begin{align*}\Gamma_1(M) = \left\{\begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \operatorname{\mathrm{SL}}_2(\operatorname{\mathrm{\mathbf{Z}}}) \text{ such that } a-1 \equiv c \equiv 0 \text{ (modulo } M\text{)}\right\},\end{align*} $$
$$ \begin{align*}\Gamma_1(M) = \left\{\begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \operatorname{\mathrm{SL}}_2(\operatorname{\mathrm{\mathbf{Z}}}) \text{ such that } a-1 \equiv c \equiv 0 \text{ (modulo } M\text{)}\right\},\end{align*} $$
and denote by
![]() $X_1(M)$
the compact modular curve (over
$X_1(M)$
the compact modular curve (over
![]() $\operatorname {\mathrm {\mathbf {C}}}$
) of level
$\operatorname {\mathrm {\mathbf {C}}}$
) of level
![]() $\Gamma _1(M)$
. Let
$\Gamma _1(M)$
. Let
be the set of cusps of
![]() $X_1(M)$
, and let
$X_1(M)$
, and let
![]() $C_M^0$
be those cusps in
$C_M^0$
be those cusps in
![]() $C_M$
of the form
$C_M$
of the form
![]() $\Gamma _1(M) \cdot \frac {a}{b}$
with
$\Gamma _1(M) \cdot \frac {a}{b}$
with
![]() $\gcd (a,b)=1$
and
$\gcd (a,b)=1$
and
![]() $a \not \equiv 0 \text { (modulo } M \text {)}$
(in the case
$a \not \equiv 0 \text { (modulo } M \text {)}$
(in the case
![]() $b=0$
, we have the cusp
$b=0$
, we have the cusp
![]() ${\Gamma _1(M)\cdot \infty }$
).
${\Gamma _1(M)\cdot \infty }$
).
Let
![]() $H_1(X_1(M), C_M, \operatorname {\mathrm {\mathbf {Z}}})$
be the singular homology of
$H_1(X_1(M), C_M, \operatorname {\mathrm {\mathbf {Z}}})$
be the singular homology of
![]() $X_1(M)$
relative to
$X_1(M)$
relative to
![]() $C_M$
. If
$C_M$
. If
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are in
$\beta $
are in
![]() $\mathbb {P}^1(\operatorname {\mathrm {\mathbf {Q}}})$
, let
$\mathbb {P}^1(\operatorname {\mathrm {\mathbf {Q}}})$
, let
be the class of the hyperbolic geodesic from
![]() $\alpha $
to
$\alpha $
to
![]() $\beta $
in
$\beta $
in
![]() $X_1(M)$
. The group
$X_1(M)$
. The group
![]() $H_1(X_1(M), C_M, \operatorname {\mathrm {\mathbf {Z}}})$
carries an action of various Hecke operators, which we now recall.
$H_1(X_1(M), C_M, \operatorname {\mathrm {\mathbf {Z}}})$
carries an action of various Hecke operators, which we now recall.
If
![]() $\ell $
is a prime number, the
$\ell $
is a prime number, the
![]() $\ell $
th Hecke operator
$\ell $
th Hecke operator
![]() $T_{\ell }$
is the double coset operator
$T_{\ell }$
is the double coset operator
 $\Gamma _1(M) \begin {pmatrix} 1 & 0 \\ 0 & \ell \end {pmatrix} \Gamma _1(M)$
. As usual, we denote
$\Gamma _1(M) \begin {pmatrix} 1 & 0 \\ 0 & \ell \end {pmatrix} \Gamma _1(M)$
. As usual, we denote
![]() $T_{\ell }$
by
$T_{\ell }$
by
![]() $U_{\ell }$
is
$U_{\ell }$
is
![]() $\ell $
divides M. The Atkin–Lehner involution
$\ell $
divides M. The Atkin–Lehner involution
![]() $W_M$
is the involution of
$W_M$
is the involution of
![]() $H_1(X_1(M), C_M, \operatorname {\mathrm {\mathbf {Z}}})$
induced by the map
$H_1(X_1(M), C_M, \operatorname {\mathrm {\mathbf {Z}}})$
induced by the map
![]() $z \mapsto -\frac {1}{Mz}$
of the upper half-plane.
$z \mapsto -\frac {1}{Mz}$
of the upper half-plane.
For any
![]() $x \in (\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }$
, we denote by
$x \in (\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }$
, we denote by
![]() $\langle x \rangle $
the corresponding diamond operator, which is the automorphism of
$\langle x \rangle $
the corresponding diamond operator, which is the automorphism of
![]() $X_1(M)$
induced by the action of any matrix
$X_1(M)$
induced by the action of any matrix
 $\begin {pmatrix} a & b \\ c & d \end {pmatrix} \in \Gamma _0(M)$
such that
$\begin {pmatrix} a & b \\ c & d \end {pmatrix} \in \Gamma _0(M)$
such that
This gives by functoriality an action of
![]() $(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
on
$(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
on
![]() $H_1(X_1(M), C_M, \operatorname {\mathrm {\mathbf {Z}}})$
. Note that diamond operators act on the set of cusps
$H_1(X_1(M), C_M, \operatorname {\mathrm {\mathbf {Z}}})$
. Note that diamond operators act on the set of cusps
![]() $C_M$
and that this action preserves
$C_M$
and that this action preserves
![]() $C_M^0$
. We say that two cusps c and
$C_M^0$
. We say that two cusps c and
![]() $c'$
are in the same diamond orbit if there exists
$c'$
are in the same diamond orbit if there exists
![]() $x \in (\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }$
such that
$x \in (\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }$
such that
![]() $\langle x \rangle \cdot c = c'$
.
$\langle x \rangle \cdot c = c'$
.
There are also dual Hecke operators: if T is one of the operators defined above, we let
![]() $T^* = W_M^{-1} T W_M$
. As is well known (cf. [Reference Diamond and Shurman1, Theorem 5.5.3]), we have
$T^* = W_M^{-1} T W_M$
. As is well known (cf. [Reference Diamond and Shurman1, Theorem 5.5.3]), we have
![]() $\langle x \rangle ^* = \langle x \rangle ^{-1}$
(for all
$\langle x \rangle ^* = \langle x \rangle ^{-1}$
(for all
![]() $x \in (\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }$
) and
$x \in (\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }$
) and
![]() $T_{\ell }^* = \langle \ell \rangle ^{-1} T_{\ell }$
(for all primes
$T_{\ell }^* = \langle \ell \rangle ^{-1} T_{\ell }$
(for all primes
![]() $\ell \nmid M$
).
$\ell \nmid M$
).
1.2 (Dual) Manin symbols
Let
![]() $\xi _M : \operatorname {\mathrm {\mathbf {Z}}}[\Gamma _1(M) \backslash \operatorname {\mathrm {SL}}_2(\operatorname {\mathrm {\mathbf {Z}}})] \rightarrow H_1(X_1(M), C_M, \operatorname {\mathrm {\mathbf {Z}}})$
be the (modified) Manin map: it sends a coset
$\xi _M : \operatorname {\mathrm {\mathbf {Z}}}[\Gamma _1(M) \backslash \operatorname {\mathrm {SL}}_2(\operatorname {\mathrm {\mathbf {Z}}})] \rightarrow H_1(X_1(M), C_M, \operatorname {\mathrm {\mathbf {Z}}})$
be the (modified) Manin map: it sends a coset
 $\Gamma _1(M) \cdot \begin {pmatrix} a & b \\ c & d \end {pmatrix}$
to
$\Gamma _1(M) \cdot \begin {pmatrix} a & b \\ c & d \end {pmatrix}$
to
![]() $\{-\frac {d}{Mb}, -\frac {c}{Ma}\}$
(it is the usual Manin map sending
$\{-\frac {d}{Mb}, -\frac {c}{Ma}\}$
(it is the usual Manin map sending
 $\Gamma _1(M) \cdot \begin {pmatrix} a & b \\ c & d \end {pmatrix}$
to
$\Gamma _1(M) \cdot \begin {pmatrix} a & b \\ c & d \end {pmatrix}$
to
![]() $\{\frac {b}{d}, \frac {a}{c}\}$
composed with the Atkin–Lehner involution
$\{\frac {b}{d}, \frac {a}{c}\}$
composed with the Atkin–Lehner involution
![]() $W_M$
). Manin showed that
$W_M$
). Manin showed that
![]() $W_M \circ \xi _M$
is surjective, and therefore
$W_M \circ \xi _M$
is surjective, and therefore
![]() $\xi _M$
is surjective (cf. [Reference Manin7, Section 1.6]).
$\xi _M$
is surjective (cf. [Reference Manin7, Section 1.6]).
Let
![]() $S_M^0 \subset \Gamma _1(M) \backslash \operatorname {\mathrm {SL}}_2(\operatorname {\mathrm {\mathbf {Z}}})$
be the subset consisting of
$S_M^0 \subset \Gamma _1(M) \backslash \operatorname {\mathrm {SL}}_2(\operatorname {\mathrm {\mathbf {Z}}})$
be the subset consisting of
 $\Gamma _1(M) \cdot \begin {pmatrix} a & b \\ c & d \end {pmatrix}$
with
$\Gamma _1(M) \cdot \begin {pmatrix} a & b \\ c & d \end {pmatrix}$
with
![]() $M \nmid c$
and
$M \nmid c$
and
![]() $M \nmid d$
. The restriction
$M \nmid d$
. The restriction
is surjective (cf. [Reference Fukaya, Kato and Sharifi3, Section 2.1.3]).
1.3 Algebraic K-theory and motivic cohomology
Fix an algebraic closure
![]() $\overline {\operatorname {\mathrm {\mathbf {Q}}}}$
of
$\overline {\operatorname {\mathrm {\mathbf {Q}}}}$
of
![]() $\operatorname {\mathrm {\mathbf {Q}}}$
. For any integer
$\operatorname {\mathrm {\mathbf {Q}}}$
. For any integer
![]() $M \geq 4$
, choose a primitive Mth root of unity
$M \geq 4$
, choose a primitive Mth root of unity
![]() $\zeta _M \in \overline {\operatorname {\mathrm {\mathbf {Q}}}}$
such that for all
$\zeta _M \in \overline {\operatorname {\mathrm {\mathbf {Q}}}}$
such that for all
![]() $M' \mid M$
, we have
$M' \mid M$
, we have
![]() $\zeta _{M'} = \zeta _M^{M/M'}$
.
$\zeta _{M'} = \zeta _M^{M/M'}$
.
We have a canonical group isomorphism
sending
![]() $a \in (\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }$
to the Galois automorphism characterized by
$a \in (\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }$
to the Galois automorphism characterized by
![]() $\zeta _M \mapsto \zeta _M^a$
. The complex conjugation of
$\zeta _M \mapsto \zeta _M^a$
. The complex conjugation of
![]() $ \operatorname {\mathrm {Gal}}(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _M)/\operatorname {\mathrm {\mathbf {Q}}})$
corresponds to the class of
$ \operatorname {\mathrm {Gal}}(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _M)/\operatorname {\mathrm {\mathbf {Q}}})$
corresponds to the class of
![]() $-1$
in
$-1$
in
![]() $(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }$
under that isomorphism.
$(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }$
under that isomorphism.
If A is a commutative ring, let
![]() $K_2(A)$
be the second K-group of A, as defined by Quillen. For any
$K_2(A)$
be the second K-group of A, as defined by Quillen. For any
![]() $x,y \in A^{\times }$
, there is an element
$x,y \in A^{\times }$
, there is an element
![]() $\{ x, y \}$
of
$\{ x, y \}$
of
![]() $K_2(A)$
, called the Steinberg symbol of x and y. It is bilinear in x and y and has the property that if
$K_2(A)$
, called the Steinberg symbol of x and y. It is bilinear in x and y and has the property that if
![]() $x+y=1$
, then
$x+y=1$
, then
![]() $\{ x, y \} = 1$
.
$\{ x, y \} = 1$
.
There is an action of
![]() $\operatorname {\mathrm {Gal}}(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _M)/\operatorname {\mathrm {\mathbf {Q}}})$
(and in particular of the complex conjugation) on
$\operatorname {\mathrm {Gal}}(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _M)/\operatorname {\mathrm {\mathbf {Q}}})$
(and in particular of the complex conjugation) on
![]() $K_2(\operatorname {\mathrm {\mathbf {Z}}}[\zeta _M, \frac {1}{M}])$
. We denote by
$K_2(\operatorname {\mathrm {\mathbf {Z}}}[\zeta _M, \frac {1}{M}])$
. We denote by
![]() $\mathcal {K}_M$
the largest quotient of
$\mathcal {K}_M$
the largest quotient of
![]() $K_2(\operatorname {\mathrm {\mathbf {Z}}}[\zeta _M, \frac {1}{M}]) \otimes \operatorname {\mathrm {\mathbf {Z}}}[\frac {1}{2}]$
on which the complex conjugation acts trivially. Note that
$K_2(\operatorname {\mathrm {\mathbf {Z}}}[\zeta _M, \frac {1}{M}]) \otimes \operatorname {\mathrm {\mathbf {Z}}}[\frac {1}{2}]$
on which the complex conjugation acts trivially. Note that
![]() $\mathcal {K}_M$
is a
$\mathcal {K}_M$
is a
![]() $(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
-module.
$(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
-module.
1.4 Sharifi’s
 $\varpi _M$
map and summary of known results
$\varpi _M$
map and summary of known results
The map
![]() $\operatorname {\mathrm {\mathbf {Z}}}[S_M^0] \rightarrow \mathcal {K}_M$
given by
$\operatorname {\mathrm {\mathbf {Z}}}[S_M^0] \rightarrow \mathcal {K}_M$
given by
 $$ \begin{align*}\Gamma_1(M) \cdot \begin{pmatrix} a & b \\ c & d \end{pmatrix} \mapsto \{ 1 - \zeta_M^c, 1-\zeta_M^d \}\end{align*} $$
$$ \begin{align*}\Gamma_1(M) \cdot \begin{pmatrix} a & b \\ c & d \end{pmatrix} \mapsto \{ 1 - \zeta_M^c, 1-\zeta_M^d \}\end{align*} $$
factors through
![]() $\xi _M^0$
(cf. [Reference Fukaya, Kato and Sharifi3, Section 2.1.4]), and thus induces a map
$\xi _M^0$
(cf. [Reference Fukaya, Kato and Sharifi3, Section 2.1.4]), and thus induces a map
Let us note that our map
![]() $\varpi _M$
is, in the notation of [Reference Sharifi and Venkatesh9, Proposition 4.3.2], equal to
$\varpi _M$
is, in the notation of [Reference Sharifi and Venkatesh9, Proposition 4.3.2], equal to
![]() $\Pi _M^{\circ }\circ W_M$
. Sharifi made the following conjecture.
$\Pi _M^{\circ }\circ W_M$
. Sharifi made the following conjecture.
Conjecture 1.1 (Sharifi)
The restriction of
![]() $\varpi _M$
to
$\varpi _M$
to
![]() $H_1(X_0(M), \operatorname {\mathrm {\mathbf {Z}}})$
is annihilated by the Hecke operators
$H_1(X_0(M), \operatorname {\mathrm {\mathbf {Z}}})$
is annihilated by the Hecke operators
![]() $T_{\ell }-\ell \langle \ell \rangle - 1$
for primes
$T_{\ell }-\ell \langle \ell \rangle - 1$
for primes
![]() $\ell $
not dividing M and by the Hecke operators
$\ell $
not dividing M and by the Hecke operators
![]() $U_{\ell }-1$
for primes
$U_{\ell }-1$
for primes
![]() $\ell \mid M$
.
$\ell \mid M$
.
This is equivalent to [Reference Sharifi and Venkatesh9, Conjecture 4.3.5(a)], where the authors use dual Hecke operators but use
![]() $\Pi _M^{\circ } = \varpi _M \circ W_M$
instead of
$\Pi _M^{\circ } = \varpi _M \circ W_M$
instead of
![]() $\varpi _M$
. As Sharifi and Venkatesh mention right after [Reference Sharifi and Venkatesh9, Theorem 4.3.6], it is expected that the conjecture holds without restricting
$\varpi _M$
. As Sharifi and Venkatesh mention right after [Reference Sharifi and Venkatesh9, Theorem 4.3.6], it is expected that the conjecture holds without restricting
![]() $\varpi _M$
to
$\varpi _M$
to
![]() $H_1(X_0(M), \operatorname {\mathrm {\mathbf {Z}}})$
.
$H_1(X_0(M), \operatorname {\mathrm {\mathbf {Z}}})$
.
This conjecture has a history of partial results: [Reference Fukaya and Kazuya4, Reference Lecouturier and Wang5] and most recently [Reference Sharifi and Venkatesh9]. Let us recall the main results of Sharifi–Venkatesh and Fukaya–Kato on this conjecture.
Theorem 1.2 (Sharifi–Venkatesh)
The restriction of
![]() $\varpi _M$
to
$\varpi _M$
to
![]() $H_1(X_0(M), \operatorname {\mathrm {\mathbf {Z}}})$
is annihilated by the Hecke operators
$H_1(X_0(M), \operatorname {\mathrm {\mathbf {Z}}})$
is annihilated by the Hecke operators
![]() $T_{\ell }-\ell \langle \ell \rangle - 1$
for primes
$T_{\ell }-\ell \langle \ell \rangle - 1$
for primes
![]() $\ell $
not dividing M.
$\ell $
not dividing M.
This follows from [Reference Sharifi and Venkatesh9, Theorem 4.3.7]. Therefore, to prove Conjecture 1.1, it only remains to consider the Hecke operators
![]() $U_{\ell }-1$
for primes
$U_{\ell }-1$
for primes
![]() $\ell \mid M$
. Fukaya–Kato do get a result including
$\ell \mid M$
. Fukaya–Kato do get a result including
![]() $U_{\ell }-1$
, but they have to tensor with
$U_{\ell }-1$
, but they have to tensor with
![]() $\operatorname {\mathrm {\mathbf {Z}}}_p$
where
$\operatorname {\mathrm {\mathbf {Z}}}_p$
where
![]() $p\geq 5$
is a prime dividing M.
$p\geq 5$
is a prime dividing M.
Theorem 1.3 (Fukaya–Kato)
Let
![]() $p\geq 5$
be a prime dividing M. The map
$p\geq 5$
be a prime dividing M. The map
is annihilated by the Hecke operators
![]() $T_{\ell }-\ell \langle \ell \rangle - 1$
for primes
$T_{\ell }-\ell \langle \ell \rangle - 1$
for primes
![]() $\ell $
not dividing M and by the Hecke operators
$\ell $
not dividing M and by the Hecke operators
![]() $U_{\ell }-1$
for primes
$U_{\ell }-1$
for primes
![]() $\ell \mid M$
.
$\ell \mid M$
.
We refer to [Reference Fukaya and Kazuya4, Theorem 5.2.3(1)] for this result. Let us note that Fukaya and Kato actually consider (the p-ordinary part of)
![]() $H^1(Y_1(M), \operatorname {\mathrm {\mathbf {Z}}}_p)$
instead of
$H^1(Y_1(M), \operatorname {\mathrm {\mathbf {Z}}}_p)$
instead of
![]() $H_1(X_1(M), C_M, \operatorname {\mathrm {\mathbf {Z}}}_p)$
. These two groups are canonically isomorphic, but the isomorphism transfers dual Hecke operators (i.e.,
$H_1(X_1(M), C_M, \operatorname {\mathrm {\mathbf {Z}}}_p)$
. These two groups are canonically isomorphic, but the isomorphism transfers dual Hecke operators (i.e.,
![]() $T_{\ell }^*$
,
$T_{\ell }^*$
,
![]() $U_{\ell }^*$
or
$U_{\ell }^*$
or
![]() $\langle x \rangle ^{-1}$
) to usual Hecke operators (i.e.,
$\langle x \rangle ^{-1}$
) to usual Hecke operators (i.e.,
![]() $T_{\ell }$
,
$T_{\ell }$
,
![]() $U_{\ell }$
or
$U_{\ell }$
or
![]() $\langle x \rangle $
).
$\langle x \rangle $
).
1.5 Our main results
Another important aspect of Sharifi’s theory is the way in which the maps
![]() $\varpi _M$
relate with each other when varying M. This has been studied under some assumptions in [Reference Fukaya and Kazuya4, Reference Williams11]. If p is a prime, there are two degeneracy maps
$\varpi _M$
relate with each other when varying M. This has been studied under some assumptions in [Reference Fukaya and Kazuya4, Reference Williams11]. If p is a prime, there are two degeneracy maps
![]() $\pi _1, \pi _2 : X_1(Mp) \rightarrow X_1(M)$
given on the upper half-plane by
$\pi _1, \pi _2 : X_1(Mp) \rightarrow X_1(M)$
given on the upper half-plane by
![]() $\pi _1 : z\mapsto z$
and
$\pi _1 : z\mapsto z$
and
![]() $\pi _2 : z \mapsto pz$
. On the K-side, there is a norm map
$\pi _2 : z \mapsto pz$
. On the K-side, there is a norm map
![]() $\operatorname {\mathrm {Norm}} : \mathcal {K}_{Mp} \rightarrow \mathcal {K}_M$
. Our main result is the following.
$\operatorname {\mathrm {Norm}} : \mathcal {K}_{Mp} \rightarrow \mathcal {K}_M$
. Our main result is the following.
Theorem 1.4 Let
![]() $p\geq 2$
be a prime number, and let
$p\geq 2$
be a prime number, and let
![]() $M \geq 4$
. Let
$M \geq 4$
. Let
![]() $C \subset C_{Mp}^0$
be a subset of cusps which are all in the same orbit under the action of
$C \subset C_{Mp}^0$
be a subset of cusps which are all in the same orbit under the action of
![]() $\operatorname {\mathrm {Ker}}((\operatorname {\mathrm {\mathbf {Z}}}/Mp\operatorname {\mathrm {\mathbf {Z}}})^{\times } \rightarrow (\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times })$
(the action being given by diamond operators as recalled above).
$\operatorname {\mathrm {Ker}}((\operatorname {\mathrm {\mathbf {Z}}}/Mp\operatorname {\mathrm {\mathbf {Z}}})^{\times } \rightarrow (\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times })$
(the action being given by diamond operators as recalled above).
-
(i) Assume that p divides M. We have a commutative diagram

-
(ii) Assume that p does not divide M. We have a commutative diagram

Here,
 $\langle p \rangle $
is the pth diamond operator, induced by the action of a matrix
$\langle p \rangle $
is the pth diamond operator, induced by the action of a matrix
 $\begin {pmatrix} a & b \\ c & d \end {pmatrix} \in \Gamma _0(M)$
with
$\begin {pmatrix} a & b \\ c & d \end {pmatrix} \in \Gamma _0(M)$
with
 $d \equiv p \text { (modulo }M\text {)}$
on
$d \equiv p \text { (modulo }M\text {)}$
on
 $X_1(M)$
.
$X_1(M)$
.
Remark 1.5
-
(i) Theorem 1.4(i) has been proved by Fukaya and Kato in [Reference Fukaya and Kazuya4, Theorem 5.2.3(2)] after tensoring by
 $\operatorname {\mathrm {\mathbf {Z}}}_p$
for
$\operatorname {\mathrm {\mathbf {Z}}}_p$
for
 $p\geq 5$
. They use
$p\geq 5$
. They use
 $H^2(G_{\operatorname {\mathrm {\mathbf {Q}}}(\zeta _M)}, \operatorname {\mathrm {\mathbf {Z}}}_p(2))$
instead of
$H^2(G_{\operatorname {\mathrm {\mathbf {Q}}}(\zeta _M)}, \operatorname {\mathrm {\mathbf {Z}}}_p(2))$
instead of
 $\mathcal {K}_M \otimes \operatorname {\mathrm {\mathbf {Z}}}_p$
. The étale Chern class map (cf. [Reference Tate10]) provides an isomorphism
$\mathcal {K}_M \otimes \operatorname {\mathrm {\mathbf {Z}}}_p$
. The étale Chern class map (cf. [Reference Tate10]) provides an isomorphism  $$ \begin{align*}K_2\left(\operatorname{\mathrm{\mathbf{Z}}}\left[\zeta_M, \frac{1}{M}\right]\right) \otimes \operatorname{\mathrm{\mathbf{Z}}}_p \simeq H^2_{\text{\'et}}\left(\operatorname{\mathrm{\mathbf{Z}}}\left[\zeta_M, \frac{1}{M}\right], \operatorname{\mathrm{\mathbf{Z}}}_p(2)\right) \text{ .}\end{align*} $$
$$ \begin{align*}K_2\left(\operatorname{\mathrm{\mathbf{Z}}}\left[\zeta_M, \frac{1}{M}\right]\right) \otimes \operatorname{\mathrm{\mathbf{Z}}}_p \simeq H^2_{\text{\'et}}\left(\operatorname{\mathrm{\mathbf{Z}}}\left[\zeta_M, \frac{1}{M}\right], \operatorname{\mathrm{\mathbf{Z}}}_p(2)\right) \text{ .}\end{align*} $$
Since
 $H^2_{\mathrm {\'et}}(\operatorname {\mathrm {\mathbf {Z}}}[\zeta _M, \frac {1}{M}], \operatorname {\mathrm {\mathbf {Z}}}_p(2))$
is a subgroup
$H^2_{\mathrm {\'et}}(\operatorname {\mathrm {\mathbf {Z}}}[\zeta _M, \frac {1}{M}], \operatorname {\mathrm {\mathbf {Z}}}_p(2))$
is a subgroup
 $H^2(G_{\operatorname {\mathrm {\mathbf {Q}}}(\zeta _M)}, \operatorname {\mathrm {\mathbf {Z}}}_p(2))$
and
$H^2(G_{\operatorname {\mathrm {\mathbf {Q}}}(\zeta _M)}, \operatorname {\mathrm {\mathbf {Z}}}_p(2))$
and
 $\mathcal {K}_M$
is identified with the fixed part by the complex conjugation in
$\mathcal {K}_M$
is identified with the fixed part by the complex conjugation in
 $K_2(\operatorname {\mathrm {\mathbf {Z}}}[\zeta _M, \frac {1}{M}]) \otimes \operatorname {\mathrm {\mathbf {Z}}}_p$
, we get a canonical embedding
$K_2(\operatorname {\mathrm {\mathbf {Z}}}[\zeta _M, \frac {1}{M}]) \otimes \operatorname {\mathrm {\mathbf {Z}}}_p$
, we get a canonical embedding  $$ \begin{align*}\mathcal{K}_M \otimes \operatorname{\mathrm{\mathbf{Z}}}_p \hookrightarrow H^2(G_{\operatorname{\mathrm{\mathbf{Q}}}(\zeta_M)}, \operatorname{\mathrm{\mathbf{Z}}}_p(2)) \text{ .}\end{align*} $$
$$ \begin{align*}\mathcal{K}_M \otimes \operatorname{\mathrm{\mathbf{Z}}}_p \hookrightarrow H^2(G_{\operatorname{\mathrm{\mathbf{Q}}}(\zeta_M)}, \operatorname{\mathrm{\mathbf{Z}}}_p(2)) \text{ .}\end{align*} $$
Fukaya and Kato’s map actually takes values in
 $\mathcal {K}_M$
(by construction). They also do not need to restrict to the subset C of
$\mathcal {K}_M$
(by construction). They also do not need to restrict to the subset C of
 $C_{Mp}^0$
. Their techniques rely on p-adic Hodge theory.
$C_{Mp}^0$
. Their techniques rely on p-adic Hodge theory. -
(ii) Similarly, Theorem 1.4(ii) has been proved (for the absolute homology) by Scott in [Reference Williams11, Theorem 7] after tensoring by
 $\operatorname {\mathrm {\mathbf {Z}}}_{\ell }$
for a prime
$\operatorname {\mathrm {\mathbf {Z}}}_{\ell }$
for a prime
 $\ell \neq p$
dividing M (Scott’s p is our
$\ell \neq p$
dividing M (Scott’s p is our
 $\ell $
and vice versa). Scott relies on the techniques of Fukaya and Kato.
$\ell $
and vice versa). Scott relies on the techniques of Fukaya and Kato. -
(iii) Thus, the main novelty of our result is to work with
 $\operatorname {\mathrm {\mathbf {Z}}}$
coefficients. This is because we rely instead on the motivic techniques of Sharifi and Venkatesh.
$\operatorname {\mathrm {\mathbf {Z}}}$
coefficients. This is because we rely instead on the motivic techniques of Sharifi and Venkatesh. -
(iv) It would be interesting to allow less restrictive conditions on C, and in particular replace
 $H_1(X_1(M), \operatorname {\mathrm {\mathbf {Z}}})$
in the bottom line of our diagrams by a relative homology group. We were actually able to improve slightly our result when C contains the cusp
$H_1(X_1(M), \operatorname {\mathrm {\mathbf {Z}}})$
in the bottom line of our diagrams by a relative homology group. We were actually able to improve slightly our result when C contains the cusp
 $\infty $
(cf. diagrams (5.7) and (5.11)). We were not able to go beyond these results because the techniques of Sharifi and Venkatesh essentially deal with the absolute homology of modular curves.
$\infty $
(cf. diagrams (5.7) and (5.11)). We were not able to go beyond these results because the techniques of Sharifi and Venkatesh essentially deal with the absolute homology of modular curves. -
(v) The techniques of Sharifi and Venkatesh, combined with the result of Section 4 actually show that the restriction of
 $\varpi _M$
to
$\varpi _M$
to
 $H_1(X_1(M), C_{\infty }, \operatorname {\mathrm {\mathbf {Z}}})$
is annihilated by
$H_1(X_1(M), C_{\infty }, \operatorname {\mathrm {\mathbf {Z}}})$
is annihilated by
 $T_{\ell }-\ell \langle \ell \rangle - 1$
for primes
$T_{\ell }-\ell \langle \ell \rangle - 1$
for primes
 $\ell $
not dividing M, where
$\ell $
not dividing M, where
 $C_{\infty }$
are the cusps of
$C_{\infty }$
are the cusps of
 $X_1(M)$
in the same diamond orbit as
$X_1(M)$
in the same diamond orbit as
 $\infty $
. This is a slight improvement on Theorem 1.2 (which holds for the restriction of
$\infty $
. This is a slight improvement on Theorem 1.2 (which holds for the restriction of
 $\varpi _M$
to
$\varpi _M$
to
 $H_1(X_1(M), \operatorname {\mathrm {\mathbf {Z}}})$
).
$H_1(X_1(M), \operatorname {\mathrm {\mathbf {Z}}})$
).
By combining Theorem 1.4 and the results of Fukaya and Kato, one gets the following result.
Theorem 1.6 Let
![]() $M \geq 4$
. The map
$M \geq 4$
. The map
![]() $H_1(X_1(M), \operatorname {\mathrm {\mathbf {Z}}}[\frac {1}{6}]) \rightarrow \mathcal {K}_M \otimes \operatorname {\mathrm {\mathbf {Z}}}[\frac {1}{6}]$
obtained by restricting
$H_1(X_1(M), \operatorname {\mathrm {\mathbf {Z}}}[\frac {1}{6}]) \rightarrow \mathcal {K}_M \otimes \operatorname {\mathrm {\mathbf {Z}}}[\frac {1}{6}]$
obtained by restricting
![]() $\varpi _M$
to
$\varpi _M$
to
![]() $H_1(X_1(M), \operatorname {\mathrm {\mathbf {Z}}})$
and inverting
$H_1(X_1(M), \operatorname {\mathrm {\mathbf {Z}}})$
and inverting
![]() $6$
is annihilated by the Hecke operator
$6$
is annihilated by the Hecke operator
![]() $U_{\ell }-1$
for all primes
$U_{\ell }-1$
for all primes
![]() $\ell $
dividing M. Here,
$\ell $
dividing M. Here,
![]() $U_{\ell }$
is the classical Hecke operator of index
$U_{\ell }$
is the classical Hecke operator of index
![]() $\ell $
, corresponding to the double coset of
$\ell $
, corresponding to the double coset of
 $\begin {pmatrix} 1 & 0 \\ 0 & \ell \end {pmatrix}$
.
$\begin {pmatrix} 1 & 0 \\ 0 & \ell \end {pmatrix}$
.
Remark 1.7
-
(i) As mentioned above, Theorem 1.6 goes beyond Theorem 1.2. Our result thus completes the proof of Conjecture 1.1 for the absolute homology, after inverting
 $6$
.
$6$
. -
(ii) Fukaya and Kato proved Theorem 1.6 after tensoring with
 $\operatorname {\mathrm {\mathbf {Z}}}_p$
for a prime
$\operatorname {\mathrm {\mathbf {Z}}}_p$
for a prime
 $p\geq 5$
dividing M (cf. Theorem 1.3). Our trick is to use Theorem 1.3 after adding p to the level, and then descend using Theorem 1.4(ii). The reason we have to invert
$p\geq 5$
dividing M (cf. Theorem 1.3). Our trick is to use Theorem 1.3 after adding p to the level, and then descend using Theorem 1.4(ii). The reason we have to invert
 $6$
is that Fukaya and Kato assume that
$6$
is that Fukaya and Kato assume that
 $p \nmid 6$
(note that
$p \nmid 6$
(note that
 $2$
is inverted anyway in the definition of
$2$
is inverted anyway in the definition of
 $\varpi _M$
). It would be nice to be able to avoid inverting
$\varpi _M$
). It would be nice to be able to avoid inverting
 $3$
in our result.
$3$
in our result.
The plan of this paper is as follows: in Section 2, we recall some basic facts and notation about various kinds of homology and cohomology groups. In Section 3, we recall some constructions of Sharifi and Venkatesh. In Section 4, we explain how to use the cocycle of Sharifi and Venkatesh to produce a map on a certain relative homology group. Finally, in Section 5, we prove Theorems 1.4 and 1.6.
2 Background and notation regarding homology and cohomology
Let
![]() $\Gamma $
be a torsion-free finite index subgroup of
$\Gamma $
be a torsion-free finite index subgroup of
![]() $\operatorname {\mathrm {SL}}_2(\operatorname {\mathrm {\mathbf {Z}}})$
(e.g.,
$\operatorname {\mathrm {SL}}_2(\operatorname {\mathrm {\mathbf {Z}}})$
(e.g.,
![]() $\Gamma = \Gamma _1(M)$
for
$\Gamma = \Gamma _1(M)$
for
![]() $M \geq 3$
). Let
$M \geq 3$
). Let
![]() $Y = \Gamma \backslash \mathfrak {h}$
be the open modular curve of level
$Y = \Gamma \backslash \mathfrak {h}$
be the open modular curve of level
![]() $\Gamma $
, where
$\Gamma $
, where
![]() $\mathfrak {h}$
is the upper half-plane. We denote by X the corresponding compactified modular curve: we have
$\mathfrak {h}$
is the upper half-plane. We denote by X the corresponding compactified modular curve: we have
![]() $X = Y \cup C$
where
$X = Y \cup C$
where
![]() $C = \Gamma \backslash \mathbf {P}^1(\operatorname {\mathrm {\mathbf {Q}}})$
is the set of cusps of X.
$C = \Gamma \backslash \mathbf {P}^1(\operatorname {\mathrm {\mathbf {Q}}})$
is the set of cusps of X.
We denote by
![]() $H_1(X, C, \operatorname {\mathrm {\mathbf {Z}}})$
the first singular homology group of X relative to C. We have the following exact sequence coming from the long exact sequence for the pair
$H_1(X, C, \operatorname {\mathrm {\mathbf {Z}}})$
the first singular homology group of X relative to C. We have the following exact sequence coming from the long exact sequence for the pair
![]() $(X,C)$
:
$(X,C)$
:
where the map
![]() $\operatorname {\mathrm {\mathbf {Z}}}[C] \rightarrow \operatorname {\mathrm {\mathbf {Z}}}$
is the degree map.
$\operatorname {\mathrm {\mathbf {Z}}}[C] \rightarrow \operatorname {\mathrm {\mathbf {Z}}}$
is the degree map.
The Poincaré duality yields a perfect bilinear pairing
![]() $H_1(X, C, \operatorname {\mathrm {\mathbf {Z}}}) \times H_1(Y, \operatorname {\mathrm {\mathbf {Z}}}) \rightarrow \operatorname {\mathrm {\mathbf {Z}}}$
(also called the intersection pairing, due to its interpretation in terms of intersection number of cycles). Under this duality, (2.1) becomes
$H_1(X, C, \operatorname {\mathrm {\mathbf {Z}}}) \times H_1(Y, \operatorname {\mathrm {\mathbf {Z}}}) \rightarrow \operatorname {\mathrm {\mathbf {Z}}}$
(also called the intersection pairing, due to its interpretation in terms of intersection number of cycles). Under this duality, (2.1) becomes
where the map
![]() $\operatorname {\mathrm {\mathbf {Z}}}[C] \rightarrow H_1(Y \operatorname {\mathrm {\mathbf {Z}}})$
sends
$\operatorname {\mathrm {\mathbf {Z}}}[C] \rightarrow H_1(Y \operatorname {\mathrm {\mathbf {Z}}})$
sends
![]() $c \in C$
to the class of a little oriented circle around c.
$c \in C$
to the class of a little oriented circle around c.
If G is a group and T is a left G-module, we say that
![]() $c : G \rightarrow T$
is a
$c : G \rightarrow T$
is a
![]() $1$
-cocycle if for all
$1$
-cocycle if for all
![]() $g,g' \in G$
we have
$g,g' \in G$
we have
![]() $c(gg') = c(g)+g\cdot c(g')$
. The first cohomology group
$c(gg') = c(g)+g\cdot c(g')$
. The first cohomology group
![]() $H^1(G,T)$
can be computed as the abelian group of
$H^1(G,T)$
can be computed as the abelian group of
![]() $1$
-cocycles
$1$
-cocycles
![]() $c : G \rightarrow T$
modulo the cocycles of the form
$c : G \rightarrow T$
modulo the cocycles of the form
![]() $c(g) = gx-x$
for some
$c(g) = gx-x$
for some
![]() $x \in T$
(independent of g).
$x \in T$
(independent of g).
Similarly, using the projective resolution of
![]() $\operatorname {\mathrm {\mathbf {Z}}}$
as a
$\operatorname {\mathrm {\mathbf {Z}}}$
as a
![]() $\operatorname {\mathrm {\mathbf {Z}}}[G]$
-module in terms of inhomogeneous chains, one can compute the first homology group
$\operatorname {\mathrm {\mathbf {Z}}}[G]$
-module in terms of inhomogeneous chains, one can compute the first homology group
![]() $H_1(G,T)$
as
$H_1(G,T)$
as
where
![]() $Z \subset \operatorname {\mathrm {\mathbf {Z}}}[G] \otimes _{\operatorname {\mathrm {\mathbf {Z}}}} T$
is the kernel of the map sending
$Z \subset \operatorname {\mathrm {\mathbf {Z}}}[G] \otimes _{\operatorname {\mathrm {\mathbf {Z}}}} T$
is the kernel of the map sending
![]() $[g] \otimes x$
to
$[g] \otimes x$
to
![]() $g^{-1}x-x$
(for
$g^{-1}x-x$
(for
![]() $g \in G$
and
$g \in G$
and
![]() $x \in T$
) and B is generated by the elements of the form
$x \in T$
) and B is generated by the elements of the form
![]() $[gg'] \otimes x - [g] \otimes x - [g'] \otimes g^{-1}x$
for
$[gg'] \otimes x - [g] \otimes x - [g'] \otimes g^{-1}x$
for
![]() $g,g' \in G$
and
$g,g' \in G$
and
![]() $x \in T$
.
$x \in T$
.
Finally, let us recall that since
![]() $\Gamma $
is torsion-free, it is isomorphic to the fundamental group of Y, and therefore we have canonical group isomorphisms
$\Gamma $
is torsion-free, it is isomorphic to the fundamental group of Y, and therefore we have canonical group isomorphisms
3 Reminders from the work of Sharifi and Venkatesh
Sharifi and Venkatesh constructed a
![]() $1$
-cocycle
$1$
-cocycle
Here,
carries a left action of
![]() $\operatorname {\mathrm {SL}}_2(\operatorname {\mathrm {\mathbf {Z}}})$
induced by the natural right action of
$\operatorname {\mathrm {SL}}_2(\operatorname {\mathrm {\mathbf {Z}}})$
induced by the natural right action of
![]() $\operatorname {\mathrm {SL}}_2(\operatorname {\mathrm {\mathbf {Z}}})$
on
$\operatorname {\mathrm {SL}}_2(\operatorname {\mathrm {\mathbf {Z}}})$
on
![]() $\mathbf {G}_m^2$
given by
$\mathbf {G}_m^2$
given by
 $$ \begin{align*}(z_1, z_2) \cdot \begin{pmatrix} a & b \\ c & d \end{pmatrix} = \left(z_1^az_2^c, z_1^bz_2^d\right) \text{ .}\end{align*} $$
$$ \begin{align*}(z_1, z_2) \cdot \begin{pmatrix} a & b \\ c & d \end{pmatrix} = \left(z_1^az_2^c, z_1^bz_2^d\right) \text{ .}\end{align*} $$
Furthermore,
![]() $\operatorname {\mathrm {\mathbf {Z}}}\cdot \{ -z_1, -z_2 \}$
is the subgroup of
$\operatorname {\mathrm {\mathbf {Z}}}\cdot \{ -z_1, -z_2 \}$
is the subgroup of
![]() $ {\mathbf {K}}_2$
generated by the Steinberg symbol of
$ {\mathbf {K}}_2$
generated by the Steinberg symbol of
![]() $-z_1$
and
$-z_1$
and
![]() $-z_2$
. The cocycle
$-z_2$
. The cocycle
![]() $\Theta $
actually takes values in
$\Theta $
actually takes values in
![]() $ {\mathbf {K}}_2^{(0)}/ \{ -z_1, -z_2 \}$
, where
$ {\mathbf {K}}_2^{(0)}/ \{ -z_1, -z_2 \}$
, where
![]() $ {\mathbf {K}}_2^{(0)}$
is the subgroup of
$ {\mathbf {K}}_2^{(0)}$
is the subgroup of
![]() $ {\mathbf {K}}_2$
fixed by the pushforward
$ {\mathbf {K}}_2$
fixed by the pushforward
![]() $[m]_*$
of the multiplication by m map for all
$[m]_*$
of the multiplication by m map for all
![]() $m \in \mathbf {N}$
(cf. [Reference Sharifi and Venkatesh9, Section 4.1.2]).
$m \in \mathbf {N}$
(cf. [Reference Sharifi and Venkatesh9, Section 4.1.2]).
Let us recall a characterization of
![]() $\Theta $
. Let
$\Theta $
. Let
where D runs through all the irreducible divisors of
![]() $\mathbf {G}_m^2$
. There is a divisor map
$\mathbf {G}_m^2$
. There is a divisor map
![]() $\partial : {\mathbf {K}}_2 \rightarrow {\mathbf {K}}_1$
sending a Steinberg symbol
$\partial : {\mathbf {K}}_2 \rightarrow {\mathbf {K}}_1$
sending a Steinberg symbol
![]() $\{ f, g\}$
to the element of
$\{ f, g\}$
to the element of
![]() $K_1$
whose component in D is
$K_1$
whose component in D is
where v is the valuation coming from D (cf. [Reference Sharifi and Venkatesh9, equation (2.6)]). The map
![]() $\partial $
induces an embedding
$\partial $
induces an embedding
(cf. [Reference Sharifi and Venkatesh9, Section 3.2 and Lemma 4.1.2]). As in [Reference Sharifi and Venkatesh9, Section 3.2], for any
![]() $a, c \in \operatorname {\mathrm {\mathbf {Z}}}$
with
$a, c \in \operatorname {\mathrm {\mathbf {Z}}}$
with
![]() $\gcd (a,c)=1$
, there is a special element
$\gcd (a,c)=1$
, there is a special element
which is supported on the divisor
![]() $D : 1-z_1^az_2^c=0$
and is given there by the function
$D : 1-z_1^az_2^c=0$
and is given there by the function
![]() $1-z_1^bz_2^d$
for any
$1-z_1^bz_2^d$
for any
![]() $b, d\in \operatorname {\mathrm {\mathbf {Z}}}$
such that
$b, d\in \operatorname {\mathrm {\mathbf {Z}}}$
such that
![]() $ad-bc=1$
(this is independent of the choice of b and d).
$ad-bc=1$
(this is independent of the choice of b and d).
For any
 $\gamma = \begin {pmatrix} a & b \\ c & d \end {pmatrix} \in \operatorname {\mathrm {SL}}_2(\operatorname {\mathrm {\mathbf {Z}}})$
,
$\gamma = \begin {pmatrix} a & b \\ c & d \end {pmatrix} \in \operatorname {\mathrm {SL}}_2(\operatorname {\mathrm {\mathbf {Z}}})$
,
![]() $\Theta (\gamma )$
is characterized by the equality
$\Theta (\gamma )$
is characterized by the equality
in
![]() $K_1$
(cf. [Reference Sharifi and Venkatesh9, Proposition 3.3.1]). As in the proof of [Reference Sharifi and Venkatesh9, Proposition 3.3.4], one sees that
$K_1$
(cf. [Reference Sharifi and Venkatesh9, Proposition 3.3.1]). As in the proof of [Reference Sharifi and Venkatesh9, Proposition 3.3.4], one sees that
![]() $\Theta (\gamma )=0$
if
$\Theta (\gamma )=0$
if
![]() $\gamma (0)=0$
, i.e., if
$\gamma (0)=0$
, i.e., if
 $\gamma = \begin {pmatrix} 1 & 0 \\ m & 1 \end {pmatrix}$
for some
$\gamma = \begin {pmatrix} 1 & 0 \\ m & 1 \end {pmatrix}$
for some
![]() $m \in \operatorname {\mathrm {\mathbf {Z}}}$
(this follows from the injectivity of
$m \in \operatorname {\mathrm {\mathbf {Z}}}$
(this follows from the injectivity of
![]() $\partial : {\mathbf {K}}_2^{(0)}/\operatorname {\mathrm {\mathbf {Z}}}\cdot \{ -z_1, -z_2 \} \hookrightarrow {\mathbf {K}}_1$
).
$\partial : {\mathbf {K}}_2^{(0)}/\operatorname {\mathrm {\mathbf {Z}}}\cdot \{ -z_1, -z_2 \} \hookrightarrow {\mathbf {K}}_1$
).
Finally, let us recall how Sharifi and Venkatesh (cf. [Reference Sharifi and Venkatesh9, Section 4.2.1]) specialize
![]() $\Theta $
to a cocycle
$\Theta $
to a cocycle
(for every
![]() $M \geq 4$
). Here, the action of
$M \geq 4$
). Here, the action of
![]() $ \Gamma _0(M)$
on
$ \Gamma _0(M)$
on
![]() $K_2(\operatorname {\mathrm {\mathbf {Z}}}[\zeta _M, \frac {1}{M}])$
is given as follows: we have a surjective group homomorphism
$K_2(\operatorname {\mathrm {\mathbf {Z}}}[\zeta _M, \frac {1}{M}])$
is given as follows: we have a surjective group homomorphism
given by
 $$ \begin{align*}\begin{pmatrix} a & b \\ c & d \end{pmatrix} \mapsto d \text{ (modulo }M\text{)} \text{ ,}\end{align*} $$
$$ \begin{align*}\begin{pmatrix} a & b \\ c & d \end{pmatrix} \mapsto d \text{ (modulo }M\text{)} \text{ ,}\end{align*} $$
and
![]() $(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }$
acts on
$(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }$
acts on
![]() $K_2(\operatorname {\mathrm {\mathbf {Z}}}[\zeta _M, \frac {1}{M}])$
via our identification
$K_2(\operatorname {\mathrm {\mathbf {Z}}}[\zeta _M, \frac {1}{M}])$
via our identification
![]() $(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times } \simeq \operatorname {\mathrm {Gal}}(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _M)/\operatorname {\mathrm {\mathbf {Q}}})$
.
$(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times } \simeq \operatorname {\mathrm {Gal}}(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _M)/\operatorname {\mathrm {\mathbf {Q}}})$
.
The idea is to “evaluate”
![]() $\Theta (\gamma )$
at
$\Theta (\gamma )$
at
![]() $(z_1, z_2) = (1, \zeta _M)$
. To “evaluate” at
$(z_1, z_2) = (1, \zeta _M)$
. To “evaluate” at
![]() $(z_1, z_2) = (1, \zeta _M)$
, a naive idea would be to send a Steinberg symbol
$(z_1, z_2) = (1, \zeta _M)$
, a naive idea would be to send a Steinberg symbol
![]() $\{f, g\} \in {\mathbf {K}}_2$
to
$\{f, g\} \in {\mathbf {K}}_2$
to
This does not make sense in general because
![]() $f(1, \zeta _M)$
or
$f(1, \zeta _M)$
or
![]() $g(1, \zeta _M)$
may not be well defined (f or g may have a pole or zero at
$g(1, \zeta _M)$
may not be well defined (f or g may have a pole or zero at
![]() $(1, \zeta _M)$
).
$(1, \zeta _M)$
).
The idea of Sharifi and Venkatesh is to prove that
![]() $\Theta (\gamma )$
is actually a combination of Steinberg symbols which can be evaluated at
$\Theta (\gamma )$
is actually a combination of Steinberg symbols which can be evaluated at
![]() $(1, \zeta _M)$
. They make this precise by using motivic cohomology groups. We refer to [Reference Sharifi and Venkatesh9, Section 2.1] for the precise definition and results they are using regarding motivic cohomology groups. In particular, if
$(1, \zeta _M)$
. They make this precise by using motivic cohomology groups. We refer to [Reference Sharifi and Venkatesh9, Section 2.1] for the precise definition and results they are using regarding motivic cohomology groups. In particular, if
![]() ${U \subset \mathbf {G}_m^2}$
is an open subset, there is a motivic cohomology group
${U \subset \mathbf {G}_m^2}$
is an open subset, there is a motivic cohomology group
![]() $H^2(U, 2)$
(which is an abelian group). As explained in [Reference Sharifi and Venkatesh9, Remark 2.2.3], the functorial map
$H^2(U, 2)$
(which is an abelian group). As explained in [Reference Sharifi and Venkatesh9, Remark 2.2.3], the functorial map
![]() $H^2(U, 2) \rightarrow H^2(\operatorname {\mathrm {\mathbf {Q}}}(\mathbf {G}_m^2), 2)$
is injective and
$H^2(U, 2) \rightarrow H^2(\operatorname {\mathrm {\mathbf {Q}}}(\mathbf {G}_m^2), 2)$
is injective and
![]() $H^2(\operatorname {\mathrm {\mathbf {Q}}}(\mathbf {G}_m^2), 2)$
is canonically identified with
$H^2(\operatorname {\mathrm {\mathbf {Q}}}(\mathbf {G}_m^2), 2)$
is canonically identified with
![]() $ {\mathbf {K}}_2$
.
$ {\mathbf {K}}_2$
.
As noted in [Reference Sharifi and Venkatesh9, Section 4.2.1], for all
 $\gamma = \begin {pmatrix} a & b \\ c & d \end {pmatrix} \in \Gamma _0(M)$
, the element
$\gamma = \begin {pmatrix} a & b \\ c & d \end {pmatrix} \in \Gamma _0(M)$
, the element
lies in the image of
![]() $H^2(U_{\gamma }, 2)/\{-z_1, -z_2\}$
, where
$H^2(U_{\gamma }, 2)/\{-z_1, -z_2\}$
, where
![]() $U_{\gamma }$
is the open subset of
$U_{\gamma }$
is the open subset of
![]() $\mathbf {G}_m^2$
, which is the complement of
$\mathbf {G}_m^2$
, which is the complement of
![]() $\{z_1^bz_2^d = 1\} \cup \{z_2=1\}$
. Since
$\{z_1^bz_2^d = 1\} \cup \{z_2=1\}$
. Since
![]() $(1, \zeta _M) \in U_{\gamma }$
, there is a functorial map
$(1, \zeta _M) \in U_{\gamma }$
, there is a functorial map
By [Reference Sharifi and Venkatesh9, Corollary 4.2.5],
![]() $\Theta _M(\gamma ) := s_M^*(\Theta (\gamma ))$
actually belongs to the subgroup
$\Theta _M(\gamma ) := s_M^*(\Theta (\gamma ))$
actually belongs to the subgroup
of
![]() $K_2(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _M))/\operatorname {\mathrm {\mathbf {Z}}}\cdot \{-1, -\zeta _M\}$
.
$K_2(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _M))/\operatorname {\mathrm {\mathbf {Z}}}\cdot \{-1, -\zeta _M\}$
.
We therefore have a
![]() $1$
-cocycle
$1$
-cocycle
By [Reference Sharifi and Venkatesh9, Proposition 4.2.1], the cocycle
![]() $\Theta _M$
is parabolic. This means that if
$\Theta _M$
is parabolic. This means that if
![]() $c \in \mathbf {P}^1(\operatorname {\mathrm {\mathbf {Q}}})$
and
$c \in \mathbf {P}^1(\operatorname {\mathrm {\mathbf {Q}}})$
and
![]() $\Gamma _c \subset \Gamma _0(M)$
is the stabilizer of c, then the restriction of
$\Gamma _c \subset \Gamma _0(M)$
is the stabilizer of c, then the restriction of
![]() $\Theta _M$
to
$\Theta _M$
to
![]() $\Gamma _c$
is a coboundary, i.e., of the form
$\Gamma _c$
is a coboundary, i.e., of the form
![]() $\gamma \mapsto \gamma \cdot x -x$
for some
$\gamma \mapsto \gamma \cdot x -x$
for some
![]() $x \in K_2(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _M))/\operatorname {\mathrm {\mathbf {Z}}}\cdot \{-1, -\zeta _M\}$
(depending on c a priori).
$x \in K_2(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _M))/\operatorname {\mathrm {\mathbf {Z}}}\cdot \{-1, -\zeta _M\}$
(depending on c a priori).
4 From cocycles to relative homology
In this section, we explain how the cocycle
![]() $\Theta _M$
defined in (3.2) gives rise to a group homomorphism
$\Theta _M$
defined in (3.2) gives rise to a group homomorphism
where
![]() $C_0$
is the set of cusps of
$C_0$
is the set of cusps of
![]() $X_1(M)$
which are in the same diamond orbit as the cusp
$X_1(M)$
which are in the same diamond orbit as the cusp
![]() $\Gamma _1(M) \cdot 0$
.
$\Gamma _1(M) \cdot 0$
.
Recall that we have denoted by
![]() $\mathcal {K}_M$
the largest quotient of
$\mathcal {K}_M$
the largest quotient of
![]() $K_2(\operatorname {\mathrm {\mathbf {Z}}}[\zeta _M, \frac {1}{M}]) \otimes \operatorname {\mathrm {\mathbf {Z}}}[\frac {1}{2}]$
on which the complex conjugation acts trivially. Note that since the Steinberg symbol
$K_2(\operatorname {\mathrm {\mathbf {Z}}}[\zeta _M, \frac {1}{M}]) \otimes \operatorname {\mathrm {\mathbf {Z}}}[\frac {1}{2}]$
on which the complex conjugation acts trivially. Note that since the Steinberg symbol
![]() $\{-1, -\zeta _M\}$
has order dividing
$\{-1, -\zeta _M\}$
has order dividing
![]() $2$
, its image in
$2$
, its image in
![]() $\mathcal {K}_M$
is trivial. Furthermore, the action of
$\mathcal {K}_M$
is trivial. Furthermore, the action of
![]() $(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }$
on
$(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }$
on
![]() $\mathcal {K}_M$
factors through
$\mathcal {K}_M$
factors through
![]() $(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
(by definition).
$(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
(by definition).
Recall that we have a group homomorphism
![]() $\Gamma _0(M) \rightarrow (\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }$
given by
$\Gamma _0(M) \rightarrow (\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }$
given by
![]() $\gamma \mapsto \langle \gamma \rangle $
, where if
$\gamma \mapsto \langle \gamma \rangle $
, where if
 $\gamma = \begin {pmatrix} a & b \\ c & d \end {pmatrix}$
, we let
$\gamma = \begin {pmatrix} a & b \\ c & d \end {pmatrix}$
, we let
![]() $\langle \gamma \rangle = d \text { (modulo }M\text {)}$
. Therefore, a (left)
$\langle \gamma \rangle = d \text { (modulo }M\text {)}$
. Therefore, a (left)
![]() $(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
-module can be considered naturally as a (left)
$(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
-module can be considered naturally as a (left)
![]() $\Gamma _0(M)$
-module. In particular, this is the case of
$\Gamma _0(M)$
-module. In particular, this is the case of
![]() $H_1(X_1(M), C_0, \operatorname {\mathrm {\mathbf {Z}}})$
, on which
$H_1(X_1(M), C_0, \operatorname {\mathrm {\mathbf {Z}}})$
, on which
![]() $(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
acts via diamond operators.
$(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
acts via diamond operators.
There is a map
given by
![]() $\gamma \mapsto \{0, \gamma 0\}$
. The map f is a
$\gamma \mapsto \{0, \gamma 0\}$
. The map f is a
![]() $1$
-cocycle, since for all
$1$
-cocycle, since for all
![]() $\gamma , \gamma ' \in \Gamma _0(M)$
, we have
$\gamma , \gamma ' \in \Gamma _0(M)$
, we have
 $$ \begin{align*} f(\gamma \gamma') &= \{0, \gamma\gamma' 0\} \\& = \{0, \gamma 0\} + \{\gamma0, \gamma \gamma' 0\} \\& = f(\gamma) + \langle \gamma \rangle f(\gamma') \text{ .} \end{align*} $$
$$ \begin{align*} f(\gamma \gamma') &= \{0, \gamma\gamma' 0\} \\& = \{0, \gamma 0\} + \{\gamma0, \gamma \gamma' 0\} \\& = f(\gamma) + \langle \gamma \rangle f(\gamma') \text{ .} \end{align*} $$
We shall need the following result, which allows us to transfer a
![]() $1$
-cocycle to a map on homology.
$1$
-cocycle to a map on homology.
Proposition 4.1 Let T be a (left)
![]() $(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
-module (where
$(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
-module (where
![]() $M>3$
). Let
$M>3$
). Let
![]() $u : \Gamma _0(M) \rightarrow T$
be a
$u : \Gamma _0(M) \rightarrow T$
be a
![]() $1$
-cocycle satisfying
$1$
-cocycle satisfying
![]() $u(\gamma )=0$
for any
$u(\gamma )=0$
for any
![]() $\gamma \in \Gamma _1(M)$
such that there exists
$\gamma \in \Gamma _1(M)$
such that there exists
![]() $c \in \mathbf {P}^1(\operatorname {\mathrm {\mathbf {Q}}})$
with
$c \in \mathbf {P}^1(\operatorname {\mathrm {\mathbf {Q}}})$
with
![]() $\gamma c = c$
. Then u factors through the map
$\gamma c = c$
. Then u factors through the map
![]() $f : \Gamma _0(M) \rightarrow H_1(X_1(M), C_0, \operatorname {\mathrm {\mathbf {Z}}})$
, thus inducing a morphism of left
$f : \Gamma _0(M) \rightarrow H_1(X_1(M), C_0, \operatorname {\mathrm {\mathbf {Z}}})$
, thus inducing a morphism of left
![]() $(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
-modules
$(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
-modules
![]() $\tilde {u} : H_1(X_1(M), C_0, \operatorname {\mathrm {\mathbf {Z}}}) \rightarrow T$
.
$\tilde {u} : H_1(X_1(M), C_0, \operatorname {\mathrm {\mathbf {Z}}}) \rightarrow T$
.
Proof For notational simplicity, let
![]() $G = (\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times } / \pm 1$
,
$G = (\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times } / \pm 1$
,
![]() $\Gamma _0 = \Gamma _0(M)/\pm 1$
, and
$\Gamma _0 = \Gamma _0(M)/\pm 1$
, and
![]() $\Gamma _1 = \Gamma _1(M) \subset \Gamma _0$
. Recall that if
$\Gamma _1 = \Gamma _1(M) \subset \Gamma _0$
. Recall that if
![]() $\gamma \in \Gamma _0$
, we let
$\gamma \in \Gamma _0$
, we let
![]() $\langle \gamma \rangle \in G$
be the class of the lower-right corner of
$\langle \gamma \rangle \in G$
be the class of the lower-right corner of
![]() $\gamma $
. For any
$\gamma $
. For any
![]() $c \in \mathbf {P}^1(\operatorname {\mathrm {\mathbf {Q}}})$
, let
$c \in \mathbf {P}^1(\operatorname {\mathrm {\mathbf {Q}}})$
, let
![]() $\gamma _c \in \Gamma _1$
be a generator of the stabilizer of c in
$\gamma _c \in \Gamma _1$
be a generator of the stabilizer of c in
![]() $\Gamma _1$
.
$\Gamma _1$
.
By assumption, we have
![]() $u(\gamma _c) = 0$
for all
$u(\gamma _c) = 0$
for all
![]() $c \in \mathbf {P}^1(\operatorname {\mathrm {\mathbf {Q}}})$
. Thus, u induces a group homomorphism
$c \in \mathbf {P}^1(\operatorname {\mathrm {\mathbf {Q}}})$
. Thus, u induces a group homomorphism
![]() $u' : \operatorname {\mathrm {\mathbf {Z}}}[G \times \Gamma _0]/I \rightarrow T$
given by
$u' : \operatorname {\mathrm {\mathbf {Z}}}[G \times \Gamma _0]/I \rightarrow T$
given by
![]() $u'(g, \gamma ) = g\cdot u(\gamma )$
, where I is the subgroup of
$u'(g, \gamma ) = g\cdot u(\gamma )$
, where I is the subgroup of
![]() $ \operatorname {\mathrm {\mathbf {Z}}}[G \times \Gamma _0]$
generated by the elements
$ \operatorname {\mathrm {\mathbf {Z}}}[G \times \Gamma _0]$
generated by the elements
![]() $(g, \gamma \gamma ') - (g, \gamma ) - (g\langle \gamma \rangle , \gamma ')$
and by the
$(g, \gamma \gamma ') - (g, \gamma ) - (g\langle \gamma \rangle , \gamma ')$
and by the
![]() $(1, \gamma _c) - (1, 1)$
for all
$(1, \gamma _c) - (1, 1)$
for all
![]() $g \in G$
,
$g \in G$
,
![]() $\gamma , \gamma ' \in \Gamma _0(M)$
and
$\gamma , \gamma ' \in \Gamma _0(M)$
and
![]() $c \in \mathbf {P}^1(\operatorname {\mathrm {\mathbf {Q}}})$
.
$c \in \mathbf {P}^1(\operatorname {\mathrm {\mathbf {Q}}})$
.
It suffices to prove that the map
sending
![]() $(g, \gamma )$
to
$(g, \gamma )$
to
![]() $g\cdot \{0, \gamma 0 \}$
is an isomorphism. Note that
$g\cdot \{0, \gamma 0 \}$
is an isomorphism. Note that
![]() $\varphi $
is well defined since
$\varphi $
is well defined since
 $$ \begin{align*} \{0, \gamma_c 0\}&= \{0, c\} + \{c, \gamma_c c\} + \{\gamma_c c, \gamma_c 0\} \\&= (1-\langle \gamma_c \rangle) \cdot \{ 0, c\} \\& = 0 \end{align*} $$
$$ \begin{align*} \{0, \gamma_c 0\}&= \{0, c\} + \{c, \gamma_c c\} + \{\gamma_c c, \gamma_c 0\} \\&= (1-\langle \gamma_c \rangle) \cdot \{ 0, c\} \\& = 0 \end{align*} $$
(we have used the fact that
![]() $\gamma _c \in \Gamma _1$
, so the diamond operator
$\gamma _c \in \Gamma _1$
, so the diamond operator
![]() $\langle \gamma _c \rangle $
is trivial).
$\langle \gamma _c \rangle $
is trivial).
Let us first prove that
![]() $\varphi $
is surjective. Any element of
$\varphi $
is surjective. Any element of
![]() $H_1(X_1(M), C_0, \operatorname {\mathrm {\mathbf {Z}}})$
is a combination of modular symbols of the form
$H_1(X_1(M), C_0, \operatorname {\mathrm {\mathbf {Z}}})$
is a combination of modular symbols of the form
![]() $\{\alpha , \beta \}$
where
$\{\alpha , \beta \}$
where
![]() $\alpha , \beta \in \mathbf {P}^1(\operatorname {\mathrm {\mathbf {Q}}})$
project onto
$\alpha , \beta \in \mathbf {P}^1(\operatorname {\mathrm {\mathbf {Q}}})$
project onto
![]() $C_0$
in
$C_0$
in
![]() $X_1(M)$
. This latter condition means that
$X_1(M)$
. This latter condition means that
![]() $\alpha = \gamma 0$
and
$\alpha = \gamma 0$
and
![]() $\beta = \gamma ' 0$
for some
$\beta = \gamma ' 0$
for some
![]() $\gamma , \gamma ' \in \Gamma _0(M)$
. Note that
$\gamma , \gamma ' \in \Gamma _0(M)$
. Note that
 $$ \begin{align*} \{\alpha, \beta\} &= \{\alpha, 0\} + \{0, \beta\} \\&= \{0, \gamma' 0\} - \{0, \gamma 0\} \text{ ,} \end{align*} $$
$$ \begin{align*} \{\alpha, \beta\} &= \{\alpha, 0\} + \{0, \beta\} \\&= \{0, \gamma' 0\} - \{0, \gamma 0\} \text{ ,} \end{align*} $$
so
![]() $H_1(X_1(M), C_0, \operatorname {\mathrm {\mathbf {Z}}})$
is generated by the elements of the form
$H_1(X_1(M), C_0, \operatorname {\mathrm {\mathbf {Z}}})$
is generated by the elements of the form
![]() $\{0, \gamma 0\}$
for
$\{0, \gamma 0\}$
for
![]() $\gamma \in \Gamma _0(M)$
. We have thus proved that
$\gamma \in \Gamma _0(M)$
. We have thus proved that
![]() $\varphi $
is surjective. To prove that
$\varphi $
is surjective. To prove that
![]() $\varphi $
is injective, it is enough to show that
$\varphi $
is injective, it is enough to show that
![]() $ \operatorname {\mathrm {\mathbf {Z}}}[G \times \Gamma _0]/I$
is a free
$ \operatorname {\mathrm {\mathbf {Z}}}[G \times \Gamma _0]/I$
is a free
![]() $\operatorname {\mathrm {\mathbf {Z}}}$
-module of the same rank as
$\operatorname {\mathrm {\mathbf {Z}}}$
-module of the same rank as
![]() $H_1(X_1(M), C_0, \operatorname {\mathrm {\mathbf {Z}}})$
.
$H_1(X_1(M), C_0, \operatorname {\mathrm {\mathbf {Z}}})$
.
Since
![]() $M>3$
, the group
$M>3$
, the group
![]() $\Gamma _1$
is torsion-free and we have
$\Gamma _1$
is torsion-free and we have
![]() $H_1(\Gamma _1, \operatorname {\mathrm {\mathbf {Z}}}) \simeq H_1(Y_1(M), \operatorname {\mathrm {\mathbf {Z}}})$
(cf. (2.4)). By Shapiro’s lemma for group homology, we have
$H_1(\Gamma _1, \operatorname {\mathrm {\mathbf {Z}}}) \simeq H_1(Y_1(M), \operatorname {\mathrm {\mathbf {Z}}})$
(cf. (2.4)). By Shapiro’s lemma for group homology, we have
![]() $H_1(\Gamma _1, \operatorname {\mathrm {\mathbf {Z}}}) \kern1.2pt{\simeq}\kern1.2pt H_1(\Gamma _0, \operatorname {\mathrm {\mathbf {Z}}}[G])$
. Using the description of group homology in terms of inhomogeneous chains (cf. (2.3)), one gets a short exact sequence
$H_1(\Gamma _1, \operatorname {\mathrm {\mathbf {Z}}}) \kern1.2pt{\simeq}\kern1.2pt H_1(\Gamma _0, \operatorname {\mathrm {\mathbf {Z}}}[G])$
. Using the description of group homology in terms of inhomogeneous chains (cf. (2.3)), one gets a short exact sequence
where
![]() $\partial (g, \gamma ) = g\cdot \langle \gamma \rangle ^{-1} - g$
and J is the subgroup of
$\partial (g, \gamma ) = g\cdot \langle \gamma \rangle ^{-1} - g$
and J is the subgroup of
![]() $\operatorname {\mathrm {\mathbf {Z}}}[G \times \Gamma _0]$
generated by
$\operatorname {\mathrm {\mathbf {Z}}}[G \times \Gamma _0]$
generated by
for
![]() $g \in G$
,
$g \in G$
,
![]() $\gamma , \gamma ' \in \Gamma _0(M)$
. The last map
$\gamma , \gamma ' \in \Gamma _0(M)$
. The last map
![]() $\operatorname {\mathrm {\mathbf {Z}}}[G] \rightarrow \operatorname {\mathrm {\mathbf {Z}}}$
is the augmentation (degree) map (note that J is indeed in the kernel of
$\operatorname {\mathrm {\mathbf {Z}}}[G] \rightarrow \operatorname {\mathrm {\mathbf {Z}}}$
is the augmentation (degree) map (note that J is indeed in the kernel of
![]() $\partial $
).
$\partial $
).
As in (2.2), we have an exact sequence
where
![]() $C_M$
is the set of cusps of
$C_M$
is the set of cusps of
![]() $Y_1(M)$
. Here, the map
$Y_1(M)$
. Here, the map
![]() $ \operatorname {\mathrm {\mathbf {Z}}}[C_M]$
sends a cusp c to the homology class of a small loop around c in
$ \operatorname {\mathrm {\mathbf {Z}}}[C_M]$
sends a cusp c to the homology class of a small loop around c in
![]() $Y_1(M)$
.
$Y_1(M)$
.
Under the isomorphism
![]() $H_1(Y_1(M), \operatorname {\mathrm {\mathbf {Z}}}) \simeq H_1(\Gamma _0, \operatorname {\mathrm {\mathbf {Z}}}[G])$
and the embedding
$H_1(Y_1(M), \operatorname {\mathrm {\mathbf {Z}}}) \simeq H_1(\Gamma _0, \operatorname {\mathrm {\mathbf {Z}}}[G])$
and the embedding
![]() $H_1(\Gamma _0, \operatorname {\mathrm {\mathbf {Z}}}[G]) \hookrightarrow \operatorname {\mathrm {\mathbf {Z}}}[G \times \Gamma _0]/J$
described above, the map
$H_1(\Gamma _0, \operatorname {\mathrm {\mathbf {Z}}}[G]) \hookrightarrow \operatorname {\mathrm {\mathbf {Z}}}[G \times \Gamma _0]/J$
described above, the map
![]() $\operatorname {\mathrm {\mathbf {Z}}}[C_M] \rightarrow H_1(\Gamma _0, \operatorname {\mathrm {\mathbf {Z}}}[G])$
sends a cusp c to the class of
$\operatorname {\mathrm {\mathbf {Z}}}[C_M] \rightarrow H_1(\Gamma _0, \operatorname {\mathrm {\mathbf {Z}}}[G])$
sends a cusp c to the class of
![]() $(1,\gamma _c) - (1,1)$
in
$(1,\gamma _c) - (1,1)$
in
![]() $\operatorname {\mathrm {\mathbf {Z}}}[G \times \Gamma _0]/J$
.
$\operatorname {\mathrm {\mathbf {Z}}}[G \times \Gamma _0]/J$
.
Thus, we have an exact sequence
where
![]() $I'$
is the subgroup of
$I'$
is the subgroup of
![]() $ \operatorname {\mathrm {\mathbf {Z}}}[G \times \Gamma _0]$
generated by the elements
$ \operatorname {\mathrm {\mathbf {Z}}}[G \times \Gamma _0]$
generated by the elements
and by the
![]() $(1, \gamma _c) - (1, 1)$
for all
$(1, \gamma _c) - (1, 1)$
for all
![]() $g \in G$
,
$g \in G$
,
![]() $\gamma , \gamma ' \in \Gamma _0(M)$
and
$\gamma , \gamma ' \in \Gamma _0(M)$
and
![]() $c \in \mathbf {P}^1(\operatorname {\mathrm {\mathbf {Q}}})$
.
$c \in \mathbf {P}^1(\operatorname {\mathrm {\mathbf {Q}}})$
.
The involution
![]() $G \rightarrow G$
given by
$G \rightarrow G$
given by
![]() $g \mapsto g^{-1}$
induces an isomorphism
$g \mapsto g^{-1}$
induces an isomorphism
![]() $ \operatorname {\mathrm {\mathbf {Z}}}[G \times \Gamma _0]/I' \xrightarrow {\sim } \operatorname {\mathrm {\mathbf {Z}}}[G \times \Gamma _0]/I$
. This shows that
$ \operatorname {\mathrm {\mathbf {Z}}}[G \times \Gamma _0]/I' \xrightarrow {\sim } \operatorname {\mathrm {\mathbf {Z}}}[G \times \Gamma _0]/I$
. This shows that
![]() $ \operatorname {\mathrm {\mathbf {Z}}}[G \times \Gamma _0]/I$
is a free
$ \operatorname {\mathrm {\mathbf {Z}}}[G \times \Gamma _0]/I$
is a free
![]() $\operatorname {\mathrm {\mathbf {Z}}}$
-module of rank
$\operatorname {\mathrm {\mathbf {Z}}}$
-module of rank
![]() $\operatorname {\mathrm {rk}}_{\operatorname {\mathrm {\mathbf {Z}}}} H_1(X_1(M), \operatorname {\mathrm {\mathbf {Z}}}) + \#G -1$
. We have
$\operatorname {\mathrm {rk}}_{\operatorname {\mathrm {\mathbf {Z}}}} H_1(X_1(M), \operatorname {\mathrm {\mathbf {Z}}}) + \#G -1$
. We have
![]() $\# G = \# C_0$
, and the exact sequence (cf. (2.1))
$\# G = \# C_0$
, and the exact sequence (cf. (2.1))
shows that
![]() $\operatorname {\mathrm {rk}}_{\operatorname {\mathrm {\mathbf {Z}}}} \operatorname {\mathrm {\mathbf {Z}}}[G \times \Gamma _0]/I = \operatorname {\mathrm {rk}}_{\operatorname {\mathrm {\mathbf {Z}}}} H_1(X_1(M), C_0, \operatorname {\mathrm {\mathbf {Z}}})$
, as wanted.
$\operatorname {\mathrm {rk}}_{\operatorname {\mathrm {\mathbf {Z}}}} \operatorname {\mathrm {\mathbf {Z}}}[G \times \Gamma _0]/I = \operatorname {\mathrm {rk}}_{\operatorname {\mathrm {\mathbf {Z}}}} H_1(X_1(M), C_0, \operatorname {\mathrm {\mathbf {Z}}})$
, as wanted.
Let us apply Proposition 4.1 to
![]() $T = \mathcal {K}_M$
and
$T = \mathcal {K}_M$
and
![]() $u : \Gamma _0(M) \rightarrow T$
induced by
$u : \Gamma _0(M) \rightarrow T$
induced by
![]() $\Theta _M$
. Since u is parabolic and
$\Theta _M$
. Since u is parabolic and
![]() $\Gamma _1(M)$
acts trivially on T, the condition that u vanishes on parabolic elements of
$\Gamma _1(M)$
acts trivially on T, the condition that u vanishes on parabolic elements of
![]() $\Gamma _1(M)$
is satisfied. Therefore, we get a
$\Gamma _1(M)$
is satisfied. Therefore, we get a
![]() $(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
-equivariant homomorphism
$(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
-equivariant homomorphism
5 Proofs of the theorems
We start with the following lemma (we thank Venkatesh for explaining this to us).
Lemma 5.1 Let
![]() $M \geq 4$
and
$M \geq 4$
and
![]() $p\geq 2$
be a prime. Let
$p\geq 2$
be a prime. Let
 $\alpha = \begin {pmatrix} 1 & 0 \\ 0 & p \end {pmatrix}$
. Let
$\alpha = \begin {pmatrix} 1 & 0 \\ 0 & p \end {pmatrix}$
. Let
![]() $\phi _p : \Gamma _0(Mp) \rightarrow \Gamma _0(M)$
be the group homomorphism sending
$\phi _p : \Gamma _0(Mp) \rightarrow \Gamma _0(M)$
be the group homomorphism sending
 $\begin {pmatrix} a & b \\ c & d \end {pmatrix}$
to
$\begin {pmatrix} a & b \\ c & d \end {pmatrix}$
to
 $\begin {pmatrix} a & pb \\ c/p & d \end {pmatrix}$
. We have a commutative diagram
$\begin {pmatrix} a & pb \\ c/p & d \end {pmatrix}$
. We have a commutative diagram

where
![]() $\alpha _*$
is the trace map induced by
$\alpha _*$
is the trace map induced by
![]() $\alpha $
.
$\alpha $
.
Proof Since
![]() $\partial : {\mathbf {K}}_2^{(0)}/\operatorname {\mathrm {\mathbf {Z}}} \cdot \{-z_1, -z_2\} \hookrightarrow {\mathbf {K}}_1$
is injective, it suffices to prove that the following diagram is commutative:
$\partial : {\mathbf {K}}_2^{(0)}/\operatorname {\mathrm {\mathbf {Z}}} \cdot \{-z_1, -z_2\} \hookrightarrow {\mathbf {K}}_1$
is injective, it suffices to prove that the following diagram is commutative:

In other words, if
 $\gamma = \begin {pmatrix} a & b \\ c & d \end {pmatrix} \in \Gamma _0(Mp)$
, then it suffices to check that
$\gamma = \begin {pmatrix} a & b \\ c & d \end {pmatrix} \in \Gamma _0(Mp)$
, then it suffices to check that
(cf. (3.1) for the definition of the symbol
![]() $\langle b , d \rangle $
).
$\langle b , d \rangle $
).
As in [Reference Sharifi and Venkatesh9, equation (3.2)], we have
![]() $\langle b , d \rangle = \gamma ^* \langle 0, 1 \rangle $
where
$\langle b , d \rangle = \gamma ^* \langle 0, 1 \rangle $
where
![]() $\gamma ^* : {\mathbf {K}}_1 \rightarrow {\mathbf {K}}_1$
is the pullback induced by the right action of
$\gamma ^* : {\mathbf {K}}_1 \rightarrow {\mathbf {K}}_1$
is the pullback induced by the right action of
![]() $\gamma $
on
$\gamma $
on
![]() $\mathbf {G}_m^2$
. Note that we have
$\mathbf {G}_m^2$
. Note that we have
![]() $\gamma ^* = (\gamma ^{-1})_*$
. Thus, we have
$\gamma ^* = (\gamma ^{-1})_*$
. Thus, we have
 $$ \begin{align*}\alpha_* \langle b, d \rangle &= \alpha_* (\gamma^{-1})_* \langle 0, 1 \rangle = (\gamma^{-1}\cdot \alpha)_* \langle 0, 1 \rangle = (\alpha^{-1} \cdot \gamma^{-1}\cdot\alpha)_* \alpha_* \langle 0, 1 \rangle \\&=(\alpha^{-1} \cdot \gamma \cdot\alpha)^* \alpha_* \langle 0, 1 \rangle \text{ .}\end{align*} $$
$$ \begin{align*}\alpha_* \langle b, d \rangle &= \alpha_* (\gamma^{-1})_* \langle 0, 1 \rangle = (\gamma^{-1}\cdot \alpha)_* \langle 0, 1 \rangle = (\alpha^{-1} \cdot \gamma^{-1}\cdot\alpha)_* \alpha_* \langle 0, 1 \rangle \\&=(\alpha^{-1} \cdot \gamma \cdot\alpha)^* \alpha_* \langle 0, 1 \rangle \text{ .}\end{align*} $$
Let us prove that
![]() $\alpha _*\langle 0 , 1 \rangle = \langle 0, 1 \rangle $
. By definition,
$\alpha _*\langle 0 , 1 \rangle = \langle 0, 1 \rangle $
. By definition,
![]() $\langle 0 , 1 \rangle $
is the function
$\langle 0 , 1 \rangle $
is the function
![]() $1-z_1^{-1}$
on the divisor
$1-z_1^{-1}$
on the divisor
![]() $z_2=1$
of
$z_2=1$
of
![]() $\mathbf {G}_m^2$
. Furthermore, right multiplication by
$\mathbf {G}_m^2$
. Furthermore, right multiplication by
![]() $\alpha $
on
$\alpha $
on
![]() $\mathbf {G}_m^2$
is given by
$\mathbf {G}_m^2$
is given by
![]() $(z_1, z_2) \mapsto (z_1, z_2^p)$
. Thus, the divisor
$(z_1, z_2) \mapsto (z_1, z_2^p)$
. Thus, the divisor
![]() $z_2=1$
is mapped to itself by right multiplication by
$z_2=1$
is mapped to itself by right multiplication by
![]() $\alpha $
. Therefore (cf. [Reference Sharifi and Venkatesh9, Remark 2.3.3]),
$\alpha $
. Therefore (cf. [Reference Sharifi and Venkatesh9, Remark 2.3.3]),
![]() $\alpha _*\langle 0 , 1 \rangle $
is the norm of
$\alpha _*\langle 0 , 1 \rangle $
is the norm of
![]() $1-z_1^{-1}$
via the identity map
$1-z_1^{-1}$
via the identity map
![]() $K_1(\operatorname {\mathrm {\mathbf {Q}}}(z_1)) \rightarrow K_1(\operatorname {\mathrm {\mathbf {Q}}}(z_1))$
, on the divisor
$K_1(\operatorname {\mathrm {\mathbf {Q}}}(z_1)) \rightarrow K_1(\operatorname {\mathrm {\mathbf {Q}}}(z_1))$
, on the divisor
![]() $z_2=1$
. This proves that
$z_2=1$
. This proves that
![]() $\alpha _*\langle 0 , 1 \rangle = \langle 0, 1 \rangle $
.
$\alpha _*\langle 0 , 1 \rangle = \langle 0, 1 \rangle $
.
Since
 $\alpha ^{-1} \cdot \gamma \cdot \alpha = \begin {pmatrix} a & pb \\ c/p & d \end {pmatrix}$
, we get
$\alpha ^{-1} \cdot \gamma \cdot \alpha = \begin {pmatrix} a & pb \\ c/p & d \end {pmatrix}$
, we get
![]() $\alpha _* \langle b, d \rangle = \langle pb, d \rangle $
. This proves (5.1), and concludes the proof of Lemma 5.1.
$\alpha _* \langle b, d \rangle = \langle pb, d \rangle $
. This proves (5.1), and concludes the proof of Lemma 5.1.
We are now ready to prove Theorem 1.4. Let
and let
be as in Lemma 5.1. Let
![]() $f : \mathbf {G}_m^2 \rightarrow \mathbf {G}_m^2$
given by
$f : \mathbf {G}_m^2 \rightarrow \mathbf {G}_m^2$
given by
(note that f is induced by the right action of the matrix
![]() $\alpha $
of Lemma 5.1).
$\alpha $
of Lemma 5.1).
Let
![]() $U = U_{\gamma }$
be as in Section 3 and
$U = U_{\gamma }$
be as in Section 3 and
Both U and
![]() $U'$
are open subschemes of
$U'$
are open subschemes of
![]() $\mathbf {G}_m^2$
, and we have
$\mathbf {G}_m^2$
, and we have
![]() $(1, \zeta _M) \in U$
and
$(1, \zeta _M) \in U$
and
![]() $(1, \zeta \cdot \zeta _{Mp}) \in U'$
for all pth root of unity
$(1, \zeta \cdot \zeta _{Mp}) \in U'$
for all pth root of unity
![]() $\zeta $
.
$\zeta $
.
Consider the following Cartesian diagram of schemes:

where
![]() $s_M$
is given by the closed point
$s_M$
is given by the closed point
![]() $(1, \zeta _M) \in U$
, and X makes the diagram Cartesian by definition.
$(1, \zeta _M) \in U$
, and X makes the diagram Cartesian by definition.
Lemma 5.2 We have a natural isomorphism of schemes over
![]() $\operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}})$
:
$\operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}})$
:
where the maps
![]() $\operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _M)) \rightarrow \operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}[T, T^{-1}])$
and
$\operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _M)) \rightarrow \operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}[T, T^{-1}])$
and
![]() $\operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}[t, t^{-1}]) \rightarrow \operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}[T, T^{-1}])$
are given by
$\operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}[t, t^{-1}]) \rightarrow \operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}[T, T^{-1}])$
are given by
![]() $T \mapsto \zeta _M$
and
$T \mapsto \zeta _M$
and
![]() $T \mapsto t^p$
, respectively.
$T \mapsto t^p$
, respectively.
Under this isomorphism, the map
![]() $X \rightarrow \operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _M))$
is the projection onto the first factor. The compositum map
$X \rightarrow \operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _M))$
is the projection onto the first factor. The compositum map
![]() $X \rightarrow U' \hookrightarrow \operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}[z_1, z_2, z_1^{-1}, z_2^{-1}])$
is given by the compositum of the projection
$X \rightarrow U' \hookrightarrow \operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}[z_1, z_2, z_1^{-1}, z_2^{-1}])$
is given by the compositum of the projection
and of the map
![]() $ \operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}[t, t^{-1}]) \rightarrow \operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}[z_1, z_2, z_1^{-1}, z_2^{-1}])$
defined by
$ \operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}[t, t^{-1}]) \rightarrow \operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}[z_1, z_2, z_1^{-1}, z_2^{-1}])$
defined by
![]() $z_1 \mapsto 1$
and
$z_1 \mapsto 1$
and
![]() ${z_2 \mapsto t}$
.
${z_2 \mapsto t}$
.
Proof Let Y be such that the following diagram is Cartesian:

We claim that there is a natural isomorphism
![]() $Y \simeq X$
. To prove that, it is enough to prove that we have a commutative diagram
$Y \simeq X$
. To prove that, it is enough to prove that we have a commutative diagram

It suffices to prove that the image of Y (which we view as a closed subscheme of
![]() $\mathbf {G}_m^2$
) is contained in
$\mathbf {G}_m^2$
) is contained in
![]() $U'$
. This follows from the fact that
$U'$
. This follows from the fact that
![]() $f^{-1}(1, \zeta _M) \subset U'$
.
$f^{-1}(1, \zeta _M) \subset U'$
.
To conclude the proof of Lemma 5.2, note that there is a commutative diagram

Lemma 5.2 yields a more concrete description of X: we have
This latter isomorphism can be rewritten more simply in a way which depends on whether p divides M or not.
5.1 The case
 $p \mid M$
$p \mid M$
Assume first that p divides M. Then
![]() $X \simeq \operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _{Mp}))$
and the map
$X \simeq \operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _{Mp}))$
and the map
![]() $X \rightarrow U'$
comes from the point
$X \rightarrow U'$
comes from the point
![]() $(1, \zeta _{Mp}) \in U'$
. Applying the functor
$(1, \zeta _{Mp}) \in U'$
. Applying the functor
![]() $H^2( \cdot , 2)$
to (5.2) (cf. [Reference Sharifi and Venkatesh9, Lemma 2.1.1]), we get a commutative diagram
$H^2( \cdot , 2)$
to (5.2) (cf. [Reference Sharifi and Venkatesh9, Lemma 2.1.1]), we get a commutative diagram

and hence a commutative diagram

As explained in Section 3, we have
and
Since
![]() $U'$
is an open subset of
$U'$
is an open subset of
![]() $U_{\gamma '}$
, we have a functorial embedding
$U_{\gamma '}$
, we have a functorial embedding
Thus, we have
By Lemma 5.1, we have
Therefore, using (5.4), we get
![]() $s_{M}^*(\Theta (\gamma )) = \operatorname {\mathrm {Norm}}(s_{Mp}^*(\Theta (\gamma ')))$
, i.e.,
$s_{M}^*(\Theta (\gamma )) = \operatorname {\mathrm {Norm}}(s_{Mp}^*(\Theta (\gamma ')))$
, i.e.,
By Proposition 4.1, equation (5.5) yields the following commutative diagram:

where
![]() $C_0'$
(resp.
$C_0'$
(resp.
![]() $C_0$
) is the set of cusps of
$C_0$
) is the set of cusps of
![]() $X_1(Mp)$
(resp.
$X_1(Mp)$
(resp.
![]() $X_1(M)$
) in the same diamond orbit as
$X_1(M)$
) in the same diamond orbit as
![]() $0$
. The top horizontal map (resp. bottom horizontal map) is equivariant for the action of
$0$
. The top horizontal map (resp. bottom horizontal map) is equivariant for the action of
![]() $(\operatorname {\mathrm {\mathbf {Z}}}/Mp\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
(resp.
$(\operatorname {\mathrm {\mathbf {Z}}}/Mp\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
(resp.
![]() $(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
).
$(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
).
After applying the Atkin–Lehner involution
![]() $W_{Mp}$
and
$W_{Mp}$
and
![]() $W_M$
to the two lines of (5.6), we get a commutative diagram
$W_M$
to the two lines of (5.6), we get a commutative diagram

where
![]() $C_{\infty }'$
(resp.
$C_{\infty }'$
(resp.
![]() $C_{\infty }$
) is the set of cusps of
$C_{\infty }$
) is the set of cusps of
![]() $X_1(Mp)$
(resp.
$X_1(Mp)$
(resp.
![]() $X_1(M)$
) in the same orbit as
$X_1(M)$
) in the same orbit as
![]() $\infty $
. We have used the facts that
$\infty $
. We have used the facts that
![]() $\varpi _{Mp} = \tilde {\Theta }_{Mp} \circ W_{Mp}$
and
$\varpi _{Mp} = \tilde {\Theta }_{Mp} \circ W_{Mp}$
and
![]() $\varpi _{M} = \tilde {\Theta }_{M} \circ W_{M}$
. This follows from [Reference Sharifi and Venkatesh9, Proposition 4.3.3], where the authors use usual Manin symbols (whereas our map
$\varpi _{M} = \tilde {\Theta }_{M} \circ W_{M}$
. This follows from [Reference Sharifi and Venkatesh9, Proposition 4.3.3], where the authors use usual Manin symbols (whereas our map
![]() $\varpi _M$
uses Manin symbols twisted by the Atkin–Lehner involution).
$\varpi _M$
uses Manin symbols twisted by the Atkin–Lehner involution).
Note that
![]() $\varpi _{Mp}$
and
$\varpi _{Mp}$
and
![]() $\varpi _{M}$
are anti-equivariant for the actions of
$\varpi _{M}$
are anti-equivariant for the actions of
![]() $(\operatorname {\mathrm {\mathbf {Z}}}/Mp\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
and
$(\operatorname {\mathrm {\mathbf {Z}}}/Mp\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
and
![]() $(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
, respectively. This means that for any
$(\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
, respectively. This means that for any
![]() $x \in H_1(X_1(Mp), C_{\infty }', \operatorname {\mathrm {\mathbf {Z}}})$
and
$x \in H_1(X_1(Mp), C_{\infty }', \operatorname {\mathrm {\mathbf {Z}}})$
and
![]() $g \in (\operatorname {\mathrm {\mathbf {Z}}}/Mp\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
, we have
$g \in (\operatorname {\mathrm {\mathbf {Z}}}/Mp\operatorname {\mathrm {\mathbf {Z}}})^{\times }/\pm 1$
, we have
(and similarly for
![]() $\varpi _M$
). Indeed, we have
$\varpi _M$
). Indeed, we have
![]() $W_{Mp} \circ \langle g \rangle = \langle g^{-1} \rangle \circ W_{Mp}$
. This could also have been checked easily directly on the definition of
$W_{Mp} \circ \langle g \rangle = \langle g^{-1} \rangle \circ W_{Mp}$
. This could also have been checked easily directly on the definition of
![]() $\varpi _{Mp}$
and
$\varpi _{Mp}$
and
![]() $\varpi _{M}$
in terms of dual Manin symbols. Let us note that (5.8) is true independently on whether p divides M or not.
$\varpi _{M}$
in terms of dual Manin symbols. Let us note that (5.8) is true independently on whether p divides M or not.
Now, let C be a subset of cusps of
![]() $X_1(Mp)$
as in Theorem 1.4. If
$X_1(Mp)$
as in Theorem 1.4. If
![]() $C \subset C_{\infty }'$
, then Theorem 1.4 follows from (5.7) (we just restrict
$C \subset C_{\infty }'$
, then Theorem 1.4 follows from (5.7) (we just restrict
![]() $\varpi _{Mp}$
to
$\varpi _{Mp}$
to
![]() $H_1(X_1(Mp), C, \operatorname {\mathrm {\mathbf {Z}}}) \subset H_1(X_1(Mp), C_{\infty }', \operatorname {\mathrm {\mathbf {Z}}})$
). Let us explain how to deduce the general case from this special case.
$H_1(X_1(Mp), C, \operatorname {\mathrm {\mathbf {Z}}}) \subset H_1(X_1(Mp), C_{\infty }', \operatorname {\mathrm {\mathbf {Z}}})$
). Let us explain how to deduce the general case from this special case.
Fix
![]() $c \in \mathbf {P}^1(\operatorname {\mathrm {\mathbf {Q}}})$
such that
$c \in \mathbf {P}^1(\operatorname {\mathrm {\mathbf {Q}}})$
such that
![]() $\Gamma _1(Mp)\cdot c \in C$
. An element of
$\Gamma _1(Mp)\cdot c \in C$
. An element of
![]() $H_1(X_1(Mp), C, \operatorname {\mathrm {\mathbf {Z}}})$
is of the form
$H_1(X_1(Mp), C, \operatorname {\mathrm {\mathbf {Z}}})$
is of the form
![]() $\{c, \gamma c\}$
for some
$\{c, \gamma c\}$
for some
![]() $\gamma \in \Gamma _0(Mp)$
. The assumption that all the elements of C are in the same diamond orbit under
$\gamma \in \Gamma _0(Mp)$
. The assumption that all the elements of C are in the same diamond orbit under
![]() $\operatorname {\mathrm {Ker}}((\operatorname {\mathrm {\mathbf {Z}}}/Mp\operatorname {\mathrm {\mathbf {Z}}})^{\times } \rightarrow (\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times })$
means that we can actually choose
$\operatorname {\mathrm {Ker}}((\operatorname {\mathrm {\mathbf {Z}}}/Mp\operatorname {\mathrm {\mathbf {Z}}})^{\times } \rightarrow (\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times })$
means that we can actually choose
![]() $\gamma $
in
$\gamma $
in
![]() $\Gamma _0(Mp) \cap \Gamma _1(M)$
.
$\Gamma _0(Mp) \cap \Gamma _1(M)$
.
We have
 $$ \begin{align*} \{c, \gamma c\} &= \{c, \infty\} + \{\infty, \gamma \infty\} + \{\gamma \infty, \gamma c\} \\& = \{\infty, \gamma \infty\} + (\langle \gamma \rangle - 1)\cdot \{\infty, c \} \text{ ,} \end{align*} $$
$$ \begin{align*} \{c, \gamma c\} &= \{c, \infty\} + \{\infty, \gamma \infty\} + \{\gamma \infty, \gamma c\} \\& = \{\infty, \gamma \infty\} + (\langle \gamma \rangle - 1)\cdot \{\infty, c \} \text{ ,} \end{align*} $$
where
![]() $\langle \gamma \rangle $
is the diamond operator associated with
$\langle \gamma \rangle $
is the diamond operator associated with
![]() $\gamma $
. Since
$\gamma $
. Since
![]() $\gamma \in \Gamma _0(Mp) \cap \Gamma _1(M)$
, we have
$\gamma \in \Gamma _0(Mp) \cap \Gamma _1(M)$
, we have
![]() $ \pi _2\left ( (\langle \gamma \rangle - 1)\cdot \{\infty , c \}\right ) = 0$
. Thus, we have
$ \pi _2\left ( (\langle \gamma \rangle - 1)\cdot \{\infty , c \}\right ) = 0$
. Thus, we have
We also have
in
![]() $ \mathcal {K}_M$
since by (5.8) we have
$ \mathcal {K}_M$
since by (5.8) we have
Thus, we have
 $$ \begin{align*} \operatorname{\mathrm{Norm}}(\varpi_{Mp}( \{c, \gamma c\} )) &= \operatorname{\mathrm{Norm}}(\varpi_{Mp}( \{\infty, \gamma \infty\} )) \\& = \varpi_M(\pi_2( \{\infty, \gamma \infty\} )) \\& =\varpi_M(\pi_2( \{c, \gamma c\} )) \text{ .} \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Norm}}(\varpi_{Mp}( \{c, \gamma c\} )) &= \operatorname{\mathrm{Norm}}(\varpi_{Mp}( \{\infty, \gamma \infty\} )) \\& = \varpi_M(\pi_2( \{\infty, \gamma \infty\} )) \\& =\varpi_M(\pi_2( \{c, \gamma c\} )) \text{ .} \end{align*} $$
This concludes the proof of Theorem 1.4 in the case
![]() $p \mid M$
.
$p \mid M$
.
5.2 The case
 $p \nmid M$
$p \nmid M$
Assume now that p does not divide M. Note that in this case we have
![]() $(1, \zeta _M) \in U'$
. By (5.3), there is an isomorphism
$(1, \zeta _M) \in U'$
. By (5.3), there is an isomorphism
such that:
-
• The map
 $X \rightarrow U'$
is given by the two inclusions
$X \rightarrow U'$
is given by the two inclusions
 $(1, \zeta _M^{p^*}) \in U'$
and
$(1, \zeta _M^{p^*}) \in U'$
and
 $(1, \zeta _{Mp}) \in U'$
, where
$(1, \zeta _{Mp}) \in U'$
, where
 $p^* \in (\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }$
is the inverse of p modulo M.
$p^* \in (\operatorname {\mathrm {\mathbf {Z}}}/M\operatorname {\mathrm {\mathbf {Z}}})^{\times }$
is the inverse of p modulo M. -
• The map
 $X \rightarrow \operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _{M}))$
is given by the canonical map
$X \rightarrow \operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _{M}))$
is given by the canonical map
 $\operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _{Mp})) \rightarrow \operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _{M}))$
and the identity map
$\operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _{Mp})) \rightarrow \operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _{M}))$
and the identity map
 $\operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _{M})) \rightarrow \operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _{M}))$
.
$\operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _{M})) \rightarrow \operatorname {\mathrm {Spec}}(\operatorname {\mathrm {\mathbf {Q}}}(\zeta _{M}))$
.
Applying the functor
![]() $H^2( \cdot , 2)$
to (5.2) (cf. [Reference Sharifi and Venkatesh9, Lemma 2.1.1]), we get the following commutative diagram:
$H^2( \cdot , 2)$
to (5.2) (cf. [Reference Sharifi and Venkatesh9, Lemma 2.1.1]), we get the following commutative diagram:

Combining Lemma 5.1 and (5.9), we get
By (5.8), we have
As in (5.7), we then get a commutative diagram

(note that both
![]() $\pi _1$
and
$\pi _1$
and
![]() $\langle p \rangle \pi _2$
send
$\langle p \rangle \pi _2$
send
![]() $C_{\infty }'$
to
$C_{\infty }'$
to
![]() $C_{\infty }$
, so that this diagram makes sense). An argument identical to the one when
$C_{\infty }$
, so that this diagram makes sense). An argument identical to the one when
![]() $p\mid M$
shows that the diagram of Theorem 1.4 commutes. This concludes the proof of Theorem 1.4.
$p\mid M$
shows that the diagram of Theorem 1.4 commutes. This concludes the proof of Theorem 1.4.
5.3 Proof of Theorem 1.6
Let us now prove Theorem 1.6. Let
![]() $M \geq 4$
and
$M \geq 4$
and
![]() $p \geq 5$
be a prime. One needs to prove that
$p \geq 5$
be a prime. One needs to prove that
is annihilated by the operator
![]() $U_{\ell }-1$
for any prime
$U_{\ell }-1$
for any prime
![]() $\ell \mid M$
. If
$\ell \mid M$
. If
![]() $p \mid M$
, then this is a result of Fukaya and Kato (cf. Theorem 1.3). Therefore, we shall assume in what follows that p does not divide M.
$p \mid M$
, then this is a result of Fukaya and Kato (cf. Theorem 1.3). Therefore, we shall assume in what follows that p does not divide M.
By Theorem 1.4(ii), we have a commutative diagram

By the result of Fukaya and Kato, one knows that
![]() $\varpi _{Mp} \otimes \operatorname {\mathrm {\mathbf {Z}}}_p$
is annihilated by the Hecke operator
$\varpi _{Mp} \otimes \operatorname {\mathrm {\mathbf {Z}}}_p$
is annihilated by the Hecke operator
![]() $U_{\ell }-1$
. Since
$U_{\ell }-1$
. Since
![]() $\pi _1-\langle p \rangle \pi _2$
commutes with the action of
$\pi _1-\langle p \rangle \pi _2$
commutes with the action of
![]() $U_{\ell }-1$
on both sides, it suffices to prove that
$U_{\ell }-1$
on both sides, it suffices to prove that
is surjective. Note that
by the Universal Coefficient Theorem (as
![]() $H_0(X, \operatorname {\mathrm {\mathbf {Z}}})$
is torsion-free).
$H_0(X, \operatorname {\mathrm {\mathbf {Z}}})$
is torsion-free).
By the Nakayama lemma, the surjectivity of our map
![]() $ H_1(X_1(Mp), \operatorname {\mathrm {\mathbf {Z}}}_p) \rightarrow H_1(X_1(M), \operatorname {\mathrm {\mathbf {Z}}}_p)$
is equivalent to the surjectivity of the map
$ H_1(X_1(Mp), \operatorname {\mathrm {\mathbf {Z}}}_p) \rightarrow H_1(X_1(M), \operatorname {\mathrm {\mathbf {Z}}}_p)$
is equivalent to the surjectivity of the map
By the Poincaré duality, it suffices to prove that
is injective. Note that
![]() $H_1(X_1(M), \operatorname {\mathrm {\mathbf {Z}}}/p\operatorname {\mathrm {\mathbf {Z}}})$
is canonically isomorphic to the parabolic cohomology
$H_1(X_1(M), \operatorname {\mathrm {\mathbf {Z}}}/p\operatorname {\mathrm {\mathbf {Z}}})$
is canonically isomorphic to the parabolic cohomology
![]() $H^1_p(\Gamma _1(M), \operatorname {\mathrm {\mathbf {Z}}}/p\operatorname {\mathrm {\mathbf {Z}}})$
, i.e., the subgroup of
$H^1_p(\Gamma _1(M), \operatorname {\mathrm {\mathbf {Z}}}/p\operatorname {\mathrm {\mathbf {Z}}})$
, i.e., the subgroup of
![]() $H^1(\Gamma _1(M), \operatorname {\mathrm {\mathbf {Z}}}/p\operatorname {\mathrm {\mathbf {Z}}})$
consisting of classes of cocycles which are coboundaries when restricted to stabilizers of cusps.
$H^1(\Gamma _1(M), \operatorname {\mathrm {\mathbf {Z}}}/p\operatorname {\mathrm {\mathbf {Z}}})$
consisting of classes of cocycles which are coboundaries when restricted to stabilizers of cusps.
Thus, it is enough for us to prove that the map
is injective. By [Reference Edixhoven and Khare2, Lemma 1], the map
is injective.
By the inflation-restriction exact sequence, we have an exact sequence
Since
![]() $(\operatorname {\mathrm {\mathbf {Z}}}/p\operatorname {\mathrm {\mathbf {Z}}})^{\times }$
has order prime to p, we have
$(\operatorname {\mathrm {\mathbf {Z}}}/p\operatorname {\mathrm {\mathbf {Z}}})^{\times }$
has order prime to p, we have
![]() $H^1((\operatorname {\mathrm {\mathbf {Z}}}/p\operatorname {\mathrm {\mathbf {Z}}})^{\times }, \operatorname {\mathrm {\mathbf {Z}}}/p\operatorname {\mathrm {\mathbf {Z}}})=0$
, so the map
$H^1((\operatorname {\mathrm {\mathbf {Z}}}/p\operatorname {\mathrm {\mathbf {Z}}})^{\times }, \operatorname {\mathrm {\mathbf {Z}}}/p\operatorname {\mathrm {\mathbf {Z}}})=0$
, so the map
is injective. We then conclude that the map
is injective. This proves the injectivity of (5.13), and thus concludes the proof of Theorem 1.6.
Acknowledgment
The first author would like to thank Akshay Venkatesh for a useful discussion concerning this work, especially regarding Lemma 5.1. We would like to thank the anonymous referee for providing detailed and useful comments, which helped to greatly improve the exposition.