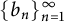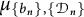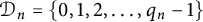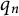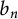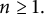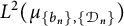1 Introduction
Let
![]() $\mu $
be a compactly supported Borel probability measure on
$\mu $
be a compactly supported Borel probability measure on
![]() ${\mathbb R}^d$
. We say that
${\mathbb R}^d$
. We say that
![]() $\mu $
is a spectral measure if there exists a countable set
$\mu $
is a spectral measure if there exists a countable set
![]() $\Lambda $
of
$\Lambda $
of
![]() ${\mathbb R}^d$
such that
${\mathbb R}^d$
such that
![]() $E(\Lambda )=\{e^{2\pi i \langle \lambda , x\rangle }:\lambda \in \Lambda \}$
forms an orthonormal basis for
$E(\Lambda )=\{e^{2\pi i \langle \lambda , x\rangle }:\lambda \in \Lambda \}$
forms an orthonormal basis for
![]() $L^2(\mu )$
. In this case,
$L^2(\mu )$
. In this case,
![]() $\Lambda $
is called a spectrum of
$\Lambda $
is called a spectrum of
![]() $\mu .$
Spectral theory for the Lebesgue measure on sets has been studied extensively since it is initialed by Fuglede in 1974 [Reference Fuglede16].
$\mu .$
Spectral theory for the Lebesgue measure on sets has been studied extensively since it is initialed by Fuglede in 1974 [Reference Fuglede16].
There exist probability measures that are not the restriction of the Lebesgue measure to bounded sets, but they admit spectra. In 1998, Jorgensen and Pedersen [Reference Jorgensen and Pedersen18] constructed the first example of a singular, non-atomic spectral measure
![]() $\mu _{4,\{0,2\}}$
(i.e., the one-fourth standard Cantor measure) and proved that the set
$\mu _{4,\{0,2\}}$
(i.e., the one-fourth standard Cantor measure) and proved that the set
 $$ \begin{align*}\Lambda=\Big\{\sum_{k=0}^n4^kd_k:d_k\in\{0,1\},n\geq 0\Big\}\end{align*} $$
$$ \begin{align*}\Lambda=\Big\{\sum_{k=0}^n4^kd_k:d_k\in\{0,1\},n\geq 0\Big\}\end{align*} $$
is a spectrum of
![]() $\mu _{4,\{0,2\}}$
. Following this discovery, more interesting spectral measures were found and new spectra for
$\mu _{4,\{0,2\}}$
. Following this discovery, more interesting spectral measures were found and new spectra for
![]() $\mu _{4,\{0,2\}}$
were found (see [Reference An and He2, Reference Dai5, Reference Dai, Fu and Yan6, Reference Dai and Sun8, Reference Dutkay, Han and Sun10, Reference Łaba and Wang19, Reference Li20]). Subsequently, some singular phenomena different from the spectral theory of Lebesgue measures were discovered. For example, there exists only one spectrum with containing
$\mu _{4,\{0,2\}}$
were found (see [Reference An and He2, Reference Dai5, Reference Dai, Fu and Yan6, Reference Dai and Sun8, Reference Dutkay, Han and Sun10, Reference Łaba and Wang19, Reference Li20]). Subsequently, some singular phenomena different from the spectral theory of Lebesgue measures were discovered. For example, there exists only one spectrum with containing
![]() $0$
for
$0$
for
![]() $L^2[0,1]$
, while a given singular spectral measure
$L^2[0,1]$
, while a given singular spectral measure
![]() $\mu $
has more than one spectrum which is not obtained by the translations of each other [Reference Dutkay, Han and Sun10, Reference Fu, He and Wen14]. Another surprising and interesting difference is that the Fourier expansions of functions in
$\mu $
has more than one spectrum which is not obtained by the translations of each other [Reference Dutkay, Han and Sun10, Reference Fu, He and Wen14]. Another surprising and interesting difference is that the Fourier expansions of functions in
![]() $L^2(\mu _{4,\{0,2\}})$
with respect to different spectra may have different convergence properties. Strichartz [Reference Strichartz22, Reference Strichartz23] proved that for any continuous function on
$L^2(\mu _{4,\{0,2\}})$
with respect to different spectra may have different convergence properties. Strichartz [Reference Strichartz22, Reference Strichartz23] proved that for any continuous function on
![]() ${\mathbb R}$
, its Fourier expansion with respect to
${\mathbb R}$
, its Fourier expansion with respect to
![]() $\Lambda $
is uniformly convergent; but Dutkay et al. showed in [Reference Dutkay, Han and Sun11] that there exists a continuous function on
$\Lambda $
is uniformly convergent; but Dutkay et al. showed in [Reference Dutkay, Han and Sun11] that there exists a continuous function on
![]() ${\mathbb R}$
whose Fourier expansion with respect to the spectrum
${\mathbb R}$
whose Fourier expansion with respect to the spectrum
![]() $17\Lambda $
is divergent at
$17\Lambda $
is divergent at
![]() $0$
. Based on the above exotic phenomena, a natural question is raised:
$0$
. Based on the above exotic phenomena, a natural question is raised:
For a given spectral measure, can we find all spectra?
It is quite challenging to “characterize” all the spectra (no example is known with this property). Motivated by the above problem, many researchers concentrated their work on investigating self-similar/self-affine/Moran spectral measures and the construction of their spectra from various aspects (see [Reference An, Fu and Lai1, Reference An and Wang3, Reference Chen, Liu and Wang4, Reference Dai, He and Lai7–Reference Dutkay, Han and Sun10, Reference Dutkay and Haussermann12, Reference Fu, He and Wen14, Reference Hu and Lau17, Reference Lu, Dong and Liu21, Reference Yan25] and the references therein).
Nowadays, there are a few of literature on this topic to construct new spectra. Most of this literature deals with the issue of self-similar/self-affine measures. Various of new spectra have been constructed for the measure
![]() $\mu _{4,\{0,2\}}$
by Dutkay et al. [Reference Dutkay, Han and Sun10], for self-similar measure with consecutive digits by Dai et al. [Reference Dai, He and Lai7], Dai [Reference Dai5], for infinite Bernoulli convolution by Li [Reference Li20], Fu et al. [Reference Fu, He and Wen14], for certain self-affine measures on
$\mu _{4,\{0,2\}}$
by Dutkay et al. [Reference Dutkay, Han and Sun10], for self-similar measure with consecutive digits by Dai et al. [Reference Dai, He and Lai7], Dai [Reference Dai5], for infinite Bernoulli convolution by Li [Reference Li20], Fu et al. [Reference Fu, He and Wen14], for certain self-affine measures on
![]() ${\mathbb R}^d$
by Deng et al. [Reference Deng, Dong and Li9], etc. Besides these results, some answers for spectral Moran measures have been given in [Reference Fu and Wang15, Reference Wang and Yin24]. Motivated by these, the main focus of this paper is to study the classification of spectra of the so-called Moran measures with consecutive digits, where
${\mathbb R}^d$
by Deng et al. [Reference Deng, Dong and Li9], etc. Besides these results, some answers for spectral Moran measures have been given in [Reference Fu and Wang15, Reference Wang and Yin24]. Motivated by these, the main focus of this paper is to study the classification of spectra of the so-called Moran measures with consecutive digits, where
![]() $\mu _{4,\{0,2\}}$
and Cantor measures with consecutive digits are special cases.
$\mu _{4,\{0,2\}}$
and Cantor measures with consecutive digits are special cases.
Let
![]() $\{b_n\}_{n=1}^{\infty }$
be a sequence of integers larger than 1 and
$\{b_n\}_{n=1}^{\infty }$
be a sequence of integers larger than 1 and
![]() ${\mathcal D}_{n}=\{0,1,2,\ldots ,q_n-1\}$
for each
${\mathcal D}_{n}=\{0,1,2,\ldots ,q_n-1\}$
for each
![]() $n\geq 1,$
there exists a Borel probability measure
$n\geq 1,$
there exists a Borel probability measure
![]() $\mu _{\{b_n\},\{{\mathcal D}_n\}},$
which is defined by the following infinite convolutions of finite measures:
$\mu _{\{b_n\},\{{\mathcal D}_n\}},$
which is defined by the following infinite convolutions of finite measures:
where
![]() $rE=\{rx:x\in E\},~\delta _E=\frac {1}{\#E}\sum _{e\in E}\delta _e$
(
$rE=\{rx:x\in E\},~\delta _E=\frac {1}{\#E}\sum _{e\in E}\delta _e$
(
![]() $\#E$
is the cardinality of the finite set
$\#E$
is the cardinality of the finite set
![]() $E,~\delta _e$
is the Dirac measure at the point
$E,~\delta _e$
is the Dirac measure at the point
![]() $e\in {\mathbb R}$
) and the convergence is in a weak sense. Note that
$e\in {\mathbb R}$
) and the convergence is in a weak sense. Note that
![]() ${\mathcal D}_n=\{0,1,2,\ldots ,q_n-1\}$
, we call the measure
${\mathcal D}_n=\{0,1,2,\ldots ,q_n-1\}$
, we call the measure
![]() $\mu _{\{b_n\},\{{\mathcal D}_n\}}$
a Moran measure with consecutive digits. In particular, when
$\mu _{\{b_n\},\{{\mathcal D}_n\}}$
a Moran measure with consecutive digits. In particular, when
![]() $b_n=b$
and
$b_n=b$
and
![]() ${\mathcal D}_n=\{0,1,\ldots ,q-1\}:={\mathcal D}$
for all
${\mathcal D}_n=\{0,1,\ldots ,q-1\}:={\mathcal D}$
for all
![]() $n \in {\mathbb N}$
, then the measure
$n \in {\mathbb N}$
, then the measure
![]() $\mu _{\{b_n\},\{{\mathcal D}_n\}}$
is reduced to the self-similar measure
$\mu _{\{b_n\},\{{\mathcal D}_n\}}$
is reduced to the self-similar measure
![]() $\mu _{b,{\mathcal D}}$
(see [Reference Falconer13]).
$\mu _{b,{\mathcal D}}$
(see [Reference Falconer13]).
Let us first recall the known results on the spectrality of the measure
![]() $\mu _{\{b_n\},\{{\mathcal D}_n\}}$
. In the self-similar case, Dai, He, and Lai [Reference Dai, He and Lai7] showed that the measure
$\mu _{\{b_n\},\{{\mathcal D}_n\}}$
. In the self-similar case, Dai, He, and Lai [Reference Dai, He and Lai7] showed that the measure
![]() $\mu _{b,{\mathcal D}}$
is spectral if and only if
$\mu _{b,{\mathcal D}}$
is spectral if and only if
![]() $q|b$
. Recently, An and He [Reference An and He2] proved that if
$q|b$
. Recently, An and He [Reference An and He2] proved that if
![]() $q_n|b_n$
for all
$q_n|b_n$
for all
![]() $n\geq 1,$
then
$n\geq 1,$
then
![]() $\mu _{\{b_n\},\{{\mathcal D}_n\}}$
is a spectral measure. Continuing the above research, the main goal of this paper is to investigate the structure of spectra for the Moran spectral measure
$\mu _{\{b_n\},\{{\mathcal D}_n\}}$
is a spectral measure. Continuing the above research, the main goal of this paper is to investigate the structure of spectra for the Moran spectral measure
![]() $\mu _{\{b_n\},\{{\mathcal D}_n\}}$
.
$\mu _{\{b_n\},\{{\mathcal D}_n\}}$
.
The starting point of our approach is to analyze the precise structure of the zero set of the Fourier transform
![]() $\widehat {\mu }_{\{b_n\},\{{\mathcal D}_n\}}$
, and then we introduce the maximal orthonormal sets, as candidates for the spectra of the measure
$\widehat {\mu }_{\{b_n\},\{{\mathcal D}_n\}}$
, and then we introduce the maximal orthonormal sets, as candidates for the spectra of the measure
![]() $\mu _{\{b_n\},\{{\mathcal D}_n\}}$
. We shows that there is one-to-one correspondence between a maximal orthonormal set and a tree mapping (Theorem 1.2). More precisely, we decomposed the maximal orthonormal sets of the measure
$\mu _{\{b_n\},\{{\mathcal D}_n\}}$
. We shows that there is one-to-one correspondence between a maximal orthonormal set and a tree mapping (Theorem 1.2). More precisely, we decomposed the maximal orthonormal sets of the measure
![]() $\mu _{\{b_n\},\{{\mathcal D}_n\}}$
using
$\mu _{\{b_n\},\{{\mathcal D}_n\}}$
using
![]() ${{\mathcal C}_j}$
-adic expansion and put them into a labeling of the tree.
${{\mathcal C}_j}$
-adic expansion and put them into a labeling of the tree.
Definition 1.1 Let
![]() $b_n=q_nr_n$
for all
$b_n=q_nr_n$
for all
![]() $n\geq 1,$
we say that
$n\geq 1,$
we say that
![]() $\tau $
is a tree mapping if it is a map
$\tau $
is a tree mapping if it is a map
![]() $\tau :{\mathcal D}_{0,*}\rightarrow {\mathbb Z}$
which satisfies:
$\tau :{\mathcal D}_{0,*}\rightarrow {\mathbb Z}$
which satisfies:
(i)
![]() $\tau (0^{n})=0$
for all
$\tau (0^{n})=0$
for all
![]() $n\geq 1,$
$n\geq 1,$
(ii) for all
![]() $n\geq 1,~\tau (\sigma _{1}\dots \sigma _n) \in (\sigma _{n}+q_n{\mathbb Z})\bigcap \{-1,0,1,\ldots ,q_nr_{n+1}-2\},$
$n\geq 1,~\tau (\sigma _{1}\dots \sigma _n) \in (\sigma _{n}+q_n{\mathbb Z})\bigcap \{-1,0,1,\ldots ,q_nr_{n+1}-2\},$
(iii) for any word
![]() $\sigma \in {\mathcal D}_{0,n}(n\geq 1),$
there exists
$\sigma \in {\mathcal D}_{0,n}(n\geq 1),$
there exists
![]() $\sigma '\in {\mathcal D}_{n,\infty }$
such that
$\sigma '\in {\mathcal D}_{n,\infty }$
such that
![]() $\tau \big ((\sigma \sigma ')|_j\big )=0$
for all j sufficiently large.
$\tau \big ((\sigma \sigma ')|_j\big )=0$
for all j sufficiently large.
Given a tree mapping
![]() $\tau $
, we define the following sets:
$\tau $
, we define the following sets:
and
 $$ \begin{align*} \Lambda(\tau)=\Big\{\sum_{k=1}^{\infty}\tau(\sigma|_{k})r_k b_1\dots b_{k-1}\big|\sigma\in{\mathcal D}(\tau)\Big\}. \end{align*} $$
$$ \begin{align*} \Lambda(\tau)=\Big\{\sum_{k=1}^{\infty}\tau(\sigma|_{k})r_k b_1\dots b_{k-1}\big|\sigma\in{\mathcal D}(\tau)\Big\}. \end{align*} $$
It will play a special role in the following theorem, which gives a characterization of the maximal orthogonal set of
![]() $L^2(\mu _{\{b_n\},\{{\mathcal D}_n\}})$
.
$L^2(\mu _{\{b_n\},\{{\mathcal D}_n\}})$
.
Theorem 1.2 The set
![]() $\Lambda $
with
$\Lambda $
with
![]() $0\in \Lambda $
is a maximal orthonormal set of
$0\in \Lambda $
is a maximal orthonormal set of
![]() $\mu _{\{b_n\},\{{\mathcal D}_n\}}$
if and only if there exists a tree mapping
$\mu _{\{b_n\},\{{\mathcal D}_n\}}$
if and only if there exists a tree mapping
![]() $\tau $
such that
$\tau $
such that
![]() $\Lambda =\Lambda (\tau )$
.
$\Lambda =\Lambda (\tau )$
.
While a maximal orthonormal set is not necessarily a spectrum since it may lack of completeness in
![]() $L^2(\mu _{\{b_n\},\{{\mathcal D}_n\}}).$
So what we need to do is to investigate under what conditions on
$L^2(\mu _{\{b_n\},\{{\mathcal D}_n\}}).$
So what we need to do is to investigate under what conditions on
![]() $\tau $
such that the set
$\tau $
such that the set
![]() $ \Lambda (\tau )$
to be a spectrum for the measure
$ \Lambda (\tau )$
to be a spectrum for the measure
![]() $\mu _{\{b_n\},\{{\mathcal D}_n\}}$
. We first introduce a good path to ensure the above maximal orthogonal set
$\mu _{\{b_n\},\{{\mathcal D}_n\}}$
. We first introduce a good path to ensure the above maximal orthogonal set
![]() $ E\big (\Lambda (\tau )\big )$
to be a complete set in
$ E\big (\Lambda (\tau )\big )$
to be a complete set in
![]() $L^2(\mu _{\{b_n\},\{{\mathcal D}_n\}}).$
$L^2(\mu _{\{b_n\},\{{\mathcal D}_n\}}).$
Theorem 1.3 Let
![]() $\{q_n,b_n\}_{n=1}^\infty $
be a sequence of positive integers larger than 1 with
$\{q_n,b_n\}_{n=1}^\infty $
be a sequence of positive integers larger than 1 with
![]() $q_n|b_n$
for all
$q_n|b_n$
for all
![]() $n\in {\mathbb N}$
and
$n\in {\mathbb N}$
and
![]() $\sup _{n\geq 1}\{b_n\}<\infty $
. Let
$\sup _{n\geq 1}\{b_n\}<\infty $
. Let
![]() $\tau $
be a tree mapping of
$\tau $
be a tree mapping of
![]() $\mu _{\{b_n\},\{{\mathcal D}_n\}}$
. Suppose there is a constant integer
$\mu _{\{b_n\},\{{\mathcal D}_n\}}$
. Suppose there is a constant integer
![]() $N>0$
such that for any word
$N>0$
such that for any word
![]() $\sigma \in {\mathcal D}_{0,k}(k\geq 1),$
there exists
$\sigma \in {\mathcal D}_{0,k}(k\geq 1),$
there exists
![]() $\sigma '\in {\mathcal D}_{k,\infty }$
such that
$\sigma '\in {\mathcal D}_{k,\infty }$
such that
![]() $\sigma \sigma '\in {\mathcal D}(\tau )$
and one of the following two conditions is satisfied:
$\sigma \sigma '\in {\mathcal D}(\tau )$
and one of the following two conditions is satisfied:
(i)
![]() $\tau \big ((\sigma \sigma ')|_{k+j}\big )=0~$
for all
$\tau \big ((\sigma \sigma ')|_{k+j}\big )=0~$
for all
![]() $j\geq 1;$
$j\geq 1;$
(ii)
![]() $\tau \big ((\sigma \sigma ')|_{k+j}\big )=0$
for all
$\tau \big ((\sigma \sigma ')|_{k+j}\big )=0$
for all
![]() $1\leq j\leq n,\ \tau \big ((\sigma \sigma ')|_{k+n+1}\big )\in q_{k+n+1}{\mathbb Z}\backslash \{0\}$
and
$1\leq j\leq n,\ \tau \big ((\sigma \sigma ')|_{k+n+1}\big )\in q_{k+n+1}{\mathbb Z}\backslash \{0\}$
and
Then
![]() $\Lambda (\tau )$
is a spectrum of
$\Lambda (\tau )$
is a spectrum of
![]() $\mu _{\{b_n\},\{{\mathcal D}_n\}}.$
$\mu _{\{b_n\},\{{\mathcal D}_n\}}.$
We remark that (1.2) shows that the efficient length of the word
![]() $\sigma \sigma '$
is uniformly bounded, that is to say,
$\sigma \sigma '$
is uniformly bounded, that is to say,
![]() $\sigma '$
is crucial in the proof of the completeness. However, the length of
$\sigma '$
is crucial in the proof of the completeness. However, the length of
![]() $\sigma \sigma '$
i.e.,
$\sigma \sigma '$
i.e.,
![]() $\max \Big \{j\geq 1:\tau \big ((\sigma \sigma ')|_{k+j}\big )\neq 0 \Big \}$
may be not uniformly bounded since it also depends on the choice of n in
$\max \Big \{j\geq 1:\tau \big ((\sigma \sigma ')|_{k+j}\big )\neq 0 \Big \}$
may be not uniformly bounded since it also depends on the choice of n in
![]() $0^n$
.
$0^n$
.
Next, we consider other digits that can be used for the base expansion of the integers in the candidate set
![]() $\Lambda $
, and give a sufficient condition when these will generate spectra for the measure
$\Lambda $
, and give a sufficient condition when these will generate spectra for the measure
![]() $\mu _{\{b_n\},\{{\mathcal D}_n\}}$
.
$\mu _{\{b_n\},\{{\mathcal D}_n\}}$
.
Definition 1.4 We say that
![]() $\tau $
is a generalized tree mapping if it is a mapping
$\tau $
is a generalized tree mapping if it is a mapping
![]() $\tau :{\mathcal D}_{0,*}\rightarrow {\mathbb Z}$
, which satisfies:
$\tau :{\mathcal D}_{0,*}\rightarrow {\mathbb Z}$
, which satisfies:
(i)
![]() $\tau (\sigma _{1}\sigma _2\dots \sigma _{n})=0$
if
$\tau (\sigma _{1}\sigma _2\dots \sigma _{n})=0$
if
![]() $\sigma _n=0$
;
$\sigma _n=0$
;
(ii)
![]() $\tau (\sigma _{1}\sigma _2\dots \sigma _{n}) \in \sigma _{n}+q_n{\mathbb Z}$
if
$\tau (\sigma _{1}\sigma _2\dots \sigma _{n}) \in \sigma _{n}+q_n{\mathbb Z}$
if
![]() $\sigma _n \neq 0$
.
$\sigma _n \neq 0$
.
We say that
![]() $\sigma \in {\mathcal D}_{0,\infty }$
is a useful word about the generalized tree mapping
$\sigma \in {\mathcal D}_{0,\infty }$
is a useful word about the generalized tree mapping
![]() $\tau $
if there exists an integer
$\tau $
if there exists an integer
![]() $\tau ^\diamond (\sigma )\in {\mathbb Z}$
satisfying
$\tau ^\diamond (\sigma )\in {\mathbb Z}$
satisfying
 $$ \begin{align*}\tau^\diamond(\sigma)\equiv\sum_{k=1}^n\tau(\sigma|_k)r_kB_{k-1}\quad \pmod{r_{n+1}B_n}, \qquad \text{for all}\ n\ge 1.\end{align*} $$
$$ \begin{align*}\tau^\diamond(\sigma)\equiv\sum_{k=1}^n\tau(\sigma|_k)r_kB_{k-1}\quad \pmod{r_{n+1}B_n}, \qquad \text{for all}\ n\ge 1.\end{align*} $$
Given a generalized tree mapping
![]() $\tau $
, we let
$\tau $
, we let
Theorem 1.5 Let
![]() $\{q_n,b_n\}_{n=1}^\infty $
be a sequence of positive integers larger than 1 with
$\{q_n,b_n\}_{n=1}^\infty $
be a sequence of positive integers larger than 1 with
![]() $q_n|b_n$
for all
$q_n|b_n$
for all
![]() $n\in {\mathbb N}$
and
$n\in {\mathbb N}$
and
![]() $\sup _{n\geq 1}\{b_n\}<\infty $
. Let
$\sup _{n\geq 1}\{b_n\}<\infty $
. Let
![]() $\tau $
be a generalized tree mapping,
$\tau $
be a generalized tree mapping,
(i)
![]() $\Lambda ^\diamond (\tau )$
is a maximal orthogonal set of
$\Lambda ^\diamond (\tau )$
is a maximal orthogonal set of
![]() $\mu _{\{b_n\},\{{\mathcal D}_n\}}$
;
$\mu _{\{b_n\},\{{\mathcal D}_n\}}$
;
(ii) if
![]() $\sup _{\sigma \in {\mathcal D}_{0,*}}|\tau (\sigma )|<\infty $
, then
$\sup _{\sigma \in {\mathcal D}_{0,*}}|\tau (\sigma )|<\infty $
, then
![]() $\Lambda ^\diamond (\tau )$
is a spectrum of
$\Lambda ^\diamond (\tau )$
is a spectrum of
![]() $\mu _{\{b_n\},\{{\mathcal D}_n\}}$
.
$\mu _{\{b_n\},\{{\mathcal D}_n\}}$
.
The paper is organized as follows. In Section 2, we recall some preliminary results on basic criterion for spectral measures to prove our main results in the sequel, and characterize all the maximal orthonormal sets
![]() $\Lambda $
for
$\Lambda $
for
![]() $L^2(\mu _{\{b_n\},\{{\mathcal D}_n\}})$
. Theorem 1.3 is proved in Section 3. In Section 4, the proof of Theorem 1.5 is given.
$L^2(\mu _{\{b_n\},\{{\mathcal D}_n\}})$
. Theorem 1.3 is proved in Section 3. In Section 4, the proof of Theorem 1.5 is given.
2 Preliminaries and maximal orthogonal set
In this section, we first give some necessary definitions and facts that we need in the proof of the main theorem. Subsequently, we characterize all the maximal orthogonal sets
![]() $\Lambda $
for
$\Lambda $
for
![]() $L^2(\mu _{\{b_n\},\{{\mathcal D}_n\}})$
via a tree mapping (see Definition 1.1).
$L^2(\mu _{\{b_n\},\{{\mathcal D}_n\}})$
via a tree mapping (see Definition 1.1).
2.1 A criterion for spectral measures
Let
![]() $\mu $
be a probability measure with compact support on
$\mu $
be a probability measure with compact support on
![]() ${\mathbb R}.$
As usual, we define the Fourier transform of the measure
${\mathbb R}.$
As usual, we define the Fourier transform of the measure
![]() $\mu $
,
$\mu $
,
A countable set
![]() $\Lambda \subseteq {\mathbb R}$
is called an orthonormal set/ maximal orthonormal set/spectrum, respectively, of
$\Lambda \subseteq {\mathbb R}$
is called an orthonormal set/ maximal orthonormal set/spectrum, respectively, of
![]() $\mu $
if
$\mu $
if
![]() $E(\Lambda ):=\{e^{ 2\pi i\lambda x}:\lambda \in \Lambda \}$
is an orthonormal set/maximal orthogonal set/orthonormal basis, respectively, for
$E(\Lambda ):=\{e^{ 2\pi i\lambda x}:\lambda \in \Lambda \}$
is an orthonormal set/maximal orthogonal set/orthonormal basis, respectively, for
![]() $L^{2}(\mu ).$
It is easy to show that
$L^{2}(\mu ).$
It is easy to show that
![]() $\Lambda $
is an orthogonal set of
$\Lambda $
is an orthogonal set of
![]() $\mu $
if and only if
$\mu $
if and only if
![]() $\widehat {\mu }(\lambda _{i}-\lambda _{j})=0$
for any
$\widehat {\mu }(\lambda _{i}-\lambda _{j})=0$
for any
![]() $\lambda _{i}\neq \lambda _{j}\in \Lambda $
, which is equivalent to
$\lambda _{i}\neq \lambda _{j}\in \Lambda $
, which is equivalent to
where
![]() $\mathcal {Z}(f):=\{\xi :f(\xi )=0\}$
is the set of the roots of the function
$\mathcal {Z}(f):=\{\xi :f(\xi )=0\}$
is the set of the roots of the function
![]() $f(\xi ).$
$f(\xi ).$
Combining (1.1) and (2.1), we can conclude that
 $$ \begin{align*} \widehat{\mu}_{{\{b_n\},\{{\mathcal D}_n\}}}(\xi)=\prod_{j=1}^{\infty} M_{{\mathcal D}_j}\Big(\frac{\xi}{b_1b_2\dots b_j}\Big), \end{align*} $$
$$ \begin{align*} \widehat{\mu}_{{\{b_n\},\{{\mathcal D}_n\}}}(\xi)=\prod_{j=1}^{\infty} M_{{\mathcal D}_j}\Big(\frac{\xi}{b_1b_2\dots b_j}\Big), \end{align*} $$
where
A direct calculation shows that
where
![]() $q_j\nmid a$
means that
$q_j\nmid a$
means that
![]() $q_j$
does not divide
$q_j$
does not divide
![]() $a.$
Hence, the zero of
$a.$
Hence, the zero of
![]() $\widehat {\mu }_{\{b_n\},\{{\mathcal D}_n\}}$
is given by
$\widehat {\mu }_{\{b_n\},\{{\mathcal D}_n\}}$
is given by
where
![]() $r_j=b_j/q_j$
for all
$r_j=b_j/q_j$
for all
![]() $j\geq 1$
and
$j\geq 1$
and
![]() $B_j=b_0b_1\cdots b_j$
with
$B_j=b_0b_1\cdots b_j$
with
![]() $b_0=1$
.
$b_0=1$
.
To this end, we introduce a fundamental criterion for spectral measures, which is a direct application of Stone–Weierstrass Theorem and Parseval’s identity. For any
![]() $\xi \in {\mathbb R}$
, denote
$\xi \in {\mathbb R}$
, denote
Theorem 2.1 [Reference Jorgensen and Pedersen18]
Let
![]() $\mu $
be a Borel probability measure with compact support on
$\mu $
be a Borel probability measure with compact support on
![]() ${\mathbb R}$
, and let
${\mathbb R}$
, and let
![]() $\Lambda \subseteq {\mathbb R}$
be a countable subset. Then:
$\Lambda \subseteq {\mathbb R}$
be a countable subset. Then:
(i)
![]() $\Lambda $
is an orthonormal set of
$\Lambda $
is an orthonormal set of
![]() $\mu $
if and only if
$\mu $
if and only if
![]() $Q(\xi )\le 1$
for any
$Q(\xi )\le 1$
for any
![]() $\xi \in {\mathbb R};$
$\xi \in {\mathbb R};$
(ii)
![]() $\Lambda $
is a spectrum of
$\Lambda $
is a spectrum of
![]() $\mu $
if and only if
$\mu $
if and only if
![]() $Q(\xi )\equiv 1$
for any
$Q(\xi )\equiv 1$
for any
![]() $\xi \in {\mathbb R};$
$\xi \in {\mathbb R};$
(iii)
![]() $Q(\xi )$
is an entire function in the complex plane if
$Q(\xi )$
is an entire function in the complex plane if
![]() $\Lambda $
is an orthogonal set of
$\Lambda $
is an orthogonal set of
![]() $\mu .$
$\mu .$
2.2 Maximal orthogonal sets
We start with some notations for simplicity. Fix such an integer
![]() $n\geq 0,$
let
$n\geq 0,$
let
be the set of all words with length
![]() $k.$
We adopt that
$k.$
We adopt that
![]() ${\mathcal D}_{n,*}=\bigcup _{k=1}^\infty {\mathcal D}_{n,k}\bigcup \{\emptyset \}$
is the set of all the finite words beginning with
${\mathcal D}_{n,*}=\bigcup _{k=1}^\infty {\mathcal D}_{n,k}\bigcup \{\emptyset \}$
is the set of all the finite words beginning with
![]() ${\mathcal D}_{n+1}$
and
${\mathcal D}_{n+1}$
and
![]() ${\mathcal D}_{n,\infty }=\{\sigma _{n+1}\sigma _{n+2}\ldots : \sigma _k\in {\mathcal D}_k, k\geq n+1 \}$
is the set of all the infinite words beginning with
${\mathcal D}_{n,\infty }=\{\sigma _{n+1}\sigma _{n+2}\ldots : \sigma _k\in {\mathcal D}_k, k\geq n+1 \}$
is the set of all the infinite words beginning with
![]() ${\mathcal D}_{n+1}$
. For any
${\mathcal D}_{n+1}$
. For any
![]() $\sigma =\sigma _{n+1}\sigma _{n+2}\dots \sigma _{n+k}\in {\mathcal D}_{n,*},$
we use
$\sigma =\sigma _{n+1}\sigma _{n+2}\dots \sigma _{n+k}\in {\mathcal D}_{n,*},$
we use
![]() $|\sigma |=k$
to be its length and
$|\sigma |=k$
to be its length and
![]() $\sigma \mid _j:=\sigma _{n+1}\sigma _{n+2}\dots \sigma _{n+j}(1\leq j \leq |\sigma |).$
For any
$\sigma \mid _j:=\sigma _{n+1}\sigma _{n+2}\dots \sigma _{n+j}(1\leq j \leq |\sigma |).$
For any
![]() $\sigma \in {\mathcal D}_{n,*}$
and
$\sigma \in {\mathcal D}_{n,*}$
and
![]() $\sigma '\in {\mathcal D}_{n',*}\bigcup {\mathcal D}_{n',\infty },$
the word
$\sigma '\in {\mathcal D}_{n',*}\bigcup {\mathcal D}_{n',\infty },$
the word
![]() $\sigma \sigma '$
is their nature conjunction. In particular,
$\sigma \sigma '$
is their nature conjunction. In particular,
![]() $\emptyset I=I$
and
$\emptyset I=I$
and
![]() $0^\infty =000\dots .$
$0^\infty =000\dots .$
For simplicity, we set
![]() $b_0=1$
and
$b_0=1$
and
![]() $B_k=b_0b_1b_2\dots b_k$
for all
$B_k=b_0b_1b_2\dots b_k$
for all
![]() $k\geq 1$
. Given a tree mapping
$k\geq 1$
. Given a tree mapping
![]() $\tau $
, recall that
$\tau $
, recall that
For any
![]() $\sigma \in {\mathcal D}(\tau )$
, we let
$\sigma \in {\mathcal D}(\tau )$
, we let
 $$ \begin{align} \tau(\sigma)=\sum_{k=1}^{\infty}\tau(\sigma|_{k})r_kB_{k-1} \quad \text{and} \quad \Lambda(\tau)=\{\tau(\sigma)|\sigma\in{\mathcal D}(\tau)\}, \end{align} $$
$$ \begin{align} \tau(\sigma)=\sum_{k=1}^{\infty}\tau(\sigma|_{k})r_kB_{k-1} \quad \text{and} \quad \Lambda(\tau)=\{\tau(\sigma)|\sigma\in{\mathcal D}(\tau)\}, \end{align} $$
which plays a special role in Theorem 1.2.
Before giving a proof of Theorem 1.2, we give the following lemma.
Lemma 2.2 Let
![]() $\mathcal {C}_n=\{-1,0,1,\ldots ,q_nr_{n+1}-2\}$
and
$\mathcal {C}_n=\{-1,0,1,\ldots ,q_nr_{n+1}-2\}$
and
![]() $\textbf {C}_n=\mathcal {C}_{1}\times \cdots \times \mathcal {C}_n$
for all
$\textbf {C}_n=\mathcal {C}_{1}\times \cdots \times \mathcal {C}_n$
for all
![]() $n\geq 1.$
Then for any
$n\geq 1.$
Then for any
![]() $k\in {\mathbb Z}(k\neq 0),$
there exists a unique word
$k\in {\mathbb Z}(k\neq 0),$
there exists a unique word
![]() $\sigma =\sigma _{1}\sigma _{2}\dots \sigma _n\in \textbf {C}_n$
with
$\sigma =\sigma _{1}\sigma _{2}\dots \sigma _n\in \textbf {C}_n$
with
![]() $\sigma _n\neq 0,$
such that
$\sigma _n\neq 0,$
such that
Moreover, if
![]() $k=0,$
then
$k=0,$
then
![]() $\sigma =\sigma _{1}=0.$
$\sigma =\sigma _{1}=0.$
Proof For any
![]() $k\in {\mathbb Z}$
and
$k\in {\mathbb Z}$
and
![]() $|k|<q_1r_2,$
let
$|k|<q_1r_2,$
let
 $$ \begin{align*} \sigma= \begin{cases} 1(-1),\qquad\qquad k=-(q_1r_2-1),\\ (q_1r_2+k)(-1),\quad-(q_1r_2-1)<k<0,\\ k, \qquad\qquad\qquad0\leq k<q_1r_2-1,\\ -11,\qquad\qquad\quad k=q_1r_2-1,\nonumber \end{cases} \end{align*} $$
$$ \begin{align*} \sigma= \begin{cases} 1(-1),\qquad\qquad k=-(q_1r_2-1),\\ (q_1r_2+k)(-1),\quad-(q_1r_2-1)<k<0,\\ k, \qquad\qquad\qquad0\leq k<q_1r_2-1,\\ -11,\qquad\qquad\quad k=q_1r_2-1,\nonumber \end{cases} \end{align*} $$
then
![]() $k=\pi (\sigma ).$
When
$k=\pi (\sigma ).$
When
![]() $|k|>q_1r_2,$
then k can be decomposed uniquely as
$|k|>q_1r_2,$
then k can be decomposed uniquely as
![]() $k=c_{1}+k_{1}q_1r_2,$
where
$k=c_{1}+k_{1}q_1r_2,$
where
![]() $c_{1}\in {\mathcal C}_{1}.$
If
$c_{1}\in {\mathcal C}_{1}.$
If
![]() $|k_{1}|<q_2r_3,$
then
$|k_{1}|<q_2r_3,$
then
![]() $k_{1}$
has to be decomposed as in the previous step. Otherwise, we further decompose
$k_{1}$
has to be decomposed as in the previous step. Otherwise, we further decompose
![]() $k_{1}$
in a similar way and we get
$k_{1}$
in a similar way and we get
![]() $|k_n|<q_{n+1}r_{n+2}$
after finite number k steps. The expansion is unique since each decomposition is unique.
$|k_n|<q_{n+1}r_{n+2}$
after finite number k steps. The expansion is unique since each decomposition is unique.
Now, we can give the proof of Theorem 1.2.
Proof of Theorem 1.2
Suppose
![]() $\Lambda =\Lambda (\tau )$
for some tree mapping
$\Lambda =\Lambda (\tau )$
for some tree mapping
![]() $\tau .$
We show that it is a maximal orthogonal of
$\tau .$
We show that it is a maximal orthogonal of
![]() $\mu _{\{b_n\},\{{\mathcal D}_n\}}.$
To see this, we firstly show the orthogonality of
$\mu _{\{b_n\},\{{\mathcal D}_n\}}.$
To see this, we firstly show the orthogonality of
![]() $\Lambda $
. Pick two distinct
$\Lambda $
. Pick two distinct
![]() $\lambda ,\lambda '\in \Lambda ,$
by the definition of
$\lambda ,\lambda '\in \Lambda ,$
by the definition of
![]() $\Lambda (\tau ),$
we can find
$\Lambda (\tau ),$
we can find
![]() $\sigma \neq \sigma '\in {\mathcal D}(\tau )$
such that
$\sigma \neq \sigma '\in {\mathcal D}(\tau )$
such that
 $$ \begin{align*}\lambda=\sum_{j=1}^{\infty}\tau(\sigma|_{j})r_jB_{j-1}\quad \text{and}\quad \lambda'=\sum_{j=1}^{\infty}\tau(\sigma'|_{j})r_jB_{j-1}.\end{align*} $$
$$ \begin{align*}\lambda=\sum_{j=1}^{\infty}\tau(\sigma|_{j})r_jB_{j-1}\quad \text{and}\quad \lambda'=\sum_{j=1}^{\infty}\tau(\sigma'|_{j})r_jB_{j-1}.\end{align*} $$
Let k be the first index such that
![]() $\sigma |_{k}\neq \sigma '|_{k}.$
Then, for some integer
$\sigma |_{k}\neq \sigma '|_{k}.$
Then, for some integer
![]() $M,$
we can write
$M,$
we can write
By (ii) in Definition 1.1,
![]() $\tau (\sigma |_{k})$
and
$\tau (\sigma |_{k})$
and
![]() $\tau (\sigma '|_{k})$
are in distinct residue classes of
$\tau (\sigma '|_{k})$
are in distinct residue classes of
![]() $q_k.$
This implies
$q_k.$
This implies
![]() $\lambda -\lambda ' \in \mathcal {Z}(\widehat {\mu }_{\{b_n\},\{{\mathcal D}_n\}})$
and then
$\lambda -\lambda ' \in \mathcal {Z}(\widehat {\mu }_{\{b_n\},\{{\mathcal D}_n\}})$
and then
![]() $\Lambda (\tau )$
is orthogonal.
$\Lambda (\tau )$
is orthogonal.
With respect to the maximality of the orthogonal set
![]() $\Lambda ,$
the proof is by contradiction. Suppose
$\Lambda ,$
the proof is by contradiction. Suppose
![]() $\theta \in {\mathbb R}\backslash \Lambda $
and
$\theta \in {\mathbb R}\backslash \Lambda $
and
![]() $\theta $
is orthogonal to all elements in
$\theta $
is orthogonal to all elements in
![]() $\Lambda .$
Since
$\Lambda .$
Since
![]() $0\in \Lambda $
, it gets that
$0\in \Lambda $
, it gets that
![]() $\theta =\theta -0\in \mathcal {Z}(\widehat {\mu }_{\{b_n\},\{{\mathcal D}_n\}}).$
Hence, by (2.2), there exists
$\theta =\theta -0\in \mathcal {Z}(\widehat {\mu }_{\{b_n\},\{{\mathcal D}_n\}}).$
Hence, by (2.2), there exists
![]() $k\in {\mathbb Z}$
such that
$k\in {\mathbb Z}$
such that
![]() $\theta =r_kB_{k-1}a,$
where
$\theta =r_kB_{k-1}a,$
where
![]() $a\in {\mathbb Z}$
and
$a\in {\mathbb Z}$
and
![]() $q_k$
does not divide
$q_k$
does not divide
![]() $a.$
By Lemma 2.2, it yields that
$a.$
By Lemma 2.2, it yields that
where
![]() $\epsilon _{j}\in {\mathcal C}_{j}(k\leq j\leq k+l)$
and
$\epsilon _{j}\in {\mathcal C}_{j}(k\leq j\leq k+l)$
and
![]() $q_k$
does not divide
$q_k$
does not divide
![]() $\epsilon _{k}.$
Consequently, it can infer that
$\epsilon _{k}.$
Consequently, it can infer that
Note that there exists unique
![]() $\sigma _{s}(0\leq \sigma _{s}\leq q_s-1)$
such that
$\sigma _{s}(0\leq \sigma _{s}\leq q_s-1)$
such that
Denote
![]() $\epsilon _{s}=\sigma _{s}=0$
for all
$\epsilon _{s}=\sigma _{s}=0$
for all
![]() $s>k+l.$
Since
$s>k+l.$
Since
![]() $\theta \notin \Lambda ,$
we can find the smallest integer
$\theta \notin \Lambda ,$
we can find the smallest integer
![]() $\alpha $
such that
$\alpha $
such that
![]() $\tau (\sigma _{1}\dots \sigma _{\alpha })\neq \epsilon _{\alpha }.$
By (iii) in the definition of
$\tau (\sigma _{1}\dots \sigma _{\alpha })\neq \epsilon _{\alpha }.$
By (iii) in the definition of
![]() $\tau ,$
we can find
$\tau ,$
we can find
 $$ \begin{align*}\lambda=\sum_{j=1}^{\alpha}\tau(\sigma|_j)r_jB_{j-1}+MB_\alpha\end{align*} $$
$$ \begin{align*}\lambda=\sum_{j=1}^{\alpha}\tau(\sigma|_j)r_jB_{j-1}+MB_\alpha\end{align*} $$
for some integer
![]() $M.$
Then there exists
$M.$
Then there exists
![]() $M'$
such that
$M'$
such that
By (ii) in the definition of
![]() $\tau ,~\tau (\sigma |_{\alpha })\equiv \sigma _{\alpha }~(\mathrm {mod}~q_\alpha ),$
which is also congruent to
$\tau ,~\tau (\sigma |_{\alpha })\equiv \sigma _{\alpha }~(\mathrm {mod}~q_\alpha ),$
which is also congruent to
![]() $\epsilon _{\alpha }$
by our construction. This implies
$\epsilon _{\alpha }$
by our construction. This implies
![]() $\theta -\lambda $
is not in the zero set of
$\theta -\lambda $
is not in the zero set of
![]() $\widehat {\mu }_{\{b_n\},\{{\mathcal D}_n\}}$
since
$\widehat {\mu }_{\{b_n\},\{{\mathcal D}_n\}}$
since
![]() $q_\alpha \mid \big (\epsilon _{\alpha }-\tau (\sigma |_{\alpha })\big ).$
It contradicts to
$q_\alpha \mid \big (\epsilon _{\alpha }-\tau (\sigma |_{\alpha })\big ).$
It contradicts to
![]() $\theta $
being orthogonal to all
$\theta $
being orthogonal to all
![]() $\lambda \in \Lambda .$
$\lambda \in \Lambda .$
Conversely, suppose we are given a maximal orthogonal set
![]() $\Lambda $
of
$\Lambda $
of
![]() $\mu _{\{b_n\},\{{\mathcal D}_n\}}$
with
$\mu _{\{b_n\},\{{\mathcal D}_n\}}$
with
![]() $0\in \Lambda .$
Then
$0\in \Lambda .$
Then
![]() $\Lambda \subset \mathcal {Z}(\widehat {\mu }_{\{b_n\},\{{\mathcal D}_n\}}).$
Hence, we expand
$\Lambda \subset \mathcal {Z}(\widehat {\mu }_{\{b_n\},\{{\mathcal D}_n\}}).$
Hence, we expand
![]() $\lambda /r_1~(\lambda \in \Lambda )$
with Lemma 2.2 and get
$\lambda /r_1~(\lambda \in \Lambda )$
with Lemma 2.2 and get
 $$ \begin{align} \lambda=\sum_{j=1}^{k}\epsilon_{\lambda,j}r_jB_{j-1}: =\sum_{j=1}^{\infty}\epsilon_{\lambda,j}r_jB_{j-1}, \end{align} $$
$$ \begin{align} \lambda=\sum_{j=1}^{k}\epsilon_{\lambda,j}r_jB_{j-1}: =\sum_{j=1}^{\infty}\epsilon_{\lambda,j}r_jB_{j-1}, \end{align} $$
where
![]() $\epsilon _{\lambda ,j}\in {\mathcal C}_j(1\leq j\leq k)$
with
$\epsilon _{\lambda ,j}\in {\mathcal C}_j(1\leq j\leq k)$
with
![]() $\epsilon _{\lambda ,k}\neq 0$
and
$\epsilon _{\lambda ,k}\neq 0$
and
![]() $\epsilon _{\lambda ,j}=0$
for all
$\epsilon _{\lambda ,j}=0$
for all
![]() $j\geq k+1.$
Note that all
$j\geq k+1.$
Note that all
![]() $\epsilon _{0,n}$
are zero. We first consider
$\epsilon _{0,n}$
are zero. We first consider
![]() $\epsilon _{\lambda ,1}$
the first coefficients of
$\epsilon _{\lambda ,1}$
the first coefficients of
![]() $\lambda $
’s. As
$\lambda $
’s. As
![]() $\epsilon _{\lambda ,1}$
can be written uniquely as
$\epsilon _{\lambda ,1}$
can be written uniquely as
![]() $i_k+q_1\alpha _k\in {\mathcal C}_1$
for some
$i_k+q_1\alpha _k\in {\mathcal C}_1$
for some
![]() $i_k\in {\mathcal D}_1=\{0,1,\ldots ,q_1-1\},$
we claim that
$i_k\in {\mathcal D}_1=\{0,1,\ldots ,q_1-1\},$
we claim that
(Here
![]() $\alpha _i$
depends only on i but not on
$\alpha _i$
depends only on i but not on
![]() $\lambda ,$
hence the set has
$\lambda ,$
hence the set has
![]() $q_1$
elements.) In fact, the orthogonality of
$q_1$
elements.) In fact, the orthogonality of
![]() $\Lambda $
implies that
$\Lambda $
implies that
![]() $\{\epsilon _{\lambda ,1}\}_{\lambda \in \Lambda }\subseteq \{i+q_1\alpha _i:i\in {\mathcal D}_1\}$
. On the other hand, if
$\{\epsilon _{\lambda ,1}\}_{\lambda \in \Lambda }\subseteq \{i+q_1\alpha _i:i\in {\mathcal D}_1\}$
. On the other hand, if
![]() $\{\epsilon _{\lambda ,1}\}_{\lambda \in \Lambda }\subsetneqq \{i+q_1\alpha _i:i\in {\mathcal D}_1\},$
then there exists
$\{\epsilon _{\lambda ,1}\}_{\lambda \in \Lambda }\subsetneqq \{i+q_1\alpha _i:i\in {\mathcal D}_1\},$
then there exists
![]() $0\leq i'\leq q_1-1$
such that
$0\leq i'\leq q_1-1$
such that
![]() $q_1\nmid (\epsilon _{\lambda ,1}-i')$
for all
$q_1\nmid (\epsilon _{\lambda ,1}-i')$
for all
![]() $\lambda \in \Lambda ,$
which contradicts the maximality of
$\lambda \in \Lambda ,$
which contradicts the maximality of
![]() $\Lambda .$
This proves the claim.
$\Lambda .$
This proves the claim.
From the claim, we can define
![]() $\tau $
on
$\tau $
on
![]() ${\mathcal D}_{0,1}$
by
${\mathcal D}_{0,1}$
by
![]() $\tau (\sigma _1)=\sigma _1+q_1\alpha _{\sigma _1}(\sigma _1\in {\mathcal D}_1)$
and in particular
$\tau (\sigma _1)=\sigma _1+q_1\alpha _{\sigma _1}(\sigma _1\in {\mathcal D}_1)$
and in particular
![]() $\tau (0)=0.$
Similarly, we can show, for each
$\tau (0)=0.$
Similarly, we can show, for each
![]() $0\leq i_1\leq q_1-1,$
that
$0\leq i_1\leq q_1-1,$
that
and define
![]() $\tau (\sigma _1\sigma _2)=\sigma _2+q_2\alpha _{\sigma _2} (\sigma _2\in {\mathcal D}_2).$
Inductively, we can define a mapping
$\tau (\sigma _1\sigma _2)=\sigma _2+q_2\alpha _{\sigma _2} (\sigma _2\in {\mathcal D}_2).$
Inductively, we can define a mapping
![]() $\tau $
on
$\tau $
on
![]() ${\mathcal D}_{0,*}$
. By the construction of
${\mathcal D}_{0,*}$
. By the construction of
![]() $\tau ,$
it is easy to see that (i) and (ii) in Definition 1.1 are satisfied. For any
$\tau ,$
it is easy to see that (i) and (ii) in Definition 1.1 are satisfied. For any
![]() $\sigma =\sigma _1\sigma _2\dots \sigma _m\in {\mathcal D}_{0,*},$
again by the construction of
$\sigma =\sigma _1\sigma _2\dots \sigma _m\in {\mathcal D}_{0,*},$
again by the construction of
![]() $\tau ,$
there exist infinitely many
$\tau ,$
there exist infinitely many
![]() $\lambda $
such that
$\lambda $
such that
![]() $\epsilon _{\lambda ,t}=\sigma _t+q_t\alpha _{\sigma _t}$
for
$\epsilon _{\lambda ,t}=\sigma _t+q_t\alpha _{\sigma _t}$
for
![]() $1\leq t\leq m.$
Together with (2.5), fix such a k, if
$1\leq t\leq m.$
Together with (2.5), fix such a k, if
![]() $m\geq k,$
then we have
$m\geq k,$
then we have
![]() $\lambda =\sum _{j=1}^{\infty }\epsilon _{\lambda ,j}r_jB_{j-1} =\tau (\sigma 0^\infty );$
If
$\lambda =\sum _{j=1}^{\infty }\epsilon _{\lambda ,j}r_jB_{j-1} =\tau (\sigma 0^\infty );$
If
![]() $m< k,$
there exists
$m< k,$
there exists
![]() $\sigma '=\sigma _{m+1}\sigma _{m+2}\dots \sigma _k$
such that
$\sigma '=\sigma _{m+1}\sigma _{m+2}\dots \sigma _k$
such that
![]() $\epsilon _{\lambda ,n}=\tau (\sigma _1\dots \sigma _m\sigma _{m+1}\dots \sigma _n)$
for all
$\epsilon _{\lambda ,n}=\tau (\sigma _1\dots \sigma _m\sigma _{m+1}\dots \sigma _n)$
for all
![]() $m+1\leq n\leq k.$
Then
$m+1\leq n\leq k.$
Then
 $$ \begin{align*}\lambda=\sum_{j=1}^{\infty}\epsilon_{\lambda,j}r_jB_{j-1} =\tau(\sigma\sigma'0^\infty).\end{align*} $$
$$ \begin{align*}\lambda=\sum_{j=1}^{\infty}\epsilon_{\lambda,j}r_jB_{j-1} =\tau(\sigma\sigma'0^\infty).\end{align*} $$
This implies that (iii) in Definition 1.1 holds. Hence,
![]() $\tau $
is a tree mapping and
$\tau $
is a tree mapping and
![]() $\Lambda \subset \Lambda (\tau ).$
Conversely,
$\Lambda \subset \Lambda (\tau ).$
Conversely,
![]() $\Lambda (\tau )\subset \Lambda $
since
$\Lambda (\tau )\subset \Lambda $
since
![]() $\Lambda $
is a maximal orthogonal set. And then
$\Lambda $
is a maximal orthogonal set. And then
![]() $\Lambda =\Lambda (\tau ).$
$\Lambda =\Lambda (\tau ).$
3 The proof of Theorem 1.3
Theorem 1.2 shows that a countable set is a maximal orthonormal set of the measure
![]() $\mu _{\{b_n\},\{{\mathcal D}_n\}}$
if and only if it can be labeled as a tree. In this section, we will give a sufficient condition for a tree mapping to generate a spectrum. In the remainder of this paper, we always assume that the measure
$\mu _{\{b_n\},\{{\mathcal D}_n\}}$
if and only if it can be labeled as a tree. In this section, we will give a sufficient condition for a tree mapping to generate a spectrum. In the remainder of this paper, we always assume that the measure
![]() $\mu _{\{b_n\},\{{\mathcal D}_n\}}$
satisfies
$\mu _{\{b_n\},\{{\mathcal D}_n\}}$
satisfies
![]() $P=\sup _{n\geq 1}\{b_n\}<\infty $
. Given a tree mapping
$P=\sup _{n\geq 1}\{b_n\}<\infty $
. Given a tree mapping
![]() $\tau $
for
$\tau $
for
![]() $\mu _{\{b_n\},\{{\mathcal D}_n\}}$
, we recall that
$\mu _{\{b_n\},\{{\mathcal D}_n\}}$
, we recall that
and
 $$ \begin{align*}\tau(\sigma)=\sum_{k=1}^{\infty}\tau(\sigma|_{k})r_kB_{k-1},\quad \forall~\sigma\in{\mathcal D}(\tau),\end{align*} $$
$$ \begin{align*}\tau(\sigma)=\sum_{k=1}^{\infty}\tau(\sigma|_{k})r_kB_{k-1},\quad \forall~\sigma\in{\mathcal D}(\tau),\end{align*} $$
where
![]() $B_n=b_0b_1\dots b_n$
with
$B_n=b_0b_1\dots b_n$
with
![]() $b_0=1$
. Similarly, for any
$b_0=1$
. Similarly, for any
![]() $\sigma '\in {\mathcal D}_{0,n}$
, we define
$\sigma '\in {\mathcal D}_{0,n}$
, we define
 $$ \begin{align*}\tau^*(\sigma')=\sum_{k=1}^{n}\tau(\sigma'|_{k})r_kB_{k-1}.\end{align*} $$
$$ \begin{align*}\tau^*(\sigma')=\sum_{k=1}^{n}\tau(\sigma'|_{k})r_kB_{k-1}.\end{align*} $$
We list some propositions, which will be useful in the sequel. Recall that
 $$ \begin{align*}\mu_{\{b_n\},\{{\mathcal D}_n\}}(\cdot)&=\delta_{b_1^{-1}{\mathcal D}_1}\ast\delta_{({b_1b_2})^{-1}{\mathcal D}_2}\ast\dots\\&=\mu_n(\cdot)\ast\mu_{>n}(b_1b_2\dots b_n \cdot), \end{align*} $$
$$ \begin{align*}\mu_{\{b_n\},\{{\mathcal D}_n\}}(\cdot)&=\delta_{b_1^{-1}{\mathcal D}_1}\ast\delta_{({b_1b_2})^{-1}{\mathcal D}_2}\ast\dots\\&=\mu_n(\cdot)\ast\mu_{>n}(b_1b_2\dots b_n \cdot), \end{align*} $$
where
![]() $\mu _n$
is the convolutional product of the first n discrete measures and
$\mu _n$
is the convolutional product of the first n discrete measures and
Proposition 3.1 Let
![]() $\tau $
be a tree mapping. Then, for any
$\tau $
be a tree mapping. Then, for any
![]() $\xi \in {\mathbb R}$
and for any
$\xi \in {\mathbb R}$
and for any
![]() $\sigma \in {\mathcal D}(\tau ),$
we have
$\sigma \in {\mathcal D}(\tau ),$
we have
Proof Since
 $$ \begin{align*}\tau(\sigma)=\sum_{j=1}^{\infty}\tau(\sigma|_j)r_jB_{j-1} =\tau^*(\sigma|_k)+\sum_{j=k+1}^{\infty}\tau(\sigma|_j)r_jB_{j-1},\end{align*} $$
$$ \begin{align*}\tau(\sigma)=\sum_{j=1}^{\infty}\tau(\sigma|_j)r_jB_{j-1} =\tau^*(\sigma|_k)+\sum_{j=k+1}^{\infty}\tau(\sigma|_j)r_jB_{j-1},\end{align*} $$
it follows from the periodicity of
![]() $|M_{{\mathcal D}_{s}}( x)|$
that
$|M_{{\mathcal D}_{s}}( x)|$
that
 $$ \begin{align*}\widehat{\mu}_k\Big(\xi+\tau(\sigma)\Big) =\prod_{s=1}^kM_{{\mathcal D}_s}\Big(\xi+\tau(\sigma)\Big) =\prod_{s=1}^kM_{{\mathcal D}_s}\Big(\xi+\tau^*(\sigma|_k)\Big) =\widehat{\mu}_k\Big(\xi+\tau^*(\sigma|_k)\Big).\end{align*} $$
$$ \begin{align*}\widehat{\mu}_k\Big(\xi+\tau(\sigma)\Big) =\prod_{s=1}^kM_{{\mathcal D}_s}\Big(\xi+\tau(\sigma)\Big) =\prod_{s=1}^kM_{{\mathcal D}_s}\Big(\xi+\tau^*(\sigma|_k)\Big) =\widehat{\mu}_k\Big(\xi+\tau^*(\sigma|_k)\Big).\end{align*} $$
And then the result follows.
Proposition 3.2 Let
![]() $\tau $
be a tree mapping. Then, for all
$\tau $
be a tree mapping. Then, for all
![]() $k\in {\mathbb N}$
, we have
$k\in {\mathbb N}$
, we have
Proof Clearly,
![]() $\{\sigma |_k:\sigma \in {\mathcal D}(\tau )\}\subset {\mathcal D}_{0,k}.$
Conversely, it follows from (iii) of Definition 1.1 that for any word
$\{\sigma |_k:\sigma \in {\mathcal D}(\tau )\}\subset {\mathcal D}_{0,k}.$
Conversely, it follows from (iii) of Definition 1.1 that for any word
![]() $\sigma '\in {\mathcal D}_{0,k},$
there exists
$\sigma '\in {\mathcal D}_{0,k},$
there exists
![]() $\sigma "\in {\mathcal D}_{k,\infty }$
such that
$\sigma "\in {\mathcal D}_{k,\infty }$
such that
![]() $\sigma '\sigma "\in {\mathcal D}(\tau ).$
This implies
$\sigma '\sigma "\in {\mathcal D}(\tau ).$
This implies
![]() ${\mathcal D}_{0,k}\subseteq \{\sigma |_k:\sigma \in {\mathcal D}(\tau )\}$
since
${\mathcal D}_{0,k}\subseteq \{\sigma |_k:\sigma \in {\mathcal D}(\tau )\}$
since
![]() $(\sigma '\sigma ")|_k=\sigma '\in {\mathcal D}_{0,k}.$
Hence, we finish the proof.
$(\sigma '\sigma ")|_k=\sigma '\in {\mathcal D}_{0,k}.$
Hence, we finish the proof.
Proposition 3.3 Let
![]() $\tau $
be a tree mapping. Then, for all
$\tau $
be a tree mapping. Then, for all
![]() $k\geq 1$
and for any
$k\geq 1$
and for any
![]() $\xi \in {\mathbb R}$
, we have
$\xi \in {\mathbb R}$
, we have
Proof We claim that
![]() $\{\tau ^*(\sigma )\}_{\sigma \in {\mathcal D}_{0,k}}$
is a spectrum of
$\{\tau ^*(\sigma )\}_{\sigma \in {\mathcal D}_{0,k}}$
is a spectrum of
![]() $L^{2}(\mu _k).$
We can then use Theorem 2.1 to conclude our lemma. Since this set has exactly
$L^{2}(\mu _k).$
We can then use Theorem 2.1 to conclude our lemma. Since this set has exactly
![]() $q_1q_2\dots q_k$
elements, we just need to show the mutual orthogonality.
$q_1q_2\dots q_k$
elements, we just need to show the mutual orthogonality.
For any two distinct words
![]() $\sigma ,\sigma '\in {\mathcal D}_{0,k}$
, we have
$\sigma ,\sigma '\in {\mathcal D}_{0,k}$
, we have
 $$ \begin{align*}\tau^*(\sigma)=\sum_{j=1}^{k}\tau(\sigma|_j)r_jB_{j-1} \quad \text{and} \quad \tau^*(\sigma')=\sum_{j=1}^{k}\tau(\sigma'|_j)r_jB_{j-1}.\end{align*} $$
$$ \begin{align*}\tau^*(\sigma)=\sum_{j=1}^{k}\tau(\sigma|_j)r_jB_{j-1} \quad \text{and} \quad \tau^*(\sigma')=\sum_{j=1}^{k}\tau(\sigma'|_j)r_jB_{j-1}.\end{align*} $$
Let
![]() $s~(1\leq s\leq k)$
be the first index such that
$s~(1\leq s\leq k)$
be the first index such that
![]() $\sigma |_s\neq \sigma '|_s$
. Then we can obtain that
$\sigma |_s\neq \sigma '|_s$
. Then we can obtain that
for some integer M. It follows from the periodicity of the exponential function
![]() $e^{-2\pi ix}$
that
$e^{-2\pi ix}$
that
 $$ \begin{align*}M_{{\mathcal D}_s}\Big(\frac{\tau^*(\sigma)-\tau^*(\sigma')}{B_s}\Big)= M_{{\mathcal D}_s}\Big(\frac{\tau(\sigma|_s)-\tau(\sigma'|_s)}{q_s}\Big)=0,\end{align*} $$
$$ \begin{align*}M_{{\mathcal D}_s}\Big(\frac{\tau^*(\sigma)-\tau^*(\sigma')}{B_s}\Big)= M_{{\mathcal D}_s}\Big(\frac{\tau(\sigma|_s)-\tau(\sigma'|_s)}{q_s}\Big)=0,\end{align*} $$
where the last equation holds because (ii) in the definition of maximal mapping implies that
![]() $q_s$
does not divide
$q_s$
does not divide
![]() $\tau (\sigma |_s)-\tau (\sigma '|_s)$
. Since
$\tau (\sigma |_s)-\tau (\sigma '|_s)$
. Since
 $$ \begin{align*}\widehat{\mu}_k(\xi)=\prod_{j=1}^k\Big|M_{{\mathcal D}_j}\Big(\frac{\xi}{B_j}\Big)\Big|,\end{align*} $$
$$ \begin{align*}\widehat{\mu}_k(\xi)=\prod_{j=1}^k\Big|M_{{\mathcal D}_j}\Big(\frac{\xi}{B_j}\Big)\Big|,\end{align*} $$
it follows that
![]() $\widehat {\mu }_k\big (\tau ^*(\sigma )-\tau ^*(\sigma ')\big )=0$
. And thus the desired result follows.
$\widehat {\mu }_k\big (\tau ^*(\sigma )-\tau ^*(\sigma ')\big )=0$
. And thus the desired result follows.
We divide the proof of Theorem 1.3 into several lemmas.
Lemma 3.4 Assume that for any
![]() $1\leq j\leq t, c_{k+j}\in \{-1,0,1,\ldots ,q_{k+j}r_{k+j+1}-2\}$
satisfies
$1\leq j\leq t, c_{k+j}\in \{-1,0,1,\ldots ,q_{k+j}r_{k+j+1}-2\}$
satisfies
Let
![]() $|\xi |\leq r_{k+1}-1/q_k,~~ \eta _1=\xi /b_{k+1}$
and
$|\xi |\leq r_{k+1}-1/q_k,~~ \eta _1=\xi /b_{k+1}$
and
then one has
for all
![]() $2 \leq n \leq t,$
where
$2 \leq n \leq t,$
where
![]() $P=\sup _{n\geq 1}\{b_n\}<\infty $
.
$P=\sup _{n\geq 1}\{b_n\}<\infty $
.
Proof With an easy calculation, it can infer that
 $$ \begin{align*}\eta_n=\frac{\xi+c_{k+1}r_{k+1}+\sum_{j=2}^{n-1}c_{k+j}r_{k+j}b_{k+1}\dots b_{k+j-1}}{b_{k+1}\dots b_{k+n}},\quad \forall 2\leq n \leq t.\end{align*} $$
$$ \begin{align*}\eta_n=\frac{\xi+c_{k+1}r_{k+1}+\sum_{j=2}^{n-1}c_{k+j}r_{k+j}b_{k+1}\dots b_{k+j-1}}{b_{k+1}\dots b_{k+n}},\quad \forall 2\leq n \leq t.\end{align*} $$
On the upper bound, it follows
![]() $c_{k+j}\in \{-1,0,1,\ldots ,q_{k+j}r_{k+j+1}-2\}$
for all
$c_{k+j}\in \{-1,0,1,\ldots ,q_{k+j}r_{k+j+1}-2\}$
for all
![]() $1\leq j\leq n$
, then
$1\leq j\leq n$
, then
 $$ \begin{align} |\eta_n|&=\left|\frac{\xi+c_{k+1}r_{k+1}+\sum_{j=2}^{n-1}c_{k+j}r_{k+j}b_{k+1}\dots b_{k+j-1}}{b_{k+1}\dots b_{k+n}}\right| \nonumber \\ &\leq\frac{r_{k+1}\!-\!1/q_k\!+\!(q_{k+1}r_{k+2}\!-\!2)r_{k+1} +\!\cdots\!+(q_{k+n-1}r_{k+n}\!-\!2) r_{k+n-1}b_{k+1}\dots b_{k+n-2}}{b_{k+1}b_{k+2}\!\dots\! b_{k+n}} \nonumber \\ &\leq\frac{r_{k+n}b_{k+1}\dots b_{k+n-1}-r_{k+n-1}b_{k+1}\dots b_{k+n-2}}{b_{k+1}\dots b_{k+n}} \nonumber \\ &=\frac{1}{q_{k+n}}\Big(1-\frac{1}{q_{k+n-1}r_{k+n}}\Big) \leq \frac{1}{q_{k+n}}\Big(1-\frac{1}{P^2}\Big), \end{align} $$
$$ \begin{align} |\eta_n|&=\left|\frac{\xi+c_{k+1}r_{k+1}+\sum_{j=2}^{n-1}c_{k+j}r_{k+j}b_{k+1}\dots b_{k+j-1}}{b_{k+1}\dots b_{k+n}}\right| \nonumber \\ &\leq\frac{r_{k+1}\!-\!1/q_k\!+\!(q_{k+1}r_{k+2}\!-\!2)r_{k+1} +\!\cdots\!+(q_{k+n-1}r_{k+n}\!-\!2) r_{k+n-1}b_{k+1}\dots b_{k+n-2}}{b_{k+1}b_{k+2}\!\dots\! b_{k+n}} \nonumber \\ &\leq\frac{r_{k+n}b_{k+1}\dots b_{k+n-1}-r_{k+n-1}b_{k+1}\dots b_{k+n-2}}{b_{k+1}\dots b_{k+n}} \nonumber \\ &=\frac{1}{q_{k+n}}\Big(1-\frac{1}{q_{k+n-1}r_{k+n}}\Big) \leq \frac{1}{q_{k+n}}\Big(1-\frac{1}{P^2}\Big), \end{align} $$
where the last inequality holds since
![]() $P=\sup _{n\geq 1}\{b_n\}$
.
$P=\sup _{n\geq 1}\{b_n\}$
.
On the lower bound, for
![]() $\eta _1$
, a direct calculation shows that
$\eta _1$
, a direct calculation shows that
For
![]() $\eta _2=\frac {1}{b_{k+2}} \left (\eta _{1} +\frac {c_{k+1}}{q_{k+1}} \right ),$
since
$\eta _2=\frac {1}{b_{k+2}} \left (\eta _{1} +\frac {c_{k+1}}{q_{k+1}} \right ),$
since
it follows that
 $$ \begin{align*} |\eta_2|\geq \frac{1}{b_{k+2}}\left( 1-\frac{1}{q_{k+1}}\Big(1-\frac{1}{P^2}\Big)\right)> \frac{1}{2P}\geq\frac{1}{P^3}. \end{align*} $$
$$ \begin{align*} |\eta_2|\geq \frac{1}{b_{k+2}}\left( 1-\frac{1}{q_{k+1}}\Big(1-\frac{1}{P^2}\Big)\right)> \frac{1}{2P}\geq\frac{1}{P^3}. \end{align*} $$
For
![]() $\eta _3=\frac {1}{b_{k+3}} \left (\eta _{2} +\frac {c_{k+2}}{q_{k+2}} \right ),$
where
$\eta _3=\frac {1}{b_{k+3}} \left (\eta _{2} +\frac {c_{k+2}}{q_{k+2}} \right ),$
where
![]() $c_{k+2}\in \{-1,0,1,\ldots ,q_{k+2}r_{k+3}-2\},$
one has the following two cases:
$c_{k+2}\in \{-1,0,1,\ldots ,q_{k+2}r_{k+3}-2\},$
one has the following two cases:
(i) if
![]() $c_{k+2}=0$
, then
$c_{k+2}=0$
, then
![]() $\eta _3=\frac {1}{b_{k+3}} \eta _{2}$
, and hence
$\eta _3=\frac {1}{b_{k+3}} \eta _{2}$
, and hence
(ii) if
![]() $c_{k+2} \not =0,$
then
$c_{k+2} \not =0,$
then
 $$ \begin{align*} |\eta_3|> \frac{1}{b_{k+3}} \left( \frac{1}{q_{k+2}}-\frac{1}{q_{k+2}}\Big(1-\frac{1}{P^2}\Big) \right)=\frac{1}{q_{k+2}b_{k+3}P^2}\geq \frac{1}{P^4}. \end{align*} $$
$$ \begin{align*} |\eta_3|> \frac{1}{b_{k+3}} \left( \frac{1}{q_{k+2}}-\frac{1}{q_{k+2}}\Big(1-\frac{1}{P^2}\Big) \right)=\frac{1}{q_{k+2}b_{k+3}P^2}\geq \frac{1}{P^4}. \end{align*} $$
Noting that
![]() $\frac {1}{P^4}\leq \frac {1}{q_{k+3}}\Big (1-\frac {1}{P^2}\Big ).$
Then we get that
$\frac {1}{P^4}\leq \frac {1}{q_{k+3}}\Big (1-\frac {1}{P^2}\Big ).$
Then we get that
Continuing the above procedure several times, we can obtain, for all
![]() $2 \leq n \leq t$
, that
$2 \leq n \leq t$
, that
Hence, the lemma is proved.
Since
![]() $\sup _{n\geq 1}\{b_n\}<\infty $
and
$\sup _{n\geq 1}\{b_n\}<\infty $
and
![]() $q_n|b_n,$
there are only finitely many
$q_n|b_n,$
there are only finitely many
![]() $(b_n,{\mathcal D}_n),$
say that
$(b_n,{\mathcal D}_n),$
say that
![]() $\big (b(1),{\mathcal D}(1)\big ),\ \big (b(2),{\mathcal D}(2)\big ),\ldots ,\big (b(N),{\mathcal D}(N)\big )$
with
$\big (b(1),{\mathcal D}(1)\big ),\ \big (b(2),{\mathcal D}(2)\big ),\ldots ,\big (b(N),{\mathcal D}(N)\big )$
with
![]() $D(i)=\{0,1,\ldots ,q_{(i)}-1\}$
for some
$D(i)=\{0,1,\ldots ,q_{(i)}-1\}$
for some
![]() $N\in {\mathbb N}.$
Hence, it is easy to show that
$N\in {\mathbb N}.$
Hence, it is easy to show that
 $$ \begin{align} c_1=\min\left\{\big|M_{{\mathcal D}(i)}(\xi)\big|:|\xi|\leq \frac{1}{q_{(i)}}\Big(1-\frac{1}{P^2}\Big)\right\}>0, \end{align} $$
$$ \begin{align} c_1=\min\left\{\big|M_{{\mathcal D}(i)}(\xi)\big|:|\xi|\leq \frac{1}{q_{(i)}}\Big(1-\frac{1}{P^2}\Big)\right\}>0, \end{align} $$
and
 $$ \begin{align} c(t)=\min\left\{\big|M_{{\mathcal D}(i)}\left(\xi+\frac{j}{q(i)}\right)\big|: \begin{array}{ll} \xi\in\! \left(\left[\! \frac{1}{P^{t+1}}, \frac{1}{q_{(i)}}\Big(1\!-\!\frac{1}{P^2}\Big)\!\right]\! \cup \!\left[\! \!-\!\frac{1}{q_{(i)}}\Big(1\!-\!\frac{1}{P^2}\Big),-\frac{1}{P^{t+1}}\!\right] \right)\\ \forall j\in \left\{0, 1,\dots, q(i)-1 \right\} \end{array} \right\}>0. \end{align} $$
$$ \begin{align} c(t)=\min\left\{\big|M_{{\mathcal D}(i)}\left(\xi+\frac{j}{q(i)}\right)\big|: \begin{array}{ll} \xi\in\! \left(\left[\! \frac{1}{P^{t+1}}, \frac{1}{q_{(i)}}\Big(1\!-\!\frac{1}{P^2}\Big)\!\right]\! \cup \!\left[\! \!-\!\frac{1}{q_{(i)}}\Big(1\!-\!\frac{1}{P^2}\Big),-\frac{1}{P^{t+1}}\!\right] \right)\\ \forall j\in \left\{0, 1,\dots, q(i)-1 \right\} \end{array} \right\}>0. \end{align} $$
The following lemma will be use to prove Lemma 3.6, which is crucial in proof of completeness of the maximal orthogonal set.
Lemma 3.5 Assume that for any
![]() $1\leq j\leq t, c_{k+j}\in \{-1,0,1,\ldots ,q_{k+j}r_{k+j+1}-2\}$
satisfies
$1\leq j\leq t, c_{k+j}\in \{-1,0,1,\ldots ,q_{k+j}r_{k+j+1}-2\}$
satisfies
Let
![]() $|\xi |\leq r_{k+1}-1/q_k$
, and let
$|\xi |\leq r_{k+1}-1/q_k$
, and let
 $$ \begin{align*}\eta=\xi+c_{k+1}r_{k+1}+\sum_{j=2}^tc_{k+j}r_{k+j}b_{k+1}\dots b_{k+j-1},\end{align*} $$
$$ \begin{align*}\eta=\xi+c_{k+1}r_{k+1}+\sum_{j=2}^tc_{k+j}r_{k+j}b_{k+1}\dots b_{k+j-1},\end{align*} $$
then there exists a constant
![]() $C(t)\in (0,1)$
(only depending on t) such that
$C(t)\in (0,1)$
(only depending on t) such that
![]() $|\widehat {\mu }_{>k}(\eta )|\geq C(t).$
$|\widehat {\mu }_{>k}(\eta )|\geq C(t).$
Proof We define
![]() $\eta _1=\frac {\xi }{b_{k+1}}$
and
$\eta _1=\frac {\xi }{b_{k+1}}$
and
 $$ \begin{align*}\eta_n=\frac{\xi+c_{k+1}r_{k+1}+\sum_{j=2}^{n-1}c_{k+j}r_{k+j}b_{k+1}\dots b_{k+j-1}}{b_{k+1}\dots b_{k+n}},\quad \forall 2\leq n \leq t.\end{align*} $$
$$ \begin{align*}\eta_n=\frac{\xi+c_{k+1}r_{k+1}+\sum_{j=2}^{n-1}c_{k+j}r_{k+j}b_{k+1}\dots b_{k+j-1}}{b_{k+1}\dots b_{k+n}},\quad \forall 2\leq n \leq t.\end{align*} $$
According to the fact that
 $$ \begin{align*}\Big|\widehat{\mu}_{>k}(\eta)\Big|=\prod_{s=1}^\infty \Big|M_{{\mathcal D}_{k+s}}\Big(\frac{\eta}{b_{k+1}\dots b_{k+s}}\Big)\Big|,\end{align*} $$
$$ \begin{align*}\Big|\widehat{\mu}_{>k}(\eta)\Big|=\prod_{s=1}^\infty \Big|M_{{\mathcal D}_{k+s}}\Big(\frac{\eta}{b_{k+1}\dots b_{k+s}}\Big)\Big|,\end{align*} $$
it follows from the periodicity of
![]() $|M_{{\mathcal D}_{k+s}}( x)|$
and
$|M_{{\mathcal D}_{k+s}}( x)|$
and
![]() $c_{k+1}\in q_{k+1}{\mathbb Z}\backslash \{0\}$
that
$c_{k+1}\in q_{k+1}{\mathbb Z}\backslash \{0\}$
that
 $$ \begin{align*} \Big|\widehat{\mu}_{>k}(\eta)\Big|=\Big|M_{{\mathcal D}_{k+1}}\Big(\eta_1\Big)\Big|\cdot \prod_{s=2}^{t}\Big|M_{{\mathcal D}_{k+s}}\Big(\eta_s+\frac{a_{k+s}}{q_{k+s}}\Big)\Big|\cdot \prod_{s=t+1}^{\infty}\Big|M_{{\mathcal D}_{k+s}}\Big(\frac{\eta}{b_{k+1}\dots b_{k+s}}\Big)\Big|, \end{align*} $$
$$ \begin{align*} \Big|\widehat{\mu}_{>k}(\eta)\Big|=\Big|M_{{\mathcal D}_{k+1}}\Big(\eta_1\Big)\Big|\cdot \prod_{s=2}^{t}\Big|M_{{\mathcal D}_{k+s}}\Big(\eta_s+\frac{a_{k+s}}{q_{k+s}}\Big)\Big|\cdot \prod_{s=t+1}^{\infty}\Big|M_{{\mathcal D}_{k+s}}\Big(\frac{\eta}{b_{k+1}\dots b_{k+s}}\Big)\Big|, \end{align*} $$
where
![]() $a_{k+s} \equiv c_{k+s}~(\mathrm {mod}~q_{k+s})$
with
$a_{k+s} \equiv c_{k+s}~(\mathrm {mod}~q_{k+s})$
with
![]() $a_{k+s}\in \{0,1,\ldots ,q_{k+s}-1\}$
for
$a_{k+s}\in \{0,1,\ldots ,q_{k+s}-1\}$
for
![]() $2\leq s\leq t.$
$2\leq s\leq t.$
We estimate the products one by one. From the proof of Lemma 3.4, it can infer that
And thus we have, together with (3.2), that
For any
![]() $2\leq s\leq t$
, using Lemma 3.4 again, we also have that
$2\leq s\leq t$
, using Lemma 3.4 again, we also have that
It follows from (3.3) that
For
![]() $s\geq t+1,$
we set
$s\geq t+1,$
we set
for convenience. Thus, we conclude that
Using (3.2) again, it gets that
 $$ \begin{align} \prod_{s=t+1}^{\infty}\Big|M_{{\mathcal D}_{k+s}}\Big(\frac{\eta}{b_{k+1}\dots b_{k+s}}\Big)\Big| &=\Big|M_{{\mathcal D}_{k+t+1}}\Big(\frac{\gamma}{b_{k+t+1}}\Big)\Big|\cdot \prod_{m=2}^{\infty}\Big|M_{{\mathcal D}_{k+t+s}}\Big(\frac{\gamma}{b_{k+t+1}\dots b_{k+t+m}}\Big)\Big|\nonumber\\ &=\Big|M_{{\mathcal D}_{k+t+1}}\Big(\frac{\gamma}{b_{k+t+1}}\Big)\Big|\cdot \prod_{m=2}^{\infty} \Big|\frac{\sin q_{k+t+m}\pi\gamma (b_{k+t+1}\dots b_{k+t+m})^{-1}}{q_{k+t+m} \sin \pi \gamma (b_{k+t+1}\dots b_{k+t+m})^{-1}}\Big)\Big|\nonumber\\ &\geq c_1\cdot \prod_{m=2}^{\infty} \Big|\frac{\sin q_{k+t+m}\pi\gamma (b_{k+t+1}\dots b_{k+t+m})^{-1}}{q_{k+t+m} \pi \gamma (b_{k+t+1}\dots b_{k+t+m})^{-1}}\Big)\Big|. \end{align} $$
$$ \begin{align} \prod_{s=t+1}^{\infty}\Big|M_{{\mathcal D}_{k+s}}\Big(\frac{\eta}{b_{k+1}\dots b_{k+s}}\Big)\Big| &=\Big|M_{{\mathcal D}_{k+t+1}}\Big(\frac{\gamma}{b_{k+t+1}}\Big)\Big|\cdot \prod_{m=2}^{\infty}\Big|M_{{\mathcal D}_{k+t+s}}\Big(\frac{\gamma}{b_{k+t+1}\dots b_{k+t+m}}\Big)\Big|\nonumber\\ &=\Big|M_{{\mathcal D}_{k+t+1}}\Big(\frac{\gamma}{b_{k+t+1}}\Big)\Big|\cdot \prod_{m=2}^{\infty} \Big|\frac{\sin q_{k+t+m}\pi\gamma (b_{k+t+1}\dots b_{k+t+m})^{-1}}{q_{k+t+m} \sin \pi \gamma (b_{k+t+1}\dots b_{k+t+m})^{-1}}\Big)\Big|\nonumber\\ &\geq c_1\cdot \prod_{m=2}^{\infty} \Big|\frac{\sin q_{k+t+m}\pi\gamma (b_{k+t+1}\dots b_{k+t+m})^{-1}}{q_{k+t+m} \pi \gamma (b_{k+t+1}\dots b_{k+t+m})^{-1}}\Big)\Big|. \end{align} $$
On the other hand, for any
![]() $m\geq 2$
, it can be easily checked that
$m\geq 2$
, it can be easily checked that
 $$ \begin{align*}\Big|\frac{q_{k+t+m}\pi\gamma}{b_{k+t+1}\dots b_{k+t+m}}\Big| \leq\frac{\pi(1-\frac{1}{P^2})}{q_{k+t+1}b_{k+t+2}\dots b_{k+t+m-1}r_{k+t+m}} \leq \frac{\pi(1-\frac{1}{P^2})}{2^{m-1}}.\end{align*} $$
$$ \begin{align*}\Big|\frac{q_{k+t+m}\pi\gamma}{b_{k+t+1}\dots b_{k+t+m}}\Big| \leq\frac{\pi(1-\frac{1}{P^2})}{q_{k+t+1}b_{k+t+2}\dots b_{k+t+m-1}r_{k+t+m}} \leq \frac{\pi(1-\frac{1}{P^2})}{2^{m-1}}.\end{align*} $$
Combined this with (3.6), we can obtain from the monotonicity of
![]() $|\sin x/x|$
in
$|\sin x/x|$
in
![]() $[0,\pi ]$
and
$[0,\pi ]$
and
![]() $\sin x/x\geq 1-6^{-1}x^2$
for
$\sin x/x\geq 1-6^{-1}x^2$
for
![]() $x\in [0,\pi /2]$
that
$x\in [0,\pi /2]$
that
 $$ \begin{align} \prod_{s=t+1}^{\infty}\Big|M_{{\mathcal D}_{k+s}}\Big(\frac{\eta}{b_{k+1}\dots b_{k+s}}\Big)\Big|\geq c_1\cdot \prod_{m=1}^\infty \Big(1-\frac{\pi^2(1-\frac{1}{p^2})^2}{6\cdot 4^m}\Big):=c'>0. \end{align} $$
$$ \begin{align} \prod_{s=t+1}^{\infty}\Big|M_{{\mathcal D}_{k+s}}\Big(\frac{\eta}{b_{k+1}\dots b_{k+s}}\Big)\Big|\geq c_1\cdot \prod_{m=1}^\infty \Big(1-\frac{\pi^2(1-\frac{1}{p^2})^2}{6\cdot 4^m}\Big):=c'>0. \end{align} $$
Combined with (3.4), (3.5), and (3.7), we get that
Therefore, the desired result follows from
![]() $C(t)=c_1c(t)^{t-1}c'$
.
$C(t)=c_1c(t)^{t-1}c'$
.
Lemma 3.6 For any word
![]() $\sigma \in {\mathcal D}_{0,k}(k\geq 1),$
let
$\sigma \in {\mathcal D}_{0,k}(k\geq 1),$
let
![]() $\sigma \sigma '\in {\mathcal D}(\tau )$
satisfying (1.2) given as in Theorem 1.3. Let
$\sigma \sigma '\in {\mathcal D}(\tau )$
satisfying (1.2) given as in Theorem 1.3. Let
![]() $|\xi |\leq r_{k+1}-1/q_k$
, and let
$|\xi |\leq r_{k+1}-1/q_k$
, and let
 $$ \begin{align*}\eta=\xi+\frac{\sum_{j=1}^{\infty}\tau\big((\sigma\sigma')|_{k+j}\big)r_{k+j}B_{k+j-1}}{B_{k}}.\end{align*} $$
$$ \begin{align*}\eta=\xi+\frac{\sum_{j=1}^{\infty}\tau\big((\sigma\sigma')|_{k+j}\big)r_{k+j}B_{k+j-1}}{B_{k}}.\end{align*} $$
Then there exists a constant c such that
![]() $|\widehat {\mu }_{>k}(\eta )|\geq c.$
$|\widehat {\mu }_{>k}(\eta )|\geq c.$
Proof We distinguish two cases to prove it.
Case I. When
![]() $\sigma '=0^\infty $
with
$\sigma '=0^\infty $
with
![]() $\tau \big ((\sigma \sigma ')|_j\big )=0$
for any
$\tau \big ((\sigma \sigma ')|_j\big )=0$
for any
![]() $ j\geq k+1,$
thus
$ j\geq k+1,$
thus
![]() $\eta =\xi $
and
$\eta =\xi $
and
It is easy to check that
![]() $|\widehat {\mu }_{>k}(\eta )|\geq c'>0,$
where
$|\widehat {\mu }_{>k}(\eta )|\geq c'>0,$
where
![]() $c'$
is given as in (3.7).
$c'$
is given as in (3.7).
Case II. When
![]() $\sigma '=0^n\delta (n\in {\mathbb N},\delta \in {\mathcal D}_{k+n,\infty })$
with
$\sigma '=0^n\delta (n\in {\mathbb N},\delta \in {\mathcal D}_{k+n,\infty })$
with
![]() $\tau \big ((\sigma \sigma ')|_{k+j}\big )=0~(\forall ~1\leq j\leq n),$
$\tau \big ((\sigma \sigma ')|_{k+j}\big )=0~(\forall ~1\leq j\leq n),$
Together with the periodicity of
![]() $|M_{{\mathcal D}_{k+s}}( x)|$
, it implies that
$|M_{{\mathcal D}_{k+s}}( x)|$
, it implies that
 $$ \begin{align} |\widehat{\mu}_{>k}(\eta)|&=\prod_{s=1}^\infty \Big|M_{{\mathcal D}_{k+s}}\Big(\frac{\eta}{b_{k+1}\dots b_{k+s}}\Big)\Big| \nonumber\\ &=\prod_{s=1}^{n} \Big|M_{{\mathcal D}_{k+s}}\Big(\frac{\eta}{b_{k+1}\dots b_{k+s}}\Big)\Big|\cdot \prod_{s=n+1}^{\infty}\Big|M_{{\mathcal D}_{k+s}}\Big(\frac{\eta}{b_{k+1}\dots b_{k+s}}\Big)\Big|\nonumber\\ &=\prod_{s=1}^{n} \Big|M_{{\mathcal D}_{k+s}}\Big(\frac{\xi}{b_{k+1}\dots b_{k+s}}\Big)\Big|\cdot |\widehat{\mu}_{>k+n}(\gamma)|, \end{align} $$
$$ \begin{align} |\widehat{\mu}_{>k}(\eta)|&=\prod_{s=1}^\infty \Big|M_{{\mathcal D}_{k+s}}\Big(\frac{\eta}{b_{k+1}\dots b_{k+s}}\Big)\Big| \nonumber\\ &=\prod_{s=1}^{n} \Big|M_{{\mathcal D}_{k+s}}\Big(\frac{\eta}{b_{k+1}\dots b_{k+s}}\Big)\Big|\cdot \prod_{s=n+1}^{\infty}\Big|M_{{\mathcal D}_{k+s}}\Big(\frac{\eta}{b_{k+1}\dots b_{k+s}}\Big)\Big|\nonumber\\ &=\prod_{s=1}^{n} \Big|M_{{\mathcal D}_{k+s}}\Big(\frac{\xi}{b_{k+1}\dots b_{k+s}}\Big)\Big|\cdot |\widehat{\mu}_{>k+n}(\gamma)|, \end{align} $$
where
 $$ \begin{align*}\gamma=\frac{\eta}{b_{k+1}\!\dots\! b_{k+n}}=\frac{\xi}{b_{k+1}\!\dots\! b_{k+n}} +\tau\big((\sigma\sigma')|_{k+n+1}\big)c_{k+n+1} +\!\sum_{j=2}^\infty\! \tau\big((\sigma\sigma')|_{k+n+j}\big)r_{k+n+j}b_{k+n+1}\!\dots b_{k+n+j-1}.\end{align*} $$
$$ \begin{align*}\gamma=\frac{\eta}{b_{k+1}\!\dots\! b_{k+n}}=\frac{\xi}{b_{k+1}\!\dots\! b_{k+n}} +\tau\big((\sigma\sigma')|_{k+n+1}\big)c_{k+n+1} +\!\sum_{j=2}^\infty\! \tau\big((\sigma\sigma')|_{k+n+j}\big)r_{k+n+j}b_{k+n+1}\!\dots b_{k+n+j-1}.\end{align*} $$
Since
![]() $\max \Big \{j:\tau \big ((\sigma \sigma ')|_{k+n+j}\big )\neq 0, ~~ j\geq 1 \Big \}\leq N$
, it follows that
$\max \Big \{j:\tau \big ((\sigma \sigma ')|_{k+n+j}\big )\neq 0, ~~ j\geq 1 \Big \}\leq N$
, it follows that
![]() $\gamma $
can be rewritten as
$\gamma $
can be rewritten as
 $$ \begin{align*}\gamma=\frac{\xi}{b_{k+1}\!\dots\! b_{k+n}} +\tau\big((\sigma\sigma')|_{k+n+1}\big)c_{k+n+1} +\!\sum_{j=2}^N\! \tau\big((\sigma\sigma')|_{k+n+j}\big)r_{k+n+j}b_{k+n+1}\!\dots b_{k+n+j-1}.\end{align*} $$
$$ \begin{align*}\gamma=\frac{\xi}{b_{k+1}\!\dots\! b_{k+n}} +\tau\big((\sigma\sigma')|_{k+n+1}\big)c_{k+n+1} +\!\sum_{j=2}^N\! \tau\big((\sigma\sigma')|_{k+n+j}\big)r_{k+n+j}b_{k+n+1}\!\dots b_{k+n+j-1}.\end{align*} $$
Using Lemma 3.5, there exists a constant
![]() $C(N)\in (0,1)$
(only depending on N) such that
$C(N)\in (0,1)$
(only depending on N) such that
Note that
![]() $|\xi |\leq r_{k+1}-1/q_k$
, we also have
$|\xi |\leq r_{k+1}-1/q_k$
, we also have
 $$ \begin{align} \prod_{s=1}^{n} \Big|M_{{\mathcal D}_{k+s}}\Big(\frac{\xi}{b_{k+1}\dots b_{k+s}}\Big)\Big|\geq \prod_{s=1}^\infty \Big|M_{{\mathcal D}_{k+s}}\Big(\frac{\xi}{b_{k+1}\dots b_{k+s}}\Big)\Big|=|\widehat{\mu}_{>k}(\xi)|\geq c', \end{align} $$
$$ \begin{align} \prod_{s=1}^{n} \Big|M_{{\mathcal D}_{k+s}}\Big(\frac{\xi}{b_{k+1}\dots b_{k+s}}\Big)\Big|\geq \prod_{s=1}^\infty \Big|M_{{\mathcal D}_{k+s}}\Big(\frac{\xi}{b_{k+1}\dots b_{k+s}}\Big)\Big|=|\widehat{\mu}_{>k}(\xi)|\geq c', \end{align} $$
where the last inequality holds from Case I.
Combined with (3.8), (3.9), and (3.10), we get that
Let
![]() $c=C(N)c'$
, we can obtain the desired result.
$c=C(N)c'$
, we can obtain the desired result.
Now, we have all ingredients for the proof of Theorem 1.3.
Proof of Theorem 1.3.
Since
![]() $\tau $
is a tree mapping, it follows that
$\tau $
is a tree mapping, it follows that
![]() $\Lambda (\tau )$
is a maximal orthogonal set. By Theorem 2.1, we have
$\Lambda (\tau )$
is a maximal orthogonal set. By Theorem 2.1, we have
 $$ \begin{align*}Q(\xi)&=\sum_{I\in{\mathcal D}(\tau)}\Big|\widehat{\mu}_{\{b_n\},\{{\mathcal D}_n\}} \Big(\xi+\tau(I)\Big)\Big|^2\\ &=\sum_{n=0}^\infty \sum_{I\in{\mathcal D}(\tau),l_{\tau}(I)=n}\Big|\widehat{\mu}_{\{b_n\},\{{\mathcal D}_n\}} \Big(\xi+\tau(I)\Big)\Big|^2\leq1, \quad \forall~\xi\in{\mathbb R}.\end{align*} $$
$$ \begin{align*}Q(\xi)&=\sum_{I\in{\mathcal D}(\tau)}\Big|\widehat{\mu}_{\{b_n\},\{{\mathcal D}_n\}} \Big(\xi+\tau(I)\Big)\Big|^2\\ &=\sum_{n=0}^\infty \sum_{I\in{\mathcal D}(\tau),l_{\tau}(I)=n}\Big|\widehat{\mu}_{\{b_n\},\{{\mathcal D}_n\}} \Big(\xi+\tau(I)\Big)\Big|^2\leq1, \quad \forall~\xi\in{\mathbb R}.\end{align*} $$
Here,
![]() $l_{\tau }(I)$
is the smallest integer n such that
$l_{\tau }(I)$
is the smallest integer n such that
![]() $\tau (I|_k)=0$
for all
$\tau (I|_k)=0$
for all
![]() $k\geq n$
. Moreover, fixed
$k\geq n$
. Moreover, fixed
![]() $\xi \in (0,1),$
for any
$\xi \in (0,1),$
for any
![]() $\epsilon>0,$
there exists an integer
$\epsilon>0,$
there exists an integer
![]() $N_\epsilon $
such that
$N_\epsilon $
such that
 $$ \begin{align} \sum_{I\in{\mathcal D}(\tau),l_{\tau}(I)\geq N_\epsilon}\Big|\widehat{\mu}_{\{b_n\},\{{\mathcal D}_n\}} \Big(\xi+\tau(I)\Big)\Big|^2<\epsilon. \end{align} $$
$$ \begin{align} \sum_{I\in{\mathcal D}(\tau),l_{\tau}(I)\geq N_\epsilon}\Big|\widehat{\mu}_{\{b_n\},\{{\mathcal D}_n\}} \Big(\xi+\tau(I)\Big)\Big|^2<\epsilon. \end{align} $$
From Theorem 2.1, we only need to show that
![]() $Q(\xi )\geq 1$
for all
$Q(\xi )\geq 1$
for all
![]() $\xi \in (0,1).$
Together with Proposition 3.1, it can infer that
$\xi \in (0,1).$
Together with Proposition 3.1, it can infer that
 $$ \begin{align*} Q(\xi)&\geq \sum_{I\in{\mathcal D}(\tau),l_{\tau}(I)< N_\epsilon}\Big|\widehat{\mu}_{\{b_n\},\{{\mathcal D}_n\}} \Big(\xi+\tau(I)\Big)\Big|^2\nonumber\\ &=\sum_{I\in{\mathcal D}(\tau),l_{\tau}(I)< N_\epsilon}\lim_{k\rightarrow\infty}\Big|\widehat{\mu}_{k} \Big(\xi+\tau^*(I|_k)\Big)\Big|^2\nonumber\\ &=\lim_{k\rightarrow\infty}\sum_{I'\in{\mathcal D}(\tau),l_{\tau}(I)< N_\epsilon}\Big|\widehat{\mu}_{k} \Big(\xi+\tau^*(I|_k)\Big)\Big|^2. \end{align*} $$
$$ \begin{align*} Q(\xi)&\geq \sum_{I\in{\mathcal D}(\tau),l_{\tau}(I)< N_\epsilon}\Big|\widehat{\mu}_{\{b_n\},\{{\mathcal D}_n\}} \Big(\xi+\tau(I)\Big)\Big|^2\nonumber\\ &=\sum_{I\in{\mathcal D}(\tau),l_{\tau}(I)< N_\epsilon}\lim_{k\rightarrow\infty}\Big|\widehat{\mu}_{k} \Big(\xi+\tau^*(I|_k)\Big)\Big|^2\nonumber\\ &=\lim_{k\rightarrow\infty}\sum_{I'\in{\mathcal D}(\tau),l_{\tau}(I)< N_\epsilon}\Big|\widehat{\mu}_{k} \Big(\xi+\tau^*(I|_k)\Big)\Big|^2. \end{align*} $$
Using the condition of Theorem 1.3, it follows that
 $$ \begin{align} Q(\xi)&\geq \lim_{k\rightarrow\infty}\sum_{\sigma\in{\mathcal D}_{0,k},l_\tau(\sigma\sigma')<N_\epsilon} \!\Big|\widehat{\mu}_{k} \Big(\xi+\tau^*\big((\sigma\sigma')|_k\big)\Big)\Big|^2 \nonumber\\ &=\lim_{k\rightarrow\infty}\!\sum_{\sigma\in{\mathcal D}_{0,k},l_\tau(\sigma\sigma')<N_\epsilon} \Big|\widehat{\mu}_k \Big(\xi+\tau^*\big(\sigma\big)\Big)\Big|^2, \end{align} $$
$$ \begin{align} Q(\xi)&\geq \lim_{k\rightarrow\infty}\sum_{\sigma\in{\mathcal D}_{0,k},l_\tau(\sigma\sigma')<N_\epsilon} \!\Big|\widehat{\mu}_{k} \Big(\xi+\tau^*\big((\sigma\sigma')|_k\big)\Big)\Big|^2 \nonumber\\ &=\lim_{k\rightarrow\infty}\!\sum_{\sigma\in{\mathcal D}_{0,k},l_\tau(\sigma\sigma')<N_\epsilon} \Big|\widehat{\mu}_k \Big(\xi+\tau^*\big(\sigma\big)\Big)\Big|^2, \end{align} $$
where
![]() $\sigma '$
are given as in the theorem. It can easily be checked that
$\sigma '$
are given as in the theorem. It can easily be checked that
 $$ \begin{align*} \Big|\widehat{\mu}_{\{b_n\},\{{\mathcal D}_n\}} \Big(\xi+\tau(\sigma\sigma')\Big)\Big| &=\Big|\widehat{\mu}_k\Big(\xi+\tau^{*}(\sigma)\Big)\Big|\cdot \Big|\widehat{\mu}_{>k}\\ &\quad \Big(\frac{\xi+\tau^{*}(\sigma)}{B_k} \!+\frac{\sum_{j=1}^{\infty}\tau\big((\sigma\sigma')|_{k+j}\big)r_{k+j}B_{k+j-1}}{B_{k}}\Big)\Big|, \end{align*} $$
$$ \begin{align*} \Big|\widehat{\mu}_{\{b_n\},\{{\mathcal D}_n\}} \Big(\xi+\tau(\sigma\sigma')\Big)\Big| &=\Big|\widehat{\mu}_k\Big(\xi+\tau^{*}(\sigma)\Big)\Big|\cdot \Big|\widehat{\mu}_{>k}\\ &\quad \Big(\frac{\xi+\tau^{*}(\sigma)}{B_k} \!+\frac{\sum_{j=1}^{\infty}\tau\big((\sigma\sigma')|_{k+j}\big)r_{k+j}B_{k+j-1}}{B_{k}}\Big)\Big|, \end{align*} $$
and
 $$ \begin{align*} \Big|\frac{\xi+\tau^{*}(\sigma)}{B_k}\Big|=\Big|\frac{\xi+ \sum_{j=1}^k \tau(\sigma|_j)r_jB_{j-1}}{B_k}\Big| \leq r_{k+1}-\frac{1}{q_k}. \end{align*} $$
$$ \begin{align*} \Big|\frac{\xi+\tau^{*}(\sigma)}{B_k}\Big|=\Big|\frac{\xi+ \sum_{j=1}^k \tau(\sigma|_j)r_jB_{j-1}}{B_k}\Big| \leq r_{k+1}-\frac{1}{q_k}. \end{align*} $$
Therefore, combining with Lemma 3.6, we get
where c is given in Lemma 3.6. Together with (3.11), it yields that
 $$ \begin{align*}\sum_{\sigma\in{\mathcal D}_{0,k},l_\tau(\sigma\sigma')\geq N_\epsilon} \Big|\widehat{\mu}_k \Big(\xi+\tau^*\big(\sigma\big)\Big)\Big|^2 \leq\frac{1}{c^2}\sum_{\sigma\in{\mathcal D}_{0,k},l_\tau(\sigma\sigma') \geq N_\epsilon} \Big|\widehat{\mu}_{\{b_n\},\{{\mathcal D}_n\}} \Big(\xi+\tau^*\big(\sigma\big)\Big)\Big|^2 <\frac{\epsilon}{c^2}.\end{align*} $$
$$ \begin{align*}\sum_{\sigma\in{\mathcal D}_{0,k},l_\tau(\sigma\sigma')\geq N_\epsilon} \Big|\widehat{\mu}_k \Big(\xi+\tau^*\big(\sigma\big)\Big)\Big|^2 \leq\frac{1}{c^2}\sum_{\sigma\in{\mathcal D}_{0,k},l_\tau(\sigma\sigma') \geq N_\epsilon} \Big|\widehat{\mu}_{\{b_n\},\{{\mathcal D}_n\}} \Big(\xi+\tau^*\big(\sigma\big)\Big)\Big|^2 <\frac{\epsilon}{c^2}.\end{align*} $$
Applying Propositions 3.2 and 3.3, we infer that
 $$ \begin{align*} \sum_{\sigma\in{\mathcal D}_{0,k},l_\tau(\sigma\sigma')<N_\epsilon} \Big|\widehat{\mu}_k \Big(\xi+\tau^*\big(\sigma\big)\Big)\Big|^2+\sum_{\sigma\in{\mathcal D}_{0,k},l_\tau(\sigma\sigma')\geq N_\epsilon} \Big|\widehat{\mu}_k \Big(\xi+\tau^*\big(\sigma\big)\Big)\Big|^2=1. \end{align*} $$
$$ \begin{align*} \sum_{\sigma\in{\mathcal D}_{0,k},l_\tau(\sigma\sigma')<N_\epsilon} \Big|\widehat{\mu}_k \Big(\xi+\tau^*\big(\sigma\big)\Big)\Big|^2+\sum_{\sigma\in{\mathcal D}_{0,k},l_\tau(\sigma\sigma')\geq N_\epsilon} \Big|\widehat{\mu}_k \Big(\xi+\tau^*\big(\sigma\big)\Big)\Big|^2=1. \end{align*} $$
Then using (3.12), we obtain that
 $$ \begin{align*} Q(\xi)\geq\lim_{k\rightarrow\infty} \Big(1-\sum_{\sigma\in{\mathcal D}_{0,k},l_\tau(\sigma\sigma')\geq N_\epsilon} \Big|\widehat{\mu}_k \Big(\xi+\tau^*\big(\sigma\big)\Big)\Big|^2\Big) \geq1-\frac{\epsilon}{c^2}. \end{align*} $$
$$ \begin{align*} Q(\xi)\geq\lim_{k\rightarrow\infty} \Big(1-\sum_{\sigma\in{\mathcal D}_{0,k},l_\tau(\sigma\sigma')\geq N_\epsilon} \Big|\widehat{\mu}_k \Big(\xi+\tau^*\big(\sigma\big)\Big)\Big|^2\Big) \geq1-\frac{\epsilon}{c^2}. \end{align*} $$
Hence,
![]() $Q(\xi )\geq 1$
and this completes the proof of Theorem 1.3.
$Q(\xi )\geq 1$
and this completes the proof of Theorem 1.3.
4 The proof of Theorem 1.5
The aim of this section is to prove Theorem 1.5. Recall that
![]() $\sigma \in {\mathcal D}_{0,\infty }$
is a useful word about the generalized tree mapping
$\sigma \in {\mathcal D}_{0,\infty }$
is a useful word about the generalized tree mapping
![]() $\tau $
if there exists an integer
$\tau $
if there exists an integer
![]() $\tau ^\diamond (\sigma )\in {\mathbb Z}$
satisfying
$\tau ^\diamond (\sigma )\in {\mathbb Z}$
satisfying
 $$ \begin{align*}\tau^\diamond(\sigma)\equiv\sum_{k=1}^n\tau(\sigma|_k)r_kB_{k-1} \quad\pmod{r_{n+1}B_n}, \qquad \text{for all}\ n\ge 1.\end{align*} $$
$$ \begin{align*}\tau^\diamond(\sigma)\equiv\sum_{k=1}^n\tau(\sigma|_k)r_kB_{k-1} \quad\pmod{r_{n+1}B_n}, \qquad \text{for all}\ n\ge 1.\end{align*} $$
It is easy to see that if
![]() $\sigma \in {\mathcal D}_{0,\infty }$
is a useful word, then the associated
$\sigma \in {\mathcal D}_{0,\infty }$
is a useful word, then the associated
![]() $\tau ^\diamond (\sigma )$
is unique. Given a generalized tree mapping
$\tau ^\diamond (\sigma )$
is unique. Given a generalized tree mapping
![]() $\tau $
, we let
$\tau $
, we let
Proof of Theorem 1.5.
(i) We first show that
![]() $\Lambda ^\diamond (\tau )$
is an orthogonal set of
$\Lambda ^\diamond (\tau )$
is an orthogonal set of
![]() $\mu _{\{b_n\},\{{\mathcal D}_n\}}$
. For any two distinct words
$\mu _{\{b_n\},\{{\mathcal D}_n\}}$
. For any two distinct words
![]() $\sigma ,\sigma '\in {\mathcal D}^\diamond (\tau )$
, we let n be the first index such that
$\sigma ,\sigma '\in {\mathcal D}^\diamond (\tau )$
, we let n be the first index such that
![]() $\sigma |_n \neq \sigma '|_n$
. Since
$\sigma |_n \neq \sigma '|_n$
. Since
 $$ \begin{align*}\tau^\diamond(\sigma)\equiv\sum_{k=1}^n\tau(\sigma|_k)r_kB_{k-1} \!\quad\pmod{r_{n+1}B_n} \quad\! \text{and}\! \quad \tau^\diamond(\sigma')\equiv\sum_{k=1}^n\tau(\sigma'|_k)r_kB_{k-1} \quad\pmod{r_{n+1}B_n},\end{align*} $$
$$ \begin{align*}\tau^\diamond(\sigma)\equiv\sum_{k=1}^n\tau(\sigma|_k)r_kB_{k-1} \!\quad\pmod{r_{n+1}B_n} \quad\! \text{and}\! \quad \tau^\diamond(\sigma')\equiv\sum_{k=1}^n\tau(\sigma'|_k)r_kB_{k-1} \quad\pmod{r_{n+1}B_n},\end{align*} $$
it follows that
for some integer M. Using the definition of the generalized tree mapping, we know that
Together with (2.2), we also have that
Hence,
![]() $\Lambda ^\diamond (\tau )$
is an orthogonal set of
$\Lambda ^\diamond (\tau )$
is an orthogonal set of
![]() $\mu _{\{b_n\},\{{\mathcal D}_n\}}$
.
$\mu _{\{b_n\},\{{\mathcal D}_n\}}$
.
Next, we show the maximality of
![]() $\Lambda ^\diamond (\tau )$
by contradiction. Suppose that there exists a
$\Lambda ^\diamond (\tau )$
by contradiction. Suppose that there exists a
![]() $\theta \in {\mathbb R}\backslash \Lambda ^\diamond (\tau )$
such that
$\theta \in {\mathbb R}\backslash \Lambda ^\diamond (\tau )$
such that
![]() $\theta $
is orthogonal to all elements in
$\theta $
is orthogonal to all elements in
![]() $\Lambda ^\diamond (\tau )$
. Note that
$\Lambda ^\diamond (\tau )$
. Note that
![]() $0\in \Lambda ^\diamond (\tau )$
, we have that
$0\in \Lambda ^\diamond (\tau )$
, we have that
![]() $\theta \in \mathcal {Z}(\widehat {\mu }_{\{b_n\},\{{\mathcal D}_n\}})$
. Hence, by (2.2), there exists
$\theta \in \mathcal {Z}(\widehat {\mu }_{\{b_n\},\{{\mathcal D}_n\}})$
. Hence, by (2.2), there exists
![]() $k\in {\mathbb Z}$
such that
$k\in {\mathbb Z}$
such that
![]() $\theta =r_kB_{k-1}a,$
where
$\theta =r_kB_{k-1}a,$
where
![]() $a\in {\mathbb Z}$
and
$a\in {\mathbb Z}$
and
![]() $q_k$
does not divide
$q_k$
does not divide
![]() $a.$
By Lemma 2.2, it yields that
$a.$
By Lemma 2.2, it yields that
where
![]() $\epsilon _{j}\in {\mathcal C}_{j}=\{-1,0,1,\ldots ,q_jr_{j+1}-2\}(k\leq j\leq k+l)$
and
$\epsilon _{j}\in {\mathcal C}_{j}=\{-1,0,1,\ldots ,q_jr_{j+1}-2\}(k\leq j\leq k+l)$
and
![]() $q_k$
does not divide
$q_k$
does not divide
![]() $\epsilon _{k}.$
Consequently, it can infer that
$\epsilon _{k}.$
Consequently, it can infer that
where
![]() $q_k$
does not divide
$q_k$
does not divide
![]() $\epsilon _{k}.$
Note that there exists unique
$\epsilon _{k}.$
Note that there exists unique
![]() $\sigma _j~(0\leq \sigma _j\leq q_j-1)$
such that
$\sigma _j~(0\leq \sigma _j\leq q_j-1)$
such that
Denote
![]() $\sigma _j=0$
for all
$\sigma _j=0$
for all
![]() $1\leq j<k$
and let
$1\leq j<k$
and let
![]() $\sigma =\sigma _1\sigma _2\dots \sigma _{k+l}$
. By the definition of useful words, it can be easily checked that
$\sigma =\sigma _1\sigma _2\dots \sigma _{k+l}$
. By the definition of useful words, it can be easily checked that
![]() $\sigma 0^\infty $
is a useful word.
$\sigma 0^\infty $
is a useful word.
Since
![]() $\theta \notin \Lambda ^\diamond (\tau ),$
we can find the smallest integer
$\theta \notin \Lambda ^\diamond (\tau ),$
we can find the smallest integer
![]() $\alpha $
such that
$\alpha $
such that
![]() $\tau (\sigma _{1}\dots \sigma _{\alpha })\neq \epsilon _{\alpha }.$
Hence,
$\tau (\sigma _{1}\dots \sigma _{\alpha })\neq \epsilon _{\alpha }.$
Hence,
for some integer M. Using the definition of the generalized tree mapping again, we know that
![]() $(\sigma 0^\infty )|_{\alpha }\equiv \sigma _{\alpha }~(\mathrm {mod}~q_\alpha ),$
which is also congruent to
$(\sigma 0^\infty )|_{\alpha }\equiv \sigma _{\alpha }~(\mathrm {mod}~q_\alpha ),$
which is also congruent to
![]() $\epsilon _{\alpha }$
by our construction. It implies that
$\epsilon _{\alpha }$
by our construction. It implies that
and thus
![]() $\theta -\tau ^\diamond (\sigma 0^\infty )\notin \widehat {\mu }_{\{b_n\},\{{\mathcal D}_n\}}$
. This contradicts the assumption and the maximality of
$\theta -\tau ^\diamond (\sigma 0^\infty )\notin \widehat {\mu }_{\{b_n\},\{{\mathcal D}_n\}}$
. This contradicts the assumption and the maximality of
![]() $\Lambda ^\diamond (\tau )$
follows.
$\Lambda ^\diamond (\tau )$
follows.
(ii) Together with the conclusion (i) and Theorem 1.2, there exists a tree mapping
![]() $\tau _1$
such that
$\tau _1$
such that
![]() $\Lambda ^\diamond (\tau )=\Lambda (\tau _1)$
. For any
$\Lambda ^\diamond (\tau )=\Lambda (\tau _1)$
. For any
![]() $\sigma '\in {\mathcal D}_{0,k}~(k\geq 1)$
, by the definition of the tree mapping
$\sigma '\in {\mathcal D}_{0,k}~(k\geq 1)$
, by the definition of the tree mapping
![]() $\tau _1$
, there is an infinite word
$\tau _1$
, there is an infinite word
![]() $\sigma "\in {\mathcal D}_{k,\infty }$
such that
$\sigma "\in {\mathcal D}_{k,\infty }$
such that
![]() $\sigma '\sigma "\in {\mathcal D}(\tau _1)$
. Since
$\sigma '\sigma "\in {\mathcal D}(\tau _1)$
. Since
![]() $\Lambda ^\diamond (\tau )=\Lambda (\tau _1)$
, it follows that there exists
$\Lambda ^\diamond (\tau )=\Lambda (\tau _1)$
, it follows that there exists
![]() $\sigma \in {\mathcal D}^\diamond (\tau )$
such that
$\sigma \in {\mathcal D}^\diamond (\tau )$
such that
![]() $\tau ^\diamond (\sigma )=\tau _1(\sigma '\sigma ").$
Note that
$\tau ^\diamond (\sigma )=\tau _1(\sigma '\sigma ").$
Note that
![]() $\sigma |_k0^\infty $
is a useful word, we can find
$\sigma |_k0^\infty $
is a useful word, we can find
![]() $\sigma "'\in {\mathcal D}(\tau _1)$
such that
$\sigma "'\in {\mathcal D}(\tau _1)$
such that
![]() $\tau ^\diamond (\sigma |_k0^\infty )=\tau _1(\sigma "')$
. Hence, one has that
$\tau ^\diamond (\sigma |_k0^\infty )=\tau _1(\sigma "')$
. Hence, one has that
A direct calculation shows that
 $$ \begin{align*}\mid\tau_1^*\big((\sigma'\sigma")|_n\big)-\tau_1^*(\sigma"'|_n)\mid\leq \sum_{j=1}^{n}(q_jr_{j+1}-2)r_jB_{j-1}<r_{n+1}B_n.\end{align*} $$
$$ \begin{align*}\mid\tau_1^*\big((\sigma'\sigma")|_n\big)-\tau_1^*(\sigma"'|_n)\mid\leq \sum_{j=1}^{n}(q_jr_{j+1}-2)r_jB_{j-1}<r_{n+1}B_n.\end{align*} $$
Together with (4.2), it implies that
![]() $\tau _1^*\big ((\sigma '\sigma ")|_n\big )=\tau _1^*(\sigma "'|_n)$
for all
$\tau _1^*\big ((\sigma '\sigma ")|_n\big )=\tau _1^*(\sigma "'|_n)$
for all
![]() $1\leq n\leq k$
and thus we have that
$1\leq n\leq k$
and thus we have that
Hence, we rewrite
![]() $\sigma "'$
as
$\sigma "'$
as
![]() $\sigma "'=\sigma '\delta $
with
$\sigma "'=\sigma '\delta $
with
![]() $\delta \in {\mathcal D}_{k,\infty }$
. Since
$\delta \in {\mathcal D}_{k,\infty }$
. Since
![]() $\sup _{\sigma \in {\mathcal D}_{0,*}}|\tau (\sigma )|<\infty $
, there exists a constant M such that
$\sup _{\sigma \in {\mathcal D}_{0,*}}|\tau (\sigma )|<\infty $
, there exists a constant M such that
![]() $|\tau (\sigma )|<2^M$
for all
$|\tau (\sigma )|<2^M$
for all
![]() $\sigma \in {\mathcal D}_{0,*}$
. Then
$\sigma \in {\mathcal D}_{0,*}$
. Then
 $$ \begin{align} |\tau_1(\sigma'\delta)|=|\tau^\diamond(\sigma|_k0^\infty)|\leq 2^M\sum_{j=1}^k r_jB_{j-1}\leq 2^{M+1}r_kB_{k-1}. \end{align} $$
$$ \begin{align} |\tau_1(\sigma'\delta)|=|\tau^\diamond(\sigma|_k0^\infty)|\leq 2^M\sum_{j=1}^k r_jB_{j-1}\leq 2^{M+1}r_kB_{k-1}. \end{align} $$
Repeating the procedure of (4.1), we also have that
where
![]() $\vartheta _j\in {\mathcal C}_j$
for all
$\vartheta _j\in {\mathcal C}_j$
for all
![]() $k\leq j\leq k+\ell $
. Then it is easy to check that
$k\leq j\leq k+\ell $
. Then it is easy to check that
 $$ \begin{align*} 2^{M+1} r_kB_{k-1}&=|\vartheta_kr_kB_{k-1}+\vartheta_{k+1}r_{k+1}B_k+\cdots+ \vartheta_{k+\ell}r_{k+\ell}B_{k+\ell-1}|\\ &\geq r_{k+\ell}B_{k+\ell-1}-\sum_{j=k}^{k+\ell-1}(q_jr_{j+1}-2)r_jB_{j-1}\\ &\geq r_{k+\ell-1}B_{k+\ell-2}. \end{align*} $$
$$ \begin{align*} 2^{M+1} r_kB_{k-1}&=|\vartheta_kr_kB_{k-1}+\vartheta_{k+1}r_{k+1}B_k+\cdots+ \vartheta_{k+\ell}r_{k+\ell}B_{k+\ell-1}|\\ &\geq r_{k+\ell}B_{k+\ell-1}-\sum_{j=k}^{k+\ell-1}(q_jr_{j+1}-2)r_jB_{j-1}\\ &\geq r_{k+\ell-1}B_{k+\ell-2}. \end{align*} $$
Consequently, it can infer that
and thus
![]() $\ell \leq M+2$
.
$\ell \leq M+2$
.
We let m be the largest order of the expansion of
![]() $\tau (\sigma '\delta )$
with respect to the base
$\tau (\sigma '\delta )$
with respect to the base
![]() $\{{\mathcal C}_j\}_{j=1}^\infty $
. Using (4.3) and (4.4), it can obtain that
$\{{\mathcal C}_j\}_{j=1}^\infty $
. Using (4.3) and (4.4), it can obtain that
Therefore, it follows from the definition of m that
Hence, the conclusion (ii) follows form Theorem 1.3.