Hostname: page-component-7dd5485656-gs9qr Total loading time: 0 Render date: 2025-10-31T18:22:37.327Z Has data issue: false hasContentIssue false
  • English
  • Français

Fukaya categories of surfaces, spherical objects and mapping class groups

Part of: Symplectic geometry, contact geometry

Published online by Cambridge University Press:  18 March 2021

Denis Auroux  and
Ivan Smith
Denis Auroux
Affiliation:
Department of Mathematics, Harvard University, Cambridge, MA 02138, USA; E-mail: auroux@math.harvard.edu.
Ivan Smith
Affiliation:
Centre for Mathematical Sciences, University of Cambridge, CB3 0WB, England; E-mail: is200@cam.ac.uk.

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that every spherical object in the derived Fukaya category of a closed surface of genus at least 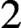$2$ whose Chern character represents a nonzero Hochschild homology class is quasi-isomorphic to a simple closed curve equipped with a rank 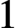$1$ local system. (The homological hypothesis is necessary.) This largely answers a question of Haiden, Katzarkov and Kontsevich. It follows that there is a natural surjection from the autoequivalence group of the Fukaya category to the mapping class group. The proofs appeal to and illustrate numerous recent developments: quiver algebra models for wrapped categories, sheafifying the Fukaya category, equivariant Floer theory for finite and continuous group actions and homological mirror symmetry. An application to high-dimensional symplectic mapping class groups is included.

MSC classification

Primary: 53D37: Mirror symmetry, symplectic aspects; homological mirror symmetry; Fukaya category

Information

Type
Topology
Information
Forum of Mathematics, Sigma , Volume 9 , 2021 , e26
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Abouzaid, M., ‘On the Fukaya categories of higher genus surfaces’, Adv. Math. 217(3) (2008), 1192–1235.CrossRefGoogle Scholar
Abouzaid, M., ‘A geometric criterion for generating the Fukaya category’, Publ. Math. Inst. Hautes Études Sci. 112 (2010), 191–240.CrossRefGoogle Scholar
Abouzaid, M., ‘Family Floer cohomology and mirror symmetry’, in Proceedings of the International Congress of Mathematicians—Seoul 2014. Vol. II (Kyung Moon Sa, Seoul, South Korea, 2014), 813–836.Google Scholar
Abouzaid, M., ‘The family Floer functor is faithful’, J. Eur. Math. Soc. (JEMS) 19(7) (2017), 2139–2217.CrossRefGoogle Scholar
Abouzaid, M., Auroux, D., Efimov, A. I., Katzarkov, L. and Orlov, D., ‘Homological mirror symmetry for punctured spheres’, J. Amer. Math. Soc. 26(4) (2013), 1051–1083.CrossRefGoogle Scholar
Abouzaid, M., Auroux, D. and Katzarkov, L., ‘Lagrangian fibrations on blowups of toric varieties and mirror symmetry for hypersurfaces’, Publ. Math. Inst. Hautes Études Sci. 123 (2016), 199–282.CrossRefGoogle Scholar
Abouzaid, M. and Seidel, P., ‘An open string analogue of Viterbo functoriality’, Geom. Topol. 14(2) (2010), 627–718.CrossRefGoogle Scholar
Abouzaid, M. and Smith, I., ‘Exact Lagrangians in plumbings’, Geom. Funct. Anal. 22(4) (2012), 785–831.CrossRefGoogle Scholar
Abreu, M. and McDuff, D., ‘Topology of symplectomorphism groups of rational ruled surfaces’, J. Amer. Math. Soc. 13(4) (2000), 971–1009.CrossRefGoogle Scholar
André, Y., ‘Différentielles non commutatives et théorie de Galois différentielle ou aux différences’, Ann. Sci. Éc. Norm. Supér. (4) 34(5) (2001), 685–739.CrossRefGoogle Scholar
Auroux, D., ‘Asymptotically holomorphic families of symplectic submanifolds’, Geom. Funct. Anal. 7(6) (1997), 971–995.CrossRefGoogle Scholar
Borisov, L. A. and Horja, R. P., ‘On the $K$-theory of smooth toric DM stacks’, in Snowbird Lectures on String Geometry, Contemp. Math. vol. 401 (American Mathematical Society, Providence, RI, 2006), 21–42.CrossRefGoogle Scholar
Brion, M., ‘Some structure theorems for algebraic groups’, in Algebraic Groups: Structure and Actions, Proc. Sympos. Pure Math. vol. 94 (American Mathematical Society, Providence, RI, 2017), 53–126.CrossRefGoogle Scholar
Burban, I. and Drozd, Y., ‘Coherent sheaves on rational curves with simple double points and transversal intersections’, Duke Math. J. 121(2) (2004), 189–229.Google Scholar
Chang, H.-C., Erickson, J., Letscher, D., de Mesmay, A., Schleimer, S., Sedgwick, E., Thurston, D. and Tillmann, S., ‘Tightening curves on surfaces via local moves’, in Proceedings of the Twenty-Ninth Annual ACM-SIAM Symposium on Discrete Algorithms (SIAM, Philadelphia, PA, 2018), 121–135.Google Scholar
Ganatra, S., ‘Automatically generating Fukaya categories and computing quantum cohomology’, Preprint, 2016, arXiv:1605.07702.Google Scholar
Ganatra, S., ‘Symplectic cohomology and duality for the wrapped Fukaya category’, Preprint, YYYY, arXiv:1304.7312.Google Scholar
Ganatra, S., Pardon, J. and Shende, V., ‘Sectorial descent for wrapped Fukaya categories’, Preprint, YYYY, arXiv:1809.03427.Google Scholar
Gromov, M., ‘Pseudo holomorphic curves in symplectic manifolds’, Invent. Math. 82(2) (1985), 307–347.CrossRefGoogle Scholar
Haiden, F., Katzarkov, L. and Kontsevich, M., ‘Flat surfaces and stability structures’, Publ. Math. Inst. Hautes Études Sci. 126 (2017), 247–318.CrossRefGoogle Scholar
Hanselman, J., Rasmussen, J. and Watson, L., ‘Bordered Floer homology for manifolds with torus boundary via immersed curves’, Preprint, YYYY, arXiv:1604.03466.Google Scholar
Hass, J. and Scott, P., ‘Intersections of curves on surfaces’, Israel J. Math. 51(1–2) (1985), 90–120.CrossRefGoogle Scholar
Hass, J. and Scott, P., ‘Shortening curves on surfaces’, Topology 33(1) (1994), 25–43.CrossRefGoogle Scholar
Kartal, Y. Baris, ‘Dynamical invariants of mapping torus categories’, Preprint, YYYY, arXiv:1809.04046.Google Scholar
Lee, H., ‘Homological mirror symmetry for open Riemann surfaces from pair-of-pants decompositions’, Preprint, YYYY, arXiv:1608.04473.Google Scholar
Nazarova, L. A. and Roĭter, A. V., ‘A certain problem of I. M. Gel’fand’, Funktsional. Anal. i Prilozhen. 7(4) (1973), 54–69.Google Scholar
Ritter, A. F. and Smith, I., ‘The monotone wrapped Fukaya category and the open-closed string map’, Selecta Math. (N.S.) 23(1) (2017), 533–642.CrossRefGoogle Scholar
Schaller, P. S, ‘Mapping class groups of hyperbolic surfaces and automorphism groups of graphs’, Compos. Math. 122(3) (2000), 243–260.CrossRefGoogle Scholar
Seidel, P., Fukaya Categories and Picard–Lefschetz Theory, Zurich Lectures in Advanced Mathematics (European Mathematical Society, Zürich, 2008).CrossRefGoogle Scholar
Seidel, P., ‘Homological mirror symmetry for the genus two curve’, J. Algebraic Geom. 20(4) (2011), 727–769.CrossRefGoogle Scholar
Seidel, P., ‘Lagrangian homology spheres in $\left({A}_m\right)$ Milnor fibres via ${\mathbb{C}}^{\ast }$-equivariant ${A}_{\infty }$-modules’, Geom. Topol. 16(4) (2012), 2343–2389.CrossRefGoogle Scholar
Seidel, P., Abstract Analogues of Flux as Symplectic Invariants, Mém. Soc. Math. Fr. (N.S.) vol. 137, 132 (Soc. Math. France., Marseilles, 2014).Google Scholar
Seidel, P., ‘Lectures on categorical dynamics and symplectic topology’, unpublished manuscript (2014). URL: http://math.mit.edu/~seidel/.Google Scholar
Seidel, P., Homological Mirror Symmetry for the Quartic Surface, Mem. Amer. Math. Soc. 236, 1116 (Amer. Math. Soc., Providence, RI , 2015).Google Scholar
Seidel, P., ‘Picard-Lefschetz theory and dilating ${\mathbb{C}}^{\ast }$-actions’, J. Topol. 8(4) (2015), 1167–1201. With an appendix available at arXiv:1403.7571v2.CrossRefGoogle Scholar
Sheridan, N., ‘Homological mirror symmetry for Calabi-Yau hypersurfaces in projective space’, Invent. Math. 199(1) (2015), 1–186.CrossRefGoogle Scholar
Shklyarov, D., ‘Hirzebruch–Riemann–Roch-type formula for DG algebras’, Proc. Lond. Math. Soc. (3) 106(1) (2013), 1–32.CrossRefGoogle Scholar
Smith, I., ‘Floer cohomology and pencils of quadrics’, Invent. Math. 189(1) (2012), 149–250.CrossRefGoogle Scholar
Steinitz, E., ‘Polyeder und Raumeinteilungen’, in Encyclopädie der mathematischen Wissenschaften, Band 3 (Geometries) (IIIAB12) (B.G. Teubner Verlag, Leipzig, 1916) 1–139.Google Scholar
Steinitz, E. and Rademacher, H., Vorlesungen über die Theorie der Polyeder unter Einschluss der Elemente der Topologie (Springer-Verlag, Berlin, 1976). Reprint of the 1934 original, Grundlehren der Mathematischen Wissenschaften, 41.CrossRefGoogle Scholar
Weibel, C., ‘The negative $K$-theory of normal surfaces’, Duke Math. J. 108(1) (2001), 1–35.CrossRefGoogle Scholar