Hostname: page-component-7dd5485656-wlg5v Total loading time: 0 Render date: 2025-10-31T01:54:38.707Z Has data issue: false hasContentIssue false
  • English
  • Français

KOSTANT'S PROBLEM AND PARABOLIC SUBGROUPS

Published online by Cambridge University Press:  30 July 2009

JOHAN KÅHRSTRÖM
JOHAN KÅHRSTRÖM*
Affiliation:
Department of Mathematics, Uppsala University, SE-751 06 Uppsala, Sweden e-mail: johank@math.uu.se
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 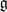be a finite dimensional complex semi-simple Lie algebra with Weyl group W and simple reflections S. For I ⊆ S let 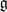I be the corresponding semi-simple subalgebra of 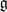. Denote by WI the Weyl group of 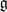I and let w○ and wI○ be the longest elements of W and WI, respectively. In this paper we show that the answer to Kostant's problem, i.e. whether the universal enveloping algebra surjects onto the space of all ad-finite linear transformations of a given module, is the same for the simple highest weight 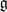I-module LI(x) of highest weight x ⋅ 0, x ∈ WI, as the answer for the simple highest weight 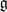-module L(xwI○w○) of highest weight xwI○w○ ⋅ 0. We also give a new description of the unique quasi-simple quotient of the Verma module Δ(e) with the same annihilator as L(y), y ∈ W.

Information

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 52 , Issue 1 , January 2010 , pp. 19 - 32
Copyright
Copyright © Glasgow Mathematical Journal Trust 2009

References

REFERENCES

1.Andersen, H. H. and Stroppel, C., Twisting functors on , Represent. Theory 7 (2003), 681–699.CrossRefGoogle Scholar
2.Bernšteĭn, J. N. and Gelfand, S. I., Tensor products of finite- and infinite-dimensional representations of semisimple Lie algebras, Compositio Math. 41 (2) (1980), 245–285.Google Scholar
3.Bernšteĭn, I. N., Gelfand, I. M. and Gelfand, S. I., A certain category of -modules. Funkcional. Anal. i Prilozen. 10 (2) (1976), 1–8.Google Scholar
4.Conze, N., Algèbres d'opérateurs différentiels et quotients des algèbres enveloppantes, Bull. Soc. Math. France 102 (1974), 379–415.CrossRefGoogle Scholar
5.Conze-Berline, N. and Duflo, M., Sur les représentations induites des groupes semi-simples complexes. Compositio Math. 34 (3) (1977), 307–336.Google Scholar
6.Dixmier, J., Enveloping algebras, Graduate Studies in Mathematics, 11, (American Mathematical Society, Prodivence, RI, 1996).Google Scholar
7.Duflo, M., Sur la classification des idéaux primitifs dans l'algèbre enveloppante d'une algèbre de Lie semi-simple, Ann. Math. 105 (1977), 107–120.CrossRefGoogle Scholar
8.Gabber, O. and Joseph, A., On the Bernstein–Gelfand–Gelfand resolution and the Duflo Sum formula, Compositio Math. 43 (Fasc. 1) 1981, 108–131.Google Scholar
9.Happel, D., Triangulated categories in the representation theory of finite-dimensional algebras, London Mathematical Society Lecture Notes Series, Vol. 119 (Cambridge University Press, Cambridge, UK, 1988).CrossRefGoogle Scholar
10.Humphreys, J., Representations of semisimple Lie algebras in the BGG category O, Graduate Studies in Mathematics 94 (American Mathematical Society, Providence, RI, 2008).Google Scholar
11.Jantzen, J. C., Moduln mit einem höchsten Gewicht, Lecture Notes in Mathematics, Vol. 750 (Springer-Verlag, Berlin, 1979), ii–195.CrossRefGoogle Scholar
12.Jantzen, J. C., Einhüllende Algebren halbeinfacher Lie-Algebren, u Ergebnisse der Mathematik und ihrer Grenzgebiete (3), Vol. 3 (Springer-Verlag, Berlin, 1983).CrossRefGoogle Scholar
13.Joseph, A., A characteristic variety for the primitive spectrum of a semisimple Lie algebra, Non-commutative harmonic analysis (Actes Colloq., Marseille-Luminy, 1976), 102–118. Lecture Notes in Mathematics, Vol. 587, Springer, Berlin, 1977.Google Scholar
14.Joseph, A., Dixmier's problem for Verma and principal series submodules, J. Lond. Math. Soc. 20 (1979), 193–204.CrossRefGoogle Scholar
15.Joseph, A., Kostant's problem, Goldie rank and the Gelfand–Kirillov conjecture, Invent. Math. 56 (1980), 191–213.CrossRefGoogle Scholar
16.Joseph, A., Goldie rank in the enveloping algebra of a semisimple Lie algebra, I, J. Algebra 65 (1980), 269–283.CrossRefGoogle Scholar
17.Joseph, A., Kostant's problem and Goldie rank, Noncommutative harmonic analysis and Lie groups (Marseille, 1980), 249–266, Lecture Notes in Mathematics, 880 (Springer, Berlin-New York, 1981).Google Scholar
18.Joseph, A., A sum rule for scale factors in the Goldie rank polynomials, J. Algebra 118 (2) (1988), 276–311.CrossRefGoogle Scholar
19.Kåhrström, J., Mazorchuk, V., A new approach to Kostant's problem, preprint arXiv:0712.3117.Google Scholar
20.Kazhdan, D. and Lusztig, G., Representations of Coxeter groups and Hecke algebras, Invent. Math. 53 (2) (1979), 165–184.CrossRefGoogle Scholar
21.Khomenko, O. and Mazorchuk, V., Structure of modules induced from simple modules with minimal annihilator, Can. J. Math. 56 (2) (2004), 293–309.CrossRefGoogle Scholar
22.Khomenko, O. and Mazorchuk, V., On Arkhipov's and Enright's functors, Math. Z. 249 (2) (2005), 357–386.CrossRefGoogle Scholar
23.Lusztig, G., Characters of reductive groups over a finite field, in Annals of Mathematics Studies, Vol. 107 (Princeton University Press, Princeton, NJ, 1984).Google Scholar
24.Lusztig, G., Cells in affine Weyl groups, in Advanced Studies in Pure Mathematics, Vol. 6 (North-Holland, Amsterdam, 1985).Google Scholar
25.Lusztig, G., Cells in affine Weyl groups, II, Algebra 109 (2) (1987), 536–548.CrossRefGoogle Scholar
26.Mazorchuk, V., A twisted approach to Kostant's problem, Glasgow Math. J. 47 (2005), 549–561.CrossRefGoogle Scholar
27.Mazorchuk, V. and Stroppel, C., Categorification of (induced) cell modules and the rough structure of generalised Verma modules, Adv. Math. 219 (4) (2008), 1363–1426.CrossRefGoogle Scholar
28.Mazorchuk, V. and Stroppel, C., Categorification of Wedderburn's basis for [Sn], Arch. Math. (Basel) 91 (1) (2008), 1–11.CrossRefGoogle Scholar
29.Miličić, D. and Soergel, W., The composition series of modules induced from Whittaker modules, Comment. Math. Helv. 72 (4) (1997), 503–520.CrossRefGoogle Scholar
30.Stroppel, C., Category : Gradings and translation functors, J. Algebra 268 (1) (2003), 301–326.CrossRefGoogle Scholar
31.Stroppel, C., Composition factors of quotients of the universal enveloping algebra by primitive ideals, J. Lond. Math. Soc. (2) 70 (3) (2004), 643–658.CrossRefGoogle Scholar
32.Vogan, D., Ordering of the primitive spectrum of a semisimple Lie algebra, Math. Ann. 248 (3) (1980), 195–203.CrossRefGoogle Scholar