Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gul, M.
and
Ganapathisubramani, B.
2022.
Experimental observations on turbulent boundary layers subjected to a step change in surface roughness.
Journal of Fluid Mechanics,
Vol. 947,
Issue. ,
Garcia-Mayoral, Ricardo
Durbin, Paul
McKeon, Beverley J.
Piomelli, Ugo
Sandberg, Richard D.
Bensow, Rickard
Bettle, Mark
Knopp, Tobias A.
Krumbein, Andreas
Roy, Christopher J.
Gargiulo, Aldo
Lowe, K T.
and
Toxopeus, Serge L.
2022.
Modeling of high-Re, incompressible, non-equilibrium, rough-wall boundary layers for naval applications under NATO-AVT349.
Potsis, Theodore
and
Stathopoulos, Ted
2022.
A Novel Computational Approach for an Improved Expression of the Spectral Content in the Lower Atmospheric Boundary Layer.
Buildings,
Vol. 12,
Issue. 6,
p.
788.
Zhang, Jiaojiao
Liu, Shengna
and
Zheng, Liancun
2022.
Turbulent boundary layer heat transfer of CuO–water nanofluids on a continuously moving plate subject to convective boundary.
Zeitschrift für Naturforschung A,
Vol. 77,
Issue. 4,
p.
369.
Li, Mogeng
de Silva, Charitha M.
Chung, Daniel
Pullin, Dale I.
Marusic, Ivan
and
Hutchins, Nicholas
2022.
Modelling the downstream development of a turbulent boundary layer following a step change of roughness.
Journal of Fluid Mechanics,
Vol. 949,
Issue. ,
Ding, Shan-Shan
Placidi, Marco
Carpentieri, Matteo
and
Robins, Alan
2023.
Neutrally- and stably-stratified boundary layers adjustments to a step change in surface roughness.
Experiments in Fluids,
Vol. 64,
Issue. 4,
He, Xibo
and
Liu, Hongyou
2023.
The effect of turbulent motions on particle spatial distribution in high-Reynolds-number particle-laden flows.
Journal of Fluid Mechanics,
Vol. 976,
Issue. ,
Mondal, Kingshuk
Kethavath, Naveen N.
Abhinay, Kondu
and
Ghaisas, Niranjan S.
2023.
Large Eddy Simulation Study of Atmospheric Boundary Layer Flow over an Abrupt Rough-to-Smooth Surface Roughness Transition.
Boundary-Layer Meteorology,
Segalini, Antonio
and
Janzon, Erik
2023.
An Asymptotic Theory for the Flow over Heterogeneous Roughness.
Boundary-Layer Meteorology,
Vol. 186,
Issue. 3,
p.
637.
Li, Mogeng
Baars, Woutijn J.
Marusic, Ivan
and
Hutchins, Nicholas
2023.
Quantifying inner-outer interactions in noncanonical wall-bounded flows.
Physical Review Fluids,
Vol. 8,
Issue. 8,
Ismail, Umair
2023.
Direct Numerical Simulation of a Turbulent Boundary Layer Encountering a Smooth-to-Rough Step Change.
Energies,
Vol. 16,
Issue. 4,
p.
1709.
Hutchins, N.
Ganapathisubramani, B.
Schultz, M.P.
and
Pullin, D.I.
2023.
Defining an equivalent homogeneous roughness length for turbulent boundary layers developing over patchy or heterogeneous surfaces.
Ocean Engineering,
Vol. 271,
Issue. ,
p.
113454.
García-Mayoral, Ricardo
Chung, Daniel
Durbin, Paul
Hutchins, Nicholas
Knopp, Tobias
McKeon, Beverley J.
Piomelli, Ugo
and
Sandberg, Richard D.
2024.
Challenges and perspective on the modelling of high-Re, incompressible, non-equilibrium, rough-wall boundary layers.
Journal of Turbulence,
Ding, Shan-Shan
Carpentieri, Matteo
Robins, Alan
and
Placidi, Marco
2024.
Statistical properties of neutrally and stably stratified boundary layers in response to an abrupt change in surface roughness.
Journal of Fluid Mechanics,
Vol. 986,
Issue. ,
Cooke, Justin
Jerolmack, Douglas
and
Park, George Ilhwan
2024.
Mesoscale structure of the atmospheric boundary layer across a natural roughness transition.
Proceedings of the National Academy of Sciences,
Vol. 121,
Issue. 13,
Ramani, A.
Schilt, L.
Nugroho, B.
Busse, A.
Jelly, T. O.
Monty, J. P.
and
Hutchins, N.
2024.
An assessment of effective slope as a parameter for turbulent drag prediction over multi-scaled roughness.
Experiments in Fluids,
Vol. 65,
Issue. 6,
Jensen, Rune M.
and
Forooghi, Pourya
2025.
A study of turbulent flow over patchy roughness.
Journal of Fluid Mechanics,
Vol. 1006,
Issue. ,
Gustenyov, Nikolay
and
Bailey, Sean C. C.
2025.
Effects of the formation of shear-driven liquid-surface waves on the gas-phase turbulent boundary layer.
Experiments in Fluids,
Vol. 66,
Issue. 7,
Cooke, Justin P.
Jerolmack, Douglas J.
and
Park, George Ilhwan
2025.
The Evolution of Turbulence Producing Motions in the Neutral ABL Across a Natural Roughness Transition.
Journal of Geophysical Research: Atmospheres,
Vol. 130,
Issue. 5,
Cooke, Justin P.
Park, George I.
Jerolmack, Douglas J.
and
Arratia, Paulo E.
2025.
Alternative scaling for roughness transitions in turbulent flows: The role of the internal boundary layer.
Physical Review Fluids,
Vol. 10,
Issue. 8,
 $k_{s0}^{+}\approx 160$ is maintained on the rough surface, while the friction Reynolds number
$k_{s0}^{+}\approx 160$ is maintained on the rough surface, while the friction Reynolds number  $Re_{\tau 0}$ ranges from 7100 to 21 000. For the Group-ks cases,
$Re_{\tau 0}$ ranges from 7100 to 21 000. For the Group-ks cases,  $Re_{\tau 0}\approx 14\,000$ is maintained while
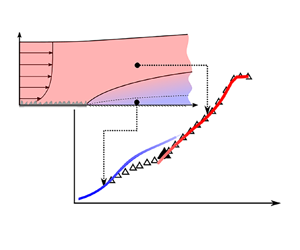
$Re_{\tau 0}\approx 14\,000$ is maintained while  $k_{s0}^{+}$ ranges from 111 to 228. The wall-shear stress on the downstream smooth surface is measured directly using oil-film interferometry to redress previously reported uncertainties in the skin-friction coefficient recovery trends. In the early development following the roughness transition, the flow in the internal layer is not in equilibrium with the wall-shear stress. This conflicts with the common practise of modelling the mean velocity profile as two log laws below and above the internal layer height, as first proposed by Elliott (Trans. Am. Geophys. Union, vol. 39, 1958, pp. 1048–1054). As a solution to this, the current data are used to model the recovering mean velocity semi-empirically by blending the corresponding rough-wall and smooth-wall profiles. The over-energised large-scale motions leave a strong footprint in the near-wall region of the energy spectrum, the frequency and magnitude of which exhibit dependence on
$k_{s0}^{+}$ ranges from 111 to 228. The wall-shear stress on the downstream smooth surface is measured directly using oil-film interferometry to redress previously reported uncertainties in the skin-friction coefficient recovery trends. In the early development following the roughness transition, the flow in the internal layer is not in equilibrium with the wall-shear stress. This conflicts with the common practise of modelling the mean velocity profile as two log laws below and above the internal layer height, as first proposed by Elliott (Trans. Am. Geophys. Union, vol. 39, 1958, pp. 1048–1054). As a solution to this, the current data are used to model the recovering mean velocity semi-empirically by blending the corresponding rough-wall and smooth-wall profiles. The over-energised large-scale motions leave a strong footprint in the near-wall region of the energy spectrum, the frequency and magnitude of which exhibit dependence on  $Re_{\tau 0}$ and
$Re_{\tau 0}$ and  $k_{s0}^{+}$, respectively. The energy distribution in near-wall small scales is mostly unaffected by the presence of the outer flow with rough-wall characteristics, which can be used as a surrogate measure to extract the local friction velocity.
$k_{s0}^{+}$, respectively. The energy distribution in near-wall small scales is mostly unaffected by the presence of the outer flow with rough-wall characteristics, which can be used as a surrogate measure to extract the local friction velocity.

