Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-10-31T23:05:50.143Z Has data issue: false hasContentIssue false
  • English
  • Français

Local balance and cross-scale flux of available potential energy

Published online by Cambridge University Press:  08 February 2010

M. JEROEN MOLEMAKER  and
JAMES C. McWILLIAMS
M. JEROEN MOLEMAKER*
Affiliation:
Institute of Geophysics and Planetary Physics, UCLA Los Angeles, CA 90095-1567, USA
JAMES C. McWILLIAMS
Affiliation:
Institute of Geophysics and Planetary Physics, UCLA Los Angeles, CA 90095-1567, USA
*
†Email address for correspondence: nmolem@atmos.ucla.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Gravitational available potential energy is a central concept in an energy analysis of flows in which buoyancy effects are dynamically important. These include, but are not limited to, most geophysical flows with persistently stable density stratification. The volume-integrated available potential energy 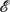ap is defined as the difference between the gravitational potential energy of the system and the potential energy of a reference state with the lowest potential energy that can be reached by adiabatic material rearrangement; 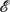ap determines how much energy is available for conservative dynamical exchange with kinetic energy 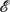k. In this paper we introduce new techniques for computing the local available potential energy density Eap in numerical simulations that allow for a more accurate and complete analysis of the available potential energy and its dynamical balances as part of the complete energy cycle of a flow. In particular, the definition of Eap and an associated gravitation disturbance field 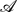permit us to make a spectral decomposition of its dynamical balance and examine the cross-scale energy flux. Several examples illustrate the spatial structure of Eap and its evolutionary influences. The greatest attention is given to an analysis of a turbulent-equilibrium simulation Eady-like vertical-shear flow with rotation and stable stratification. In this regime Eap exhibits a vigorous forward energy cascade from the mesoscale through the submesoscale range – first in a scale range dominated by frontogenesis and positive buoyancy-flux conversion from 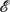ap to 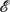k and then, after strong frontal instability and frontogenetic arrest, in a coupled kinetic-potential energy inertial-cascade range with negative buoyancy-flux conversion – en route to fine-scale dissipation of both energy components.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 645 , 25 February 2010 , pp. 295 - 314
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Andrews, D. 1981 A note on potential energy density in a stratified compressible fluid. J. Fluid Mech. 107, 227–236.CrossRefGoogle Scholar
Bray, N. & Fofonoff, N. 1981 Available potential energy for MODE eddies. J. Phys. Oceanogr. 11, 30–47.2.0.CO;2>CrossRefGoogle Scholar
Capet, X., McWilliams, J., Molemaker, M. & Shepetkin, A. 2008 a Mesoscale to submesoscale transition in the California Current System: flow structure and eddy flux. J. Phys. Oceanogr. 38, 29–43.CrossRefGoogle Scholar
Capet, X., McWilliams, M., Molemaker, M. & Shepetkin, A. 2008 b Mesoscale to submesoscale transition in the California Current System: frontal processes. J. Phys. Oceanogr. 38, 44–64.CrossRefGoogle Scholar
Charney, J. 1971 Geostrophic turbulence. J. Atmos. Sci. 28, 1087–1095.2.0.CO;2>CrossRefGoogle Scholar
Eady, E. 1949 Long waves and cyclone waves. Tellus 1, 33–52.CrossRefGoogle Scholar
Henyey, F. S. 1983 Hamiltonian description of stratified fluid dynamics. Phys. Fluids 26, 40–47.CrossRefGoogle Scholar
Holliday, D. & McIntyre, M. 1981 On potential energy density in an incompressible, stratified flow. J. Fluid Mech. 107, 221–225.CrossRefGoogle Scholar
Huang, R. 1998 On available potential energy in a Boussinesq ocean. J. Phys. Oceanogr. 28, 669–678.2.0.CO;2>CrossRefGoogle Scholar
Kaneda, Y., Ishihara, I., Yokokawa, M., Itakura, K. & Uno, A. 2003 Energy dissipation rate and energy spectrum in high resolution direct numerical simulation of turbulence in a periodic box. Phys. Fluids 15, L21–L24.CrossRefGoogle Scholar
Lindborg, E. 2006 The energy cascade in a strongly stratified fluid. J. Fluid Mech. 550, 207–242.CrossRefGoogle Scholar
Lindborg, E. & Brethouwer, G. 2007 Stratified turbulence forced in rotational and divergent modes. J. Fluid Mech. 586, 83–108.CrossRefGoogle Scholar
Lorenz, E. 1955 Available energy and the maintenance of the general circulation. Tellus 7, 157–167.CrossRefGoogle Scholar
Lorenz, E. 1967 The Nature and Theory of the General Circulation of the Atmosphere. World Meteorological Organization.Google Scholar
McDougall, T. 1987 Neutral surfaces. J. Phys. Oceanogr. 17, 1950–1964.2.0.CO;2>CrossRefGoogle Scholar
Molemaker, M., McWilliams, J. & Yavneh, I. 2005 Baroclinic instability and loss of balance. J. Phys. Oceanogr. 35, 1505–1517.CrossRefGoogle Scholar
Molemaker, M., McWilliams, J. & Capet, X. 2010 Balanced and unbalanced routes to dissipation in equilibrated Eady flow. J. Fluid Mech. (in press).CrossRefGoogle Scholar
Muller, P., McWilliams, J. & Molemaker, M. 2005 Routes to dissipation in the ocean: the 2D/3D turbulence conundrum. In Marine Turbulence: Theories, Observations and Models (ed. Baumert, H., Simpson, J. & Sundermann, J.), pp. 397–405. Cambridge University Press.Google Scholar
Pedlosky, J. 1987 Geophysical Fluid Dynamics. Springer.CrossRefGoogle Scholar
Reid, R., Elliot, B. & Olson, D. 1981 Available potential energy: a clarification. J. Phys. Oceanogr. 11, 15–30.2.0.CO;2>CrossRefGoogle Scholar
Riley, J. & Lindborg, E. 2008 Stratified turbulence: a possible interpretation of some geophysical turbulence measurements. J. Atmos. Sci. 65, 2416–2424.CrossRefGoogle Scholar
Shepherd, T. 1993 A unified theory of available potential energy. Atmos.-Ocean 31, 1–26.CrossRefGoogle Scholar
Stone, P. 1966 On non-geostrophic baroclinic instability. J. Atmos. Sci. 23, 390–400.2.0.CO;2>CrossRefGoogle Scholar
Toole, J. 1998 Turbulent mixing in the ocean. In Oceanic Modelling and Parameterization (ed. Chassignet, E. & Verron, J.), vol. C 516, pp. 171–189, NATO Science Series. Kluwer Academic.CrossRefGoogle Scholar
Tseng, Y.-H. & Ferziger, J. 2001 Mixing and available potential energy in stratified flows. Phys. Fluids 13, 1281–1293.CrossRefGoogle Scholar
Winters, K., Lombard, P., Riley, J. & D'Asaro, E. 1995 Available potential energy and mixing in density-stratified fluids. J. Fluid Mech. 289, 115–128.CrossRefGoogle Scholar