Hostname: page-component-669899f699-tzmfd Total loading time: 0 Render date: 2025-05-04T16:28:39.882Z Has data issue: false hasContentIssue false
  • English
  • Français

Shear-induced modulation on thermal convection over rough plates

Published online by Cambridge University Press:  15 February 2022

Tian-Cheng Jin ,
Jian-Zhao Wu ,
Yi-Zhao Zhang ,
Yu-Lu Liu  and
Quan Zhou Open the ORCID record for Quan Zhou [Opens in a new window]
Tian-Cheng Jin
Affiliation:
Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, Shanghai University, Shanghai 200072, PR China
Jian-Zhao Wu*
Affiliation:
Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, Shanghai University, Shanghai 200072, PR China
Yi-Zhao Zhang
Affiliation:
Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, Shanghai University, Shanghai 200072, PR China
Yu-Lu Liu
Affiliation:
Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, Shanghai University, Shanghai 200072, PR China
Quan Zhou*
Affiliation:
Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, Shanghai University, Shanghai 200072, PR China
*
†Email addresses for correspondence: jianzhao_wu@shu.edu.cn, qzhou@shu.edu.cn
†Email addresses for correspondence: jianzhao_wu@shu.edu.cn, qzhou@shu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

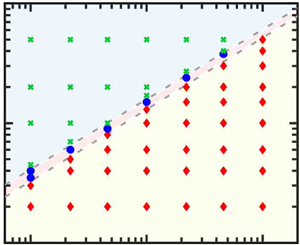
External modulation on thermal convection has been studied extensively to achieve the control of flow structures and heat-transfer efficiency. In this paper, we carry out direct numerical simulations on Rayleigh–Bénard convection accounting for both the modulation of wall shear and roughness over the Rayleigh number range $1.0 \times 10^6 \le Ra \le 1.0 \times 10^8$, the wall shear Reynolds number range $0 \le Re_w \le 5000$, the aspect-ratio range $2 \le \varGamma \le 4{\rm \pi}$, and the dimensionless roughness height range $0 \le h \le 0.2$ at fixed Prandtl number $Pr = 1$. Under the combined actions of wall shear and roughness, with increasing $Re_w$, the heat flux is initially enhanced in the buoyancy-dominant regime, then has an abrupt transition near the critical shear Reynolds number $Re_{w,cr}$, and finally enters the purely diffusion regime dominated by shear. Based on the crossover of the kinetic energy production between the buoyancy-dominant and shear-dominant regimes, a physical model is proposed to predict the transitional scaling behaviour between $Re_{w,cr}$ and $Ra$, i.e. $Re_{w,cr} \sim Ra^{9/14}$, which agrees well with our numerical results. The reason for the observed heat-transport enhancement in the buoyancy-dominant regime is further explained by the fact that the moving rough plates introduce an external shear to strengthen the large-scale circulation (LSC) in the vertical direction and serve as a conveyor belt to increase the chances of the interaction between the LSC and secondary flows within cavities, which triggers more thermal plumes, efficiently transports the trapped hot (cold) fluids outside cavities.

JFM classification

Turbulent Flows: Turbulent convection
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 936 , 10 April 2022 , A28
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Abtahi, A. & Floryan, J.M. 2017 Natural convection and thermal drift. J. Fluid Mech. 826, 553–582.CrossRefGoogle Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81 (2), 503–537.CrossRefGoogle Scholar
Blass, A., Tabak, P., Verzicco, R., Stevens, R.J.A.M. & Lohse, D. 2021 The effect of Prandtl number on turbulent sheared thermal convection. J. Fluid Mech. 910, A37.CrossRefGoogle Scholar
Blass, A., Zhu, X.J., Verzicco, R., Lohse, D. & Stevens, R.J.A.M. 2020 Flow organization and heat transfer in turbulent wall sheared thermal convection. J. Fluid Mech. 897, A22.CrossRefGoogle ScholarPubMed
Bluestein, H.B. 2013 Severe Convective Storms and Tornadoes, vol. 10, pp. 95–104. Springer.CrossRefGoogle Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35 (7), 58.CrossRefGoogle ScholarPubMed
Domaradzki, J.A. & Metcalfe, R.W. 1988 Direct numerical simulations of the effects of shear on turbulent Rayleigh–Bénard convection. J. Fluid Mech. 193, 499–531.CrossRefGoogle Scholar
Dong, D.L., Wang, B.F., Dong, Y.H., Huang, Y.X., Jiang, N., Liu, Y.L., Lu, Z.M., Qiu, X., Tang, Z.Q. & Zhou, Q. 2020 Influence of spatial arrangements of roughness elements on turbulent Rayleigh–Bénard convection. Phys. Fluids 32 (4), 045114.Google Scholar
Du, Y.B. & Tong, P. 1998 Enhanced heat transport in turbulent convection over a rough surface. Phys. Rev. Lett. 81 (5), 987–990.CrossRefGoogle Scholar
Du, Y.B. & Tong, P. 2000 Turbulent thermal convection in a cell with ordered rough boundaries. J. Fluid Mech. 407, 57–84.CrossRefGoogle Scholar
Fadlun, E.A., Verzicco, R., Orlandi, P. & Mohd-Yusof, J. 2000 Combined immersed-boundary finite-difference methods for three-dimensional complex flow simulations. J. Comput. Phys. 161 (1), 35–60.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Hossain, M.Z. & Floryan, J.M. 2020 On the role of surface grooves in the reduction of pressure losses in heated channels. Phys. Fluids 32 (8), 083610.CrossRefGoogle Scholar
Huang, S.-D., Kaczorowski, M., Ni, R. & Xia, K.-Q. 2013 Confinement-induced heat transport enhancement in turbulent thermal convection. Phys. Rev. Lett. 111, 104501.CrossRefGoogle ScholarPubMed
Jiang, H.C., Zhu, X.J., Mathai, V., Verzicco, R., Lohse, D. & Sun, C. 2018 Controlling heat transport and flow structures in thermal turbulence using ratchet surfaces. Phys. Rev. Lett. 120 (4), 044501.CrossRefGoogle ScholarPubMed
Langham, J., Eaves, T.S. & Kerswell, R.R. 2020 Stably stratified exact coherent structures in shear flow: the effect of Prandtl number. J. Fluid Mech. 882, A10.CrossRefGoogle Scholar
Lohse, D. & Xia, K.Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42 (1), 335–364.CrossRefGoogle Scholar
MacDonald, M., Hutchins, N., Lohse, D. & Chung, D. 2019 Heat transfer in rough-wall turbulent thermal convection in the ultimate regime. Phys. Rev. Fluids 4 (7), 071501.CrossRefGoogle Scholar
Pirozzoli, S., Bernardini, M., Verzicco, R. & Orlandi, P. 2017 Mixed convection in turbulent channels with unstable stratification. J. Fluid Mech. 821, 482–516.CrossRefGoogle Scholar
van der Poel, E.P., Verzicco, R., Grossmann, S. & Lohse, D. 2015 Plume emission statistics in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 772, 5–15.CrossRefGoogle Scholar
Roche, P.E., Castaing, B., Chabaud, B. & Hébral, B. 2001 Observation of the $1/2$ power law in Rayleigh–Bénard convection. Phys. Rev. E 63 (4), 045303.CrossRefGoogle Scholar
Rusaouën, E., Liot, O., Castaing, B., Salort, J. & Chillà, F. 2018 Thermal transfer in Rayleigh–Bénard cell with smooth or rough boundaries. J. Fluid Mech. 837, 443–460.CrossRefGoogle Scholar
Scagliarini, A., Einarsson, H., Gylfason, Á. & Toschi, F. 2015 Law of the wall in an unstably stratified turbulent channel flow. J. Fluid Mech. 781, R5.CrossRefGoogle Scholar
Scagliarini, A., Gylfason, Á. & Toschi, F. 2014 Heat-flux scaling in turbulent Rayleigh–Bénard convection with an imposed longitudinal wind. Phys. Rev. E 89 (4), 043012.CrossRefGoogle ScholarPubMed
Shen, Y., Tong, P. & Xia, K.Q. 1996 Turbulent convection over rough surfaces. Phys. Rev. Lett. 76 (6), 908–911.CrossRefGoogle ScholarPubMed
Shishkina, O. & Wagner, C. 2011 Modelling the influence of wall roughness on heat transfer in thermal convection. J. Fluid Mech. 686, 568–582.CrossRefGoogle Scholar
Solomon, T.H. & Gollub, J.P. 1990 Sheared boundary layers in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 64 (20), 2382–2385.CrossRefGoogle ScholarPubMed
Tisserand, J.C., Creyssels, M., Gasteuil, Y., Pabiou, H., Gibert, M., Castaing, B. & Chillà, F. 2011 Comparison between rough and smooth plates within the same Rayleigh–Bénard cell. Phys. Fluids 23 (1), 015105.CrossRefGoogle Scholar
Tummers, M.J. & Steunebrink, M. 2019 Effect of surface roughness on heat transfer in Rayleigh–Bénard convection. Intl J. Heat Mass Transfer 139, 1056–1064.CrossRefGoogle Scholar
Vishnu, R. & Sameen, A. 2020 Heat transfer scaling in natural convection with shear due to rotation. Phys. Rev. Fluids 5 (11), 113504.CrossRefGoogle Scholar
Wagner, S. & Shishkina, O. 2015 Heat flux enhancement by regular surface roughness in turbulent thermal convection. J. Fluid Mech. 763, 109–135.CrossRefGoogle Scholar
Wang, B.F., Zhou, Q. & Sun, C. 2020 Vibration-induced boundary-layer destabilization achieves massive heat-transport enhancement. Sci. Adv. 6 (21), eaaz8239.CrossRefGoogle ScholarPubMed
Wei, P., Chan, T.S., Ni, R., Zhao, X.Z. & Xia, K.Q. 2014 Heat transport properties of plates with smooth and rough surfaces in turbulent thermal convection. J. Fluid Mech. 740, 28–46.CrossRefGoogle Scholar
Xie, Y.C. & Xia, K.Q. 2017 Turbulent thermal convection over rough plates with varying roughness geometries. J. Fluid Mech. 825, 573–599.CrossRefGoogle Scholar
Yang, J.L., Zhang, Y.Z., Jin, T.C., Dong, Y.H., Wang, B.F. & Zhou, Q. 2021 The $Pr$-dependence of the critical roughness height in two-dimensional turbulent Rayleigh–Bénard convection. J. Fluid Mech. 911, A52.CrossRefGoogle Scholar
Zhang, Y.Z., Sun, C., Bao, Y. & Zhou, Q. 2018 How surface roughness reduces heat transport for small roughness heights in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 836, R2.CrossRefGoogle Scholar
Zhang, Y.Z., Xia, S.N., Dong, Y.H., Wang, B.F. & Zhou, Q. 2019 An efficient parallel algorithm for DNS of buoyancy-driven turbulent flows. J. Hydrodyn. 31 (6), 1159–1169.CrossRefGoogle Scholar
Zhou, Q. & Xia, K.Q. 2013 Thermal boundary layer structure in turbulent Rayleigh–Bénard convection in a rectangular cell. J. Fluid Mech. 721, 199–224.CrossRefGoogle Scholar
Zhu, X.J., Stevens, R.J.A.M., Shishkina, O., Verzicco, R. & Lohse, D. 2019 $Nu\sim Ra^{1/2}$ scaling enabled by multiscale wall roughness in Rayleigh–Bénard turbulence. J. Fluid Mech. 869, R4.CrossRefGoogle Scholar
Zhu, X.J., Stevens, R.J.A.M., Verzicco, R. & Lohse, D. 2017 Roughness-facilitated local $1/2$ scaling does not imply the onset of the ultimate regime of thermal convection. Phys. Rev. Lett. 119 (15), 154501.CrossRefGoogle Scholar
Zonta, F. & Soldati, A. 2018 Stably stratified wall-bounded turbulence. Appl. Mech. Rev. 70 (4), 040801.CrossRefGoogle Scholar

Jin et al. supplementary movie 1

See word file for movie caption

Download Jin et al. supplementary movie 1(Video)
Video 3.6 MB

Jin et al. supplementary movie 2

See word file for movie caption

Download Jin et al. supplementary movie 2(Video)
Video 3.2 MB

Jin et al. supplementary movie 3

See word file for movie caption

Download Jin et al. supplementary movie 3(Video)
Video 341.4 KB

Jin et al. supplementary movie 4

See word file for movie caption

Download Jin et al. supplementary movie 4(Video)
Video 5.2 MB
Supplementary material: File

Jin et al. supplementary material

Captions for movies 1-4

Download Jin et al. supplementary material(File)
File 1.8 KB