Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-12-04T07:26:00.865Z Has data issue: false hasContentIssue false
  • English
  • Français

Spanwise-coherent hydrodynamic waves around flat plates and airfoils

Published online by Cambridge University Press:  20 September 2021

Leandra I. Abreu Open the ORCID record for Leandra I. Abreu [Opens in a new window] ,
Alvaro Tanarro ,
André V.G. Cavalieri Open the ORCID record for André V.G. Cavalieri [Opens in a new window] ,
Philipp Schlatter Open the ORCID record for Philipp Schlatter [Opens in a new window] ,
Ricardo Vinuesa Open the ORCID record for Ricardo Vinuesa [Opens in a new window] ,
Ardeshir Hanifi Open the ORCID record for Ardeshir Hanifi [Opens in a new window]  and
Dan S. Henningson Open the ORCID record for Dan S. Henningson [Opens in a new window]
Leandra I. Abreu*
Affiliation:
São Paulo State University (UNESP), Campus of São João da Boa Vista, 13876-750, SP, Brazil Divisão de Engenharia Aeronáutica, Instituto Tecnológico de Aeronáutica, 12228-900, São José dos Campos, SP, Brazil
Alvaro Tanarro
Affiliation:
FLOW, KTH Engineering Mechanics, Royal Institute of Technology, SE-100 44 Stockholm, Sweden
André V.G. Cavalieri
Affiliation:
Divisão de Engenharia Aeronáutica, Instituto Tecnológico de Aeronáutica, 12228-900, São José dos Campos, SP, Brazil
Philipp Schlatter
Affiliation:
FLOW, KTH Engineering Mechanics, Royal Institute of Technology, SE-100 44 Stockholm, Sweden
Ricardo Vinuesa
Affiliation:
FLOW, KTH Engineering Mechanics, Royal Institute of Technology, SE-100 44 Stockholm, Sweden
Ardeshir Hanifi
Affiliation:
FLOW, KTH Engineering Mechanics, Royal Institute of Technology, SE-100 44 Stockholm, Sweden
Dan S. Henningson
Affiliation:
FLOW, KTH Engineering Mechanics, Royal Institute of Technology, SE-100 44 Stockholm, Sweden
*
†Email address for correspondence: leandra.abreu@unesp.br
Get access Rights & Permissions [Opens in a new window]

Abstract

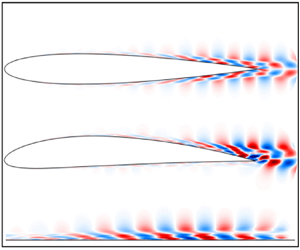
We investigate spanwise-coherent structures in the turbulent flow around airfoils, motivated by their connection with trailing-edge noise. We analyse well-resolved large-eddy simulations (LES) of the flow around NACA 0012 and NACA 4412 airfoils, both at a Reynolds number of 400 000 based on the chord length. Spectral proper orthogonal decomposition performed on the data reveals that the most energetic coherent structures are hydrodynamic waves, extending over the turbulent boundary layers around the airfoils with significant amplitudes near the trailing edge. Resolvent analysis was used to model such structures, using the mean field as a base flow. We then focus on evaluating the dependence of such structures on the domain size, to ensure that they are not an artefact of periodic boundary conditions in small computational boxes. To this end, we performed incompressible LES of a zero-pressure-gradient turbulent boundary layer, for three different spanwise sizes, with the momentum-thickness Reynolds number matching those near the airfoils trailing edge. The same coherent hydrodynamic waves were observed for the three domains. Such waves are accurately modelled as the most amplified flow response from resolvent analysis. The signature of such wide structures is seen in non-premultiplied spanwise wavenumber spectra, which collapse for the three computational domains. These results suggest that the spanwise-elongated structures are not domain-size dependent for the studied simulations, indicating thus the presence of very wide structures in wall-bounded turbulent flows.

JFM classification

Acoustics: Aeroacoustics Acoustics: Hydrodynamic noise
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 927 , 25 November 2021 , A1
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abreu, L.I., Cavalieri, A.V.G., Schlatter, P., Vinuesa, R. & Henningson, D.S. 2020 a Resolvent modelling of near-wall coherent structures in turbulent channel flow. Intl J. Heat Fluid Flow 85, 108662.CrossRefGoogle Scholar
Abreu, L.I., Cavalieri, A.V.G., Schlatter, P., Vinuesa, R. & Henningson, D.S. 2020 b Spectral proper orthogonal decomposition and resolvent analysis of near-wall coherent structures in turbulent pipe flows. J. Fluid Mech. 900, A11.CrossRefGoogle Scholar
Åkervik, E., Ehrenstein, U., Gallaire, F. & Henningson, D.S. 2008 Global two-dimensional stability measures of the flat plate boundary-layer flow. Eur. J. Mech. B/Fluids 27 (5), 501–513.CrossRefGoogle Scholar
del Alamo, J.C. & Jimenez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.CrossRefGoogle Scholar
Alfonsi, G., Primavera, L., Passoni, G. & Restano, C. 2001 Proper orthogonal decomposition of turbulent channel flow. In Computational Fluid Dynamics 2000 (ed. N. Satofuka), 1st edn, vol. 1, pp. 473–478. Springer.CrossRefGoogle Scholar
Amiet, R. 1976 Noise due to turbulent flow past a trailing edge. J. Sound Vib. 47 (3), 387–393.CrossRefGoogle Scholar
Araya, D.B., Colonius, T. & Dabiri, J.O. 2017 Transition to bluff-body dynamics in the wake of vertical-axis wind turbines. J. Fluid Mech. 813, 346–381.CrossRefGoogle Scholar
Aubry, N., Holmes, P., Lumley, J.L. & Stone, E. 1988 a The dynamics of coherent structures in the wall region of a turbulent boundary layer. J. Fluid Mech. 192, 115–173.CrossRefGoogle Scholar
Aubry, N., Holmes, P., Lumley, J.L. & Stone, E. 1988 b The dynamics of coherent structures in the wall region of a turbulent boundary layer. J. Fluid Mech. 192, 115–173.CrossRefGoogle Scholar
Beneddine, S., Sipp, D., Arnault, A., Dandois, J. & Lesshafft, L. 2016 Conditions for validity of mean flow stability analysis. J. Fluid Mech. 798, 485–504.CrossRefGoogle Scholar
Berkooz, G., Holmes, P. & Lumley, J.L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25 (1), 539–575.CrossRefGoogle Scholar
Borée, J. 2003 Extended proper orthogonal decomposition: a tool to analyse correlated events in turbulent flows. Exp. Fluids 35 (2), 188–192.CrossRefGoogle Scholar
Cavalieri, A., Rodríguez, D., Jordan, P., Colonius, T. & Gervais, Y. 2013 Wavepackets in the velocity field of turbulent jets. J. Fluid Mech. 730, 559–592.CrossRefGoogle Scholar
Cavalieri, A.V.G., Jordan, P. & Lesshafft, L. 2019 Wave-packet models for jet dynamics and sound radiation. Appl. Mech. Rev. 71 (2), 020802.CrossRefGoogle Scholar
Chevalier, M., Lundbladh, A. & Henningson, D.S. 2007 Simson–a pseudo-spectral solver for incompressible boundary layer flow. Tech Rep. TRITA-MEK 2007:07. KTH Mechanics.Google Scholar
Dergham, G., Sipp, D. & Robinet, J.-C. 2013 Stochastic dynamics and model reduction of amplifier flows: the backward facing step flow. J. Fluid Mech. 719, 406–430.CrossRefGoogle Scholar
Eitel-Amor, G., Örlü, R. & Schlatter, P. 2014 Simulation and validation of a spatially evolving turbulent boundary layer up to $Re_{\theta }=8300$. Intl J. Heat Fluid Flow 47, 57–69.CrossRefGoogle Scholar
Ffowcs Williams, J.E. & Hall, L.H. 1970 Aerodynamic sound generation by turbulent flow in the vicinity of a scattering half plane. J. Fluid Mech. 40 (04), 657–670.CrossRefGoogle Scholar
Fischer, P.F., Lottes, J.W. & Kerkemeier, S.G. 2008 NEK5000: Open Source spectral element CFD solver. Available at: http://nek5000.mcs.anl.gov (Accessed July 30, 2018).Google Scholar
Freund, J.B. & Colonius, T. 2009 Turbulence and sound-field pod analysis of a turbulent jet. Intl J. Aeroacoust. 8 (4), 337–354.CrossRefGoogle Scholar
Garnaud, X., Lesshafft, L., Schmid, P. & Huerre, P. 2013 The preferred mode of incompressible jets: linear frequency response analysis. J. Fluid Mech. 716, 189–202.CrossRefGoogle Scholar
Hellström, L.H.O., Marusic, I. & Smits, A.J. 2016 Self-similarity of the large-scale motions in turbulent pipe flow. J. Fluid Mech. 792, R1.CrossRefGoogle Scholar
Hussain, A.K.M.F. & Reynolds, W.C. 1972 The mechanics of an organized wave in turbulent shear flow. Part 2. Experimental results. J. Fluid Mech. 54 (2), 241–261.CrossRefGoogle Scholar
Jeun, J., Nichols, J.W. & Jovanović, M.R. 2016 Input-output analysis of high-speed axisymmetric isothermal jet noise. Phys. Fluids 28 (4), 047101.CrossRefGoogle Scholar
Jiménez, J. 1998 The largest scales of turbulent wall flows. CTR Annual Research Briefs 137, 54.Google Scholar
Jiménez, J. 2013 Near-wall turbulence. Phys. Fluids 25 (10), 101302.CrossRefGoogle Scholar
Jovanovic, M.R. & Bamieh, B. 2005 Componentwise energy amplification in channel flows. J. Fluid Mech. 534, 145–183.CrossRefGoogle Scholar
Kaplan, O., Jordan, P., Cavalieri, A.V.G. & Brès, G.A. 2021 Nozzle dynamics and wavepackets in turbulent jets. J. Fluid Mech. 923, A22.CrossRefGoogle Scholar
Komminaho, J., Lundbladh, A. & Johansson, A.V. 1996 Very large structures in plane turbulent Couette flow. J. Fluid Mech. 320, 259–285.CrossRefGoogle Scholar
Lesshafft, L., Semeraro, O., Jaunet, V., Cavalieri, A.V.G. & Jordan, P. 2019 Resolvent-based modeling of coherent wave packets in a turbulent jet. Phys. Rev. Fluids 4 (6), 063901.CrossRefGoogle Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Effect of the computational domain on direct simulations of turbulent channels up to $Re_{\tau }=4200$. Phys. Fluids 26 (1), 011702.CrossRefGoogle Scholar
Lumley, J.L. 2007 Stochastic Tools in Turbulence. Courier Corporation.Google Scholar
McKeon, B.J. 2017 The engine behind (wall) turbulence: perspectives on scale interactions. J. Fluid Mech. 817, P1.CrossRefGoogle Scholar
McKeon, B.J. & Sharma, A.S. 2010 A critical-layer framework for turbulent pipe flow. J. Fluid Mech. 658, 336–382.CrossRefGoogle Scholar
Noack, B.R., Afanasiev, K., Morzynski, M., Tadmor, G. & Thiele, F. 2003 A hierarchy of low-dimensional models for the transient and post-transient cylinder wake. J. Fluid Mech. 497, 335–363.CrossRefGoogle Scholar
Nogueira, P.A.S., Cavalieri, A.V.G., Hanifi, A. & Henningson, D.S. 2020 Resolvent analysis in unbounded flows: role of free-stream modes. Theor. Comput. Fluid Dyn. 34, 163–176.CrossRefGoogle Scholar
Nogueira, P.A.S., Cavalieri, A.V.G. & Jordan, P. 2017 A model problem for sound radiation by an installed jet. J. Sound Vib. 391, 95–115.CrossRefGoogle Scholar
Österlund, J.M., Johansson, A.V., Nagib, H.M. & Hites, M.H. 2000 A note on the overlap region in turbulent boundary layers. Phys. Fluids 12 (1), 1–4.CrossRefGoogle Scholar
Pérez-Saborid, M. 2019 A simple matlab program to compute differentiation matrices for arbitrary meshes via lagrangian interpolation. arXiv:1910.13256.Google Scholar
Picard, C. & Delville, J. 2000 Pressure velocity coupling in a subsonic round jet. Intl J. Heat Fluid Flow 21 (3), 359–364.CrossRefGoogle Scholar
Sandberg, R. & Sandham, N. 2008 Direct numerical simulation of turbulent flow past a trailing edge and the associated noise generation. J. Fluid Mech. 596, 353–385.CrossRefGoogle Scholar
Sano, A., Abreu, L.I., Cavalieri, A.V.G. & Wolf, W.R. 2019 Trailing-edge noise from the scattering of spanwise-coherent structures. Phys. Rev. Fluids 4 (9), 094602.CrossRefGoogle Scholar
Schlatter, P., Li, Q., Örlü, R., Hussain, F. & Henningson, D.S. 2014 On the near-wall vortical structures at moderate Reynolds numbers. Eur. J. Mech. B/Fluids 48, 75–93.CrossRefGoogle Scholar
Schlatter, P. & Örlü, R. 2012 Turbulent boundary layers at moderate reynolds numbers: inflow length and tripping effects. J. Fluid Mech. 710, 5–34.CrossRefGoogle Scholar
Schlatter, P., Stolz, S. & Kleiser, L. 2004 Les of transitional flows using the approximate deconvolution model. Intl J. Heat Fluid Flow 25 (3), 549–558.CrossRefGoogle Scholar
Schmid, P.J. & Henningson, D.S. 2001 Stability and Transition in Shear Flows, vol. 142. Springer Science and Business Media.CrossRefGoogle Scholar
Schmidt, O.T., Towne, A., Rigas, G., Colonius, T. & Brès, G.A. 2018 Spectral analysis of jet turbulence. J. Fluid Mech. 855, 953–982.CrossRefGoogle Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.CrossRefGoogle Scholar
Sinha, A., Rodríguez, D., Brès, G.A. & Colonius, T. 2014 Wavepacket models for supersonic jet noise. J. Fluid Mech. 742, 71–95.CrossRefGoogle Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. I. Coherent structures. Q. Appl. Maths 45 (3), 561–571.CrossRefGoogle Scholar
Tanarro, Á., Vinuesa, R. & Schlatter, P. 2020 Effect of adverse pressure gradients on turbulent wing boundary layers. J. Fluid Mech. 883, A8.CrossRefGoogle Scholar
Tinney, C. & Jordan, P. 2008 The near pressure field of co-axial subsonic jets. J. Fluid Mech. 611, 175–204.CrossRefGoogle Scholar
Towne, A., Schmidt, O.T. & Colonius, T. 2018 Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis. J. Fluid Mech. 847, 821–867.CrossRefGoogle Scholar
Trefethen, L. 2000 Spectral Methods in MATLAB. SIAM.CrossRefGoogle Scholar
Vinuesa, R., Bobke, A., Örlü, R. & Schlatter, P. 2016 On determining characteristic length scales in pressure-gradient turbulent boundary layers. Phys. Fluids 28 (5), 055101.CrossRefGoogle Scholar
Wei, M. & Freund, J.B. 2006 A noise-controlled free shear flow. J. Fluid Mech. 546, 123–152.CrossRefGoogle Scholar