Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-10-31T23:05:55.248Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent structures in a statistically three-dimensional boundary layer

Published online by Cambridge University Press:  21 November 2018

Kevin Kevin Open the ORCID record for Kevin Kevin [Opens in a new window] ,
Jason Monty  and
Nicholas Hutchins
Kevin Kevin*
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
Jason Monty
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
Nicholas Hutchins
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
*
†Email address for correspondence: kevin.kevin@unimelb.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the behaviour of large-scale coherent structures in a spanwise-heterogeneous turbulent boundary layer, using particle image velocimetry on multiple orthogonal planes. The statistical three-dimensionality is imposed by a herringbone riblet surface, although the key results presented here will be common to many cases of wall turbulence with embedded secondary flows in the form of mean streamwise vortices. 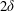Instantaneous velocity fields in the logarithmic layer reveal elongated low-momentum streaks located over the upwash-flow region, where their spanwise spacing is forced by the $2\unicode[STIX]{x1D6FF}$ periodicity of the herringbone pattern. These streaks largely resemble the turbulence structures that occur naturally (and randomly located) in spanwise-homogeneous smooth-/rough-wall boundary layers, although here they are directly formed by the roughness pattern. In the far outer region, the large spanwise spacing permits the streaks to aggressively meander. The mean secondary flows are the time-averaged artefact of the unsteady and spanwise asymmetric large-scale roll modes that accompany these meandering streaks. Interestingly, this meandering, or instability, gives rise to a pronounced streamwise periodicity (i.e. an alternating coherent pattern) in the spatial statistics, at wavelengths of approximately 4.5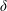$\unicode[STIX]{x1D6FF}$. Overall, the observed behaviours largely resemble the streak-instability model that has been proposed for the buffer region, only here at a much larger scale and at a forced spanwise spacing. This observation further confirms recent observations that such features may occur at an entire hierarchy of scales throughout the turbulent boundary layer.

JFM classification

Boundary Layers: Boundary layer control Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 859 , 25 January 2019 , pp. 543 - 565
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.Google Scholar
Anderson, W., Barros, J. M., Christensen, K. T. & Awasthi, A. 2015 Numerical and experimental study of mechanisms responsible for turbulent secondary flows in boundary layer flows over spanwise heterogeneous roughness. J. Fluid Mech. 768, 316–347.Google Scholar
Bai, H. L., Kevin, K., Hutchins, N. & Monty, J. P. 2018 Turbulence modifications in a turbulent boundary layer over a rough wall with spanwise-alternating roughness strips. Phys. Fluids 30 (5), 055105.Google Scholar
Baidya, R., de Silva, C. M., Huang, Y., Castillo, L., Marusic, I. & Hutchins, N. 2016 Developing turbulent boundary layer using spanwise-periodic trips. In 20th Australasian Fluid Mechanics Conference. Perth, Australia.Google Scholar
Barros, J. M. & Christensen, K. T. 2014 Observations of turbulent secondary flows in a rough-wall boundary layer. J. Fluid Mech. 748, R1.Google Scholar
Bradshaw, P. 1965 The effect of wind-tunnel screens on nominally two-dimensional boundary layers. J. Fluid Mech. 22, 679–687.Google Scholar
Bradshaw, P. 1987 Turbulent secondary flows. Annu. Rev. Fluid Mech. 19 (1), 53–74.Google Scholar
Canton, J., Örlü, R., Chin, C., Hutchins, N., Monty, J. & Schlatter, P. 2016 On large-scale friction control in trubulent wall flow in low Reynolds number channels. Flow Turbul. Combust. 97, 811–827.Google Scholar
Chauhan, K., Philip, J., de Silva, C. M., Hutchins, N. & Marusic, I. 2014 The turbulent/non-turbulent interface and entrainment in a boundary layer. J. Fluid Mech. 742, 119–151.Google Scholar
Choi, H., Jeon, W.-P. & Kim, J. 2008 Control of flow over a bluff body. Annu. Rev. Fluid Mech. 40, 113–139.Google Scholar
Choi, K.-S., Jukes, T. & Whalley, R. 2011 Turbulent boundary-layer control with plasma actuators. Phil. Trans. R. Soc. Lond. A 369 (1940), 1443–1458.Google Scholar
Christensen, K. T.2001 Experimental investigation of acceleration and velocity fields in turbulent channel flow. PhD thesis, University of Illinois at Urbana-Champaign.Google Scholar
Chung, D., Monty, J. P. & Hutchins, N. 2018 Similarity and structure of wall-turbulence with lateral wall shear stress variations. J. Fluid Mech. 847, 591–613.Google Scholar
Colombini, M. 1993 Turbulence-driven secondary flows and formation of sand ridges. J. Fluid Mech. 254, 701–719.Google Scholar
Elsinga, G. E., Adrian, R. J., Oudheusden, B. W. & Van Scarano, F. 2010 Three-dimensional vortex organization in a high-Reynolds-number supersonic turbulent boundary layer. J. Fluid Mech. 644, 35–60.Google Scholar
Erhard, P., Etling, D., Müller, U., Riedel, U., Sreenivasan, K. R. & Warnatz, J. 2010 Prandtl-essentials of Fluid Mechanics, vol. 158. Springer Science & Business Media.Google Scholar
Flores, O. & Jiménez, J. 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22 (7), 071704.Google Scholar
Flores, O., Jiménez, J. & del Álamo, J. C. 2007 Vorticity organization in the outer layer of turbulent channels with disturbed walls. J. Fluid Mech. 591, 145–154.Google Scholar
Furuya, Y., Nakamura, I. & Osaka, H. 1979 Three-dimensional structure of a nominally planar turbulent boundary layer. Trans. ASME J. Fluids Engng 101 (3), 326–330.Google Scholar
Godard, G. & Stanislas, M. 2006 Control of a decelerating boundary layer. Part 1. Optimization of passive vortex generators. Aerosol Sci. Technol. 10, 181–191.Google Scholar
Guala, M., Tomkins, C. D., Christensen, K. T. & Adrian, R. J. 2012 Vortex organization in a turbulent boundary layer overlying sparse roughness elements. J. Hydraul Res. 50 (5), 465–481.Google Scholar
Harun, Z., Monty, J. P., Mathis, R. & Marusic, I. 2013 Pressure gradient effects on the large-scale structure of turbulent boundary layers. J. Fluid Mech. 715, 477–498.Google Scholar
Hinze, J. 1967 Secondary currents in wall turbulence. Phys. Fluids (Suppl.) 10, S122–S125.Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hwang, Y. & Cossu, C. 2010 Self-sustained processed at large scales in turbulent channel flow. Phys. Rev. Lett. 105 (4), 044505.Google Scholar
Hwang, Y. & Cossu, C. 2011 Self-sustained processes in the logarithmic layer of turbulent channel flows. Phys. Fluids 23 (6), 061702.Google Scholar
Ikeda, S. 1981 Self-formed straight channels in sandy beds. J. Hydraul. Div. ASCE 107 (4), 389–406.Google Scholar
Iuso, G., Onorato, M., Spazzini, P. G. & Di Cicca, G. M. 2002 Wall turbulence manipulation by large-scale streamwise vortices. J. Fluid Mech. 473, 23–58.Google Scholar
Jacobi, A. M. & Shah, R. K. 1995 Heat transfer surface enhancement through the use of longitudinal vortices: a review of recent progress. Exp. Therm. Fluid Sci. 11, 295–309.Google Scholar
Jeong, J., Hussain, F., Schoppa, W. & Kim, J. 1997 Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.Google Scholar
Kevin, Monty, J. P., Bai, H. L., Pathikonda, G., Nugroho, B., Barros, J. M., Christensen, K. T. & Hutchins, N. 2017 Cross-stream stereoscopic particle image velocimetry of a modified turbulent boundary layer over directional surface pattern. J. Fluid Mech. 813, 412–435.Google Scholar
Kevin, Nugroho, B., Monty, J. P., Hutchins, N., Pathikonda, G., Barros, J. M. & Christensen, K. T. 2015 Dissecting a modified turbulent boundary layer using particle image velocimetry. In 7th Australian Conference on Laser Diagnostics in Fluid Mechanics and Combustion, Melbourne, Australia.Google Scholar
Krogstadt, P.-Å. & Antonia, R. A. 1999 Surface roughness effects in turbulent boundary layers. Exp. Fluids 27 (5), 450–460.Google Scholar
Lee, J., Lee, J. H., Choi, J. I. & Sung, H. J. 2014 Spatial organization of large- and very-large-scale motions in a turbulent channel flow. J. Fluid Mech. 749, 818–840.Google Scholar
Lee, J. H., Kevin, Monty, J. P. & Hutchins, N. 2016 Validating under-resolved turbulence intensities for PIV experiments in canonical wall-bounded turbulence. Exp. Fluids 57 (8), 129.Google Scholar
Lin, J. C. 2002 Review of research on low-profile vortex generators to control boundary-layer separation. Prog. Aerosp. Sci. 38 (4), 389–420.Google Scholar
Luchini, P., Manzo, F. & Pozzi, A. 1991 Resistance of a grooved surface to parallel flow and cross-flow. J. Fluid Mech. 228, 87–109.Google Scholar
Mehta, R. D. & Hoffmann, P. H. 1987 Boundary layer two-dimensionality in wind tunnels. Exp. Fluids 5 (5), 358–360.Google Scholar
Mejia-Alvarez, R. & Christensen, K. T. 2013 Wall-parallel stereo particle-image velocimetry measurements in the roughness sublayer of turbulent flow overlying highly irregular roughness. Phys. Fluids 25 (1), 115109.Google Scholar
Nezu, I. & Nakagawa, H. 1984 Cellular secondary currents in straight conduit. J. Hydraul. Engng ASCE 110 (2), 173–193.Google Scholar
Nugroho, B., Gnanamanickam, E., Kevin, K., Monty, J. & Hutchins, N. 2014 Roll-modes generated in turbulent boundary layers with passive surface modifications. In 52nd Aerospace Sciences Meeting, p. 0197. AIAA.Google Scholar
Nugroho, B., Hutchins, N. & Monty, J. P. 2013 Large-scale spanwise periodicity in a turbulent boundary layer induced by highly ordered and directional surface roughness. Intl J. Heat Fluid Flow 41, 90–102.Google Scholar
Perry, A. E. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.Google Scholar
Rao, D. M. & Kariya, T. T. 1988 Boundary-layer submerged vortex generators for separation control-an exploratory study. In AIAA, ASME, SIAM, and APS, National Fluid Dynamics Congress, vol. 1, pp. 839–846.Google Scholar
Schlatter, P., Li, Q., Örlü, R., Hussain, F. & Henningson, D. S. 2014 On the near-wall vortical structures at moderate reynolds numbers. Eur. J. Mech. (B/Fluids) 48, 75–93.Google Scholar
Schoppa, W. & Hussain, F. 1998 A large scale control strategy for drag reduction in turbulent boundary layers. Phys. Fluids 10 (5), 1049–1051.Google Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at reynolds numbers up to 𝛿+ ≈ 2000. Phys. Fluids 25 (10), 105102.Google Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2014 Two-point statistics for turbulent boundary layers and channels at Reynolds numbers up to 𝛿+ ≈ 2000. Phys. Fluids 26 (10), 105109.Google Scholar
de Silva, C. M., Kevin, Baidya, R., Hutchins, N. & Marusic, I. 2018 Large coherence of spanwise velocity in turbulent boundary layers. J. Fluid Mech. 847, 161–185.Google Scholar
Soldati, A. 2002 Influence of large-scale streamwise vortical ehd flows on wall turbulence. Intl J. Heat Fluid Flow 23, 441–443.Google Scholar
Squire, D. T., Morril-Winter, C., Hutchins, N., Marusic, I., Schultz, M. P. & Klewicki, J. C. 2016 Smooth- and rough-wall boundary layer structure from high spatial range particle image velocimetry. Phys. Rev. Fluids 1 (6), 064402.Google Scholar
Stroh, A., Hasegawa, Y., Kriegseis, J. & Frohnapfel, B. 2016 Secondary vortices over surfaces with spanwise varying drag. J. Turbul. 17 (12), 1142–1158.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, vol. 2. Cambridge University Press.Google Scholar
Vanderwel, C. & Ganapathisubramani, B. 2015 Effects of spanwise spacing on large-scale secondary flows in rough-wall turbulent boundary layers. J. Fluid Mech. 774, R2.Google Scholar
Volino, R. J., Schultz, M. P. & Flack, K. A. 2007 Turbulence structure in rough- and smooth-wall boundary layers. J. Fluid Mech. 592, 263–293.Google Scholar
Volino, R. J., Schultz, M. P. & Flack, K. A. 2009 Turbulence structure in a boundary layer with two-dimensional roughness. J. Fluid Mech. 635, 75–101.Google Scholar
Volino, R. J., Schultz, M. P. & Flack, K. A. 2011 Turbulence structure in boundary layers over periodic two- and three-dimensional roughness. J. Fluid Mech. 676, 172–190.Google Scholar
Wang, Z. Q. & Cheng, N. S. 2006 Time-mean structure of secondary flows in open channel with longitudinal bedforms. Adv. Water Resour. 29 (11), 521–542.Google Scholar
Willingham, D., Anderson, W., Christensen, K. T. & Barros, J. M. 2014 Turbulent boundary layer flow over transverse aerodynamic roughness transitions: induced mixing and flow characterization. Phys. Fluids 26 (2), 025117.Google Scholar
Wu, Y. & Christensen, K. T. 2010 Spatial structure of a turbulent boundary layer with irregular surface roughness. J. Fluid Mech. 655, 380–418.Google Scholar
Xu, F., Zhong, S. & Zhang, S. 2018 Vortical structures and development of laminar flow over convergent-divergent riblets. Phys. Fluids 30 (5), 051901.Google Scholar
Yang, J. & Anderson, W. 2018 Numerical study of turbulent channel flow over surfaces with varying variable spanwise heterogeneities: topographically-driven secondary flows affect outer-layer similarity of turbulent length scales. Flow Turbul. Combust. 100 (1), 1–17.Google Scholar