No CrossRef data available.
Article contents
FACTORIZATION OF OPERATORS THROUGH SUBSPACES OF 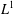 $L^{1}$-SPACES
$L^{1}$-SPACES
Published online by Cambridge University Press: 08 November 2016
Abstract
We analyze domination properties and factorization of operators in Banach spaces through subspaces of 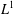 $L^{1}$-spaces. Using vector measure integration and extending classical arguments based on scalar integral bounds, we provide characterizations of operators factoring through subspaces of
$L^{1}$-spaces. Using vector measure integration and extending classical arguments based on scalar integral bounds, we provide characterizations of operators factoring through subspaces of 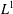 $L^{1}$-spaces of finite measures. Some special cases involving positivity and compactness of the operators are considered.
$L^{1}$-spaces of finite measures. Some special cases involving positivity and compactness of the operators are considered.
MSC classification
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 103 , Issue 3 , December 2017 , pp. 313 - 328
- Copyright
- © 2016 Australian Mathematical Publishing Association Inc.
Footnotes
Research supported by MINECO/FEDER under projects MTM2014-53009-P (J. M. Calabuig), MTM2014-54182-P (J. Rodríguez) and MTM2012-36740-C02-02 (E. A. Sánchez-Pérez).


