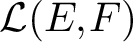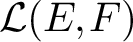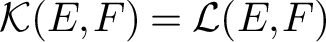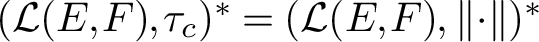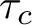1. Introduction
The famous James theorem states that a Banach space E is reflexive if and only if every bounded linear functional on E attains its norm. By using this characterisation, one can check that if every bounded linear operator from a Banach space E into a Banach space F is norm-attaining, then E must be reflexive, whereas the range space F is not forced to be reflexive in general. Indeed, every bounded linear operator from a reflexive space into a Banach space that satisfies the Schur property is compact (by the Eberlein-Šmulian theorem) and any compact operator from a reflexive space into an arbitrary Banach space is norm-attaining. Therefore, it seems natural to wonder whether it is possible to guarantee the existence of a non-norm-attaining operator from the existence of a noncompact operator. This brings us back to the 1970s when J.R. Holub proved that this is, in fact, true under approximation property assumptions (see [Reference Holub16, Theorem 2]). Almost 30 years later, J. Mujica improved Holub’s result by using the compact approximation property (see [Reference Mujica25, Theorem 2.1]), which is a weaker assumption than the approximation property. However, both results require the reflexivity on both domain and range spaces, so the following question arises naturally:
Given a reflexive space E and an arbitrary Banach space F, under which assumptions may we guarantee the existence of non-norm-attaining operators in
![]() $\mathcal {L}(E, F)$
?
$\mathcal {L}(E, F)$
?
Coming back to Holub and Mujica’s results, we would like to highlight what they proved in the direction of the above question. For a background on necessary definitions and notations, we refer the reader to Section 2. In what follows,
![]() $\tau _c$
denotes the topology of compact convergence and
$\tau _c$
denotes the topology of compact convergence and
![]() $\|\cdot \|$
denotes the norm topology in
$\|\cdot \|$
denotes the norm topology in
![]() $\mathcal {L}(E, F)$
.
$\mathcal {L}(E, F)$
.
Theorem [Reference Holub16, Theorem 2] and [Reference Mujica25, Theorem 2.1]
Let E and F be both reflexive spaces.
-
(a) If
 $\mathcal {L}(E,F)$
is nonreflexive, there is a non-norm-attaining operator
$\mathcal {L}(E,F)$
is nonreflexive, there is a non-norm-attaining operator
 $S \in \mathcal {L}(E,F)$
.
$S \in \mathcal {L}(E,F)$
. -
(b) If E or F has the (compact) approximation property, then the following statements are equivalent:
-
(i) There exists a non-norm-attaining operator
 $S \in \mathcal {L}(E,F)$
;
$S \in \mathcal {L}(E,F)$
; -
(ii)
 $\mathcal {L}(E,F)\neq \mathcal {K}(E,F)$
;
$\mathcal {L}(E,F)\neq \mathcal {K}(E,F)$
; -
(iii)
 $\mathcal {L}(E,F)$
is nonreflexive;
$\mathcal {L}(E,F)$
is nonreflexive; -
(iv)
 $(\mathcal {L}(E,F), \|\cdot \|)^* \neq (\mathcal {L} (E,F), \tau _c)^*$
.
$(\mathcal {L}(E,F), \|\cdot \|)^* \neq (\mathcal {L} (E,F), \tau _c)^*$
.
-
The proof of the above result relies on the fact that if F is a reflexive space, then
![]() $\mathcal {L}(E, F)$
is the dual space of the projective tensor product
$\mathcal {L}(E, F)$
is the dual space of the projective tensor product
![]() $E \widehat {\otimes }_\pi F^*$
. However, if the range space F is nonreflexive, then
$E \widehat {\otimes }_\pi F^*$
. However, if the range space F is nonreflexive, then
![]() $\mathcal {L}(E,F)$
is always nonreflexive (see, for instance, [Reference Ruckle30]).
$\mathcal {L}(E,F)$
is always nonreflexive (see, for instance, [Reference Ruckle30]).
As a way of extending the above results to the case of nonreflexive range spaces, we borrow some of the techniques used by R.C. James (see [Reference James17, Reference James18]). As a matter of fact, one of his results [Reference James18, Theorem 1] implies that a separable Banach space E is nonreflexive if and only if given
![]() $0 < \theta < 1$
, there exists a sequence
$0 < \theta < 1$
, there exists a sequence
![]() $(x_n^*)$
in
$(x_n^*)$
in
![]() $B_{E^*}$
such that
$B_{E^*}$
such that
 $x_n^* \stackrel {w^*}{\longrightarrow } 0$
and
$x_n^* \stackrel {w^*}{\longrightarrow } 0$
and
![]() $\operatorname {\mbox {dist }} (0, \operatorname {\mathrm {co}} \{ x_n^* : n \in \mathbb {N} \})> \theta $
, which in turn is equivalent to the existence of a relatively weak-star compact set
$\operatorname {\mbox {dist }} (0, \operatorname {\mathrm {co}} \{ x_n^* : n \in \mathbb {N} \})> \theta $
, which in turn is equivalent to the existence of a relatively weak-star compact set
![]() $K \subseteq B_{E^*}$
such that
$K \subseteq B_{E^*}$
such that
 $0 \in \overline {K}^{w^*}$
and
$0 \in \overline {K}^{w^*}$
and
![]() $0 \not \in \overline {\operatorname {\mathrm {co}}}^{\left \Vert \cdot \right \Vert }(K)$
. This motivates us to define the following property.
$0 \not \in \overline {\operatorname {\mathrm {co}}}^{\left \Vert \cdot \right \Vert }(K)$
. This motivates us to define the following property.
Definition 1.1. We say that a pair
![]() $(E, F)$
of Banach spaces has the James property if there exists a relatively weak operator topology (WOT)-compact set
$(E, F)$
of Banach spaces has the James property if there exists a relatively weak operator topology (WOT)-compact set
![]() $K \subseteq \mathcal {L}(E, F)$
such that
$K \subseteq \mathcal {L}(E, F)$
such that
![]() $0 \in \overline {K}^{WOT}$
and
$0 \in \overline {K}^{WOT}$
and
![]() $0 \not \in \overline {\operatorname {\mathrm {co}}}^{\left \Vert \cdot \right \Vert }(K)$
.
$0 \not \in \overline {\operatorname {\mathrm {co}}}^{\left \Vert \cdot \right \Vert }(K)$
.
We will prove that the James property is a sufficient condition to guarantee the existence of an operator that does not attain its norm, which is our first aim in the present article.
Theorem A. Let E and F be Banach spaces. If the pair
![]() $(E, F)$
has the James property, then there exists a non-norm-attaining operator in
$(E, F)$
has the James property, then there exists a non-norm-attaining operator in
![]() $\mathcal {L}(E, F)$
.
$\mathcal {L}(E, F)$
.
Next, we prove that
![]() $(\mathcal {L}(E,F), \|\cdot \|)^*$
does not coincide with
$(\mathcal {L}(E,F), \|\cdot \|)^*$
does not coincide with
![]() $(\mathcal {L}(E,F),\tau _c)^*$
whenever a pair
$(\mathcal {L}(E,F),\tau _c)^*$
whenever a pair
![]() $(E, F)$
satisfies the James property (see Proposition 3.1). From this, we can see that whenever the pair
$(E, F)$
satisfies the James property (see Proposition 3.1). From this, we can see that whenever the pair
![]() $(E, F)$
has the James property, the Banach space
$(E, F)$
has the James property, the Banach space
![]() $\mathcal {L}(E, F)$
cannot be reflexive due to [Reference Mujica25, Lemma 2.3].
$\mathcal {L}(E, F)$
cannot be reflexive due to [Reference Mujica25, Lemma 2.3].
We observe, for a reflexive space E and an arbitrary Banach space F, that (1) the unit ball of
![]() $\mathcal {K}(E,F)$
is closed in the strong operator topology if and only if it is sequentially closed in this topology (see Lemma 3.4) and (2)
$\mathcal {K}(E,F)$
is closed in the strong operator topology if and only if it is sequentially closed in this topology (see Lemma 3.4) and (2)
![]() $\mathcal {K}(E,F) = \mathcal {L}(E,F)$
implies that
$\mathcal {K}(E,F) = \mathcal {L}(E,F)$
implies that
![]() $(\mathcal {L}(E,F), \|\cdot \|)^* = (\mathcal {L}(E,F), \tau _c)^*$
by using the result [Reference Feder and Saphar12, Theorem 1] due to M. Feder and P. Saphar. In addition, we consider the concept of the pointwise-bounded compact approximation property for a pair of Banach spaces in the way it is done in [Reference Bonde3] (see Definition 2.1) and prove that
$(\mathcal {L}(E,F), \|\cdot \|)^* = (\mathcal {L}(E,F), \tau _c)^*$
by using the result [Reference Feder and Saphar12, Theorem 1] due to M. Feder and P. Saphar. In addition, we consider the concept of the pointwise-bounded compact approximation property for a pair of Banach spaces in the way it is done in [Reference Bonde3] (see Definition 2.1) and prove that
![]() $\mathcal {K}(E,F) = \mathcal {L} (E,F)$
when either (3) the norm-closed unit ball of
$\mathcal {K}(E,F) = \mathcal {L} (E,F)$
when either (3) the norm-closed unit ball of
![]() $\mathcal {K}(E,F)$
is closed in the strong operator topology or (4)
$\mathcal {K}(E,F)$
is closed in the strong operator topology or (4)
![]() $(\mathcal {L}(E,F), \| \cdot \|)^* = (\mathcal {L}(E,F), \tau _c)^*$
under the just mentioned approximation property assumption (see Lemma 3.7). Combining (1)–(4) together with Theorem A, we get a generalisation of Holub and Mujica’s results, where we no longer need reflexivity on the target space F and E and F might not have the bounded compact approximation property (CAP) (see Example 2.2).
$(\mathcal {L}(E,F), \| \cdot \|)^* = (\mathcal {L}(E,F), \tau _c)^*$
under the just mentioned approximation property assumption (see Lemma 3.7). Combining (1)–(4) together with Theorem A, we get a generalisation of Holub and Mujica’s results, where we no longer need reflexivity on the target space F and E and F might not have the bounded compact approximation property (CAP) (see Example 2.2).
Theorem B. Let E be a reflexive space and F be an arbitrary Banach space. Consider the following conditions:
-
(a)
 $\mathcal {K}(E, F) = \mathcal {L}(E, F)$
.
$\mathcal {K}(E, F) = \mathcal {L}(E, F)$
. -
(b) Every operator from E into F attains its norm.
-
(c) The unit ball
 $B_{\mathcal {K}(E, F)}$
is closed in the strong operator topology.
$B_{\mathcal {K}(E, F)}$
is closed in the strong operator topology. -
(d)
 $(\mathcal {L}(E,F), \tau _c)^* = (\mathcal {L}(E, F), \left \Vert \cdot \right \Vert )^*$
.
$(\mathcal {L}(E,F), \tau _c)^* = (\mathcal {L}(E, F), \left \Vert \cdot \right \Vert )^*$
.
Then, we always have (a)
![]() $\Longrightarrow $
(b)
$\Longrightarrow $
(b)
![]() $\Longrightarrow $
(c) and (a)
$\Longrightarrow $
(c) and (a)
![]() $\Longrightarrow $
(d)
$\Longrightarrow $
(d)
![]() $\Longrightarrow $
(c). Additionally, if the pair
$\Longrightarrow $
(c). Additionally, if the pair
![]() $(E,F)$
has the bounded compact approximation property, then (c)
$(E,F)$
has the bounded compact approximation property, then (c)
![]() $\Longrightarrow $
(a) and therefore all of the statements are equivalent.
$\Longrightarrow $
(a) and therefore all of the statements are equivalent.
The following diagram summarises most of the results included in this article. In what follows, E is supposed to be any reflexive space and F is any arbitrary Banach space. See Definition 2.1 in Section 2 for the definition of the pointwise-bounded compact approximation property (BCAP).
Finally, as an application of Theorem B, we connect the Schur property with the case where every operator attains its norm and obtain the following characterisation, which follows from Theorem 3.10.

Theorem C. Let F be a Banach space. The following statements are equivalent:
-
(a) F has the Schur property.
-
(b)
 $\mathcal {K}(E, F) = \mathcal {L}(E, F)$
for every reflexive space E.
$\mathcal {K}(E, F) = \mathcal {L}(E, F)$
for every reflexive space E. -
(c)
 $\operatorname {NA}(E, F) = \mathcal {L}(E, F)$
for every reflexive space E.
$\operatorname {NA}(E, F) = \mathcal {L}(E, F)$
for every reflexive space E. -
(d)
 $\mathcal {K} (G, F) = \mathcal {L} (G, F)$
for every reflexive space G with basis.
$\mathcal {K} (G, F) = \mathcal {L} (G, F)$
for every reflexive space G with basis. -
(e)
 $\operatorname {NA} (G,F) = \mathcal {L} (G,F)$
for every reflexive space G with basis.
$\operatorname {NA} (G,F) = \mathcal {L} (G,F)$
for every reflexive space G with basis.
2. Preliminaries
Throughout the article, E and F will be Banach spaces over a field
![]() $\mathbb {K}$
, which can be either real or complex numbers. We denote by
$\mathbb {K}$
, which can be either real or complex numbers. We denote by
![]() $B_E$
and
$B_E$
and
![]() $S_E$
the closed unit ball and the unit sphere of the Banach space E, respectively. For a subset K of E,
$S_E$
the closed unit ball and the unit sphere of the Banach space E, respectively. For a subset K of E,
![]() $\operatorname {\mathrm {co}} (K)$
(respectively,
$\operatorname {\mathrm {co}} (K)$
(respectively,
![]() $\overline {\operatorname {\mathrm {co}}} (K)$
) denotes the convex hull (respectively, closed convex hull) of K. The space of all bounded linear operators from E into F is denoted by
$\overline {\operatorname {\mathrm {co}}} (K)$
) denotes the convex hull (respectively, closed convex hull) of K. The space of all bounded linear operators from E into F is denoted by
![]() $\mathcal {L}(E, F)$
. The symbol
$\mathcal {L}(E, F)$
. The symbol
![]() $\mathcal {K}(E, F)$
(respectively,
$\mathcal {K}(E, F)$
(respectively,
![]() $\mathcal {W}(E,F)$
) stands for the space of all compact operators (respectively, weakly compact operators) from E into F, whereas the symbol
$\mathcal {W}(E,F)$
) stands for the space of all compact operators (respectively, weakly compact operators) from E into F, whereas the symbol
![]() $\mathcal {F}(E, F)$
is used to denote the space of all finite-rank operators. Finally, let us recall that an operator
$\mathcal {F}(E, F)$
is used to denote the space of all finite-rank operators. Finally, let us recall that an operator
![]() $T \in \mathcal {L}(E, F)$
attains its norm or is norm-attaining if there exists
$T \in \mathcal {L}(E, F)$
attains its norm or is norm-attaining if there exists
![]() $x \in B_E$
such that
$x \in B_E$
such that
![]() $\|T(x)\| = \|T\|$
. By
$\|T(x)\| = \|T\|$
. By
![]() $\operatorname {NA}(E,F)$
we mean the set of all norm-attaining operators from E into F. If
$\operatorname {NA}(E,F)$
we mean the set of all norm-attaining operators from E into F. If
![]() $E = F$
, then we simply write
$E = F$
, then we simply write
![]() $\operatorname {NA}(E)$
instead of
$\operatorname {NA}(E)$
instead of
![]() $\operatorname {NA}(E, E)$
and we do the same with the above classes of operators.
$\operatorname {NA}(E, E)$
and we do the same with the above classes of operators.
We will be using different topologies in
![]() $\mathcal {L}(E, F)$
. We denote by
$\mathcal {L}(E, F)$
. We denote by
![]() $\tau _c$
the topology of compact convergence; that is, the topology of uniform convergence on compact subsets of E. The WOT is defined by the basic neighbourhoods
$\tau _c$
the topology of compact convergence; that is, the topology of uniform convergence on compact subsets of E. The WOT is defined by the basic neighbourhoods
 $$ \begin{align*} N(T; A, B, \varepsilon) := \big\{ S \in \mathcal{L}(E, F): |y^*(T - S)(x)| < \varepsilon, \mbox{ for every } y^* \in B, x \in A \big\}, \end{align*} $$
$$ \begin{align*} N(T; A, B, \varepsilon) := \big\{ S \in \mathcal{L}(E, F): |y^*(T - S)(x)| < \varepsilon, \mbox{ for every } y^* \in B, x \in A \big\}, \end{align*} $$
where A and B are arbitrary finite sets in E and
![]() $F^*$
, respectively, and
$F^*$
, respectively, and
![]() $\varepsilon> 0$
. Thus, in the WOT, a net
$\varepsilon> 0$
. Thus, in the WOT, a net
![]() $(T_{\alpha })$
converges to T if and only if
$(T_{\alpha })$
converges to T if and only if
![]() $(y^*(T_{\alpha }(x)))$
converges to
$(y^*(T_{\alpha }(x)))$
converges to
![]() $y^*{(T(x))}$
for every
$y^*{(T(x))}$
for every
![]() $x \in E$
and
$x \in E$
and
![]() $y^* \in F^*$
. Analogously, the strong operator topology (SOT) is defined by the basic neighbourhoods
$y^* \in F^*$
. Analogously, the strong operator topology (SOT) is defined by the basic neighbourhoods
 $$ \begin{align*} N(T; A, \varepsilon) := \big\{ S \in \mathcal{L}(E, F): \|(T - S)(x)\| < \varepsilon, \mbox{ for every } x \in A \big\}, \end{align*} $$
$$ \begin{align*} N(T; A, \varepsilon) := \big\{ S \in \mathcal{L}(E, F): \|(T - S)(x)\| < \varepsilon, \mbox{ for every } x \in A \big\}, \end{align*} $$
where A is an arbitrary finite set in E and
![]() $\varepsilon> 0$
. Thus, a net
$\varepsilon> 0$
. Thus, a net
![]() $(T_{\alpha })$
converges in the SOT to T if and only if
$(T_{\alpha })$
converges in the SOT to T if and only if
![]() $(T_{\alpha }(x))$
converges in norm to
$(T_{\alpha }(x))$
converges in norm to
![]() $T(x)$
for every
$T(x)$
for every
![]() $x \in E$
. We will deal with SOT and WOT closures of bounded sets in
$x \in E$
. We will deal with SOT and WOT closures of bounded sets in
![]() $\mathcal {L}(E,F)$
. It is worth mentioning that for a bounded convex set in
$\mathcal {L}(E,F)$
. It is worth mentioning that for a bounded convex set in
![]() $\mathcal {L}(E,F)$
, the WOT closure and the SOT closure coincide [Reference Dunford and Schwartz10, Corollary VI.1.5]. Thus, the SOT and the WOT in some results in this article can be interchanged. For a more detailed exposition on topologies in
$\mathcal {L}(E,F)$
, the WOT closure and the SOT closure coincide [Reference Dunford and Schwartz10, Corollary VI.1.5]. Thus, the SOT and the WOT in some results in this article can be interchanged. For a more detailed exposition on topologies in
![]() $\mathcal {L}(E, F)$
, we refer the reader to [Reference Defant and Floret8, Reference Dunford and Schwartz10].
$\mathcal {L}(E, F)$
, we refer the reader to [Reference Defant and Floret8, Reference Dunford and Schwartz10].
Let us present now the necessary definitions on approximation properties we will need. A Banach space E is said to have the approximation property (AP) if the identity operator
![]() $\operatorname {\mathrm {Id}}_E$
in
$\operatorname {\mathrm {Id}}_E$
in
![]() $\mathcal {L}(E)$
belongs to
$\mathcal {L}(E)$
belongs to
 $\overline { \mathcal {F} (E)}^{\tau _c}$
. Given
$\overline { \mathcal {F} (E)}^{\tau _c}$
. Given
![]() $\lambda \geqslant 1$
, E is said to have the
$\lambda \geqslant 1$
, E is said to have the
![]() $\lambda$
-bounded approximation property (
$\lambda$
-bounded approximation property (
![]() $\lambda $
-BAP) when
$\lambda $
-BAP) when
![]() $\operatorname {\mathrm {Id}}_E$
belongs to
$\operatorname {\mathrm {Id}}_E$
belongs to
 $\lambda \overline {B_{\mathcal {F}(E)}}^{\tau _c}$
. A Banach space is said to have the bounded approximation property (BAP) if it has the
$\lambda \overline {B_{\mathcal {F}(E)}}^{\tau _c}$
. A Banach space is said to have the bounded approximation property (BAP) if it has the
![]() $\lambda $
-BAP for some
$\lambda $
-BAP for some
![]() $\lambda \geqslant 1$
. In the special case when
$\lambda \geqslant 1$
. In the special case when
![]() $\lambda = 1$
, we say that E has the metric approximation property (MAP). Also, recall that E is said to have the CAP if the identity operator
$\lambda = 1$
, we say that E has the metric approximation property (MAP). Also, recall that E is said to have the CAP if the identity operator
![]() $\operatorname {\mathrm {Id}}_E$
in
$\operatorname {\mathrm {Id}}_E$
in
![]() $\mathcal {L}(E)$
belongs to
$\mathcal {L}(E)$
belongs to
 $\overline { \mathcal {K} (E)}^{\tau _c}$
. The
$\overline { \mathcal {K} (E)}^{\tau _c}$
. The
![]() $\lambda $
-bounded compact approximation property (
$\lambda $
-bounded compact approximation property (
![]() $\lambda $
-BCAP), BCAP and metric compact approximation property (MCAP) for a Banach space E can be defined in an analogous way. It is known that a reflexive space has the AP if and only if it has the MAP (see [Reference Grothendieck14]). Analogously, every reflexive space with the CAP also has the MCAP (see [Reference Cho and Johnson5, Proposition 1 and Remark 1]). We refer the reader to [Reference Lindenstrauss and Tzafriri22, Reference Lindenstrauss and Tzafriri23] and [Reference Casazza, Johnson and Lindenstrauss4] for background.
$\lambda $
-BCAP), BCAP and metric compact approximation property (MCAP) for a Banach space E can be defined in an analogous way. It is known that a reflexive space has the AP if and only if it has the MAP (see [Reference Grothendieck14]). Analogously, every reflexive space with the CAP also has the MCAP (see [Reference Cho and Johnson5, Proposition 1 and Remark 1]). We refer the reader to [Reference Lindenstrauss and Tzafriri22, Reference Lindenstrauss and Tzafriri23] and [Reference Casazza, Johnson and Lindenstrauss4] for background.
On the other hand, E. Bonde introduced in [Reference Bonde3] the AP and
![]() $\lambda $
-BAP for pairs of Banach spaces in the following way: a pair
$\lambda $
-BAP for pairs of Banach spaces in the following way: a pair
![]() $(E,F)$
of Banach spaces is said to have the AP if any operator
$(E,F)$
of Banach spaces is said to have the AP if any operator
![]() $T \in \mathcal {L} (E,F)$
belongs to
$T \in \mathcal {L} (E,F)$
belongs to
 $\overline { \mathcal {F} (E,F)}^{\tau _c}$
. If
$\overline { \mathcal {F} (E,F)}^{\tau _c}$
. If
![]() $\lambda \geqslant 1$
and every operator
$\lambda \geqslant 1$
and every operator
![]() $T \in \mathcal {L} (E,F)$
belongs to
$T \in \mathcal {L} (E,F)$
belongs to
 $\lambda \|T\|\overline {B_{\mathcal {F}(E,F)}}^{\tau _c}$
, then
$\lambda \|T\|\overline {B_{\mathcal {F}(E,F)}}^{\tau _c}$
, then
![]() $(E,F)$
is said to have the
$(E,F)$
is said to have the
![]() $\lambda $
-BAP or simply the BAP.
$\lambda $
-BAP or simply the BAP.
It is clear that if E or F has the AP (respectively, BAP), then the pair
![]() $(E,F)$
has the AP (respectively, BAP). It is observed in [Reference Bonde3, Section 4] that there are pairs of Banach spaces
$(E,F)$
has the AP (respectively, BAP). It is observed in [Reference Bonde3, Section 4] that there are pairs of Banach spaces
![]() $(E,F)$
with the BAP such that E and F do not have the BAP. Similarly, we have the following.
$(E,F)$
with the BAP such that E and F do not have the BAP. Similarly, we have the following.
Definition 2.1. The pair
![]() $(E,F)$
of Banach spaces is said to have the compact approximation property (CAP) if every operator
$(E,F)$
of Banach spaces is said to have the compact approximation property (CAP) if every operator
![]() $T \in \mathcal {L} (E,F)$
belongs to
$T \in \mathcal {L} (E,F)$
belongs to
 $\overline {\mathcal {K} (E,F)}^{\tau _c}$
. If
$\overline {\mathcal {K} (E,F)}^{\tau _c}$
. If
![]() $\lambda \geqslant 1$
and every operator
$\lambda \geqslant 1$
and every operator
![]() $T \in \mathcal {L} (E,F)$
belongs to
$T \in \mathcal {L} (E,F)$
belongs to
 $\lambda \|T\|\overline {B_{\mathcal {K}(E,F)}}^{\tau _c}$
, then
$\lambda \|T\|\overline {B_{\mathcal {K}(E,F)}}^{\tau _c}$
, then
![]() $(E,F)$
is said to have the
$(E,F)$
is said to have the
![]() $\lambda $
-BCAP or simply the BCAP. In the case when
$\lambda $
-BCAP or simply the BCAP. In the case when
![]() $\lambda =1$
, we say that the pair
$\lambda =1$
, we say that the pair
![]() $(E,F)$
has the MCAP.
$(E,F)$
has the MCAP.
Moreover, as one of the anonymous referees and Miguel Martín suggested, we say that the pair
![]() $(E,F)$
has the pointwise-BCAP if for every operator
$(E,F)$
has the pointwise-BCAP if for every operator
![]() $T \in \mathcal {L} (E,F)$
there is a constant
$T \in \mathcal {L} (E,F)$
there is a constant
![]() $\lambda _T \geqslant 1$
such that
$\lambda _T \geqslant 1$
such that
 $T\in \lambda _T \overline {B_{\mathcal {K}(E,F)}}^{\tau _c}$
.
$T\in \lambda _T \overline {B_{\mathcal {K}(E,F)}}^{\tau _c}$
.
Let us note that the BCAP implies the pointwise-BCAP and the pointwise-BCAP implies the CAP. In addition, for a Banach space E, the pair
![]() $(E,E)$
has the BCAP if and only if it has the pointwise-BCAP (just take
$(E,E)$
has the BCAP if and only if it has the pointwise-BCAP (just take
![]() $\lambda :=\lambda _I$
with I the identity on E from the definition of the pointwise-BCAP and note that
$\lambda :=\lambda _I$
with I the identity on E from the definition of the pointwise-BCAP and note that
 $T=T \circ I \subseteq \overline {\{T \circ K: K \in \lambda _I B_{\mathcal {K}(E,E)}\}}^{\tau _c}\subseteq \lambda \|T\|\overline {B_{\mathcal {K}(E,E)}}^{\tau _c}$
for every
$T=T \circ I \subseteq \overline {\{T \circ K: K \in \lambda _I B_{\mathcal {K}(E,E)}\}}^{\tau _c}\subseteq \lambda \|T\|\overline {B_{\mathcal {K}(E,E)}}^{\tau _c}$
for every
![]() $T \in \mathcal {L} (E,E)$
). However, we do not know whether the pointwise-BCAP of a pair
$T \in \mathcal {L} (E,E)$
). However, we do not know whether the pointwise-BCAP of a pair
![]() $(E,F)$
is equivalent to the BCAP or the CAP for an arbitrary Banach space F even if E is assumed to be reflexive. The next example shows that a pair
$(E,F)$
is equivalent to the BCAP or the CAP for an arbitrary Banach space F even if E is assumed to be reflexive. The next example shows that a pair
![]() $(E,F)$
might have the BCAP even if E and F do not have the CAP.
$(E,F)$
might have the BCAP even if E and F do not have the CAP.
Example 2.2. In [Reference Bonde3, Example 4.2], it is shown that whenever E is a subspace of
![]() $\ell _{p_1}$
and F is a subspace of
$\ell _{p_1}$
and F is a subspace of
![]() $\ell _{p_2}$
with
$\ell _{p_2}$
with
![]() $1\leqslant p_2 < 2 <p_1 <\infty $
, the pair
$1\leqslant p_2 < 2 <p_1 <\infty $
, the pair
![]() $(E,F)$
has the BAP and therefore the BCAP. Nevertheless, for every
$(E,F)$
has the BAP and therefore the BCAP. Nevertheless, for every
![]() $1<p<\infty $
with
$1<p<\infty $
with
![]() $p\neq 2$
there is a subspace of
$p\neq 2$
there is a subspace of
![]() $\ell _p$
failing the CAP (see [Reference Davie6] and [Reference Lindenstrauss and Tzafriri22, Theorem 1.g.4 and Remark 2 in pg. 111]). In particular, there are Banach spaces E and F such that
$\ell _p$
failing the CAP (see [Reference Davie6] and [Reference Lindenstrauss and Tzafriri22, Theorem 1.g.4 and Remark 2 in pg. 111]). In particular, there are Banach spaces E and F such that
![]() $(E,F)$
has the BCAP and E and F do not have the CAP. Therefore, assuming that a pair
$(E,F)$
has the BCAP and E and F do not have the CAP. Therefore, assuming that a pair
![]() $(E,F)$
of Banach spaces has the BCAP is more general than E or F having the CAP.
$(E,F)$
of Banach spaces has the BCAP is more general than E or F having the CAP.
3 The Results
In this section, we shall prove Theorems A, B, C and their consequences. We start by proving Theorem A. To do so, let us recall that a set
![]() $B \subseteq B_{E^*}$
is called a James boundary of a Banach space E if for every
$B \subseteq B_{E^*}$
is called a James boundary of a Banach space E if for every
![]() $x \in S_E$
there exists
$x \in S_E$
there exists
![]() $f \in B$
such that
$f \in B$
such that
![]() $f(x) = 1$
. For a subset G of
$f(x) = 1$
. For a subset G of
![]() $E^*$
, we shall denote by
$E^*$
, we shall denote by
![]() $w(E, G)$
the weak topology of X induced by G.
$w(E, G)$
the weak topology of X induced by G.
Proof of Theorem A. Let us assume by contradiction that every operator from E into F attains its norm. Then, the family
 $$ \begin{align*} B:= \Big\{ x \otimes y^*: x \in S_E, y^* \in S_{F^*} \Big\} \end{align*} $$
$$ \begin{align*} B:= \Big\{ x \otimes y^*: x \in S_E, y^* \in S_{F^*} \Big\} \end{align*} $$
is a James boundary of
![]() $\mathcal {L}(E, F)$
. Indeed, for an arbitrary operator
$\mathcal {L}(E, F)$
. Indeed, for an arbitrary operator
![]() $T \in \mathcal {L}(E, F) = \operatorname {NA}(E, F)$
, take
$T \in \mathcal {L}(E, F) = \operatorname {NA}(E, F)$
, take
![]() $x \in S_E$
to be such that
$x \in S_E$
to be such that
![]() $\|T(x)\| = \|T\|$
and then
$\|T(x)\| = \|T\|$
and then
![]() $y^* \in S_{F^*}$
to be such that
$y^* \in S_{F^*}$
to be such that
![]() $|y^*(T(x))| = \|T(x)\| = \|T\|$
. Now, because
$|y^*(T(x))| = \|T(x)\| = \|T\|$
. Now, because
![]() $(E, F)$
has the James property, there exists a relatively WOT-compact set
$(E, F)$
has the James property, there exists a relatively WOT-compact set
![]() $K \subseteq \mathcal {L}(E, F)$
such that
$K \subseteq \mathcal {L}(E, F)$
such that
![]() $0 \in \overline {K}^{WOT}$
and
$0 \in \overline {K}^{WOT}$
and
![]() $0 \not \in \overline {\operatorname {\mathrm {co}}}^{\left \Vert \cdot \right \Vert }(K)$
. By the uniform boundedness principle, the set
$0 \not \in \overline {\operatorname {\mathrm {co}}}^{\left \Vert \cdot \right \Vert }(K)$
. By the uniform boundedness principle, the set
![]() $\overline {K}^{WOT}$
is norm-bounded. Note that the WOT-topology is the topology of pointwise convergence on B, so it coincides with
$\overline {K}^{WOT}$
is norm-bounded. Note that the WOT-topology is the topology of pointwise convergence on B, so it coincides with
![]() $w(\mathcal {L}(E, F), B)$
. By hypothesis,
$w(\mathcal {L}(E, F), B)$
. By hypothesis,
![]() $\overline {K}^{WOT}$
is WOT-compact or, equivalently,
$\overline {K}^{WOT}$
is WOT-compact or, equivalently,
![]() $w(\mathcal {L}(E, F), B)$
-compact. By a theorem of Pfitzner (see [Reference Pfitzner27] or [Reference Fabian, Habala, Hájek, Montesinos and Zizler11, Theorem 3.121]), we have that
$w(\mathcal {L}(E, F), B)$
-compact. By a theorem of Pfitzner (see [Reference Pfitzner27] or [Reference Fabian, Habala, Hájek, Montesinos and Zizler11, Theorem 3.121]), we have that
![]() $\overline {K}^{WOT}$
is weakly compact. Therefore,
$\overline {K}^{WOT}$
is weakly compact. Therefore,
![]() $0 \in \overline {K}^{WOT} = \overline {K}^w$
, which in particular gives that
$0 \in \overline {K}^{WOT} = \overline {K}^w$
, which in particular gives that
![]() $0 \in \overline {\operatorname {\mathrm {co}}}^w(K) = \overline {\operatorname {\mathrm {co}}}^{\left \Vert \cdot \right \Vert }(K)$
. This contradiction yields a non-norm-attaining operator
$0 \in \overline {\operatorname {\mathrm {co}}}^w(K) = \overline {\operatorname {\mathrm {co}}}^{\left \Vert \cdot \right \Vert }(K)$
. This contradiction yields a non-norm-attaining operator
![]() $T \in \mathcal {L}(E, F)$
as desired. □
$T \in \mathcal {L}(E, F)$
as desired. □
Let us observe that if a pair
![]() $(E,F)$
of Banach spaces has the James property, then the dual of
$(E,F)$
of Banach spaces has the James property, then the dual of
![]() $\mathcal {L}(E, F)$
endowed with the norm topology does not coincide with the dual of
$\mathcal {L}(E, F)$
endowed with the norm topology does not coincide with the dual of
![]() $\mathcal {L}(E, F)$
endowed with the topology
$\mathcal {L}(E, F)$
endowed with the topology
![]() $\tau _c$
of compact convergence. As a matter of fact, if K is a subset of E given as in Definition 1.1, then there exists
$\tau _c$
of compact convergence. As a matter of fact, if K is a subset of E given as in Definition 1.1, then there exists
![]() $\varphi \in (\mathcal {L}(E, F), \|\cdot \|)^*$
such that
$\varphi \in (\mathcal {L}(E, F), \|\cdot \|)^*$
such that
![]() $0 = \operatorname {\mathrm {Re}} \varphi (0)> \sup \left \{ \operatorname {\mathrm {Re}} \varphi (T): T \in \overline {\operatorname {\mathrm {co}}}(K) \right \}$
thanks to the Hahn-Banach separation theorem. This implies that
$0 = \operatorname {\mathrm {Re}} \varphi (0)> \sup \left \{ \operatorname {\mathrm {Re}} \varphi (T): T \in \overline {\operatorname {\mathrm {co}}}(K) \right \}$
thanks to the Hahn-Banach separation theorem. This implies that
![]() $\varphi $
cannot be in
$\varphi $
cannot be in
![]() $(\mathcal {L}(E, F), \tau _c)^*$
because
$(\mathcal {L}(E, F), \tau _c)^*$
because
![]() $0 \in \overline {\operatorname {\mathrm {co}}}^{WOT}(K) = \overline {\operatorname {\mathrm {co}}}^{\tau _c}(K)$
. Moreover, using [Reference Mujica25, Lemma 2.3], we see that if
$0 \in \overline {\operatorname {\mathrm {co}}}^{WOT}(K) = \overline {\operatorname {\mathrm {co}}}^{\tau _c}(K)$
. Moreover, using [Reference Mujica25, Lemma 2.3], we see that if
![]() $(\mathcal {L} (E,F), \| \cdot \|)^* \neq (\mathcal {L} (E,F), \tau _c)^*$
, then the space
$(\mathcal {L} (E,F), \| \cdot \|)^* \neq (\mathcal {L} (E,F), \tau _c)^*$
, then the space
![]() $\mathcal {L} (E,F)$
cannot be reflexive. Summarising, we obtain the following result.
$\mathcal {L} (E,F)$
cannot be reflexive. Summarising, we obtain the following result.
Proposition 3.1. Let E and F be Banach spaces. If the pair
![]() $(E, F)$
has the James property, then
$(E, F)$
has the James property, then
-
(i)
 $(\mathcal {L}(E, F), \|\cdot \|)^* \not = (\mathcal {L}(E, F), \tau _c)^*$
.
$(\mathcal {L}(E, F), \|\cdot \|)^* \not = (\mathcal {L}(E, F), \tau _c)^*$
. -
(ii)
 $\mathcal {L}(E, F)$
is nonreflexive.
$\mathcal {L}(E, F)$
is nonreflexive.
One easy consequence of Theorem A is that if E is reflexive and a pair
![]() $(E,F)$
has the James property, then
$(E,F)$
has the James property, then
![]() $\mathcal {K}(E,F)$
cannot be equal to the whole space
$\mathcal {K}(E,F)$
cannot be equal to the whole space
![]() $\mathcal {L} (E,F)$
. As a matter of fact, the following result gives us a rather general observation.
$\mathcal {L} (E,F)$
. As a matter of fact, the following result gives us a rather general observation.
Proposition 3.2. Let E be a reflexive space and F be an arbitrary Banach space. If
![]() $\mathcal {K}(E, F) = \mathcal {L}(E, F)$
, then
$\mathcal {K}(E, F) = \mathcal {L}(E, F)$
, then
![]() $(\mathcal {L}(E, F), \|\cdot \|)^* = (\mathcal {L}(E, F), \tau _c)^*$
.
$(\mathcal {L}(E, F), \|\cdot \|)^* = (\mathcal {L}(E, F), \tau _c)^*$
.
Proof. Let
![]() $D: E \widehat {\otimes }_\pi F^* \longrightarrow (\mathcal {L}(E, F), \tau _c)^*$
be defined by
$D: E \widehat {\otimes }_\pi F^* \longrightarrow (\mathcal {L}(E, F), \tau _c)^*$
be defined by
![]() $D (z)(T):= \sum _{n=1}^{\infty } y_n^*(T(x_n))$
for every
$D (z)(T):= \sum _{n=1}^{\infty } y_n^*(T(x_n))$
for every
![]() $z \in E \widehat {\otimes }_\pi F^*$
with
$z \in E \widehat {\otimes }_\pi F^*$
with
![]() $z = \sum _{n=1}^{\infty } x_n \otimes y_n^*$
and
$z = \sum _{n=1}^{\infty } x_n \otimes y_n^*$
and
![]() $T \in \mathcal {L}(E, F)$
. It is well known that D is a surjective map (see, for example, [Reference Defant and Floret8, Section 5.5, pg. 62]). Therefore, we have that
$T \in \mathcal {L}(E, F)$
. It is well known that D is a surjective map (see, for example, [Reference Defant and Floret8, Section 5.5, pg. 62]). Therefore, we have that
![]() $(\mathcal {L}(E, F), \tau _c)^* =( E \widehat {\otimes }_\pi F^* )/ \ker D.$
On the other hand, from the result [Reference Feder and Saphar12, Theorem 1], we have that the map
$(\mathcal {L}(E, F), \tau _c)^* =( E \widehat {\otimes }_\pi F^* )/ \ker D.$
On the other hand, from the result [Reference Feder and Saphar12, Theorem 1], we have that the map
![]() $V: E \widehat {\otimes }_\pi F^* \longrightarrow (\mathcal {K}(E, F), \|\cdot \|)^*$
defined by
$V: E \widehat {\otimes }_\pi F^* \longrightarrow (\mathcal {K}(E, F), \|\cdot \|)^*$
defined by
![]() $V(z)(T) := \sum _{n=1}^{\infty } y_n^*(T(x_n))$
for
$V(z)(T) := \sum _{n=1}^{\infty } y_n^*(T(x_n))$
for
![]() $z = \sum _{n=1}^{\infty } x_n \otimes y_n^*$
and
$z = \sum _{n=1}^{\infty } x_n \otimes y_n^*$
and
![]() $T \in \mathcal {K}(E, F)$
satisfies the following: for every
$T \in \mathcal {K}(E, F)$
satisfies the following: for every
![]() $\varphi \in (\mathcal {K}(E, F), \|\cdot \|)^*$
, there exists
$\varphi \in (\mathcal {K}(E, F), \|\cdot \|)^*$
, there exists
![]() $v \in E \widehat {\otimes }_\pi F^*$
such that
$v \in E \widehat {\otimes }_\pi F^*$
such that
![]() $\varphi = V(v)$
and
$\varphi = V(v)$
and
![]() $\|\varphi \| = \|v\|$
. In particular, we have that
$\|\varphi \| = \|v\|$
. In particular, we have that
![]() $(\mathcal {K}(E, F), \|\cdot \|)^* = (E \widehat {\otimes }_\pi F^*) / \ker V$
. Thus, if
$(\mathcal {K}(E, F), \|\cdot \|)^* = (E \widehat {\otimes }_\pi F^*) / \ker V$
. Thus, if
![]() $\mathcal {K}(E, F) = \mathcal {L}(E, F)$
, then
$\mathcal {K}(E, F) = \mathcal {L}(E, F)$
, then
![]() $D(z)(T) = V(z)(T)$
for every
$D(z)(T) = V(z)(T)$
for every
![]() $z \in E \widehat {\otimes }_\pi F^*$
and every
$z \in E \widehat {\otimes }_\pi F^*$
and every
![]() $T \in \mathcal {K}(E, F)$
; hence,
$T \in \mathcal {K}(E, F)$
; hence,
![]() $\ker D = \ker V$
and
$\ker D = \ker V$
and
![]() $(\mathcal {L}(E,F), \| \cdot \|)^* =(\mathcal {L}(E, F), \tau _c)^*$
. □
$(\mathcal {L}(E,F), \| \cdot \|)^* =(\mathcal {L}(E, F), \tau _c)^*$
. □
Let us now go towards the proof of Theorem B. We show the following result, which will help us to prove that if
![]() $(E, F)$
does not satisfy the James property, then
$(E, F)$
does not satisfy the James property, then
 $\overline {B_{\mathcal {K}(E, F)}}^{SOT}$
coincides with
$\overline {B_{\mathcal {K}(E, F)}}^{SOT}$
coincides with
![]() $B_{\mathcal {K}(E, F)}$
. Recall that the sequential closure of a set in a topological space is the family of all limit points of sequences on the set in consideration.
$B_{\mathcal {K}(E, F)}$
. Recall that the sequential closure of a set in a topological space is the family of all limit points of sequences on the set in consideration.
Lemma 3.3. Let E and F be Banach spaces. Suppose that there exists a norm-closed convex set
![]() $C \subseteq \mathcal {L}(E, F)$
that is not sequentially closed in the strong operator topology. Then
$C \subseteq \mathcal {L}(E, F)$
that is not sequentially closed in the strong operator topology. Then
![]() $(E, F)$
has the James property.
$(E, F)$
has the James property.
Proof. Suppose that
![]() $C \subseteq \mathcal {L}(E, F)$
is norm-closed but not SOT-sequentially closed. This implies that there exists a sequence of operators
$C \subseteq \mathcal {L}(E, F)$
is norm-closed but not SOT-sequentially closed. This implies that there exists a sequence of operators
![]() $(R_n) \subseteq C$
such that
$(R_n) \subseteq C$
such that
![]() $(R_n)$
converges in the SOT (and therefore in the WOT) to an operator
$(R_n)$
converges in the SOT (and therefore in the WOT) to an operator
![]() $R \notin C$
. We may (and we do) suppose that
$R \notin C$
. We may (and we do) suppose that
![]() $R = 0$
. Set
$R = 0$
. Set
![]() $K:= \{R_n:n \in \mathbb {N}\} \subseteq \mathcal {L}(E, F)$
. Therefore, K is relatively WOT-compact,
$K:= \{R_n:n \in \mathbb {N}\} \subseteq \mathcal {L}(E, F)$
. Therefore, K is relatively WOT-compact,
![]() $0 \in \overline {K}^{WOT}$
but
$0 \in \overline {K}^{WOT}$
but
![]() $0$
cannot be in
$0$
cannot be in
![]() $\overline {\operatorname {\mathrm {co}}}(K)$
by hypothesis. Therefore,
$\overline {\operatorname {\mathrm {co}}}(K)$
by hypothesis. Therefore,
![]() $(E, F)$
has the James property. □
$(E, F)$
has the James property. □
It is not difficult to check that for a bounded subset C of
![]() $\mathcal {L} (E,F)$
, with E separable, the SOT-closure of C coincides with the SOT-sequential closure of C. Namely, if
$\mathcal {L} (E,F)$
, with E separable, the SOT-closure of C coincides with the SOT-sequential closure of C. Namely, if
![]() $D=\{x_n: n \in \mathbb {N}\}$
is a countable norm-dense subset of E and C is a bounded subset of
$D=\{x_n: n \in \mathbb {N}\}$
is a countable norm-dense subset of E and C is a bounded subset of
![]() $\mathcal {L} (E,F)$
with
$\mathcal {L} (E,F)$
with
![]() $T \in \overline {C}^{SOT}$
, then for each
$T \in \overline {C}^{SOT}$
, then for each
![]() $n\in \mathbb {N}$
we can pick
$n\in \mathbb {N}$
we can pick
![]() $T_n \in C$
such that
$T_n \in C$
such that
 $\|T_n(x_m)-T(x_m)\| \leqslant \frac {1}{n}$
for every
$\|T_n(x_m)-T(x_m)\| \leqslant \frac {1}{n}$
for every
![]() $m\leqslant n$
. Because
$m\leqslant n$
. Because
![]() $(T_n)$
is a uniformly bounded sequence of operators converging in norm on a dense set, it follows from a routine computation that
$(T_n)$
is a uniformly bounded sequence of operators converging in norm on a dense set, it follows from a routine computation that
![]() $T_n(x)$
converges in norm to
$T_n(x)$
converges in norm to
![]() $T(x)$
for every
$T(x)$
for every
![]() $x \in E$
, so T is in the SOT-sequential closure of C.
$x \in E$
, so T is in the SOT-sequential closure of C.
Furthermore, the following result shows that the unit ball of
![]() $\mathcal {K} (E,F)$
is SOT-closed if it is SOT-sequentially closed under the assumption that E has the separable complementation property. Recall that a Banach space E is said to have the separable complementation property if for every separable subspace Y in E there is a separable subspace Z with
$\mathcal {K} (E,F)$
is SOT-closed if it is SOT-sequentially closed under the assumption that E has the separable complementation property. Recall that a Banach space E is said to have the separable complementation property if for every separable subspace Y in E there is a separable subspace Z with
![]() $Y \subseteq Z \subseteq E$
and Z is complemented in E. It is worth mentioning that D. Amir and J. Lindenstrauss proved in [Reference Amir and Lindenstrauss2] that every weakly compactly generated Banach space (and therefore every reflexive space) has the separable complementation property.
$Y \subseteq Z \subseteq E$
and Z is complemented in E. It is worth mentioning that D. Amir and J. Lindenstrauss proved in [Reference Amir and Lindenstrauss2] that every weakly compactly generated Banach space (and therefore every reflexive space) has the separable complementation property.
Lemma 3.4. Let E be a Banach space with the separable complementation property and F be an arbitrary Banach space. Then, the unit ball
![]() $B_{\mathcal {K}(E,F)}$
is SOT-closed if and only if it is SOT-sequentially closed.
$B_{\mathcal {K}(E,F)}$
is SOT-closed if and only if it is SOT-sequentially closed.
Proof. It is enough to check that if
![]() $B_{\mathcal {K}(E,F)}$
is not SOT-closed then it is not SOT-sequentially closed. Suppose that T is an operator that belongs to the SOT-closure of
$B_{\mathcal {K}(E,F)}$
is not SOT-closed then it is not SOT-sequentially closed. Suppose that T is an operator that belongs to the SOT-closure of
![]() $B_{\mathcal {K}(E,F)}$
but not to
$B_{\mathcal {K}(E,F)}$
but not to
![]() $B_{\mathcal {K}(E,F)}$
. Note that T is noncompact; hence, there exists a separable subspace
$B_{\mathcal {K}(E,F)}$
. Note that T is noncompact; hence, there exists a separable subspace
![]() $E_0$
of E such that
$E_0$
of E such that
![]() $T|_{E_0}$
is noncompact. Choose a separable subspace Z of E such that
$T|_{E_0}$
is noncompact. Choose a separable subspace Z of E such that
![]() $E_0 \subseteq Z \subseteq E$
and Z is complemented in E. Note that
$E_0 \subseteq Z \subseteq E$
and Z is complemented in E. Note that
![]() $T|_{Z}$
is noncompact and belongs to the SOT-closure of
$T|_{Z}$
is noncompact and belongs to the SOT-closure of
![]() $B_{\mathcal {K} (Z, F)}$
. Because Z is separable, we have that
$B_{\mathcal {K} (Z, F)}$
. Because Z is separable, we have that
![]() $T|_Z$
is indeed in the SOT-sequential closure of
$T|_Z$
is indeed in the SOT-sequential closure of
![]() $B_{\mathcal {K} (Z,F)}$
. Let
$B_{\mathcal {K} (Z,F)}$
. Let
![]() $(K_n)$
be a sequence in
$(K_n)$
be a sequence in
![]() $B_{\mathcal {K} (Z,F)}$
converging to
$B_{\mathcal {K} (Z,F)}$
converging to
![]() $T|_Z$
in the SOT. Letting P be a projection from E onto Z, it is immediate that
$T|_Z$
in the SOT. Letting P be a projection from E onto Z, it is immediate that
![]() $T|_Z \circ P$
is noncompact and
$T|_Z \circ P$
is noncompact and
![]() $K_n \circ P$
is SOT-convergent to
$K_n \circ P$
is SOT-convergent to
![]() $T|_Z \circ P$
. This proves that
$T|_Z \circ P$
. This proves that
![]() $B_{\mathcal {K}(E,F)}$
is not SOT-sequentially closed. □
$B_{\mathcal {K}(E,F)}$
is not SOT-sequentially closed. □
It is worth mentioning, however, that the SOT-closure and SOT-sequential closure are different in general, as the following remark shows.
Remark 3.5. In general, it is not true that the SOT-sequential closure of a bounded convex set C in
![]() $\mathcal {L}(E,F)$
coincides with the SOT-closure of C. An example is given by
$\mathcal {L}(E,F)$
coincides with the SOT-closure of C. An example is given by
 $$ \begin{align*} C := &\Big\{ T \in B_{\mathcal{L}(\ell_2(\omega_1))} \colon \mbox{there is} \ \alpha<\omega_1 \ \mbox{such that } \left(T(x)\right)_{\beta}=0 \ \mbox{for every} \\ &\quad \beta>\alpha,~x\in \ell_2(\omega_1) \Big\}. \end{align*} $$
$$ \begin{align*} C := &\Big\{ T \in B_{\mathcal{L}(\ell_2(\omega_1))} \colon \mbox{there is} \ \alpha<\omega_1 \ \mbox{such that } \left(T(x)\right)_{\beta}=0 \ \mbox{for every} \\ &\quad \beta>\alpha,~x\in \ell_2(\omega_1) \Big\}. \end{align*} $$
It is immediate that C is SOT-sequentially closed. Nevertheless, because the canonical projections
![]() $P_\alpha \in \mathcal {L}(\ell _2(\omega _1))$
with
$P_\alpha \in \mathcal {L}(\ell _2(\omega _1))$
with
![]() $\alpha <\omega _1$
, defined by
$\alpha <\omega _1$
, defined by
 $\left (P_\alpha (x)\right )_\beta =x_\beta $
if
$\left (P_\alpha (x)\right )_\beta =x_\beta $
if
![]() $\beta \leqslant \alpha $
and
$\beta \leqslant \alpha $
and
![]() $0$
otherwise are in C and satisfy that
$0$
otherwise are in C and satisfy that
![]() $\{P_\alpha \}_{\alpha <\omega _1}$
SOT-converges to the identity, which is not in C, it follows that C is not SOT-closed.
$\{P_\alpha \}_{\alpha <\omega _1}$
SOT-converges to the identity, which is not in C, it follows that C is not SOT-closed.
Notice that if E is reflexive, then it has the separable complementation property. By Lemma 3.4,
![]() $B_{\mathcal {K}(E, F)}$
is SOT-closed if and only if it is SOT-sequentially closed. Therefore, if we assume that
$B_{\mathcal {K}(E, F)}$
is SOT-closed if and only if it is SOT-sequentially closed. Therefore, if we assume that
 $\overline {B_{\mathcal {K}(E, F)}}^{SOT} \not = B_{\mathcal {K}(E, F)}$
, then
$\overline {B_{\mathcal {K}(E, F)}}^{SOT} \not = B_{\mathcal {K}(E, F)}$
, then
![]() $(E, F)$
has the James property by Lemma 3.3. Therefore, we have the following result.
$(E, F)$
has the James property by Lemma 3.3. Therefore, we have the following result.
Proposition 3.6. Let E and F be Banach spaces. If
 $\overline {B_{\mathcal {K}(E, F)}}^{SOT} \not = B_{\mathcal {K}(E, F)}$
, then
$\overline {B_{\mathcal {K}(E, F)}}^{SOT} \not = B_{\mathcal {K}(E, F)}$
, then
![]() $(E, F)$
has the James property.
$(E, F)$
has the James property.
In order to prove Theorem B, we also need the following lemma. We thank Miguel Martín and one of the anonymous referees for suggesting the use of the pointwise-BCAP instead of the BCAP in the following lemma.
Lemma 3.7. Let E and F be Banach spaces. Suppose that the pair
![]() $(E,F)$
has the pointwise-BCAP. Then
$(E,F)$
has the pointwise-BCAP. Then
![]() $\mathcal {K} (E,F) = \mathcal {L}(E,F)$
if and only if the unit ball
$\mathcal {K} (E,F) = \mathcal {L}(E,F)$
if and only if the unit ball
![]() $B_{\mathcal {K}(E,F)}$
is SOT-closed.
$B_{\mathcal {K}(E,F)}$
is SOT-closed.
Proof. First, note that because the pair
![]() $(E,F)$
has the pointwise-BCAP, we have
$(E,F)$
has the pointwise-BCAP, we have
 $\mathcal {L}(E,F)=\bigcup _{\lambda>0} \lambda \overline { B_{\mathcal {K}(E,F)}}^{\tau _c}$
. Because
$\mathcal {L}(E,F)=\bigcup _{\lambda>0} \lambda \overline { B_{\mathcal {K}(E,F)}}^{\tau _c}$
. Because
 $\overline { B_{\mathcal {K}(E,F)}}^{\tau _c} \subseteq \overline { B_{\mathcal {K}(E,F)}}^{SOT}$
, we have that
$\overline { B_{\mathcal {K}(E,F)}}^{\tau _c} \subseteq \overline { B_{\mathcal {K}(E,F)}}^{SOT}$
, we have that
 $\mathcal {L}(E,F)=\bigcup _{\lambda>0} \lambda \overline { B_{\mathcal {K}(E,F)}}^{SOT}.$
So, if we assume
$\mathcal {L}(E,F)=\bigcup _{\lambda>0} \lambda \overline { B_{\mathcal {K}(E,F)}}^{SOT}.$
So, if we assume
![]() $B_{\mathcal {K}(E,F)}$
to be SOT-closed, then
$B_{\mathcal {K}(E,F)}$
to be SOT-closed, then
 $$ \begin{align*} \mathcal{L}(E,F)= \bigcup_{\lambda>0} \lambda\overline{ B_{\mathcal{K}(E,F)}}^{SOT}=\bigcup_{\lambda>0} \lambda B_{\mathcal{K}(E,F)} =\mathcal{K}(E,F). \end{align*} $$
$$ \begin{align*} \mathcal{L}(E,F)= \bigcup_{\lambda>0} \lambda\overline{ B_{\mathcal{K}(E,F)}}^{SOT}=\bigcup_{\lambda>0} \lambda B_{\mathcal{K}(E,F)} =\mathcal{K}(E,F). \end{align*} $$
The other implication is immediate. □
Let us finally recall the following conditions and prove Theorem B as a consequence of Theorem A, Proposition 3.1, Proposition 3.2, Proposition 3.6 and Lemma 3.7.
-
(a)
 $\mathcal {K}(E, F) = \mathcal {L}(E, F)$
.
$\mathcal {K}(E, F) = \mathcal {L}(E, F)$
. -
(b) Every operator from E into F attains its norm.
-
(c) The unit ball
 $B_{\mathcal {K}(E, F)}$
is closed in the strong operator topology.
$B_{\mathcal {K}(E, F)}$
is closed in the strong operator topology. -
(d)
 $(\mathcal {L}(E,F), \tau _c)^* = (\mathcal {L}(E, F), \left \Vert \cdot \right \Vert )^*$
.
$(\mathcal {L}(E,F), \tau _c)^* = (\mathcal {L}(E, F), \left \Vert \cdot \right \Vert )^*$
.
Proof of Theorem B. Let E be reflexive and F be an arbitrary Banach space. It was noted in the Introduction that (a)
![]() $\Longrightarrow $
(b) holds. Moreover, (b) implies that
$\Longrightarrow $
(b) holds. Moreover, (b) implies that
![]() $(E,F)$
does not have the James property (by applying Theorem A), which in turn implies (c) (by applying Proposition 3.6). On the other hand, Proposition 3.2 shows (a)
$(E,F)$
does not have the James property (by applying Theorem A), which in turn implies (c) (by applying Proposition 3.6). On the other hand, Proposition 3.2 shows (a)
![]() $\Longrightarrow $
(d). By Proposition 3.1, (d) implies that
$\Longrightarrow $
(d). By Proposition 3.1, (d) implies that
![]() $(E,F)$
does not have the James Property and, therefore, it implies (c) (by applying Proposition 3.6). Finally, if the pair
$(E,F)$
does not have the James Property and, therefore, it implies (c) (by applying Proposition 3.6). Finally, if the pair
![]() $(E,F)$
has the BCAP, then the implication (c)
$(E,F)$
has the BCAP, then the implication (c)
![]() $\Longrightarrow $
(a) follows from Lemma 3.7 and all statements (a)–(d) are equivalent. □
$\Longrightarrow $
(a) follows from Lemma 3.7 and all statements (a)–(d) are equivalent. □
M.I. Ostrovskii asked in [Reference Maslyuchenko and Plichko24, §12, pg. 65] whether there exist infinite-dimensional Banach spaces on which every operator attains its norm (this question is also asked in [Reference Khatskevich, Ostrovskii and Shulman20, Problem 8] and [Reference Guirao, Montesinos and Zizler15, Problem 217]). By Holub’s theorem [Reference Holub16], if such an infinite-dimensional Banach space exists, it cannot have the AP. Theorem 3.8 is a generalisation of this fact. Let us recall that given a (norm-closed) operator ideal
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\lambda \geqslant 1$
, a Banach space E is said to have the
$\lambda \geqslant 1$
, a Banach space E is said to have the
![]() $\lambda $
-
$\lambda $
-
![]() $\mathcal {A}$
-approximation property (
$\mathcal {A}$
-approximation property (
![]() $\lambda $
-
$\lambda $
-
![]() $\mathcal {A}$
-AP) if the identity operator
$\mathcal {A}$
-AP) if the identity operator
![]() $\operatorname {\mathrm {Id}}_E$
belongs to
$\operatorname {\mathrm {Id}}_E$
belongs to
 $\overline {\{ T \in \mathcal {A} (E,E) : \|T \| \leqslant \lambda \}}^{\tau _c}$
. We say that E has the bounded-
$\overline {\{ T \in \mathcal {A} (E,E) : \|T \| \leqslant \lambda \}}^{\tau _c}$
. We say that E has the bounded-
![]() $\mathcal {A}$
-AP if it has the
$\mathcal {A}$
-AP if it has the
![]() $\lambda $
-
$\lambda $
-
![]() $\mathcal {A}$
-AP for some
$\mathcal {A}$
-AP for some
![]() $\lambda \geqslant 1$
. This general approximation property has been studied, for instance, in [Reference Grønbœk and Willis13, Reference Lima and Oja21, Reference Oja26, Reference Reinov29].
$\lambda \geqslant 1$
. This general approximation property has been studied, for instance, in [Reference Grønbœk and Willis13, Reference Lima and Oja21, Reference Oja26, Reference Reinov29].
Theorem 3.8. If there is an infinite-dimensional Banach space E such that every operator on
![]() $\mathcal {L}(E)$
attains its norm, then E does not have the bounded
$\mathcal {L}(E)$
attains its norm, then E does not have the bounded
![]() $\mathcal {A}$
-approximation property for any nontrivial ideal
$\mathcal {A}$
-approximation property for any nontrivial ideal
![]() $\mathcal {A}$
(i.e., for any ideal
$\mathcal {A}$
(i.e., for any ideal
![]() $\mathcal {A}\neq \mathcal {L}(E)$
).
$\mathcal {A}\neq \mathcal {L}(E)$
).
Proof. As highlighted in [Reference Maslyuchenko and Plichko24, §12, pg. 66], due to a result of N.J. Kalton, if such a Banach space E exists, then it must be separable. Therefore, the SOT-closure of the set
![]() $B := \{T \in \mathcal {A} (E,E) : \|T \| \leqslant 1\}$
in
$B := \{T \in \mathcal {A} (E,E) : \|T \| \leqslant 1\}$
in
![]() $\mathcal {L}(E)$
coincides with its SOT-sequential closure. Thus, if every operator on
$\mathcal {L}(E)$
coincides with its SOT-sequential closure. Thus, if every operator on
![]() $\mathcal {L}(E)$
attains its norm, then B is SOT-closed by Lemma 3.3. Suppose that E has the bounded
$\mathcal {L}(E)$
attains its norm, then B is SOT-closed by Lemma 3.3. Suppose that E has the bounded
![]() $\mathcal {A}$
-approximation property. Then, because
$\mathcal {A}$
-approximation property. Then, because
 $\overline {B}^{\tau _c} \subseteq \overline {B}^{SOT}=B $
, we have that B contains a multiple of the identity and therefore
$\overline {B}^{\tau _c} \subseteq \overline {B}^{SOT}=B $
, we have that B contains a multiple of the identity and therefore
![]() $\mathcal {A}$
contains the identity on E, so
$\mathcal {A}$
contains the identity on E, so
![]() $\mathcal {A}=\mathcal {L}(E)$
. □
$\mathcal {A}=\mathcal {L}(E)$
. □
We finally present the proof of Theorem C as a direct consequence of Theorem B and Proposition 3.9. Recall that a Banach space E has the Schur property if every weakly convergent sequence is norm convergent. It is known that a Banach space F has the Schur property if and only if every weakly compact operator from E into F is compact for any Banach space E (see, for example, [Reference Pietsch28, Section 3.2, pg. 61]). Also, it is proved in [Reference Dowling, Freeman, Lennard, Odell, Randrianantoanina and Turett9, Theorem 1] that a Banach space F has the Schur property if and only if the weak Grothendieck compactness principle holds in F; that is, every weakly compact subset of F is contained in the closed convex hull of a weakly null sequence. Then W.B. Johnson et al. gave an alternative proof in [Reference Johnson, Lillemets and Oja19, Theorem 1.1] for this result by using the Davis-Figiel-Johnson-Pełczyński factorisation theorem [Reference Davis, Figiel, Johnson and Pełczyński7]. Moreover, it was observed in [Reference Johnson, Lillemets and Oja19, Theorem 3.3] that a Banach space F has the Schur property if and only if
![]() $\mathcal {W}_\infty (E, F) \subseteq \mathcal {W} (E,F)$
for every Banach space E (see the precise definition of these sets just after Proposition 3.9).
$\mathcal {W}_\infty (E, F) \subseteq \mathcal {W} (E,F)$
for every Banach space E (see the precise definition of these sets just after Proposition 3.9).
The following result will be used as an important tool in the proof of Theorem 3.10.
Proposition 3.9. Let F be a Banach space. If F fails to have the Schur property, then there exists a reflexive space with basis E such that
![]() $\mathcal {K}(E,F) \neq \mathcal {L}(E,F)$
.
$\mathcal {K}(E,F) \neq \mathcal {L}(E,F)$
.
Proof. Take
![]() $(x_n) \subseteq S_F$
to be a weakly null sequence in F, which is not norm null. Because the absolute closed convex hull of
$(x_n) \subseteq S_F$
to be a weakly null sequence in F, which is not norm null. Because the absolute closed convex hull of
![]() $\{x_n: n \in \mathbb {N}\}$
is weakly compact, the operator
$\{x_n: n \in \mathbb {N}\}$
is weakly compact, the operator
![]() $T \in \mathcal {L}(\ell _1 ,F)$
given by
$T \in \mathcal {L}(\ell _1 ,F)$
given by
![]() $T (e_n) := x_n$
for each
$T (e_n) := x_n$
for each
![]() $n \in \mathbb {N}$
defines a weakly compact operator (which is not compact). By the Davis-Figiel-Johnson-Pełczyński factorisation theorem [Reference Davis, Figiel, Johnson and Pełczyński7], there exists a reflexive space
$n \in \mathbb {N}$
defines a weakly compact operator (which is not compact). By the Davis-Figiel-Johnson-Pełczyński factorisation theorem [Reference Davis, Figiel, Johnson and Pełczyński7], there exists a reflexive space
![]() $E_0$
such that
$E_0$
such that
![]() $T= S \circ R$
, where
$T= S \circ R$
, where
![]() $R \in \mathcal {L}(\ell _1, E_0)$
and
$R \in \mathcal {L}(\ell _1, E_0)$
and
![]() $S \in \mathcal {L}(E_0, F)$
. In particular, note that S cannot be a compact operator. Now, pick a weakly null sequence
$S \in \mathcal {L}(E_0, F)$
. In particular, note that S cannot be a compact operator. Now, pick a weakly null sequence
![]() $(v_n) \subseteq E_0$
so that
$(v_n) \subseteq E_0$
so that
![]() $S(v_n)$
does not admit a convergent subsequence. Because
$S(v_n)$
does not admit a convergent subsequence. Because
![]() $(v_n)$
is weakly null, consider a subsequence that is a basic sequence of
$(v_n)$
is weakly null, consider a subsequence that is a basic sequence of
![]() $E_0$
(see [Reference Albiac and Kalton1, Proposition 1.5.4]) and denote it again by
$E_0$
(see [Reference Albiac and Kalton1, Proposition 1.5.4]) and denote it again by
![]() $(v_n)$
. Let
$(v_n)$
. Let
![]() $E := \overline {\operatorname {span}} \{v_n\}_{n \in \mathbb {N}}$
. Then, E is a closed reflexive space with basis and
$E := \overline {\operatorname {span}} \{v_n\}_{n \in \mathbb {N}}$
. Then, E is a closed reflexive space with basis and
![]() $S(v_n)$
does not admit a convergent subsequence. Therefore, we conclude that
$S(v_n)$
does not admit a convergent subsequence. Therefore, we conclude that
![]() $\mathcal {K}(E, F) \not = \mathcal {L}(E, F)$
. □
$\mathcal {K}(E, F) \not = \mathcal {L}(E, F)$
. □
Compared to the previously known results in [Reference Johnson, Lillemets and Oja19], Theorem 3.10 not only provides a new characterisation of the Schur property in terms of norm-attaining operators but also shows that we can restrict the possible candidates for a domain space as in the below items (f)–(i) by considering only reflexive Banach spaces with basis. Recall that
![]() $T \in \mathcal {L} (E,F)$
is completely continuous if T sends weakly null sequences in E to norm null sequences in F. We denote by
$T \in \mathcal {L} (E,F)$
is completely continuous if T sends weakly null sequences in E to norm null sequences in F. We denote by
![]() $\mathcal {V}(E,F)$
the space of all completely continuous operators from E into F. Let us denote by
$\mathcal {V}(E,F)$
the space of all completely continuous operators from E into F. Let us denote by
![]() $\mathcal {W}_\infty (E,F)$
the space of all weakly
$\mathcal {W}_\infty (E,F)$
the space of all weakly
![]() $\infty $
-compact operators from E into F, which are introduced in [Reference Sinha and Karn31]. A subset C of a Banach space E is called relatively weakly
$\infty $
-compact operators from E into F, which are introduced in [Reference Sinha and Karn31]. A subset C of a Banach space E is called relatively weakly
![]() $\infty $
-compact if there exists a weakly null sequence
$\infty $
-compact if there exists a weakly null sequence
![]() $(x_n)$
in E such that
$(x_n)$
in E such that
![]() $C \subseteq \{ \sum _{n=1}^\infty a_n x_n : (a_n) \in B_{\ell _1} \}$
and an operator
$C \subseteq \{ \sum _{n=1}^\infty a_n x_n : (a_n) \in B_{\ell _1} \}$
and an operator
![]() $T \in \mathcal {L} (E,F)$
is said to be weakly
$T \in \mathcal {L} (E,F)$
is said to be weakly
![]() $\infty $
-compact if
$\infty $
-compact if
![]() $T(B_E)$
is a relatively weakly
$T(B_E)$
is a relatively weakly
![]() $\infty $
-compact subset of F.
$\infty $
-compact subset of F.
It is immediate to notice that Theorem C follows from Theorem 3.10.
Theorem 3.10. Let F be an arbitrary Banach space. The following are equivalent:
-
(a) F has the Schur property.
-
(b)
 $\mathcal {K}(E, F) = \mathcal {L}(E, F)$
for every reflexive space E.
$\mathcal {K}(E, F) = \mathcal {L}(E, F)$
for every reflexive space E. -
(c)
 $\mathcal {W}_\infty (E,F) = \mathcal {L} (E,F)$
for every reflexive space E.
$\mathcal {W}_\infty (E,F) = \mathcal {L} (E,F)$
for every reflexive space E. -
(d)
 $\mathcal {V} (E,F) = \mathcal {L}(E,F)$
for every reflexive space E.
$\mathcal {V} (E,F) = \mathcal {L}(E,F)$
for every reflexive space E. -
(e)
 $\operatorname {NA}(E, F) = \mathcal {L}(E, F)$
for every reflexive space E.
$\operatorname {NA}(E, F) = \mathcal {L}(E, F)$
for every reflexive space E. -
(f)
 $\mathcal {K} (G, F) = \mathcal {L} (G, F)$
for every reflexive space G with basis.
$\mathcal {K} (G, F) = \mathcal {L} (G, F)$
for every reflexive space G with basis. -
(g)
 $\operatorname {NA} (G,F) = \mathcal {L} (G,F)$
for every reflexive space G with basis.
$\operatorname {NA} (G,F) = \mathcal {L} (G,F)$
for every reflexive space G with basis. -
(h)
 $\mathcal {W}_\infty (G, F) = \mathcal {L} (G, F)$
for every reflexive space G with basis.
$\mathcal {W}_\infty (G, F) = \mathcal {L} (G, F)$
for every reflexive space G with basis. -
(i)
 $\mathcal {V}(G,F) = \mathcal {L} (G, F)$
for every reflexive space G with basis.
$\mathcal {V}(G,F) = \mathcal {L} (G, F)$
for every reflexive space G with basis.
Proof. The following diagram holds.

Indeed, by definition we have that
![]() $\mathcal {K}(E,F) \subseteq \mathcal {W}_\infty (E,F) \subseteq \mathcal {W} (E,F)$
for any Banach space E and F, and it is also known that
$\mathcal {K}(E,F) \subseteq \mathcal {W}_\infty (E,F) \subseteq \mathcal {W} (E,F)$
for any Banach space E and F, and it is also known that
![]() $\mathcal {K}(E,F) \subseteq \mathcal {W}_\infty (E,F) \subseteq \mathcal {V} (E,F)$
(see [Reference Johnson, Lillemets and Oja19, Proposition 3.1]). Moreover, if T is an element of
$\mathcal {K}(E,F) \subseteq \mathcal {W}_\infty (E,F) \subseteq \mathcal {V} (E,F)$
(see [Reference Johnson, Lillemets and Oja19, Proposition 3.1]). Moreover, if T is an element of
![]() $\mathcal {V}(E,F)$
with E reflexive, then
$\mathcal {V}(E,F)$
with E reflexive, then
![]() $T \in \operatorname {NA} (E,F)$
thanks to the weak sequential compactness of
$T \in \operatorname {NA} (E,F)$
thanks to the weak sequential compactness of
![]() $B_E$
. Thus, it is immediate that (a)
$B_E$
. Thus, it is immediate that (a)
![]() $\Longrightarrow $
(b)
$\Longrightarrow $
(b)
![]() $\Longrightarrow $
(c)
$\Longrightarrow $
(c)
![]() $\Longrightarrow $
(d)
$\Longrightarrow $
(d)
![]() $\Longrightarrow $
(e)
$\Longrightarrow $
(e)
![]() $\Longrightarrow $
(g) and (c)
$\Longrightarrow $
(g) and (c)
![]() $\Longrightarrow $
(h)
$\Longrightarrow $
(h)
![]() $\Longrightarrow $
(i)
$\Longrightarrow $
(i)
![]() $\Longrightarrow $
(g) hold. Because a reflexive Banach space with basis has the MAP, (f)
$\Longrightarrow $
(g) hold. Because a reflexive Banach space with basis has the MAP, (f)
![]() $\Longleftrightarrow $
(g) follows from Theorem B. Finally, (f)
$\Longleftrightarrow $
(g) follows from Theorem B. Finally, (f)
![]() $\Longrightarrow $
(a) is already obtained by Proposition 3.9. □
$\Longrightarrow $
(a) is already obtained by Proposition 3.9. □
Questions and comments. Let us conclude the article by recalling some open problems. In [Reference Holub16], Holub conjectured that if E and F are both reflexive, then
![]() $\mathcal {L}(E,F)$
is reflexive if and only if
$\mathcal {L}(E,F)$
is reflexive if and only if
![]() $\mathcal {L}(E,F)=\mathcal {K}(E,F)=NA(E,F)$
. We do not know whether, in general, when E and F are both reflexive spaces all of the implications in the diagram of the Introduction are indeed equivalences. A similar open question posed by Miguel Martín and one of the anonymous referees asks whether Theorem A is in general an equivalence; that is, whether a pair
$\mathcal {L}(E,F)=\mathcal {K}(E,F)=NA(E,F)$
. We do not know whether, in general, when E and F are both reflexive spaces all of the implications in the diagram of the Introduction are indeed equivalences. A similar open question posed by Miguel Martín and one of the anonymous referees asks whether Theorem A is in general an equivalence; that is, whether a pair
![]() $(E,F)$
has the James property whenever there exists a non-norm-attaining operator in
$(E,F)$
has the James property whenever there exists a non-norm-attaining operator in
![]() $\mathcal {L}(E,F)$
. Note that James proved that this implication holds when E is separable and
$\mathcal {L}(E,F)$
. Note that James proved that this implication holds when E is separable and
![]() $F=\mathbb {R}$
(recall the paragraph preceding Definition 1.1).
$F=\mathbb {R}$
(recall the paragraph preceding Definition 1.1).
Acknowledgements
We thank José Rodríguez for suggesting Definition 1.1 and the use of Pfitzner’s theorem to strengthen and simplify part of the content of the article. We are also grateful to Miguel Martín and anonymous referees for pointing out that only the pointwise-BCAP is needed in the proof of Lemma 3.7 and for several helpful suggestions. Finally, we thank Richard Aron, Gilles Godefroy and Manuel Maestre for fruitful conversations on the topic of the present article.
S. Dantas was supported by the Spanish AEI Project PID2019-106529GB-I00/AEI/10.13039/501100011033, by PGC2018-093794-B-I00 (MCIU/AEI/FEDER, UE), by the project OPVVV CAAS CZ.02.1.01/0.0/0.0/16_019/0000778 and by the Estonian Research Council grant PRG877. The second author was supported by the NRF (NRF-2019R1A2C1003857). The third author was partially supported by Fundación Séneca (20797/PI/18), Agencia Estatal de Investigación (MTM2017-86182-P, cofunded by ERDF, EU) and the European Social Fund (ESF) and the Youth European Initiative (YEI) under Fundación Séneca (21319/PDGI/19).