Article contents
PERIODS OF DRINFELD MODULES AND LOCAL SHTUKAS WITH COMPLEX MULTIPLICATION
Published online by Cambridge University Press: 20 March 2018
Abstract
Colmez [Périodes des variétés abéliennes a multiplication complexe, Ann. of Math. (2)138(3) (1993), 625–683; available at http://www.math.jussieu.fr/∼colmez] conjectured a product formula for periods of abelian varieties over number fields with complex multiplication and proved it in some cases. His conjecture is equivalent to a formula for the Faltings height of CM abelian varieties in terms of the logarithmic derivatives at 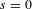 $s=0$ of certain Artin
$s=0$ of certain Artin  $L$-functions. In a series of articles we investigate the analog of Colmez’s theory in the arithmetic of function fields. There abelian varieties are replaced by Drinfeld modules and their higher-dimensional generalizations, so-called
$L$-functions. In a series of articles we investigate the analog of Colmez’s theory in the arithmetic of function fields. There abelian varieties are replaced by Drinfeld modules and their higher-dimensional generalizations, so-called  $A$-motives. In the present article we prove the product formula for the Carlitz module and we compute the valuations of the periods of a CM
$A$-motives. In the present article we prove the product formula for the Carlitz module and we compute the valuations of the periods of a CM  $A$-motive at all finite places in terms of Artin
$A$-motive at all finite places in terms of Artin  $L$-series. The latter is achieved by investigating the local shtukas associated with the
$L$-series. The latter is achieved by investigating the local shtukas associated with the  $A$-motive.
$A$-motive.
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 1 , January 2020 , pp. 175 - 208
- Copyright
- © The Author(s) 2018. Published by Cambridge University Press
Footnotes
Both authors acknowledge support by the Deutsche Forschungsgemeinschaft (DFG) in form of SFB 878.
References
A correction has been issued for this article:
- 4
- Cited by
Linked content
Please note a has been issued for this article.


