Article contents
POINCARÉ AND SOBOLEV INEQUALITIES FOR DIFFERENTIAL FORMS IN HEISENBERG GROUPS AND CONTACT MANIFOLDS
Published online by Cambridge University Press: 29 June 2020
Abstract
In this paper, we prove contact Poincaré and Sobolev inequalities in Heisenberg groups 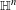 $\mathbb{H}^{n}$, where the word ‘contact’ is meant to stress that de Rham’s exterior differential is replaced by the exterior differential of the so-called Rumin complex
$\mathbb{H}^{n}$, where the word ‘contact’ is meant to stress that de Rham’s exterior differential is replaced by the exterior differential of the so-called Rumin complex 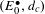 $(E_{0}^{\bullet },d_{c})$, which recovers the scale invariance under the group dilations associated with the stratification of the Lie algebra of
$(E_{0}^{\bullet },d_{c})$, which recovers the scale invariance under the group dilations associated with the stratification of the Lie algebra of 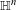 $\mathbb{H}^{n}$. In addition, we construct smoothing operators for differential forms on sub-Riemannian contact manifolds with bounded geometry, which act trivially on cohomology. For instance, this allows us to replace a closed form, up to adding a controlled exact form, with a much more regular differential form.
$\mathbb{H}^{n}$. In addition, we construct smoothing operators for differential forms on sub-Riemannian contact manifolds with bounded geometry, which act trivially on cohomology. For instance, this allows us to replace a closed form, up to adding a controlled exact form, with a much more regular differential form.
Keywords
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 2
- Cited by



