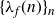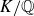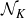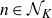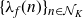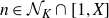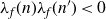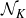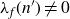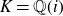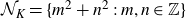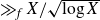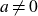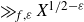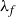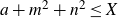1. Introduction
The study of sign patterns of real-valued multiplicative functions at consecutive integers has received a lot of attention in recent years, as a means of investigating the apparently random behaviour of multiplicative functions in interactions with additive patterns of integers. Of classical, as well as modern, interest is the particular collection of multiplicative functions that arise from the sequence of Fourier coefficients of a normalised Hecke eigencusp form f of some weight and level. Here, we study the case of forms with level 1 and without complex multiplication. In the sequel, for such a cusp form f of weight k and level 1 we write
where, as usual
![]() $e(z) \;:\!=\; e^{2\pi i z}$
for
$e(z) \;:\!=\; e^{2\pi i z}$
for
![]() $z \in \mathbb{C}$
. In this case the sequence
$z \in \mathbb{C}$
. In this case the sequence
![]() $\{\lambda_f(n)\}_n$
is real, and it is natural to study its sign changes, i.e., the set of n for which
$\{\lambda_f(n)\}_n$
is real, and it is natural to study its sign changes, i.e., the set of n for which
![]() $\lambda_f(n)\lambda_f(n+1) < 0$
.
$\lambda_f(n)\lambda_f(n+1) < 0$
.
A number of works (see e.g., [Reference Kowalski, Lau, Soundararajan and Wu6, Reference Lamzouri7]) have explored the relationship between the distribution of signs and sign changes of Fourier coefficients of cusp forms and the least quadratic non-residue problem modulo primes p. Moreover, in the spirit of exploring the mass distribution of Hecke–Maass cusp forms in the weight aspect, Ghosh and Sarnak [ Reference Ghosh and Sarnak2 ] exhibited a relationship between the distribution of “real zeros” of such forms and counts for sign changes of their coefficients.
Improving on work of Lau and Wu [
Reference Lau and Wu8
], Matomäki and Radziwiłł [
Reference Matomäki and Radziwiłł12
] obtained the optimal result that there are
![]() $\gg_f X$
sign changes for the sequence
$\gg_f X$
sign changes for the sequence
![]() $\{\lambda_f(n)\}_{n\leq X}$
. Shortly thereafter, they managed to reprove this result in a much more general context introduced in the breakthrough work [
Reference Matomäki and Radziwiłł13
] on general bounded multiplicative functions g. This new proof is based on relating short and long partial sums of
$\{\lambda_f(n)\}_{n\leq X}$
. Shortly thereafter, they managed to reprove this result in a much more general context introduced in the breakthrough work [
Reference Matomäki and Radziwiłł13
] on general bounded multiplicative functions g. This new proof is based on relating short and long partial sums of
![]() $\text{sign}(g(n))$
(using the convention
$\text{sign}(g(n))$
(using the convention
![]() $\text{sign}(0) = 0$
), discovering that sufficient cancellation in the long partial sums of g imply that in typical short intervals of bounded but large length g must change sign at least once.
$\text{sign}(0) = 0$
), discovering that sufficient cancellation in the long partial sums of g imply that in typical short intervals of bounded but large length g must change sign at least once.
More generally, given a set
![]() $\mathcal{S} \subset \mathbb{N}$
and a map
$\mathcal{S} \subset \mathbb{N}$
and a map
![]() $g\;:\; \mathbb{N} \rightarrow \mathbb{R}$
, by a sign change of g on
$g\;:\; \mathbb{N} \rightarrow \mathbb{R}$
, by a sign change of g on
![]() $\mathcal{S}$
we mean a pair of elements
$\mathcal{S}$
we mean a pair of elements
![]() $n < n'$
of
$n < n'$
of
![]() $\mathcal{S}$
such that
$\mathcal{S}$
such that
![]() $g(n)g(n') < 0$
, and such that any
$g(n)g(n') < 0$
, and such that any
![]() $n < m < n'$
belonging to
$n < m < n'$
belonging to
![]() $\mathcal{S}$
satisfies
$\mathcal{S}$
satisfies
![]() $g(m) = 0$
. One can naturally ask what, if anything, can be said about the sign changes that arise along sparse subsequences of positive integers of arithmetic interest. As an example, in [
Reference Murty14
, theorem 5], M.R. Murty unconditionally estimates the number of sign changes among the prime values
$g(m) = 0$
. One can naturally ask what, if anything, can be said about the sign changes that arise along sparse subsequences of positive integers of arithmetic interest. As an example, in [
Reference Murty14
, theorem 5], M.R. Murty unconditionally estimates the number of sign changes among the prime values
![]() $\{\lambda_f(p)\}_p$
. Using a Hoheisel-type argument, based on zero-density estimates for the corresponding Hecke L-function, he obtains cancellation in the short interval prime sums
$\{\lambda_f(p)\}_p$
. Using a Hoheisel-type argument, based on zero-density estimates for the corresponding Hecke L-function, he obtains cancellation in the short interval prime sums
for
![]() $h < x^{1-\delta}$
and some small
$h < x^{1-\delta}$
and some small
![]() $\delta = \delta(f) > 0$
, enabling him to obtain
$\delta = \delta(f) > 0$
, enabling him to obtain
![]() $\gg_f x^{\delta}$
such sign changes among prime values. We might expect this to be rather far from the truth, and that perhaps there should even be
$\gg_f x^{\delta}$
such sign changes among prime values. We might expect this to be rather far from the truth, and that perhaps there should even be
![]() $\gg_f \pi(x)$
such sign changes
$\gg_f \pi(x)$
such sign changes
![]() $p \leq x$
.
$p \leq x$
.
In this paper, instead of the sequence of primes we will consider the model set of sums of two squares,
as a setting in which strong lower bounds on the number of sign changes can be obtained. This set also reveals itself as a natural choice given the relevance of the generating function for the set of perfect squares, the Jacobi theta function, in the theory of modular forms.
In [
Reference Banerjee and Pandey1
], the authors consider the problem of counting sign changes in the sequence
![]() $\{\lambda_f(n)\}_{n \in \mathcal{N}}$
. They showed that there are
$\{\lambda_f(n)\}_{n \in \mathcal{N}}$
. They showed that there are
![]() $\gg x^{1/8-\varepsilon}$
such sign changes in (x,2x]. Their proof ultimately relies on comparing the partial sums
$\gg x^{1/8-\varepsilon}$
such sign changes in (x,2x]. Their proof ultimately relies on comparing the partial sums
where r(n) denotes the number of representations of n as a sum of two squares, and with
![]() $h = h(x) \geq x^{7/8+\varepsilon}$
. Using a contour integration argument involving Rankin–Selberg L–functions, they derive a contradiction to the assertion that
$h = h(x) \geq x^{7/8+\varepsilon}$
. Using a contour integration argument involving Rankin–Selberg L–functions, they derive a contradiction to the assertion that
![]() $\lambda_f(n) \geq 0$
(say) for all
$\lambda_f(n) \geq 0$
(say) for all
![]() $x < n \leq x+h$
. The structure of
$x < n \leq x+h$
. The structure of
![]() $\mathcal{N}$
(in particular the convolution formula
$\mathcal{N}$
(in particular the convolution formula
![]() ${r}/{4} = 1\ast \chi_{4}$
, where
${r}/{4} = 1\ast \chi_{4}$
, where
![]() $\chi_{4}$
is the non-principal character modulo 4) seems to play a crucial role.
$\chi_{4}$
is the non-principal character modulo 4) seems to play a crucial role.
In view of the result of Matomäki and Radziwiłł mentioned above, even accounting for the sparseness of
![]() $\mathcal{N}$
it seems that one ought to do better, with the optimal result expected to be
$\mathcal{N}$
it seems that one ought to do better, with the optimal result expected to be
![]() $\gg {x}/{\sqrt{\log x}} \asymp |\mathcal{N} \cap [1,x]|$
sign changes in [1, x]. It should be noted that this cannot be achieved by the method of [
Reference Banerjee and Pandey1
], which relies on Deligne’s bound
$\gg {x}/{\sqrt{\log x}} \asymp |\mathcal{N} \cap [1,x]|$
sign changes in [1, x]. It should be noted that this cannot be achieved by the method of [
Reference Banerjee and Pandey1
], which relies on Deligne’s bound
![]() $|\lambda_f(n)| \leq d(n)$
as
$|\lambda_f(n)| \leq d(n)$
as
to obtain a contradiction to the purported non-negativity of
![]() $\lambda_f(n)$
on
$\lambda_f(n)$
on
![]() $[x,x+h]$
. This forces any admissible choice of length
$[x,x+h]$
. This forces any admissible choice of length
![]() $h = h(x)$
to satisfy
$h = h(x)$
to satisfy
![]() $h \geq \exp\left((1+o(1)){\log x}/{\log\log x}\right)$
by invoking pointwise bounds on the divisor function, and the number of sign changes obtained with this argument (as discussed later) is
$h \geq \exp\left((1+o(1)){\log x}/{\log\log x}\right)$
by invoking pointwise bounds on the divisor function, and the number of sign changes obtained with this argument (as discussed later) is
![]() $\gg x/h$
.
$\gg x/h$
.
In this paper, we improve upon the main theorem in [
Reference Banerjee and Pandey1
] by making extensive use of the techniques in the more recent paper [
Reference Matomäki and Radziwiłł11
] of Matomäki and Radziwiłł, which among other things are applicable to sparsely-supported multiplicative functions (of which
![]() $f(n)1_{\mathcal{N}}(n)$
is an example). By additionally incorporating some refinements to these methods from the author’s paper [
Reference Mangerel10
] (which render their results slightly more amenable to the study Fourier coefficients of cusp forms), we in fact obtain the optimal result.
$f(n)1_{\mathcal{N}}(n)$
is an example). By additionally incorporating some refinements to these methods from the author’s paper [
Reference Mangerel10
] (which render their results slightly more amenable to the study Fourier coefficients of cusp forms), we in fact obtain the optimal result.
Corollary 1·1.
Let f be a Hecke eigencusp form without complex multiplication of weight
![]() $k\geq 2$
for the full modular group, and let X be large. Then
$k\geq 2$
for the full modular group, and let X be large. Then
![]() $\mathcal{N} \cap [1,X]$
contains
$\mathcal{N} \cap [1,X]$
contains
![]() $\gg_f {X}/{\sqrt{\log X}}$
sign changes for
$\gg_f {X}/{\sqrt{\log X}}$
sign changes for
![]() $\lambda_f$
.
$\lambda_f$
.
Remark 1·2. The restriction to non-CM holomorphic cusp forms is in place in order to ensure that
![]() $\lambda_f(p) = 0$
only on a sparse set of primes (see e.g. Lemma 2·4 for a more precise statement). It is a classical result of Hecke that for cusp forms f with complex multiplication, asymptotically half of the primes p satisfy
$\lambda_f(p) = 0$
only on a sparse set of primes (see e.g. Lemma 2·4 for a more precise statement). It is a classical result of Hecke that for cusp forms f with complex multiplication, asymptotically half of the primes p satisfy
![]() $\lambda_f(p) = 0$
, and thus the set of n with
$\lambda_f(p) = 0$
, and thus the set of n with
![]() $\lambda_f(n) \neq 0$
, irrespective of the additional condition
$\lambda_f(n) \neq 0$
, irrespective of the additional condition
![]() $n \in \mathcal{N}$
, is already sparse. The arguments in this paper would thus need to be modified by conditioning n to belong to the set of non-vanishing of
$n \in \mathcal{N}$
, is already sparse. The arguments in this paper would thus need to be modified by conditioning n to belong to the set of non-vanishing of
![]() $\lambda_f$
, in order to get a result of a similar flavour to Corollary 1·1, relative to the set of non-vanishing. We believe this is doable, but prefer to leave the resulting extension to the interesting reader.
$\lambda_f$
, in order to get a result of a similar flavour to Corollary 1·1, relative to the set of non-vanishing. We believe this is doable, but prefer to leave the resulting extension to the interesting reader.
Remark 1·3. Our arguments apply more generally to forms f of level
![]() $N > 1$
, provided of course that the coefficients
$N > 1$
, provided of course that the coefficients
![]() $\lambda_f(n)$
are real (in order for the problem of counting sign changes to be sensible).
$\lambda_f(n)$
are real (in order for the problem of counting sign changes to be sensible).
Remark 1·4. It is reasonable to ask whether the above result for holomorphic cusp forms extends to the case of Hecke–Maass cusp. A current challenge in applying the methods of this paper in this context is that it is currently not known whether, for a Hecke–Maass cusp form
![]() $\phi$
, the set of primes p for which
$\phi$
, the set of primes p for which
![]() $\lambda_{\phi}(p) = 0$
is, or is not, sparse, let alone how it distributes in arithmetic progressions (information that we would require to prove an analogue of Corollary 1·1 in this context). Moreover, to apply the results of [
Reference Mangerel10
] we would require lower bounds of the shape
$\lambda_{\phi}(p) = 0$
is, or is not, sparse, let alone how it distributes in arithmetic progressions (information that we would require to prove an analogue of Corollary 1·1 in this context). Moreover, to apply the results of [
Reference Mangerel10
] we would require lower bounds of the shape
 \begin{align*} \sum_{\substack{y < p \leq z \\ \lambda_{\phi}(p) \neq 0}} \frac{1}{p} \geq \alpha \sum_{y < p \leq z} \frac{1}{p} + O\left(\frac{1}{(\log y)^{\beta}}\right),\end{align*}
\begin{align*} \sum_{\substack{y < p \leq z \\ \lambda_{\phi}(p) \neq 0}} \frac{1}{p} \geq \alpha \sum_{y < p \leq z} \frac{1}{p} + O\left(\frac{1}{(\log y)^{\beta}}\right),\end{align*}
where
![]() $0 < \alpha, \beta \leq 1$
, uniformly over
$0 < \alpha, \beta \leq 1$
, uniformly over
![]() $2 \leq y \leq z \leq X$
(see item (ii) above Lemma 2·10). This condition is crucial to counting sign changes in a sparse set like
$2 \leq y \leq z \leq X$
(see item (ii) above Lemma 2·10). This condition is crucial to counting sign changes in a sparse set like
![]() $\mathcal{N}$
using the methods of [
Reference Mangerel10
], in contrast to what is needed to count all sign changes in
$\mathcal{N}$
using the methods of [
Reference Mangerel10
], in contrast to what is needed to count all sign changes in
![]() $\mathbb{N}$
as is done in [
Reference Matomäki and Radziwiłł12
]. As far as the author is aware, proving that such a condition is satisfied for a Hecke–Maass form
$\mathbb{N}$
as is done in [
Reference Matomäki and Radziwiłł12
]. As far as the author is aware, proving that such a condition is satisfied for a Hecke–Maass form
![]() $\phi$
is out of reach by current methods. It would be interesting to know whether the above-mentioned obstacle can be overcome by a different method.
$\phi$
is out of reach by current methods. It would be interesting to know whether the above-mentioned obstacle can be overcome by a different method.
We will actually prove a more general result that provides the optimal number of sign changes in
![]() $\{\lambda_f(n)\}_{\substack{n \in \mathcal{N}_K \\ n \leq X}}$
, where
$\{\lambda_f(n)\}_{\substack{n \in \mathcal{N}_K \\ n \leq X}}$
, where
![]() $\mathcal{N}_K$
is the sequence of positive integers arising as norms of algebraic integers in a number field
$\mathcal{N}_K$
is the sequence of positive integers arising as norms of algebraic integers in a number field
![]() $K/\mathbb{Q}$
. Following Matomäki and Radziwiłł [
Reference Matomäki and Radziwiłł11
, section 1·3], we refer to these as norm forms. An integer n is thus a norm form of K if there is an algebraic integer x in the ring of integers
$K/\mathbb{Q}$
. Following Matomäki and Radziwiłł [
Reference Matomäki and Radziwiłł11
, section 1·3], we refer to these as norm forms. An integer n is thus a norm form of K if there is an algebraic integer x in the ring of integers
![]() $\mathcal{O}_K$
of K such that
$\mathcal{O}_K$
of K such that
![]() $N_K(x) = n$
, where
$N_K(x) = n$
, where
![]() $N_K$
is the norm map on K. As the norm on
$N_K$
is the norm map on K. As the norm on
![]() $K = \mathbb{Q}(i)$
is simply
$K = \mathbb{Q}(i)$
is simply
![]() $N_{\mathbb{Q}(i)}(a+ib) = a^2+b^2$
, we have in the above notation
$N_{\mathbb{Q}(i)}(a+ib) = a^2+b^2$
, we have in the above notation
![]() $\mathcal{N} = \mathcal{N}_{\mathbb{Q}(i)}$
. Define now
$\mathcal{N} = \mathcal{N}_{\mathbb{Q}(i)}$
. Define now
 \begin{align*} \delta_K(X) \;:\!=\; \prod_{\substack{p \leq X \\ p \neq N_K(\mathfrak{a}) \text{ for } \mathfrak{a} \subset \mathcal{O}_K }} \left(1-\frac{1}{p}\right).\end{align*}
\begin{align*} \delta_K(X) \;:\!=\; \prod_{\substack{p \leq X \\ p \neq N_K(\mathfrak{a}) \text{ for } \mathfrak{a} \subset \mathcal{O}_K }} \left(1-\frac{1}{p}\right).\end{align*}
It is known (see e.g., [
Reference Odoni17
]) that
![]() $|\mathcal{N}_K \cap [1,X]| \asymp_K X \delta_K(X)$
. We prove the following:
$|\mathcal{N}_K \cap [1,X]| \asymp_K X \delta_K(X)$
. We prove the following:
Theorem 1·5.
Let
![]() $K/\mathbb{Q}$
be a number field, and let f be a Hecke eigencusp form without complex multiplication of weight
$K/\mathbb{Q}$
be a number field, and let f be a Hecke eigencusp form without complex multiplication of weight
![]() $k \geq 2$
for the full modular group. As
$k \geq 2$
for the full modular group. As
![]() $X\rightarrow \infty$
, the number of sign changes of
$X\rightarrow \infty$
, the number of sign changes of
![]() $\lambda_f$
in
$\lambda_f$
in
![]() $\mathcal{N}_K \cap [1,X]$
is
$\mathcal{N}_K \cap [1,X]$
is
![]() $\gg_{K,f} X\delta_K(X)$
.
$\gg_{K,f} X\delta_K(X)$
.
Returning to the setting of sums of two squares, we may modify the problem slightly by asking about sign changes among other patterns of integers, such as shifted sums
![]() $a + \mathcal{N} = \{a + m^2 + n^2 \;:\; m,n \in \mathbb{N}\}$
, for
$a + \mathcal{N} = \{a + m^2 + n^2 \;:\; m,n \in \mathbb{N}\}$
, for
![]() $a \in \mathbb{Z} \backslash \{0\}$
. In this case, it is more challenging to directly apply tools from multiplicative number theory. Nevertheless, using shifted convolution sum estimates among other techniques, we obtain a lower bound on the number of sign changes of
$a \in \mathbb{Z} \backslash \{0\}$
. In this case, it is more challenging to directly apply tools from multiplicative number theory. Nevertheless, using shifted convolution sum estimates among other techniques, we obtain a lower bound on the number of sign changes of
![]() $\lambda_f$
along
$\lambda_f$
along
![]() $a+\mathcal{N}$
.
$a+\mathcal{N}$
.
Theorem 1·6.
Fix
![]() $a \neq 0$
. Then for any
$a \neq 0$
. Then for any
![]() $\varepsilon > 0$
and X sufficiently large there are
$\varepsilon > 0$
and X sufficiently large there are
![]() $\gg_{\varepsilon} X^{1/2-\varepsilon}$
sign changes for
$\gg_{\varepsilon} X^{1/2-\varepsilon}$
sign changes for
![]() $\lambda_f$
in
$\lambda_f$
in
![]() $(a+\mathcal{N}) \cap [1,X]$
.
$(a+\mathcal{N}) \cap [1,X]$
.
As far as the author is concerned, this is the first non-trivial result on sign changes for shifted sums of two squares (a set of equal sparseness to
![]() $\mathcal{N}$
itself).
$\mathcal{N}$
itself).
1·1. Proof Ideas
1·1·1. Proofs of Theorem 1·5
Let f be a non-CM eigencusp form for
![]() $\text{SL}_2(\mathbb{Z})$
, and let
$\text{SL}_2(\mathbb{Z})$
, and let
![]() $K/ \mathbb{Q}$
be a number field. Denote by
$K/ \mathbb{Q}$
be a number field. Denote by
![]() $\sigma_f(n)$
the sign of
$\sigma_f(n)$
the sign of
![]() $\lambda_f(n)$
, using the convention
$\lambda_f(n)$
, using the convention
![]() $\sigma_f(n) = 0$
whenever
$\sigma_f(n) = 0$
whenever
![]() $\lambda_f(n) = 0$
.
$\lambda_f(n) = 0$
.
Let
![]() $1 \leq h \leq X$
. The proof of Theorem 1·5 follows the strategy of [
Reference Matomäki and Radziwiłł13
, corollary 3], the objective of which is to show that for all but o(X) points
$1 \leq h \leq X$
. The proof of Theorem 1·5 follows the strategy of [
Reference Matomäki and Radziwiłł13
, corollary 3], the objective of which is to show that for all but o(X) points
![]() $x \in [X,2X]$
, for X large, the two averages
$x \in [X,2X]$
, for X large, the two averages
are simultaneously
![]() $ > 0$
. The positivity of the left-hand sum implies the existence of
$ > 0$
. The positivity of the left-hand sum implies the existence of
![]() $x < n_1 \leq x+h$
such that
$x < n_1 \leq x+h$
such that
![]() $\sigma_f(n_1) > 0$
, and similarly that of the right-hand sum implies that
$\sigma_f(n_1) > 0$
, and similarly that of the right-hand sum implies that
![]() $\sigma_f(n_2) < 0$
for some
$\sigma_f(n_2) < 0$
for some
![]() $x < n_2 \leq x+h$
. This gives rise to a sign change in most short intervals
$x < n_2 \leq x+h$
. This gives rise to a sign change in most short intervals
![]() $[x,x+h]$
, and by dissecting [X, 2X] into disjoint such short intervals, yields
$[x,x+h]$
, and by dissecting [X, 2X] into disjoint such short intervals, yields
![]() $\gg X/h$
distinct sign changes.
$\gg X/h$
distinct sign changes.
Of course, as
![]() $\mathcal{N}_K$
is a sparse subset of positive integers containing
$\mathcal{N}_K$
is a sparse subset of positive integers containing
![]() $\asymp \delta_K(X) X$
integers
$\asymp \delta_K(X) X$
integers
![]() $n \in [X,2X]$
, it is not even guaranteed that the above sums have non-empty support unless h is sufficiently large. To avoid this issue we require, in particular, that
$n \in [X,2X]$
, it is not even guaranteed that the above sums have non-empty support unless h is sufficiently large. To avoid this issue we require, in particular, that
![]() $h \geq C \delta_K(X)^{-1}$
, for
$h \geq C \delta_K(X)^{-1}$
, for
![]() $C > 0$
a large constant (depending at most on K and f).
$C > 0$
a large constant (depending at most on K and f).
Depending on the class number of K, the argument must be modified. Consider first when K has class number 1 (this being in particular the case for
![]() $K = \mathbb{Q}(i)$
). Then (by Dedekind’s ideal factorisation theorem) the indicator function
$K = \mathbb{Q}(i)$
). Then (by Dedekind’s ideal factorisation theorem) the indicator function
![]() $1_{\mathcal{N}_K}$
is multiplicative. Now, naturally if we had a means of making the comparison
$1_{\mathcal{N}_K}$
is multiplicative. Now, naturally if we had a means of making the comparison
for typical
![]() $x \in [X,2X]$
and each
$x \in [X,2X]$
and each
![]() $\eta \in \{-1,+1\}$
then our problem becomes substantially easier. The key issue, that of the sparseness of support, is a main obstacle in this comparison. Fortunately, the recent work of Matomäki and Radziwiłł [
Reference Matomäki and Radziwiłł11
] is dedicated to addressing exactly such complications, and may be employed to give such a comparison theorem. Our particular application of their methods is worked out in Section 3.
$\eta \in \{-1,+1\}$
then our problem becomes substantially easier. The key issue, that of the sparseness of support, is a main obstacle in this comparison. Fortunately, the recent work of Matomäki and Radziwiłł [
Reference Matomäki and Radziwiłł11
] is dedicated to addressing exactly such complications, and may be employed to give such a comparison theorem. Our particular application of their methods is worked out in Section 3.
The problem is thus reduced to to one involving mean values of multiplicative functions with sparse support. As we show using work of Wirsing [ Reference Wirsing27 ] and of Tenenbaum [ Reference Tenenbaum23 ], respectively, we may deduce that
Whereas the former bound is of a more classical nature, the latter relies on an understanding (roughly speaking) of the prime sums
 \begin{align*} \sum_{\substack{p \leq X \\ p \in \mathcal{I}_K}} \frac{1-\text{Re}(\sigma_f(p)p^{-it})}{p}, \quad |t| \leq \log X,\end{align*}
\begin{align*} \sum_{\substack{p \leq X \\ p \in \mathcal{I}_K}} \frac{1-\text{Re}(\sigma_f(p)p^{-it})}{p}, \quad |t| \leq \log X,\end{align*}
where
![]() $\mathcal{I}_K$
is a class of ideals of the ring
$\mathcal{I}_K$
is a class of ideals of the ring
![]() $\mathcal{O}_K$
of algebraic integers of K. As a concrete example, when
$\mathcal{O}_K$
of algebraic integers of K. As a concrete example, when
![]() $K = \mathbb{Q}(i)$
and
$K = \mathbb{Q}(i)$
and
![]() $\mathcal{N}_K$
is the sequence of sums of two squares,
$\mathcal{N}_K$
is the sequence of sums of two squares,
![]() $\mathcal{I}_K$
is the set of primes
$\mathcal{I}_K$
is the set of primes
![]() $p \equiv 1 \pmod{4}$
(the collection of primes where
$p \equiv 1 \pmod{4}$
(the collection of primes where
![]() $1_{\mathcal{N}}$
is supported). By employing a (generalisation of a) hybrid Chebotarev-Sato–Tate type estimate due to R.M. Murty and V.K. Murty [
Reference Murty14
], we are able to condition on both the sign of
$1_{\mathcal{N}}$
is supported). By employing a (generalisation of a) hybrid Chebotarev-Sato–Tate type estimate due to R.M. Murty and V.K. Murty [
Reference Murty14
], we are able to condition on both the sign of
![]() $\lambda_f(p)$
as well as the ideal class of p in order to prove that these sums tend to
$\lambda_f(p)$
as well as the ideal class of p in order to prove that these sums tend to
![]() $\infty$
uniformly in
$\infty$
uniformly in
![]() $|t| \leq \log X$
as
$|t| \leq \log X$
as
![]() $X \rightarrow \infty$
.
$X \rightarrow \infty$
.
When K has class number
![]() $> 1$
the problem is rendered more complicated by the fact that the indicator
$> 1$
the problem is rendered more complicated by the fact that the indicator
![]() $1_{\mathcal{N}_K}$
is no longer a multiplicative function. Luckily, a result of Odoni (discussed in some detail in [
Reference Matomäki and Radziwiłł11
]) allows one to express
$1_{\mathcal{N}_K}$
is no longer a multiplicative function. Luckily, a result of Odoni (discussed in some detail in [
Reference Matomäki and Radziwiłł11
]) allows one to express
![]() $1_{\mathcal{N}_K}$
as a linear combination of structured multiplicative functions, and (with some work) similar techniques may then be applied to the individual terms of these linear combinations.
$1_{\mathcal{N}_K}$
as a linear combination of structured multiplicative functions, and (with some work) similar techniques may then be applied to the individual terms of these linear combinations.
1·1·2. Proofs of Theorem 1·6
Fix a non-zero integer a. To prove Theorem 1·6, we make use of more classical arguments about sign changes. Namely, we find a lower bound on the least h such that
![]() $\lambda_f(n)$
must change sign in an interval
$\lambda_f(n)$
must change sign in an interval
![]() $[x,x+h]$
for typical
$[x,x+h]$
for typical
![]() $x \in [X,2X]$
. Dually, we show by way of contradiction that if
$x \in [X,2X]$
. Dually, we show by way of contradiction that if
![]() $\lambda_f(n) \geq 0$
, say, for all
$\lambda_f(n) \geq 0$
, say, for all
![]() $x < n \leq x+h$
then we obtain contradictory upper and lower bounds for the quantity
$x < n \leq x+h$
then we obtain contradictory upper and lower bounds for the quantity
for typical
![]() $x \in [X,2X]$
, provided
$x \in [X,2X]$
, provided
![]() $h \gg X^{1/2+\varepsilon}$
. This results in
$h \gg X^{1/2+\varepsilon}$
. This results in
![]() $\gg X/h \gg X^{1/2-\varepsilon}$
distinct sign changes. Here, as above, r(n) denotes the number of representations of n as a sum of two squares.
$\gg X/h \gg X^{1/2-\varepsilon}$
distinct sign changes. Here, as above, r(n) denotes the number of representations of n as a sum of two squares.
The upper bound we need is furnished by estimates for shifted convolution sums arising from the spectral theory of automorphic forms. In this context, one obtains the square-root cancelling bound
![]() $O_f(X^{1/2+\varepsilon})$
using the work of Ravindran [
Reference Ravindran18
].
$O_f(X^{1/2+\varepsilon})$
using the work of Ravindran [
Reference Ravindran18
].
The lower bound requires more work, and principally involves restricting the sum to those n for which
![]() $|\lambda_f(n)| > X^{-\delta}$
. Assuming
$|\lambda_f(n)| > X^{-\delta}$
. Assuming
![]() $\lambda_f(n) \geq 0$
for all
$\lambda_f(n) \geq 0$
for all
![]() $x < n \leq x+h$
, it follows that then
$x < n \leq x+h$
, it follows that then
 \begin{align} & \sum_{x < n \leq x+h} \lambda_f(n)r(n-a) \geq X^{-\delta} \sum_{\substack{x < n \leq x+h \\ \lambda_f(n) > X^{-\delta}}} r(n-a) \nonumber \\[5pt] & = X^{-\delta}\left(\sum_{\substack{x < n \leq x+h \\ \lambda_f(n) \neq 0}} r(n-a) - \sum_{\substack{x < n \leq x+h \\ 0 < \lambda_f(n) \leq X^{-\delta}}} r(n-a)\right).\end{align}
\begin{align} & \sum_{x < n \leq x+h} \lambda_f(n)r(n-a) \geq X^{-\delta} \sum_{\substack{x < n \leq x+h \\ \lambda_f(n) > X^{-\delta}}} r(n-a) \nonumber \\[5pt] & = X^{-\delta}\left(\sum_{\substack{x < n \leq x+h \\ \lambda_f(n) \neq 0}} r(n-a) - \sum_{\substack{x < n \leq x+h \\ 0 < \lambda_f(n) \leq X^{-\delta}}} r(n-a)\right).\end{align}
Since, as Serre [
Reference Serre19
] showed, the set of primes p such that
![]() $\lambda_f(p) = 0$
is quite sparse, the conditon
$\lambda_f(p) = 0$
is quite sparse, the conditon
![]() $\lambda_f(n) \neq 0$
is easily dealt with using sieve theoretical arguments, and the first expression in brackets in (1·1) is shown to be of size
$\lambda_f(n) \neq 0$
is easily dealt with using sieve theoretical arguments, and the first expression in brackets in (1·1) is shown to be of size
![]() $\gg h$
for typical
$\gg h$
for typical
![]() $x \in [X,2X]$
.
$x \in [X,2X]$
.
On the other hand, the support of the second sum in (1·1) is shown to be sparse for typical x. Indeed, by exploiting the multiplicativity of
![]() $\lambda_f$
together with some Diophantine information about coefficients of cusp forms, we show that any n for which
$\lambda_f$
together with some Diophantine information about coefficients of cusp forms, we show that any n for which
![]() $0 < |\lambda_f(n) | < X^{-\delta}$
has a prime power divisor
$0 < |\lambda_f(n) | < X^{-\delta}$
has a prime power divisor
![]() $p^\nu > (\log X)^{c_1}$
for which
$p^\nu > (\log X)^{c_1}$
for which
![]() $|\lambda_f(p^\nu)| < (\log X)^{-c_2}$
, for
$|\lambda_f(p^\nu)| < (\log X)^{-c_2}$
, for
![]() $c_1,c_2 > 0$
constants depending at most on
$c_1,c_2 > 0$
constants depending at most on
![]() $\delta$
and f. Using a recent version of the Sato–Tate theorem with a quantitative error term due to Thorner [
Reference Thorner24
], we show that the set of such multiples n is a sparse set, and therefore typical length h short intervals have few such multiples. This is essentially enough to conclude that the second sum in brackets in (1·1) is o(h) for most
$\delta$
and f. Using a recent version of the Sato–Tate theorem with a quantitative error term due to Thorner [
Reference Thorner24
], we show that the set of such multiples n is a sparse set, and therefore typical length h short intervals have few such multiples. This is essentially enough to conclude that the second sum in brackets in (1·1) is o(h) for most
![]() $x \in [X,2X]$
, giving rise to the conflicting bounds
$x \in [X,2X]$
, giving rise to the conflicting bounds
(taking
![]() $\delta=\varepsilon$
small) whenever
$\delta=\varepsilon$
small) whenever
![]() $h \gg_f X^{1/2+3\varepsilon}$
.
$h \gg_f X^{1/2+3\varepsilon}$
.
1·2. Structure of the paper
The paper is structured as follows. In Section 2 we give some background results in the theory of norm forms and that of cusp forms, and we also summarise some results from multiplicative number theory of relevance in the rest of the paper. In Section 3 we prove Theorem 1·5, and in Section 4 we prove Theorem 1·6.
2. Background results
2·1. Background on norm forms
Fix
![]() $K/\mathbb{Q}$
a number field, and let
$K/\mathbb{Q}$
a number field, and let
![]() $\mathcal{N}_K$
be the sequence of norm forms of K. In general, the indicator function
$\mathcal{N}_K$
be the sequence of norm forms of K. In general, the indicator function
![]() $g_K(n) \;:\!=\; 1_{\mathcal{N}_K}(n)$
of
$g_K(n) \;:\!=\; 1_{\mathcal{N}_K}(n)$
of
![]() $\mathcal{N}_K$
is not a multiplicative function, and thus an analysis of sign changes of
$\mathcal{N}_K$
is not a multiplicative function, and thus an analysis of sign changes of
![]() $\lambda_f(n)g_K(n)$
purely on the basis of multiplicative techniques seems a priori difficult. However, Odoni [
Reference Odoni17
] showed that
$\lambda_f(n)g_K(n)$
purely on the basis of multiplicative techniques seems a priori difficult. However, Odoni [
Reference Odoni17
] showed that
![]() $g_K$
can be written as a linear combination of certain multiplicative functions that have fairly predictable values, and this will be sufficient for the proof of Theorem 1·5. The material required to these ends is drawn essentially from [
Reference Matomäki and Radziwiłł11
, section 13], which leverages Odoni’s ideas. We describe the salient points in brief detail here.
$g_K$
can be written as a linear combination of certain multiplicative functions that have fairly predictable values, and this will be sufficient for the proof of Theorem 1·5. The material required to these ends is drawn essentially from [
Reference Matomäki and Radziwiłł11
, section 13], which leverages Odoni’s ideas. We describe the salient points in brief detail here.
Let
![]() $\overline{K}$
denote the normal closure of K, and let
$\overline{K}$
denote the normal closure of K, and let
![]() $\mathcal{H}(\overline{K})$
denote the narrow class field of
$\mathcal{H}(\overline{K})$
denote the narrow class field of
![]() $\overline{K}$
. Thus,
$\overline{K}$
. Thus,
![]() $G_K \;:\!=\; \text{Gal}(\mathcal{H}(\overline{K})/\overline{K})$
is canonically isomorphic to the narrow class group
$G_K \;:\!=\; \text{Gal}(\mathcal{H}(\overline{K})/\overline{K})$
is canonically isomorphic to the narrow class group
![]() $H(\overline{K})$
of
$H(\overline{K})$
of
![]() $\overline{K}$
, via the map
$\overline{K}$
, via the map
![]() $\mathcal{C} \in H(\overline{K}) \mapsto \sigma_{\mathcal{C}}$
, the Frobenius conjugacy class of the ideal class
$\mathcal{C} \in H(\overline{K}) \mapsto \sigma_{\mathcal{C}}$
, the Frobenius conjugacy class of the ideal class
![]() $\mathcal{C}$
.
$\mathcal{C}$
.
Consider first the case of prime norm forms. Since the set of rational primes that ramify in K is finite (they all must divide the discriminant
![]() $\text{disc}(K/\mathbb{Q})$
) we will be able to ignore them in the sequel, and therefore focus mainly on the unramified primes. Any unramified rational prime p factors as
$\text{disc}(K/\mathbb{Q})$
) we will be able to ignore them in the sequel, and therefore focus mainly on the unramified primes. Any unramified rational prime p factors as
where, as
![]() $N_K(p) = p^{[K:\mathbb{Q}]}$
, we have
$N_K(p) = p^{[K:\mathbb{Q}]}$
, we have
![]() $N_K (\mathfrak{p}_l) = p^{m}$
for some
$N_K (\mathfrak{p}_l) = p^{m}$
for some
![]() $1\leq m \leq [K\;:\;\mathbb{Q}]$
. Each of the prime ideals
$1\leq m \leq [K\;:\;\mathbb{Q}]$
. Each of the prime ideals
![]() $\mathfrak{p}_l$
lying above p belongs to some class in the narrow class group
$\mathfrak{p}_l$
lying above p belongs to some class in the narrow class group
![]() $H(\overline{K})$
. Let
$H(\overline{K})$
. Let
![]() $\{C_1,\ldots,C_{h(K)}\}$
be an enumeration of these classes,
$\{C_1,\ldots,C_{h(K)}\}$
be an enumeration of these classes,
![]() $h(K) = |H(\overline{K})|$
denoting the narrow class number of
$h(K) = |H(\overline{K})|$
denoting the narrow class number of
![]() $\overline{K}$
. For each
$\overline{K}$
. For each
![]() $1 \leq i \leq [K\;:\;\mathbb{Q}]$
,
$1 \leq i \leq [K\;:\;\mathbb{Q}]$
,
![]() $1 \leq j \leq h(K)$
and rational prime p let us write
$1 \leq j \leq h(K)$
and rational prime p let us write
Following Odoni, the matrix B(p) is called the pattern of p. Let
![]() $\mathcal{B} = \{B(p)\}_p$
be the (finite) collection of all pattern matrices that occur.
$\mathcal{B} = \{B(p)\}_p$
be the (finite) collection of all pattern matrices that occur.
It will be profitable to have access to asymptotic formulae for the number of rational primes with a given pattern, which can be achieved by an application of the Chebotarev density theorem. Indeed, Odoni [
Reference Odoni17
, theorem 4·1] showed that for a given
![]() $B \in \mathcal{B}$
there is a collection
$B \in \mathcal{B}$
there is a collection
![]() $\mathcal{C}_B$
of conjugacy classes of
$\mathcal{C}_B$
of conjugacy classes of
![]() $G_K$
such that
$G_K$
such that
By the Chebotarev density theorem (see [
Reference Thorner and Zaman25
] for an unconditional result that is state-of-the-art), it thus follows that for any
![]() $B \in \mathcal{B}$
there is a positive constant
$B \in \mathcal{B}$
there is a positive constant
![]() $c(B) \;:\!=\; {|\mathcal{C}_B|}/{h(K)} > 0$
such that as
$c(B) \;:\!=\; {|\mathcal{C}_B|}/{h(K)} > 0$
such that as
![]() $X \rightarrow \infty$
(keeping K fixed),
$X \rightarrow \infty$
(keeping K fixed),
for some constant
![]() $c_K > 0$
depending only on K.
$c_K > 0$
depending only on K.
We highlight the following consequence of this. Define
Since
![]() $N_K(\alpha) = N_K(\alpha \mathcal{O}_K)$
for all
$N_K(\alpha) = N_K(\alpha \mathcal{O}_K)$
for all
![]() $\alpha \in \mathcal{O}_K$
we have
$\alpha \in \mathcal{O}_K$
we have
![]() $\mathcal{N}_K \subseteq \widehat{\mathcal{N}}_K$
, though in general these sets differ. By Dedekind’s theorem on factorisation of integral ideals,
$\mathcal{N}_K \subseteq \widehat{\mathcal{N}}_K$
, though in general these sets differ. By Dedekind’s theorem on factorisation of integral ideals,
![]() $\widehat{\mathcal{N}}_K$
is a multiplicative set, i.e.,
$\widehat{\mathcal{N}}_K$
is a multiplicative set, i.e.,
![]() $m,n \in \widehat{\mathcal{N}}_K$
iff
$m,n \in \widehat{\mathcal{N}}_K$
iff
![]() $mn \in \widehat{\mathcal{N}}_K$
.
$mn \in \widehat{\mathcal{N}}_K$
.
As discussed by Odoni [
Reference Odoni17
, p. 71], there is a collection
![]() $\mathfrak{C}$
of ideal classes such that an unramified prime
$\mathfrak{C}$
of ideal classes such that an unramified prime
![]() $p \in \mathcal{N}_K$
if, and only if,
$p \in \mathcal{N}_K$
if, and only if,
![]() $R(p) \cap \mathfrak{C} \neq \emptyset$
, where R(p) is the collection of integral ideals
$R(p) \cap \mathfrak{C} \neq \emptyset$
, where R(p) is the collection of integral ideals
![]() $\mathfrak{a} \subseteq \mathcal{O}_K$
such that
$\mathfrak{a} \subseteq \mathcal{O}_K$
such that
![]() $N_K(\mathfrak{a}) = p$
. By necessity,
$N_K(\mathfrak{a}) = p$
. By necessity,
![]() $\mathfrak{a} = \mathfrak{p}$
must then be a prime ideal, lying in some ideal class
$\mathfrak{a} = \mathfrak{p}$
must then be a prime ideal, lying in some ideal class
![]() $C_j$
containing
$C_j$
containing
![]() $\mathfrak{p}$
, and since
$\mathfrak{p}$
, and since
![]() $N_K(\mathfrak{p}) \in \mathfrak{p}$
we must have
$N_K(\mathfrak{p}) \in \mathfrak{p}$
we must have
![]() $\mathfrak{p}|p$
. Thus, there is
$\mathfrak{p}|p$
. Thus, there is
![]() $1 \leq j \leq h(K)$
such that
$1 \leq j \leq h(K)$
such that
![]() $\mathcal{C}_j \in \mathfrak{C}$
and
$\mathcal{C}_j \in \mathfrak{C}$
and
![]() $b_{1,j}(p) > 0$
. In other terms, among unramified primes,
$b_{1,j}(p) > 0$
. In other terms, among unramified primes,
 \begin{align*} p \in \mathcal{N}_K \text{ if, and only if, } \sum_{\substack{1 \leq j \leq h(K) \\ \mathcal{C}_j \in \mathfrak{C}}} b_{1,j}(p) > 0.\end{align*}
\begin{align*} p \in \mathcal{N}_K \text{ if, and only if, } \sum_{\substack{1 \leq j \leq h(K) \\ \mathcal{C}_j \in \mathfrak{C}}} b_{1,j}(p) > 0.\end{align*}
Define
![]() $\mathcal{U} \subseteq \mathcal{V} \subseteq \mathcal{B}$
the subcollections of patterns
$\mathcal{U} \subseteq \mathcal{V} \subseteq \mathcal{B}$
the subcollections of patterns
![]() $B = \{b_{i,j}\}$
such that
$B = \{b_{i,j}\}$
such that
 \begin{align*}B \in \mathcal{U} &\text{ if and only if } \sum_{j\;:\; \mathcal{C}_j \in \mathfrak{C}} b_{1,j} > 0, \\[5pt] B \in \mathcal{V} &\text{ if and only if } \sum_j b_{1,j} > 0.\end{align*}
\begin{align*}B \in \mathcal{U} &\text{ if and only if } \sum_{j\;:\; \mathcal{C}_j \in \mathfrak{C}} b_{1,j} > 0, \\[5pt] B \in \mathcal{V} &\text{ if and only if } \sum_j b_{1,j} > 0.\end{align*}
Combined with the Chebotarev density theorem, these remarks imply the following.
Lemma 2·1.
Let
![]() $\beta_K \;:\!=\; \sum_{B \in \mathcal{U}} c(B)$
and
$\beta_K \;:\!=\; \sum_{B \in \mathcal{U}} c(B)$
and
![]() $\tau_K \;:\!=\; \sum_{B \in \mathcal{V}} c(B)$
. Then
$\tau_K \;:\!=\; \sum_{B \in \mathcal{V}} c(B)$
. Then
With the above preliminaries in hand, we can now proceed towards Odoni’s decomposition theorem, as presented in [
Reference Matomäki and Radziwiłł11
, section 13]. In the sequel, define the multiplicative function
![]() $\Delta_K$
at prime powers
$\Delta_K$
at prime powers
![]() $p^{\nu}$
via
$p^{\nu}$
via
 \begin{equation}\Delta_K(p^{\nu}) \;:\!=\; \begin{cases} 1 \text{ if $p \in \widehat{\mathcal{N}}_K$} \\[5pt] 0 \text{ otherwise.} \end{cases}\end{equation}
\begin{equation}\Delta_K(p^{\nu}) \;:\!=\; \begin{cases} 1 \text{ if $p \in \widehat{\mathcal{N}}_K$} \\[5pt] 0 \text{ otherwise.} \end{cases}\end{equation}
Since
![]() $\widehat{\mathcal{N}}_K \supseteq \mathcal{N}_K$
we have
$\widehat{\mathcal{N}}_K \supseteq \mathcal{N}_K$
we have
![]() $\Delta_K(n) \geq g_K(n)$
for all integers n.
$\Delta_K(n) \geq g_K(n)$
for all integers n.
Proposition 2·2 (Matomäki–Radziwiłł, [
Reference Matomäki and Radziwiłł11
, lemma 13·3]; Odoni [
Reference Odoni17
]). There are positive real constants
![]() $\alpha = \alpha(K)$
,
$\alpha = \alpha(K)$
,
![]() $\rho = \rho(K)$
, non-negative integers
$\rho = \rho(K)$
, non-negative integers
![]() $M = M(K)$
,
$M = M(K)$
,
![]() $R = R(K)$
with
$R = R(K)$
with
![]() $R > M$
, an integer
$R > M$
, an integer
![]() $D = D(K) \geq 1$
and complex numbers
$D = D(K) \geq 1$
and complex numbers
![]() $c_i = c_i(K) \in \mathbb{C}$
for
$c_i = c_i(K) \in \mathbb{C}$
for
![]() $0 \leq i \leq R$
such that for all
$0 \leq i \leq R$
such that for all
![]() $n \in \mathbb{N}$
,
$n \in \mathbb{N}$
,
where the functions
![]() $f_i\;:\; \mathbb{N} \rightarrow \mathbb{C}$
are multiplicative with
$f_i\;:\; \mathbb{N} \rightarrow \mathbb{C}$
are multiplicative with
![]() $f_i(p)^D = \Delta_K(p)$
for all p and
$f_i(p)^D = \Delta_K(p)$
for all p and
![]() $0 \leq i \leq R$
, and satisfy the following properties for sufficiently large X:
$0 \leq i \leq R$
, and satisfy the following properties for sufficiently large X:
-
(i) for each
 $0 \leq l \leq R$
and
$0 \leq l \leq R$
and
 $2 \leq w \leq z \leq X$
,
$2 \leq w \leq z \leq X$
,  \begin{align*} \sum_{w \leq p \leq z} \frac{|f_i(p)|}{p} = \tau_K \sum_{w \leq p \leq z} \frac{1}{p} + O_K\left(\frac{1}{\log w}\right);\end{align*}
\begin{align*} \sum_{w \leq p \leq z} \frac{|f_i(p)|}{p} = \tau_K \sum_{w \leq p \leq z} \frac{1}{p} + O_K\left(\frac{1}{\log w}\right);\end{align*}
-
(ii) if
 $p \nmid \text{disc}(K/\mathbb{Q})$
then
$p \nmid \text{disc}(K/\mathbb{Q})$
then
 $f_l(p) = \Delta_K(p)$
for all
$f_l(p) = \Delta_K(p)$
for all
 $0 \leq l \leq M$
;
$0 \leq l \leq M$
; -
(iii)
 $\sum_{0 \leq l \leq M} c_l > 0$
; and
$\sum_{0 \leq l \leq M} c_l > 0$
; and
-
(iv) for each
 $M+1 \leq l \leq R$
we have
$M+1 \leq l \leq R$
we have  \begin{align*} \min_{|t| \leq 2X} \sum_{p \leq X} \frac{\Delta_K(p) - \text{Re}(f_l(p)p^{-it})}{p} \geq \rho \log\log X.\end{align*}
\begin{align*} \min_{|t| \leq 2X} \sum_{p \leq X} \frac{\Delta_K(p) - \text{Re}(f_l(p)p^{-it})}{p} \geq \rho \log\log X.\end{align*}
The utility of (iv) will become evident in Section 2·3, where we will appeal to some notions from pretentious number theory.
Proof. Claims (ii),(iii) and (iv) are explicitly stated in [
Reference Matomäki and Radziwiłł11
, lemma 13·3]. Claim (i) follows immediately from the claim
![]() $f_l(p)^D = \Delta_K(p)$
, which implies that
$f_l(p)^D = \Delta_K(p)$
, which implies that
![]() $|f_l(p)| = \Delta_K(p) \in \{0,1\}$
for all l and p. Thus, (i) follows from Lemma 2·1 and partial summation.
$|f_l(p)| = \Delta_K(p) \in \{0,1\}$
for all l and p. Thus, (i) follows from Lemma 2·1 and partial summation.
Otherwise, the only statement mentioned here that does not explicitly appear in [
Reference Matomäki and Radziwiłł11
, lemma 13·3] is the existence of D. However, the functions
![]() $f_i$
are constructed in such a way that for each
$f_i$
are constructed in such a way that for each
![]() $B \in \mathcal{B}$
there is a root of unity
$B \in \mathcal{B}$
there is a root of unity
![]() $\zeta_{i,B} \in \mu_{d_B}$
of some order
$\zeta_{i,B} \in \mu_{d_B}$
of some order
![]() $d_B \geq 1$
such that whenever
$d_B \geq 1$
such that whenever
![]() $B(p) = B$
we have
$B(p) = B$
we have
![]() $f_i(p) = \zeta_{i,B}$
[
Reference Matomäki and Radziwiłł11
, p. 77]. Since
$f_i(p) = \zeta_{i,B}$
[
Reference Matomäki and Radziwiłł11
, p. 77]. Since
![]() $\mathcal{B}$
is a finite set, this constitutes a finite set of roots of unity, and thus taking
$\mathcal{B}$
is a finite set, this constitutes a finite set of roots of unity, and thus taking
![]() $D \;:\!=\; \text{lcm}\{d_B\;:\; B \in \mathcal{B}\}$
, we obtain the required number D. This completes the proof of the proposition.
$D \;:\!=\; \text{lcm}\{d_B\;:\; B \in \mathcal{B}\}$
, we obtain the required number D. This completes the proof of the proposition.
2·2. Results from the theory of modular forms
We will need to use the following slight generalisation (to forms of weight
![]() $k > 2$
) of a hybrid of the Sato–Tate and Chebotarev theorems, due toFootnote 1 M.R. Murty and V.K. Murty.
$k > 2$
) of a hybrid of the Sato–Tate and Chebotarev theorems, due toFootnote 1 M.R. Murty and V.K. Murty.
Lemma 2·3 (Chebotarev–Sato–Tate for modular forms of weight
![]() $k \geq 2$
). Let
$k \geq 2$
). Let
![]() $M/K$
be an Abelian Galois extension and let
$M/K$
be an Abelian Galois extension and let
![]() $G = \text{Gal}(M/K)$
. Let f be a Hecke eigencusp form of weight k and level 1, without CM. If
$G = \text{Gal}(M/K)$
. Let f be a Hecke eigencusp form of weight k and level 1, without CM. If
![]() $\mathcal{C}$
is a conjugacy class of G then as
$\mathcal{C}$
is a conjugacy class of G then as
![]() $X \rightarrow \infty$
we have
$X \rightarrow \infty$
we have
where
![]() $\theta_p$
is defined implicitly via
$\theta_p$
is defined implicitly via
![]() $\lambda_f(p) = 2\cos \theta_p$
, and
$\lambda_f(p) = 2\cos \theta_p$
, and
![]() $\sigma_p$
is the Artin symbol attached to p.
$\sigma_p$
is the Artin symbol attached to p.
Proof. The argument is based on [
Reference Murty and Murty15
, theorem 1], but is simplified since we work with Abelian G (given that in our application,
![]() $G = G_K$
, the narrow Hilbert class field) and also in light of the recent breakthroughs on automorphy lifting of
$G = G_K$
, the narrow Hilbert class field) and also in light of the recent breakthroughs on automorphy lifting of
![]() $\text{Sym}^m\rho_f$
, due to Newton and Thorne [
Reference Newton and Thorne16
].
$\text{Sym}^m\rho_f$
, due to Newton and Thorne [
Reference Newton and Thorne16
].
Let
![]() $\rho_f$
be a Galois representation associated to f. Since G is Abelian, the irreducible representations of G are all 1-dimensional, thus characters. Let
$\rho_f$
be a Galois representation associated to f. Since G is Abelian, the irreducible representations of G are all 1-dimensional, thus characters. Let
![]() $\hat{G}$
be the set of characters of G. By Tauberian theorems and the orthogonality relations on
$\hat{G}$
be the set of characters of G. By Tauberian theorems and the orthogonality relations on
![]() $\hat{G}$
, it suffices to show that for any
$\hat{G}$
, it suffices to show that for any
![]() $\chi \in \hat{G}$
and
$\chi \in \hat{G}$
and
![]() $m \geq 1$
we have that
$m \geq 1$
we have that
![]() $L(s,\text{Sym}^m \rho_f \otimes \chi)$
is analytic and non-vanishing on
$L(s,\text{Sym}^m \rho_f \otimes \chi)$
is analytic and non-vanishing on
![]() $\text{Re}(s) \geq 1$
. By the general theory of automorphic L-functions, it thus suffices to show that
$\text{Re}(s) \geq 1$
. By the general theory of automorphic L-functions, it thus suffices to show that
![]() $L(s,\text{Sym}^m\rho_f \otimes \chi)$
is automorphic (see e.g. [
Reference Iwaniec and Kowalski4
, section 5·12], in particular [
Reference Iwaniec and Kowalski4
, theorem 5·42]). But by the Artin reciprocity law,
$L(s,\text{Sym}^m\rho_f \otimes \chi)$
is automorphic (see e.g. [
Reference Iwaniec and Kowalski4
, section 5·12], in particular [
Reference Iwaniec and Kowalski4
, theorem 5·42]). But by the Artin reciprocity law,
![]() $\chi$
corresponds to a Hecke character
$\chi$
corresponds to a Hecke character
![]() $\psi$
, and since
$\psi$
, and since
![]() $\text{Sym}^m\rho_f$
is automorphic over
$\text{Sym}^m\rho_f$
is automorphic over
![]() $\mathbb{Q}$
by [
Reference Newton and Thorne16
], so is
$\mathbb{Q}$
by [
Reference Newton and Thorne16
], so is
![]() $\text{Sym}^m \rho_f \otimes \psi$
, and the claim follows.
$\text{Sym}^m \rho_f \otimes \psi$
, and the claim follows.
In order to keep track of sign changes we will require some control over the set of vanishing of
![]() $\lambda_f$
. This will be aided by the following result of Serre (for the best result in this direction, however, see [
Reference Zaman and Thorner28
]).
$\lambda_f$
. This will be aided by the following result of Serre (for the best result in this direction, however, see [
Reference Zaman and Thorner28
]).
Lemma 2·4 (Serre, [
Reference Serre19
, theorem 15]). Let f be a Hecke eigencusp form of weight k and level 1 without CM. Then for any
![]() $\varepsilon > 0$
, if
$\varepsilon > 0$
, if
![]() $X \geq X_0(\varepsilon)$
we have
$X \geq X_0(\varepsilon)$
we have
Let us state the following very simple consequence of Serre’s result, which will arise repeatedly later on. Define
For
![]() $n \in \mathbb{N}$
define the multiplicative function
$n \in \mathbb{N}$
define the multiplicative function
![]() $\iota_{K,f}(n) \;:\!=\; \mu^2(n) 1_{p|n \Rightarrow p \notin B_{K,f}}$
(the fact that it is supported on squarefree integers will be used later). The following lemma is a trivial consequence of Lemma 2·4 and partial summation.
$\iota_{K,f}(n) \;:\!=\; \mu^2(n) 1_{p|n \Rightarrow p \notin B_{K,f}}$
(the fact that it is supported on squarefree integers will be used later). The following lemma is a trivial consequence of Lemma 2·4 and partial summation.
Lemma 2·5.
For any
![]() $2 \leq w \leq z \leq X$
and
$2 \leq w \leq z \leq X$
and
![]() $\varepsilon > 0$
we have
$\varepsilon > 0$
we have
2·3. Results about pretentious number theory
In the sequel, our arguments dealing with multiplicative functions will, implicitly and explicitly, use notions from pretentious number theory. A key role in that theory is played by the pretentious distance functions. Write
![]() $\mathbb{U} \;:\!=\; \{z \in \mathbb{C}\;:\; |z| \leq 1\}$
. Given
$\mathbb{U} \;:\!=\; \{z \in \mathbb{C}\;:\; |z| \leq 1\}$
. Given
![]() $y \geq 2$
and sequences
$y \geq 2$
and sequences
![]() $a \;:\!=\; \{a(p)\}_p, b \;:\!=\; \{b(p)\}_p \subset \mathbb{U}$
we define the pretentious distance between a and b up to y to be
$a \;:\!=\; \{a(p)\}_p, b \;:\!=\; \{b(p)\}_p \subset \mathbb{U}$
we define the pretentious distance between a and b up to y to be
 \begin{align*} \mathbb{D}(a,b;\;y) \;:\!=\; \left(\sum_{p \leq y} \frac{1-\text{Re}(a(p)\overline{b}(p))}{p}\right)^{1/2}.\end{align*}
\begin{align*} \mathbb{D}(a,b;\;y) \;:\!=\; \left(\sum_{p \leq y} \frac{1-\text{Re}(a(p)\overline{b}(p))}{p}\right)^{1/2}.\end{align*}
This distance satisfies the pretentious triangle inequality, i.e., if
![]() $c = \{c(p)\}_p$
is any such third sequence then
$c = \{c(p)\}_p$
is any such third sequence then
(see e.g. [
Reference Granville and Soundararajan3
, lemma 3·1]). Since
![]() $\eta(u,v) \;:\!=\; (1-\text{Re}(u\overline{w}))^{1/2}$
, well-defined for
$\eta(u,v) \;:\!=\; (1-\text{Re}(u\overline{w}))^{1/2}$
, well-defined for
![]() $u,v \in \mathbb{U}$
, satisfies
$u,v \in \mathbb{U}$
, satisfies
![]() $\eta(u,v) = \eta(u\overline{v},1) = \eta(1,\overline{u}v)$
, one can consequently show the useful inequality
$\eta(u,v) = \eta(u\overline{v},1) = \eta(1,\overline{u}v)$
, one can consequently show the useful inequality
using the notation
![]() $(ab)(p) \;:\!=\; a(p)b(p)$
for all p for prime-indexed sequences a and b. Among other things, iterating this leads to the result that
$(ab)(p) \;:\!=\; a(p)b(p)$
for all p for prime-indexed sequences a and b. Among other things, iterating this leads to the result that
Perhaps less well known is the following general, weighted variant of the pretentious triangle inequality, also due to Granville and Soundararajan [ Reference Granville and Soundararajan3 ].
Lemma 2·6.
Let
![]() $\{r(p)\}_p\subset [0,\infty)$
, and let
$\{r(p)\}_p\subset [0,\infty)$
, and let
![]() $a = \{a(p)\}_p, b = \{b(p)\}_p$
and
$a = \{a(p)\}_p, b = \{b(p)\}_p$
and
![]() $c = \{c(p)\}_p$
be as above. Then for any
$c = \{c(p)\}_p$
be as above. Then for any
![]() $y \geq 2$
,
$y \geq 2$
,
 \begin{align*} & \left(\sum_{p \leq y} r(p)(1-\text{Re}(a(p)\overline{c}(p)))\right)^{1/2} \leq \left(\sum_{p \leq y} r(p)(1-\text{Re}(a(p)\overline{b}(p)))\right)^{1/2} \\[5pt] &+ \left(\sum_{p \leq y} r(p)(1-\text{Re}(b(p)\overline{c}(p)))\right)^{1/2}.\end{align*}
\begin{align*} & \left(\sum_{p \leq y} r(p)(1-\text{Re}(a(p)\overline{c}(p)))\right)^{1/2} \leq \left(\sum_{p \leq y} r(p)(1-\text{Re}(a(p)\overline{b}(p)))\right)^{1/2} \\[5pt] &+ \left(\sum_{p \leq y} r(p)(1-\text{Re}(b(p)\overline{c}(p)))\right)^{1/2}.\end{align*}
Proof. This is alluded to below the proof of lemma 3·1 in [ Reference Granville and Soundararajan3 ]. Since the proof is not given, we give the details here, elaborating slightly on the arguments in [ Reference Granville and Soundararajan3 ] for the sake of clarity.
Observe first of all that if
![]() $z \in \mathbb{U}$
then
$z \in \mathbb{U}$
then
![]() $|z| \leq 1$
and thus
$|z| \leq 1$
and thus
It follows, therefore, that for any
![]() $z_1,z_2 \in \mathbb{U}$
,
$z_1,z_2 \in \mathbb{U}$
,
![]() $2\eta(1,z_1)\eta(1,z_2) \geq |\text{Im}(z_1)||\text{Im}(z_2)|$
. Next, note the property
$2\eta(1,z_1)\eta(1,z_2) \geq |\text{Im}(z_1)||\text{Im}(z_2)|$
. Next, note the property
whence we may deduce that
We therefore obtain that
 \begin{align*}\eta(z_1,z_2)^2 &= 1-\text{Re}(z_1\overline{z_2}) \leq 2 - \text{Re}(z_1)-\text{Re}(z_2)-\text{Im}(z_1)\text{Im}(z_2) \\[5pt] &\leq \eta(1,z_1)^2 + \eta(1,z_2)^2 + |\text{Im}(z_1)||\text{Im}(z_2)| \leq \eta(1,z_1)^2 + \eta(1,z_2)^2 + 2\eta(1,z_1)\eta(1,z_2) \\[5pt] &= (\eta(1,z_1)+\eta(1,z_2))^2.\end{align*}
\begin{align*}\eta(z_1,z_2)^2 &= 1-\text{Re}(z_1\overline{z_2}) \leq 2 - \text{Re}(z_1)-\text{Re}(z_2)-\text{Im}(z_1)\text{Im}(z_2) \\[5pt] &\leq \eta(1,z_1)^2 + \eta(1,z_2)^2 + |\text{Im}(z_1)||\text{Im}(z_2)| \leq \eta(1,z_1)^2 + \eta(1,z_2)^2 + 2\eta(1,z_1)\eta(1,z_2) \\[5pt] &= (\eta(1,z_1)+\eta(1,z_2))^2.\end{align*}
Specialising to the case
![]() $z_1= u\overline{v}$
and
$z_1= u\overline{v}$
and
![]() $z_2 = v\overline{w}$
, we obtain the preliminary inequality
$z_2 = v\overline{w}$
, we obtain the preliminary inequality
for any
![]() $u,v,w\in \mathbb{U}$
.
$u,v,w\in \mathbb{U}$
.
Next, note that by Cauchy–Schwarz we have
 \begin{align*} \sum_{p \leq y} r(p) \eta(a(p),b(p))\eta(b(p),c(p)) \leq\! \left(\sum_{p \leq y} r(p) \eta(a(p),b(p))^2\right)^{\!1/2} \!\!\left(\sum_{p \leq y} r(p) \eta(b(p),c(p))^2\right)^{\!1/2},\end{align*}
\begin{align*} \sum_{p \leq y} r(p) \eta(a(p),b(p))\eta(b(p),c(p)) \leq\! \left(\sum_{p \leq y} r(p) \eta(a(p),b(p))^2\right)^{\!1/2} \!\!\left(\sum_{p \leq y} r(p) \eta(b(p),c(p))^2\right)^{\!1/2},\end{align*}
and from this and (2·6) we obtain
 \begin{align*}& \left(\left(\sum_{p \leq y} r(p) \eta(a(p),b(p))^2\right)^{1/2} + \left(\sum_{p \leq y} r(p)\eta(b(p),c(p))^2\right)^{1/2}\right)^2 \\ &\geq \sum_{p \leq y} r(p)(\eta(a(p),b(p)) + \eta(b(p),c(p)))^2 \\[5pt] &\geq \sum_{p \leq y} r(p)\eta(a(p),c(p))^2.\end{align*}
\begin{align*}& \left(\left(\sum_{p \leq y} r(p) \eta(a(p),b(p))^2\right)^{1/2} + \left(\sum_{p \leq y} r(p)\eta(b(p),c(p))^2\right)^{1/2}\right)^2 \\ &\geq \sum_{p \leq y} r(p)(\eta(a(p),b(p)) + \eta(b(p),c(p)))^2 \\[5pt] &\geq \sum_{p \leq y} r(p)\eta(a(p),c(p))^2.\end{align*}
This implies the claim.
We specialise the above lemma as follows. Given
![]() $y \geq 2$
, a number field
$y \geq 2$
, a number field
![]() $K/\mathbb{Q}$
and multiplicative functions
$K/\mathbb{Q}$
and multiplicative functions
![]() $\phi_1,\phi_2 \;:\; \mathbb{N} \rightarrow \mathbb{C}$
, let us write
$\phi_1,\phi_2 \;:\; \mathbb{N} \rightarrow \mathbb{C}$
, let us write
 \begin{align*} \mathbb{D}_K(\phi_1,\phi_2;\;y) \;:\!=\; \left(\sum_{\substack{p \leq y \\ p \in \widehat{\mathcal{N}}_K}} \frac{1-\text{Re}(\phi_1(p)\overline{\phi_2}(p))}{p}\right)^{1/2},\end{align*}
\begin{align*} \mathbb{D}_K(\phi_1,\phi_2;\;y) \;:\!=\; \left(\sum_{\substack{p \leq y \\ p \in \widehat{\mathcal{N}}_K}} \frac{1-\text{Re}(\phi_1(p)\overline{\phi_2}(p))}{p}\right)^{1/2},\end{align*}
i.e., we set
![]() $r(p) \;:\!=\; \Delta_K(p)/p$
in the notation of the previous lemma. Trivially,
$r(p) \;:\!=\; \Delta_K(p)/p$
in the notation of the previous lemma. Trivially,
![]() $\mathbb{D}_{\mathbb{Q}}(\cdot,\cdot;\;y) = \mathbb{D}(\cdot,\cdot;\;y)$
for all
$\mathbb{D}_{\mathbb{Q}}(\cdot,\cdot;\;y) = \mathbb{D}(\cdot,\cdot;\;y)$
for all
![]() $y\geq 2$
. Note in particular that item (iv) of Proposition 2·2 is precisely the statement that
$y\geq 2$
. Note in particular that item (iv) of Proposition 2·2 is precisely the statement that
![]() $\min_{|t| \leq 2X} \mathbb{D}_K(f_l,n^{it};\;\;X)^2 \geq \rho \log\log X$
for all
$\min_{|t| \leq 2X} \mathbb{D}_K(f_l,n^{it};\;\;X)^2 \geq \rho \log\log X$
for all
![]() $M+1 \leq l \leq R$
. The above lemma allows us to conclude, analogously to (2·5), that for any
$M+1 \leq l \leq R$
. The above lemma allows us to conclude, analogously to (2·5), that for any
![]() $d \geq 1$
,
$d \geq 1$
,
for f, g multiplicative functions taking values in
![]() $\mathbb{U}$
.
$\mathbb{U}$
.
In the sequel, we take the convention that
![]() $\text{sign}(0) \;:\!=\; 0$
, and for
$\text{sign}(0) \;:\!=\; 0$
, and for
![]() $n \in \mathbb{N}$
we define the multiplicative function
$n \in \mathbb{N}$
we define the multiplicative function
![]() $\sigma_f(n) \;:\!=\; \text{sign}(\lambda_f(n))$
, which takes values in
$\sigma_f(n) \;:\!=\; \text{sign}(\lambda_f(n))$
, which takes values in
![]() $\{-1,0,1\}$
. By Lemma 2·4 we know that
$\{-1,0,1\}$
. By Lemma 2·4 we know that
![]() $\sigma_f(p) \neq 0$
for all but a zero density set of primes, and in fact by the Sato-Tate theorem we have
$\sigma_f(p) \neq 0$
for all but a zero density set of primes, and in fact by the Sato-Tate theorem we have
At several junctures of our argument we will require precise information about, in particular quantitative lower bounds for,
![]() $\mathbb{D}_K(\sigma_f,n^{it};\;X)$
, where
$\mathbb{D}_K(\sigma_f,n^{it};\;X)$
, where
![]() $|t| \leq 2X$
, among other such distances. In this direction, we prove the following.
$|t| \leq 2X$
, among other such distances. In this direction, we prove the following.
Lemma 2·7.
Let
![]() $0 \leq l \leq R$
, and let
$0 \leq l \leq R$
, and let
![]() $f_l$
be one of the functions mentioned in Proposition 2·2. Then there is a
$f_l$
be one of the functions mentioned in Proposition 2·2. Then there is a
![]() $\sigma = \sigma(K) > 0$
such that whenever
$\sigma = \sigma(K) > 0$
such that whenever
![]() $|t| \leq 2X$
we have
$|t| \leq 2X$
we have
Moreover, as
![]() $X \rightarrow \infty$
we have
$X \rightarrow \infty$
we have
Proof. We begin with the first claim. Recall from Proposition 2·2 that there is a
![]() $D = D(K) \in \mathbb{N}$
such that
$D = D(K) \in \mathbb{N}$
such that
![]() $f_l^D = \Delta_K$
, and thus
$f_l^D = \Delta_K$
, and thus
![]() $(f_l(p) \sigma_f(p))^{2D} = 1$
for all p such that
$(f_l(p) \sigma_f(p))^{2D} = 1$
for all p such that
![]() $\Delta_K(p) \lambda_f(p) \neq 0$
. It follows from Lemma 2·5 and (2·7) that
$\Delta_K(p) \lambda_f(p) \neq 0$
. It follows from Lemma 2·5 and (2·7) that
 \begin{align*}(2D) \mathbb{D}_K(\sigma_f f_l, n^{it};\;X) \geq \mathbb{D}_K((\sigma_f f_l)^{2D}, n^{2iDt};\;X)&= \left(\sum_{\substack{p \leq X \\ \Delta_K(p) \lambda_f(p) \neq 0}} \frac{1-\text{Re}(p^{-2Dit})}{p}\right)^{1/2} \\[5pt] &\geq \mathbb{D}_K(1,n^{2iDt};\;X) - O_{K,f}(1).\end{align*}
\begin{align*}(2D) \mathbb{D}_K(\sigma_f f_l, n^{it};\;X) \geq \mathbb{D}_K((\sigma_f f_l)^{2D}, n^{2iDt};\;X)&= \left(\sum_{\substack{p \leq X \\ \Delta_K(p) \lambda_f(p) \neq 0}} \frac{1-\text{Re}(p^{-2Dit})}{p}\right)^{1/2} \\[5pt] &\geq \mathbb{D}_K(1,n^{2iDt};\;X) - O_{K,f}(1).\end{align*}
If
![]() $D|t| \leq 10/\log X$
then the claim is trivial, so we may assume otherwise that
$D|t| \leq 10/\log X$
then the claim is trivial, so we may assume otherwise that
![]() $|t| > 10/\log X$
. Now, for
$|t| > 10/\log X$
. Now, for
![]() $\eta \in (0,1/3)$
set
$\eta \in (0,1/3)$
set
![]() $N_{X,\eta} \;:\!=\; \exp((\log X)^{2/3+\eta})$
and let
$N_{X,\eta} \;:\!=\; \exp((\log X)^{2/3+\eta})$
and let
![]() $Y \;:\!=\; \max\{N_{X,\eta}, e^{1/|Dt|}\} \leq X$
. By [
Reference Matomäki and Radziwiłł11
, lemma 13·3(ii)] we have
$Y \;:\!=\; \max\{N_{X,\eta}, e^{1/|Dt|}\} \leq X$
. By [
Reference Matomäki and Radziwiłł11
, lemma 13·3(ii)] we have
 \begin{align*} \mathbb{D}_K(1,n^{2iDt};\;X)^2 \geq \sum_{B \in \mathcal{V}} \text{Re}\left( \sum_{\substack{Y < p \leq X \\ B(p) = B}} \frac{1-p^{2iDt}}{p}\right) + O_K(1) = \tau_K \sum_{Y < p \leq X} \frac{1-\text{Re}(p^{2iDt})}{p} + O_K(1),\end{align*}
\begin{align*} \mathbb{D}_K(1,n^{2iDt};\;X)^2 \geq \sum_{B \in \mathcal{V}} \text{Re}\left( \sum_{\substack{Y < p \leq X \\ B(p) = B}} \frac{1-p^{2iDt}}{p}\right) + O_K(1) = \tau_K \sum_{Y < p \leq X} \frac{1-\text{Re}(p^{2iDt})}{p} + O_K(1),\end{align*}
(where
![]() $\tau_K$
is defined as in Lemma 2·1). We now consider two cases. If
$\tau_K$
is defined as in Lemma 2·1). We now consider two cases. If
![]() $1 \leq D|t| \leq 2X$
then it follows from standard arguments employing the Vinogradov–Korobov zero-free region for the Riemann zeta function (see e.g. [
Reference Koukoulopoulos5
, (4·4)], taking
$1 \leq D|t| \leq 2X$
then it follows from standard arguments employing the Vinogradov–Korobov zero-free region for the Riemann zeta function (see e.g. [
Reference Koukoulopoulos5
, (4·4)], taking
![]() $q = 1$
and
$q = 1$
and
![]() $\chi$
trivial) that the latter prime sum is
$\chi$
trivial) that the latter prime sum is
 \begin{align*} \geq \tau_K \left(\log\left(\frac{\log X}{\log Y}\right) - \left|\sum_{Y < p \leq X} \frac{1}{p^{1+2iDt}}\right| \right) \geq \tau_K(\tfrac 13 - \eta) \log\log X - O_K(1).\end{align*}
\begin{align*} \geq \tau_K \left(\log\left(\frac{\log X}{\log Y}\right) - \left|\sum_{Y < p \leq X} \frac{1}{p^{1+2iDt}}\right| \right) \geq \tau_K(\tfrac 13 - \eta) \log\log X - O_K(1).\end{align*}
Thus, for
![]() $1 \leq |t| \leq 2X$
we have
$1 \leq |t| \leq 2X$
we have
On the other hand, if
![]() $10/\log X < D|t| \leq 1$
then by partial summation and the prime number theorem we have
$10/\log X < D|t| \leq 1$
then by partial summation and the prime number theorem we have
 \begin{align*}\sum_{Y < p \leq X} \frac{1-\text{Re}(p^{2iDt})}{p} &= \frac{1}{2\pi} \left(\int_0^{2\pi} (1-\cos \alpha)d\alpha\right) \cdot \log\left(\frac{\log(2D|t| \log X)}{\max\{1, D|t|\log N_{X,\eta}\}}\right) - O_K(1)\\[5pt] &\geq \left(\frac{1}{3}-\eta\right) \min\{\log\log X, \log(1+|t| \log X)\} - O_K(1).\end{align*}
\begin{align*}\sum_{Y < p \leq X} \frac{1-\text{Re}(p^{2iDt})}{p} &= \frac{1}{2\pi} \left(\int_0^{2\pi} (1-\cos \alpha)d\alpha\right) \cdot \log\left(\frac{\log(2D|t| \log X)}{\max\{1, D|t|\log N_{X,\eta}\}}\right) - O_K(1)\\[5pt] &\geq \left(\frac{1}{3}-\eta\right) \min\{\log\log X, \log(1+|t| \log X)\} - O_K(1).\end{align*}
This completes the proof of the first claim with any
![]() $0 < \sigma < \tau_K/(12D^2)$
(choosing
$0 < \sigma < \tau_K/(12D^2)$
(choosing
![]() $\eta$
appropriately small).
$\eta$
appropriately small).
For the second, let
![]() $Z = Z(X) \geq 10$
be a parameter to be chosen later and observe that if
$Z = Z(X) \geq 10$
be a parameter to be chosen later and observe that if
![]() $|t| \geq Z/\log X$
then by the first claim we obtain
$|t| \geq Z/\log X$
then by the first claim we obtain
Next, suppose
![]() $|t| \leq Z/\log X$
. As mentioned in the proof of Proposition 2·2, Odoni showed that
$|t| \leq Z/\log X$
. As mentioned in the proof of Proposition 2·2, Odoni showed that
![]() $f_l$
is constant on the set of unramified primes
$f_l$
is constant on the set of unramified primes
![]() $p \in \widehat{\mathcal{N}}_K$
with a fixed pattern
$p \in \widehat{\mathcal{N}}_K$
with a fixed pattern
![]() $B(p) = B$
, taking a root of unity depending on B as its value. Thus, let
$B(p) = B$
, taking a root of unity depending on B as its value. Thus, let
![]() $B \in \mathcal{V}$
. We know that
$B \in \mathcal{V}$
. We know that
![]() $f_j(p) = \zeta_B$
for some root of unity (possibly equal to 1) for all p with
$f_j(p) = \zeta_B$
for some root of unity (possibly equal to 1) for all p with
![]() $B(p) = B$
. As discussed in Section 2·1, there is a collection of conjugacy classes
$B(p) = B$
. As discussed in Section 2·1, there is a collection of conjugacy classes
![]() $\mathcal{C}_B$
of
$\mathcal{C}_B$
of
![]() $G_K$
for which the Frobenius
$G_K$
for which the Frobenius
![]() $\sigma_p$
of p belongs to some class
$\sigma_p$
of p belongs to some class
![]() $C \in \mathcal{C}_B$
. Applying (2·1) and partial summation, whenever
$C \in \mathcal{C}_B$
. Applying (2·1) and partial summation, whenever
![]() $|t| \leq Z/\log X$
we obtain
$|t| \leq Z/\log X$
we obtain
 \begin{align*}\mathbb{D}_K(\sigma_f f_j, n^{it};\;X)^2 &\geq \sum_{\substack{e^{\sqrt{\log X}} < p \leq X \\ B(p) = B}} \frac{1-\sigma_f(p)\text{Re}(\zeta_B p^{-it})}{p} \\[5pt] &= \frac{c(B)}{2} \log\log X + O_K(1) - \text{Re}\left(\zeta_B \sum_{C \in \mathcal{C}_B} \sum_{\substack{e^{\sqrt{\log X}} < p \leq X \\ \sigma_p \in C}} \frac{\sigma_f(p)p^{-it}}{p}\right),\end{align*}
\begin{align*}\mathbb{D}_K(\sigma_f f_j, n^{it};\;X)^2 &\geq \sum_{\substack{e^{\sqrt{\log X}} < p \leq X \\ B(p) = B}} \frac{1-\sigma_f(p)\text{Re}(\zeta_B p^{-it})}{p} \\[5pt] &= \frac{c(B)}{2} \log\log X + O_K(1) - \text{Re}\left(\zeta_B \sum_{C \in \mathcal{C}_B} \sum_{\substack{e^{\sqrt{\log X}} < p \leq X \\ \sigma_p \in C}} \frac{\sigma_f(p)p^{-it}}{p}\right),\end{align*}
where the contribution from ramified primes is absorbed in the
![]() $O_K(1)$
term. Applying partial summation, the estimate
$O_K(1)$
term. Applying partial summation, the estimate
![]() $|t| \leq Z/\log X$
and Lemma 2·3, we obtain that there is a function
$|t| \leq Z/\log X$
and Lemma 2·3, we obtain that there is a function
![]() $\varepsilon(t) \rightarrow 0$
as
$\varepsilon(t) \rightarrow 0$
as
![]() $t \rightarrow \infty$
such that for each
$t \rightarrow \infty$
such that for each
![]() $C \in \mathcal{C}_B$
,
$C \in \mathcal{C}_B$
,
 \begin{align*}&\left|\sum_{\substack{e^{\sqrt{\log X}} < p \leq X \\ \sigma_p \in C}} \frac{\sigma_f(p)p^{-it}}{p}\right| \ll (1+|t|) \int_{e^{\sqrt{\log X}}}^X \left|\sum_{\substack{p \leq Y \\ \sigma_p \in C}} \sigma_f(p)\right| \frac{du}{u^2} + \frac{1}{\sqrt{\log X}} \\[5pt] &\leq (Z \log\log X) \max_{e^{\sqrt{\log X}} \leq Y \leq X} \frac{1}{\pi(Y)} \left||\{p \leq Y\;:\; \sigma_p \in C, \sigma_f(p) \in [0,1]\}| \right.\\& \left. - |\{p \leq Y\;:\; \sigma_p \in C , \sigma_f(p) \in [-1,0]\}| \right| + \frac{1}{\sqrt{\log X}}\\[5pt] &\leq \left(\min_{e^{\sqrt{\log X}} \leq Y\leq X} \varepsilon(Y)\right) Z\log\log X.\end{align*}
\begin{align*}&\left|\sum_{\substack{e^{\sqrt{\log X}} < p \leq X \\ \sigma_p \in C}} \frac{\sigma_f(p)p^{-it}}{p}\right| \ll (1+|t|) \int_{e^{\sqrt{\log X}}}^X \left|\sum_{\substack{p \leq Y \\ \sigma_p \in C}} \sigma_f(p)\right| \frac{du}{u^2} + \frac{1}{\sqrt{\log X}} \\[5pt] &\leq (Z \log\log X) \max_{e^{\sqrt{\log X}} \leq Y \leq X} \frac{1}{\pi(Y)} \left||\{p \leq Y\;:\; \sigma_p \in C, \sigma_f(p) \in [0,1]\}| \right.\\& \left. - |\{p \leq Y\;:\; \sigma_p \in C , \sigma_f(p) \in [-1,0]\}| \right| + \frac{1}{\sqrt{\log X}}\\[5pt] &\leq \left(\min_{e^{\sqrt{\log X}} \leq Y\leq X} \varepsilon(Y)\right) Z\log\log X.\end{align*}
If we therefore define
![]() $Z=Z(X)$
via
$Z=Z(X)$
via
 \begin{align*} Z(X)^2 \;:\!=\; \left(\min_{e^{\sqrt{\log X}} \leq Y \leq X} \varepsilon(Y)\right)^{-1},\end{align*}
\begin{align*} Z(X)^2 \;:\!=\; \left(\min_{e^{\sqrt{\log X}} \leq Y \leq X} \varepsilon(Y)\right)^{-1},\end{align*}
we obtain that, uniformly over
![]() $|t| \leq 2X$
,
$|t| \leq 2X$
,
 \begin{align*} \sum_{p \leq X} \frac{\Delta_K(p) - \sigma_f(p)\text{Re}(f_j(p)p^{-it})}{p} \geq \min\{\sigma \log Z, \left(\frac{1}{2}\max_{B \in \mathcal{V}} c(B) - O(\tfrac{1}{Z})\right) \log\log X\} - O_{K,f}(1),\end{align*}
\begin{align*} \sum_{p \leq X} \frac{\Delta_K(p) - \sigma_f(p)\text{Re}(f_j(p)p^{-it})}{p} \geq \min\{\sigma \log Z, \left(\frac{1}{2}\max_{B \in \mathcal{V}} c(B) - O(\tfrac{1}{Z})\right) \log\log X\} - O_{K,f}(1),\end{align*}
and as
![]() $Z(X) \rightarrow \infty$
with X, we obtain the second claim.
$Z(X) \rightarrow \infty$
with X, we obtain the second claim.
2·4. Background on multiplicative functions
In the proof of our main theorems, we will need to estimate, both asymptotically and/or with non-trivial upper bounds, the averages of sparsely-supported multiplicative functions. The following two lemmas will be key in this endeavour. The first of these results, due to Wirsing, allows us to asymptotically estimate partial sums of non-negative multiplicative functions that are slowly growing and suitably regular on the primes; it applies immediately to any such function that is everywhere bounded by 1.
Lemma 2·8 (Wirsing [
Reference Wirsing27
]). Let
![]() $\phi\;:\; \mathbb{N} \rightarrow [0,\infty)$
be a multiplicative function for which there are constants
$\phi\;:\; \mathbb{N} \rightarrow [0,\infty)$
be a multiplicative function for which there are constants
![]() $A,B > 0$
such that
$A,B > 0$
such that
 \begin{align*} \sup_p \phi(p) \leq B, \quad \quad \sum_{p^{\nu}, \nu \geq 2} \frac{\phi(p^{\nu}) \log p^{\nu}}{p^{\nu}} \leq A.\end{align*}
\begin{align*} \sup_p \phi(p) \leq B, \quad \quad \sum_{p^{\nu}, \nu \geq 2} \frac{\phi(p^{\nu}) \log p^{\nu}}{p^{\nu}} \leq A.\end{align*}
Assume furthermore that there is
![]() $\tau > 0$
, such that
$\tau > 0$
, such that
Then, as
![]() $X \rightarrow \infty$
,
$X \rightarrow \infty$
,
 \begin{align*} \frac{1}{X}\sum_{n \leq X} \phi(n) = \left(\frac{e^{-\gamma \tau}}{\Gamma(\tau)} + o(1)\right) \prod_{p \leq X} \left(1-\frac{1}{p}\right) \sum_{k \geq 0} \frac{\phi(p^k)}{p^k}.\end{align*}
\begin{align*} \frac{1}{X}\sum_{n \leq X} \phi(n) = \left(\frac{e^{-\gamma \tau}}{\Gamma(\tau)} + o(1)\right) \prod_{p \leq X} \left(1-\frac{1}{p}\right) \sum_{k \geq 0} \frac{\phi(p^k)}{p^k}.\end{align*}
We would also like a result complementing Wirsing’s theorem that allows us to say that if g is a multiplicative function such that
![]() $|g(n)|$
satisfies the hypotheses of Lemma 2·8 then, provided g oscillates sufficiently, we have
$|g(n)|$
satisfies the hypotheses of Lemma 2·8 then, provided g oscillates sufficiently, we have
![]() $\sum_{n \leq X} g(n) = o(\sum_{n \leq X} |g(n)|)$
. The following strong result of this kind is due to Tenenbaum.
$\sum_{n \leq X} g(n) = o(\sum_{n \leq X} |g(n)|)$
. The following strong result of this kind is due to Tenenbaum.
Lemma 2·9 (Tenenbaum, [
Reference Tenenbaum23
, corollary 2·1]). Let
![]() $T \geq 1$
. Let
$T \geq 1$
. Let
![]() $g\;:\; \mathbb{N} \rightarrow \mathbb{C}$
be a multiplicative function such that
$g\;:\; \mathbb{N} \rightarrow \mathbb{C}$
be a multiplicative function such that
 \begin{align*} \sup_p |g(p)| \leq A, \quad \sum_{p^{\nu}, \nu \geq 2} \frac{|g(p^{\nu})| (\log p^{\nu})^2}{p^{\nu}} \leq B.\end{align*}
\begin{align*} \sup_p |g(p)| \leq A, \quad \sum_{p^{\nu}, \nu \geq 2} \frac{|g(p^{\nu})| (\log p^{\nu})^2}{p^{\nu}} \leq B.\end{align*}
Assume furthermore that there is a constant
![]() $\beta > 0$
such that for any
$\beta > 0$
such that for any
![]() $2 \leq y \leq x$
we have
$2 \leq y \leq x$
we have
Then as
![]() $X \rightarrow \infty$
,
$X \rightarrow \infty$
,
 \begin{align*} \left|\frac{1}{X}\sum_{n \leq X} g(n)\right| \ll_{A,B,\beta} \left(\frac{1}{X}\sum_{n \leq X} |g(n)|\right) \cdot \left(\frac{1+m_g(X;\;T)}{e^{m_g(x;T)}} + \frac{1}{\sqrt{T}} + \frac{1}{\log x}\right),\end{align*}
\begin{align*} \left|\frac{1}{X}\sum_{n \leq X} g(n)\right| \ll_{A,B,\beta} \left(\frac{1}{X}\sum_{n \leq X} |g(n)|\right) \cdot \left(\frac{1+m_g(X;\;T)}{e^{m_g(x;T)}} + \frac{1}{\sqrt{T}} + \frac{1}{\log x}\right),\end{align*}
where we have denoted
 \begin{align*} m_g(x;\;T) \;:\!=\; \min_{|t| \leq T} \sum_{p \leq X} \frac{|g(p)|-\text{Re}(g(p)p^{-it})}{p}.\end{align*}
\begin{align*} m_g(x;\;T) \;:\!=\; \min_{|t| \leq T} \sum_{p \leq X} \frac{|g(p)|-\text{Re}(g(p)p^{-it})}{p}.\end{align*}
Finally, we will need a means of comparing short and long interval averages of multiplicative functions. To this end we will apply a recent result of the author [
Reference Mangerel10
], which in this context is a slight refinement (in certain aspects) of [
Reference Matomäki and Radziwiłł11
, theorem 1·9]. To state it we will need a bit of notation. For parameters
![]() $0 < \sigma \leq A \leq 1$
,
$0 < \sigma \leq A \leq 1$
,
![]() $\gamma > 0$
and X large we define the setFootnote 2
$\gamma > 0$
and X large we define the setFootnote 2
![]() $\mathcal{M}(X;\; A,\gamma,\sigma)$
to be the collection of all multiplicative functions
$\mathcal{M}(X;\; A,\gamma,\sigma)$
to be the collection of all multiplicative functions
![]() $g\;:\; \mathbb{N} \rightarrow \mathbb{C}$
such that:
$g\;:\; \mathbb{N} \rightarrow \mathbb{C}$
such that:
-
(i)
 $|g(n)| \leq 1$
for all
$|g(n)| \leq 1$
for all
 $n \leq X$
;
$n \leq X$
; -
(ii) for all
 $z_0 \leq z \leq w \leq X$
we haveFootnote 3
$z_0 \leq z \leq w \leq X$
we haveFootnote 3
 $$\sum_{z < p \leq w} \frac{|g(p)|}{p} \geq A \sum_{z < p \leq w} \frac{1}{p} - O\left(\frac{1}{(\log z)^{\gamma}}\right);$$
$$\sum_{z < p \leq w} \frac{|g(p)|}{p} \geq A \sum_{z < p \leq w} \frac{1}{p} - O\left(\frac{1}{(\log z)^{\gamma}}\right);$$
-
(iii) if
 $t_0 = t_0(g;\;X) \in [-X,X]$
is a minimiser for the map then for every
$t_0 = t_0(g;\;X) \in [-X,X]$
is a minimiser for the map then for every \begin{align*} t \mapsto \rho(g,n^{it};\;X)^2 \;:\!=\; \sum_{p \leq X} \frac{|g(p)| - \text{Re}(g(p)p^{-it})}{p},\end{align*}
\begin{align*} t \mapsto \rho(g,n^{it};\;X)^2 \;:\!=\; \sum_{p \leq X} \frac{|g(p)| - \text{Re}(g(p)p^{-it})}{p},\end{align*}
 $t \in [-2X,2X]$
we have
$t \in [-2X,2X]$
we have  \begin{align*} \rho(g,n^{it};\;X)^2 \geq \sigma \min\{\log\log X, \log(1+|t-t_0|\log X)\} - O_A(1).\end{align*}
\begin{align*} \rho(g,n^{it};\;X)^2 \geq \sigma \min\{\log\log X, \log(1+|t-t_0|\log X)\} - O_A(1).\end{align*}
-
For
 $g \in \mathcal{M}(X;\;A,\gamma,\sigma)$
we also define
$g \in \mathcal{M}(X;\;A,\gamma,\sigma)$
we also define  \begin{align*} H(g;\;X) \;:\!=\; \prod_{p \leq X} \left(1+\frac{(|g(p)|-1)^2}{p}\right).\end{align*}
\begin{align*} H(g;\;X) \;:\!=\; \prod_{p \leq X} \left(1+\frac{(|g(p)|-1)^2}{p}\right).\end{align*}
Lemma 2·10 ([
Reference Mangerel10
, theorem 1·7]). Let
![]() $X \geq 100$
. Let
$X \geq 100$
. Let
![]() $g \in \mathcal{M}(X;\;A,\gamma,\sigma)$
and put
$g \in \mathcal{M}(X;\;A,\gamma,\sigma)$
and put
![]() $t_0 = t_0(g;\;X)$
. Let
$t_0 = t_0(g;\;X)$
. Let
![]() $10 \leq h_0 \leq X/10H(g;\;X)$
and set
$10 \leq h_0 \leq X/10H(g;\;X)$
and set
![]() $h\;:\!=\; h_0 H(g;\;X)$
. Then there is
$h\;:\!=\; h_0 H(g;\;X)$
. Then there is
![]() $\kappa = \kappa(A,\sigma) > 0$
such that
$\kappa = \kappa(A,\sigma) > 0$
such that
 \begin{align*}&\frac{1}{X}\int_X^{2X}\left|\frac{1}{h}\sum_{x \leq n \leq x+h} g(n) - \frac{1}{h}\int_{x}^{x+h} u^{it_0} du \cdot \frac{1}{X}\sum_{X \leq n \leq 2X} g(n)n^{-it_0}\right|^2 dx \\[5pt] &\ll_A \left(\left(\frac{\log\log h_0}{\log h_0}\right)^A + \frac{\log\log X}{(\log X)^{\kappa}}\right) \prod_{p \leq X} \left(1+\frac{|g(p)|-1}{p}\right)^2.\end{align*}
\begin{align*}&\frac{1}{X}\int_X^{2X}\left|\frac{1}{h}\sum_{x \leq n \leq x+h} g(n) - \frac{1}{h}\int_{x}^{x+h} u^{it_0} du \cdot \frac{1}{X}\sum_{X \leq n \leq 2X} g(n)n^{-it_0}\right|^2 dx \\[5pt] &\ll_A \left(\left(\frac{\log\log h_0}{\log h_0}\right)^A + \frac{\log\log X}{(\log X)^{\kappa}}\right) \prod_{p \leq X} \left(1+\frac{|g(p)|-1}{p}\right)^2.\end{align*}
When g is non-negative the above estimate holds with
![]() $t_0 = 0$
.
$t_0 = 0$
.
Remark 2·11. The statement that
![]() $t_0 = 0$
when g is a non-negative function is not explicitly stated in [
Reference Mangerel10
, theorem 1·7], but the fact that 0 is a minimiser of
$t_0 = 0$
when g is a non-negative function is not explicitly stated in [
Reference Mangerel10
, theorem 1·7], but the fact that 0 is a minimiser of
![]() $t \mapsto \rho(g, n^{it};\;X)$
is clear: indeed,
$t \mapsto \rho(g, n^{it};\;X)$
is clear: indeed,
![]() $\rho(g,n^{it};\;X) \geq 0$
trivially for all t, and moreover as
$\rho(g,n^{it};\;X) \geq 0$
trivially for all t, and moreover as
![]() $g(p) = \text{Re}(g(p)) = |g(p)|$
in this case we have
$g(p) = \text{Re}(g(p)) = |g(p)|$
in this case we have
As a consequence of this result, we obtain the following.
Corollary 2·12.
Let X be large and let
![]() $10 \leq h_0 \leq (\log X)^{100}$
. Let
$10 \leq h_0 \leq (\log X)^{100}$
. Let
![]() $g \in \mathcal{M}(X;\;A,\gamma,\sigma)$
and set
$g \in \mathcal{M}(X;\;A,\gamma,\sigma)$
and set
![]() $t_0 = t_0(g;\;X)$
. Let
$t_0 = t_0(g;\;X)$
. Let
![]() $\delta = \delta(X) \in (0,1)$
be a small quantity such that
$\delta = \delta(X) \in (0,1)$
be a small quantity such that
Then for all but
![]() $O(\delta X)$
integers
$O(\delta X)$
integers
![]() $x \in [X,2X]$
we have
$x \in [X,2X]$
we have
 \begin{align*} \left|\frac{1}{h} \sum_{x \leq n \leq x+h} g(n) - \frac{1}{h}\int_x^{x+h} u^{it_0} du \cdot \frac{1}{X}\sum_{X \leq n \leq 2X} g(n)n^{-it_0}\right| \ll \delta \prod_{p \leq X}\left(1+\frac{|g(p)|-1}{p}\right).\end{align*}
\begin{align*} \left|\frac{1}{h} \sum_{x \leq n \leq x+h} g(n) - \frac{1}{h}\int_x^{x+h} u^{it_0} du \cdot \frac{1}{X}\sum_{X \leq n \leq 2X} g(n)n^{-it_0}\right| \ll \delta \prod_{p \leq X}\left(1+\frac{|g(p)|-1}{p}\right).\end{align*}
If g is non-negative then the same estimate holds with
![]() $t_0 = 0$
.
$t_0 = 0$
.
Proof. Since
![]() $g \in \mathcal{M}(X;\;A,\gamma,\sigma)$
, Lemma 2·10 together with Chebyshev’s integral inequality yields that the measure of
$g \in \mathcal{M}(X;\;A,\gamma,\sigma)$
, Lemma 2·10 together with Chebyshev’s integral inequality yields that the measure of
![]() $x \in [X,2X]$
for which the claimed bound does not hold is
$x \in [X,2X]$
for which the claimed bound does not hold is
 \begin{align*}&\!\!\leq \delta^{-2}\prod_{p \leq X} \!\left(\!1+ \frac{|g(p)|-1}{p}\!\right)^{\!-2}\! \int_X^{2X} \!\left|\frac{1}{h} \sum_{x \leq n \leq x+h} \!g(n) - \frac{1}{h}\int_x^{x+h} \!u^{it_0} du \cdot \frac{1}{X}\sum_{X \leq n \leq 2X} g(n)n^{-it_0} \right|^2 dx \\[5pt] &\ll \delta^{-2}X\left(\frac{\log\log h_0}{\log h_0}\right)^A \leq \delta X.\end{align*}
\begin{align*}&\!\!\leq \delta^{-2}\prod_{p \leq X} \!\left(\!1+ \frac{|g(p)|-1}{p}\!\right)^{\!-2}\! \int_X^{2X} \!\left|\frac{1}{h} \sum_{x \leq n \leq x+h} \!g(n) - \frac{1}{h}\int_x^{x+h} \!u^{it_0} du \cdot \frac{1}{X}\sum_{X \leq n \leq 2X} g(n)n^{-it_0} \right|^2 dx \\[5pt] &\ll \delta^{-2}X\left(\frac{\log\log h_0}{\log h_0}\right)^A \leq \delta X.\end{align*}
As in Lemma 2·10, when g is non-negative the same conclusion applies with
![]() $t_0 = 0$
. Since
$t_0 = 0$
. Since
![]() $x\mapsto \sum_{x \leq n \leq x+h} g(n)$
is piecewise constant, the claimed cardinality bound for integer
$x\mapsto \sum_{x \leq n \leq x+h} g(n)$
is piecewise constant, the claimed cardinality bound for integer
![]() $x \in [X,2X]$
is equivalent to the measure bound for real
$x \in [X,2X]$
is equivalent to the measure bound for real
![]() $x \in [X,2X]$
.
$x \in [X,2X]$
.
3. Proofs of Theorem 1·5
In this section we will prove Theorem 1·5. We briefly describe here the idea of the argument. Recall the notation
 \begin{align*} \delta_K(X) = \prod_{\substack{p \leq X \\ p \notin \widehat{\mathcal{N}}_K}} (1-1/p).\end{align*}
\begin{align*} \delta_K(X) = \prod_{\substack{p \leq X \\ p \notin \widehat{\mathcal{N}}_K}} (1-1/p).\end{align*}
Suppose we can show that for large enough X and
![]() $h = h(X) \ll \delta_K(X)^{-1}$
there are
$h = h(X) \ll \delta_K(X)^{-1}$
there are
![]() $\geq 3X/4$
integers
$\geq 3X/4$
integers
![]() $x \in [X,2X]$
for which each of the following inequalities hold:
$x \in [X,2X]$
for which each of the following inequalities hold:
By the union bound, it would follow that for
![]() $\geq X/2$
integers
$\geq X/2$
integers
![]() $x \in [X,2X]$
there are integers
$x \in [X,2X]$
there are integers
![]() $n_1,n_2 \in [x,x+h]$
such that
$n_1,n_2 \in [x,x+h]$
such that
![]() $n_j \in \mathcal{N}_K$
and
$n_j \in \mathcal{N}_K$
and
![]() $\sigma_f(n_1)\sigma_f(n_2) < 0$
. This implies the existence of a sign change for
$\sigma_f(n_1)\sigma_f(n_2) < 0$
. This implies the existence of a sign change for
![]() $\lambda_f(n)$
as n ranges over norm forms
$\lambda_f(n)$
as n ranges over norm forms
![]() $\mathcal{N}_K \cap [x,x+h]$
in
$\mathcal{N}_K \cap [x,x+h]$
in
![]() $\geq X/2$
such sets. Choosing greedily a subset of these endpoints x such that each pair of consecutive points are
$\geq X/2$
such sets. Choosing greedily a subset of these endpoints x such that each pair of consecutive points are
![]() $>h$
from one another, we deduce that each of these sign changes is distinct, and their number is
$>h$
from one another, we deduce that each of these sign changes is distinct, and their number is
![]() $\gg X/h \gg \delta_K(X) X$
. This would thus yield Theorem 1·5.
$\gg X/h \gg \delta_K(X) X$
. This would thus yield Theorem 1·5.
In order to verify (3·1) we will compare, using Corollary 2·12, such short sums to corresponding long sums. We will then apply the results of the previous section in order to estimate these long sums.
Recall once again that
where
![]() $B_{K,f} \;:\!=\; \{p: \lambda_f(p) = 0\} \cup \{p\;:\; p|\text{disc}(K/\mathbb{Q})\}$
, and the definition of
$B_{K,f} \;:\!=\; \{p: \lambda_f(p) = 0\} \cup \{p\;:\; p|\text{disc}(K/\mathbb{Q})\}$
, and the definition of
![]() $\Delta_K$
in (2·4).
$\Delta_K$
in (2·4).
Lemma 3·1.
With the notation of Proposition 2·2, let
![]() $M+1 \leq l \leq R$
, let
$M+1 \leq l \leq R$
, let
![]() $u \in [-X,X]$
and let
$u \in [-X,X]$
and let
![]() $g \in \{1,\sigma_f\}$
. Then the following bounds hold as
$g \in \{1,\sigma_f\}$
. Then the following bounds hold as
![]() $X \rightarrow \infty$
:
$X \rightarrow \infty$
:
 \begin{align} \left|\frac{1}{X}\sum_{n \leq X} \sigma_f(n)\Delta_K(n)\iota_{K,f}(n)n^{-iu}\right| = o_{K,f}\left(\prod_{p \leq X} \left(1+\frac{\Delta_K(p)-1}{p}\right)\right) \end{align}
\begin{align} \left|\frac{1}{X}\sum_{n \leq X} \sigma_f(n)\Delta_K(n)\iota_{K,f}(n)n^{-iu}\right| = o_{K,f}\left(\prod_{p \leq X} \left(1+\frac{\Delta_K(p)-1}{p}\right)\right) \end{align}
 \begin{align} \left|\frac{1}{X}\sum_{n \leq X} g(n)f_l(n)\iota_{K,f}(n) n^{-iu}\right| = o_{K,f}\left(\prod_{p \leq X} \left(1+\frac{\Delta_K(p)-1}{p}\right)\right). \end{align}
\begin{align} \left|\frac{1}{X}\sum_{n \leq X} g(n)f_l(n)\iota_{K,f}(n) n^{-iu}\right| = o_{K,f}\left(\prod_{p \leq X} \left(1+\frac{\Delta_K(p)-1}{p}\right)\right). \end{align}
Proof. Note that
![]() $0 \leq \Delta_K\iota_{K,f} \leq 1$
, and combining Lemmas 2·1 and 2·5 with partial summation we have
$0 \leq \Delta_K\iota_{K,f} \leq 1$
, and combining Lemmas 2·1 and 2·5 with partial summation we have
 \begin{align*} \sum_{p \leq X} \frac{\Delta_K(p)\iota_{K,f}(p) \log p}{p} & = \sum_{p \leq X} \frac{\Delta_K(p) \log p}{p} + O\left(\sum_{p \leq X} \frac{(1-\iota_{K,f}(p))\log p}{p}\right)\\[5pt] &= \tau_K \log X + O_{\varepsilon}((\log X)^{3/4+\varepsilon}).\end{align*}
\begin{align*} \sum_{p \leq X} \frac{\Delta_K(p)\iota_{K,f}(p) \log p}{p} & = \sum_{p \leq X} \frac{\Delta_K(p) \log p}{p} + O\left(\sum_{p \leq X} \frac{(1-\iota_{K,f}(p))\log p}{p}\right)\\[5pt] &= \tau_K \log X + O_{\varepsilon}((\log X)^{3/4+\varepsilon}).\end{align*}
Hence, Lemma 2·8 applies, and we obtain
By Mertens’ theorem and Lemma 2·5, we obtain that
 \begin{align*}\prod_{p \leq X} \left(1-\frac{1}{p}\right)\left(1+\frac{\Delta_K(p)\iota_{K,f}(p)}{p}\right) & \asymp \exp\left(\sum_{p \leq X} \frac{\Delta_K(p)\iota_{K,f}(p)-1}{p}\right)\\[5pt] &= \exp\left(\sum_{p \leq X} \frac{\Delta_K(p)-1}{p} + O_{K,f}(1)\right) \\[5pt] &\asymp_{K,f} \prod_{p \leq X} \left(1+\frac{\Delta_K(p)-1}{p}\right),\end{align*}
\begin{align*}\prod_{p \leq X} \left(1-\frac{1}{p}\right)\left(1+\frac{\Delta_K(p)\iota_{K,f}(p)}{p}\right) & \asymp \exp\left(\sum_{p \leq X} \frac{\Delta_K(p)\iota_{K,f}(p)-1}{p}\right)\\[5pt] &= \exp\left(\sum_{p \leq X} \frac{\Delta_K(p)-1}{p} + O_{K,f}(1)\right) \\[5pt] &\asymp_{K,f} \prod_{p \leq X} \left(1+\frac{\Delta_K(p)-1}{p}\right),\end{align*}
which in light of the previous estimate gives (3·2).
Estimates (3·3) and (3·4) are consequences of Lemma 2·7. Indeed, we have
![]() $|\sigma_f \Delta_K n^{-iu}|, |gf_l n^{-iu}| \leq \Delta_K$
, with equality at primes except on the sparse set
$|\sigma_f \Delta_K n^{-iu}|, |gf_l n^{-iu}| \leq \Delta_K$
, with equality at primes except on the sparse set
![]() $B_{K,f}$
. In the notation of Lemma 2·9, taking
$B_{K,f}$
. In the notation of Lemma 2·9, taking
![]() $T = (\log X)^2$
,
$T = (\log X)^2$
,
 \begin{align*}m_{\phi}(X;\;T) &= \min_{|t| \leq T} \sum_{p \leq X} \frac{\Delta_K(p) - \text{Re}(\phi(p)p^{-it})}{p} - O_{K,f}(1) \\[5pt] &\geq \min_{|t| \leq T} \mathbb{D}_K(\phi ,n^{i(t-u)};\;X)^2 - O_{K,f}(1) \rightarrow \infty,\end{align*}
\begin{align*}m_{\phi}(X;\;T) &= \min_{|t| \leq T} \sum_{p \leq X} \frac{\Delta_K(p) - \text{Re}(\phi(p)p^{-it})}{p} - O_{K,f}(1) \\[5pt] &\geq \min_{|t| \leq T} \mathbb{D}_K(\phi ,n^{i(t-u)};\;X)^2 - O_{K,f}(1) \rightarrow \infty,\end{align*}
as
![]() $X \rightarrow \infty$
whenever
$X \rightarrow \infty$
whenever
![]() $\phi = \sigma_f \Delta_Kn^{-iu}$
or
$\phi = \sigma_f \Delta_Kn^{-iu}$
or
![]() $\phi = g f_l n^{-iu}$
, for
$\phi = g f_l n^{-iu}$
, for
![]() $M+1 \leq l \leq R$
and
$M+1 \leq l \leq R$
and
![]() $|u| \leq X$
. Finally, if, more simply,
$|u| \leq X$
. Finally, if, more simply,
![]() $\phi = f_ln^{-iu}$
then by Proposition 2·2 we have
$\phi = f_ln^{-iu}$
then by Proposition 2·2 we have
Note that Lemma 2·9 applies since all of the functions in play are bounded by 1, and the lower bound on sums
![]() $\sum_{y \leq p \leq x} \Delta_K(p)/p$
is an immediate consequence of Lemma 2·1. We thus get that each of the quantities on the LHS of (3·3) and (3·4) is bounded from above by
$\sum_{y \leq p \leq x} \Delta_K(p)/p$
is an immediate consequence of Lemma 2·1. We thus get that each of the quantities on the LHS of (3·3) and (3·4) is bounded from above by
 \begin{align*} \ll_{K,f} \!\left(\frac{1}{X} \sum_{n \leq X} \Delta_K(n)\right) \cdot \left(\frac{1+m_{\phi}(X;(\log X)^2)}{e^{m_{\phi}(X;(\log X)^2)}} + \frac{1}{\log X}\right) = o_{K,f}\!\left(\prod_{p \leq X} \left(1+\frac{\Delta_K(p)-1}{p}\right)\!\right),\end{align*}
\begin{align*} \ll_{K,f} \!\left(\frac{1}{X} \sum_{n \leq X} \Delta_K(n)\right) \cdot \left(\frac{1+m_{\phi}(X;(\log X)^2)}{e^{m_{\phi}(X;(\log X)^2)}} + \frac{1}{\log X}\right) = o_{K,f}\!\left(\prod_{p \leq X} \left(1+\frac{\Delta_K(p)-1}{p}\right)\!\right),\end{align*}
where in the last step the bracketed sum was estimated using Lemma 2·8, just as in (3·2). This completes the proof.
Finally, let us note that as
![]() $\Delta_K(p) \in \{0,1\}$
we have
$\Delta_K(p) \in \{0,1\}$
we have
 \begin{align*} H(\Delta_K;\;X) = \prod_{p \leq X} \left(1+\frac{(\Delta_K(p)-1)^2}{p}\right) = \prod_{p \leq X} \left(1+\frac{1-\Delta_K(p)}{p}\right) = \delta_K(X)^{-1}.\end{align*}
\begin{align*} H(\Delta_K;\;X) = \prod_{p \leq X} \left(1+\frac{(\Delta_K(p)-1)^2}{p}\right) = \prod_{p \leq X} \left(1+\frac{1-\Delta_K(p)}{p}\right) = \delta_K(X)^{-1}.\end{align*}
We will use this fact in what follows.
Proof of Theorem
1·5. Let
![]() $\delta \in (0,1/4)$
be a small parameter. In light of the discussion at the beginning of this section, it will suffice to show that for all but
$\delta \in (0,1/4)$
be a small parameter. In light of the discussion at the beginning of this section, it will suffice to show that for all but
![]() $O(\delta X)$
choices of
$O(\delta X)$
choices of
![]() $x \in [X,2X]$
we obtain, for both
$x \in [X,2X]$
we obtain, for both
![]() $\eta \in \{-1,+1\}$
, the positive lower bound
$\eta \in \{-1,+1\}$
, the positive lower bound
Since
![]() $|\sigma_f(n)| +\eta \sigma_f(n) \geq 0$
for
$|\sigma_f(n)| +\eta \sigma_f(n) \geq 0$
for
![]() $\eta \in \{-1,+1\}$
, by positivity the latter sum is
$\eta \in \{-1,+1\}$
, by positivity the latter sum is
since
![]() $\iota_{K,f}(n) = 0$
whenever
$\iota_{K,f}(n) = 0$
whenever
![]() $\sigma_f(n) = 0$
. By Proposition 2·2 we may use the decomposition of
$\sigma_f(n) = 0$
. By Proposition 2·2 we may use the decomposition of
![]() $g_K$
as a linear combination of multiplicative functions to write this last sum as
$g_K$
as a linear combination of multiplicative functions to write this last sum as
![]() $\mathcal{L}(x) + \mathcal{S}(x)$
, where we define
$\mathcal{L}(x) + \mathcal{S}(x)$
, where we define
 \begin{align*}\mathcal{L}(x) &\;:\!=\; \sum_{0 \leq l \leq M} c_l \sum_{x \leq n \leq x+h} f_l(n)\iota_{K,f}(n)(1 + \eta \sigma_f(n)) \\[5pt] &= \left(\sum_{0 \leq l \leq M} c_l\right) \sum_{x \leq n \leq x+h} \Delta_K(n)\iota_{K,f}(n)(1+\eta \sigma_f(n)), \\[5pt] \mathcal{S}(x) &\;:\!=\; \sum_{M+1 \leq l \leq R} c_l \sum_{x \leq n \leq x+h} f_l(n)\iota_{K,f}(n)(1 + \eta \sigma_f(n)),\end{align*}
\begin{align*}\mathcal{L}(x) &\;:\!=\; \sum_{0 \leq l \leq M} c_l \sum_{x \leq n \leq x+h} f_l(n)\iota_{K,f}(n)(1 + \eta \sigma_f(n)) \\[5pt] &= \left(\sum_{0 \leq l \leq M} c_l\right) \sum_{x \leq n \leq x+h} \Delta_K(n)\iota_{K,f}(n)(1+\eta \sigma_f(n)), \\[5pt] \mathcal{S}(x) &\;:\!=\; \sum_{M+1 \leq l \leq R} c_l \sum_{x \leq n \leq x+h} f_l(n)\iota_{K,f}(n)(1 + \eta \sigma_f(n)),\end{align*}
where we re-expressed
![]() $\mathcal{L}$
using the fact that
$\mathcal{L}$
using the fact that
![]() $\iota_{K,f}(n) = 0$
unless
$\iota_{K,f}(n) = 0$
unless
![]() $(n,\text{disc}(K/\mathbb{Q})) = 1$
, in which case
$(n,\text{disc}(K/\mathbb{Q})) = 1$
, in which case
![]() $f_l(n) = \Delta_K(n)$
for all
$f_l(n) = \Delta_K(n)$
for all
![]() $0 \leq l \leq M$
. Combining Proposition 2·2 with Lemmas 2·4 and 2·7, note that
$0 \leq l \leq M$
. Combining Proposition 2·2 with Lemmas 2·4 and 2·7, note that
![]() $\phi \in \mathcal{M}(X;\;\tau_K, 1/4-\eta, (1-3\eta)\tau_K/(12D^2)\}$
whenever
$\phi \in \mathcal{M}(X;\;\tau_K, 1/4-\eta, (1-3\eta)\tau_K/(12D^2)\}$
whenever
![]() $\phi = \sigma_f f_l$
for any
$\phi = \sigma_f f_l$
for any
![]() $0 \leq l \leq R$
and
$0 \leq l \leq R$
and
![]() $\eta > 0$
is sufficiently small; when
$\eta > 0$
is sufficiently small; when
![]() $\phi = f_l$
the same lemmas also imply that
$\phi = f_l$
the same lemmas also imply that
![]() $\phi \in \mathcal{M}(X;\;\tau_K, 1/4-\eta,\rho)$
.
$\phi \in \mathcal{M}(X;\;\tau_K, 1/4-\eta,\rho)$
.
Let us show first that
To see this, we note first of all that for any
![]() $t_0 \in [-X,X]$
and
$t_0 \in [-X,X]$
and
![]() $g \in \{1,\sigma_f\}$
, Lemma 3·1 shows that for each
$g \in \{1,\sigma_f\}$
, Lemma 3·1 shows that for each
![]() $M+1 \leq l \leq R$
,
$M+1 \leq l \leq R$
,
 \begin{align*} \frac{1}{X}\left|\sum_{X \leq n \leq 2X} f_l(n)g(n)\iota_{K,f}(n)n^{-it_0}\right| & \ll \max_{Y \in [X,2X]} \frac{1}{Y}\left|\sum_{n \leq Y} f_l(n)g(n)n^{-it_0}\right| \\[5pt] & = o_{K,f}\left(\prod_{p \leq X}\left(1+\frac{\Delta_K(p)-1}{p}\right)\right).\end{align*}
\begin{align*} \frac{1}{X}\left|\sum_{X \leq n \leq 2X} f_l(n)g(n)\iota_{K,f}(n)n^{-it_0}\right| & \ll \max_{Y \in [X,2X]} \frac{1}{Y}\left|\sum_{n \leq Y} f_l(n)g(n)n^{-it_0}\right| \\[5pt] & = o_{K,f}\left(\prod_{p \leq X}\left(1+\frac{\Delta_K(p)-1}{p}\right)\right).\end{align*}
Moreover, choosing X sufficiently large,
![]() $h_0$
sufficiently large in terms of
$h_0$
sufficiently large in terms of
![]() $\delta$
and writing
$\delta$
and writing
![]() $h = h_0H(\Delta_K;\;X)$
, we may combine this with Corollary 2·12 and the triangle inequality to deduce that for each
$h = h_0H(\Delta_K;\;X)$
, we may combine this with Corollary 2·12 and the triangle inequality to deduce that for each
![]() $M+1 \leq l \leq R$
, for all but
$M+1 \leq l \leq R$
, for all but
![]() $O(\delta X)$
choices of
$O(\delta X)$
choices of
![]() $x \in [X,2X]$
we have
$x \in [X,2X]$
we have
 \begin{align*}&\left|\frac{1}{h}\sum_{x \leq n \leq x+h} f_l(n)g(n)\iota_{K,f}(n) \right| \\[5pt] &\ll \left|\frac{1}{h}\sum_{x \leq n \leq x+h} f_l(n)g(n)\iota_{K,f}(n) - \frac{1}{h}\int_x^{x+h} u^{it_0} du \cdot \frac{1}{X}\sum_{X \leq n \leq 2X} f_l(n)g(n)\iota_{K,f}(n) n^{-it_0}\right| \\[5pt] & \quad + \frac{1}{X}\left|\sum_{X \leq n \leq 2X} f_l(n)g(n)\iota_{K,f}(n)n^{-it_0}\right| \\[5pt] & \quad \ll_{K,f} \delta \prod_{p \leq X} \left(1 + \frac{\Delta_K(p)-1}{p}\right),\end{align*}
\begin{align*}&\left|\frac{1}{h}\sum_{x \leq n \leq x+h} f_l(n)g(n)\iota_{K,f}(n) \right| \\[5pt] &\ll \left|\frac{1}{h}\sum_{x \leq n \leq x+h} f_l(n)g(n)\iota_{K,f}(n) - \frac{1}{h}\int_x^{x+h} u^{it_0} du \cdot \frac{1}{X}\sum_{X \leq n \leq 2X} f_l(n)g(n)\iota_{K,f}(n) n^{-it_0}\right| \\[5pt] & \quad + \frac{1}{X}\left|\sum_{X \leq n \leq 2X} f_l(n)g(n)\iota_{K,f}(n)n^{-it_0}\right| \\[5pt] & \quad \ll_{K,f} \delta \prod_{p \leq X} \left(1 + \frac{\Delta_K(p)-1}{p}\right),\end{align*}
where in the above,
![]() $t_0 = t_0(f_l g;\;X)$
. Combining all of the
$t_0 = t_0(f_l g;\;X)$
. Combining all of the
![]() $R-M = O_K(1)$
exceptional sets in this way, we see that for all but
$R-M = O_K(1)$
exceptional sets in this way, we see that for all but
![]() $O_{K,f}(\delta X)$
choices of
$O_{K,f}(\delta X)$
choices of
![]() $x \in [X,2X]$
, we obtain by the triangle inequality that
$x \in [X,2X]$
, we obtain by the triangle inequality that
 \begin{align*} |\mathcal{S}(x)| \leq \sum_{M+1 \leq l \leq R} |c_l| \sum_{g \in \{1,\sigma_f\}} \left|\sum_{x \leq n \leq x+h} f_l(n)g(n)\iota_{K,f}(n)\right| \ll_{K,f} \delta h \prod_{p \leq X} \left(1+\frac{\Delta_K(p)-1}{p}\right).\end{align*}
\begin{align*} |\mathcal{S}(x)| \leq \sum_{M+1 \leq l \leq R} |c_l| \sum_{g \in \{1,\sigma_f\}} \left|\sum_{x \leq n \leq x+h} f_l(n)g(n)\iota_{K,f}(n)\right| \ll_{K,f} \delta h \prod_{p \leq X} \left(1+\frac{\Delta_K(p)-1}{p}\right).\end{align*}
Next, write
 \begin{align*}\mathcal{L}(x) &= \left(\sum_{0 \leq l \leq M} c_l\right) \sum_{x \leq n \leq x+h} \Delta_K(n) \iota_{K,f}(n)(1+\eta \sigma_f(n)) = \left(\sum_{0 \leq l \leq M} c_l\right) \left( \mathcal{L}_1(x) + \eta \mathcal{L}_2(x)\right).\end{align*}
\begin{align*}\mathcal{L}(x) &= \left(\sum_{0 \leq l \leq M} c_l\right) \sum_{x \leq n \leq x+h} \Delta_K(n) \iota_{K,f}(n)(1+\eta \sigma_f(n)) = \left(\sum_{0 \leq l \leq M} c_l\right) \left( \mathcal{L}_1(x) + \eta \mathcal{L}_2(x)\right).\end{align*}
Combining Lemma 3·1 with Corollary 2·12 as above, we may deduce in the same way that for all but
![]() $O_{K,f}(\delta X)$
choices of
$O_{K,f}(\delta X)$
choices of
![]() $x \in [X,2X]$
we have
$x \in [X,2X]$
we have
Furthermore, if we set
then by Corollary 2·12 we once again have (taking
![]() $t_0 = 0$
since
$t_0 = 0$
since
![]() $\Delta_K\iota_{K,f} \geq 0$
) that for all but
$\Delta_K\iota_{K,f} \geq 0$
) that for all but
![]() $O_{K,f}(\delta X)$
choices of
$O_{K,f}(\delta X)$
choices of
![]() $x \in [X,2X]$
,
$x \in [X,2X]$
,
 \begin{align*} |\mathcal{L}_1(x)| \geq \frac{h}{X} \tilde{\mathcal{L}}_1(X) - h\Bigg|\frac 1h \mathcal{L}_1(x) - \frac 1X \tilde{\mathcal{L}}_1(X) \Bigg| \geq \frac{h}{X} \tilde{\mathcal{L}}_1(X) - O_{K,f}\!\left(\delta h\prod_{p \leq X}\left(1+\frac{\Delta_K(p)-1}{p}\right)\!\right)\!.\end{align*}
\begin{align*} |\mathcal{L}_1(x)| \geq \frac{h}{X} \tilde{\mathcal{L}}_1(X) - h\Bigg|\frac 1h \mathcal{L}_1(x) - \frac 1X \tilde{\mathcal{L}}_1(X) \Bigg| \geq \frac{h}{X} \tilde{\mathcal{L}}_1(X) - O_{K,f}\!\left(\delta h\prod_{p \leq X}\left(1+\frac{\Delta_K(p)-1}{p}\right)\!\right)\!.\end{align*}
Combining all of these facts together (and taking unions over exceptional sets), we deduce that for all but
![]() $O_{K,f}(\delta X)$
choices of
$O_{K,f}(\delta X)$
choices of
![]() $x \in [X,2X]$
we have, simultaneously for both
$x \in [X,2X]$
we have, simultaneously for both
![]() $\eta \in \{-1,+1\}$
,
$\eta \in \{-1,+1\}$
,
 \begin{align*}&\sum_{x \leq n \leq x+h} g_K(n)\iota_{K,f}(n)(1+\eta \sigma_f(n)) \\[5pt] &\geq \left(\sum_{0 \leq l \leq M} c_l\right) \cdot \frac{h}{X} \sum_{X \leq n \leq 2X} \Delta_K(n)\iota_{K,f}(n) - O\left(\delta h \prod_{p \leq X} \left(1+\frac{\Delta_K(p)-1}{p}\right)\right) \\[5pt] &\geq \left(c-O_{K,f}(\delta)\right) h \prod_{p \leq X} \left(1+\frac{\Delta_K(p)-1}{p}\right),\end{align*}
\begin{align*}&\sum_{x \leq n \leq x+h} g_K(n)\iota_{K,f}(n)(1+\eta \sigma_f(n)) \\[5pt] &\geq \left(\sum_{0 \leq l \leq M} c_l\right) \cdot \frac{h}{X} \sum_{X \leq n \leq 2X} \Delta_K(n)\iota_{K,f}(n) - O\left(\delta h \prod_{p \leq X} \left(1+\frac{\Delta_K(p)-1}{p}\right)\right) \\[5pt] &\geq \left(c-O_{K,f}(\delta)\right) h \prod_{p \leq X} \left(1+\frac{\Delta_K(p)-1}{p}\right),\end{align*}
for some
![]() $c = c(K,f) > 0$
, where in the last estimate we used (3·2). Choosing
$c = c(K,f) > 0$
, where in the last estimate we used (3·2). Choosing
![]() $\delta$
sufficiently small as a function of K and f, we thus obtain
$\delta$
sufficiently small as a function of K and f, we thus obtain
for
![]() $\geq (1-O_{K,f}(\delta))X \geq 3X/4$
choices of
$\geq (1-O_{K,f}(\delta))X \geq 3X/4$
choices of
![]() $x \in [X,2X]$
. Since now
$x \in [X,2X]$
. Since now
![]() $h_0$
was simply chosen sufficiently large in terms of
$h_0$
was simply chosen sufficiently large in terms of
![]() $\delta$
, we can take it of some large size
$\delta$
, we can take it of some large size
![]() $O_{K,f}(1)$
, in which case
$O_{K,f}(1)$
, in which case
![]() $h = h_0H(\Delta_K;\;X) \asymp_{K,f} \delta_K(X)^{-1}$
, and the claim follows.
$h = h_0H(\Delta_K;\;X) \asymp_{K,f} \delta_K(X)^{-1}$
, and the claim follows.
4. Proofs of Theorem 1·6
Fix an integer
![]() $a \neq 0$
. The proof of Theorem 1·6 relies on two propositions.
$a \neq 0$
. The proof of Theorem 1·6 relies on two propositions.
Proposition 4·1.
Let
![]() $\delta > 0$
and suppose
$\delta > 0$
and suppose
![]() $X^{\varepsilon} < h \leq X^{1-\varepsilon}$
. Then for all but
$X^{\varepsilon} < h \leq X^{1-\varepsilon}$
. Then for all but
![]() $O(X/(\log \log X)^{1/10})$
choices of
$O(X/(\log \log X)^{1/10})$
choices of
![]() $x \in [X,2X]$
we have
$x \in [X,2X]$
we have
 \begin{align*} \sum_{\substack{x < n \leq x+ h \\ 0 < |\lambda_f(n)| < X^{-\delta}}} r(n+a) \ll_{\varepsilon,\delta,f} \frac{h}{(\log\log X)^{1/10}}.\end{align*}
\begin{align*} \sum_{\substack{x < n \leq x+ h \\ 0 < |\lambda_f(n)| < X^{-\delta}}} r(n+a) \ll_{\varepsilon,\delta,f} \frac{h}{(\log\log X)^{1/10}}.\end{align*}
Proposition 4·2.
Let
![]() $X^{1/3 + \varepsilon} < h \leq X^{1-\varepsilon}$
. Then for all but
$X^{1/3 + \varepsilon} < h \leq X^{1-\varepsilon}$
. Then for all but
![]() $O(X/(\log \log X)^{1/10})$
choices of
$O(X/(\log \log X)^{1/10})$
choices of
![]() $x \in [X,2X]$
we have
$x \in [X,2X]$
we have
 \begin{align*} \sum_{\substack{x < n \leq x + h \\ \lambda_f(n) \neq 0}} r(n+a) \gg_{\varepsilon,f} h.\end{align*}
\begin{align*} \sum_{\substack{x < n \leq x + h \\ \lambda_f(n) \neq 0}} r(n+a) \gg_{\varepsilon,f} h.\end{align*}
Proof of Theorem 4·1 and 4·2. Let
![]() $X^{1/2+3\varepsilon} < h \leq X^{1-\varepsilon}$
and let
$X^{1/2+3\varepsilon} < h \leq X^{1-\varepsilon}$
and let
![]() $\eta \in (0,1/4)$
be a small parameter. Assume for the sake of contradiction that
$\eta \in (0,1/4)$
be a small parameter. Assume for the sake of contradiction that
(the corresponding case where
![]() $\lambda_f(n) > 0$
on
$\lambda_f(n) > 0$
on
![]() $[x,x+h]$
is completely similar). Thus, for all but
$[x,x+h]$
is completely similar). Thus, for all but
![]() $\leq \eta X$
choices of
$\leq \eta X$
choices of
![]() $x \in [X,2X]$
, we have that
$x \in [X,2X]$
, we have that
![]() $\lambda_f(n)r(n-a)$
has the same sign for all
$\lambda_f(n)r(n-a)$
has the same sign for all
![]() $n \in [x,x+h]$
. For such an x,
$n \in [x,x+h]$
. For such an x,
 \begin{align*} \sum_{x < n \leq x+h} |\lambda_f(n)| r(n-a) = \sum_{x < n \leq x+h} \lambda_f(n)r(n-a) \ll \max_{X < y \leq 3X} \left|\sum_{n \leq y} \lambda_f(n)r(n-a)\right|.\end{align*}
\begin{align*} \sum_{x < n \leq x+h} |\lambda_f(n)| r(n-a) = \sum_{x < n \leq x+h} \lambda_f(n)r(n-a) \ll \max_{X < y \leq 3X} \left|\sum_{n \leq y} \lambda_f(n)r(n-a)\right|.\end{align*}
By a shifted convolution sum estimate of Ravindran [ Reference Ravindran18 ], we obtain
 \begin{align*} \left|\sum_{x < n \leq x+h} \lambda_f(n)r(n-a)\right| \ll_{\varepsilon,f} X^{1/2+\varepsilon}.\end{align*}
\begin{align*} \left|\sum_{x < n \leq x+h} \lambda_f(n)r(n-a)\right| \ll_{\varepsilon,f} X^{1/2+\varepsilon}.\end{align*}
On the other hand, for any small
![]() $\delta >0$
we have
$\delta >0$
we have
 \begin{align*}&\sum_{x < n \leq x+ h} |\lambda_f(n)| r(n-a) \\[5pt] &\geq X^{-\delta} \sum_{\substack{x < n \leq x+ h \\ |\lambda_f(n)| \geq X^{-\delta}}} r(n-a) = X^{-\delta}\left(\sum_{\substack{x < n \leq x+ h \\ \lambda_f(n) \neq 0}} r(n+a) - \sum_{\substack{x < n \leq x + h \\ 0 < |\lambda_f(n)| < X^{-\delta}}} r(n-a)\right).\end{align*}
\begin{align*}&\sum_{x < n \leq x+ h} |\lambda_f(n)| r(n-a) \\[5pt] &\geq X^{-\delta} \sum_{\substack{x < n \leq x+ h \\ |\lambda_f(n)| \geq X^{-\delta}}} r(n-a) = X^{-\delta}\left(\sum_{\substack{x < n \leq x+ h \\ \lambda_f(n) \neq 0}} r(n+a) - \sum_{\substack{x < n \leq x + h \\ 0 < |\lambda_f(n)| < X^{-\delta}}} r(n-a)\right).\end{align*}
By Propositions 4·1 and 4·2, respectively, we have
 \begin{align*}\sum_{\substack{x < n \leq x + h \\ 0 < |\lambda_f(n)| < X^{-\delta}}} r(n-a) \ll_{\varepsilon,\delta,f} \frac{h}{(\log\log X)^{1/5}}, \quad \quad\sum_{\substack{x < n \leq x+ h \\ \lambda_f(n) \neq 0}} r(n-a) \gg_{\varepsilon,f} h\end{align*}
\begin{align*}\sum_{\substack{x < n \leq x + h \\ 0 < |\lambda_f(n)| < X^{-\delta}}} r(n-a) \ll_{\varepsilon,\delta,f} \frac{h}{(\log\log X)^{1/5}}, \quad \quad\sum_{\substack{x < n \leq x+ h \\ \lambda_f(n) \neq 0}} r(n-a) \gg_{\varepsilon,f} h\end{align*}
for all but
![]() $O(X/(\log \log X)^{1/10})$
choices of
$O(X/(\log \log X)^{1/10})$
choices of
![]() $x \in [X,2X]$
.
$x \in [X,2X]$
.
It therefore follows that if
![]() $X \geq X_0(\delta,\eta)$
then for all but
$X \geq X_0(\delta,\eta)$
then for all but
![]() $\leq 2\eta X$
choices of
$\leq 2\eta X$
choices of
![]() $x \in [X,2X]$
we have
$x \in [X,2X]$
we have
Choosing
![]() $\delta = \varepsilon$
sufficiently small and X larger in terms of f and
$\delta = \varepsilon$
sufficiently small and X larger in terms of f and
![]() $\varepsilon$
if necessary, we deduce that
$\varepsilon$
if necessary, we deduce that
![]() $h \ll_{\varepsilon,f} X^{1/2+2\varepsilon}$
, which is a contradiction for X large enough.
$h \ll_{\varepsilon,f} X^{1/2+2\varepsilon}$
, which is a contradiction for X large enough.
Thus, there is a constant
![]() $c > 0$
such that for
$c > 0$
such that for
![]() $\geq cX$
choices of
$\geq cX$
choices of
![]() $x \in [X,2X]$
$x \in [X,2X]$
![]() $\lambda_f$
changes sign on
$\lambda_f$
changes sign on
![]() $(a+\mathcal{N}) \cap [x,x+h]$
. By the greedy selection argument mentioned at the beginning of Section 3, it follows that there are
$(a+\mathcal{N}) \cap [x,x+h]$
. By the greedy selection argument mentioned at the beginning of Section 3, it follows that there are
![]() $\gg X/h \gg_{\varepsilon,f} X^{1/2-3\varepsilon}$
distinct such n, all of which produce a sign change, and the theorem is proved.
$\gg X/h \gg_{\varepsilon,f} X^{1/2-3\varepsilon}$
distinct such n, all of which produce a sign change, and the theorem is proved.
4·1. Proofs of Proposition 4·1
In order to prove Proposition 4·1 we will deduce from the condition
![]() $0 < |\lambda_f(n)| < X^{-\delta}$
that n is divisible by a large prime power
$0 < |\lambda_f(n)| < X^{-\delta}$
that n is divisible by a large prime power
![]() $p^k$
with a small Fourier coefficient
$p^k$
with a small Fourier coefficient
![]() $|\lambda_f(p^k)|$
. The following lemma plays an important role in showing that the number of multiples of all such prime powers is quite small.
$|\lambda_f(p^k)|$
. The following lemma plays an important role in showing that the number of multiples of all such prime powers is quite small.
Lemma 4·3.
Let
![]() $c \in (0,1/4)$
be fixed and let
$c \in (0,1/4)$
be fixed and let
![]() $2 \leq Z \leq X$
. Then
$2 \leq Z \leq X$
. Then
 \begin{align*} \sum_{\substack{Z \leq p^\nu \leq X \\ 0 < |\lambda_f(p^\nu)| \leq (\log X)^{-c}}} \frac{1}{p^\nu} \ll_f \frac{\log\log X}{(\log X)^c} + \frac{1}{(\log (Z+\log X))^{1/5}}.\end{align*}
\begin{align*} \sum_{\substack{Z \leq p^\nu \leq X \\ 0 < |\lambda_f(p^\nu)| \leq (\log X)^{-c}}} \frac{1}{p^\nu} \ll_f \frac{\log\log X}{(\log X)^c} + \frac{1}{(\log (Z+\log X))^{1/5}}.\end{align*}
Similarly, we have
 \begin{align*} \sum_{\substack{Z \leq p^{\nu} \leq X \\ \lambda_f(p^{\nu}) = 0}} \frac{1}{p^{\nu}} \ll_f \frac{1}{(\log Z)^{1/5}}.\end{align*}
\begin{align*} \sum_{\substack{Z \leq p^{\nu} \leq X \\ \lambda_f(p^{\nu}) = 0}} \frac{1}{p^{\nu}} \ll_f \frac{1}{(\log Z)^{1/5}}.\end{align*}
Proof. By Thorner’s quantitative version of the Sato–Tate theorem [
Reference Thorner24
, theorem 1·1], for any
![]() $\Delta > 0$
we have
$\Delta > 0$
we have
By Lemma 2·4, we also have
Applying these two results with
![]() $\Delta = (\log X)^{-c}$
,
$\Delta = (\log X)^{-c}$
,
![]() $0 < c < 1/4$
, then using partial summation, for any
$0 < c < 1/4$
, then using partial summation, for any
![]() $2 \leq Y \leq X$
we obtain
$2 \leq Y \leq X$
we obtain
 \begin{align*}\sum_{\substack{Y < p^\nu \leq X \\ 0 < |\lambda_f(p^\nu)| < (\log X)^{-c}}} \frac{1}{p^\nu} &= \mu_{ST}([-\Delta,\Delta]) \log\left(\log X/\log Y\right) + O\left(\int_Y^X \frac{du}{u(\log u)^{6/5}}\right) \\[5pt] &= \mu_{ST}([-\Delta,\Delta]) \log\left(\log X/\log Y\right) + O\left(\frac{1}{(\log Y)^{1/5}}\right) \\[5pt] &\ll \frac{\log\log X}{(\log X)^{c}} + \frac{1}{(\log Y)^{1/5}}.\end{align*}
\begin{align*}\sum_{\substack{Y < p^\nu \leq X \\ 0 < |\lambda_f(p^\nu)| < (\log X)^{-c}}} \frac{1}{p^\nu} &= \mu_{ST}([-\Delta,\Delta]) \log\left(\log X/\log Y\right) + O\left(\int_Y^X \frac{du}{u(\log u)^{6/5}}\right) \\[5pt] &= \mu_{ST}([-\Delta,\Delta]) \log\left(\log X/\log Y\right) + O\left(\frac{1}{(\log Y)^{1/5}}\right) \\[5pt] &\ll \frac{\log\log X}{(\log X)^{c}} + \frac{1}{(\log Y)^{1/5}}.\end{align*}
Now, it is known that there is a constant
![]() $C_f > 0$
such that if
$C_f > 0$
such that if
![]() $\lambda_f(p^\nu) \neq 0$
then
$\lambda_f(p^\nu) \neq 0$
then
![]() $|\lambda_f(p^\nu)| \geq p^{-C_f\nu}$
. Indeed, as argued in [
Reference Luca, Radziwiłł and Shparlinski9
], writing
$|\lambda_f(p^\nu)| \geq p^{-C_f\nu}$
. Indeed, as argued in [
Reference Luca, Radziwiłł and Shparlinski9
], writing
![]() $a_f(n) \;:\!=\; \lambda_f(n)n^{(k-1)/2}$
for all n we have that
$a_f(n) \;:\!=\; \lambda_f(n)n^{(k-1)/2}$
for all n we have that
![]() $a_f(n)$
is an algebraic integer in some number field
$a_f(n)$
is an algebraic integer in some number field
![]() $K_f$
of (finite) degree
$K_f$
of (finite) degree
![]() $d_f \geq 1$
, and so for each
$d_f \geq 1$
, and so for each
![]() $n = p^\nu$
with
$n = p^\nu$
with
![]() $a_f(n) \neq 0$
its norm
$a_f(n) \neq 0$
its norm
![]() $N_{K_f}(a_f(p^\nu)) \geq 1$
. On the other hand, for each automorphism
$N_{K_f}(a_f(p^\nu)) \geq 1$
. On the other hand, for each automorphism
![]() $\sigma$
of
$\sigma$
of
![]() $K_f$
it is well known (see [
Reference Shimura20
]) that
$K_f$
it is well known (see [
Reference Shimura20
]) that
![]() $\{\sigma(a_f(n))\}_n$
is the sequence of coefficients of an eigencusp form of weight k and level 1, and we obtain
$\{\sigma(a_f(n))\}_n$
is the sequence of coefficients of an eigencusp form of weight k and level 1, and we obtain
 \begin{align*} 1 \leq N_{K_f}(a_f(p^\nu)) = |a_f(p^{\nu})| \prod_{\substack{\sigma \in \text{Aut}(K_f) \\ \sigma \neq 1}} |\sigma(a_f(p^\nu))| \leq |\lambda_f(p^\nu)| d(p^{\nu})^{d_f-1} p^{\nu d_f(k-1)/2},\end{align*}
\begin{align*} 1 \leq N_{K_f}(a_f(p^\nu)) = |a_f(p^{\nu})| \prod_{\substack{\sigma \in \text{Aut}(K_f) \\ \sigma \neq 1}} |\sigma(a_f(p^\nu))| \leq |\lambda_f(p^\nu)| d(p^{\nu})^{d_f-1} p^{\nu d_f(k-1)/2},\end{align*}
using Deligne’s bound
![]() $|\sigma(a_f(p^{\nu}))| \leq d(p^{\nu}) p^{\nu(k-1)/2}$
for each
$|\sigma(a_f(p^{\nu}))| \leq d(p^{\nu}) p^{\nu(k-1)/2}$
for each
![]() $\sigma \neq 1$
in the last inequality. From this, the claim
$\sigma \neq 1$
in the last inequality. From this, the claim
![]() $|\lambda_f(p^\nu)| \geq p^{-C_f \nu}$
follows with any
$|\lambda_f(p^\nu)| \geq p^{-C_f \nu}$
follows with any
![]() $C_f > d_f(k-1)/2$
.
$C_f > d_f(k-1)/2$
.
Therefore, if
![]() $0 < |\lambda_f(p^\nu)| < (\log X)^{-c}$
then
$0 < |\lambda_f(p^\nu)| < (\log X)^{-c}$
then
![]() $p^{\nu} > (\log X)^{\eta}$
with
$p^{\nu} > (\log X)^{\eta}$
with
![]() $\eta \;:\!=\; c/C_f$
, and so we immediately have that
$\eta \;:\!=\; c/C_f$
, and so we immediately have that
 \begin{align*} \sum_{\substack{Z < p^\nu \leq X \\ 0 < |\lambda_f(p^\nu)| < (\log X)^{-c}}} \frac{1}{p^\nu} = \sum_{\substack{\max\{(\log X)^{\eta},Z\} < p^\nu \leq X \\ 0 < |\lambda_f(p^\nu)| < (\log X)^{-c}}} \frac{1}{p^\nu} \ll \frac{1}{(\log(Z + (\log X)^{\eta}))^{1/5}},\end{align*}
\begin{align*} \sum_{\substack{Z < p^\nu \leq X \\ 0 < |\lambda_f(p^\nu)| < (\log X)^{-c}}} \frac{1}{p^\nu} = \sum_{\substack{\max\{(\log X)^{\eta},Z\} < p^\nu \leq X \\ 0 < |\lambda_f(p^\nu)| < (\log X)^{-c}}} \frac{1}{p^\nu} \ll \frac{1}{(\log(Z + (\log X)^{\eta}))^{1/5}},\end{align*}
and the first claim follows.
The second claim is proven more directly by appealing to Lemma 2·4 and partial summation.
To leverage the bound in Lemma 4·3 we require the following upper bound for correlations of r(n) supported on multiples of prime powers
![]() $p^k$
, provided they are not too close to h in size.
$p^k$
, provided they are not too close to h in size.
Lemma 4·4.
Let
![]() $X^{\varepsilon} \leq h \leq X$
. Then for any
$X^{\varepsilon} \leq h \leq X$
. Then for any
![]() $p^\nu \leq h^{1-\varepsilon}$
we have
$p^\nu \leq h^{1-\varepsilon}$
we have
 \begin{align*} \sum_{\substack{x < n \leq x+h \\ p^\nu || n}} r(n+a) \ll_{\varepsilon} \frac{h}{p^\nu}.\end{align*}
\begin{align*} \sum_{\substack{x < n \leq x+h \\ p^\nu || n}} r(n+a) \ll_{\varepsilon} \frac{h}{p^\nu}.\end{align*}
Proof. Write
![]() $r'(n) = r(n)/4$
, which is multiplicative and divisor-bounded. By Shiu’s theorem [
Reference Shiu21
], the sum in question is bounded above by
$r'(n) = r(n)/4$
, which is multiplicative and divisor-bounded. By Shiu’s theorem [
Reference Shiu21
], the sum in question is bounded above by
 \begin{align*} 4\sum_{\substack{x+ a < m \leq x+h+a \\ m \equiv a\pmod{p^{\nu}}}} r'(m) \ll_{\varepsilon} \frac{h}{p^{\nu}}\prod_{p' \leq X} \left(1+\frac{r'(p')-1}{p'}\right) \ll \frac{h}{p^{\nu}},\end{align*}
\begin{align*} 4\sum_{\substack{x+ a < m \leq x+h+a \\ m \equiv a\pmod{p^{\nu}}}} r'(m) \ll_{\varepsilon} \frac{h}{p^{\nu}}\prod_{p' \leq X} \left(1+\frac{r'(p')-1}{p'}\right) \ll \frac{h}{p^{\nu}},\end{align*}
as claimed.
Proof of Proposition
4·1. Suppose
![]() $n \leq X$
satisfies
$n \leq X$
satisfies
![]() $0 < |\lambda_f(n)| < X^{-\delta}$
. Writing out the prime factorization of n and using multiplicativity, we observe that
$0 < |\lambda_f(n)| < X^{-\delta}$
. Writing out the prime factorization of n and using multiplicativity, we observe that
 \begin{align*} X^{-\delta} > \prod_{p^k||n} |\lambda_f(p^k)| \geq \left(\min_{p^k||n} |\lambda_f(p^k)|\right)^{\omega(n)} > 0,\end{align*}
\begin{align*} X^{-\delta} > \prod_{p^k||n} |\lambda_f(p^k)| \geq \left(\min_{p^k||n} |\lambda_f(p^k)|\right)^{\omega(n)} > 0,\end{align*}
where
![]() $\omega(n)$
denotes the number of distinct prime factors of n. Since
$\omega(n)$
denotes the number of distinct prime factors of n. Since
![]() $\omega(n) \leq C\;{\log X}/{\log} {\log X}$
for some
$\omega(n) \leq C\;{\log X}/{\log} {\log X}$
for some
![]() $C > 0$
absolute, we deduce that if n satisfies
$C > 0$
absolute, we deduce that if n satisfies
![]() $0 < |\lambda_f(n)| < X^{-\delta}$
then there is a prime power
$0 < |\lambda_f(n)| < X^{-\delta}$
then there is a prime power
![]() $p^k || n$
for which
$p^k || n$
for which
Set
![]() $c \;:\!=\; \min\{\delta/C,1/5\}$
, and call
$c \;:\!=\; \min\{\delta/C,1/5\}$
, and call
Then it suffices to bound, for all but
![]() $O(X/(\log \log X)^{1/10})$
choices of
$O(X/(\log \log X)^{1/10})$
choices of
![]() $x \in [X,2X]$
, the sum
$x \in [X,2X]$
, the sum
 \begin{align*} \sum_{\substack{x < n \leq x + h \\ \exists p^\nu || n , p^\nu \in \mathcal{P}_c}} r(n+a).\end{align*}
\begin{align*} \sum_{\substack{x < n \leq x + h \\ \exists p^\nu || n , p^\nu \in \mathcal{P}_c}} r(n+a).\end{align*}
We split the set
![]() $\mathcal{P}_c$
into three ranges:
$\mathcal{P}_c$
into three ranges:
We immediately note that since
![]() $h < X^{1-\varepsilon}$
there is at most one multiple of any prime power
$h < X^{1-\varepsilon}$
there is at most one multiple of any prime power
![]() $p^\nu$
from range (iii) in any interval
$p^\nu$
from range (iii) in any interval
![]() $(x,x+h]$
, and since (by arguing as in the proof of Lemma 4·3) there are
$(x,x+h]$
, and since (by arguing as in the proof of Lemma 4·3) there are
![]() $\ll X/(\log X)^{1+c'}$
such prime powers in
$\ll X/(\log X)^{1+c'}$
such prime powers in
![]() $\mathcal{P}_c$
, for some
$\mathcal{P}_c$
, for some
![]() $c ' > 0$
depending on c, we may ignore the range
$c ' > 0$
depending on c, we may ignore the range
![]() $p^\nu > X^{1-\varepsilon}$
by excluding at most
$p^\nu > X^{1-\varepsilon}$
by excluding at most
![]() $O(X/(\log X)^{1+c'})$
intervals
$O(X/(\log X)^{1+c'})$
intervals
![]() $[x,x+h]$
.
$[x,x+h]$
.
Next, consider range (i). Combining Lemmas 4·4 and 4·3 we obtain that
 \begin{align*} \sum_{\substack{x < n \leq x + h \\ \exists p^\nu \in \mathcal{P}_c \cap [2,h^{1-\varepsilon}] \\ p^\nu || n}} r(n+a) & \ll \sum_{\substack{p^\nu \leq h^{1-\varepsilon} \\ p^\nu \in \mathcal{P}_c}} \sum_{\substack{x < n \leq x + h \\ p^\nu||n}} r(n+a) \ll_{\varepsilon} h\sum_{\substack{p^\nu \leq h^{1-\varepsilon} \\ 0 < |\lambda_f(p^\nu)| < (\log x)^{-c}}} \frac{1}{p^\nu} \\[5pt] & \ll_{\delta,f} \frac{h}{(\log\log X)^{1/5}}.\end{align*}
\begin{align*} \sum_{\substack{x < n \leq x + h \\ \exists p^\nu \in \mathcal{P}_c \cap [2,h^{1-\varepsilon}] \\ p^\nu || n}} r(n+a) & \ll \sum_{\substack{p^\nu \leq h^{1-\varepsilon} \\ p^\nu \in \mathcal{P}_c}} \sum_{\substack{x < n \leq x + h \\ p^\nu||n}} r(n+a) \ll_{\varepsilon} h\sum_{\substack{p^\nu \leq h^{1-\varepsilon} \\ 0 < |\lambda_f(p^\nu)| < (\log x)^{-c}}} \frac{1}{p^\nu} \\[5pt] & \ll_{\delta,f} \frac{h}{(\log\log X)^{1/5}}.\end{align*}
Note that this holds for every
![]() $x \in [X,2X]$
.
$x \in [X,2X]$
.
Finally, consider range (ii). Observe that by the same argument as in Lemma 4·4 (splitting into dyadic intervals [X,2X] and [2X,4X] and replacing h by y for
![]() $y \in \{X,2X\}$
in each respective case),
$y \in \{X,2X\}$
in each respective case),
 \begin{align*} \sum_{\substack{X < n \leq 4X \\ p^\nu||n}} r(n+a) \ll_{\varepsilon} \frac{X}{p^\nu}.\end{align*}
\begin{align*} \sum_{\substack{X < n \leq 4X \\ p^\nu||n}} r(n+a) \ll_{\varepsilon} \frac{X}{p^\nu}.\end{align*}
Thus, on combining this with Lemma 4·3 we obtain
 \begin{align*} \sum_{\substack{X < n \leq 4X \\ \exists p^\nu \in \mathcal{P}_c \cap (h^{1-\varepsilon} ,X^{1-\varepsilon}] \\ p^\nu||n}} r(n+a) \ll_{\varepsilon} \frac{X}{(\log \log X)^{1/5}},\end{align*}
\begin{align*} \sum_{\substack{X < n \leq 4X \\ \exists p^\nu \in \mathcal{P}_c \cap (h^{1-\varepsilon} ,X^{1-\varepsilon}] \\ p^\nu||n}} r(n+a) \ll_{\varepsilon} \frac{X}{(\log \log X)^{1/5}},\end{align*}
in light of the condition
![]() $h \geq X^{\varepsilon}$
. By positivity, we deduce from this that
$h \geq X^{\varepsilon}$
. By positivity, we deduce from this that
 \begin{align*} \sum_{X < m \leq 2X} \sum_{\substack{m < n \leq m+h \\ \exists p^\nu \in (h^{1-\varepsilon}, X^{1-\varepsilon}] \cap \mathcal{P}_c \\ p^\nu||n }} r(n+a) \leq h \sum_{\substack{X < n \leq 2X+h \\ \exists p^\nu \in (h^{1-\varepsilon},X^{1-\varepsilon}] \cap \mathcal{P}_c \\ p^\nu||n}} r(n+a) \ll \frac{hX}{(\log \log X)^{1/5}}.\end{align*}
\begin{align*} \sum_{X < m \leq 2X} \sum_{\substack{m < n \leq m+h \\ \exists p^\nu \in (h^{1-\varepsilon}, X^{1-\varepsilon}] \cap \mathcal{P}_c \\ p^\nu||n }} r(n+a) \leq h \sum_{\substack{X < n \leq 2X+h \\ \exists p^\nu \in (h^{1-\varepsilon},X^{1-\varepsilon}] \cap \mathcal{P}_c \\ p^\nu||n}} r(n+a) \ll \frac{hX}{(\log \log X)^{1/5}}.\end{align*}
By Markov’s inequality, we thus obtain that for all but
![]() $O(X/(\log \log X)^{1/10})$
we have
$O(X/(\log \log X)^{1/10})$
we have
 \begin{align*} \sum_{\substack{m < n \leq m+h \\ \exists p^\nu \in (h^{1-\varepsilon}, X^{1-\varepsilon}] \cap \mathcal{P}_c \\ p^\nu||n}} r(n+a) \ll \frac{h}{(\log \log X)^{1/10}}.\end{align*}
\begin{align*} \sum_{\substack{m < n \leq m+h \\ \exists p^\nu \in (h^{1-\varepsilon}, X^{1-\varepsilon}] \cap \mathcal{P}_c \\ p^\nu||n}} r(n+a) \ll \frac{h}{(\log \log X)^{1/10}}.\end{align*}
Combined with the bound for the primes
![]() $p^\nu \leq h^{1-\varepsilon}$
and
$p^\nu \leq h^{1-\varepsilon}$
and
![]() $p^{\nu} > X^{1-\varepsilon}$
, the claim follows.
$p^{\nu} > X^{1-\varepsilon}$
, the claim follows.
4·2. Proof of Proposition 4·2
To prove Proposition 4·2 we sieve out short intervals
![]() $[x,x+h]$
by the sparse set of prime powers
$[x,x+h]$
by the sparse set of prime powers
![]() $p^\nu$
satisfying
$p^\nu$
satisfying
![]() $\lambda_f(p^{\nu}) = 0$
. To accomplish this we make use of an estimate for r(n) in arithmetic progressions
$\lambda_f(p^{\nu}) = 0$
. To accomplish this we make use of an estimate for r(n) in arithmetic progressions
![]() $ n\leq y$
,
$ n\leq y$
,
![]() $n \equiv a \pmod{q}$
with
$n \equiv a \pmod{q}$
with
![]() $q \leq y^{1/10}$
, say. Asymptotic formulae of this kind, with power saving error term for the fairly wide range
$q \leq y^{1/10}$
, say. Asymptotic formulae of this kind, with power saving error term for the fairly wide range
![]() $q \leq y^{2/3-\varepsilon}$
, were given by R.A. Smith [
Reference Smith22
, theorem 9]. The following improvement of these results is due to Tolev [
Reference Tolev26
].
$q \leq y^{2/3-\varepsilon}$
, were given by R.A. Smith [
Reference Smith22
, theorem 9]. The following improvement of these results is due to Tolev [
Reference Tolev26
].
Lemma 4·5 (Tolev [
Reference Tolev26
]). Let y be large,
![]() $q \leq y^{2/3}$
be squarefree and let a be a residue class modulo q with
$q \leq y^{2/3}$
be squarefree and let a be a residue class modulo q with
![]() $(a,q) = 1$
. Then
$(a,q) = 1$
. Then
 \begin{align*} \sum_{\substack{n \leq y \\ n \equiv a \pmod{q}}} r(n) = \pi \prod_{p | q} \left(1-\frac{\chi_{4}(p)}{p}\right) \frac{y}{q} + O_{\varepsilon}\left(y^{\varepsilon}\left(q^{1/2} + y^{1/3}\right)\right),\end{align*}
\begin{align*} \sum_{\substack{n \leq y \\ n \equiv a \pmod{q}}} r(n) = \pi \prod_{p | q} \left(1-\frac{\chi_{4}(p)}{p}\right) \frac{y}{q} + O_{\varepsilon}\left(y^{\varepsilon}\left(q^{1/2} + y^{1/3}\right)\right),\end{align*}
where
![]() $\chi_4$
is the non-principal character mod 4.
$\chi_4$
is the non-principal character mod 4.
Proof of Proposition
4·2. Let
![]() $z \;:\!=\; (\log X)^{1/2}$
and let
$z \;:\!=\; (\log X)^{1/2}$
and let
 \begin{align*} P = P(z) \;:\!=\; \prod_{\substack{3 \leq p \leq z \\ \exists \nu \geq 1 \text{ with } \lambda_f(p^\nu) = 0}} p.\end{align*}
\begin{align*} P = P(z) \;:\!=\; \prod_{\substack{3 \leq p \leq z \\ \exists \nu \geq 1 \text{ with } \lambda_f(p^\nu) = 0}} p.\end{align*}
By the prime number theorem, we have
![]() $P \leq \exp(2z) \ll_{\varepsilon} X^{\varepsilon}$
.
$P \leq \exp(2z) \ll_{\varepsilon} X^{\varepsilon}$
.
We may lower bound the sum in question by
 \begin{align}\geq \sum_{\substack{x < n \leq x + h \\ 2 \nmid n \\ \lambda_f(n) \neq 0}} r(n+a) \geq \sum_{\substack{x < n \leq x + h \\ 2 \nmid n \\ (n,P(z)) = 1}} r(n+a) - \sum_{\substack{x < n \leq x + h \\ \exists p > z, k \geq 1 \\ \lambda_f(p^k) = 0 \\ p^k||n }} r(n+a).\end{align}
\begin{align}\geq \sum_{\substack{x < n \leq x + h \\ 2 \nmid n \\ \lambda_f(n) \neq 0}} r(n+a) \geq \sum_{\substack{x < n \leq x + h \\ 2 \nmid n \\ (n,P(z)) = 1}} r(n+a) - \sum_{\substack{x < n \leq x + h \\ \exists p > z, k \geq 1 \\ \lambda_f(p^k) = 0 \\ p^k||n }} r(n+a).\end{align}
To estimate the first sum we use Möbius inversion together with Lemma 4·5, getting
 \begin{align*} & \sum_{\substack{x < n \leq x + h \\ 2 \nmid n \\ (n,P(z)) = 1}} r(n+a)= \sum_{\substack{d|P}} \mu(d) \sum_{\substack{x<n \leq x+ h \\ 2 \nmid n \\ d|n}} r(n+a) \\ &= \sum_{e|(a,P)} \mu(e) r'(e) \sum_{\substack{d'|P/e \\ (d',a/e) = 1}} \mu(d') \sum_{\substack{x/e < m \leq (x+h)/e \\ m \equiv 1 \pmod{2} \\ m \equiv 0 \pmod{d'}}} r(m+a/e) \\[5pt] &= \frac{\pi h}{2} \sum_{e|(a,P)} \frac{\mu(e)r'(e)}{e} \sum_{\substack{d'|P/e \\ (d',a/e) = 1}} \frac{\mu(d')}{d'} \prod_{p|d'} \left(1-\frac{\chi_4(p)}{p}\right) + O_{\varepsilon}\left(X^{\varepsilon} \left(\sum_{d|P} d^{\tfrac 12} + X^{\tfrac 13+\varepsilon} \tau(P) \!\right)\!\right) \\[5pt] &= \frac{\pi h}{2} \prod_{p|(a,P)} \left(1-\frac{r'(p)}{p-1+\chi_4(p)/p}\right) \prod_{\substack{3 \leq p\leq z \\ \lambda_f(p) = 0}} \left(1-\frac{1+\chi_4(p)}{p} + \frac{\chi_4(p)}{p^2}\right) + O_{\varepsilon}\left(X^{1/3+\varepsilon} \right).\end{align*}
\begin{align*} & \sum_{\substack{x < n \leq x + h \\ 2 \nmid n \\ (n,P(z)) = 1}} r(n+a)= \sum_{\substack{d|P}} \mu(d) \sum_{\substack{x<n \leq x+ h \\ 2 \nmid n \\ d|n}} r(n+a) \\ &= \sum_{e|(a,P)} \mu(e) r'(e) \sum_{\substack{d'|P/e \\ (d',a/e) = 1}} \mu(d') \sum_{\substack{x/e < m \leq (x+h)/e \\ m \equiv 1 \pmod{2} \\ m \equiv 0 \pmod{d'}}} r(m+a/e) \\[5pt] &= \frac{\pi h}{2} \sum_{e|(a,P)} \frac{\mu(e)r'(e)}{e} \sum_{\substack{d'|P/e \\ (d',a/e) = 1}} \frac{\mu(d')}{d'} \prod_{p|d'} \left(1-\frac{\chi_4(p)}{p}\right) + O_{\varepsilon}\left(X^{\varepsilon} \left(\sum_{d|P} d^{\tfrac 12} + X^{\tfrac 13+\varepsilon} \tau(P) \!\right)\!\right) \\[5pt] &= \frac{\pi h}{2} \prod_{p|(a,P)} \left(1-\frac{r'(p)}{p-1+\chi_4(p)/p}\right) \prod_{\substack{3 \leq p\leq z \\ \lambda_f(p) = 0}} \left(1-\frac{1+\chi_4(p)}{p} + \frac{\chi_4(p)}{p^2}\right) + O_{\varepsilon}\left(X^{1/3+\varepsilon} \right).\end{align*}
Note that as P is odd,
![]() $2\nmid (a,P)$
and thus the products above are
$2\nmid (a,P)$
and thus the products above are
![]() $> 0$
. Furthermore, since
$> 0$
. Furthermore, since
![]() $\sum_{p \;:\; \lambda_f(p) = 0} {1}/{p} < \infty$
, for
$\sum_{p \;:\; \lambda_f(p) = 0} {1}/{p} < \infty$
, for
![]() $h > X^{1/3+2\varepsilon}$
the product over
$h > X^{1/3+2\varepsilon}$
the product over
![]() $3 \leq p \leq z$
with
$3 \leq p \leq z$
with
![]() $\lambda_f(p) = 0$
converges, and thus we deduce the existence of a constant
$\lambda_f(p) = 0$
converges, and thus we deduce the existence of a constant
![]() $c_{f,a} > 0$
such that
$c_{f,a} > 0$
such that
 \begin{align*} \sum_{\substack{x < n \leq x+h \\ 2 \nmid n \\ (n,P(z)) = 1}} r(n+a) = (c_{f,a}+o(1)) h.\end{align*}
\begin{align*} \sum_{\substack{x < n \leq x+h \\ 2 \nmid n \\ (n,P(z)) = 1}} r(n+a) = (c_{f,a}+o(1)) h.\end{align*}
Next, we upper bound the second sum in (4·1) similarly as in Proposition 4·1. For
![]() $p^k \leq h^{1-\varepsilon}$
we use Lemmas 4·3 and 4·4 to get
$p^k \leq h^{1-\varepsilon}$
we use Lemmas 4·3 and 4·4 to get
 \begin{align*} \sum_{\substack{x < n \leq x + h \\ \exists p > z, \nu \geq 1 \\ p^\nu \leq h^{1-\varepsilon} \\ \lambda_f(p^\nu) = 0 \\ p^\nu||n }} r(n+a) \ll_{\varepsilon} h\sum_{\substack{z < p^\nu \leq h^{1-\varepsilon} \\ \lambda_f(p^\nu) = 0}} \frac{1}{p^\nu} \ll_f \frac{h}{(\log z)^{1/5}} \ll \frac{h}{(\log \log X)^{1/5}},\end{align*}
\begin{align*} \sum_{\substack{x < n \leq x + h \\ \exists p > z, \nu \geq 1 \\ p^\nu \leq h^{1-\varepsilon} \\ \lambda_f(p^\nu) = 0 \\ p^\nu||n }} r(n+a) \ll_{\varepsilon} h\sum_{\substack{z < p^\nu \leq h^{1-\varepsilon} \\ \lambda_f(p^\nu) = 0}} \frac{1}{p^\nu} \ll_f \frac{h}{(\log z)^{1/5}} \ll \frac{h}{(\log \log X)^{1/5}},\end{align*}
and, if
![]() $x\in [X,2X]$
is chosen outside of a set of size
$x\in [X,2X]$
is chosen outside of a set of size
![]() $\ll X/(\log \log X)^{1/10}$
then we also have
$\ll X/(\log \log X)^{1/10}$
then we also have
 \begin{align*} \sum_{\substack{x < n \leq x + h \\ \exists p > z, \nu \geq 1 \\ p^\nu > h^{1-\varepsilon} \\ \lambda_f(p^\nu) = 0 \\ p^\nu||n }} r(n+a) \ll_{\varepsilon,f} \frac{h}{(\log \log X)^{1/10}}.\end{align*}
\begin{align*} \sum_{\substack{x < n \leq x + h \\ \exists p > z, \nu \geq 1 \\ p^\nu > h^{1-\varepsilon} \\ \lambda_f(p^\nu) = 0 \\ p^\nu||n }} r(n+a) \ll_{\varepsilon,f} \frac{h}{(\log \log X)^{1/10}}.\end{align*}
Adding up the two contributions, we get that
 \begin{align*} \sum_{\substack{x < n \leq x + h \\ \exists p > z, \nu \geq 1 \\ \lambda_f(p^\nu) = 0, p^\nu||n }} r(n+a) \ll_f \frac{h}{(\log\log X)^{1/10}}.\end{align*}
\begin{align*} \sum_{\substack{x < n \leq x + h \\ \exists p > z, \nu \geq 1 \\ \lambda_f(p^\nu) = 0, p^\nu||n }} r(n+a) \ll_f \frac{h}{(\log\log X)^{1/10}}.\end{align*}
To summarise, we have shown the existence of a constant
![]() $c_{f,a} > 0$
such that if
$c_{f,a} > 0$
such that if
![]() $h > X^{1/3+2\varepsilon}$
then
$h > X^{1/3+2\varepsilon}$
then
 \begin{align*} \sum_{\substack{ x < n \leq x+ h \\ \lambda_f(n) \neq 0}} r(n+a) \geq (c_{f,a}+o(1)) h + O_f\left(\frac{h}{(\log\log X)^{1/10}} \right) \gg_f h\end{align*}
\begin{align*} \sum_{\substack{ x < n \leq x+ h \\ \lambda_f(n) \neq 0}} r(n+a) \geq (c_{f,a}+o(1)) h + O_f\left(\frac{h}{(\log\log X)^{1/10}} \right) \gg_f h\end{align*}
for all but
![]() $O(X/(\log \log X)^{1/10})$
choices of
$O(X/(\log \log X)^{1/10})$
choices of
![]() $x \in [X,2X]$
, and the claim follows.
$x \in [X,2X]$
, and the claim follows.
Acknowledgements
The author thanks the anonymous referee for a careful reading of the paper and for helpful comments that improved its exposition. He is also indebted to Oleksiy Klurman, Youness Lamzouri, Maksym Radziwiłł and Asif Zaman for their advice and encouragement.
Most of this work was completed during a research visit at Queen’s University. The author would like to thank Queen’s for their support.