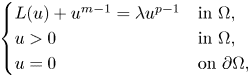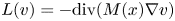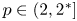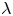Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Colasuonno, Francesca
and
Noris, Benedetta
2023.
Asymptotics for a high-energy solution of a supercritical problem.
Nonlinear Analysis,
Vol. 227,
Issue. ,
p.
113166.
Batahri, Asma Amira
Attar, Ahmed
and
Dieb, Abdelrazek
2025.
A non-local scalar field problem: existence, multiplicity and asymptotic behavior.
Complex Variables and Elliptic Equations,
Vol. 70,
Issue. 3,
p.
412.