No CrossRef data available.
Article contents
Unbalanced optimal total variation transport problems and generalized Wasserstein barycenters
Published online by Cambridge University Press: 04 June 2021
Abstract
In this paper, we establish a Kantorovich duality for unbalanced optimal total variation transport problems. As consequences, we recover a version of duality formula for partial optimal transports established by Caffarelli and McCann; and we also get another proof of Kantorovich–Rubinstein theorem for generalized Wasserstein distance 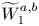 $\widetilde {W}_1^{a,b}$ proved before by Piccoli and Rossi. Then we apply our duality formula to study generalized Wasserstein barycenters. We show the existence of these barycenters for measures with compact supports. Finally, we prove the consistency of our barycenters.
$\widetilde {W}_1^{a,b}$ proved before by Piccoli and Rossi. Then we apply our duality formula to study generalized Wasserstein barycenters. We show the existence of these barycenters for measures with compact supports. Finally, we prove the consistency of our barycenters.
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 3 , June 2022 , pp. 674 - 700
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh



