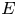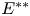Order continuity of Arens extensions of regular multilinear operators

Geraldo Botelho; Luis Alberto Garcia

doi:10.1017/prm.2023.89

Order continuity of Arens extensions of regular multilinear operators

Part of: Measures, integration, derivative, holomorphy Normed linear spaces and Banach spaces; Banach lattices Topological linear spaces and related structures Special classes of linear operators

Published online by Cambridge University Press: 11 September 2023

Geraldo Botelho and

Luis Alberto Garcia

Show author details

Geraldo Botelho: Affiliation:
Faculdade de Matemática, Universidade Federal de Uberlândia, 38.400-902 Uberlândia, Brazil (botelho@ufu.br)
Luis Alberto Garcia: Affiliation:
Instituto de Matemática e Estatística, Universidade de São Paulo, 05.508-090 São Paulo, Brazil (luisgarcia@ime.usp.br)

Article contents

Abstract
Introduction
Background
The counterexample
Operators between Riesz spaces
Operators between Banach lattices
References

Rights & Permissions

Abstract

First we give a counterexample showing that recent results on separate order continuity of Arens extensions of multilinear operators cannot be improved to get separate order continuity on the product of the whole of the biduals. Then we establish conditions on the operators and/or on the underlying Riesz spaces/Banach lattices so that the extensions are order continuous on the product of the whole biduals. We also prove that all Arens extensions of any regular multilinear operator are order continuous in at least one variable and we study when Arens extensions of regular homogeneous polynomials on a Banach lattice $E$ are order continuous on $E^{**}$.

Keywords

Riesz spaces Banach lattices Arens extension separate order continuity

MSC classification

Primary: 46A40: Ordered topological linear spaces, vector lattices

Secondary: 46B42: Banach lattices 46G25: (Spaces of) multilinear mappings, polynomials 47B65: Positive operators and order-bounded operators

Type: Research Article
Information: Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 22

DOI: https://doi.org/10.1017/prm.2023.89 [Opens in a new window]
Copyright: Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

1. Introduction

The second adjoint $u^{**}$ of a linear operator $u$, which is a bidual extension of $u$, is a powerful tool in several areas of mathematics. For multilinear operators, this role has been played by Arens extensions. This has been extensively studied over the past 70 years since its introduction by Arens in his seminal paper, [Reference Arens3]. In order to state the two recent results that have motivated our work, let us fix some notation. By $E^\sim$ we denote the order dual of a Riesz space $E$, hence $E^{\sim \sim } = (E^\sim )^\sim$ denotes its second order dual. For a Banach lattice $E$, $E^*$ denotes its topological dual, hence $E^{**}$ stands for its bidual. The symbols $(E^\sim )_n^{\sim }$ and $(E^*)_n^{*}$ stand for the corresponding subspaces formed by the order continuous functionals. The results that motivated our research are the following:

• Buskes and Roberts (2019) [Reference Buskes and Roberts10, Theorem 3.4]: If $A \colon E_1 \times \cdots \times E_m \longrightarrow F$ is an $m$-linear operator of order bounded variation between Riesz spaces, then its Arens extension $A^{\ast [m+1]} \colon E_1^{\sim \sim } \times \cdots \times E_m^{\sim \sim } \longrightarrow F^{\sim \sim }$ is separately order continuous on $(E_1^\sim )_n^{\sim } \times \cdots \times (E_m^\sim )_n^{\sim }.$
• Boyd, Ryan and Snigireva (2021) [Reference Boyd, Ryan and Snigireva7, Theorem 1]: If $A \colon E_1 \times \cdots \times E_m \longrightarrow F$ is a regular $m$-linear operator between Banach lattices, with $F$ Dedekind complete, then its Arens extension $A^{\ast [m+1]}\colon E_1^{**} \times \cdots \times E_m^{**} \longrightarrow F^{**}$ is separately order continuous on $(E_1^*)_n^{*} \times \cdots \times (E_m^*)_n^{*}.$

The obvious question is whether or not these results can be improved to get order continuity on $E_1^{\sim \sim } \times \cdots \times E_m^{\sim \sim }$ and $E_1^{**} \times \cdots \times E_m^{**}$, respectively. By means of a simple but efficient counterexample we show that this is not the case (cf. Section 3). Actually the counterexample, which is the bilinear form $A$ on $\ell _1 \times c_0$ given by the duality $c_0^* = \ell _1$, discloses an interesting phenomenon: its Arens extension $A^{***}$ is not separately order continuous on $\ell _1^{**} \times c_0^{**}$ (more precisely, it is order continuous in the first variable but not in the second one), while the other Arens extension of $A$ is. We then proceed to find conditions on the operator and/or on the underlying spaces so that all Arens extensions are separately order continuous on the product of the whole of the biduals. In § 4 we prove that this holds for finite sums of multiplicative operators from Riesz spaces to Archimedean $f$-algebras, in particular for operators of finite type between arbitrary Riesz spaces. The main result of § 4 (Theorem 4.6): (i) implies that all Arens extensions of any regular multilinear operator between Riesz spaces are order continuous in at least one variable, (ii) implies that all Arens extensions of a regular homogeneous polynomial from the Riesz space $E$ to a Riesz space $F$ are order continuous at the origin on $E^{\sim \sim }$, (iii) improves the results of Boyd, Ryan and Snigireva and of Buskes and Roberts for regular operators (see Remark 4.7). In the final § 5 we give sufficient conditions on the Banach lattices $E_1,\, \ldots,\, E_m$ so that Arens extensions of any regular $m$-linear operator from $E_1 \times \cdots \times E_m$ to an arbitrary Banach lattice $F$ are separately order continuous on $E_1^{**} \times \cdots \times E_m^{**}$; and conditions so that Arens extensions of regular homogeneous polynomials on a Banach lattice $E$ are order continuous on $E^{**}$.

In § 2 we discuss briefly the notion of order continuity of linear operators and recall the characterization of the Arens extensions of regular multilinear operators between Riesz spaces that shall fit our purposes. Although these extensions are usually called Aron-Berner extensions in the case of operators between Banach spaces (see [Reference Aron and Berner4, Reference Dineen13]), for simplicity we shall refer to Arens extensions even for operators between Banach lattices.

2. Background

Our references to Riesz spaces, Banach lattices and regular linear operators are the canonical ones [Reference Aliprantis and Burkinshaw2, Reference Meyer–Nieberg17, Reference Schaefer19].

The following three definitions of order convergence can be found in the literature (see [Reference Abramovich and Sirotkin1]). A net $(x_{\alpha })_{\alpha \in \Omega }$ in a Riesz space $E$ is said to be:

• order convergent to $x\in E$ if there is a net $(y_{\alpha })_{\alpha \in \Omega }$ in $E$ such that $y_{\alpha }\downarrow 0$ and $|x_{\alpha }-x|\leq y_{\alpha }$ for every $\alpha \in \Omega$.
• 1-convergent to $x\in E$ if there are a net $(y_{\alpha })_{\alpha \in \Omega }$ in $E$ and $\alpha _{0}\in \Omega$ such that $y_{\alpha }\downarrow 0$ and $|x_{\alpha }-x|\leq y_{\alpha }$ for every $\alpha \geq \alpha _{0}$.
• 2-convergent to $x\in E$ is there are a net $(y_{\beta })_{\beta \in \Gamma }$ in $E$ such that $y_{\beta }\downarrow 0$ and for every $\beta \in \Gamma$ there exists $\alpha _{0}\in \Omega$ such that $|x_{\alpha }-x|\leq y_{\beta }$ for any $\alpha \geq \alpha _{0}$.

If $E$ is Dedekind complete, then the notions of 1-convergence and 2-convergence coincide [Reference Abramovich and Sirotkin1], but otherwise they may be different (see [Reference Abramovich and Sirotkin1, Example 1.4]).

Order continuity can be considered with respect to any of these three notions of order convergence: a linear operator $T \colon E \longrightarrow F$ between Riesz spaces is said to be order continuous (1-order continuous, 2-order continuous, respectively) if $(T(x_{\alpha }))_{\alpha \in \Omega }$ is order convergent (1-convergent, 2-convergent, respectively) to zero in $F$ whenever $(x_{\alpha })_{\alpha \in \Omega }$ is order convergent (1-convergent, 2-convergent, respectively) to zero in $E$.

The following coincidences are known (see [Reference Aliprantis and Burkinshaw2, Theorem 1.56] or [Reference Meyer–Nieberg17, Proposition 1.3.9]):

• If $F$ is Dedekind complete, then $T$ is order continuous if and only if $T$ is 1-order continuous.
• If $E$ and $F$ are Dedekind complete, then $T$ is order continuous if and only if $T$ is 1-order continuous if and only if $T$ is 2-order continuous.

In most cases in this paper we will investigate the order continuity of regular linear operators from $E^{\sim \sim }$ to $F^{\sim \sim }$, where $E$ and $F$ are Riesz spaces, or from $E^{**}$ to $F^{**}$, where $E$ and $F$ are Banach lattices. Since all these spaces are Dedekind complete, we are free to use any of the three notions of order continuity. We shall denote the order convergence by $x_\alpha \stackrel {o}{\longrightarrow } x$.

For the theory of regular multilinear operators and regular homogeneous polynomials we refer to [Reference Bu and Buskes9, Reference Buskes and Roberts10, Reference Loane16]. An $m$-linear operator $A \colon E_1 \times \cdots \times E_m \longrightarrow F$ is separately order continuous (separately 1-order continuous, separately 2-order continuous) if for all $j \in \{1,\, \ldots,\, m\}$ and $x_k \in E_k,\, k = 1,\,\ldots,\, m,\, k\neq j$, the linear operator

\[ x_j \in E_j \mapsto A(x_1, \ldots, x_m) \in F \]

is order continuous (1-order continuous, 2-order continuous). For the definition of joint order continuity see [Reference Boyd, Ryan and Snigireva7, p. 234]. If $A$ is a regular operator between Banach lattices with $F$ Dedekind complete, then $A$ is separately order continuous if and only if $A$ is jointly order continuous [Reference Boyd, Ryan and Snigireva7, Theorem 2].

Now we recall the description of the Arens extensions of regular multilinear operators between Riesz spaces as presented in [Reference Botelho and Garcia6]. By $J_E \colon E \longrightarrow E^{\sim \sim }$ we denote the canonical operator ($J_E(x)(x'') = x''(x)$), which happens to be a Riesz homomorphism.

Given Riesz spaces $E_1,\, \ldots,\, E_m,\,F$, the space of regular $m$-linear operators from $E_1 \times \cdots \times E_m$ to $F$ is denoted by ${\mathcal {L}}_r(E_1,\, \ldots,\, E_m;F)$. When $F$ is the scalar field we write ${\mathcal {L}}_r(E_1,\, \ldots,\, E_m)$. We use $S_m$ to denote the set of permutations of $\{1,\, \ldots,\, m\}$.

Let $m\in \mathbb {N}$ and $\rho \in S_{m}$ be given. For an $m$-linear form $C\colon E_{1}\times \cdots \times E_{m}\longrightarrow \mathbb {R}$, define the $m$-linear form

\[ C_{\rho}\colon E_{\rho(1)}\times\cdots\times E_{\rho(m)}\longrightarrow \mathbb{R},~ C_{\rho}(x_{1},\ldots,x_{m})=C(x_{\rho^{{-}1}(1)},\ldots,x_{\rho^{{-}1}(x_{m})}), \]

where $x_{j}\in E_{\rho (j)},\, j=1,\,\ldots,\,m$. Furthermore, for each $i=1,\,\ldots,\,m-1$, and $x_{\rho (i)}^{\prime \prime }\in E_{\rho (i)}^{\sim \sim }$, consider the regular linear operator

(2.1)\begin{equation} \overline{x_{\rho(i)}^{\prime\prime}}\colon \mathcal{L}_{r}(E_{\rho(i)},\ldots,E_{\rho(m)})\longrightarrow \mathcal{L}_{r}(E_{\rho(i+1)},\ldots,E_{\rho(m)}), \quad \overline{x_{\rho(i)}^{\prime\prime}}(B)=x_{\rho(i)}^{\prime\prime}\circ B^{i}, \end{equation}

where $B^{i}\colon E_{\rho (i+1)}\times \cdots \times E_{\rho (m)}\longrightarrow E_{\rho (i)}^{\sim }$ is given by

\[ B^{i}(x_{i+1},\ldots,x_{m})(x_{i})=B(x_{i},x_{i+1},\ldots,x_{m}), \text{ for all } x_{j}\in E_{\rho(j)}, \quad j=i,\ldots,m. \]

In the case $i=m$ we define $\overline {x_{\rho (m)}^{\prime \prime }}\colon E_{\rho (m)}^{\sim }\longrightarrow \mathbb {R}$ by $\overline {x_{\rho (m)}^{\prime \prime }}(x_{\rho (m)})=x_{\rho (m)}^{\prime \prime }(x_{\rho (m)})$.

The Arens extension of the regular $m$-linear operator $A\colon E_{1}\times \cdots \times E_{m}\longrightarrow F$ is the regular $m$-linear operator $AR_{m}^{\rho }(A)\colon E_{1}^{\sim \sim }\times \cdots \times E_{m}^{\sim \sim }\longrightarrow F^{\sim \sim }$ given by

\[ AR_{m}^{\rho}(A)(x_{1}^{\prime\prime},\ldots,x_{m}^{\prime\prime})(y^{\prime})=\big(\overline{x_{\rho(m)}^{\prime\prime}}\circ\cdots\circ \overline{x_{\rho(1)}^{\prime\prime}}\big)((y^{\prime}\circ A)_{\rho}), \]

for all $x_{1}^{\prime \prime }\in E_{1}^{\sim \sim },\,\ldots,\,x_{m}^{\prime \prime }\in E_{m}^{\sim \sim }$ and every $y^{\prime }\in F^{\sim }$. Although the notation is a bit different, these are exactly the Arens extensions studied in [Reference Botelho and Garcia6].

According to [Reference Botelho and Garcia6, Theorem 2.2], $AR_{m}^{\rho }(A)$ is a regular $m$-linear operator that extends $A$ in the sense that $AR_{m}^{\rho }(A)\circ (J_{E_{1}},\,\ldots,\,J_{E_{m}})=J_{F}\circ A.$ Moreover, $AR_{m}^{\rho }(A)$ is positive for positive $A$.

The extension $A^{\ast [m+1]}$ from [Reference Boyd, Ryan and Snigireva7, Reference Buskes and Roberts10] is recovered by considering the permutation $\theta (m) = 1,\, \theta (m-1) = 2,\, \ldots,\,\theta (2) = m-1,\, \theta (1) = m$, that is, $AR_m^\theta (A) = A^{*[m+1]}$. In particular, $AR_2^\theta (A) = A^{***}$ in the bilinear case $m = 2$.

3. The counterexample

Consider the positive bilinear form given by the duality bracket $(c_0,\,\ell _1)$:

\[ A\colon \ell_{1}\times c_{0}\longrightarrow \mathbb{R}, A((x_{n})_{n=1}^{\infty},(y_{n})_{n=1}^{\infty})=\displaystyle\sum_{n=1}^{\infty}x_{n}y_{n}. \]

The two Arens extensions of $A$ shall be denoted by $A^{***} =AR_2^\theta (A)$ and $AR_2^{\rm id}(A)$, where id is the identity permutation. As announced, we shall prove that $AR_2^{\rm id}(A)$ is separately order continuous on $\ell _1^{**} \times c_0^{**}$ and that $A^{***}$ is order continuous in the first variable but not in the second one. Although everything can be proved directly to this bilinear form, to avoid unnecessary repetitions we shall apply some results that will be proved later.

From Theorem 4.6 we know that $A^{***} \colon \ell _{1}^{\ast \ast }\times c_{0}^{\ast \ast }\longrightarrow \mathbb {R}$ is order continuous in the first variable. Suppose that $A^{***}$ is order continuous in the second variable, that is, for every $x^{\ast \ast }\in \ell _{1}^{\ast \ast }$, the linear functional $A^{***}(x^{\ast \ast },\,\bullet )\colon c_{0}^{\ast \ast }\longrightarrow \mathbb {R}$, defined by $A^{***}(x^{\ast \ast },\,\bullet )(y^{**}) = A^{***}(x^{**},\, y^{**})$, is order continuous. Denoting by $\psi \colon \ell _{1}\longrightarrow c_{0}^{*}$ the canonical isometric isomorphism, note that $\psi$ and $\psi ^{-1}\colon c_{0}^{\ast }\longrightarrow \ell _{1}$, $\psi ^{-1}(\varphi )=(\varphi (e_{n}))_{n=1}^{\infty }$, are positive operators, hence $\psi$ is a Riesz homomorphism [Reference Aliprantis and Burkinshaw2, Theorem 2.15]. Moreover, $\psi (x)=A_\theta (\bullet,\, x)$ for every $x\in \ell _{1}$, where $A_{\theta }(\bullet,\,x)\colon c_{0}\longrightarrow \mathbb {R}$ is given by $A_{\theta }(\bullet,\,x)(y)=A_{\theta }(y,\,x)$.

Claim 1. $\psi ^{\ast \ast }(x^{\ast \ast })=A^{***}(x^{\ast \ast },\,\bullet )$ for every $x^{\ast \ast }\in \ell _{1}^{\ast \ast }$.

Indeed, given $y^{\ast \ast }\in c_{0}^{\ast \ast }$ and $x\in \ell _{1}$, noting that $A_{\theta }^{1}\colon \ell _{1}\longrightarrow c_{0}^{\ast }$ is given by $A_{\theta }^{1}(x)(y)=A_{\theta }(y,\,x)$, we have $A_{\theta }^{1}(x)=A_{\theta }(\bullet,\,x)$, hence

\begin{align*} \psi^{{\ast}}(y^{{\ast}{\ast}})(x)& =y^{{\ast}{\ast}}(\psi(x))\nonumber\\& =y^{{\ast}{\ast}}(A_{\theta}({\bullet},x))=y^{{\ast}{\ast}}(A_{\theta}^{1}(x))=(y^{{\ast}{\ast}}\circ A_{\theta}^{1})(x)=\overline{y^{{\ast}{\ast}}}(A_{\theta})(x), \end{align*}

proving that $\psi ^{\ast }(y^{\ast \ast })=\overline {y^{\ast \ast }}(A_{\theta })$. Therefore, for $x^{\ast \ast }\in \ell _{1}^{\ast \ast }$ and $y^{\ast \ast }\in c_{0}^{\ast \ast }$, bearing in mind that $A^{***} =AR_2^\theta (A)$ ,

\begin{align*} \psi^{{\ast}{\ast}}(x^{{\ast}{\ast}})(y^{{\ast}{\ast}})& =x^{{\ast}{\ast}}(\psi^{{\ast}}(y^{{\ast}{\ast}}))\\& =x^{{\ast}{\ast}}(\overline{y^{{\ast}{\ast}}}(A_{\theta}))=AR_{2}^{\theta}(A)(x^{{\ast}{\ast}},y^{{\ast}{\ast}}) = A^{***}(x^{{\ast}{\ast}}, \bullet)(y^{{\ast}{\ast}}). \end{align*}

Claim 2. $x^{**}\in \ell _{1}^{\ast \ast }$ is order continuous on $\ell _1^*$ if and only if $\psi ^{\ast \ast }(x^{\ast \ast })\in c_{0}^{\ast \ast \ast }$ is order continuous on $c_0^{**}$.

Let $x^{**}\in \ell _{1}^{\ast \ast }$ be such that $\psi ^{\ast \ast }(x^{\ast \ast })\in c_{0}^{\ast \ast \ast }$ is order continuous on $c_0^{**}$. Supposing that $x^{\ast \ast }$ fails to be order continuous on $\ell _1^*$, the positive functional $|x^{\ast \ast }|\in \ell _{1}^{\ast \ast }$ is not order continuous on $\ell _1^*$ either [Reference Aliprantis and Burkinshaw2, Theorem 1.56]. Then there is a net $(x_{\alpha }^{\ast })_{\alpha \in \Omega }$ in $\ell _{1}^{\ast }$ such that $x_{\alpha }^{\ast }\downarrow 0$ but $\displaystyle \inf _{\alpha \in \Omega }|x^{\ast \ast }|(x_{\alpha }^{\ast })> 0$. For each $\alpha \in \Omega$ let $y_{\alpha }^{\ast \ast }\in c_{0}^{\ast \ast }$ be such that $\psi ^{\ast }(y_{\alpha }^{\ast \ast })=x_{\alpha }^{\ast }$. Thus

\[ y_{\alpha}^{{\ast}{\ast}}=(\psi^{{\ast}})^{{-}1}(x_{\alpha}^{{\ast}})=(\psi^{{-}1})^{{\ast}}(x_{\alpha}^{{\ast}})\downarrow 0 \text{ in } c_{0}^{{\ast}{\ast}} \]

because $(\psi ^{-1})^{\ast }$ is positive and order continuous [Reference Aliprantis and Burkinshaw2, Theorem 1.73]. By assumption $\psi ^{\ast \ast }(x^{\ast \ast })$ is order continuous on $c_0^{**}$, so is $|\psi ^{\ast \ast }(x^{\ast \ast })|$ [Reference Aliprantis and Burkinshaw2, Theorem 1.56]. Since $\psi$ is a Riesz homomorphism, $\psi ^{\ast \ast }$ is as well, so $\psi ^{\ast \ast }(|x^{\ast \ast }|)(y_{\alpha }^{\ast \ast })=|\psi ^{\ast \ast }(x^{\ast \ast })|(y_{\alpha }^{\ast \ast })\downarrow 0$, from which it follows that

\[ 0=\inf_{\alpha\in\Omega}\psi^{{\ast}{\ast}}(|x^{{\ast}{\ast}}|)(y_{\alpha}^{{\ast}{\ast}})= \inf_{\alpha\in\Omega}|x^{{\ast}{\ast}}|(\psi^{{\ast}}(y_{\alpha}^{{\ast}{\ast}})) =\inf_{\alpha\in\Omega}|x^{{\ast}{\ast}}|(x_{\alpha}^{{\ast}})>0. \]

This contradiction proves that $x^{\ast \ast }\in \ell _{1}^{\ast \ast }$ is order continuous on $\ell _1^*$ . The reverse implication if straightforward.

Claim 3. $\ell _{1}^{\ast \ast }$ contains a functional that fails to be order continuous on $\ell _1^*$.

Let $c$ be the space of convergent real sequences and consider the positive linear functional $\varphi \in c^*$ given by $\varphi ((x_{n})_{n=1}^{\infty })=\displaystyle \lim _{n\rightarrow \infty }x_{n}$. Since $c$ is a majorizing subspace of $\ell _{\infty }$, $\varphi$ admits a positive extension $\widetilde {\varphi }\in \ell _{\infty }^{\ast }$ [Reference Aliprantis and Burkinshaw2, Theorem 1.32]. Suppose that $\widetilde {\varphi }$ is $\sigma$-order continuous on $\ell _\infty$. For each $n\in \mathbb {N}$ let $x_{n}=(1,\,\ldots,\,1,\,0,\,\ldots ) = e_1 + \cdots + e_n\in c$ and $y=(1,\,1,\,\ldots )\in c$. Note that $0\leq x_{n}\uparrow y$ and, since $\widetilde {\varphi }$ is a positive $\sigma$-order continuous operator, $0\leq \widetilde {\varphi }(x_{n})\uparrow \widetilde {\varphi }(y)$ (see [Reference Aliprantis and Burkinshaw2, p. 46]). So,

\[ 1=\widetilde{\varphi}(y)=\sup_{n\in\mathbb{N}}\widetilde{\varphi}(x_{n})=0, \]

which proves that $\widetilde {\varphi }\in \ell _{\infty }^{\ast }$ is not $\sigma$-order continuous on $\ell _\infty$. Considering the canonical Riesz isomorphism $\phi \colon \ell _{\infty }\longrightarrow \ell _{1}^{\ast }$, there is $z^{\ast \ast }\in \ell _{1}^{\ast \ast }$ such that $\phi ^{\ast }(z^{\ast \ast })=\widetilde {\varphi }$. Since $\widetilde {\varphi }\in \ell _{\infty }^{\ast }$ fails to be $\sigma$-order continuous, there is a sequence $(z_{n})_{n=1}^{\infty }$ in $\ell _{\infty }$ such that $z_{n}\downarrow 0$ and $\displaystyle \inf _{n\in \mathbb {N}}\widetilde {\varphi }(z_{n})>0$. Furthermore, for each $n \in \mathbb {N}$ there is $y_{n}^{\ast }\in \ell _{1}^{\ast }$ such that $\phi ^{-1}(y_{n}^{\ast })=z_{n}$, hence $y_{n}^{\ast }=\phi (z_{n})\downarrow$ because $\phi$ is positive, so $0\leq y_{n}^{\ast }\downarrow$. Suppose that there exists $y^{\ast }\in \ell _{1}^{\ast }$ such that $0< y^{\ast }\leq y_{n}^{\ast }$ for every $n\in \mathbb {N}$. On the one hand, as $\phi ^{-1}$ is positive,

\[ 0 \leq \phi^{{-}1}(y^{{\ast}})\leq \phi^{{-}1}(y_{n}^{{\ast}})=z_{n} \mbox{ for every } n, \]

from which we conclude that $\phi ^{-1}(y^{\ast })=0$, and so $y^{\ast }=0$ because $\phi ^{-1}$ is injective. This shows that $y_{n}^{\ast }\downarrow 0$ in $\ell _{1}^{\ast }$. On the other hand,

\begin{align*} \inf_{n\in\mathbb{N}}z^{{\ast}{\ast}}(y_{n}^{{\ast}})& = \inf_{n\in\mathbb{N}}(\phi^{{\ast}})^{{-}1}(\widetilde{\varphi})(y_{n}^{{\ast}})\\ & =\inf_{n\in\mathbb{N}}(\phi^{{-}1})^{{\ast}}(\widetilde{\varphi})(y_{n}^{{\ast}}) =\inf_{n\in\mathbb{N}}\widetilde{\varphi}(\phi^{{-}1}(y_{n}^{{\ast}})) =\inf_{n\in\mathbb{N}}\widetilde{\varphi}(z_{n})>0, \end{align*}

proving that $z^{\ast \ast }$ is not order continuous on $\ell _\infty$, as claimed.

Finally, combining claims 1 and 2 we have that $A^{***}(z^{**},\, \bullet )= \psi ^{**}(z^{**})$ is not order continuous on $c_0^{**}$. We have established that $A^{***}$ is order continuous in the first variable and fails to be order continuous in the second variable.

As to the other Arens extension of $A$, namely $AR_{2}^{\rm id}(A)\colon \ell _{1}^{\ast \ast }\times c_{0}^{\ast \ast }\longrightarrow \mathbb {R}$, since $c_{0}^{\ast } = \ell _{1}$ has order continuous norm, Corollary 5.1 guarantees that $AR_{2}^{id}(A)$ is separately order continuous, hence jointly order continuous by [Reference Boyd, Ryan and Snigireva7, Theorem 2].

Since the bilinear form $A$ is regular and of bounded order variation, this example shows that the results of Buskes and Roberts and of Boyd, Ryan and Snigireva quoted in the introduction cannot be improved to get separate order continuity on the product of the whole biduals.

4. Operators between Riesz spaces

In this section we present our results on order continuity to the whole of the bidual of Arens extensions of multilinear operators on Riesz spaces. The main result of the section, namely Theorem 4.6, is a multipurpose result: in this section it will be used to prove that Arens extensions of regular homogeneous polynomials are always order continuous at the origin on the whole of the bidual of the domain space, to extend [Reference Boyd, Ryan and Snigireva7, Theorem 1] and to show that Arens extensions are always order continuous in at least one variable. Furthermore, Theorem 4.6 will be helpful a couple of times in the next section.

Recall that a Riesz algebra $\mathcal {A}$ is a Riesz space which is an associative algebra with respect to a product $\ast$ such that $x\ast y\geq 0$ for all $x,\,y\in \mathcal {A}^{+}$. And that a Riesz algebra $(\mathcal {A},\,\ast )$ is an $f$-algebra if $x\wedge y=0$ in $\mathcal {A}$ implies that $(x\ast z)\wedge y=(z\ast x)\wedge y=0$ for every $z\in \mathcal {A}^{+}.$ The following Riesz spaces are $f$–algebras: $\mathbb {R}$, $C(X)$ and $C_{b}(X)$-spaces, where $X$ is a topological space, $\ell _{\infty }(X)$ and $\mathbb {R}^{X}$-spaces, where $X$ is a nonempty set, $L_{\infty }(\mu )$-spaces, and spaces of measurable functions on measure spaces (see [Reference Aliprantis and Burkinshaw2, p. 126]). If $(\mathcal {A},\,\ast )$ is an $f$-algebra, then the Arens product $\odot$ , defined as follows, makes ${\mathcal {A}}^{\sim \sim }$ an $f$-algebra [Reference Yilmaz20]: for $x\in \mathcal {A}$, $y^{\prime }\in \mathcal {A}^{\sim }$ and $x^{\prime \prime },\, y^{\prime \prime }\in \mathcal {A}^{\sim \sim }$,

\begin{align*} y^{\prime}\cdot x& \colon \mathcal{A}\longrightarrow \mathbb{R},~ (y^{\prime}\cdot x)(y)=y^{\prime}(x\ast y).\\ x^{\prime\prime}\diamond y^{\prime}& \colon \mathcal{A}\longrightarrow \mathbb{R}, \quad (x^{\prime\prime}\diamond y^{\prime})(y)=x^{\prime\prime}(y^{\prime}\cdot y).\\ x^{\prime\prime}\odot y^{\prime\prime}& \colon \mathcal{A}^{{\sim}}\longrightarrow \mathbb{R}, \quad (x^{\prime\prime}\odot y^{\prime\prime})(z^{\prime})=x^{\prime\prime}(y^{\prime\prime}\diamond z^{\prime} ). \end{align*}

An operator $A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m};\mathcal {A})$ is multiplicative if there are regular linear operators $T_{i}\colon E_{i}\longrightarrow \mathcal {A},\, i=1,\,\ldots,\,m$, such that $A(x_{1},\,\ldots,\,x_{m})=T_{1}(x_{1})\ast \cdots \ast T_{m}(x_{m})$ for all $x_{1}\in E_{1},\,\ldots,\,x_{m}\in E_{m}$.

Since Arens extensions $AR_{m}^{\rho }(A)$ of multilinear operators $A$ are mappings between Dedekind complete spaces, we can use any of the three notions of order continuous linear operators to investigate the separate order continuity of $AR_{m}^{\rho }(A)$.

Proposition 4.1 Let $E_{1},\,\ldots,\,E_{m}$ be Riesz spaces and $(\mathcal {A},\,\ast )$ be an Archimedean $f$-algebra. If $A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m};\mathcal {A})$ is a finite sum of multiplicative operators, then all Arens extensions of $A$, $AR_{m}^{\rho }(A)$, $\rho \in S_{m}$, coincide and are separately order continuous.

Proof. Given a multiplicative operator $B\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m};\mathcal {A})$, let $T_{i}\colon E_{i}\longrightarrow \mathcal {A},\, i=1,\,\ldots,\,m$, be such that $B(x_{1},\,\ldots,\,x_{m})=T_{1}(x_{1})\ast \cdots \ast T_{m}(x_{m})$ for all $x_{1}\in E_{1},\,\ldots,\,x_{m}\in E_{m}$. By [Reference Botelho and Garcia6, Remark 3.3 and the proof of Theorem 3.2] we have that, for each $\rho \in S_{m}$ and all $x_{1}^{\prime \prime }\in E_{1}^{\sim \sim },\,\ldots,\,x_{m}^{\prime \prime }\in E_{m}^{\sim \sim }$,

\[ AR_{m}^{\rho}(B)(x_{1}^{\prime\prime},\ldots,x_{m}^{\prime\prime})=T_{\rho(m)}^{\prime\prime}(x_{\rho(m)}^{\prime\prime})\odot \cdots\odot T_{\rho(1)}^{\prime\prime}(x_{\rho(1)}^{\prime\prime}). \]

The Arens product $\odot$ makes $\mathcal {A}^{\sim \sim }$ a Dedekind complete, hence Archimedean, commutative $f$-algebra [Reference Yilmaz20, Corollaries 3.5 and 3.6], so

\[ AR_{m}^{\rho}(B)(x_{1}^{\prime\prime},\ldots,x_{m}^{\prime\prime})=T_{1}^{\prime\prime}(x_{1}^{\prime\prime})\odot \cdots\odot T_{m}^{\prime\prime}(x_{m}^{\prime\prime}), \]

which gives, in particular, that all Arens extensions of $A$ coincide. In order to check that $AR_{m}^{\rho }(B)$ is separately order continuous, let $j\in \{1,\,\ldots.m\}$, $x_{i}^{\prime \prime }\in E_{i}^{\sim \sim },\, i=1,\,\ldots,\,m$, with $i\neq j$ be given and let $(x_{\alpha _{j}}^{\prime \prime })_{\alpha _{j}\in \Omega _{j}}$ be a net in $E_{j}^{\sim \sim }$ such that $x_{\alpha _{j}}^{\prime \prime } \xrightarrow {\, o \,} 0$. There exists a net $(z_{\alpha _{j}}^{\prime \prime })_{\alpha _{j}\in \Omega _{j}}$ such that $z_{\alpha _{j}}^{\prime \prime } \downarrow 0$ and $|x_{\alpha _{j}}^{\prime \prime }|\leq z_{\alpha _{j}}^{\prime \prime }$ for every $\alpha _{j}\in \Omega _{j}$. The functional

\[ \varphi:=|T_{1}^{\prime\prime}(x_{1}^{\prime\prime})|\odot\cdots\odot |T_{j-1}^{\prime\prime}(x_{j-1}^{\prime\prime})|\odot |T_{j+1}^{\prime\prime}(x_{j+1}^{\prime\prime})|\odot \cdots\odot |T_{m}^{\prime\prime}(x_{m}^{\prime\prime})|\in \mathcal{A}^{{\sim}{\sim}} \]

is positive. Using again that the product $\odot$ is commutative and [Reference Aliprantis and Burkinshaw2, Exercise 12, p. 131],

\begin{align*} & |AR_{m}^{\rho}(B)(x_{1}^{\prime\prime},\ldots,x_{\alpha_{j}}^{\prime\prime},\ldots,x_{m}^{\prime\prime})|=| T_{1}^{\prime\prime}(x_{1}^{\prime\prime})\odot\cdots\odot T_{j}^{\prime\prime}(x_{\alpha_{j}}^{\prime\prime})\odot \cdots\odot T_{m}^{\prime\prime}(x_{m}^{\prime\prime})|\\ & \quad =|T_{1}^{\prime\prime}(x_{1}^{\prime\prime})|\odot\cdots\odot |T_{j-1}^{\prime}(x_{j-1}^{\prime\prime})|\odot |T_{j}^{\prime\prime}(x_{\alpha_{j}}^{\prime\prime})|\odot |T_{j+1}^{\prime\prime}(x_{j+1}^{\prime\prime})|\odot \cdots\odot |T_{m}^{\prime\prime}(x_{m}^{\prime\prime})|\\ & \quad =|T_{j}^{\prime\prime}(x_{\alpha_{j}}^{\prime\prime})|\odot \big(|T_{1}^{\prime\prime}(x_{1}^{\prime\prime})|\odot\cdots\odot |T_{j-1}^{\prime\prime}(x_{j-1}^{\prime\prime})|\odot |T_{j+1}^{\prime\prime}(x_{j+1}^{\prime\prime})|\odot \cdots\odot |T_{m}^{\prime\prime}(x_{m}^{\prime\prime})|\big)\\ & \quad =|T_{j}^{\prime\prime}(x_{\alpha_{j}}^{\prime\prime})|\odot \varphi\leq |T_{j}^{\prime\prime}|(|x_{\alpha_{j}}^{\prime\prime}|)\odot \varphi\leq |T_{j}^{\prime\prime}|(z_{\alpha_{j}}^{\prime\prime})\odot \varphi. \end{align*}

Now it is enough to prove that $|T_{j}^{\prime \prime }|(z_{\alpha _{j}}^{\prime \prime })\odot \varphi \downarrow 0$. Let $0\leq y^{\prime }\in \mathcal {A}^{\sim }$ be given. Then $\varphi \diamond y^{\prime }$ is positive and, since $|T_{j}^{\prime \prime }|$ is order continuous and positive [Reference Aliprantis and Burkinshaw2, Theorems 1.56 and 1.73],

\[ \big(|T_{j}^{\prime\prime}|(z_{\alpha_{j}}^{\prime\prime})\odot \varphi\big)(y^{\prime})=|T_{j}^{\prime\prime}|(z_{\alpha_{j}}^{\prime\prime})(\varphi\diamond y^{\prime})\downarrow 0, \]

from which it follows that $(|T_{j}^{\prime \prime }|(z_{\alpha _{j}}^{\prime \prime })\odot \varphi )\downarrow 0$ [Reference Aliprantis and Burkinshaw2, Theorem 1.18] and gives the separate order continuity of $AR_{m}^{\rho }(B)$.

The linearity of the correspondence $A \mapsto AR_{m}^{\rho }(A)$ gives the result for finite sums of multiplicative operators.

Since scalar-valued Riesz multimorphisms are multiplicative [Reference Kusraev and Kusraeva14, Theorem 6], Proposition 4.1 yields the following.

Corollary 4.2 All Arens extensions of a finite sum of scalar-valued Riesz multimorphisms coincide and are separately order continuous.

An operator $A \in {\mathcal {L}}_r(E_1,\, \ldots,\, E_m;F)$ is of finite type if there are $n\in \mathbb {N}$, functionals $\varphi _{j}^{i}\in E_{i}^{\sim }$ and vectors $y_{j}\in F$, $j=1,\,\ldots,\,n$, $i=1,\,\ldots,\,m$, such that

\[ A(x_{1},\ldots,x_{m})=\sum_{j=1}^{n} \varphi_{j}^{1}(x_{1})\cdots \varphi_{j}^{m}(x_{m})y_{j} \text{ for all } x_{i}\in E_{i}, \quad i=1,\ldots,m. \]

Corollary 4.3 All Arens extensions of a multilinear operator of finite type coincide, are of finite type and are separately order continuous.

Proof. It is not difficult to check that if $A \in {\mathcal {L}}_r(E_1,\, \ldots,\, E_m)$ is separately order continuous and $y \in F$, then the operator

\[ (x_1, \ldots, x_m) \in E_1 \times \cdots \times E_m \mapsto A(x_1, \ldots, x_m)y \in F, \]

is separately order continuous as well. Now the result follows from Proposition 4.1 and from its proof.

To proceed to the main results of the section we need some preparation.

Lemma 4.4 Let $E_{1},\,\ldots,\,E_{m},\, F$ be Riesz spaces with $F$ Dedekind complete and $(B_{\alpha })_\alpha$ be a net in $\mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m}; F)$. Then $B_{\alpha }\downarrow 0$ if and only if $B_{\alpha }(x_{1},\,\ldots,\,x_{m})\downarrow 0$ in $F$ for all $x_{1}\in E_{1}^{+},\,\ldots,\, x_{m}\in E_{m}^{+}$.

Proof. It is straightforward that $B_{\alpha }\downarrow 0$ if $B_{\alpha }(x_{1},\,\ldots,\,x_{m})\downarrow 0$ in $F$ for all $x_{1}\in E_{1}^{+},\,\ldots,\, x_{m}\in E_{m}^{+}$. We prove the other implication by induction on $m$. The case $m=1$ follows from the Riesz-Kantorovich theorem [Reference Aliprantis and Burkinshaw2, Theorem 1.18]. Assume that the result holds for $n$ and let $(B_{\alpha })_\alpha$ be a net in $\mathcal {L}_{r}(E_{1},\,\ldots,\,E_{n+1}; F)$ such that $B_{\alpha }\downarrow 0$. Consider the canonical Riesz isomorphism

\[ \psi\colon \mathcal{L}_{r}(E_{1},\ldots,E_{n+1}; F)\longrightarrow \mathcal{L}_{r}(E_{1};\mathcal{L}_{r}(E_{2}\ldots,E_{n+1}; F)). \]

We have $0\leq \psi (B_{\alpha })\downarrow$ because $\psi$ is positive. Let $T \in \mathcal {L}_{r}(E_{1};\mathcal {L}_{r}(E_{2}\ldots,\,E_{n+1}; F))$ be such that $0\leq T\leq \psi (B_{\alpha })$ for every $\alpha$. Since $\psi ^{-1}$ is positive, $0 \leq \psi ^{-1}(T)\leq B_{\alpha }\downarrow 0$, hence $0\leq \psi ^{-1}(T)\leq 0$, which proves that $\psi (B_{\alpha })\downarrow 0$ in $\mathcal {L}_{r}(E_{1};\mathcal {L}_{r}(E_{2}\ldots,\,E_{n+1}; F))$. The linear case of the result gives that $\psi (B_{\alpha })(x_{1})\downarrow 0$ in $\mathcal {L}_{r}(E_{2}\ldots,\,E_{n+1}; F)$ for every $x_{1}\in E_{1}^{+}$. The induction hypothesis gives that, regardless of the $x_{2}\in E_{2}^{+},\,\ldots,\,x_{n+1}\in E_{n+1}^{+}$,

\[ B_{\alpha}(x_{1},x_{2},\ldots,x_{n+1})=\psi(B_{\alpha})(x_{1})(x_{2},\ldots,x_{n+1})\downarrow 0, \]

completing the proof.

Lemma 4.5 Let $E_{1},\,\ldots,\,E_{m}$ be Riesz spaces, $\rho \in S_{m}$, $k \in \{1,\,\ldots,\,m-1\}$ and $x_{\rho (k)}^{\prime \prime }\in (E_{\rho (k)}^{\sim })_{n}^{\sim }$. Then the operator

\[ \overline{x_{\rho(k)}^{\prime\prime}}\colon \mathcal{L}_{r}(E_{\rho(k)},\ldots,E_{\rho(m)})\longrightarrow \mathcal{L}_{r}(E_{\rho(k+1)},\ldots,E_{\rho(m)}), \]

defined in (2.1), is order continuous.

Proof. We already know that $\overline {x_{\rho (k)}^{\prime \prime }}$ is a regular linear operator, $\big |\overline {x_{\rho (k)}^{\prime \prime }} \big |\leq \overline {|x_{\rho (k)}^{\prime \prime }|}$ because $B^{k}$ is positive for every positive $B\in \mathcal {L}_{r}(E_{\rho (k)},\,\ldots,\,E_{\rho (m)})$, so

\[ \overline{|x_{\rho(k)}^{\prime\prime}|}(B)=|x_{\rho(k)}^{\prime\prime}|\circ B^{k}\geq{\pm} x_{\rho(k)}^{\prime\prime}\circ B^{k}={\pm} \big(x_{\rho(k)}^{\prime\prime}\circ B^{k}\big)={\pm} \overline{x_{\rho(k)}^{\prime\prime}}( B). \]

Let $(A_{\alpha })_{\alpha \in \Omega }$ be a net in $\mathcal {L}_{r}(E_{\rho (k)},\,\ldots,\,E_{\rho (m)})$ such that $A_{\alpha }\xrightarrow {\, o\, } 0$. Then there are a net $(B_{\alpha })_{\alpha \in \Omega }$ in $\mathcal {L}_{r}(E_{\rho (k)},\,\ldots,\,E_{\rho (m)})$ and $\alpha _{0}\in \Omega$ such that $B_{\alpha }\downarrow 0$ and $|A_{\alpha }|\leq B_{\alpha }$ for every $\alpha \geq \alpha _{0}$. Thus,

\[ \big|\overline{x_{\rho(k)}^{\prime\prime}}(A_{\alpha})\big|\leq \big|\overline{x_{\rho(k)}^{\prime\prime}}\big|(|A_{\alpha}|)\leq \overline{|x_{\rho(k)}^{\prime\prime}|}(|A_{\alpha}|)\leq \overline{|x_{\rho(k)}^{\prime\prime}|}(B_{\alpha}) \text{ for every } \alpha\geq \alpha_{0}. \]

For $x_{i}\in E_{\rho (i)}^{+}$, $i\in \{k,\,\ldots,\,m\}$, Lemma 4.4 gives

\[ B_{\alpha}^{k}(x_{k+1},\ldots,x_{m})(x_{k})=B_{\alpha}(x_{k},x_{k+1},\ldots,x_{m})\downarrow 0. \]

By [Reference Aliprantis and Burkinshaw2, Theorem 1.18] it follows that $B_{\alpha }^{k}(x_{k+1},\,\ldots,\,x_{m})\downarrow 0$. Since $x_{\rho (k)}^{\prime \prime }$ is an order continuous functional, $|x_{\rho (k)}^{\prime \prime }|$ is a positive order continuous operator [Reference Aliprantis and Burkinshaw2, Theorem 1.56], so $|x_{\rho (k)}^{\prime \prime }|(B_{\alpha }^{k}(x_{k+1},\,\ldots,\,x_{m}))\downarrow 0$, that is, $\overline {|x_{\rho (k)}^{\prime \prime }|}(B_{\alpha })(x_{k+1},\,\ldots,\,x_{m})\downarrow 0.$ Calling on Lemma 4.4 once again it follows that $\overline {|x_{\rho (k)}^{\prime \prime }|}(B_{\alpha })\downarrow 0$, proving that $\overline {x_{\rho (k)}^{\prime \prime }}$ is order continuous.

Theorem 4.6 Let $E_{1},\,\ldots,\,E_{m},\, F$ be Riesz spaces, $\rho \in S_{m}$ and $A\in \mathcal {L}_{r}(E_{1},\,\ldots, \,E_{m};F)$.

(a) For all $j\in \{1,\,\ldots,\,m\}$, $x_{\rho (i)}^{\prime \prime }\in E_{\rho (i)}^{\sim \sim },\, i=1,\,\ldots,\,j-1$, and $x_{\rho (i)}^{\prime \prime }\in (E_{\rho (i)}^{\sim })_{n}^{\sim },\, i=j+1,\,\ldots,\,m$, the operator
(4.1)\begin{equation} x''_{\rho(j)} \in E_{\rho(j)}^{{\sim}{\sim}} \mapsto AR_{m}^{\rho}(A)(x_{1}^{\prime\prime},\ldots,x_{{\rho(j)}}^{\prime\prime},\ldots,x_{m}^{\prime\prime}) \in F^{{\sim}{\sim}} \end{equation}
is order continuous on $E_{\rho (j)}^{\sim \sim }$.
(b) $AR_{m}^{\rho }(A)$ is separately order continuous on $(E_{1}^{\sim })_{n}^{\sim }\times \cdots \times (E_{m}^{\sim })_{n}^{\sim }$.
(c) $AR_{m}^{\rho }(A)$ is order continuous in the $\rho (m)$-th variable on the whole of $E_{\rho (m)}^{\sim \sim }$.

Proof. It is clear that (b) and (c) follow from (a) (for (c) just take $j = m$ in (a)). To prove (a), take $j\in \{1,\,\ldots,\,m\}$, $x_{\rho (i)}^{\prime \prime }\in E_{\rho (i)}^{\sim \sim },\, i=1,\,\ldots,\,j-1$, and $x_{\rho (i)}^{\prime \prime }\in (E_{\rho (i)}^{\sim })_{n}^{\sim },\, i=j+1,\,\ldots,\,m$. Given a net $(x_{\alpha _{\rho (j)}}^{\prime \prime })_{\alpha _{\rho (j)}\in \Omega _{\rho (j)}}$ in $E_{\rho (j)}^{\sim \sim }$ such that $x_{\alpha _{\rho (j)}}^{\prime \prime } \xrightarrow {\, o \, } 0$, there is a net $(z_{\alpha _{\rho (j)}}^{\prime \prime })_{\alpha _{\rho (j)}\in \Omega _{\rho (j)}}$ in $E_{\rho (j)}^{\sim \sim }$ and $\alpha _{\rho (j)_{0}}$ such that $z_{\alpha _{\rho (j)}}^{\prime \prime }\downarrow 0$ and $|x_{\alpha _{\rho (j)}}^{\prime \prime }|\leq z_{\alpha _{\rho (j)}}^{\prime \prime }$ for every $\alpha _{\rho (j)}\geq \alpha _{\rho (j)_{0}}$. Let $A_{1},\, A_{2}\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m};F)$ be positive operators such that $A=A_{1}-A_{2}$ and put $B:=A_{1}+A_{2}$. Of course $B$ is positive. Denoting the operator in (4.1) by $AR_{m}^{\rho }(A)_{x_{\rho (1)}^{\prime \prime },\,\ldots,\,x_{\rho (j-1)}^{\prime \prime },\,x_{\rho (j+1)}^{\prime \prime },\,\ldots,\,x_{\rho (m)}^{\prime \prime }}$, for every $\alpha _{\rho (j)}\geq \alpha _{\rho (j)_{0}}$,

\begin{align*} & |AR_{m}^{\rho}(A)_{x_{\rho(1)}^{\prime\prime},\ldots,x_{\rho(j-1)}^{\prime\prime},x_{\rho(j+1)}^{\prime\prime},\ldots,x_{\rho(m)}^{\prime\prime}}(x_{\alpha_{\rho(j)}}^{\prime\prime})| =|AR_{m}^{\rho}(A)(x_{1}^{\prime\prime},\ldots,x_{\alpha_{\rho(j)}}^{\prime\prime},\ldots,x_{m}^{\prime\prime})|\\ & \quad \leq |AR_{m}^{\rho}(A)|(|x_{1}^{\prime\prime}|,\ldots,|x_{\alpha_{\rho(j)}}^{\prime\prime}|,\ldots,|x_{m}^{\prime\prime}|)\\ & \quad = |AR_{m}^{\rho}(A_{1})-AR_{m}^{\rho}(A_{2})|(|x_{1}^{\prime\prime}|,\ldots,|x_{\alpha_{\rho(j)}}^{\prime\prime}|,\ldots,|x_{m}^{\prime\prime}|)\\ & \quad \leq \big(AR_{m}^{\rho}(A_{1})+AR_{m}^{\rho}(A_{2}) \big) (|x_{1}^{\prime\prime}|,\ldots,|x_{\alpha_{\rho(j)}}^{\prime\prime}|,\ldots,|x_{m}^{\prime\prime}|)\\ & \quad = AR_{m}^{\rho}(B)(|x_{1}^{\prime\prime}|,\ldots,|x_{\alpha_{\rho(j)}}^{\prime\prime}|,\ldots,|x_{m}^{\prime\prime}|)\\ & \quad =AR_{m}^{\rho}(B)_{|x_{\rho(1)}^{\prime\prime}|,\ldots,|x_{\rho(j-1)}^{\prime\prime}|,|x_{\rho(j+1)}^{\prime\prime}|,\ldots,|x_{\rho(m)}^{\prime\prime}|}(|x_{\alpha_{\rho(j)}}^{\prime\prime}|)\\ & \quad \leq AR_{m}^{\rho}(B)_{|x_{\rho(1)}^{\prime\prime}|,\ldots,|x_{\rho(j-1)}^{\prime\prime}|,|x_{\rho(j+1)}^{\prime\prime}|,\ldots,|x_{\rho(m)}^{\prime\prime}|}(z_{\alpha_{\rho(j)}}^{\prime\prime}). \end{align*}

As Arens extensions of positive operators are positive, it follows that

\[ 0\leq AR_{m}^{\rho}(B)_{|x_{\rho(1)}^{\prime\prime}|,\ldots,|x_{\rho(j-1)}^{\prime\prime}|,|x_{\rho(j+1)}^{\prime\prime}|,\ldots,|x_{\rho(m)}^{\prime\prime}|}(z_{\alpha_{\rho(j)}}^{\prime\prime})\downarrow. \]

Setting $T:=\overline {|x_{\rho (m)}^{\prime \prime }|}\circ \cdots \circ \overline {|x_{\rho (j+1)}^{\prime \prime }|}$, since each $|x_{\rho (i)}^{\prime \prime }|,\, i=j+1,\,\ldots,\,m$, is order continuous, by Lemma 4.5 it follows that $\overline {|x_{\rho (i)}^{\prime \prime }|}$ is order continuous, so $T$ is order continuous and positive. On the other hand, it is clear that, for every positive $y^{\prime }\in F^{\sim }$,

\[ S:=\big(\overline{|x_{\rho(j-1)}^{\prime\prime}|}\circ \cdots\circ \overline{|x_{\rho(1)}^{\prime\prime}|}\big)((y^{\prime}\circ B)_{\rho})\in \mathcal{L}_{r}(E_{\rho(j)},\ldots,\ldots,E_{\rho(m)}) \]

is positive. From $z_{\alpha _{\rho (j)}}^{\prime \prime }\downarrow 0$ we conclude that $\overline {z_{\alpha _{\rho (j)}}^{\prime \prime }}(S)\downarrow 0$, therefore $T(\overline {z_{\alpha _{\rho (j)}}^{\prime \prime }}(S))\downarrow 0$. It follows that, for every positive $y^{\prime }\in F^{\sim }$,

\begin{align*} & AR_{m}^{\rho}(B)_{|x_{\rho(1)}^{\prime\prime}|,\ldots,|x_{\rho(j-1)}^{\prime\prime}|,|x_{\rho(j+1)}^{\prime\prime}|,\ldots,|x_{\rho(m)}^{\prime\prime}|}(z_{\alpha_{\rho(j)}}^{\prime\prime})(y^{\prime})\\ & \quad =AR_{m}^{\rho}(B)(|x_{1}^{\prime\prime}|,\ldots,z_{\alpha_{\rho(j)}}^{\prime\prime},\ldots,|x_{m}^{\prime\prime}|)(y^{\prime})\\ & \quad =\big(\overline{|x_{\rho(m)}^{\prime\prime}|}\circ\cdots\circ \overline{|x_{\rho(j+1)}^{\prime\prime}|}\circ \overline{z_{\alpha_{\rho(j)}}^{\prime\prime}}\circ \overline{|x_{\rho(j-1)}^{\prime\prime}|}\circ \cdots\circ \overline{|x_{\rho(1)}^{\prime\prime}|}\big)((y^{\prime}\circ B)_{\rho})\\ & \quad =\big(T\circ \overline{z_{\alpha_{\rho(j)}}^{\prime\prime}}\circ \overline{|x_{\rho(j-1)}^{\prime\prime}|}\circ \cdots\circ \overline{|x_{\rho(1)}^{\prime\prime}|}\big)((y^{\prime}\circ B)_{\rho})\\ & \quad =T\big(\big(\overline{z_{\alpha_{\rho(j)}}^{\prime\prime}}\circ \overline{|x_{\rho(j-1)}^{\prime\prime}|}\circ \cdots\circ \overline{|x_{\rho(1)}^{\prime\prime}|}\big)((y^{\prime}\circ B)_{\rho})\big)\\ & \quad =T\big(\overline{z_{\alpha_{\rho(j)}}^{\prime\prime}}\big(\big(\overline{|x_{\rho(j-1)}^{\prime\prime}|}\circ \cdots\circ \overline{|x_{\rho(1)}^{\prime\prime}|}\big)((y^{\prime}\circ B)_{\rho})\big)\big)=T(\overline{z_{\alpha_{\rho(j)}}^{\prime\prime}}(S))\downarrow 0. \end{align*}

Lemma 4.4 gives that $AR_{m}^{\rho }(B)_{|x_{\rho (1)}^{\prime \prime }|,\,\ldots,\,|x_{\rho (j-1)}^{\prime \prime }|,\,|x_{\rho (j+1)}^{\prime \prime }|,\,\ldots,\,|x_{\rho (m)}^{\prime \prime }|}(z_{\alpha _{\rho (j)}}^{\prime \prime })\downarrow 0$, and this allows us to conclude that $AR_{m}^{\rho }(A)_{x_{\rho (1)}^{\prime \prime },\,\ldots,\,x_{\rho (j-1)}^{\prime \prime },\,x_{\rho (j+1)}^{\prime \prime },\,\ldots,\,x_{\rho (m)}^{\prime \prime }}$ is order continuous.

Remark 4.7 Theorem 4.6 improves [Reference Boyd, Ryan and Snigireva7, Theorem 1] in the sense that it holds for all Arens extensions, it holds for operators between Riesz spaces, it drops the assumption of $F$ being Dedekind complete and it assures the order continuity on the whole bidual in one of the variables. For regular operators, it improves [Reference Buskes and Roberts10, Theorem 3.4] by taking into account all Arens extensions and by assuring the order continuity on the whole bidual in one of the variables. In particular, Theorem 4.6(b) provides an alternative proof of [Reference Boyd, Ryan and Snigireva7, Theorem 1] and of [Reference Buskes and Roberts10, Theorem 3.4] for regular operators between Riesz spaces and (c) shows that $A^{\ast [m+1]}=AR_{m}^{\theta }(A)$ is order continuous in the first variable on the whole of $E_1^{\sim \sim }$.

Recall that an $m$-homogeneous polynomial $P \colon E \longrightarrow F$ between Riesz spaces is positive if the corresponding symmetric $m$-linear operator $\check P$ is positive, and that $P$ is regular, in symbols $P \in {\mathcal {P}}_r(^mE;F)$, if $P$ can be written as the difference of two positive polynomials.

The Arens extensions of a regular polynomial $P \in {\mathcal {P}}_r(^mE;F)$ are the polynomials associated to the Arens extensions of $\check P$, that is: for $\rho \in S_m$, the Arens extension of $P$ with respect to $\rho$ is the polynomial

\[ AR_m^\rho(P) \colon E^{{\sim}{\sim}} \longrightarrow F^{{\sim}{\sim}}, \quad AR_m^\rho(P)(x'') =AR_m^\rho(\check P)(x'', \ldots, x''). \]

In [Reference Buskes and Roberts10, Theorem 3.5] it is proved that $AR_m^\theta (P)$ is order continuous on $(E^\sim )_n^{\sim }$. We can go a bit further at the origin:

Proposition 4.8 All Arens extensions of a polynomial $P \in {\mathcal {P}}_r(^mE;F)$ are order continuous at the origin on $E^{\sim \sim }$, meaning that $AR_m^\rho (P)(x_{\alpha }^{\prime \prime })\xrightarrow {\, o\,} 0$ in $F^{\sim \sim }$ for every $\rho \in S_m$ and any $(x_{\alpha }^{\prime \prime })_{\alpha \in \Omega }$ in $E^{\sim \sim }$ such that $x_{\alpha }^{\prime \prime }\xrightarrow {\, o \,} 0$ in $E^{\sim \sim }$.

Proof. Write $P=P_{1}-P_{2}$, where $P_1$ and $P_2$ are positive $m$-homogeneous polynomials, and let $\check {P}_{1},\, \check {P}_{2}\colon E^{m}\longrightarrow F$ be the positive symmetric $m$-linear operators associated to $P_1$ and $P_2$, respectively. Let $(x_{\alpha }^{\prime \prime })_{\alpha \in \Omega }$ be a net in $E^{\sim \sim }$ such that $x_{\alpha }^{\prime \prime }\xrightarrow {\, o \,} 0$. There are a net $(z_{\alpha }^{\prime \prime })_{\alpha \in \Omega }$ in $E^{\sim \sim }$ and $\alpha _{0}\in \Omega$ such that $z_{\alpha }^{\prime \prime }\downarrow 0$ and $|x_{\alpha }^{\prime \prime }|\leq z_{\alpha }^{\prime \prime }$ for every $\alpha \geq \alpha _{0}$. For a permutation $\rho \in S_m$, we know from Theorem 4.6 that the operator

\[ x'' \in E^{{\sim}{\sim}} \mapsto AR_m^{\rho}(\check{P}_1 + \check{P}_2)(z''_{\alpha_0}, \ldots, z''_{\alpha_0}, x'', z''_{\alpha_0}, \ldots, z''_{\alpha_0}), \]

where $x''$ is placed at the $\rho (m)$-th coordinate, is order continuous. For $\alpha \geq \alpha _{0}$ we have $z_{\alpha }^{\prime \prime }\leq z_{\alpha _{0}}^{\prime \prime }$, so, using that $AR_m^{\rho }(\check {P}_1 + \check {P}_2)$ is positive,

\begin{align*} |AR_m^\rho(P)(x_{\alpha}^{\prime\prime})|& =|AR_m^\rho(P_1 - P_2)(x_{\alpha}^{\prime\prime})| = |AR_m^\rho((P_1 - P_2)^{{\vee}})(x_{\alpha}^{\prime\prime}, \ldots , x_{\alpha}^{\prime\prime})| \\ & =|AR_{m}^{\rho}(\check{P}_{1}-\check{P}_{2})(x_{\alpha}^{\prime\prime},\ldots,x_{\alpha}^{\prime\prime})|\leq |AR_{m}^{\rho}(\check{P}_{1}-\check{P}_{2})|(|x_{\alpha}^{\prime\prime}|,\ldots,|x_{\alpha}^{\prime\prime}|)\\ & \leq |AR_{m}^{\rho}(\check{P}_{1}-\check{P}_{2})|(z_{\alpha}^{\prime\prime},\ldots,z_{\alpha}^{\prime\prime}) \leq AR_{m}^{\rho}(\check{P}_{1}+\check{P}_{2})(z_{\alpha}^{\prime\prime},\ldots,z_{\alpha}^{\prime\prime}) \\ & \leq AR_{m}^{\rho}(\check{P}_{1}+\check{P}_{2})(z_{\alpha_{0}}^{\prime\prime},\ldots,z_{\alpha_{0}}^{\prime\prime}, z_{\alpha}^{\prime\prime},z_{\alpha_{0}}^{\prime\prime},\ldots,z_{\alpha_{0}}^{\prime\prime})\downarrow 0. \end{align*}

This proves that $AR_m^\rho (P)(x_{\alpha }^{\prime \prime })\xrightarrow {\, o\,} 0$.

In [Reference Boyd, Ryan and Snigireva8] it is proved that, for a regular homogeneous polynomial, order continuity at one point does not imply order continuity at every point in general. The result above shall be useful later.

5. Operators between Banach lattices

In this section we give conditions on the Banach lattices $E_1,\, \ldots,\, E_m$ so that, for every Banach lattice $F$, all Arens extensions of any regular $m$-linear operator from $E_1 \times \cdots \times E_m$ to $F$ are separately order continuous on $E_1^{**} \times \cdots \times E_m^{**}$. Consequences on order continuity of extensions of regular homogeneous polynomials shall also be obtained.

If the dual $E^{\ast }$ of a Banach lattice $E$ has order continuous norm, then $E^{\ast \ast }=(E^{\ast })_{n}^{\ast }$ [Reference Meyer–Nieberg17, Theorem 2.4.2]. So, the following is immediate from Theorem 4.6 .

Corollary 5.1 Let $E_{1},\,\ldots,\, E_{m},\, F$ be Banach lattices, $A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m};F)$ and $\rho \in S_{m}$. If $E_{j}^{\ast }$ has order continuous norm for $j=1,\,\ldots,\,m$, $j\neq \rho (1)$, then the Arens extension $AR_{m}^{\rho }(A)$ of $A$ is separately order continuous on $E_1^{**} \times \cdots \times E_m^{**}$.

The next result makes clear what type of condition should be asked to get order continuity of Arens extensions on the product of the whole of the biduals.

Proposition 5.2 Let $m \geq 2$ and $E_{1},\, \ldots,\,E_{m}$ be Banach lattices such that the Arens extension $A^{\ast [m+1]}$ of any form $A \in {\mathcal {L}}_r(E_1,\, \ldots,\, E_m)$ is separately order continuous on $E_{1}^{\ast \ast }\times \cdots \times E_{m}^{\ast \ast }$. Then, for every operator $T\in \mathcal {L}_{r}(E_{i};E_{j}^{\ast }),\,\ i,\,j=1,\,\ldots,\,m$, $i\neq j$, the functional $T^{\ast \ast }(x_{i}^{\ast \ast })$ is order continuous on $E_{j}^{\ast \ast }$ for every $x_{i}^{\ast \ast }\in E_{i}^{\ast \ast }$.

Proof. Let $i,\,j=1,\,\ldots,\,m,\, i\neq j$, and $T\in \mathcal {L}_{r}(E_{i};E_{j}^{\ast })$ be given. For $k=1,\,\ldots,\,m,\, i \neq k\neq j$, choose $0 \neq \varphi _{k}\in E_{k}^{\ast }$ and consider the regular $m$-linear form

\[ A\colon E_{1}\times\cdots\times E_{m}\longrightarrow \mathbb{R},~A(x_{1},\ldots,x_{m})=\Bigg(\displaystyle\prod_{ \substack{k=1 \\ k\neq i, j}}^{m}\varphi_{k}(x_{k})\Bigg)T(x_{i})(x_{j}). \]

Of course we can assume $i< j$. Using the Davie–Gamelin description of the Arens extensions [Reference Davie and Gamelin12], for $x_l^{**} \in E_l^{**}$ and nets $(x_{\alpha _{l}})_{\alpha _{l}\in \Omega _{l}}$ in $E_{l}$ such that $x_{l}^{\ast \ast }=\omega ^{\ast }-\displaystyle \lim _{\alpha _{l}}J_{E_{l}}(x_{\alpha _{l}}),\, l=1,\,\ldots,\,m$, we have

\begin{align*} & A^{{\ast}[m+1]}(x_{1}^{{\ast}{\ast}},\ldots,x_{i}^{{\ast}{\ast}},\ldots,x_{j}^{{\ast}{\ast}},\ldots,x_{m}^{{\ast}{\ast}})=\lim_{\alpha_{1}}\cdots\lim_{\alpha_{i}}\cdots\lim_{\alpha_{j}}\cdots\lim_{\alpha_{m}} A(x_{\alpha_{1}},\ldots,x_{\alpha_{m}})\\ & \quad =\lim_{\alpha_{1}}\cdots\lim_{\alpha_{i}}\cdots\lim_{\alpha_{j}}\cdots\lim_{\alpha_{m}} \Bigg(\displaystyle\prod_{ \substack{k=1 \\ k\neq i, j}}^{m}\varphi_{k}(x_{\alpha_{k}})\Bigg)T(x_{\alpha_{i}})(x_{\alpha_{j}})\\ & \quad=\lim_{\alpha_{1}}\cdots\lim_{\alpha_{i}}\cdots\lim_{\alpha_{j}}\cdots\lim_{\alpha_{m-1}} \Bigg(\displaystyle\prod_{ \substack{k=1 \\ k\neq i, j}}^{m-1}\varphi_{k}(x_{\alpha_{k}})\Bigg)T(x_{\alpha_{i}})(x_{\alpha_{j}})\lim_{\alpha_{m}} J_{E_{m}}(x_{\alpha_{m}})(\varphi_{m}) \\ & \quad=\lim_{\alpha_{1}}\cdots\lim_{\alpha_{i}}\cdots\lim_{\alpha_{j}}\cdots\lim_{\alpha_{m-1}} \Bigg(\displaystyle\prod_{ \substack{k=1 \\ k\neq i, j}}^{m-1}\varphi_{k}(x_{\alpha_{k}})\Bigg)T(x_{\alpha_{i}})(x_{\alpha_{j}}) x_{m}^{{\ast}{\ast}}(\varphi_{m})\\ & \quad \vdots\\ & \quad=\prod_{ \substack{k=i+1\\ k\neq j}}^{m}x_{k}^{{\ast}{\ast}}(\varphi_{k})\lim_{\alpha_{1}}\cdots\lim_{\alpha_{i}}\Bigg(\displaystyle\prod_{ \substack{k=1}}^{i-1}\varphi_{k}(x_{\alpha_{k}})\Bigg) x_{j}^{{\ast}{\ast}}( T(x_{\alpha_{i}}))\\ & \quad=\prod_{ \substack{k=i+1\\ k\neq j}}^{m}x_{k}^{{\ast}{\ast}}(\varphi_{k})\lim_{\alpha_{1}}\cdots\lim_{\alpha_{i-1}}\Bigg(\displaystyle\prod_{ \substack{k=1}}^{i-1}\varphi_{k}(x_{\alpha_{k}})\Bigg) \lim_{\alpha_{i}}T^{{\ast}}(x_{j}^{{\ast}{\ast}})( x_{\alpha_{i}})\\ & \quad=\prod_{ \substack{k=1\\ k\neq i, j}}^{m}x_{k}^{{\ast}{\ast}}(\varphi_{k}) \lim_{\alpha_{i}} J_{E_{i}}( x_{\alpha_{i}})(T^{{\ast}}(x_{j}^{{\ast}{\ast}}))=\Bigg(\prod_{ \substack{k=1\\ k\neq i, j}}^{m}x_{k}^{{\ast}{\ast}}(\varphi_{k})\Bigg)x_{i}^{{\ast}{\ast}}(T^{{\ast}}(x_{j}^{{\ast}{\ast}}))\\ & \quad =\Bigg(\prod_{ \substack{k=1\\ k\neq i, j}}^{m}x_{k}^{{\ast}{\ast}}(\varphi_{k})\Bigg) T^{{\ast}{\ast}}(x_{i}^{{\ast}{\ast}})(x_{j}^{{\ast}{\ast}}). \end{align*}

Choosing $x_{k}\in E_{k}$ so that $\varphi _k(x_{k})=1$, $i \neq k \neq j$, we get

\begin{align*} A^{{\ast}[m+1]}(J_{E_{1}}(x_{1}),\ldots,x_{i}^{{\ast}{\ast}},\ldots, x_{j}^{{\ast}{\ast}},\ldots,J_{E_{m}}(x_{m})) =T^{{\ast}{\ast}}(x_{i}^{{\ast}{\ast}})(x_{j}^{{\ast}{\ast}}). \end{align*}

Since $A^{\ast [m+1]}$ is separately order continuous by assumption, the functional $T^{\ast \ast }(x_{i}^{\ast \ast })$ is order continuous for every $x_{i}^{\ast \ast }\in E_{i}^{\ast \ast }$.

Although the next results hold, with the obvious modifications, for all Arens extensions $AR_{m}^{\rho }(A)$ of a regular $m$-linear operator $A$, to make the proofs more readable we shall restrict ourselves to the extension $A^{\ast [m+1]}=AR_{m}^{\theta }(A)$.

Lemma 5.3 Let $E_{1},\, \ldots,\,E_{m}$ be Banach lattices, $A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m})$ and $i\in \{1,\,\ldots,\,m\}$. If $x_{1}\in E_{1},\,\ldots,\,x_{i-1}\in E_{i-1}$, and $x_{i+1}^{\ast \ast }\in E_{i+1}^{\ast \ast },\,\ldots,\,x_{m}^{\ast \ast }\in E_{m}^{\ast \ast }$, then the operator

\[ A^{{\ast}[m+1]}(J_{E_{1}}(x_{1}),\ldots,J_{E_{i-1}}(x_{i-1}),\bullet,x_{i+1}^{{\ast}{\ast}},\ldots,x_{m}^{{\ast}{\ast}})\colon E_{i}^{{\ast}{\ast}}\longrightarrow\mathbb{R} \]

is $\omega ^{\ast }$-continuous and

\begin{align*} & A^{{\ast}[m+1]}(J_{E_{1}}(x_{1}),\ldots,J_{E_{i-1}}(x_{i-1}),x_{i}^{{\ast}{\ast}},\ldots,x_{m}^{{\ast}{\ast}})\\& \quad =\big(\overline{x_{i}^{{\ast}{\ast}}}\circ \cdots\circ \overline{x_{m}^{{\ast}{\ast}}}\big)(A_{\theta})(x_{i-1},\ldots,x_{1}). \end{align*}

Proof. Let $(x_{\alpha _{i}}^{\ast \ast })_{\alpha _{i}\in \Omega _{i}}$ be a net in $E_{i}^{\ast \ast }$ such that $x_{\alpha _{i}}^{\ast \ast }\xrightarrow {\, \omega ^{\ast } \,} x_{i}^{\ast \ast }\in E_{i}^{\ast \ast }$. For every $x_{i}^{\ast }\in E_{i}^{\ast }$ we have $x_{i}^{\ast \ast }(x_{i}^{\ast })=\displaystyle \lim _{\alpha _{i}}x_{\alpha _{i}}^{\ast \ast }(x_{i}^{\ast })$. Given $x_{1}\in E_{1},\,\ldots,\,x_{i-1}\in E_{i-1}$ and $x_{j}^{\ast \ast }\in E_{j}^{\ast \ast },\, j=i+1,\,\ldots,\,m$,

\begin{align*} & A^{{\ast}[m+1]}(J_{E_{1}}(x_{1}),\ldots,J_{E_{i-1}}(x_{i-1}),x_{i}^{{\ast}{\ast}},\ldots,x_{m}^{{\ast}{\ast}})\\ & \quad =\big(\overline{J_{E_{1}}(x_{1})}\circ\cdots\circ \overline{J_{E_{i-1}}(x_{i-1})}\circ \overline{x_{i}^{{\ast}{\ast}}}\circ \cdots\circ \overline{x_{m}^{{\ast}{\ast}}}\big)(A_{\theta})\\ & \quad =\overline{J_{E_{1}}(x_{1})}\big(\big(\overline{J_{E_{2}}(x_{2})}\circ\cdots\circ \overline{J_{E_{i-1}}(x_{i-1})}\circ \overline{x_{i}^{{\ast}{\ast}}}\circ \cdots\circ \overline{x_{m}^{{\ast}{\ast}}}\big)(A_{\theta})\big)\\ & \quad =J_{E_{1}}(x_{1})\big(\big(\overline{J_{E_{2}}(x_{2})}\circ\cdots\circ \overline{J_{E_{i-1}}(x_{i-1})}\circ \overline{x_{i}^{{\ast}{\ast}}}\circ \cdots\circ \overline{x_{m}^{{\ast}{\ast}}}\big)(A_{\theta})\big)\\ & \quad =\big(\overline{J_{E_{2}}(x_{2})}\circ\cdots\circ \overline{J_{E_{i-1}}(x_{i-1})}\circ \overline{x_{i}^{{\ast}{\ast}}}\circ \cdots\circ \overline{x_{m}^{{\ast}{\ast}}}\big)(A_{\theta})(x_{1})\\ & \quad =\overline{J_{E_{2}}(x_{2})}\big(\big(\overline{J_{E_{3}}(x_{3})} \circ\cdots\circ \overline{J_{E_{i-1}}(x_{i-1})}\circ \overline{x_{i}^{{\ast}{\ast}}}\circ \cdots\circ \overline{x_{m}^{{\ast}{\ast}}}\big)(A_{\theta})\big)(x_{1})\\ & \quad =J_{E_{2}}(x_{2})\big(\big(\big(\overline{J_{E_{3}}(x_{3})}\circ\cdots\circ \overline{J_{E_{i-1}}(x_{i-1})}\circ \overline{x_{i}^{{\ast}{\ast}}}\circ \cdots\circ \overline{x_{m}^{{\ast}{\ast}}}\big)(A_{\theta})\big)^{m-1}(x_{1})\big)\\ & \quad =\big(\big(\overline{J_{E_{3}}(x_{3})}\circ\cdots\circ \overline{J_{E_{i-1}}(x_{i-1})}\circ \overline{x_{i}^{{\ast}{\ast}}}\circ \cdots\circ \overline{x_{m}^{{\ast}{\ast}}}\big)(A_{\theta})\big)^{m-1}(x_{1})(x_{2})\\ & \quad =\big(\overline{J_{E_{3}}(x_{3})}\circ\cdots\circ \overline{J_{E_{i-1}}(x_{i-1})}\circ \overline{x_{i}^{{\ast}{\ast}}}\circ \cdots\circ \overline{x_{m}^{{\ast}{\ast}}}\big)(A_{\theta})(x_{2},x_{1})\\ & \quad \vdots\\ & \quad =\big(\overline{x_{i}^{{\ast}{\ast}}}\circ \cdots\circ \overline{x_{m}^{{\ast}{\ast}}}\big)(A_{\theta})(x_{i-1},\ldots,x_{1})\\ & \quad =\overline{x_{i}^{{\ast}{\ast}}}\big(\big(\overline{x_{i+1}^{{\ast}{\ast}}}\circ \cdots\circ \overline{x_{m}^{{\ast}{\ast}}}\big)(A_{\theta})\big)(x_{i-1},\ldots,x_{1})\\ & \quad =x_{i}^{{\ast}{\ast}}\big(\big(\big(\overline{x_{i+1}^{{\ast}{\ast}}}\circ \cdots\circ \overline{x_{m}^{{\ast}{\ast}}}\big)(A_{\theta})\big)^{m-i+1}(x_{i-1},\ldots,x_{1})\big)\\ & \stackrel{(\Delta)}{=}\displaystyle\lim_{\alpha_{i}}x_{\alpha_{i}}^{{\ast}{\ast}}\big(\big(\big(\overline{x_{i+1}^{{\ast}{\ast}}}\circ \cdots\circ \overline{x_{m}^{{\ast}{\ast}}}\big)(A_{\theta})\big)^{m-i+1}(x_{i-1},\ldots,x_{1}))\\ & \quad =\displaystyle\lim_{\alpha_{i}}A^{{\ast}[m+1]}(J_{E_{1}}(x_{1}),\ldots,J_{E_{i-1}}(x_{i-1}),x_{\alpha_{i}}^{{\ast}{\ast}},\ldots,x_{m}^{{\ast}{\ast}}), \end{align*}

where, in $(\Delta )$, we used that $((\overline {x_{i+1}^{\ast \ast }}\circ \cdots \circ \overline {x_{m}^{\ast \ast }})(A_{\theta }))^{m-i+1}(x_{i-1},\,\ldots,\,x_{1})\in E_{i}^{\ast }$.

Definition 5.4 Let $\mathcal {P}$ be a property of linear functionals on Banach lattices. We say that:

• A form $A\colon E_{1}^{\ast \ast }\times \cdots \times E_{m}^{\ast \ast } \longrightarrow \mathbb {R}$, where $E_1,\, \ldots,\, E_m$ are Banach lattices, has $\mathcal {P}$-separately if for all $j \in \{1,\, \ldots,\, m\}$ and $x_{i}^{\ast \ast }\in E_{i}^{\ast \ast },\, i=1,\,\ldots,\,m$, $i\neq j$, the functional
\[ A_{x_{1}^{{\ast}{\ast}},\ldots, x_{j-1}^{{\ast}{\ast}},x_{j+1}^{{\ast}{\ast}},\ldots,x_{m}^{{\ast}{\ast}}}\colon E_{j}^{{\ast}{\ast}}\longrightarrow \mathbb{R},~x_j^{**} \mapsto A(x_1^{**}, \ldots, x_m^{**}), \]
has property $\mathcal {P}$.
• $\mathcal {P}$ is an Arens property if, regardless of positive $m \geq 2$, the Banach lattices $E_1,\, \ldots,\, E_m$ and the form $A \in {\mathcal {L}}_r(E_1,\, \ldots,\, E_m)$, the Arens extension $A^{\ast [m+1]}$ of $A$ has $\mathcal {P}$ in the first variable, in the sense that the operator $A^{\ast [m+1]}_{x_{2}^{\ast \ast },\, \ldots,\,x_{m}^{\ast \ast }}\colon E_{1}^{\ast \ast }\longrightarrow \mathbb {R}$ has $\mathcal {P}$ for all $x_2^{\ast \ast } \in E_2^{**},\, \ldots,\, x_m^{\ast \ast } \in E_m^{**}$.

Example 5.5 Order continuity (Theorem 4.6(c)) and $\omega ^*$-continuity [Reference Dineen13, p. 413] are Arens properties.

Theorem 5.6 Let $\mathcal {P}$ be an Arens property, $m \geq 2$ and $E_{1},\, \ldots,\,E_{m}$ be Banach lattices. Suppose that:

(a) For $j=2,\,\ldots,\,m-1,$ and $i=1,\,\ldots,\,m-j$, every regular linear operator from $E_{j}$ to $E_{j+i}^{\ast }$ is weakly compact;
(b) For all $k=2,\,\ldots,\,m$, $x_{1}^{\ast \ast }\in E_{1}^{\ast \ast }$ and $T\in \mathcal {L}_{r}(E_{1};E_{k}^{\ast })$, the functional $T^{\ast \ast }(x_{1}^{\ast \ast })\in E_{k}^{\ast \ast \ast }$ has property $\mathcal {P}$.

Then, for every form $A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m})$, the Arens extension $A^{\ast [m+1]} \colon E_{1}^{\ast \ast }\times \cdots \times E_{m}^{\ast \ast } \longrightarrow \mathbb {R}$ has $\mathcal {P}$-separately.

Proof. We shall proceed by induction on $m$. Given $A\in \mathcal {L}_{r}(E_{1},\,E_{2})$, $A^{***}$ has property $\mathcal {P}$ in the first variable because $\mathcal {P}$ is an Arens property. Let us prove that, for every $x_{1}^{\ast \ast }\in E_{1}^{\ast \ast }$, $A^{***}(x_{1}^{\ast \ast },\,\bullet )\in E_{2}^{\ast \ast \ast }$ has property $\mathcal {P}$. Recall that $A_{\theta }\colon E_{2}\times E_{1}\longrightarrow \mathbb {R}$ and consider the regular linear operator $T:=A_{\theta }^{1}\colon E_{1}\longrightarrow E_{2}^{\ast }$, $T(x_{2})(x_{1})=A_{\theta }(x_{1},\,x_{2})$. For all $x_{2}^{\ast \ast }\in E_{2}^{\ast \ast }$ and $x_{2}\in E_{1}$,

\[ T^{{\ast}}(x_{2}^{{\ast}{\ast}})(x_{2})=x_{2}^{{\ast}{\ast}}(T(x_{2}))=x_{2}^{{\ast}{\ast}}(A_{\theta}^{1}(x_{2}))=(x_{2}^{{\ast}{\ast}}\circ A_{\theta}^{1})(x_{2})=\overline{x_{2}^{{\ast}{\ast}}}(A_{\theta})(x_{2}), \]

that is, $T^{\ast }(x_{2}^{\ast \ast })=\overline {x_{2}^{\ast \ast }}(A_{\theta }).$ So, for all $x_{1}^{\ast \ast }\in E_{1}^{\ast \ast },\, x_{2}^{\ast \ast }\in E_{2}^{\ast \ast }$,

\[ T^{{\ast}{\ast}}(x_{1}^{{\ast}{\ast}})(x_{2}^{{\ast}{\ast}})=x_{1}^{{\ast}{\ast}}(T^{{\ast}}(x_{2}^{{\ast}{\ast}}))=x_{1}^{{\ast}{\ast}}\big(\overline{x_{2}^{{\ast}{\ast}}}(A_{\theta})\big)=\big(\overline{x_{1}^{{\ast}{\ast}}}\circ \overline{x_{2}^{{\ast}{\ast}}}\big)(A_{\theta})=A^{***}(x_{1}^{{\ast}{\ast}},x_{2}^{{\ast}{\ast}}). \]

Since $T^{\ast \ast }(x_{1}^{\ast \ast })$ has property $\mathcal {P}$ by assumption, it follows that $A^{***}(x_{1}^{\ast \ast },\,\bullet )$ has property $\mathcal {P}$. This shows that the result holds for $m=2$.

Assume now that the result holds for $n$ and let us prove it holds for $n+1$. To do so we suppose that conditions (a) and (b) hold for $n+1$. Let $A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{n+1})$ be given. For every $x_{i}^{\ast \ast }\in E_{i}^{\ast \ast },\, i=2,\,\ldots,\,n+1$, we have

\[ \overline{x_{n-i+2}^{{\ast}{\ast}}}\colon\mathcal{L}_{r}(E_{n-i+2},\ldots,E_{1})\longrightarrow \mathcal{L}_{r}(E_{n-i+1},\ldots,E_{1}),\quad \overline{x_{n-i+2}^{{\ast}{\ast}}}(B)=x_{n-i+2}^{{\ast}{\ast}}\circ B^{i}, \]

where $B^{i}\colon E_{n-i+1}\times \cdots \times E_{1}\longrightarrow E_{n-i+2}^{\ast },\, B^{i}(x_{i+1},\,\ldots,\,x_{n+1})(x_{i})=B(x_{i},\,x_{i+1}, \ldots,\,x_{n+1})$. And for each $x_{1}^{\ast \ast }\in E_{1}^{\ast \ast }$, the functional $\overline {x_{1}^{\ast \ast }}\colon E_{1}^{\ast }\longrightarrow \mathbb {R}$ is given by $\overline {x_{1}^{\ast \ast }}=x_{1}^{\ast \ast }$. Moreover,

\begin{align*} A^{{\ast}[n+2]}(x_{1}^{{\ast}{\ast}},\ldots,x_{n+1}^{{\ast}{\ast}})& =\big(\overline{x_{1}^{{\ast}{\ast}}}\circ \cdots\circ \overline{x_{n+1}^{{\ast}{\ast}}}\big)(A_{\theta})=\big(\overline{x_{1}^{{\ast}{\ast}}}\circ \cdots\circ \overline{x_{n}^{{\ast}{\ast}}}\big)\big(\overline{x_{n+1}^{{\ast}{\ast}}}(A_{\theta})\big)\\ & =\big(\overline{x_{n+1}^{{\ast}{\ast}}}(A_{\theta})\big)^{{\ast}[n+1]}(x_{1}^{{\ast}{\ast}},\ldots,x_{n}^{{\ast}{\ast}}). \end{align*}

Since $\overline {x_{n+1}^{\ast \ast }}(A_{\theta })\in \mathcal {L}_{r}(E_{n},\,\ldots,\,E_{1})$, by the induction hypothesis we have that $(\overline {x_{n+1}^{\ast \ast }}(A_{\theta }))^{\ast [n+1]}$ has $\mathcal {P}$-separately, so $A^{\ast [n+2]}$ has property $\mathcal {P}$ in the first $n$ variables. To prove that $A^{\ast [n+2]}$ has property $\mathcal {P}$ in the $(n+1)$-th variable, let $x_{i}^{\ast \ast }\in E_{i}^{\ast \ast },\, i=1,\,\ldots,\,n$, be given. Our job is to show that $A^{\ast [n+2]}(x_{1}^{\ast \ast },\,\ldots,\,x_{n}^{\ast \ast },\,\bullet )\colon E_{n+1}^{\ast \ast }\longrightarrow \mathbb {R}$ has property $\mathcal {P}$. Recall that $A_{\theta }\colon E_{n+1}\times \cdots \times E_{1}\longrightarrow \mathbb {R}$ is given by $A_{\theta }(x_{1},\,\ldots,\,x_{n+1})=A(x_{n+1},\,\ldots,\,x_{1})$ and $A_{\theta }^{1}\colon E_{n}\times \cdots \times E_{1}\longrightarrow E_{n+1}^{\ast },\, A_{\theta }^{1}(x_{2},\,\ldots,\,x_{n+1})(x_{1})=A_{\theta }(x_{1},\,x_{2},\,\ldots,\,x_{n+1})$. Given $x_{3}\in E_{n-1},\,\ldots,\,x_{n+1}\in E_{1}$, consider the regular linear operator

\[ A_{x_{3},\ldots,x_{n+1}}\colon E_{n}\longrightarrow E_{n+1}^{{\ast}},\quad A_{x_{3},\ldots,x_{n+1}}(x_{2})=A_{\theta}^{1}(x_{2},x_{3},\ldots,x_{n+1}). \]

Given $x_{n+1}^{\ast \ast }\in E_{n+1}^{\ast \ast }$, take a net $(x_{\alpha _2})_{\alpha _2}$ in $E_{n}$ such that $J_{E_{n}}(x_{\alpha _2}) \stackrel {\omega ^*} \longrightarrow x_{n}^{\ast \ast }$ and apply the $\omega ^{\ast }$-$\omega ^{\ast }$-continuity of $[A_{x_{3},\,\ldots,\,x_{n+1}}]^{\ast \ast }$ and Lemma 5.3 for $i=n+1$ and $i=n$ to obtain

(5.1)\begin{align} & [A_{x_{3},\ldots,x_{n+1}}]^{{\ast}{\ast}}(x_{n}^{{\ast}{\ast}})(x_{n+1}^{{\ast}{\ast}})\nonumber\\ & \quad=\lim_{\alpha_{2}}[A_{x_{3},\ldots,x_{n+1}}]^{{\ast}{\ast}}(J_{E_{n}}(x_{\alpha_{2}}))(x_{n+1}^{{\ast}{\ast}})\nonumber\\ & \quad=\lim_{\alpha_{2}}J_{E_{n+1}^{{\ast}}}(A_{x_{3},\ldots,x_{n+1}}(x_{\alpha_{2}}))(x_{n+1}^{{\ast}{\ast}})\nonumber\\ & \quad=\lim_{\alpha_{2}}x_{n+1}^{{\ast}{\ast}}(A_{x_{3},\ldots,x_{n+1}}(x_{\alpha_{2}}))=\lim_{\alpha_{2}}x_{n+1}^{{\ast}{\ast}}(A_{\theta}^{1}(x_{\alpha_{2}},x_{3},\ldots,x_{n+1}))\nonumber\\ & \quad=\lim_{\alpha_{2}}\overline{x_{n+1}^{{\ast}{\ast}}}(A_{\theta})(x_{\alpha_{2}},x_{3},\ldots,x_{n+1})\nonumber\\ & \quad=\lim_{\alpha_{2}} A^{{\ast}[n+2]}(J_{E_{1}}(x_{n+1}),\ldots,J_{E_{n-1}}(x_{3}),J_{E_{n}}(x_{\alpha_{2}}),x_{n+1}^{{\ast}{\ast}})\nonumber\\ & \quad=A^{{\ast}[n+2]}(J_{E_{1}}(x_{n+1}),\ldots,J_{E_{n-1}}(x_{3}),x_{n}^{{\ast}{\ast}},x_{n+1}^{{\ast}{\ast}}). \end{align}

For $x_{n}^{\ast \ast }\in E_{n}^{\ast \ast }$ and $x_{4}\in E_{n-2},\,\ldots,\,x_{n+1}\in E_{1}$, consider the regular linear operator $A_{x_{4},\,\ldots,\,x_{n+1},\,x_{n}^{\ast \ast }}\colon$ $E_{n-1}\longrightarrow E_{n+1}^{\ast }$ given by

\[ A_{x_{4},\ldots,x_{n+1},x_{n}^{{\ast}{\ast}}}(x_{3})(x_{1})=A^{{\ast}[n+2]}(J_{E_{1}}(x_{n+1}),\ldots,J_{E_{n-1}}(x_{3}),x_{n}^{{\ast}{\ast}},J_{E_{n+1}}(x_{1})). \]

On the one hand, for every $x_{3}\in E_{n-1}$ the functional $[A_{x_{4},\,\ldots,\,x_{n+1},\,x_{n}^{\ast \ast }}(x_{3})]^{\ast \ast }$ is a $\omega ^{\ast }$-continuous extension of $A_{x_{4},\,\ldots,\,x_{n+1},\,x_{n}^{\ast \ast }}(x_{3})$. On the other hand, since $A_{x_3, \ldots, x_{n+1}}$ is weakly compact by assumption, for every $x_{n}^{\ast \ast }\in E_{n}^{\ast \ast }$ the functional $[A_{x_{3},\,\ldots,\,x_{n+1}}]^{\ast \ast }(x_{n}^{\ast \ast })$ is $\omega ^{\ast }$-continuous. Taking a net $(x_{\alpha _{1}})_{\alpha _{1}}$ in $E_{n+1}$ such that $J_{E_{n+1}}(x_{\alpha _{1}}) \stackrel {\omega ^*} \longrightarrow x_{n+1}^{\ast \ast }$,

(5.2)\begin{align} & [A_{x_{4},\ldots,x_{n+1},x_{n}^{{\ast}{\ast}}}(x_{3})]^{{\ast}{\ast}}(x_{n+1}^{{\ast}{\ast}})=\lim_{\alpha_{1}}[A_{x_{4},\ldots,x_{n+1},x_{n}^{{\ast}{\ast}}}(x_{3})]^{{\ast}{\ast}}(J_{E_{n+1}}(x_{\alpha_{1}}))\nonumber\\ & \quad =\lim_{\alpha_{1}}J_{E_{n+1}}(x_{\alpha_{1}})(A_{x_{4},\ldots,x_{n+1},x_{n}^{{\ast}{\ast}}}(x_{3}))\nonumber\\ & \quad =\lim_{\alpha_{1}}A_{x_{4},\ldots,x_{n+1},x_{n}^{{\ast}{\ast}}}(x_{3})(x_{\alpha_{1}})\nonumber\\ & \quad =\lim_{\alpha_{1}}A^{{\ast}[n+2]}(J_{E_{1}}(x_{n+1}),\ldots,J_{E_{n-1}}(x_{3}),x_{n}^{{\ast}{\ast}},J_{E_{n+1}}(x_{\alpha_{1}}))\nonumber\\ & \quad =\lim_{\alpha_{1}}[A_{x_{3},\ldots,x_{n+1}}]^{{\ast}{\ast}}(x_{n}^{{\ast}{\ast}})(J_{E_{n+1}}(x_{\alpha_{1}}))=[A_{x_{3},\ldots,x_{n+1}}]^{{\ast}{\ast}}(x_{n}^{{\ast}{\ast}})(x_{n+1}^{{\ast}{\ast}})\nonumber\\ & \stackrel{(5.1)}{=}A^{{\ast}[n+2]}(J_{E_{1}}(x_{n+1}),\ldots,J_{E_{n-1}}(x_{3}),x_{n}^{{\ast}{\ast}},x_{n+1}^{{\ast}{\ast}}). \end{align}

Take a net $(x_{\alpha _{3}})_{\alpha _{3}}$ in $E_{n-1}$ such that $J_{E_{n-1}}(x_{\alpha _{3}}) \stackrel {\omega ^*} \longrightarrow x_{n-1}^{\ast \ast }$. Using that $[A_{x_{4},\,\ldots,\,x_{n+1},\,x_{n}^{\ast \ast }}]^{\ast \ast }$ is $\omega ^{\ast }$-$\omega ^{\ast }$-continuous and calling on Lemma 5.3 for $i = n-1$, for each $x_{n+1}^{\ast \ast }\in E_{n+1}^{\ast \ast }$ we have

(5.3)\begin{align} & [A_{x_{4},\ldots,x_{n+1},x_{n}^{{\ast}{\ast}}}]^{{\ast}{\ast}}(x_{n-1}^{{\ast}{\ast}})(x_{n+1}^{{\ast}{\ast}})=\lim_{\alpha_{3}}[A_{x_{4},\ldots,x_{n+1},x_{n}^{{\ast}{\ast}}}]^{{\ast}{\ast}}(J_{E_{n-1}}(x_{\alpha_{3}}))(x_{n+1}^{{\ast}{\ast}})\nonumber\\ & \quad =\lim_{\alpha_{3}}J_{E_{n+1}^{{\ast}}}(A_{x_{4},\ldots,x_{n+1},x_{n}^{{\ast}{\ast}}}(x_{\alpha_{3}}))(x_{n+1}^{{\ast}{\ast}})\nonumber\\ & \quad =\lim_{\alpha_{3}}x_{n+1}^{{\ast}{\ast}}(A_{x_{4},\ldots,x_{n+1},x_{n}^{{\ast}{\ast}}}(x_{\alpha_{3}}))=\lim_{\alpha_{3}}[A_{x_{4},\ldots,x_{n+1},x_{n}^{{\ast}{\ast}}}(x_{\alpha_{3}})]^{{\ast}{\ast}}(x_{n+1}^{{\ast}{\ast}})\nonumber\nonumber\\ & \stackrel{\textrm{(5.2)}}{=}\lim_{\alpha_{3}} A^{{\ast}[n+2]}(J_{E_{1}}(x_{n+1}),\ldots,J_{E_{n-1}}(x_{\alpha_{3}}),x_{n}^{{\ast}{\ast}},x_{n+1}^{{\ast}{\ast}})\nonumber\\ & \quad =A^{{\ast}[n+2]}(J_{E_{1}}(x_{n+1}),\ldots,J_{E_{n-2}}(x_{4}),x_{n-1}^{{\ast}{\ast}},x_{n}^{{\ast}{\ast}},x_{n+1}^{{\ast}{\ast}}). \end{align}

For $x_{n-1}^{\ast \ast }\in E_{n-1}^{\ast \ast },\, x_{n}^{\ast \ast }\in E_{n}^{\ast \ast }$ and $x_{5}\in E_{n-3},\,\ldots,\,x_{n+1}\in E_{1}$, consider the regular linear operator $A_{x_{5},\,\ldots,\,x_{n+1},\,x_{n-1}^{\ast \ast },\,x_{n}^{\ast \ast }}\colon E_{n-2}\longrightarrow E_{n+1}^{\ast }$ given by

\begin{align*} & A_{x_{5},\ldots,x_{n+1},x_{n-1}^{{\ast}{\ast}},x_{n}^{{\ast}{\ast}}}(x_{4})(x_{1})\\& \quad =A^{{\ast}[n+2]}(J_{E_{1}}(x_{n+1}),\ldots,J_{E_{n-2}}(x_{4}),x_{n-1}^{{\ast}{\ast}},x_{n}^{{\ast}{\ast}},J_{E_{n+1}}(x_{1})). \end{align*}

For every $x_{4}\in E_{n-2}$ the functional $[A_{x_{5},\,\ldots,\,x_{n+1},\,x_{n-1}^{\ast \ast },\,x_{n}^{\ast \ast }}(x_{4})]^{\ast \ast }$ is a $\omega ^{\ast }$-continuous extension of $A_{x_{5},\,\ldots,\,x_{n+1},\,x_{n-1}^{\ast \ast },\,x_{n}^{\ast \ast }}(x_{4})$. On the other hand, since $A_{x_{4},\,\ldots,\,x_{n+1},\,x_{n}^{**}}$ is weakly compact by assumption, for every $x_{n-1}^{\ast \ast }\in E_{n-1}^{\ast \ast }$ the functional $[A_{x_{4},\,\ldots,\,x_{n+1},\,x_{n}^{\ast \ast }}]^{\ast \ast }(x_{n-1}^{\ast \ast })$ is $\omega ^{\ast }$-continuous on $E_{n-2}$. So, repeating the procedure using (5.3) we get

(5.4)\begin{align} & [A_{x_{5},\ldots,x_{n+1},x_{n-1}^{{\ast}{\ast}},x_{n}^{{\ast}{\ast}}}(x_{4})]^{{\ast}{\ast}}(x_{n+1}^{{\ast}{\ast}})\nonumber\\ & \quad=A^{{\ast}[n+2]}(J_{E_{1}}(x_{n+1}),\ldots,J_{E_{n-2}}(x_{4}),x_{n-1}^{{\ast}{\ast}},x_{n}^{{\ast}{\ast}},x_{n+1}^{{\ast}{\ast}}). \end{align}

Since the operator $[A_{x_{5},\,\ldots,\,x_{n+1},\,x_{n-1}^{\ast \ast },\,x_{n}^{\ast \ast }}]^{\ast \ast }$ is $\omega ^{\ast }$-$\omega ^{\ast }$-continuous, for every $x_{n+1}^{\ast \ast }\in E_{n+1}^{\ast \ast }$, taking a net $(x_{\alpha _{4}})_{\alpha _{4}}$ in $E_{n-2}$ such that $J_{E_{n-2}}(x_{\alpha _{4}}) \stackrel {\omega ^*} \longrightarrow x_{n-2}^{\ast \ast }$, using Lemma 5.3 for $i = n-2$ and ( 5.4) we have

\begin{align*} & [A_{x_{5},\ldots,x_{n+1},x_{n-1}^{{\ast}{\ast}},x_{n}^{{\ast}{\ast}}}]^{{\ast}{\ast}}(x_{n-2}^{{\ast}{\ast}})(x_{n+1}^{{\ast}{\ast}})\\ & \quad =A^{{\ast}[n+2]}(J_{E_{1}}(x_{n+1}),\ldots,J_{E_{n-3}}(x_{5}),x_{n-2}^{{\ast}{\ast}},x_{n-1}^{{\ast}{\ast}},x_{n}^{{\ast}{\ast}},x_{n+1}^{{\ast}{\ast}}). \end{align*}

Repeating the procedure $(n-3)$ times, we end up with

(5.5)\begin{equation} [A_{x_{n+1},x_{3}^{{\ast}{\ast}},\ldots,x_{n}^{{\ast}{\ast}}}]^{{\ast}{\ast}}(x_{2}^{{\ast}{\ast}})(x_{n+1}^{{\ast}{\ast}})=A^{{\ast}[n+2]}(J_{E_{1}}(x_{n+1}),x_{2}^{{\ast}{\ast}},\ldots,x_{n+1}^{{\ast}{\ast}}) \end{equation}

for every $x_{n+1}^{\ast \ast }\in E_{n+1}^{\ast \ast }$, where, for each $x_{n+1}\in E_{1}$ and $x_{i}^{\ast \ast }\in E_{i}^{\ast \ast },\, i=3,\,\ldots,\,n$, $A_{x_{n+1},\,x_{3}^{\ast \ast },\,\ldots,\,x_{n}^{\ast \ast }}\colon$ $E_{2}\longrightarrow E_{n+1}^{\ast }$ is the regular linear operator given by

\[ A_{x_{n+1},x_{3}^{{\ast}{\ast}},\ldots,x_{n}^{{\ast}{\ast}}}(x_{n})(x_{1})= A^{{\ast}[n+2]}(J_{E_{1}}(x_{n+1}),J_{E_{2}}(x_{n}),x_{3}^{{\ast}{\ast}},\ldots,x_{n}^{{\ast}{\ast}},J_{E_{n+1}}(x_{1})). \]

Finally, given $x_{i}^{\ast \ast }\in E_{i}^{\ast \ast },\, i=2,\,\ldots,\,n$, the regular linear operator $A_{x_{2}^{\ast \ast },\,\ldots,\,x_{n}^{\ast \ast }}\colon E_{1} \longrightarrow E_{n+1}^{\ast }$ defined by

\[ A_{x_{2}^{{\ast}{\ast}},\ldots,x_{n}^{{\ast}{\ast}}}(x_{n+1})(x_{1})= A^{{\ast}[n+2]}(J_{E_{1}}(x_{n+1}),x_{2}^{{\ast}{\ast}},\ldots,x_{n}^{{\ast}{\ast}},J_{E_{n+1}}(x_{1})), \]

is weakly compact by condition (ii) for $n+1$. So, for every $x_{2}^{\ast \ast }\in E_{2}^{\ast \ast }$, $[A_{x_{n+1},\,x_{3}^{\ast \ast },\,\ldots,\,x_{n}^{\ast \ast }}]^{\ast \ast }(x_{2}^{\ast \ast })$ is $\omega ^{\ast }$-continuous, therefore

(5.6)\begin{align} & [A_{x_{2}^{{\ast}{\ast}},\ldots,x_{n}^{{\ast}{\ast}}}(x_{n+1})]^{{\ast}{\ast}}(x_{n+1}^{{\ast}{\ast}})=\lim_{\alpha_{1}}[A_{x_{2}^{{\ast}{\ast}},\ldots,x_{n}^{{\ast}{\ast}}}(x_{n+1})]^{{\ast}{\ast}}(J_{E_{n+1}}(x_{\alpha_{1}}))\nonumber\\ & \quad =\lim_{\alpha_{1}}J_{E_{n+1}}(x_{\alpha_{1}})(A_{x_{2}^{{\ast}{\ast}},\ldots,x_{n}^{{\ast}{\ast}}}(x_{n+1}))=\lim_{\alpha_{1}}A_{x_{2}^{{\ast}{\ast}},\ldots,x_{n}^{{\ast}{\ast}}}(x_{n+1})(x_{\alpha_{1}})\nonumber\nonumber\\ & \quad =\lim_{\alpha_{1}} A^{{\ast}[n+2]}(J_{E_{1}}(x_{n+1}),x_{2}^{{\ast}{\ast}},\ldots,x_{n}^{{\ast}{\ast}},J_{E_{n+1}}(x_{\alpha_{1}}))\nonumber\\ & \quad =\lim_{\alpha_{1}} [A_{x_{n+1},x_{3}^{{\ast}{\ast}},\ldots,x_{n}^{{\ast}{\ast}}}]^{{\ast}{\ast}}(x_{2}^{{\ast}{\ast}})(J_{E_{n+1}}(x_{\alpha_{1}}))=[A_{x_{n+1},x_{3}^{{\ast}{\ast}},\ldots,x_{n}^{{\ast}{\ast}}}]^{{\ast}{\ast}}(x_{2}^{{\ast}{\ast}})(x_{n+1}^{{\ast}{\ast}})\nonumber\nonumber\\ & \stackrel{\textrm{(5.5)}}{=}A^{{\ast}[n+2]}(J_{E_{1}}(x_{n+1}),x_{2}^{{\ast}{\ast}},\ldots,x_{n+1}^{{\ast}{\ast}}). \end{align}

For the final time, taking a net $(x_{\alpha _{n+1}})_{\alpha _{n+1}}$ in $E_{1}$ such that $J_{E_{1}}(x_{\alpha _{n+1}}) \stackrel {\omega ^*} \longrightarrow x_{1}^{\ast \ast }$, the $\omega ^{\ast }$-$\omega ^{\ast }$ continuity of $[A_{x_{2}^{\ast },\,\ldots,\,x_{n}^{\ast \ast }}]^{\ast \ast }$ and Lemma 5.3 for $i = 1$ give, for every $x_{n+1}^{\ast \ast }\in E_{n+1}^{\ast \ast }$,

\begin{align*} & [A_{x_{2}^{{\ast}{\ast}},\ldots,x_{n}^{{\ast}{\ast}}}]^{**}(x_{1}^{{\ast}{\ast}})(x_{n+1}^{{\ast}{\ast}})=\lim_{\alpha_{n+1}}[A_{x_{2}^{{\ast}{\ast}},\ldots,x_{n}^{{\ast}{\ast}}}]^{{\ast}{\ast}}(J_{E_{1}}(x_{\alpha_{n+1}})(x_{n+1}^{{\ast}{\ast}})\\ & \quad =\lim_{\alpha_{n+1}}J_{E_{n+1}^{{\ast}}}(A_{x_{2}^{{\ast}{\ast}},\ldots,x_{n}^{{\ast}{\ast}}}(x_{\alpha_{n+1}}))(x_{n+1}^{{\ast}{\ast}})\\ & \quad =\lim_{\alpha_{n+1}}x_{n+1}^{{\ast}{\ast}}(A_{x_{2}^{{\ast}{\ast}},\ldots,x_{n}^{{\ast}{\ast}}}(x_{\alpha_{n+1}}))=\lim_{\alpha_{n+1}}[A_{x_{2}^{{\ast}{\ast}},\ldots,x_{n}^{{\ast}{\ast}}}(x_{\alpha_{n+1}})]^{{\ast}{\ast}}(x_{n+1}^{{\ast}{\ast}})\\ & \quad \stackrel{\textrm{(5.6)}}{=}\lim_{\alpha_{n+1}} A^{{\ast}[n+2]}(J_{E_{1}}(x_{\alpha_{n+1}}),x_{2}^{{\ast}{\ast}},\ldots,x_{n+1}^{{\ast}{\ast}})=A^{{\ast}[n+2]}(x_{1}^{{\ast}{\ast}},\ldots,x_{n+1}^{{\ast}{\ast}}). \end{align*}

This proves that $[A_{x_{2}^{\ast \ast },\,\ldots,\,x_{n}^{\ast \ast }}]^{\ast \ast }(x_{1}^{\ast \ast }) = A^{\ast [n+2]}(x_{1}^{\ast \ast },\,\ldots,\,x_{n}^{\ast \ast },\,\bullet )$. By condition (b) for $n+1$ we know that $[A_{x_{2}^{\ast \ast },\,\ldots,\,x_{n}^{\ast \ast }}]^{\ast \ast }(x_{1}^{\ast \ast })$ has property $\mathcal {P}$, so $A^{\ast [n+2]}(x_{1}^{\ast \ast },\,\ldots,\,x_{n}^{\ast \ast },\,\bullet )$ has property $\mathcal {P}$, which completes the proof.

Theorem 5.6 gives sufficient conditions for Arens extensions of regular multilinear forms to be separately order continuous on the product of the whole of the biduals. Now we derive the case of vector-valued regular multilinear operators.

Theorem 5.7 Let $m \geq 2$ and $E_{1},\, \ldots,\,E_{m}$ be Banach lattices such that:

(a) For $j=2,\,\ldots,\,m-1,$ and $i=1,\,\ldots,\,m-j$, every regular linear operator from $E_{j}$ to $E_{j+i}^{\ast }$ is weakly compact;
(b) For all $k=2,\,\ldots,\,m$, $x_{1}^{\ast \ast }\in E_{1}^{\ast \ast }$ and $T\in \mathcal {L}_{r}(E_{1};E_{k}^{\ast })$, the functional $T^{\ast \ast }(x_{1}^{\ast \ast })$ is order continuous on $E_{k}^{\ast \ast \ast }$.

Then, for every Banach lattice $F$ and any $A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m};F)$, the Arens extension $A^{\ast [m+1]}$ is separately order continuous on $E_{1}^{\ast \ast }\times \cdots \times E_{m}^{\ast \ast }$.

Proof. Let $A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m};F)$ and $y^{\ast }\in F^{\ast }$ be given. Since $y^{\ast }\circ A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m})$ and order continuity is an Arens property, by Theorem 5.6 the extension $(y^* \circ A)^{\ast [m+1]}$ is separately order continuous. For all $x_{i}^{\ast \ast }\in E_{i}^{\ast \ast },\, i=1,\,\ldots,\,m$,

\[ A^{{\ast}[m+1]}(x_{1}^{{\ast}{\ast}},\ldots,x_{m}^{{\ast}{\ast}})(y^{{\ast}})=(y^{{\ast}}\circ A)^{*[m+1]}(x_{1}^{{\ast}{\ast}},\ldots,x_{m}^{{\ast}{\ast}}). \]

For each $j\in \{1,\,\ldots,\,m\}$ let $x_{j}^{\ast \ast }\in E_{j}^{\ast \ast }$ and let $(x_{\alpha _{j}}^{\ast \ast })_{\alpha _{j}\in \Omega _{j}}$ be a net $E_{j}^{\ast \ast }$ such that $x_{\alpha _{j}}^{\ast \ast } \xrightarrow {\, o \, } 0$. There exists a net $(y_{\alpha _{j}}^{\ast \ast })_{\alpha _{j}\in \Omega _{j}}$ in $E_{j}^{\ast \ast }$ and $\alpha _{j_{0}}\in \Omega _{j}$ so that $y_{\alpha _{j}}^{\ast \ast }\downarrow 0$ and $|x_{\alpha _{j}}^{\ast \ast }|\leq y_{\alpha _{j}}^{\ast \ast }$ for every $\alpha _{j}\geq \alpha _{j_{0}}$. Without loss of generality, assume that $A$ and $y^{\ast }$ are positive. Since $(y^{\ast }\circ A)^{*[m+1]}(|x_{1}^{\ast \ast }|,\,\ldots,\,\bullet,\,\ldots,\,|x_{m}^{\ast \ast }|)\colon E_{j}^{\ast \ast }\longrightarrow \mathbb {R}$ is positive and order continuous,

\begin{align*} & A^{*[m+1]}(|x_{1}^{{\ast}{\ast}}|,\ldots,y_{\alpha_{j}}^{{\ast}{\ast}},\ldots,|x_{m}^{{\ast}{\ast}}|)(y^{{\ast}})\\ & \quad =(y^{{\ast}}\circ A)^{*[m+1]}(|x_{1}^{{\ast}{\ast}}|,\ldots,\bullet,\ldots,|x_{m}^{{\ast}{\ast}}|)(y_{\alpha_{j}}^{{\ast}{\ast}})\downarrow 0. \end{align*}

It follows that $A^{*[m+1]}(|x_{1}^{\ast \ast }|,\,\ldots,\,y_{\alpha _{j}}^{\ast \ast },\,\ldots,\,|x_{m}^{\ast \ast }|) \downarrow 0$ [Reference Aliprantis and Burkinshaw2, Theorem 1.18] and, for every $\alpha _{j}\geq \alpha _{j_{0}}$,

\begin{align*} |A^{*[m+1]}(x_{1}^{{\ast}{\ast}},\ldots,x_{\alpha_{j}}^{{\ast}{\ast}},\ldots,x_{m}^{{\ast}{\ast}})| & \leq A^{*[m+1]}(|x_{1}^{{\ast}{\ast}}|,\ldots,|x_{\alpha_{j}}^{{\ast}{\ast}}|,\ldots,|x_{m}^{{\ast}{\ast}}|)\\ & \leq A^{*[m+1]}(|x_{1}^{{\ast}{\ast}}|,\ldots,y_{\alpha_{j}}^{{\ast}{\ast}},\ldots,|x_{m}^{{\ast}{\ast}}|) \downarrow 0. \end{align*}

This shows that $A^{*[m+1]}(x_{1}^{\ast \ast },\,\ldots,\,x_{\alpha _{j}}^{\ast \ast },\,\ldots,\,x_{m}^{\ast \ast }) \xrightarrow {\, o \, } 0$ and proves that $A^{*[m+1]}$ is separately order continuous.

Recall that a Banach lattice $E$ is said to be a Kantorovich-Banach space (or briefly a KB-space) if increasing positive bounded sequences of $E$ are norm convergent.

Example 5.8 As to condition (a) above, we have the following examples between nonreflexive Banach lattices:

(a) Every operator from $c_0$ to $c_0^*=\ell _1$ is compact, hence weakly compact (this is Pitt's theorem).
(b) Every operator from $C(K)$, where $K$ is a compact Hausdorff space, to a KB-space is weakly compact. Just recall that KB-spaces do not contain a copy of $c_0$ [Reference Aliprantis and Burkinshaw2, Theorem 4.60] and apply [Reference Pełczyński18, Theorem 5].
(c) Since any AM-space with order unity is order isometric to a $C(K)$-space [Reference Aliprantis and Burkinshaw2, Theorem 4.29], from (b) it follows that every operator from an AM-space with order unity to a KB-space is weakly compact. And since the dual of an AM-space is a KB-space, every operator from an AM-space with order unity to its dual is weakly compact. In particular, every operator from $\ell _\infty$ to $\ell _\infty ^*$ is weakly compact.

Corollary 5.9 Let $m\geq 2$ and $E_{1},\, \ldots,\,E_{m},\, F$ be Banach lattices such that every regular operator from $E_{j}$ to $E_{j+i}^{\ast }$ is weakly compact, $j=2,\,\ldots,\,m-1,\, i=1,\,\ldots,\,m-j$. If $E_{1}^{\ast }$ has order continuous norm, then the Arens extension $A^{\ast [m+1]}$ of any operator $A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m};F)$ is separately order continuous on $E_{1}^{\ast \ast }\times \cdots \times E_{m}^{\ast \ast }$.

Proof. Condition (a) of Theorem 5.7 is given by assumption. For $x_{1}^{\ast \ast }\in E_{1}^{\ast \ast }$ and $T\in \mathcal {L}_{r}(E_{1};E_{k}^{\ast })$, $x_{1}^{\ast \ast }$ is order continuous because the norm of $E_{1}^{\ast }$ is order continuous [Reference Meyer–Nieberg17, Theorem 2.4.2]. Since $T^*$ is order continuous [Reference Aliprantis and Burkinshaw2, Theorem 1.73], $T^{**}(x_1^{**}) = x_1^{**} \circ T^*$ is order continuous as well, so condition (b) is fulfilled too.

Recall that a Banach space $E$ is Arens regular if every bounded linear operator from $E$ to $E^*$ is weakly compact (see, e.g., [Reference Dineen13]). The Banach lattices $c_0,\, \ell _\infty$ and $C(K)$, where $K$ is a compact Hausdorff space, in particular AM-spaces with order unit, are Arens regular (cf. Example 5.8).

Corollary 5.10 Let $E$ be an Arens regular Banach lattice. Then, for every Banach lattice $F$, the Arens extension $A^{\ast [m+1]}$ of any regular $m$-linear operator $A \colon E^m \longrightarrow F$ is separately order continuous on $(E^{**})^m$.

Proof. The Arens regularity of $E$ immediately gives condition (a) of Theorem 5.7 and implies that, for every $T\in \mathcal {L}_{r}(E;E^{\ast })$, $T^{**}(E^{**}) \subseteq J_{E^*}(E^*) \subseteq (E^{**})^*_n$, which gives condition (b).

We conclude this paper with one more result on order continuity of Arens extensions of homogeneous polynomials. For a polynomial $P \in {\mathcal {P}}_r(^mE;F)$, we write $P^{*[m+1]} := AR_m^{\theta }(P)$. Recall that $P$ is orthogonally additive if $P(x+y) = P(x) + P(y)$ whenever $x$ and $y$ are disjoint. The literature on orthogonally additive polynomials is extensive.

A linear operator $u\colon E \longrightarrow E^*$ is symmetric if $u(x)(y) = u(y)(x)$ for all $x,\,y \in E$. A Banach space $E$ is symetrically Arens regular if every symmetric operator from $E$ to $E^*$ is weakly compact. Of course, Arens regular spaces are symmetrically Arens regular, but there are symmetrically Arens regular spaces that fail to be Arens regular [Reference Leung15].

Proposition 5.11 Let $E,\,F$ be Banach lattices and $P \in {\mathcal {P}}_r(^mE;F)$. If either $P$ is orthogonally additive and $F = \mathbb {R}$ or $E$ is symmetrically Arens regular, then the Arens extension $P^{\ast [m+1]} \colon E^{**} \longrightarrow F^{**}$ of $P$ is order continuous on $E^{**}$.

Proof. Assume first that $P$ is orthogonally additive and $F = \mathbb {R}$. By Proposition 4.8 we know that $P^{\ast [m+1]}$ is order continuous at the origin on $E^{**}$, therefore it is order continuous at every point of $E^{**}$ by [Reference Boyd, Ryan and Snigireva8, Proposition 8].

Suppose now that $E$ is symmetrically Arens regular. It is clear that we can assume that $P$ is positive. We know that $(\check {P})^{\ast [m+1]}$ is order continuous in the first variable on $E^{**}$ (Theorem 4.6) and positive because $\check {P}$ is positive. In order to check that it is symmetric, let $\rho \in S_m$ be given. For every $\varphi \in F^*$, since $E$ is symmetrically Arens regular and $\varphi \circ \check {P}$ is symmetric, by [Reference Aron, Cole and Gamelin5, Theorem 8.3] (or [Reference Cabello Sánchez, García and Villanueva11, Corollary 6]) we know that $AR_m^{\theta }(\varphi \circ \check {P})$ is symmetric as well. So, for $x_1^{**},\, \ldots,\, x_m^{**} \in E^{**}$,

\begin{align*} (\check{P})^{{\ast}[m+1]}(x_1^{**}, \ldots, x_m^{**} )(\varphi) & = AR_m^{\theta}(\check{P})(x_1^{**}, \ldots, x_m^{**})(\varphi)\\ & = AR_m^{\theta}(\varphi \circ \check{P})(x_1^{**}, \ldots, x_m^{**})\\ & = AR_m^{\theta}(\varphi \circ \check{P})(x_{\rho(1)}^{**}, \ldots, x_{\rho(m)}^{**})\\ & = AR_m^{\theta}(\check{P})(x_{\rho(1)}^{**}, \ldots, x_{\rho(m)}^{**})(\varphi)\\ & = (\check{P})^{{\ast}[m+1]}(x_{\rho(1)}^{**}, \ldots, x_{\rho(m)}^{**} )(\varphi), \end{align*}

proving that $(\check {P})^{\ast [m+1]}$ is symmetric. The order continuity in the first variable and the symmetry yield that the positive $m$-linear operator $(\check {P})^{\ast [m+1]}$ is separately order continuous on $(E^{**})^m$. By [Reference Buskes and Roberts10, Lemma 2.6] it follows that $(\check {P})^{\ast [m+1]}$ is jointly order continuous on $(E^{**})^m$. So, if $x_{\alpha }^{**}\xrightarrow {\, o \,} x^{**}$ in $E^{**}$, then

\begin{align*} P^{{\ast}[m+1]}(x_{\alpha}^{**}) & = (\check{P})^{{\ast}[m+1]}(x_{\alpha}^{**}, \ldots, x_{\alpha}^{**}) \xrightarrow{\,\, o \,\,} (\check{P})^{{\ast}[m+1]}(x^{**}, \ldots, x^{**})\\ & = P^{{\ast}[m+1]}(x^{**}). \end{align*}

Acknowledgements

The authors thank the reviewer for the invaluable comments and suggestions that improved the final presentation of the paper. We are also grateful to R. Ryan for his helpful suggestions and for drawing our attention to [Reference Boyd, Ryan and Snigireva8].

References

Abramovich, Y. and Sirotkin, G.. On order convergence of nets. Positivity 9 (2005), 287–292.CrossRef Google Scholar

Aliprantis, C. D. and Burkinshaw, D. O.. Positive Operators (Dordrecht: Springer, 2006).CrossRef Google Scholar

Arens, R.. The adjoint of a bilinear operation. Proc. Amer. Math. Soc. 2 (1951), 839–848.CrossRef Google Scholar

Aron, R. and Berner, P.. A Hahn-Banach extension theorem for analytic mappings. Bull. Soc. Math. France 106 (1978), 3–24.CrossRef Google Scholar

Aron, R., Cole, B. and Gamelin, T.. Spectra of algebras of analytic functions on a Banach space. J. Reine Angew. Math. 415 (1991), 51–93.Google Scholar

Botelho, G. and Garcia, L. A.. Bidual extensions of Riesz multimorphisms. J. Math. Anal. Appl. 520 (2023), 1–18.CrossRef Google Scholar

Boyd, C., Ryan, R. A. and Snigireva, N.. Synnatzschke's theorem for polynomials. Positivity 25 (2021), 229–242.CrossRef Google Scholar

Boyd, C., Ryan, R. A. and Snigireva, N.. A Nakano Carrier theorem for polynomials. Proc. Amer. Math. Soc. 151 (2023), 1621–1635.Google Scholar

Bu, Q. and Buskes, G.. Polynomials on Banach lattices and positive tensor products. J. Math. Anal. Appl. 388 (2012), 845–862.CrossRef Google Scholar

Buskes, G. and Roberts, S., Arens extensions for polynomials and the Woodbury–Schep formula, Positivity and Noncommutative Analysis, (Trends Math., Birkhäuser, 2019), pp. 37–48.CrossRef Google Scholar

Cabello Sánchez, F., García, R. and Villanueva, I.. Extension of multilinear operators on Banach spaces. Extr. Math. 15 (2000), 291–334.Google Scholar

Davie, A. M. and Gamelin, T. W.. A theorem on polynomial-star approximation. Proc. Amer. Math. Soc. 106 (1989), 351–356.CrossRef Google Scholar

Dineen, S.. Complex Analysis on Infinite Dimensional Spaces (London: Springer, 1999).CrossRef Google Scholar

Kusraev, A. G. and Kusraeva, Z. A., Factorization of order bounded disjointness preserving multilinear operators, modern methods in operator theory and harmonic analysis, Springer Proc. Math. Stat., Vol. 291 (Springer, 2019), pp. 217–236.CrossRef Google Scholar

Leung, D. H.. Some remarks on regular Banach spaces. Glasg. Math. J. 38 (1996), 243–248.CrossRef Google Scholar

Loane, J., Polynomials on vector lattices, PhD Thesis, National University of Ireland, Galway, 2007.Google Scholar

Meyer–Nieberg, P.. Banach Lattices (New York: Springer-Verlag, 1991).CrossRef Google Scholar

Pełczyński, A.. Projections in certain Banach spaces. Stud. Math. 19 (1960), 209–228.CrossRef Google Scholar

Schaefer, H. H.. Banach Lattices and Positive Operators (Berlin: Springer, 1974).CrossRef Google Scholar

Yilmaz, R.. The Arens triadjoints of some bilinear maps. Filomat 28 (2014), 963–979.CrossRef Google Scholar

Article contents

Order continuity of Arens extensions of regular multilinear operators

Abstract

Keywords

MSC classification

1. Introduction

2. Background

3. The counterexample

4. Operators between Riesz spaces

5. Operators between Banach lattices

Acknowledgements

References

Save article to Kindle

Save article to Dropbox

Save article to Google Drive

Reply to: Submit a response

Your details

You have entered the maximum number of contributors

Conflicting interests