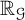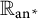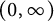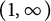1 Introduction
We generalize the theory of multisummability in the positive real direction, as discussed in [Reference Balser2, Reference Tougeron9, Reference Van den Dries and Speissegger12], to certain nonconvergent power series with real nonnegative exponents (introduced in [Reference Van den Dries and Speissegger11, p. 4377]). Examples of such series are Dirichlet series (after the change of variables
![]() $s=-\log x$
), and asymptotic expansions of certain solutions of differential equations [Reference Wasow13] and of certain functions appearing in Dulac’s problem [Reference Il’yashenko3].
$s=-\log x$
), and asymptotic expansions of certain solutions of differential equations [Reference Wasow13] and of certain functions appearing in Dulac’s problem [Reference Il’yashenko3].
Our main motivation here comes from o-minimality: summation processes induce a quasianalyticity property which is usually needed to prove that a given structure is o-minimal. In their paper [Reference Van den Dries, Macintyre and Marker10], Van den Dries, Macintyre, and Marker show that neither Euler’s gamma function
![]() $\Gamma $
restricted to
$\Gamma $
restricted to
![]() $(0,+\infty )$
, nor the Riemann zeta function
$(0,+\infty )$
, nor the Riemann zeta function
![]() $\zeta $
restricted to
$\zeta $
restricted to
![]() $(1,+\infty )$
, are definable in the o-minimal structure
$(1,+\infty )$
, are definable in the o-minimal structure
![]() ${\mathbb {R}_{\mathrm {an,exp}}}$
[Reference Van den Dries, Macintyre and Marker10, Theorem 5.11 and Corollary 5.14]. Subsequently, Van den Dries and Speissegger constructed the o-minimal expansions
${\mathbb {R}_{\mathrm {an,exp}}}$
[Reference Van den Dries, Macintyre and Marker10, Theorem 5.11 and Corollary 5.14]. Subsequently, Van den Dries and Speissegger constructed the o-minimal expansions
![]() $(\mathbb {R}_{\text {an}^*},\exp )$
[Reference Van den Dries and Speissegger11, Reference Van den Dries and Speissegger12] and
$(\mathbb {R}_{\text {an}^*},\exp )$
[Reference Van den Dries and Speissegger11, Reference Van den Dries and Speissegger12] and
![]() $(\mathbb {R}_{\mathcal {G}},\exp )$
[Reference Van den Dries and Speissegger12], and they proved that
$(\mathbb {R}_{\mathcal {G}},\exp )$
[Reference Van den Dries and Speissegger12], and they proved that
![]() $\zeta \!\!\upharpoonright _{(0,+\infty )}$
is definable in the former, but not in the latter [Reference Van den Dries and Speissegger12, Corollary 10.11], whereas
$\zeta \!\!\upharpoonright _{(0,+\infty )}$
is definable in the former, but not in the latter [Reference Van den Dries and Speissegger12, Corollary 10.11], whereas
![]() $\Gamma \!\!\upharpoonright _{(0,+\infty )}$
is definable in the latter [Reference Van den Dries and Speissegger12, Example 8.1]. At the time, it was unknown whether
$\Gamma \!\!\upharpoonright _{(0,+\infty )}$
is definable in the latter [Reference Van den Dries and Speissegger12, Example 8.1]. At the time, it was unknown whether
![]() $\Gamma \!\!\upharpoonright _{(0,+\infty )}$
was definable in the former.
$\Gamma \!\!\upharpoonright _{(0,+\infty )}$
was definable in the former.
This state of affairs thus left the following question unanswered: is there an o-minimal expansion of the real field in which both
![]() $\Gamma \!\!\upharpoonright _{(0,+\infty )}$
and
$\Gamma \!\!\upharpoonright _{(0,+\infty )}$
and
![]() $\zeta \!\!\upharpoonright _{(1,+\infty )}$
are definable? Based on additional information gained from Rolin and Servi’s paper [Reference Rolin and Servi7] about the structures
$\zeta \!\!\upharpoonright _{(1,+\infty )}$
are definable? Based on additional information gained from Rolin and Servi’s paper [Reference Rolin and Servi7] about the structures
![]() $(\mathbb {R}_{\text {an}^*},\exp )$
and
$(\mathbb {R}_{\text {an}^*},\exp )$
and
![]() $(\mathbb {R}_{\mathcal {G}},\exp )$
, we show in a separate paper (in preparation) that
$(\mathbb {R}_{\mathcal {G}},\exp )$
, we show in a separate paper (in preparation) that
![]() $\Gamma \!\!\upharpoonright _{(0,+\infty )}$
is not definable in
$\Gamma \!\!\upharpoonright _{(0,+\infty )}$
is not definable in
![]() $(\mathbb {R}_{\text {an}^*},\exp )$
either. So to answer the question in the affirmative, we need to come up with an o-minimal structure that properly expands both the expansion of the real field by
$(\mathbb {R}_{\text {an}^*},\exp )$
either. So to answer the question in the affirmative, we need to come up with an o-minimal structure that properly expands both the expansion of the real field by
![]() $\Gamma \!\!\upharpoonright _{(0,+\infty )}$
and the expansion of the real field by
$\Gamma \!\!\upharpoonright _{(0,+\infty )}$
and the expansion of the real field by
![]() $\zeta \!\!\upharpoonright _{(1,+\infty )}$
.
$\zeta \!\!\upharpoonright _{(1,+\infty )}$
.
Indeed, we construct here an o-minimal expansion of the real field that expands
![]() $(\mathbb {R}_{\mathcal {G}},\exp )$
and in which
$(\mathbb {R}_{\mathcal {G}},\exp )$
and in which
![]() $\zeta \!\!\upharpoonright _{(1,+\infty )}$
is definable (see the Main Corollary).
$\zeta \!\!\upharpoonright _{(1,+\infty )}$
is definable (see the Main Corollary).
To recap, for an indeterminate
![]() $X = (X_1, \dots , X_n)$
, we denote by
$X = (X_1, \dots , X_n)$
, we denote by
![]() $\mathbb {C}\left [\!\left [X^*\right ]\!\right ]$
the set of all generalized power series of the form
$\mathbb {C}\left [\!\left [X^*\right ]\!\right ]$
the set of all generalized power series of the form
![]() $F(X) = \sum _{\alpha \in [0,\infty )^n} a_{\alpha } X^{\alpha }$
, where each
$F(X) = \sum _{\alpha \in [0,\infty )^n} a_{\alpha } X^{\alpha }$
, where each
![]() $a_{\alpha } \in \mathbb {C}$
and the support
$a_{\alpha } \in \mathbb {C}$
and the support
is contained in a product
![]() $A_1 \times \cdots \times A_n$
of sets
$A_1 \times \cdots \times A_n$
of sets
![]() $A_i \subset [0,\infty )$
that are well ordered with respect to the usual ordering of the real numbers (see [Reference Van den Dries and Speissegger11, Section 4] for details). The series
$A_i \subset [0,\infty )$
that are well ordered with respect to the usual ordering of the real numbers (see [Reference Van den Dries and Speissegger11, Section 4] for details). The series
![]() $F(X)$
converges if there exists
$F(X)$
converges if there exists
![]() $r>0$
such that
$r>0$
such that
![]() $\|F\|_r:= \sum _{\alpha } |a_{\alpha }|r^{\alpha } < \infty $
; we denote by
$\|F\|_r:= \sum _{\alpha } |a_{\alpha }|r^{\alpha } < \infty $
; we denote by
![]() $\mathbb {C}\left \{X^*\right \}$
the set of all convergent generalized power series [Reference Van den Dries and Speissegger11, Section 5].
$\mathbb {C}\left \{X^*\right \}$
the set of all convergent generalized power series [Reference Van den Dries and Speissegger11, Section 5].
The generalized power series that we extend the notion of multisummability to have special support: we call a set
![]() $A \subseteq \mathbb {R}$
natural if
$A \subseteq \mathbb {R}$
natural if
![]() $A \cap (-\infty ,a)$
is finite, for every
$A \cap (-\infty ,a)$
is finite, for every
![]() $a \in \mathbb {R}$
; and we call a set
$a \in \mathbb {R}$
; and we call a set
![]() $A \subseteq \mathbb {R}^n$
natural if
$A \subseteq \mathbb {R}^n$
natural if
![]() $A \subseteq A_1 \times \cdots \times A_n$
with each
$A \subseteq A_1 \times \cdots \times A_n$
with each
![]() $A_i \subseteq \mathbb {R}$
natural. Restricting our attention to generalized power series with natural support allows us to use such objects as asymptotic expansions of germs (see Proposition 2.16). This has already been exploited in [Reference Kaiser, Rolin and Speissegger4], where the o-minimality of the expansion of the real field by certain Dulac germs is proven.
$A_i \subseteq \mathbb {R}$
natural. Restricting our attention to generalized power series with natural support allows us to use such objects as asymptotic expansions of germs (see Proposition 2.16). This has already been exploited in [Reference Kaiser, Rolin and Speissegger4], where the o-minimality of the expansion of the real field by certain Dulac germs is proven.
In Sections 2 and 3, we define a notion of multisummability in the positive real direction for generalized power series of natural support, appropriately named generalized multisummability in the positive real direction (or simply generalized multisummability in the real direction when working in the logarithmic chart of the Riemann surface of the logarithm, as we do throughout this paper). We verify that the resulting system
![]() $\mathcal {G}^*$
of algebras (both of functions and of germs) satisfies the axioms in [Reference Rolin and Servi7], leading to the following: let the language
$\mathcal {G}^*$
of algebras (both of functions and of germs) satisfies the axioms in [Reference Rolin and Servi7], leading to the following: let the language
![]() $\mathcal {L}_{\mathcal {G}^*}$
and the structure
$\mathcal {L}_{\mathcal {G}^*}$
and the structure
![]() $\mathbb {R}_{\mathcal {G}^*}$
be as in [Reference Rolin and Servi7, Definition 1.21] for our system
$\mathbb {R}_{\mathcal {G}^*}$
be as in [Reference Rolin and Servi7, Definition 1.21] for our system
![]() $\mathcal {G}^*$
of algebras in place of
$\mathcal {G}^*$
of algebras in place of
![]() $\mathcal {A}$
there.
$\mathcal {A}$
there.
Main Theorem
-
(1) The structure
 $\mathbb {R}_{\mathcal {G}^*}$
is model complete, o-minimal and polynomially bounded and has field of exponents
$\mathbb {R}_{\mathcal {G}^*}$
is model complete, o-minimal and polynomially bounded and has field of exponents
 $\mathbb {R}$
.
$\mathbb {R}$
. -
(2) The structure
 $\mathbb {R}_{\mathcal {G}^*}$
admits quantifier elimination in the language
$\mathbb {R}_{\mathcal {G}^*}$
admits quantifier elimination in the language
 $\mathcal {L}_{\mathcal {G}^*} \cup \{(\cdot )^{-1}\}$
.
$\mathcal {L}_{\mathcal {G}^*} \cup \{(\cdot )^{-1}\}$
.
By construction, all functions defined on compact polydisks by convergent generalized power series with natural support are definable in
![]() $\mathbb {R}_{\mathcal {G}^*}$
; and we show in Section 2 that the same holds for all functions defined on compact sets by standard power series that are multisummable in the positive real direction. Recall that, for
$\mathbb {R}_{\mathcal {G}^*}$
; and we show in Section 2 that the same holds for all functions defined on compact sets by standard power series that are multisummable in the positive real direction. Recall that, for
![]() $x\in \left [0,e^{-2}\right ]$
,
$x\in \left [0,e^{-2}\right ]$
,
![]() $\zeta \left (-\log x\right )$
is the sum of the generalized power series
$\zeta \left (-\log x\right )$
is the sum of the generalized power series
![]() $\sum _{n=1}^{\infty }x^{\log n}$
, which has natural support. In particular, both
$\sum _{n=1}^{\infty }x^{\log n}$
, which has natural support. In particular, both
![]() $\exp \!\!\upharpoonright _{[0,1]}$
and
$\exp \!\!\upharpoonright _{[0,1]}$
and
![]() $\zeta (-\log x)\!\!\upharpoonright _{[0,e^{-2}]}$
are definable in
$\zeta (-\log x)\!\!\upharpoonright _{[0,e^{-2}]}$
are definable in
![]() $\mathbb {R}_{\mathcal {G}^*}$
, as is the function
$\mathbb {R}_{\mathcal {G}^*}$
, as is the function
![]() $\log \Gamma (x) - (x-\frac 12)\log x$
on the interval
$\log \Gamma (x) - (x-\frac 12)\log x$
on the interval
![]() $(1,+\infty )$
(see [Reference Van den Dries and Speissegger12, Example 8.1]). Therefore, Theorem B of [Reference Van den Dries and Speissegger12] gives the following corollary.
$(1,+\infty )$
(see [Reference Van den Dries and Speissegger12, Example 8.1]). Therefore, Theorem B of [Reference Van den Dries and Speissegger12] gives the following corollary.
Main Corollary
-
(1) The structure
 $(\mathbb {R}_{\mathcal {G}^*},\exp )$
is model complete and o-minimal, and it admits quantifier elimination in the language
$(\mathbb {R}_{\mathcal {G}^*},\exp )$
is model complete and o-minimal, and it admits quantifier elimination in the language
 $\mathcal {L}_{\mathcal {G}^*} \cup \{\exp ,\log \}$
.
$\mathcal {L}_{\mathcal {G}^*} \cup \{\exp ,\log \}$
. -
(2) The functions
 $\Gamma \!\!\upharpoonright _{(0,+\infty )}$
and
$\Gamma \!\!\upharpoonright _{(0,+\infty )}$
and
 $\zeta \!\!\upharpoonright _{(1,+\infty )}$
are definable in
$\zeta \!\!\upharpoonright _{(1,+\infty )}$
are definable in
 $(\mathbb {R}_{\mathcal {G}^*},\exp )$
.
$(\mathbb {R}_{\mathcal {G}^*},\exp )$
.
As we rely on [Reference Rolin and Servi7] for the proof of o-minimality of
![]() $\mathbb {R}_{\mathcal {G}^*}$
, the main contribution of this paper is the generalization of multisummability in the positive real direction to generalized power series of natural support and the establishment of the axioms in [Reference Rolin and Servi7] for the corresponding system
$\mathbb {R}_{\mathcal {G}^*}$
, the main contribution of this paper is the generalization of multisummability in the positive real direction to generalized power series of natural support and the establishment of the axioms in [Reference Rolin and Servi7] for the corresponding system
![]() $\mathcal {G}^*$
of algebras of functions and germs.
$\mathcal {G}^*$
of algebras of functions and germs.
As in [Reference Van den Dries and Speissegger12], our starting point here is a characterization, due to Tougeron [Reference Tougeron9], of multisummable power series in terms of infinite sums of convergent power series of decreasing radii of convergence. Thus, we move to the logarithmic chart of the Riemann surface of the logarithm, since we are working with arbitrary real exponents. Then we define a multisummable generalized power series (in the real direction) as the infinite sum of a sequence of convergent generalized power series with decreasing radii of convergence and support contained in a fixed natural set (Section 2.4).
The corresponding theory of multisummability in one variable, developed in Section 2, differs from the classical one in that there is no origin around which we can use contour integration. One example of a classical result that we cannot generalize is the following: every classical multisummable power series can be decomposed into a sum of singly summable series; we do not know if this is the case in the generalized setting (see Section 2.7 for details). However, we do obtain the crucial quasianalyticity for our system of algebras (Section 2.6).
Also, as in [Reference Van den Dries and Speissegger12], this approach lends itself naturally to define generalized multisummability in the positive real direction in several variables, and we follow the corresponding steps in [Reference Van den Dries and Speissegger12] as closely as possible (Section 3). In Section 4 and 5, we establish the axioms of [Reference Rolin and Servi7].
Remark (1) To the best of our knowledge, this is the first time [Reference Rolin and Servi7] was used to prove the o-minimality of a structure that was previously unknown to be o-minimal. The same procedure could be used to obtain the o-minimality (and related results) of the structures
![]() $\mathbb {R}_{\text {an}^*}$
[Reference Van den Dries and Speissegger11],
$\mathbb {R}_{\text {an}^*}$
[Reference Van den Dries and Speissegger11],
![]() $\mathbb {R}_{\mathcal {G}}$
[Reference Van den Dries and Speissegger12], and
$\mathbb {R}_{\mathcal {G}}$
[Reference Van den Dries and Speissegger12], and
![]() $\mathbb {R}_{\mathcal {C}}$
[Reference Rolin, Speissegger and Wilkie8]. The resulting quantifier elimination given by [Reference Rolin and Servi7, Theorem B] is new in each of these cases, and it is used in our forthcoming paper to show that
$\mathbb {R}_{\mathcal {C}}$
[Reference Rolin, Speissegger and Wilkie8]. The resulting quantifier elimination given by [Reference Rolin and Servi7, Theorem B] is new in each of these cases, and it is used in our forthcoming paper to show that
![]() $\Gamma \!\!\upharpoonright _{(0,+\infty )}$
is not definable in
$\Gamma \!\!\upharpoonright _{(0,+\infty )}$
is not definable in
![]() $(\mathbb {R}_{\text {an}^*},\exp )$
.
$(\mathbb {R}_{\text {an}^*},\exp )$
.
(2) The only closure property needed in [Reference Rolin and Servi7] but not established in [Reference Rolin, Speissegger and Wilkie8, Reference Van den Dries and Speissegger11, Reference Van den Dries and Speissegger12] is closure under infinitesimal substitutions in the convergent variables (Proposition 4.9). The proof of this in the structures discussed in the previous remark is similar to the proof given here for
![]() $\mathcal {G}^*$
.
$\mathcal {G}^*$
.
Finally, from the point of view of generalized multisummability, as in the classical theory, there is nothing special about the positive real direction. Our generalized notion works in any other direction, and one could correspondingly come up with a notion of “generalized multisummability” as done in the classical situation. This raises some interesting questions in their own right (see Section 2.7), which we do not address in this paper.
2 Generalized multisummable functions of one variable
2.1 Preliminaries
We denote by
the logarithmic chart of the Riemann surface of the logarithm, with the additional “origin” of
![]() $\overline {\mathbb {C}}$
represented by “
$\overline {\mathbb {C}}$
represented by “
![]() $-\infty $
,” where we convene that
$-\infty $
,” where we convene that
![]() $\operatorname {\mathrm {Re}}(-\infty ) = -\infty $
. For
$\operatorname {\mathrm {Re}}(-\infty ) = -\infty $
. For
![]() ${\frak r} \in \mathbb {R}$
, we let
${\frak r} \in \mathbb {R}$
, we let
be the log-disk of log-radius
![]() ${\frak r}$
. For
${\frak r}$
. For
![]() $d,{\frak r} \in \mathbb {R}$
, a log-sector is a set
$d,{\frak r} \in \mathbb {R}$
, a log-sector is a set
 $$ \begin{align*} S(d,{\frak r},\theta):= \begin{cases} \left\{u+iv \in \mathbb{C}:\ u < {\frak r}, |d-v| < \theta\right\} \cup \{-\infty\}, &\text{if } \theta \in (0,\infty), \\ H({\frak r}), &\text{if } \theta = \infty, \end{cases} \end{align*} $$
$$ \begin{align*} S(d,{\frak r},\theta):= \begin{cases} \left\{u+iv \in \mathbb{C}:\ u < {\frak r}, |d-v| < \theta\right\} \cup \{-\infty\}, &\text{if } \theta \in (0,\infty), \\ H({\frak r}), &\text{if } \theta = \infty, \end{cases} \end{align*} $$
and a log-line is a set
(We shall mainly focus on the direction
![]() $d=0$
in this paper.) We extend the standard topology on
$d=0$
in this paper.) We extend the standard topology on
![]() $\mathbb {C}$
to
$\mathbb {C}$
to
![]() $\overline {\mathbb {C}}$
by declaring the log-disks as basic open neighborhoods of
$\overline {\mathbb {C}}$
by declaring the log-disks as basic open neighborhoods of
![]() $-\infty $
. Note that the usual covering map of the Riemann surface of the logarithm is represented in the logarithmic chart by the exponential function, and we extend it to a continuous function on
$-\infty $
. Note that the usual covering map of the Riemann surface of the logarithm is represented in the logarithmic chart by the exponential function, and we extend it to a continuous function on
![]() $\overline {\mathbb {C}}$
by setting
$\overline {\mathbb {C}}$
by setting
![]() $e^{-\infty }:= 0$
. For each
$e^{-\infty }:= 0$
. For each
![]() $d \in \mathbb {R}$
, the restriction of
$d \in \mathbb {R}$
, the restriction of
![]() $e^w$
to
$e^w$
to
![]() $S(d,\infty ,\pi ) \setminus \{-\infty \}$
is injective; its inverse is the branch of the logarithm
$S(d,\infty ,\pi ) \setminus \{-\infty \}$
is injective; its inverse is the branch of the logarithm
![]() $\log _d$
in the direction d.
$\log _d$
in the direction d.
We are mostly interested in partial functions on
![]() $\overline {\mathbb {C}}$
with values in
$\overline {\mathbb {C}}$
with values in
![]() $\mathbb {C}$
. In this spirit, we call a set
$\mathbb {C}$
. In this spirit, we call a set
![]() $D \subseteq \overline {\mathbb {C}}$
a log-domain if
$D \subseteq \overline {\mathbb {C}}$
a log-domain if
![]() $D \cap \mathbb {C}$
is a domain (in particular, every domain in
$D \cap \mathbb {C}$
is a domain (in particular, every domain in
![]() $\mathbb {C}$
is a log-domain). If
$\mathbb {C}$
is a log-domain). If
![]() $D \subseteq \overline {\mathbb {C}}$
is a log-domain, a log-holomorphic function on D is a continuous function
$D \subseteq \overline {\mathbb {C}}$
is a log-domain, a log-holomorphic function on D is a continuous function
![]() $f:D \longrightarrow \mathbb {C}$
such that the restriction of f to
$f:D \longrightarrow \mathbb {C}$
such that the restriction of f to
![]() $D \cap \mathbb {C}$
is holomorphic. For example, every holomorphic function on a domain in
$D \cap \mathbb {C}$
is holomorphic. For example, every holomorphic function on a domain in
![]() $\mathbb {C}$
is log-holomorphic, and the exponential function is log-holomorphic on
$\mathbb {C}$
is log-holomorphic, and the exponential function is log-holomorphic on
![]() $\overline {\mathbb {C}}$
.
$\overline {\mathbb {C}}$
.
2.2 The logarithmic Borel and Laplace transforms
2.2.1 Logarithmic Borel transform
Let
![]() $d,{\frak r} \in \mathbb {R}$
and
$d,{\frak r} \in \mathbb {R}$
and
![]() $\theta> \pi /2$
, and write
$\theta> \pi /2$
, and write
![]() $S = S(d,{\frak r},\theta )$
. Let
$S = S(d,{\frak r},\theta )$
. Let
![]() $f:S \longrightarrow \mathbb {C}$
be such that
$f:S \longrightarrow \mathbb {C}$
be such that
![]() $f\!\!\upharpoonright _{\overline S_0}$
is bounded and log-holomorphic, for every closed log-subsector
$f\!\!\upharpoonright _{\overline S_0}$
is bounded and log-holomorphic, for every closed log-subsector
![]() $\overline S_0$
of S. Given a closed log-subsector
$\overline S_0$
of S. Given a closed log-subsector
![]() $\overline S_0 = \operatorname {\mathrm {cl}}(S(d', {\frak r}',\theta '))$
of S with
$\overline S_0 = \operatorname {\mathrm {cl}}(S(d', {\frak r}',\theta '))$
of S with
![]() $\theta '>\frac \pi 2$
, denote by
$\theta '>\frac \pi 2$
, denote by
![]() $\partial \overline S_0$
the directed path following the boundary of
$\partial \overline S_0$
the directed path following the boundary of
![]() $\overline S_0$
from the “lower left end” to the “upper left end.” We define the logarithmic Borel transform
$\overline S_0$
from the “lower left end” to the “upper left end.” We define the logarithmic Borel transform
![]() $\mathcal {B}_{d'} f: T(d') \longrightarrow \mathbb {C}$
in the direction
$\mathcal {B}_{d'} f: T(d') \longrightarrow \mathbb {C}$
in the direction
![]() $d'$
of f by
$d'$
of f by
We leave it as an exercise to check that
![]() $\mathcal {B}_{d'} f$
only depends on
$\mathcal {B}_{d'} f$
only depends on
![]() $d'$
, but not on the other parameters of
$d'$
, but not on the other parameters of
![]() $\overline S_0$
(as long as they are in the prescribed range). More is true.
$\overline S_0$
(as long as they are in the prescribed range). More is true.
Remark 2.1 If
![]() $\theta ' < \pi $
and
$\theta ' < \pi $
and
![]() $g(z):= f(\log _d z)$
, for
$g(z):= f(\log _d z)$
, for
![]() $z \in \exp (\overline S_0)$
, then the change of variables
$z \in \exp (\overline S_0)$
, then the change of variables
![]() $z = e^w$
gives that
$z = e^w$
gives that
where
![]() $\mathcal {B}_{d'} g$
denotes the Borel transform of g in the direction
$\mathcal {B}_{d'} g$
denotes the Borel transform of g in the direction
![]() $d'$
as defined in [Reference Loray5] (see also Section 5.2 of [Reference Balser2]). Thus, the following proposition is obtained from Propriétés 1–3 on page 38 of [Reference Loray5].
$d'$
as defined in [Reference Loray5] (see also Section 5.2 of [Reference Balser2]). Thus, the following proposition is obtained from Propriétés 1–3 on page 38 of [Reference Loray5].
Proposition 2.2 Set
![]() $S':= S\left (d,\infty ,\theta -\frac \pi 2\right )$
.
$S':= S\left (d,\infty ,\theta -\frac \pi 2\right )$
.
-
(1) The function
 $\mathcal {B} f: S' \longrightarrow \mathbb {C}$
defined by
$\mathcal {B} f: S' \longrightarrow \mathbb {C}$
defined by
 $\mathcal {B} f(w):= (\mathcal {B}_{\operatorname {\mathrm {Im}} w} f)(w)$
is log-holomorphic on every closed log-subsector
$\mathcal {B} f(w):= (\mathcal {B}_{\operatorname {\mathrm {Im}} w} f)(w)$
is log-holomorphic on every closed log-subsector
 $\overline S_0$
of
$\overline S_0$
of
 $S'$
.
$S'$
. -
(2) For every closed log-subsector
 $\overline S_0$
of
$\overline S_0$
of
 $S'$
, there exist
$S'$
, there exist
 $C,D>0$
such that
$C,D>0$
such that  $$ \begin{align*}|\mathcal{B} f(w)| \le C e^{De^{\operatorname{\mathrm{Re}} w}} \quad\text{for } w \in \overline S_0.\end{align*} $$
$$ \begin{align*}|\mathcal{B} f(w)| \le C e^{De^{\operatorname{\mathrm{Re}} w}} \quad\text{for } w \in \overline S_0.\end{align*} $$
-
(3) Let
 $\alpha \ge 0$
, and assume that for every closed log-subsector
$\alpha \ge 0$
, and assume that for every closed log-subsector
 $\overline S_0$
of S, we have
$\overline S_0$
of S, we have
 $|f(w)| = O\left (e^{\alpha \operatorname {\mathrm {Re}} w}\right )$
as
$|f(w)| = O\left (e^{\alpha \operatorname {\mathrm {Re}} w}\right )$
as
 $w \to -\infty $
in
$w \to -\infty $
in
 $\overline S_0$
. Then, for every closed log-subsector
$\overline S_0$
. Then, for every closed log-subsector
 $\overline S_0$
of
$\overline S_0$
of
 $S'$
, we have
$S'$
, we have
 $|\mathcal {B} f(w)| = O\left (e^{\alpha \operatorname {\mathrm {Re}} w}\right )$
as
$|\mathcal {B} f(w)| = O\left (e^{\alpha \operatorname {\mathrm {Re}} w}\right )$
as
 $w \to -\infty $
in
$w \to -\infty $
in
 $\overline S_0$
.
$\overline S_0$
.
Accordingly, we call the function
![]() $\mathcal {B} f$
defined in the proposition above the log-Borel transform of f.
$\mathcal {B} f$
defined in the proposition above the log-Borel transform of f.
For
![]() $D \subseteq \overline {\mathbb {C}}$
and
$D \subseteq \overline {\mathbb {C}}$
and
![]() $g:D \longrightarrow \mathbb {C}$
, we set
$g:D \longrightarrow \mathbb {C}$
, we set
For later use, we make the bound in Proposition 2.2(2) more precise.
Lemma 2.3 Let
![]() $\overline S_0 = \operatorname {\mathrm {cl}}(S(d', {\frak r}',\theta '))$
be a closed subsector of S with
$\overline S_0 = \operatorname {\mathrm {cl}}(S(d', {\frak r}',\theta '))$
be a closed subsector of S with
![]() $\theta ' \in \left (\frac \pi 2,\theta \right )$
, and set
$\theta ' \in \left (\frac \pi 2,\theta \right )$
, and set
![]() $S':= S\left (d',r,\theta ' - \frac \pi 2\right )$
and
$S':= S\left (d',r,\theta ' - \frac \pi 2\right )$
and
![]() $C:= \sin \left (\frac {\theta -\theta '}2\right )$
. Then
$C:= \sin \left (\frac {\theta -\theta '}2\right )$
. Then
 $$ \begin{align*}\left\|\mathcal{B} f\right\|_{S'} \le \begin{cases} \frac{\left\| f\right\|_{\overline S_0}}{C} e, &\text{if } r \le {\frak r}', \\ \frac{\left\| f\right\|_{\overline S_0}}{C} e^{e^{r-{\frak r}'}} e^{r - {\frak r}'}, &\text{if } r \ge {\frak r}'. \end{cases}\end{align*} $$
$$ \begin{align*}\left\|\mathcal{B} f\right\|_{S'} \le \begin{cases} \frac{\left\| f\right\|_{\overline S_0}}{C} e, &\text{if } r \le {\frak r}', \\ \frac{\left\| f\right\|_{\overline S_0}}{C} e^{e^{r-{\frak r}'}} e^{r - {\frak r}'}, &\text{if } r \ge {\frak r}'. \end{cases}\end{align*} $$
Proof Let
![]() $w \in S'$
; we compute
$w \in S'$
; we compute
![]() $\mathcal {B} f(w)$
by computing
$\mathcal {B} f(w)$
by computing
![]() $\mathcal {B}_d f(w)$
, where
$\mathcal {B}_d f(w)$
, where
![]() $d:= \operatorname {\mathrm {Im}} w$
and the integral is taken along the contour
$d:= \operatorname {\mathrm {Im}} w$
and the integral is taken along the contour
![]() $\delta := \partial S\left (d,\rho ,\alpha \right )$
, where
$\delta := \partial S\left (d,\rho ,\alpha \right )$
, where
![]() $\alpha := \frac {\theta -\theta '+\pi }2$
and
$\alpha := \frac {\theta -\theta '+\pi }2$
and
![]() $\rho := \min \{\operatorname {\mathrm {Re}} w, {\frak r}'\}$
. For
$\rho := \min \{\operatorname {\mathrm {Re}} w, {\frak r}'\}$
. For
![]() $\eta \in \delta $
, we distinguish two cases.
$\eta \in \delta $
, we distinguish two cases.
Case 1:
![]() $|\operatorname {\mathrm {Im}}(w-\eta )| = \alpha $
. Then
$|\operatorname {\mathrm {Im}}(w-\eta )| = \alpha $
. Then
![]() $\operatorname {\mathrm {Re}}(e^{w-\eta }) = \cos \alpha \cdot e^{\operatorname {\mathrm {Re}} w-\operatorname {\mathrm {Re}}\eta }$
; since
$\operatorname {\mathrm {Re}}(e^{w-\eta }) = \cos \alpha \cdot e^{\operatorname {\mathrm {Re}} w-\operatorname {\mathrm {Re}}\eta }$
; since
![]() $C = -\cos \alpha $
, we get
$C = -\cos \alpha $
, we get
 $$ \begin{align*} \frac1{2\pi} \left|e^w\int_{|\operatorname{\mathrm{Im}}(w-\eta)| = \pi} e^{e^{w-\eta}} f(\eta) \frac{d\eta}{e^{\eta}}\right| &\le \frac{\left\|f\right\|_{\overline S_0}}{2\pi} \int_{|\operatorname{\mathrm{Im}}(w-\eta)| = \pi} e^{\cos\alpha \cdot e^{\operatorname{\mathrm{Re}} w-\operatorname{\mathrm{Re}}\eta}} e^{\operatorname{\mathrm{Re}} w -\operatorname{\mathrm{Re}}\eta} d\eta \\ &= \frac{\left\|f\right\|_{\overline S_0}}{\pi} \int_{-\infty}^{\rho} e^{\cos\alpha \cdot e^{\operatorname{\mathrm{Re}} w -r}} e^{\operatorname{\mathrm{Re}} w-r} dr \\ &= \frac{\left\|f\right\|_{\overline S_0}}{\pi C} e^{\cos\alpha\cdot e^{\operatorname{\mathrm{Re}} w-r}}\Big|_{-\infty}^{\rho} \\ &\le \frac{\left\|f\right\|_{\overline S_0}}{C}, \end{align*} $$
$$ \begin{align*} \frac1{2\pi} \left|e^w\int_{|\operatorname{\mathrm{Im}}(w-\eta)| = \pi} e^{e^{w-\eta}} f(\eta) \frac{d\eta}{e^{\eta}}\right| &\le \frac{\left\|f\right\|_{\overline S_0}}{2\pi} \int_{|\operatorname{\mathrm{Im}}(w-\eta)| = \pi} e^{\cos\alpha \cdot e^{\operatorname{\mathrm{Re}} w-\operatorname{\mathrm{Re}}\eta}} e^{\operatorname{\mathrm{Re}} w -\operatorname{\mathrm{Re}}\eta} d\eta \\ &= \frac{\left\|f\right\|_{\overline S_0}}{\pi} \int_{-\infty}^{\rho} e^{\cos\alpha \cdot e^{\operatorname{\mathrm{Re}} w -r}} e^{\operatorname{\mathrm{Re}} w-r} dr \\ &= \frac{\left\|f\right\|_{\overline S_0}}{\pi C} e^{\cos\alpha\cdot e^{\operatorname{\mathrm{Re}} w-r}}\Big|_{-\infty}^{\rho} \\ &\le \frac{\left\|f\right\|_{\overline S_0}}{C}, \end{align*} $$
because
![]() $\cos \alpha < 0$
.
$\cos \alpha < 0$
.
Case 2:
![]() $\operatorname {\mathrm {Re}}\eta = \rho $
. Then we have
$\operatorname {\mathrm {Re}}\eta = \rho $
. Then we have
so that
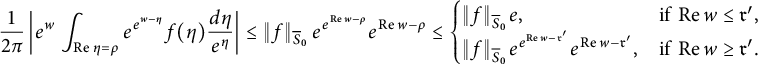 $$ \begin{align*} \frac1{2\pi} \left|e^w\int_{\operatorname{\mathrm{Re}}\eta = \rho} e^{e^{w-\eta}} f(\eta) \frac{d\eta}{e^{\eta}}\right| \le \left\|f\right\|_{\overline S_0} e^{e^{\operatorname{\mathrm{Re}} w-\rho}} e^{\operatorname{\mathrm{Re}} w - \rho} \le \begin{cases} \|f\|_{\overline S_0} e, &\text{if } \operatorname{\mathrm{Re}} w \le {\frak r}', \\ \|f\|_{\overline S_0} e^{e^{\operatorname{\mathrm{Re}} w-{\frak r}'}} e^{\operatorname{\mathrm{Re}} w - {\frak r}'}, &\text{if } \operatorname{\mathrm{Re}} w \ge {\frak r}'. \end{cases} \end{align*} $$
$$ \begin{align*} \frac1{2\pi} \left|e^w\int_{\operatorname{\mathrm{Re}}\eta = \rho} e^{e^{w-\eta}} f(\eta) \frac{d\eta}{e^{\eta}}\right| \le \left\|f\right\|_{\overline S_0} e^{e^{\operatorname{\mathrm{Re}} w-\rho}} e^{\operatorname{\mathrm{Re}} w - \rho} \le \begin{cases} \|f\|_{\overline S_0} e, &\text{if } \operatorname{\mathrm{Re}} w \le {\frak r}', \\ \|f\|_{\overline S_0} e^{e^{\operatorname{\mathrm{Re}} w-{\frak r}'}} e^{\operatorname{\mathrm{Re}} w - {\frak r}'}, &\text{if } \operatorname{\mathrm{Re}} w \ge {\frak r}'. \end{cases} \end{align*} $$
Combining the two cases, we obtain the lemma.
2.2.2 Logarithmic Laplace transform
We fix an arbitrary direction
![]() $d \in \mathbb {R}$
. Let
$d \in \mathbb {R}$
. Let
![]() $f:T(d) \longrightarrow \mathbb {C}$
be continuous, and assume that there exist
$f:T(d) \longrightarrow \mathbb {C}$
be continuous, and assume that there exist
![]() $C,D>0$
such that
$C,D>0$
such that
We let
be the Borel disk of diameter
![]() $\frac 1D$
touching the origin and centered on the ray in direction d. Correspondingly, we let
$\frac 1D$
touching the origin and centered on the ray in direction d. Correspondingly, we let
the log-Borel disk in the direction d of extent
![]() $-\log D$
; note indeed that
$-\log D$
; note indeed that
![]() $U(d,D) = \exp (V(d,D))$
. We define the log-Laplace transform
$U(d,D) = \exp (V(d,D))$
. We define the log-Laplace transform
![]() $\mathcal {L}_df:V(d,D) \longrightarrow \mathbb {C}$
in the direction d of f by
$\mathcal {L}_df:V(d,D) \longrightarrow \mathbb {C}$
in the direction d of f by
Remark 2.4 If
![]() $g(z):= f(\log _d z)$
, for
$g(z):= f(\log _d z)$
, for
![]() $z \in \mathbb {C}$
such that
$z \in \mathbb {C}$
such that
![]() $\arg z = d$
, then the change of variables
$\arg z = d$
, then the change of variables
![]() $z = e^w$
gives that
$z = e^w$
gives that
where
![]() $\mathcal {L}_{d} g$
denotes the Laplace transform of g in the direction d as defined in [Reference Loray5] (see also Section 5.1 of [Reference Balser2]). Thus, the following proposition is obtained from Propriétés 1–2 on pages 41 and 42 of [Reference Loray5].
$\mathcal {L}_{d} g$
denotes the Laplace transform of g in the direction d as defined in [Reference Loray5] (see also Section 5.1 of [Reference Balser2]). Thus, the following proposition is obtained from Propriétés 1–2 on pages 41 and 42 of [Reference Loray5].
Proposition 2.5 Let
![]() $\varphi> 0$
and set
$\varphi> 0$
and set
![]() $S:= S(d,\infty ,\varphi )$
. Let
$S:= S(d,\infty ,\varphi )$
. Let
![]() $f:S \longrightarrow \mathbb {C}$
, and assume that for every closed log-subsector
$f:S \longrightarrow \mathbb {C}$
, and assume that for every closed log-subsector
![]() $\overline S_0$
of S, the restriction
$\overline S_0$
of S, the restriction
![]() $f\!\!\upharpoonright _{\overline S_0}$
is log-holomorphic and there exist
$f\!\!\upharpoonright _{\overline S_0}$
is log-holomorphic and there exist
![]() $C,D>0$
such that
$C,D>0$
such that
![]() $|f(w)| \le Ce^{De^{\operatorname {\mathrm {Re}} w}}$
for
$|f(w)| \le Ce^{De^{\operatorname {\mathrm {Re}} w}}$
for
![]() $w \in \overline S_0$
. Then:
$w \in \overline S_0$
. Then:
-
(1) For each
 $\theta \in (0,\varphi )$
, there exists
$\theta \in (0,\varphi )$
, there exists
 $0 < R(\theta ) \le \frac 1D$
such that
$0 < R(\theta ) \le \frac 1D$
such that
 $\mathcal {L}_d f$
has a log-holomorphic extension
$\mathcal {L}_d f$
has a log-holomorphic extension
 $\mathcal {L} f: V(d,R(\theta )) \longrightarrow \mathbb {C}$
.
$\mathcal {L} f: V(d,R(\theta )) \longrightarrow \mathbb {C}$
. -
(2) Let
 $\alpha \ge 0$
, and assume that for every closed log-subsector
$\alpha \ge 0$
, and assume that for every closed log-subsector
 $\overline S_0$
of S, we have
$\overline S_0$
of S, we have
 $|f(w)| = O\left (e^{\alpha \operatorname {\mathrm {Re}} w}\right )$
as
$|f(w)| = O\left (e^{\alpha \operatorname {\mathrm {Re}} w}\right )$
as
 $w \to -\infty $
in
$w \to -\infty $
in
 $\overline S_0$
. Then, in the situation of part (1), for every closed log-subsector
$\overline S_0$
. Then, in the situation of part (1), for every closed log-subsector
 $\overline S_0$
of
$\overline S_0$
of
 $V(d,R(\theta ))$
, we have
$V(d,R(\theta ))$
, we have
 $|\mathcal {L} f(w)| = O\left (e^{\alpha \operatorname {\mathrm {Re}} w}\right )$
as
$|\mathcal {L} f(w)| = O\left (e^{\alpha \operatorname {\mathrm {Re}} w}\right )$
as
 $w \to -\infty $
in
$w \to -\infty $
in
 $\overline S_0$
.
$\overline S_0$
.
In view of the previous proposition, we call the union
![]() $V:=\bigcup _{\theta \in (0,\varphi )}V(d,R(\theta ))$
a log-sectorial domain, and we refer to the common extension
$V:=\bigcup _{\theta \in (0,\varphi )}V(d,R(\theta ))$
a log-sectorial domain, and we refer to the common extension
![]() $\mathcal {L} f:V \longrightarrow \mathbb {C}$
of
$\mathcal {L} f:V \longrightarrow \mathbb {C}$
of
![]() $\mathcal {L}_0 f$
of
$\mathcal {L}_0 f$
of
![]() $\mathcal {L}_0 f$
given by Proposition 2.5 as the log-Laplace transform of f. Note that, in practice, we shall usually restrict the domain of
$\mathcal {L}_0 f$
given by Proposition 2.5 as the log-Laplace transform of f. Note that, in practice, we shall usually restrict the domain of
![]() $\mathcal {L} f$
to a sector
$\mathcal {L} f$
to a sector
![]() $S\left (d,\log R,\theta +\frac \pi 2\right )$
for suitable
$S\left (d,\log R,\theta +\frac \pi 2\right )$
for suitable
![]() $\theta \in (0,\varphi )$
and
$\theta \in (0,\varphi )$
and
![]() $R>0$
on which it is log-holomorphic.
$R>0$
on which it is log-holomorphic.
For
![]() $f:S(d,{\frak r},\theta ) \longrightarrow \mathbb {C}$
as in Section 2.2.1, Proposition 2.2 implies that
$f:S(d,{\frak r},\theta ) \longrightarrow \mathbb {C}$
as in Section 2.2.1, Proposition 2.2 implies that
![]() $\mathcal {L}(\mathcal {B} f)$
is defined and log-holomorphic on every closed log-subsector
$\mathcal {L}(\mathcal {B} f)$
is defined and log-holomorphic on every closed log-subsector
![]() $\overline S_0$
of
$\overline S_0$
of
![]() $S(d,{\frak r},\theta )\cap V$
. Indeed,
$S(d,{\frak r},\theta )\cap V$
. Indeed,
![]() $\mathcal {L}$
is the inverse operator to
$\mathcal {L}$
is the inverse operator to
![]() $\mathcal {B}$
(see page 44 of [Reference Loray5]).
$\mathcal {B}$
(see page 44 of [Reference Loray5]).
Proposition 2.6 For
![]() $f:S(d,{\frak r},\theta ) \longrightarrow \mathbb {C}$
as in Section 2.2.1, we have
$f:S(d,{\frak r},\theta ) \longrightarrow \mathbb {C}$
as in Section 2.2.1, we have
![]() $\mathcal {L}(\mathcal {B} f) = f$
on
$\mathcal {L}(\mathcal {B} f) = f$
on
![]() $S(d,{\frak r},\theta )\cap V$
.
$S(d,{\frak r},\theta )\cap V$
.
Example 2.7 For
![]() $\alpha \in \mathbb {R}$
, we set
$\alpha \in \mathbb {R}$
, we set
![]() $p_{\alpha }(w):= e^{\alpha w}$
. Then, for
$p_{\alpha }(w):= e^{\alpha w}$
. Then, for
![]() $w \in \mathbb {R}$
, we have
$w \in \mathbb {R}$
, we have
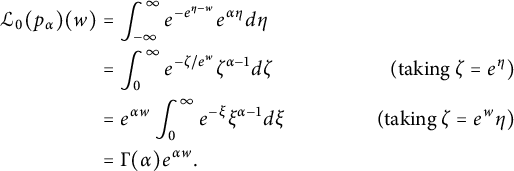 $$ \begin{align*} \mathcal{L}_0(p_{\alpha})(w) &= \int_{-\infty}^{\infty} e^{-e^{\eta-w}} e^{\alpha\eta} d\eta & \\ &=\int_0^{\infty} e^{-\zeta/e^w} \zeta^{\alpha-1} d\zeta &\text{(taking } \zeta = e^{\eta}) \\ &= e^{\alpha w} \int_0^{\infty} e^{-\xi} \xi^{\alpha-1} d\xi &\text{(taking } \zeta = e^w\eta) \\ &= \Gamma(\alpha) e^{\alpha w}. \end{align*} $$
$$ \begin{align*} \mathcal{L}_0(p_{\alpha})(w) &= \int_{-\infty}^{\infty} e^{-e^{\eta-w}} e^{\alpha\eta} d\eta & \\ &=\int_0^{\infty} e^{-\zeta/e^w} \zeta^{\alpha-1} d\zeta &\text{(taking } \zeta = e^{\eta}) \\ &= e^{\alpha w} \int_0^{\infty} e^{-\xi} \xi^{\alpha-1} d\xi &\text{(taking } \zeta = e^w\eta) \\ &= \Gamma(\alpha) e^{\alpha w}. \end{align*} $$
It follows, by analytic continuation and Proposition 2.5, that
![]() $\mathcal {L}(p_{\alpha }) = \Gamma (\alpha ) p_{\alpha }$
, and hence by Proposition 2.6 that
$\mathcal {L}(p_{\alpha }) = \Gamma (\alpha ) p_{\alpha }$
, and hence by Proposition 2.6 that
![]() $\mathcal {B}(p_{\alpha }) = \frac {p_{\alpha }}{\Gamma (\alpha )}$
.
$\mathcal {B}(p_{\alpha }) = \frac {p_{\alpha }}{\Gamma (\alpha )}$
.
2.3 Generalized power series with complex coefficients
Let now
![]() $F(X) = \sum _{\alpha \ge 0} a_{\alpha } X^{\alpha } \ \in \mathbb {C}\left \{X^*\right \}$
be such that
$F(X) = \sum _{\alpha \ge 0} a_{\alpha } X^{\alpha } \ \in \mathbb {C}\left \{X^*\right \}$
be such that
![]() $\|F\|_r < \infty $
, for some
$\|F\|_r < \infty $
, for some
![]() $r>0$
. We explain here how such a series defines a log-holomorphic function on some log-disk. Denoting by
$r>0$
. We explain here how such a series defines a log-holomorphic function on some log-disk. Denoting by
![]() $\log $
the principle branch of the logarithm on
$\log $
the principle branch of the logarithm on
![]() $\mathbb {C} \setminus (-\infty ,0]$
, we set
$\mathbb {C} \setminus (-\infty ,0]$
, we set
Then, for
![]() $w \in S(0,\infty ,\pi )$
, we have that
$w \in S(0,\infty ,\pi )$
, we have that
in other words, the entire function
![]() $p_{\alpha }$
extends the function
$p_{\alpha }$
extends the function
![]() $w \mapsto (e^w)^{\alpha }: S(0,\infty ,\pi ) \longrightarrow \mathbb {C}$
. Since
$w \mapsto (e^w)^{\alpha }: S(0,\infty ,\pi ) \longrightarrow \mathbb {C}$
. Since
![]() $|p_{\alpha }(w)| = e^{\alpha \operatorname {\mathrm {Re}} w}$
, it follows that the series
$|p_{\alpha }(w)| = e^{\alpha \operatorname {\mathrm {Re}} w}$
, it follows that the series
converges absolutely and uniformly, for
![]() $w \in H(\log r)$
. By Weierstrass’s theorem, the function
$w \in H(\log r)$
. By Weierstrass’s theorem, the function
![]() $\overline F:H(\log r)\setminus \{-\infty \} \longrightarrow \mathbb {C}$
is holomorphic, and by the previous remarks, we have
$\overline F:H(\log r)\setminus \{-\infty \} \longrightarrow \mathbb {C}$
is holomorphic, and by the previous remarks, we have
It follows, in particular, from [Reference Van den Dries and Speissegger11, Lemma 5.5] that
![]() $\overline F$
extends continuously to
$\overline F$
extends continuously to
![]() $-\infty $
and satisfies
$-\infty $
and satisfies
![]() $\overline F(-\infty ) = F(0)$
. Below, we refer to the log-holomorphic function
$\overline F(-\infty ) = F(0)$
. Below, we refer to the log-holomorphic function
![]() $\overline F$
thus defined on
$\overline F$
thus defined on
![]() $H(\log r)$
as the log-sum of
$H(\log r)$
as the log-sum of
![]() $F(X)$
.
$F(X)$
.
2.3.1 Logarithmic Borel transform of convergent generalized power series with natural support
We again fix
![]() $F(X) = \sum a_{\alpha } X^{\alpha } \in \mathbb {C}\left \{X^*\right \}$
and
$F(X) = \sum a_{\alpha } X^{\alpha } \in \mathbb {C}\left \{X^*\right \}$
and
![]() $r> 0$
such that
$r> 0$
such that
![]() $\|F\|_r < \infty .$
In addition, we assume that the support of
$\|F\|_r < \infty .$
In addition, we assume that the support of
![]() $F(X)$
—a subset of
$F(X)$
—a subset of
![]() $[0,\infty )$
by definition—is natural. Since
$[0,\infty )$
by definition—is natural. Since
![]() $\overline F$
is defined on
$\overline F$
is defined on
![]() $H(\log r) = S(0,\log r,\infty )$
, we obtain from Proposition 2.2 that its log-Borel transform
$H(\log r) = S(0,\log r,\infty )$
, we obtain from Proposition 2.2 that its log-Borel transform
![]() $\mathcal {B}\overline F$
is log-holomorphic on
$\mathcal {B}\overline F$
is log-holomorphic on
![]() $\overline {\mathbb {C}}$
.
$\overline {\mathbb {C}}$
.
In view of Example 2.7, we set
called the formal Borel transform of
![]() $F(X)$
. Note that, for
$F(X)$
. Note that, for
![]() $\sigma>0$
, we have by Binet’s second formula (see [Reference Whittaker and Watson14]) that
$\sigma>0$
, we have by Binet’s second formula (see [Reference Whittaker and Watson14]) that
Thus, for any
![]() $\sigma> 0$
, we have that
$\sigma> 0$
, we have that
 $$ \begin{align} \|\mathcal{B} F\|_{\sigma} = \sum \frac{(\sigma/r)^{\alpha}}{\Gamma(\alpha)} |a_{\alpha}| r^{\alpha} \le C(\sigma/r) \|F\|_{r}. \end{align} $$
$$ \begin{align} \|\mathcal{B} F\|_{\sigma} = \sum \frac{(\sigma/r)^{\alpha}}{\Gamma(\alpha)} |a_{\alpha}| r^{\alpha} \le C(\sigma/r) \|F\|_{r}. \end{align} $$
Since F has natural support, the sum is finite for all
![]() $\sigma $
; so the series
$\sigma $
; so the series
![]() $\mathcal {B} F(X)$
has infinite radius of convergence, and its log-sum
$\mathcal {B} F(X)$
has infinite radius of convergence, and its log-sum
![]() $\overline {\mathcal {B} F}$
is also log-holomorphic on
$\overline {\mathcal {B} F}$
is also log-holomorphic on
![]() $\overline {\mathbb {C}}$
. In summary:
$\overline {\mathbb {C}}$
. In summary:
Proposition 2.8 Let
![]() $F(X)$
be a convergent generalized power series with natural support. Then both
$F(X)$
be a convergent generalized power series with natural support. Then both
![]() $\mathcal {B}\overline {F}$
and
$\mathcal {B}\overline {F}$
and
![]() $\overline {\mathcal {B} F}$
are log-holomorphic on
$\overline {\mathcal {B} F}$
are log-holomorphic on
![]() $\overline {\mathbb {C}}$
, and we have
$\overline {\mathbb {C}}$
, and we have
![]() $\overline {\mathcal {B} F} = \mathcal {B}\overline F$
.
$\overline {\mathcal {B} F} = \mathcal {B}\overline F$
.
Proof Since
![]() $F(X)$
has natural support, we write
$F(X)$
has natural support, we write
![]() $F(X)= \sum _{n=0}^N a_n r^{\alpha _n}$
with either
$F(X)= \sum _{n=0}^N a_n r^{\alpha _n}$
with either
![]() $N \in \mathbb {N}$
, or
$N \in \mathbb {N}$
, or
![]() $N=\infty $
and
$N=\infty $
and
![]() $\lim _{n \to \infty } \alpha _n = +\infty $
. For
$\lim _{n \to \infty } \alpha _n = +\infty $
. For
![]() $w \in \mathbb {C}$
, let
$w \in \mathbb {C}$
, let
![]() $\overline S$
be the closure of the
$\overline S$
be the closure of the
![]() $\log $
-sector
$\log $
-sector
![]() $S(\operatorname {\mathrm {Im}} w,\log r,\pi )$
, and define
$S(\operatorname {\mathrm {Im}} w,\log r,\pi )$
, and define
![]() $K:\partial \overline S \longrightarrow \mathbb {C}$
by
$K:\partial \overline S \longrightarrow \mathbb {C}$
by
For
![]() $n \in \mathbb {N}$
with
$n \in \mathbb {N}$
with
![]() $n \le N$
, let
$n \le N$
, let
![]() $u_n: \partial \overline S \longrightarrow \mathbb {C}$
be defined by
$u_n: \partial \overline S \longrightarrow \mathbb {C}$
be defined by
where
![]() $p_{\alpha _n}$
is defined as in Example 2.7. Proceeding as in the proof of Lemma 2.3, we obtain a
$p_{\alpha _n}$
is defined as in Example 2.7. Proceeding as in the proof of Lemma 2.3, we obtain a
![]() $C>0$
such that
$C>0$
such that
Since
![]() $\|F\|_r < \infty $
, it follows that
$\|F\|_r < \infty $
, it follows that
![]() $\sum _n \int _{\partial \overline S} |u_n(\eta )| d\eta < \infty $
. If follows from analysis that the functions
$\sum _n \int _{\partial \overline S} |u_n(\eta )| d\eta < \infty $
. If follows from analysis that the functions
![]() $u_n$
, for each n, as well as
$u_n$
, for each n, as well as
![]() $\sum _n u_n$
and
$\sum _n u_n$
and
![]() $\sum _n |u_n|$
are integrable on
$\sum _n |u_n|$
are integrable on
![]() $\partial \overline S$
and that
$\partial \overline S$
and that
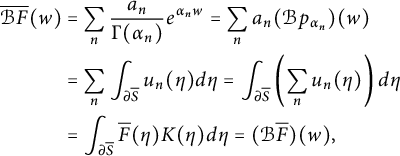 $$ \begin{align*} \overline{\mathcal{B} F}(w) &= \sum_n \frac{a_n}{\Gamma(\alpha_n)} e^{\alpha_n w}= \sum_n a_n (\mathcal{B} p_{\alpha_n})(w) \\ &= \sum_n \int_{\partial \overline S} u_n(\eta) d\eta = \int_{\partial \overline S} \left(\sum_n u_n(\eta)\right) d\eta \\ &= \int_{\partial \overline S} \overline F(\eta) K(\eta) d\eta = (\mathcal{B} \overline F)(w), \end{align*} $$
$$ \begin{align*} \overline{\mathcal{B} F}(w) &= \sum_n \frac{a_n}{\Gamma(\alpha_n)} e^{\alpha_n w}= \sum_n a_n (\mathcal{B} p_{\alpha_n})(w) \\ &= \sum_n \int_{\partial \overline S} u_n(\eta) d\eta = \int_{\partial \overline S} \left(\sum_n u_n(\eta)\right) d\eta \\ &= \int_{\partial \overline S} \overline F(\eta) K(\eta) d\eta = (\mathcal{B} \overline F)(w), \end{align*} $$
as claimed.
2.4 Generalized multisummable functions
We now define generalized multisummable functions inspired by Tougeron’s characterization of multisummable functions [Reference Tougeron9] and by their presentation in [Reference Van den Dries and Speissegger12]. However, while it was possible in [Reference Van den Dries and Speissegger12] to refer to the existing literature for summability, it is not the case in our setting. More precisely, our aim is to show a quasianalyticity result for our functions analogous to that in [Reference Van den Dries and Speissegger12, Proposition 2.18]. To this end, we need to introduce suitable Borel and Laplace transforms adapted to the generalized multisummable framework (see Section 2.5). The presentation turns out to be more readable in this setting by replacing the usual “Gevrey order” k by
![]() $1/k$
. This leads to the following definitions.
$1/k$
. This leads to the following definitions.
For
![]() $R,k \ge 0$
,
$R,k \ge 0$
,
![]() $\theta>\pi /2$
and
$\theta>\pi /2$
and
![]() $p \in \mathbb {N}$
, we set
$p \in \mathbb {N}$
, we set
Let
![]() $K \subseteq [0,\infty )$
be a nonempty finite set and
$K \subseteq [0,\infty )$
be a nonempty finite set and
![]() $r> 1$
(note that the situation studied in [Reference Van den Dries and Speissegger12] corresponds, in the current notation, to
$r> 1$
(note that the situation studied in [Reference Van den Dries and Speissegger12] corresponds, in the current notation, to
![]() $\pi /2<\theta <\pi $
and
$\pi /2<\theta <\pi $
and
![]() $K\subseteq [0,1]$
, in order to avoid dealing with the logarithmic chart), and set
$K\subseteq [0,1]$
, in order to avoid dealing with the logarithmic chart), and set
Moreover, we fix a natural set
![]() $\Delta \subseteq [0,\infty )$
and set
$\Delta \subseteq [0,\infty )$
and set
![]() $\tau := (K,R,r,\theta ,\Delta )$
(note that
$\tau := (K,R,r,\theta ,\Delta )$
(note that
![]() $\Delta = \mathbb {N}$
in [Reference Van den Dries and Speissegger12]). We define
$\Delta = \mathbb {N}$
in [Reference Van den Dries and Speissegger12]). We define
and, for
![]() $p \in \mathbb {N}$
,
$p \in \mathbb {N}$
,
and
Remark 2.9 If
![]() $0 \in K$
and
$0 \in K$
and
![]() $K' := K \setminus \{0\}$
is nonempty, then
$K' := K \setminus \{0\}$
is nonempty, then
![]() $S^{\tau } = S^{\tau '}$
and
$S^{\tau } = S^{\tau '}$
and
![]() $S^{\tau }_p = S^{\tau '}_p$
for all p, where
$S^{\tau }_p = S^{\tau '}_p$
for all p, where
![]() $\tau ' = (K',R,r,\theta ,\Delta )$
.
$\tau ' = (K',R,r,\theta ,\Delta )$
.
Definition 2.10 For each
![]() $p \in \mathbb {N}$
, let
$p \in \mathbb {N}$
, let
![]() $f_p:S^{\tau }_p \longrightarrow \mathbb {C}$
be log-holomorphic, that is, there exists a log-domain
$f_p:S^{\tau }_p \longrightarrow \mathbb {C}$
be log-holomorphic, that is, there exists a log-domain
![]() $D_p \supseteq S^{\tau }_p$
and a log-holomorphic
$D_p \supseteq S^{\tau }_p$
and a log-holomorphic
![]() $g_p:D_p \longrightarrow \mathbb {C}$
such that
$g_p:D_p \longrightarrow \mathbb {C}$
such that
![]() $f_p = g_p\!\!\upharpoonright _{S^{\tau }_p}$
. Moreover, we assume that there are generalized power series
$f_p = g_p\!\!\upharpoonright _{S^{\tau }_p}$
. Moreover, we assume that there are generalized power series
![]() $F_p(X) \in \mathbb {C}\left \{X^*\right \}$
with support contained in
$F_p(X) \in \mathbb {C}\left \{X^*\right \}$
with support contained in
![]() $\Delta $
such that
$\Delta $
such that
![]() $\|F_p\|_{\rho ^{\tau }_p} < \infty $
and
$\|F_p\|_{\rho ^{\tau }_p} < \infty $
and
Assume also that
where
![]() $\|f_p\|_{S^{\tau }_p}:= \sup _{w \in S^{\tau }_p} |f_p(w)|$
denotes the sup norm of
$\|f_p\|_{S^{\tau }_p}:= \sup _{w \in S^{\tau }_p} |f_p(w)|$
denotes the sup norm of
![]() $f_p$
on
$f_p$
on
![]() $S^{\tau }_p$
. The second of these finiteness assumptions implies that
$S^{\tau }_p$
. The second of these finiteness assumptions implies that
![]() $\sum _p f_p$
converges uniformly on
$\sum _p f_p$
converges uniformly on
![]() $S^{\tau } \setminus \{-\infty \}$
to a holomorphic function
$S^{\tau } \setminus \{-\infty \}$
to a holomorphic function
![]() $g:S^{\tau } \setminus \{-\infty \} \longrightarrow \mathbb {C}$
, while the first implies that this g extends continuously to
$g:S^{\tau } \setminus \{-\infty \} \longrightarrow \mathbb {C}$
, while the first implies that this g extends continuously to
![]() $-\infty $
, so that the resulting
$-\infty $
, so that the resulting
![]() $g:S^{\tau } \longrightarrow \mathbb {C}$
is log-holomorphic. From now on, we abbreviate this situation by writing
$g:S^{\tau } \longrightarrow \mathbb {C}$
is log-holomorphic. From now on, we abbreviate this situation by writing
Thus, for a log-holomorphic function
![]() $f:S^{\tau } \longrightarrow \mathbb {C}$
, we set
$f:S^{\tau } \longrightarrow \mathbb {C}$
, we set
 $$ \begin{align*}\|f\|_{\tau}:= \inf\left\{\max\left\{\sum_p \|F_p\|_{\rho^{\tau}_p}r^p,\sum_p \|f_p\|_{S^{\tau}_p} r^p\right\}:\ f =_{\tau} \sum_p f_p\right\} \in [0,\infty];\end{align*} $$
$$ \begin{align*}\|f\|_{\tau}:= \inf\left\{\max\left\{\sum_p \|F_p\|_{\rho^{\tau}_p}r^p,\sum_p \|f_p\|_{S^{\tau}_p} r^p\right\}:\ f =_{\tau} \sum_p f_p\right\} \in [0,\infty];\end{align*} $$
note that
![]() $\|f\|_{\tau } < \infty $
if and only if there exists a sequence
$\|f\|_{\tau } < \infty $
if and only if there exists a sequence
![]() $f_p$
such that
$f_p$
such that
![]() $f =_{\tau } \sum _p f_p$
.
$f =_{\tau } \sum _p f_p$
.
We set
It is immediate from this definition that
![]() $\mathcal {G}_{\tau }$
is a
$\mathcal {G}_{\tau }$
is a
![]() $\mathbb {C}$
-vector space under pointwise addition; moreover, if
$\mathbb {C}$
-vector space under pointwise addition; moreover, if
![]() $\Delta $
is closed under addition, then
$\Delta $
is closed under addition, then
![]() $\mathcal {G}_{\tau }$
is closed under multiplication of functions, making
$\mathcal {G}_{\tau }$
is closed under multiplication of functions, making
![]() $\mathcal {G}_{\tau }$
a
$\mathcal {G}_{\tau }$
a
![]() $\mathbb {C}$
-algebra.
$\mathbb {C}$
-algebra.
Convention 2.11 If
![]() $\Delta $
is natural, then so is its closure under addition; so we assume from now on that
$\Delta $
is natural, then so is its closure under addition; so we assume from now on that
![]() $\Delta $
is closed under addition.
$\Delta $
is closed under addition.
Example 2.12 Tougeron’s characterization implies that, if
![]() $M_K < 2$
(where
$M_K < 2$
(where
![]() $M_K$
is as in (2.2)) and
$M_K$
is as in (2.2)) and
![]() $f:S\left (0,R,{\theta M_K}\right ) \longrightarrow \mathbb {C}$
is such that
$f:S\left (0,R,{\theta M_K}\right ) \longrightarrow \mathbb {C}$
is such that
![]() $f \circ \log $
is K-summable, then
$f \circ \log $
is K-summable, then
![]() $f \in \mathcal {G}_{\tau }$
, where
$f \in \mathcal {G}_{\tau }$
, where
![]() $\tau = (K,R, r, \theta ,\mathbb {N})$
for some
$\tau = (K,R, r, \theta ,\mathbb {N})$
for some
![]() $r> 1$
.
$r> 1$
.
Definition 2.13
-
(1) We call a function f generalized multisummable in the real direction if
 $f \in \mathcal {G}_{\tau }$
for some
$f \in \mathcal {G}_{\tau }$
for some
 $\tau $
as above.
$\tau $
as above. -
(2) We call a function f generalized K-summable in the real direction if there exist
 $R'>0$
,
$R'>0$
,
 $r'>1$
,
$r'>1$
,
 $\theta '> \pi /2$
and a natural
$\theta '> \pi /2$
and a natural
 $\Delta ' \subseteq [0,\infty )$
such that
$\Delta ' \subseteq [0,\infty )$
such that
 $f \in \mathcal {G}_{\tau '}$
with
$f \in \mathcal {G}_{\tau '}$
with
 $\tau ' = (K,R',r',\theta ',\Delta ')$
.
$\tau ' = (K,R',r',\theta ',\Delta ')$
.
Example 2.14 In terms of Example 2.12, Tougeron’s characterization of multisummable functions implies that if f is K-summable in the positive real direction, then
![]() $f \circ \exp $
is generalized K-summable in the real direction.
$f \circ \exp $
is generalized K-summable in the real direction.
Let
![]() $f \in \mathcal {G}_{\tau }$
with associated functions
$f \in \mathcal {G}_{\tau }$
with associated functions
![]() $f_p$
and series
$f_p$
and series
![]() $F_p$
be as in Definition 2.10 such that
$F_p$
be as in Definition 2.10 such that
![]() $\sum _p \|F_p\|_{\rho ^{\tau }_p}r^p < 2\|f\|_{\tau }$
and
$\sum _p \|F_p\|_{\rho ^{\tau }_p}r^p < 2\|f\|_{\tau }$
and
![]() $\sum _p \|f_p\|_{S^{\tau }_p} r^p < 2\|f\|_{\tau }$
. In Proposition 2.16, we show that f has asymptotic expansion
$\sum _p \|f_p\|_{S^{\tau }_p} r^p < 2\|f\|_{\tau }$
. In Proposition 2.16, we show that f has asymptotic expansion
![]() $F(e^w)$
at
$F(e^w)$
at
![]() $-\infty $
, for the generalized power series
$-\infty $
, for the generalized power series
![]() $F(X)$
with support contained in
$F(X)$
with support contained in
![]() $\Delta $
(and hence natural), defined in (2.3). To do so, say
$\Delta $
(and hence natural), defined in (2.3). To do so, say
![]() $F_p(X) = \sum a_{p,\alpha } X^{\alpha }$
for each p, where each
$F_p(X) = \sum a_{p,\alpha } X^{\alpha }$
for each p, where each
![]() $a_{p,\alpha } \in \mathbb {R}$
, and write
$a_{p,\alpha } \in \mathbb {R}$
, and write
![]() $\rho _p$
for
$\rho _p$
for
![]() $\rho _p^{\tau }$
. Then, for each p and
$\rho _p^{\tau }$
. Then, for each p and
![]() $\alpha $
, and for arbitrary
$\alpha $
, and for arbitrary
![]() $s \in (1,r)$
, we have
$s \in (1,r)$
, we have
 $$ \begin{align*}|a_{p,\alpha}| \le \frac{\|F_p\|_{\rho_p}}{\rho_p^{\alpha}} = \frac{\|F_p\|_{\rho_p}}{R^{\alpha}} (p+1)^{\alpha M_K} \le \frac{\|F_p\|_{\rho_p}}{R^{\alpha}} s^p (p+1)^{\alpha M_K}.\end{align*} $$
$$ \begin{align*}|a_{p,\alpha}| \le \frac{\|F_p\|_{\rho_p}}{\rho_p^{\alpha}} = \frac{\|F_p\|_{\rho_p}}{R^{\alpha}} (p+1)^{\alpha M_K} \le \frac{\|F_p\|_{\rho_p}}{R^{\alpha}} s^p (p+1)^{\alpha M_K}.\end{align*} $$
Therefore, for each
![]() $\alpha $
and arbitrary
$\alpha $
and arbitrary
![]() $s \in (1,r)$
, we get
$s \in (1,r)$
, we get
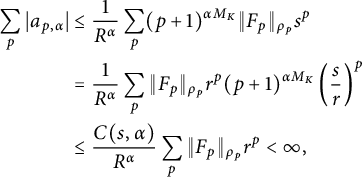 $$ \begin{align*} \sum_p |a_{p,\alpha}| &\le \frac1{R^{\alpha}} \sum_p (p+1)^{\alpha M_K} \|F_p\|_{\rho_p} s^p \\ &= \frac1{R^{\alpha}} \sum_p \|F_p\|_{\rho_p} r^p (p+1)^{\alpha M_K} \left(\frac sr\right)^p \\ &\le \frac{C(s,\alpha)}{R^{\alpha}} \sum_p \|F_p\|_{\rho_p} r^p < \infty, \end{align*} $$
$$ \begin{align*} \sum_p |a_{p,\alpha}| &\le \frac1{R^{\alpha}} \sum_p (p+1)^{\alpha M_K} \|F_p\|_{\rho_p} s^p \\ &= \frac1{R^{\alpha}} \sum_p \|F_p\|_{\rho_p} r^p (p+1)^{\alpha M_K} \left(\frac sr\right)^p \\ &\le \frac{C(s,\alpha)}{R^{\alpha}} \sum_p \|F_p\|_{\rho_p} r^p < \infty, \end{align*} $$
where
![]() $C(s,\alpha ):= \max _p (p+1)^{\alpha M_K} (s/r)^p < \infty $
. So we set
$C(s,\alpha ):= \max _p (p+1)^{\alpha M_K} (s/r)^p < \infty $
. So we set
for each
![]() $\alpha $
, and
$\alpha $
, and
which has support contained in
![]() $\Delta $
.
$\Delta $
.
Lemma 2.15 There exist
![]() $D,E> 0$
such that for all
$D,E> 0$
such that for all
![]() $p \in \mathbb {N}$
and all
$p \in \mathbb {N}$
and all
![]() $\beta \ge 0$
, we have
$\beta \ge 0$
, we have
 $$ \begin{align*}\left|f_p(w) - \sum_{\alpha < \beta} a_{\alpha,p} e^{\alpha w}\right| \le CD^{\beta} \frac{(p+1)^{\beta M_K}}{r^p} \left|e^{\beta w}\right| \quad\text{for } w \in S_p^{\tau}.\end{align*} $$
$$ \begin{align*}\left|f_p(w) - \sum_{\alpha < \beta} a_{\alpha,p} e^{\alpha w}\right| \le CD^{\beta} \frac{(p+1)^{\beta M_K}}{r^p} \left|e^{\beta w}\right| \quad\text{for } w \in S_p^{\tau}.\end{align*} $$
Proof Fix
![]() $p \in \mathbb {N}$
and
$p \in \mathbb {N}$
and
![]() $\beta \ge 0$
, and let
$\beta \ge 0$
, and let
![]() $w \in S_p^{\tau }$
. We distinguish two cases:
$w \in S_p^{\tau }$
. We distinguish two cases:
Case 1:
![]() $\operatorname {\mathrm {Re}} w < \log \rho _p$
. Then
$\operatorname {\mathrm {Re}} w < \log \rho _p$
. Then
 $$ \begin{align*} \left|f_p(w) - \sum_{\alpha < \beta} a_{p,\alpha} e^{\alpha w}\right| &= \left|\sum_{\alpha \ge \beta} a_{p,\alpha} e^{\alpha w}\right| \\ &\le \left|e^{\beta w}\right| \sum_{\alpha \ge \beta} |a_{p,\alpha}| \left|e^{(\alpha-\beta) w}\right| \\ &\le \left|e^{\beta w}\right| \sum_{\alpha \ge \beta} |a_{p,\alpha}| (\rho_p)^{\alpha-\beta} \\ &\le \frac{\left|e^{\beta w}\right|}{(\rho_p)^{\beta}} \|F_p\|_{\rho_p} \\ &\le 2\left|e^{\beta w}\right| \frac{(p+1)^{\beta M_K}}{R^{\beta} r^p} \|f\|_{\tau}, \end{align*} $$
$$ \begin{align*} \left|f_p(w) - \sum_{\alpha < \beta} a_{p,\alpha} e^{\alpha w}\right| &= \left|\sum_{\alpha \ge \beta} a_{p,\alpha} e^{\alpha w}\right| \\ &\le \left|e^{\beta w}\right| \sum_{\alpha \ge \beta} |a_{p,\alpha}| \left|e^{(\alpha-\beta) w}\right| \\ &\le \left|e^{\beta w}\right| \sum_{\alpha \ge \beta} |a_{p,\alpha}| (\rho_p)^{\alpha-\beta} \\ &\le \frac{\left|e^{\beta w}\right|}{(\rho_p)^{\beta}} \|F_p\|_{\rho_p} \\ &\le 2\left|e^{\beta w}\right| \frac{(p+1)^{\beta M_K}}{R^{\beta} r^p} \|f\|_{\tau}, \end{align*} $$
which proves the estimate in this case.
Case 2:
![]() $\operatorname {\mathrm {Re}} w \ge \log \rho _p$
. Then
$\operatorname {\mathrm {Re}} w \ge \log \rho _p$
. Then
 $$ \begin{align*} \left|f_p(w) - \sum_{\alpha < \beta} a_{p,\alpha} e^{\alpha w}\right| \le \left|f_p(w)\right| + \sum_{\alpha < \beta} |a_{p,\alpha}|\left|e^{\alpha w}\right|, \end{align*} $$
$$ \begin{align*} \left|f_p(w) - \sum_{\alpha < \beta} a_{p,\alpha} e^{\alpha w}\right| \le \left|f_p(w)\right| + \sum_{\alpha < \beta} |a_{p,\alpha}|\left|e^{\alpha w}\right|, \end{align*} $$
so we further split up the estimate:
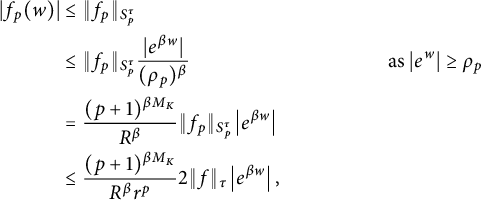 $$ \begin{align*} |f_p(w)| &\le \|f_p\|_{S_p^{\tau}} \\ &\le \|f_p\|_{S_p^{\tau}} \frac{|e^{\beta w}|}{(\rho_p)^{\beta}} &\text{as } |e^{w}| \ge \rho_p \\ &= \frac{(p+1)^{\beta M_K}}{R^{\beta}} \|f_p\|_{S_p^{\tau}} \left|e^{\beta w}\right| \\ &\le \frac{(p+1)^{\beta M_K}}{R^{\beta} r^p} 2\|f\|_{\tau} \left|e^{\beta w}\right|, \end{align*} $$
$$ \begin{align*} |f_p(w)| &\le \|f_p\|_{S_p^{\tau}} \\ &\le \|f_p\|_{S_p^{\tau}} \frac{|e^{\beta w}|}{(\rho_p)^{\beta}} &\text{as } |e^{w}| \ge \rho_p \\ &= \frac{(p+1)^{\beta M_K}}{R^{\beta}} \|f_p\|_{S_p^{\tau}} \left|e^{\beta w}\right| \\ &\le \frac{(p+1)^{\beta M_K}}{R^{\beta} r^p} 2\|f\|_{\tau} \left|e^{\beta w}\right|, \end{align*} $$
while
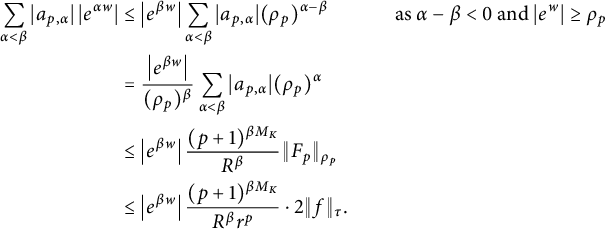 $$ \begin{align*} \sum_{\alpha < \beta} |a_{p,\alpha}| \left|e^{\alpha w}\right| &\le \left|e^{\beta w}\right| \sum_{\alpha < \beta} |a_{p,\alpha}| (\rho_p)^{\alpha-\beta} &\text{as } \alpha-\beta < 0 \text{ and } |e^{ w}| \ge \rho_p \\ &= \frac{\left|e^{\beta w}\right|}{(\rho_p)^{\beta}} \sum_{\alpha < \beta} |a_{p,\alpha}|(\rho_p)^{\alpha} \\ &\le \left|e^{\beta w}\right| \frac{(p+1)^{\beta M_K}}{R^{\beta}} \|F_p\|_{\rho_p} \\ &\le \left|e^{\beta w}\right| \frac{(p+1)^{\beta M_K}}{R^{\beta} r^p} \cdot 2\|f\|_{\tau}. \end{align*} $$
$$ \begin{align*} \sum_{\alpha < \beta} |a_{p,\alpha}| \left|e^{\alpha w}\right| &\le \left|e^{\beta w}\right| \sum_{\alpha < \beta} |a_{p,\alpha}| (\rho_p)^{\alpha-\beta} &\text{as } \alpha-\beta < 0 \text{ and } |e^{ w}| \ge \rho_p \\ &= \frac{\left|e^{\beta w}\right|}{(\rho_p)^{\beta}} \sum_{\alpha < \beta} |a_{p,\alpha}|(\rho_p)^{\alpha} \\ &\le \left|e^{\beta w}\right| \frac{(p+1)^{\beta M_K}}{R^{\beta}} \|F_p\|_{\rho_p} \\ &\le \left|e^{\beta w}\right| \frac{(p+1)^{\beta M_K}}{R^{\beta} r^p} \cdot 2\|f\|_{\tau}. \end{align*} $$
This completes the proof of Case 2 and therefore of the lemma.
Proposition 2.16 (Gevrey estimates)
For every closed log-subsector
![]() $\overline S_0$
of
$\overline S_0$
of
![]() $S^{\tau }$
, there exist
$S^{\tau }$
, there exist
![]() $D,E>0$
such that, for each
$D,E>0$
such that, for each
![]() $\beta \ge 0$
,
$\beta \ge 0$
,
 $$ \begin{align*}\left|f(w) - \sum_{\alpha < \beta} a_{\alpha} e^{\alpha w}\right| \le DE^{\beta} \Gamma\left(\beta M_K\right) \left|e^{\beta w}\right| \quad\text{for } w \in \overline S_0.\end{align*} $$
$$ \begin{align*}\left|f(w) - \sum_{\alpha < \beta} a_{\alpha} e^{\alpha w}\right| \le DE^{\beta} \Gamma\left(\beta M_K\right) \left|e^{\beta w}\right| \quad\text{for } w \in \overline S_0.\end{align*} $$
Proof Let
![]() $D,E>0$
be obtained from Lemma 2.15, and let
$D,E>0$
be obtained from Lemma 2.15, and let
![]() $\beta \ge 0$
. Since
$\beta \ge 0$
. Since
![]() $\Delta \cap [0,\beta )$
is finite we have, for
$\Delta \cap [0,\beta )$
is finite we have, for
![]() $w \in \overline S_0$
,
$w \in \overline S_0$
,
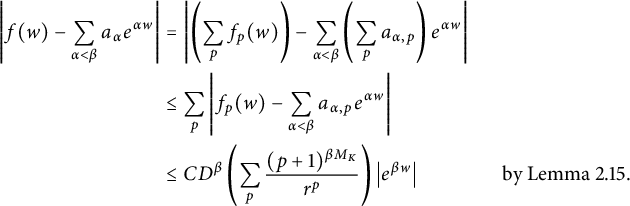 $$ \begin{align*} \left|f(w) - \sum_{\alpha < \beta} a_{\alpha} e^{\alpha w}\right| &= \left|\left(\sum_p f_p(w)\right) - \sum_{\alpha < \beta} \left(\sum_p a_{\alpha,p}\right) e^{\alpha w}\right| \\ &\le \sum_p \left|f_p(w) - \sum_{\alpha < \beta} a_{\alpha,p} e^{\alpha w}\right| \\ &\le CD^{\beta} \left(\sum_p \frac{(p+1)^{\beta M_K}}{r^p}\right) \left|e^{\beta w}\right| &\text{by Lemma 2.15}. \end{align*} $$
$$ \begin{align*} \left|f(w) - \sum_{\alpha < \beta} a_{\alpha} e^{\alpha w}\right| &= \left|\left(\sum_p f_p(w)\right) - \sum_{\alpha < \beta} \left(\sum_p a_{\alpha,p}\right) e^{\alpha w}\right| \\ &\le \sum_p \left|f_p(w) - \sum_{\alpha < \beta} a_{\alpha,p} e^{\alpha w}\right| \\ &\le CD^{\beta} \left(\sum_p \frac{(p+1)^{\beta M_K}}{r^p}\right) \left|e^{\beta w}\right| &\text{by Lemma 2.15}. \end{align*} $$
Since
![]() $\sum _p \frac {(p+1)^{\beta M_K}}{r^p} \le C'(D')^{\beta } \beta ^{\beta M_K}$
for some
$\sum _p \frac {(p+1)^{\beta M_K}}{r^p} \le C'(D')^{\beta } \beta ^{\beta M_K}$
for some
![]() $C',D'>0$
(see, for instance, the proof of [Reference Van den Dries and Speissegger12, Lemma 2.6]), the proposition now follows from Stirling’s formula for
$C',D'>0$
(see, for instance, the proof of [Reference Van den Dries and Speissegger12, Lemma 2.6]), the proposition now follows from Stirling’s formula for
![]() $\Gamma $
(see [Reference Artin1]).
$\Gamma $
(see [Reference Artin1]).
Proposition 2.16 implies that
![]() $F(e^w)$
is an asymptotic expansion of f at
$F(e^w)$
is an asymptotic expansion of f at
![]() $-\infty $
; hence, it is uniquely determined by f (and is, in particular, independent of the particular sequence
$-\infty $
; hence, it is uniquely determined by f (and is, in particular, independent of the particular sequence
![]() $\{f_p\}$
), and we write
$\{f_p\}$
), and we write
![]() $Tf(X) := F(X)$
. The map
$Tf(X) := F(X)$
. The map
![]() $T:\mathcal {G}_{\tau } \longrightarrow \mathbb {C}\left [\!\left [X^*\right ]\!\right ]$
is a
$T:\mathcal {G}_{\tau } \longrightarrow \mathbb {C}\left [\!\left [X^*\right ]\!\right ]$
is a
![]() $\mathbb {C}$
-algebra homomorphism.
$\mathbb {C}$
-algebra homomorphism.
Remark 2.17 Standard methods for proving topological completeness of function spaces (see, e.g., Rudin’s Real and Complex Analysis) show that the normed algebra
![]() $\left (\mathcal {G}_{\tau },\|\cdot \|_{\tau }\right )$
is complete; we leave the details to the reader.
$\left (\mathcal {G}_{\tau },\|\cdot \|_{\tau }\right )$
is complete; we leave the details to the reader.
Example 2.18 Assume that
![]() $K=\{0\}$
. If
$K=\{0\}$
. If
![]() $f \in \mathcal {G}_{\tau }$
, then
$f \in \mathcal {G}_{\tau }$
, then
![]() $Tf$
converges,
$Tf$
converges,
![]() $\|Tf\|_R < \infty $
and
$\|Tf\|_R < \infty $
and
![]() $f = \overline {Tf}$
. To see this, let
$f = \overline {Tf}$
. To see this, let
![]() $f =_{\tau } \sum _p f_p$
with
$f =_{\tau } \sum _p f_p$
with
![]() $Tf_p = \sum _{\alpha } a_{p,\alpha } X^{\alpha }$
for each p; then
$Tf_p = \sum _{\alpha } a_{p,\alpha } X^{\alpha }$
for each p; then
![]() $Tf = \sum _{\alpha } a_{\alpha }X^{\alpha }$
with
$Tf = \sum _{\alpha } a_{\alpha }X^{\alpha }$
with
![]() $a_{\alpha } = \sum _p a_{p,\alpha }$
as above. Since
$a_{\alpha } = \sum _p a_{p,\alpha }$
as above. Since
![]() $\rho _p^{\tau } = R$
for each p, the assumption
$\rho _p^{\tau } = R$
for each p, the assumption
![]() $\sum _p \|Tf_p\|_R r^p < \infty $
implies that
$\sum _p \|Tf_p\|_R r^p < \infty $
implies that
![]() $\sum _{p,\alpha } |a_{p,\alpha }| R^{\alpha } < \infty $
. This implies that the family
$\sum _{p,\alpha } |a_{p,\alpha }| R^{\alpha } < \infty $
. This implies that the family
![]() $\{a_{p,\alpha } e^{\alpha w}\}$
is summable on
$\{a_{p,\alpha } e^{\alpha w}\}$
is summable on
![]() $\operatorname {\mathrm {cl}} H(\log R)$
; in particular, the order of summation can be changed. Thus, we have for
$\operatorname {\mathrm {cl}} H(\log R)$
; in particular, the order of summation can be changed. Thus, we have for
![]() $w \in \operatorname {\mathrm {cl}} H(\log R)$
that
$w \in \operatorname {\mathrm {cl}} H(\log R)$
that
 $$ \begin{align*} f(w) = \sum_p f_p(w) = \sum_p \sum_{\alpha} a_{p,\alpha} e^{\alpha w} = \sum_{\alpha} \left(\sum_p a_{p,\alpha}\right) e^{\alpha w} = \sum_{\alpha} a_{\alpha} e^{\alpha w} = \overline{Tf}(w), \end{align*} $$
$$ \begin{align*} f(w) = \sum_p f_p(w) = \sum_p \sum_{\alpha} a_{p,\alpha} e^{\alpha w} = \sum_{\alpha} \left(\sum_p a_{p,\alpha}\right) e^{\alpha w} = \sum_{\alpha} a_{\alpha} e^{\alpha w} = \overline{Tf}(w), \end{align*} $$
as claimed.
Conversely, if
![]() $F \in \mathbb {R}\left [\!\left [X^*\right ]\!\right ]$
has natural support and satisfies
$F \in \mathbb {R}\left [\!\left [X^*\right ]\!\right ]$
has natural support and satisfies
![]() $\|F\|_R < \infty $
, then (the appropriate restriction of) the function
$\|F\|_R < \infty $
, then (the appropriate restriction of) the function
![]() $\overline {F}$
belongs to
$\overline {F}$
belongs to
![]() $\mathcal {G}_{\tau }$
, where
$\mathcal {G}_{\tau }$
, where
![]() $\tau = \left (K,R, r, \theta ,\Delta \right )$
with K, r,
$\tau = \left (K,R, r, \theta ,\Delta \right )$
with K, r,
![]() $\theta $
and
$\theta $
and
![]() $\Delta \supseteq \operatorname {\mathrm {supp}}(F)$
arbitrary. To see this, simply take
$\Delta \supseteq \operatorname {\mathrm {supp}}(F)$
arbitrary. To see this, simply take
![]() $f_0 := \overline F$
and
$f_0 := \overline F$
and
![]() $f_p:= 0$
, for
$f_p:= 0$
, for
![]() $p> 0$
.
$p> 0$
.
Remark 2.19 Assume that
![]() $0 \in K$
and
$0 \in K$
and
![]() $|K|>1$
, and set
$|K|>1$
, and set
![]() $K':= K \setminus \{0\}$
and
$K':= K \setminus \{0\}$
and
![]() $\tau ':= (K',R,r,\theta ,\Delta )$
. Then, by Remark 2.9, we have
$\tau ':= (K',R,r,\theta ,\Delta )$
. Then, by Remark 2.9, we have
![]() $\mathcal {G}_{\tau } = \mathcal {G}_{\tau '}$
.
$\mathcal {G}_{\tau } = \mathcal {G}_{\tau '}$
.
Recall from 2.2 that
![]() $\mu _K= \min K \in [0,\infty )$
. If
$\mu _K= \min K \in [0,\infty )$
. If
![]() $\mu _K \ge 1$
, then
$\mu _K \ge 1$
, then
![]() ${\theta \mu _K}> \frac \pi 2$
, so by Proposition 2.2, the function
${\theta \mu _K}> \frac \pi 2$
, so by Proposition 2.2, the function
![]() $\mathcal {B} f$
is defined on the sector
$\mathcal {B} f$
is defined on the sector
![]() $S\left (0, \infty , {\theta \mu _K} - \frac \pi 2\right )$
. The next proposition explains in more detail what happens when we apply the Borel transform to f.
$S\left (0, \infty , {\theta \mu _K} - \frac \pi 2\right )$
. The next proposition explains in more detail what happens when we apply the Borel transform to f.
Proposition 2.20 Let
![]() $f \in \mathcal {G}_{\tau }$
, and assume that
$f \in \mathcal {G}_{\tau }$
, and assume that
![]() $\mu _K \ge 1$
(in particular,
$\mu _K \ge 1$
(in particular,
![]() $\mathcal {B} f$
is well defined). Let
$\mathcal {B} f$
is well defined). Let
![]() $R' \in (0,R)$
and
$R' \in (0,R)$
and
![]() $r' \in (1,r)$
be such that
$r' \in (1,r)$
be such that
![]() $R' \le \frac Re \log (r/r')$
, and set
$R' \le \frac Re \log (r/r')$
, and set
![]() $K':= \left \{k-1:\ k \in K\right \}$
and
$K':= \left \{k-1:\ k \in K\right \}$
and
![]() $\tau ':= \left (K',R',r',\theta ,\Delta \right )$
. Then
$\tau ':= \left (K',R',r',\theta ,\Delta \right )$
. Then
![]() $\mathcal {B} f$
belongs to
$\mathcal {B} f$
belongs to
![]() $\mathcal {G}_{\tau '}$
and satisfies
$\mathcal {G}_{\tau '}$
and satisfies
![]() $T(\mathcal {B} f) = \mathcal {B}(Tf)$
.
$T(\mathcal {B} f) = \mathcal {B}(Tf)$
.
Proof For
![]() $p \in \mathbb {N}$
, we set
$p \in \mathbb {N}$
, we set
![]() $\rho _p:= \rho _p^{\tau }$
and
$\rho _p:= \rho _p^{\tau }$
and
![]() $\sigma _p := \rho _p^{\tau '}$
. Then, for
$\sigma _p := \rho _p^{\tau '}$
. Then, for
![]() $\alpha \ge 0$
, we have
$\alpha \ge 0$
, we have
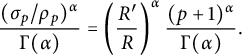 $$ \begin{align*}\frac{(\sigma_p/\rho_p)^{\alpha}}{\Gamma(\alpha)} = \left(\frac {R'}R\right)^{\alpha} \frac{(p+1)^{\alpha}}{\Gamma(\alpha)}.\end{align*} $$
$$ \begin{align*}\frac{(\sigma_p/\rho_p)^{\alpha}}{\Gamma(\alpha)} = \left(\frac {R'}R\right)^{\alpha} \frac{(p+1)^{\alpha}}{\Gamma(\alpha)}.\end{align*} $$
Claim: There exists
![]() $C = C(r,r',R,R')> 0$
such that
$C = C(r,r',R,R')> 0$
such that
 $$ \begin{align*}\left(\frac {R'}R\right)^{\alpha}\frac{(p+1)^{\alpha}}{\Gamma(\alpha)}\left(\frac {r'}r\right)^p \le C,\end{align*} $$
$$ \begin{align*}\left(\frac {R'}R\right)^{\alpha}\frac{(p+1)^{\alpha}}{\Gamma(\alpha)}\left(\frac {r'}r\right)^p \le C,\end{align*} $$
for all
![]() $p \in \mathbb {N}$
and
$p \in \mathbb {N}$
and
![]() $\alpha \ge 0$
.
$\alpha \ge 0$
.
To see the claim, note that the function
![]() $x \mapsto f_{\alpha }(x):= (x+1)^{\alpha } \left (\frac {r'}r\right )^x$
attains its maximum at
$x \mapsto f_{\alpha }(x):= (x+1)^{\alpha } \left (\frac {r'}r\right )^x$
attains its maximum at
![]() $x_{\alpha } = \frac \alpha {\log (r/r')}-1$
; so this maximum is
$x_{\alpha } = \frac \alpha {\log (r/r')}-1$
; so this maximum is
with
![]() $A:= \frac {(r'/r)^{1/\log (r/r')}}{\log (r/r')} = (e\log (r/r'))^{-1}$
independent of
$A:= \frac {(r'/r)^{1/\log (r/r')}}{\log (r/r')} = (e\log (r/r'))^{-1}$
independent of
![]() $\alpha $
. From Binet’s second formula, we get a constant
$\alpha $
. From Binet’s second formula, we get a constant
![]() $C">0$
such that, for all
$C">0$
such that, for all
![]() $\alpha \ge 0$
,
$\alpha \ge 0$
,
where
![]() $\phi (x)$
is the Stirling function. Since the latter is bounded at
$\phi (x)$
is the Stirling function. Since the latter is bounded at
![]() $\infty $
, there is a constant
$\infty $
, there is a constant
![]() $C'>0$
such that
$C'>0$
such that
Therefore,
 $$ \begin{align*} \left(\frac {R'}R\right)^{\alpha} (p+1)^{\alpha}\left(\frac {r'}r\right)^p \le \frac r{r'} \left(\frac {R'}R\right)^{\alpha} A^{\alpha} \alpha^{\alpha} \le C' \frac r{r'} \left(\frac {R'}R K e^2\right)^{\alpha} \Gamma(\alpha) \le C \Gamma(\alpha), \end{align*} $$
$$ \begin{align*} \left(\frac {R'}R\right)^{\alpha} (p+1)^{\alpha}\left(\frac {r'}r\right)^p \le \frac r{r'} \left(\frac {R'}R\right)^{\alpha} A^{\alpha} \alpha^{\alpha} \le C' \frac r{r'} \left(\frac {R'}R K e^2\right)^{\alpha} \Gamma(\alpha) \le C \Gamma(\alpha), \end{align*} $$
where
![]() $C:= C'\frac r{r'}$
, because our assumptions on
$C:= C'\frac r{r'}$
, because our assumptions on
![]() $r'$
and
$r'$
and
![]() $R'$
imply that
$R'$
imply that
![]() $Ae^2 \le \frac R{R'}$
. This proves the claim.
$Ae^2 \le \frac R{R'}$
. This proves the claim.
It follows from the claim that
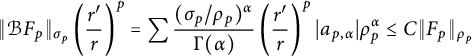 $$ \begin{align} \|\mathcal{B} F_p\|_{\sigma_p}\left(\frac {r'}r\right)^p = \sum \frac{(\sigma_p/\rho_p)^{\alpha}}{\Gamma(\alpha)}\left(\frac {r'}r\right)^p |a_{p,\alpha}|\rho_p^{\alpha} \le C\|F_p\|_{\rho_p} \end{align} $$
$$ \begin{align} \|\mathcal{B} F_p\|_{\sigma_p}\left(\frac {r'}r\right)^p = \sum \frac{(\sigma_p/\rho_p)^{\alpha}}{\Gamma(\alpha)}\left(\frac {r'}r\right)^p |a_{p,\alpha}|\rho_p^{\alpha} \le C\|F_p\|_{\rho_p} \end{align} $$
for each
![]() $p \in \mathbb {N}$
, so that
$p \in \mathbb {N}$
, so that
Next, we show
![]() $\sum \|\mathcal {B} f_p\|_{S^{\tau '}_p} (r')^p < \infty $
. If
$\sum \|\mathcal {B} f_p\|_{S^{\tau '}_p} (r')^p < \infty $
. If
![]() $|K| = \mu _K = 1$
, then (2.5) also proves that
$|K| = \mu _K = 1$
, then (2.5) also proves that
![]() $\mathcal {B} F$
is convergent and that
$\mathcal {B} F$
is convergent and that
![]() $\sum \|\mathcal {B} f_p\|_{H(\log R')} (r')^p < \infty $
; this settles the assertion in this case.
$\sum \|\mathcal {B} f_p\|_{H(\log R')} (r')^p < \infty $
; this settles the assertion in this case.
So assume that
![]() $\mu _K> 1$
or
$\mu _K> 1$
or
![]() $|K|> 1$
. By (2.5), it suffices to show that
$|K|> 1$
. By (2.5), it suffices to show that
![]() $\sum \|\mathcal {B} f_p\|_{S^{\tau '}} (r')^p < \infty $
and, for
$\sum \|\mathcal {B} f_p\|_{S^{\tau '}} (r')^p < \infty $
and, for
![]() $k \in K\setminus \{M_K\}$
, that
$k \in K\setminus \{M_K\}$
, that
![]() $\sum \|\mathcal {B} f_p\|_{S^k_p} (r')^p < \infty $
, where we set
$\sum \|\mathcal {B} f_p\|_{S^k_p} (r')^p < \infty $
, where we set
For the first estimate: since
![]() ${\theta (\mu _K-1)}< {\theta \mu _K} - \frac \pi 2$
, Lemma 2.3 shows that
${\theta (\mu _K-1)}< {\theta \mu _K} - \frac \pi 2$
, Lemma 2.3 shows that
![]() $\left \|\mathcal {B} f_p\right \|_{S^{\tau '}} \le C\left \|f_p\right \|_{S^{\tau }}$
, for some constant
$\left \|\mathcal {B} f_p\right \|_{S^{\tau '}} \le C\left \|f_p\right \|_{S^{\tau }}$
, for some constant
![]() $C>0$
that only depends on
$C>0$
that only depends on
![]() $\theta $
and
$\theta $
and
![]() $\theta '$
.
$\theta '$
.
For the second estimate: fix
![]() $k \in K\setminus \{M_K\}$
and set
$k \in K\setminus \{M_K\}$
and set
![]() $\rho ^k_p:= \rho _p^{R,k}$
,
$\rho ^k_p:= \rho _p^{R,k}$
,
![]() $k' := \min (K \setminus [\mu _K,k])$
and
$k' := \min (K \setminus [\mu _K,k])$
and
![]() $T^k_p:= S\left (0,\log \rho ^k_p,{\theta k'}\right )$
. Since
$T^k_p:= S\left (0,\log \rho ^k_p,{\theta k'}\right )$
. Since
![]() ${\theta (k'-1)} < {\theta k'} - \frac \pi 2$
, Lemma 1.3 shows that
${\theta (k'-1)} < {\theta k'} - \frac \pi 2$
, Lemma 1.3 shows that
 $$ \begin{align*}\left\|\mathcal{B} f_p\right\|_{S^k_p} \le C \left\|f_p\right\|_{T^k_p} e^{\sigma^k_p / \rho^k_p} \frac{\sigma^k_p}{\rho^k_p} = C\|f_p\|_{T^k_p} \left(e^{R'/R}\right)^{1+p} \frac{R'}R (1+p),\end{align*} $$
$$ \begin{align*}\left\|\mathcal{B} f_p\right\|_{S^k_p} \le C \left\|f_p\right\|_{T^k_p} e^{\sigma^k_p / \rho^k_p} \frac{\sigma^k_p}{\rho^k_p} = C\|f_p\|_{T^k_p} \left(e^{R'/R}\right)^{1+p} \frac{R'}R (1+p),\end{align*} $$
for some constant
![]() $C>0$
independent of p. Now note that our assumptions on
$C>0$
independent of p. Now note that our assumptions on
![]() $r'$
and
$r'$
and
![]() $R'$
imply that
$R'$
imply that
![]() $e^{R'/R}\cdot \frac {r'}r < 1$
; therefore,
$e^{R'/R}\cdot \frac {r'}r < 1$
; therefore,
![]() $D:= \max _p (1+p) \left (e^{R'/R}\right )^{(1+p)}\left (\frac {r'}r\right )^p < \infty $
. It follows that
$D:= \max _p (1+p) \left (e^{R'/R}\right )^{(1+p)}\left (\frac {r'}r\right )^p < \infty $
. It follows that
as claimed.
Finally, it remains to show that
![]() $\mathcal {B} f =_{\tau '} \sum _p \mathcal {B} f_p$
and
$\mathcal {B} f =_{\tau '} \sum _p \mathcal {B} f_p$
and
![]() $T(\mathcal {B} f) = \mathcal {B}(Tf)$
: set
$T(\mathcal {B} f) = \mathcal {B}(Tf)$
: set
![]() $g:= \sum _p \mathcal {B} f_p$
. The above estimates show that
$g:= \sum _p \mathcal {B} f_p$
. The above estimates show that
![]() $g \in \mathcal {G}_{\tau '}$
with
$g \in \mathcal {G}_{\tau '}$
with
![]() $Tg = \sum _p \mathcal {B} F_p = \mathcal {B}(Tf)$
, so we need to show that
$Tg = \sum _p \mathcal {B} F_p = \mathcal {B}(Tf)$
, so we need to show that
![]() $\mathcal {B} f = g$
. Since
$\mathcal {B} f = g$
. Since
![]() $f = \sum _p f_p$
uniformly in
$f = \sum _p f_p$
uniformly in
![]() $S^{\tau }$
, it follows from integration theory that
$S^{\tau }$
, it follows from integration theory that
![]() $\mathcal {B} f = \mathcal {B}\left (\sum _p f_p\right ) = \sum _p \mathcal {B} f_p = g$
, as required.
$\mathcal {B} f = \mathcal {B}\left (\sum _p f_p\right ) = \sum _p \mathcal {B} f_p = g$
, as required.
For later purposes, we note the following special case of Proposition 2.20:
Corollary 2.21 Let
![]() $f \in \mathcal {G}_{\tau }$
, and assume that
$f \in \mathcal {G}_{\tau }$
, and assume that
![]() $|K| \ge 1$
and
$|K| \ge 1$
and
![]() $\mu _K = 1$
. Let
$\mu _K = 1$
. Let
![]() $R' \in (0,R)$
and
$R' \in (0,R)$
and
![]() $r' \in (1,r)$
be such that
$r' \in (1,r)$
be such that
![]() $R' \le \frac Re \log (r/r')$
, and set
$R' \le \frac Re \log (r/r')$
, and set
![]() $K':= \left \{k-1:\ k \in K\right \}$
and
$K':= \left \{k-1:\ k \in K\right \}$
and
![]() $\tau ':= \left (K',R',r',\theta ,\Delta \right )$
. Then
$\tau ':= \left (K',R',r',\theta ,\Delta \right )$
. Then
![]() $\mathcal {B} f$
belongs to
$\mathcal {B} f$
belongs to
![]() $\mathcal {G}_{\tau '}$
and satisfies
$\mathcal {G}_{\tau '}$
and satisfies
![]() $T(\mathcal {B} f) = \mathcal {B}(Tf)$
.
$T(\mathcal {B} f) = \mathcal {B}(Tf)$
.
2.5 Ramified logarithmic transforms
Let
![]() $\lambda>0$
. In the classical situation, the ramified Borel transform
$\lambda>0$
. In the classical situation, the ramified Borel transform
![]() $\mathcal {B}^{\lambda } f$
of a function f is obtained from
$\mathcal {B}^{\lambda } f$
of a function f is obtained from
![]() $\mathcal {B} f$
by the change of variables
$\mathcal {B} f$
by the change of variables
![]() $z \mapsto z^{\lambda }$
. In the logarithmic chart, this means that
$z \mapsto z^{\lambda }$
. In the logarithmic chart, this means that
![]() $\mathcal {B}^{\lambda } f$
is obtained from
$\mathcal {B}^{\lambda } f$
is obtained from
![]() $\mathcal {B} f$
by the change of variables
$\mathcal {B} f$
by the change of variables
![]() $w \mapsto \lambda w$
.
$w \mapsto \lambda w$
.
2.5.1 Ramified logarithmic Borel transform
Let
![]() $d,{\frak r} \in \mathbb {R}$
and
$d,{\frak r} \in \mathbb {R}$
and
![]() $\theta> \pi $
, and write
$\theta> \pi $
, and write
![]() $S = S(d,{\frak r},\theta \lambda )$
. We denote by
$S = S(d,{\frak r},\theta \lambda )$
. We denote by
![]() $\mathbf {m}_{\lambda }:\mathbb {C} \longrightarrow \mathbb {C}$
the logarithmic ramification map defined by
$\mathbf {m}_{\lambda }:\mathbb {C} \longrightarrow \mathbb {C}$
the logarithmic ramification map defined by
![]() $\mathbf {m}_{\lambda }(w):= \lambda w$
.
$\mathbf {m}_{\lambda }(w):= \lambda w$
.
Let
![]() $f:S \longrightarrow \mathbb {C}$
be such that
$f:S \longrightarrow \mathbb {C}$
be such that
![]() $f\!\!\upharpoonright _{\widetilde S}$
is bounded and log-holomorphic, for every closed log-subsector
$f\!\!\upharpoonright _{\widetilde S}$
is bounded and log-holomorphic, for every closed log-subsector
![]() $\widetilde S$
of S. Then the map
$\widetilde S$
of S. Then the map
![]() $f \circ \mathbf {m}_{\lambda }: S(d/\lambda ,{\frak r}/\lambda ,\theta ) \longrightarrow \mathbb {C}$
has logarithmic Borel transform
$f \circ \mathbf {m}_{\lambda }: S(d/\lambda ,{\frak r}/\lambda ,\theta ) \longrightarrow \mathbb {C}$
has logarithmic Borel transform
![]() $\mathcal {B}(f \circ \mathbf {m}_{\lambda }):S\left (d/\lambda ,\infty ,\theta -\frac \pi 2\right ) \longrightarrow \mathbb {C}$
. We define the log-
$\mathcal {B}(f \circ \mathbf {m}_{\lambda }):S\left (d/\lambda ,\infty ,\theta -\frac \pi 2\right ) \longrightarrow \mathbb {C}$
. We define the log-
![]() $\lambda $
-Borel transform
$\lambda $
-Borel transform
![]() $\mathcal {B}^{\lambda } f: S\left (d,\infty ,{\theta \lambda } - \frac {\pi \lambda }{2}\right ) \longrightarrow \mathbb {C}$
of f by
$\mathcal {B}^{\lambda } f: S\left (d,\infty ,{\theta \lambda } - \frac {\pi \lambda }{2}\right ) \longrightarrow \mathbb {C}$
of f by
We immediately obtain the following from Proposition 2.2 and Example 2.7.
Corollary 2.22 Let
![]() $f:S \longrightarrow \mathbb {C}$
be such that
$f:S \longrightarrow \mathbb {C}$
be such that
![]() $f\!\!\upharpoonright _{\widetilde S}$
is bounded and log-holomorphic, for every closed log-subsector
$f\!\!\upharpoonright _{\widetilde S}$
is bounded and log-holomorphic, for every closed log-subsector
![]() $\widetilde S$
of S, and set
$\widetilde S$
of S, and set
![]() $S':= S\left (d,\infty ,{\theta \lambda } -\frac {\pi \lambda }{2}\right )$
.
$S':= S\left (d,\infty ,{\theta \lambda } -\frac {\pi \lambda }{2}\right )$
.
-
(1) For every closed log-subsector
 $\widetilde S$
of
$\widetilde S$
of
 $S'$
, the function
$S'$
, the function
 $(\mathcal {B}^{\lambda } f)\!\!\upharpoonright _{\widetilde S}$
is log-holomorphic and there exist
$(\mathcal {B}^{\lambda } f)\!\!\upharpoonright _{\widetilde S}$
is log-holomorphic and there exist
 $C,M>0$
such that
$C,M>0$
such that  $$ \begin{align*}|(\mathcal{B}^{\lambda} f)(w)| \le C e^{De^{(\operatorname{\mathrm{Re}} w)/\lambda}} \quad\text{for } w \in \widetilde S.\end{align*} $$
$$ \begin{align*}|(\mathcal{B}^{\lambda} f)(w)| \le C e^{De^{(\operatorname{\mathrm{Re}} w)/\lambda}} \quad\text{for } w \in \widetilde S.\end{align*} $$
-
(2) Let
 $\alpha \ge 0$
, and assume that for every closed log-subsector
$\alpha \ge 0$
, and assume that for every closed log-subsector
 $\widetilde S$
of S, we have
$\widetilde S$
of S, we have
 $|f(w)| = O\left (e^{\alpha \operatorname {\mathrm {Re}} w}\right )$
as
$|f(w)| = O\left (e^{\alpha \operatorname {\mathrm {Re}} w}\right )$
as
 $w \to -\infty $
in
$w \to -\infty $
in
 $\widetilde S$
. Then, for every closed log-subsector
$\widetilde S$
. Then, for every closed log-subsector
 $\widetilde S$
of
$\widetilde S$
of
 $S'$
, we have
$S'$
, we have
 $|(\mathcal {B}^{\lambda } f)(w)| = O\left (e^{\alpha \operatorname {\mathrm {Re}} w}\right )$
as
$|(\mathcal {B}^{\lambda } f)(w)| = O\left (e^{\alpha \operatorname {\mathrm {Re}} w}\right )$
as
 $w \to -\infty $
in
$w \to -\infty $
in
 $\widetilde S$
.
$\widetilde S$
. -
(3) For
 $\alpha \ge 0$
, we have
$\alpha \ge 0$
, we have
 $\mathcal {B}^{\lambda } p_{\alpha } = \frac {p_{\alpha }}{\Gamma (\alpha \lambda )}$
.
$\mathcal {B}^{\lambda } p_{\alpha } = \frac {p_{\alpha }}{\Gamma (\alpha \lambda )}$
.
2.5.2 Ramified logarithmic Laplace transform
Let
![]() $\varphi> 0$
and set
$\varphi> 0$
and set
![]() $S:= S(d,\infty ,\varphi \lambda )$
. Let
$S:= S(d,\infty ,\varphi \lambda )$
. Let
![]() $f:S \longrightarrow \mathbb {C}$
be a function, and assume that for every closed log-subsector
$f:S \longrightarrow \mathbb {C}$
be a function, and assume that for every closed log-subsector
![]() $\widetilde S$
of S, the restriction
$\widetilde S$
of S, the restriction
![]() $f\!\!\upharpoonright _{\widetilde S}$
is log-holomorphic and there exist
$f\!\!\upharpoonright _{\widetilde S}$
is log-holomorphic and there exist
![]() $C,D>0$
such that
$C,D>0$
such that
![]() $|f(w)| \le Ce^{De^{(\operatorname {\mathrm {Re}} w)/\lambda }}$
for
$|f(w)| \le Ce^{De^{(\operatorname {\mathrm {Re}} w)/\lambda }}$
for
![]() $w \in \widetilde S$
.
$w \in \widetilde S$
.
Let also
![]() $\theta \in (0,\varphi )$
; then the map
$\theta \in (0,\varphi )$
; then the map
![]() $f \circ \mathbf {m}_{\lambda }:S\left (d/\lambda ,\infty ,\theta \right ) \longrightarrow \mathbb {C}$
has logarithmic Laplace transform
$f \circ \mathbf {m}_{\lambda }:S\left (d/\lambda ,\infty ,\theta \right ) \longrightarrow \mathbb {C}$
has logarithmic Laplace transform
![]() $\mathcal {L}(f \circ \mathbf {m}_{\lambda }): S\left (d/\lambda ,{\frak r}/\lambda ,\theta + \frac \pi 2\right ) \longrightarrow \mathbb {C}$
, for some
$\mathcal {L}(f \circ \mathbf {m}_{\lambda }): S\left (d/\lambda ,{\frak r}/\lambda ,\theta + \frac \pi 2\right ) \longrightarrow \mathbb {C}$
, for some
![]() ${\frak r} \le \log (D)\lambda $
. We define the log-
${\frak r} \le \log (D)\lambda $
. We define the log-
![]() $\lambda $
-Laplace transform
$\lambda $
-Laplace transform
![]() $\mathcal {L}^{\lambda } f:S\left (d,{\frak r},{\theta \lambda } + \frac {\pi \lambda }{2}\right ) \longrightarrow \mathbb {C}$
of f by
$\mathcal {L}^{\lambda } f:S\left (d,{\frak r},{\theta \lambda } + \frac {\pi \lambda }{2}\right ) \longrightarrow \mathbb {C}$
of f by
We immediately obtain the following from Proposition 2.5 and Example 2.7.
Corollary 2.23 Let
![]() $f:S \longrightarrow \mathbb {C}$
be a function, and assume that for every closed log-subsector
$f:S \longrightarrow \mathbb {C}$
be a function, and assume that for every closed log-subsector
![]() $\widetilde S$
of S, the restriction
$\widetilde S$
of S, the restriction
![]() $f\!\!\upharpoonright _{\widetilde S}$
is log-holomorphic and there exist
$f\!\!\upharpoonright _{\widetilde S}$
is log-holomorphic and there exist
![]() $C,D>0$
such that
$C,D>0$
such that
![]() $|f(w)| \le Ce^{De^{(\operatorname {\mathrm {Re}} w)/\lambda }}$
for
$|f(w)| \le Ce^{De^{(\operatorname {\mathrm {Re}} w)/\lambda }}$
for
![]() $w \in \widetilde S$
. Let also
$w \in \widetilde S$
. Let also
![]() $\theta \in (0,\varphi )$
, and let
$\theta \in (0,\varphi )$
, and let
![]() ${\frak r} \le \log (D)\lambda $
be as above and set
${\frak r} \le \log (D)\lambda $
be as above and set
![]() $S':= S\left (d,{\frak r},{\theta \lambda } + \frac {\pi \lambda }{2}\right )$
.
$S':= S\left (d,{\frak r},{\theta \lambda } + \frac {\pi \lambda }{2}\right )$
.
-
(1) Let
 $\alpha \ge 0$
, and assume that for every closed log-subsector
$\alpha \ge 0$
, and assume that for every closed log-subsector
 $\widetilde S$
contained in S, we have
$\widetilde S$
contained in S, we have
 $|f(w)| = O\left (e^{\alpha \operatorname {\mathrm {Re}} w}\right )$
as
$|f(w)| = O\left (e^{\alpha \operatorname {\mathrm {Re}} w}\right )$
as
 $w \to -\infty $
in
$w \to -\infty $
in
 $\widetilde S$
. Then, for every closed log-subsector
$\widetilde S$
. Then, for every closed log-subsector
 $\widetilde S$
contained in
$\widetilde S$
contained in
 $S'$
, we have
$S'$
, we have
 $|(\mathcal {L}^{\lambda } f)(w)| = O\left (e^{\alpha \operatorname {\mathrm {Re}} w}\right )$
as
$|(\mathcal {L}^{\lambda } f)(w)| = O\left (e^{\alpha \operatorname {\mathrm {Re}} w}\right )$
as
 $w \to -\infty $
in
$w \to -\infty $
in
 $\widetilde S$
.
$\widetilde S$
. -
(2) For
 $\alpha \ge 0$
, we have
$\alpha \ge 0$
, we have
 $\mathcal {L}^{\lambda } p_{\alpha } = \Gamma (\alpha \lambda )p_{\alpha }$
.
$\mathcal {L}^{\lambda } p_{\alpha } = \Gamma (\alpha \lambda )p_{\alpha }$
.
For
![]() $f:S(d,{\frak r},\theta \lambda ) \longrightarrow \mathbb {C}$
as in Section 2.5.1, Corollary 2.22 implies that
$f:S(d,{\frak r},\theta \lambda ) \longrightarrow \mathbb {C}$
as in Section 2.5.1, Corollary 2.22 implies that
![]() $\mathcal {L}^{\lambda }(\mathcal {B}^{\lambda } f)$
is defined and log-holomorphic on every closed log-subsector
$\mathcal {L}^{\lambda }(\mathcal {B}^{\lambda } f)$
is defined and log-holomorphic on every closed log-subsector
![]() $\widetilde S$
contained in
$\widetilde S$
contained in
![]() $S(d,{\frak r},\theta \lambda )$
. From Proposition 2.6, we therefore obtain the following corollary.
$S(d,{\frak r},\theta \lambda )$
. From Proposition 2.6, we therefore obtain the following corollary.
Corollary 2.24 For
![]() $f:S(d,{\frak r},\theta \lambda ) \longrightarrow \mathbb {C}$
as in Section 2.5.1, we have
$f:S(d,{\frak r},\theta \lambda ) \longrightarrow \mathbb {C}$
as in Section 2.5.1, we have
![]() $\mathcal {L}^{\lambda }(\mathcal {B}^{\lambda } f) = f$
.
$\mathcal {L}^{\lambda }(\mathcal {B}^{\lambda } f) = f$
.
2.5.3 Formal Borel and Laplace transforms
Let now
![]() $F(X) = \sum a_{\alpha } X^{\alpha } \in \mathbb {C}\left \{X^*\right \}$
. In view of the above, we define the formal
$F(X) = \sum a_{\alpha } X^{\alpha } \in \mathbb {C}\left \{X^*\right \}$
. In view of the above, we define the formal
![]() $\lambda $
-Borel transform
$\lambda $
-Borel transform
and the formal
![]() $\lambda $
-Laplace transform
$\lambda $
-Laplace transform
We get the following corollary from Proposition 2.8.
Corollary 2.25 Let F be a convergent generalized power series with natural support. Then, both
![]() $\mathcal {B}^{\lambda }\overline F$
and
$\mathcal {B}^{\lambda }\overline F$
and
![]() $\overline {\mathcal {B}^{\lambda } F}$
are log-holomorphic on
$\overline {\mathcal {B}^{\lambda } F}$
are log-holomorphic on
![]() $\overline {\mathbb {C}}$
, and we have
$\overline {\mathbb {C}}$
, and we have
![]() $\mathcal {B}^{\lambda } \overline F = \overline {\mathcal {B}^{\lambda } F}$
.
$\mathcal {B}^{\lambda } \overline F = \overline {\mathcal {B}^{\lambda } F}$
.
2.5.4 Ramified Borel transforms of generalized multisummable functions
Let
![]() $K \subseteq (0,\infty )$
be finite and nonempty and
$K \subseteq (0,\infty )$
be finite and nonempty and
![]() $\lambda \le \mu _K$
, and define
$\lambda \le \mu _K$
, and define
note that
![]() $f \in \mathcal {G}_{\tau }$
if and only if
$f \in \mathcal {G}_{\tau }$
if and only if
![]() $f \circ \mathbf {m}_{\lambda } \in \mathcal {G}_{\tau (\lambda )}$
.
$f \circ \mathbf {m}_{\lambda } \in \mathcal {G}_{\tau (\lambda )}$
.
Let
![]() $f \in \mathcal {G}_{\tau }$
; by Corollary 2.22, taking
$f \in \mathcal {G}_{\tau }$
; by Corollary 2.22, taking
![]() $\theta $
there equal to
$\theta $
there equal to
![]() $\theta \cdot \frac {\mu _K}\lambda $
here, the function
$\theta \cdot \frac {\mu _K}\lambda $
here, the function
![]() $\mathcal {B}^{\lambda } f$
is defined on the log-sector
$\mathcal {B}^{\lambda } f$
is defined on the log-sector
![]() $S\left (0, \infty , {\theta \mu _K} - \frac {\pi \lambda }{2}\right )$
. Thus, we obtain the following corollary from Proposition 2.20 and Corollary 2.21.
$S\left (0, \infty , {\theta \mu _K} - \frac {\pi \lambda }{2}\right )$
. Thus, we obtain the following corollary from Proposition 2.20 and Corollary 2.21.
Corollary 2.26 Let
![]() $f \in \mathcal {G}_{\tau }$
, and assume that
$f \in \mathcal {G}_{\tau }$
, and assume that
![]() $\mu _K \ge \lambda $
(in particular,
$\mu _K \ge \lambda $
(in particular,
![]() $\mathcal {B}^{\lambda } f$
is well defined). Let
$\mathcal {B}^{\lambda } f$
is well defined). Let
![]() $R' \in (0,R)$
and
$R' \in (0,R)$
and
![]() $r' \in (1,r)$
be such that
$r' \in (1,r)$
be such that
![]() $(R')^{1/\lambda } \le \frac {R^{1/\lambda }} e \log (r/r')$
, and set
$(R')^{1/\lambda } \le \frac {R^{1/\lambda }} e \log (r/r')$
, and set
and
![]() $\tau ':= \left (K',R',r',\theta ,\Delta \right )$
. Then
$\tau ':= \left (K',R',r',\theta ,\Delta \right )$
. Then
![]() $\mathcal {B}^{\lambda } f$
belongs to
$\mathcal {B}^{\lambda } f$
belongs to
![]() $\mathcal {G}_{\tau '}$
and satisfies
$\mathcal {G}_{\tau '}$
and satisfies
![]() $T(\mathcal {B}^{\lambda } f) = \mathcal {B}^{\lambda }(Tf)$
.
$T(\mathcal {B}^{\lambda } f) = \mathcal {B}^{\lambda }(Tf)$
.
2.6 Summation and quasianalyticity
Let
![]() $K \subseteq [0,\infty )$
be nonempty and finite, and let
$K \subseteq [0,\infty )$
be nonempty and finite, and let
![]() $R>0$
,
$R>0$
,
![]() $r> 1$
,
$r> 1$
,
![]() $\theta> \pi /2$
, and
$\theta> \pi /2$
, and
![]() $\Delta \subseteq [0,\infty )$
be natural and closed under addition, and set
$\Delta \subseteq [0,\infty )$
be natural and closed under addition, and set
![]() $\tau = (K,R,r,\theta ,\Delta )$
. The goal of this section is to establish the quasianalyticity of the algebra
$\tau = (K,R,r,\theta ,\Delta )$
. The goal of this section is to establish the quasianalyticity of the algebra
![]() $\mathcal {G}_{\tau }$
(Theorem 2.28). The key ingredient is the following summation method.
$\mathcal {G}_{\tau }$
(Theorem 2.28). The key ingredient is the following summation method.
Proposition 2.27 (Summation)
Assume that
![]() $K = \{k_1, \dots , k_l\}$
with
$K = \{k_1, \dots , k_l\}$
with
![]() $0 < k_1 < \cdots < k_l < \infty $
and
$0 < k_1 < \cdots < k_l < \infty $
and
![]() $l \ge 1$
. Let
$l \ge 1$
. Let
![]() $f \in \mathcal {G}_{\tau }$
, and set
$f \in \mathcal {G}_{\tau }$
, and set
![]() $\kappa _1:= k_1$
and
$\kappa _1:= k_1$
and
![]() $\kappa _i:= k_i - k_{i-1}$
for
$\kappa _i:= k_i - k_{i-1}$
for
![]() $i=2, \dots , l$
. Then the series
$i=2, \dots , l$
. Then the series
![]() $\left (\mathcal {B}^{\kappa _1} \circ \cdots \circ \mathcal {B}^{\kappa _{l}}\right )(Tf)$
converges, and we have
$\left (\mathcal {B}^{\kappa _1} \circ \cdots \circ \mathcal {B}^{\kappa _{l}}\right )(Tf)$
converges, and we have
Proof By induction on l. If
![]() $l=1$
, then
$l=1$
, then
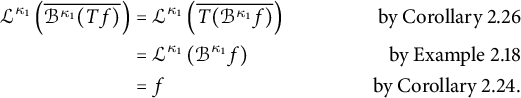 $$ \begin{align*} \mathcal{L}^{\kappa_1} \left(\overline{\mathcal{B}^{\kappa_1}(Tf)}\right) &= \mathcal{L}^{\kappa_1} \left(\overline{T(\mathcal{B}^{\kappa_1} f)}\right) &\text{by Corollary 2.26} \\ &= \mathcal{L}^{\kappa_1} \left(\mathcal{B}^{\kappa_1} f\right) &\text{by Example 2.18} \\ &= f &\text{by Corollary 2.24}. \end{align*} $$
$$ \begin{align*} \mathcal{L}^{\kappa_1} \left(\overline{\mathcal{B}^{\kappa_1}(Tf)}\right) &= \mathcal{L}^{\kappa_1} \left(\overline{T(\mathcal{B}^{\kappa_1} f)}\right) &\text{by Corollary 2.26} \\ &= \mathcal{L}^{\kappa_1} \left(\mathcal{B}^{\kappa_1} f\right) &\text{by Example 2.18} \\ &= f &\text{by Corollary 2.24}. \end{align*} $$
So we assume that
![]() $l>1$
and the proposition holds for lower values of l. Then by Corollary 2.26, the function
$l>1$
and the proposition holds for lower values of l. Then by Corollary 2.26, the function
![]() $\mathcal {B}^{\kappa _1} f$
belongs to
$\mathcal {B}^{\kappa _1} f$
belongs to
![]() $\mathcal {G}_{\tau '}$
and satisfies
$\mathcal {G}_{\tau '}$
and satisfies
![]() $T\left (\mathcal {B}^{\kappa _1} f\right ) = \mathcal {B}^{\kappa _1}(Tf)$
, where
$T\left (\mathcal {B}^{\kappa _1} f\right ) = \mathcal {B}^{\kappa _1}(Tf)$
, where
![]() $\tau ' = (K',R',r',\theta ,\Delta )$
for
$\tau ' = (K',R',r',\theta ,\Delta )$
for
![]() $K' := \left (k_2-k_1, \dots , k_l-k_1\right )$
and some appropriate
$K' := \left (k_2-k_1, \dots , k_l-k_1\right )$
and some appropriate
![]() $R'>0$
and
$R'>0$
and
![]() $r'>1$
. From the inductive hypothesis applied to
$r'>1$
. From the inductive hypothesis applied to
![]() $\mathcal {B}^{k_1} f$
, we get that
$\mathcal {B}^{k_1} f$
, we get that
![]() $\left (\mathcal {B}^{\kappa _l} \circ \cdots \circ \mathcal {B}^{\kappa _{2}}\right ) \left (T\left (\mathcal {B}^{\kappa _1}f\right )\right )$
converges, so that
$\left (\mathcal {B}^{\kappa _l} \circ \cdots \circ \mathcal {B}^{\kappa _{2}}\right ) \left (T\left (\mathcal {B}^{\kappa _1}f\right )\right )$
converges, so that
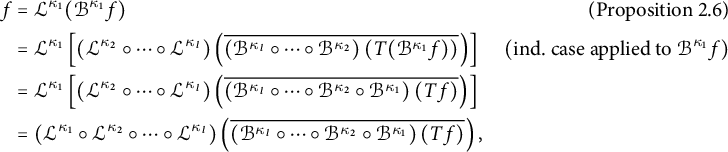 $$ \begin{align*} f &= \mathcal{L}^{\kappa_1}(\mathcal{B}^{\kappa_1} f) &\text{(Proposition 2.6)}\\ &= \mathcal{L}^{\kappa_1}\left[\left(\mathcal{L}^{\kappa_{2}} \circ \cdots \circ \mathcal{L}^{\kappa_l}\right) \left(\overline{\left(\mathcal{B}^{\kappa_l} \circ \cdots \circ \mathcal{B}^{\kappa_{2}}\right) (T(\mathcal{B}^{\kappa_1}f))}\right)\right] &(\text{ind. case applied to } \mathcal{B}^{\kappa_1} f) \\ &= \mathcal{L}^{\kappa_1}\left[\left(\mathcal{L}^{\kappa_{2}} \circ \cdots \circ \mathcal{L}^{\kappa_l}\right)\left(\overline{\left(\mathcal{B}^{\kappa_l} \circ \cdots \circ \mathcal{B}^{\kappa_{2}} \circ \mathcal{B}^{\kappa_1}\right)(Tf)}\right)\right] \\ &= \left(\mathcal{L}^{\kappa_1} \circ \mathcal{L}^{\kappa_{2}} \circ \cdots \circ \mathcal{L}^{\kappa_l}\right) \left(\overline{\left(\mathcal{B}^{\kappa_l} \circ \cdots \circ \mathcal{B}^{\kappa_{2}}\circ \mathcal{B}^{\kappa_1}\right) (Tf)}\right), \end{align*} $$
$$ \begin{align*} f &= \mathcal{L}^{\kappa_1}(\mathcal{B}^{\kappa_1} f) &\text{(Proposition 2.6)}\\ &= \mathcal{L}^{\kappa_1}\left[\left(\mathcal{L}^{\kappa_{2}} \circ \cdots \circ \mathcal{L}^{\kappa_l}\right) \left(\overline{\left(\mathcal{B}^{\kappa_l} \circ \cdots \circ \mathcal{B}^{\kappa_{2}}\right) (T(\mathcal{B}^{\kappa_1}f))}\right)\right] &(\text{ind. case applied to } \mathcal{B}^{\kappa_1} f) \\ &= \mathcal{L}^{\kappa_1}\left[\left(\mathcal{L}^{\kappa_{2}} \circ \cdots \circ \mathcal{L}^{\kappa_l}\right)\left(\overline{\left(\mathcal{B}^{\kappa_l} \circ \cdots \circ \mathcal{B}^{\kappa_{2}} \circ \mathcal{B}^{\kappa_1}\right)(Tf)}\right)\right] \\ &= \left(\mathcal{L}^{\kappa_1} \circ \mathcal{L}^{\kappa_{2}} \circ \cdots \circ \mathcal{L}^{\kappa_l}\right) \left(\overline{\left(\mathcal{B}^{\kappa_l} \circ \cdots \circ \mathcal{B}^{\kappa_{2}}\circ \mathcal{B}^{\kappa_1}\right) (Tf)}\right), \end{align*} $$
as claimed.
Theorem 2.28 (Quasianalyticity)
The map
![]() $T:\mathcal {G}_{\tau } \longrightarrow \mathbb {C}\left [\!\left [X^*\right ]\!\right ]$
is injective.
$T:\mathcal {G}_{\tau } \longrightarrow \mathbb {C}\left [\!\left [X^*\right ]\!\right ]$
is injective.
2.7 Open questions
-
(1) Let f be generalized K-summable in the real direction, where
 $K = (k_1, \dots , k_l)$
. Do there exist generalized
$K = (k_1, \dots , k_l)$
. Do there exist generalized
 $(k_i)$
-summable functions
$(k_i)$
-summable functions
 $g_i$
, for
$g_i$
, for
 $i=1, \dots , l$
, such that
$i=1, \dots , l$
, such that
 $f = g_1 + \cdots + g_l$
?
$f = g_1 + \cdots + g_l$
?This question is motivated by the following: let f be a K-summable function in the positive real direction (in the classical sense, at the origin; to avoid branching, let’s assume
 $k_1> \frac 12$
). Then by Example 2.14, the function
$k_1> \frac 12$
). Then by Example 2.14, the function
 $f \circ \exp $
belongs to
$f \circ \exp $
belongs to
 $\mathcal {G}_{\tau }$
for some
$\mathcal {G}_{\tau }$
for some
 $\tau = (K,R,r,\theta ,\mathbb {N})$
; indeed, Tougeron’s characterization implies that
$\tau = (K,R,r,\theta ,\mathbb {N})$
; indeed, Tougeron’s characterization implies that
 $f \circ \exp =_{\tau } \sum _p f_p \circ \exp $
for functions
$f \circ \exp =_{\tau } \sum _p f_p \circ \exp $
for functions
 $f_p$
that are holomorphic at the origin. This property of being holomorphic at the origin can be used, via Cauchy integration, to show that there exist
$f_p$
that are holomorphic at the origin. This property of being holomorphic at the origin can be used, via Cauchy integration, to show that there exist
 $(k_i)$
-summable functions
$(k_i)$
-summable functions
 $g_i$
, for
$g_i$
, for
 $i=1, \dots , l$
, such that
$i=1, \dots , l$
, such that
 $f = g_1 + \cdots + g_l$
. However, for general
$f = g_1 + \cdots + g_l$
. However, for general
 $g \in \mathcal {G}_{\tau }$
with
$g \in \mathcal {G}_{\tau }$
with
 $g =_{\tau } \sum _p g_p$
, the functions
$g =_{\tau } \sum _p g_p$
, the functions
 $g_p \circ \log $
have essential singularities at the origin, so the Cauchy integration argument used for f does not work for
$g_p \circ \log $
have essential singularities at the origin, so the Cauchy integration argument used for f does not work for
 $g \circ \log $
to write g as a sum of a generalized
$g \circ \log $
to write g as a sum of a generalized
 $(k_i)$
-summable functions.
$(k_i)$
-summable functions. -
(2) From the point of view of multisummability, there is nothing special about the real direction chosen here. (We are only interested in the real direction here, because we are aiming to construct algebras of real functions.) Indeed, one can similarly define generalized K-summable functions in any direction d. However, it is not clear to us what the right generalization of “generalized multisummable” (without specified direction) should be: in the classical case, all multisummable functions are
 $2\pi i$
-periodic in the logarithmic chart, and they are defined to be multisummable if they are multisummable in all but finitely many directions in
$2\pi i$
-periodic in the logarithmic chart, and they are defined to be multisummable if they are multisummable in all but finitely many directions in
 $\mathbb {R}/2\pi \mathbb {Z}$
. In contrast, the logarithmic sums of generalized convergent power series are not
$\mathbb {R}/2\pi \mathbb {Z}$
. In contrast, the logarithmic sums of generalized convergent power series are not
 $ai$
-periodic for any
$ai$
-periodic for any
 $a>0$
in general (take, for instance, the function
$a>0$
in general (take, for instance, the function
 $e^{\alpha w} + e^{\beta w}$
with
$e^{\alpha w} + e^{\beta w}$
with
 $\alpha $
and
$\alpha $
and
 $\beta $
linearly independent over
$\beta $
linearly independent over
 $\mathbb {Q}$
), so generalized multisummable functions in the real direction aren’t either. Possibly, the right way to define “generalized multisummable” would be to look for something like Stokes phenomena in differential equations over (quotients of) convergent generalized power series.
$\mathbb {Q}$
), so generalized multisummable functions in the real direction aren’t either. Possibly, the right way to define “generalized multisummable” would be to look for something like Stokes phenomena in differential equations over (quotients of) convergent generalized power series. -
(3) Is there a Ramis–Sibuya theorem (see [Reference Ramis and Sibuya6]) for ordinary differential equations involving quotients of convergent generalized power series? As hinted at in Question 2, such a theorem might inform the correct definition of the term “generalized multisummable.”
3 Generalized multisummable functions in several variables
The extension of the notion “generalized multisummable in the real direction” to several variables roughly follows the treatment in [Reference Van den Dries and Speissegger12, Section 2] of the notion “multisummable in the positive real direction,” keeping in mind that we work in the logarithmic chart. Since we will not need to work with the ramified Borel and Laplace operators any more, we will revert here to the classical notation for Gevrey orders used in [Reference Van den Dries and Speissegger12].
It will be useful for the definitions below to set
![]() $\operatorname {\mathrm {Im}}(-\infty ) = \arg 0 = 0$
.
$\operatorname {\mathrm {Im}}(-\infty ) = \arg 0 = 0$
.
Notation For
![]() $k = (k_1, \dots , k_m) \in [0, \infty )^m$
and
$k = (k_1, \dots , k_m) \in [0, \infty )^m$
and
![]() $w = (w_1, \dots , w_m) \in \overline {\mathbb {C}}^m$
, we put
$w = (w_1, \dots , w_m) \in \overline {\mathbb {C}}^m$
, we put
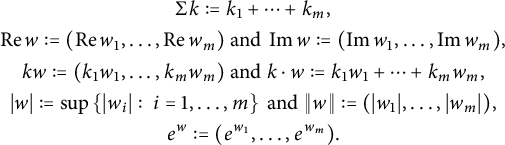 $$ \begin{gather*} \Sigma k := k_1 + \cdots + k_m, \\ \operatorname{\mathrm{Re}} w:= (\operatorname{\mathrm{Re}} w_1, \dots, \operatorname{\mathrm{Re}} w_m) \text{ and } \operatorname{\mathrm{Im}} w:= (\operatorname{\mathrm{Im}} w_1, \dots, \operatorname{\mathrm{Im}} w_m), \\ kw:= (k_1w_1, \dots, k_mw_m) \text{ and } k \cdot w := k_1w_1 + \cdots + k_mw_m, \\ |w| := \sup\left\{|w_i|:\ i=1,\dots, m\right\} \text{ and } \|w\|:= (|w_1|, \dots, |w_m|), \\ e^w := (e^{w_1}, \dots, e^{w_m}). \end{gather*} $$
$$ \begin{gather*} \Sigma k := k_1 + \cdots + k_m, \\ \operatorname{\mathrm{Re}} w:= (\operatorname{\mathrm{Re}} w_1, \dots, \operatorname{\mathrm{Re}} w_m) \text{ and } \operatorname{\mathrm{Im}} w:= (\operatorname{\mathrm{Im}} w_1, \dots, \operatorname{\mathrm{Im}} w_m), \\ kw:= (k_1w_1, \dots, k_mw_m) \text{ and } k \cdot w := k_1w_1 + \cdots + k_mw_m, \\ |w| := \sup\left\{|w_i|:\ i=1,\dots, m\right\} \text{ and } \|w\|:= (|w_1|, \dots, |w_m|), \\ e^w := (e^{w_1}, \dots, e^{w_m}). \end{gather*} $$
Moreover, if
![]() $z = (z_1, \dots , z_m) \in \mathbb {C}^m$
is such that
$z = (z_1, \dots , z_m) \in \mathbb {C}^m$
is such that
![]() $\arg z_i \in (-\pi , \pi )$
for each i, we also set
$\arg z_i \in (-\pi , \pi )$
for each i, we also set
where
![]() $\log $
denotes the standard branch of the logarithm. Finally, if
$\log $
denotes the standard branch of the logarithm. Finally, if
![]() $\alpha \in [0,\infty )^m$
and
$\alpha \in [0,\infty )^m$
and
![]() $r \in (0,\infty )^m$
, we put
$r \in (0,\infty )^m$
, we put
If
![]() $X \subseteq \overline {\mathbb {C}}^m$
and
$X \subseteq \overline {\mathbb {C}}^m$
and
![]() $1\le \nu < m$
, and if
$1\le \nu < m$
, and if
![]() $a \in \mathbb {C}^{\nu }$
and
$a \in \mathbb {C}^{\nu }$
and
![]() $b \in \mathbb {C}^{m-\nu }$
, then we let
$b \in \mathbb {C}^{m-\nu }$
, then we let
be the fibers of X over a and b, respectively.
If
![]() ${\frak r}, \widetilde {\frak r} \in \mathbb {R}^m$
, we write
${\frak r}, \widetilde {\frak r} \in \mathbb {R}^m$
, we write
![]() ${\frak r} \leq \widetilde {\frak r}$
if
${\frak r} \leq \widetilde {\frak r}$
if
![]() ${\frak r}_i \leq \widetilde {{\frak r}_i}$
for each i (and similarly with “
${\frak r}_i \leq \widetilde {{\frak r}_i}$
for each i (and similarly with “
![]() $<$
” in place of “
$<$
” in place of “
![]() $\leq $
”).
$\leq $
”).
3.1 Convergent generalized power series
Let
![]() $X = (X_1, \dots , X_m)$
. Similar to the one-variable case, we denote by
$X = (X_1, \dots , X_m)$
. Similar to the one-variable case, we denote by
![]() $\mathbb {C}\left [\!\left [X^*\right ]\!\right ]$
the set of all generalized power series of the form
$\mathbb {C}\left [\!\left [X^*\right ]\!\right ]$
the set of all generalized power series of the form
![]() $F(X) = \sum _{\alpha \in [0,\infty )^m} a_{\alpha } X^{\alpha }$
, where each
$F(X) = \sum _{\alpha \in [0,\infty )^m} a_{\alpha } X^{\alpha }$
, where each
![]() $a_{\alpha } \in \mathbb {C}$
and the support
$a_{\alpha } \in \mathbb {C}$
and the support
is contained in a Cartesian product of well-ordered subsets of
![]() $[0,\infty )$
(see [Reference Van den Dries and Speissegger11, Section 4] for details). The series
$[0,\infty )$
(see [Reference Van den Dries and Speissegger11, Section 4] for details). The series
![]() $F(X)$
converges if there exists a polyradius
$F(X)$
converges if there exists a polyradius
![]() $r \in (0,\infty )^m$
such that
$r \in (0,\infty )^m$
such that
![]() $\|F\|_r:= \sum _{\alpha } |a_{\alpha }|r^{\alpha } < \infty $
; we denote by
$\|F\|_r:= \sum _{\alpha } |a_{\alpha }|r^{\alpha } < \infty $
; we denote by
![]() $\mathbb {C}\left \{X^*\right \}$
the set of all convergent generalized power series [Reference Van den Dries and Speissegger11, Section 5].
$\mathbb {C}\left \{X^*\right \}$
the set of all convergent generalized power series [Reference Van den Dries and Speissegger11, Section 5].
For
![]() ${\frak r} \in \mathbb {R}^m$
, we let
${\frak r} \in \mathbb {R}^m$
, we let
be the log-disk of log-polyradius
![]() $\frak r$
. For an set
$\frak r$
. For an set
![]() $D \subseteq \overline {\mathbb {C}}^m$
, we set
$D \subseteq \overline {\mathbb {C}}^m$
, we set
We call set
![]() $D \subseteq \overline {\mathbb {C}}^m$
a log-domain if
$D \subseteq \overline {\mathbb {C}}^m$
a log-domain if
![]() $D \cap \mathbb {C}^m$
is a domain. If
$D \cap \mathbb {C}^m$
is a domain. If
![]() $D \subseteq \overline {\mathbb {C}}^m$
is a log-domain, a log-holomorphic function on D is a continuous function
$D \subseteq \overline {\mathbb {C}}^m$
is a log-domain, a log-holomorphic function on D is a continuous function
![]() $f:D \longrightarrow \mathbb {C}$
such that the restriction of f to
$f:D \longrightarrow \mathbb {C}$
such that the restriction of f to
![]() $D \cap \mathbb {C}^m$
is holomorphic.
$D \cap \mathbb {C}^m$
is holomorphic.
Let
![]() $F(X) = \sum _{\alpha \in [0,\infty )^m} a_{\alpha } X^{\alpha } \in \mathbb {C}\left [\!\left [X^*\right ]\!\right ]$
such that
$F(X) = \sum _{\alpha \in [0,\infty )^m} a_{\alpha } X^{\alpha } \in \mathbb {C}\left [\!\left [X^*\right ]\!\right ]$
such that
![]() $\|F\|_r < \infty $
. Similar to Section 2.3, there is a log-holomorphic function
$\|F\|_r < \infty $
. Similar to Section 2.3, there is a log-holomorphic function
![]() $\overline F: H(\log r) \longrightarrow \mathbb {C}$
, called the log-sum of F, such that
$\overline F: H(\log r) \longrightarrow \mathbb {C}$
, called the log-sum of F, such that
![]() $\overline F(w) := F(e^w)$
whenever
$\overline F(w) := F(e^w)$
whenever
![]() $|\operatorname {\mathrm {Im}} w| < \pi /2$
.
$|\operatorname {\mathrm {Im}} w| < \pi /2$
.
3.2 Logarithmic polydomains
We define here the logarithmic versions of the domains discussed in [Reference Van den Dries and Speissegger12, Section 2]. Let
![]() ${\frak r} \in \mathbb {R}^m$
,
${\frak r} \in \mathbb {R}^m$
,
![]() $\theta>\pi /2 $
and
$\theta>\pi /2 $
and
![]() $k \in [0,\infty )^m$
, and put
$k \in [0,\infty )^m$
, and put
Note that if
![]() $m=1$
, then
$m=1$
, then
![]() $S^k({\frak r}, \theta ) = S(0,{\frak r}, \theta /k)$
, where the latter is the sector defined in Section 2.1. The reason for allowing
$S^k({\frak r}, \theta ) = S(0,{\frak r}, \theta /k)$
, where the latter is the sector defined in Section 2.1. The reason for allowing
![]() $k_i=0$
is that we need our class of log-polysectors to be closed under taking Cartesian products with log-disks; for instance, if
$k_i=0$
is that we need our class of log-polysectors to be closed under taking Cartesian products with log-disks; for instance, if
![]() $m>1$
and
$m>1$
and
![]() $k = (k', 0)$
with
$k = (k', 0)$
with
![]() $k' \in [0,\infty )^{m-1}$
, then
$k' \in [0,\infty )^{m-1}$
, then
![]() $S^k({\frak r}, \theta ) = S^{k'}({\frak r}', \theta ) \times H({\frak r}_m)$
. Finally, our polystrips are “in the real multidirection”; they can easily be defined in any multidirection,Footnote
1
but we shall not do this here as we do not need to for our purposes.
$S^k({\frak r}, \theta ) = S^{k'}({\frak r}', \theta ) \times H({\frak r}_m)$
. Finally, our polystrips are “in the real multidirection”; they can easily be defined in any multidirection,Footnote
1
but we shall not do this here as we do not need to for our purposes.
Next, for
![]() $p \in \mathbb {N}$
we put, by adapting [Reference Van den Dries and Speissegger12, Section 2] to the logarithmic chart,
$p \in \mathbb {N}$
we put, by adapting [Reference Van den Dries and Speissegger12, Section 2] to the logarithmic chart,
 $$ \begin{align*} H_p^k({\frak r}) &:= \left\{w \in H({\frak r}):\ k \cdot \operatorname{\mathrm{Re}} w < k \cdot {\frak r} - \log(1+p))\right\} &(\textit{log}\text{-}k{\text{-}\textit{polydisk}}), \\ S_p^{k}({\frak r}, \theta) &:= S^k({\frak r}, \theta) \cup H_p^k({\frak r}). \end{align*} $$
$$ \begin{align*} H_p^k({\frak r}) &:= \left\{w \in H({\frak r}):\ k \cdot \operatorname{\mathrm{Re}} w < k \cdot {\frak r} - \log(1+p))\right\} &(\textit{log}\text{-}k{\text{-}\textit{polydisk}}), \\ S_p^{k}({\frak r}, \theta) &:= S^k({\frak r}, \theta) \cup H_p^k({\frak r}). \end{align*} $$
Note that
 $$ \begin{align*}\exp\left(H^k_p({\frak r})\right) = D^k_p\left(e^{\frak r}\right) = \left\{z \in D\left(e^{\frak r}\right):\ \|z\|^k < \frac{e^{k\cdot {\frak r}}}{1+p}\right\},\end{align*} $$
$$ \begin{align*}\exp\left(H^k_p({\frak r})\right) = D^k_p\left(e^{\frak r}\right) = \left\{z \in D\left(e^{\frak r}\right):\ \|z\|^k < \frac{e^{k\cdot {\frak r}}}{1+p}\right\},\end{align*} $$
corresponding to [Reference Van den Dries and Speissegger12, Definition 2.1]. Thus, for a nonempty finite
![]() $K \subseteq [0,\infty )^m$
, we set
$K \subseteq [0,\infty )^m$
, we set
and for
![]() $p \in \mathbb {N}$
,
$p \in \mathbb {N}$
,
Note that if
![]() $z \in S_p^K({\frak r}, \theta )$
and
$z \in S_p^K({\frak r}, \theta )$
and
![]() $t \le 0$
, then
$t \le 0$
, then
![]() $t+z \in S_p^K({\frak r}, \theta )$
; in particular,
$t+z \in S_p^K({\frak r}, \theta )$
; in particular,
![]() $S_p^K({\frak r}, \theta )$
is connected.
$S_p^K({\frak r}, \theta )$
is connected.
3.3 Generalized multisummable functions
We now fix
![]() $R \in (0,\infty )^m$
,
$R \in (0,\infty )^m$
,
![]() $r>1$
,
$r>1$
,
![]() $\theta> \pi /2$
, a nonempty finite
$\theta> \pi /2$
, a nonempty finite
![]() $K \subseteq [0,\infty )^m$
and a natural
$K \subseteq [0,\infty )^m$
and a natural
![]() $\Delta \subseteq [0,\infty )^m$
that is closed under addition, and we set
$\Delta \subseteq [0,\infty )^m$
that is closed under addition, and we set
![]() $\tau := (K,R,r,\theta ,\Delta )$
. In this situation, we write
$\tau := (K,R,r,\theta ,\Delta )$
. In this situation, we write
We need to introduce the following norms for generalized power series: let
![]() $U \subseteq \mathbb {C}^m$
be an open neighborhood of the origin such that
$U \subseteq \mathbb {C}^m$
be an open neighborhood of the origin such that
![]() $|z| \in U$
for every
$|z| \in U$
for every
![]() $z \in U$
. For a generalized power series
$z \in U$
. For a generalized power series
![]() $F \in \mathbb {C}\left \{X^*\right \}$
, we set
$F \in \mathbb {C}\left \{X^*\right \}$
, we set
It follows from the previous section that, if
![]() $\|F\|_{U} < \infty $
, then F is convergent and the log-sum of F extends to a log-holomorphic function
$\|F\|_{U} < \infty $
, then F is convergent and the log-sum of F extends to a log-holomorphic function
![]() $\overline F: U \longrightarrow \mathbb {C}$
such that
$\overline F: U \longrightarrow \mathbb {C}$
such that
![]() $\left \|\overline F\right \|_U \le \|F\|_U$
, where
$\left \|\overline F\right \|_U \le \|F\|_U$
, where
![]() $\left \|\overline F\right \|_U$
denotes the sup norm of
$\left \|\overline F\right \|_U$
denotes the sup norm of
![]() $\overline F$
on U.
$\overline F$
on U.
Similar to Section 2.4, we now define generalized multisummable functions in several variables. The role of the usual norm
![]() $\|\cdot \|_{\rho }$
on generalized power series there is taken on here by the norm
$\|\cdot \|_{\rho }$
on generalized power series there is taken on here by the norm
![]() $\|\cdot \|_U$
as defined above, where
$\|\cdot \|_U$
as defined above, where
![]() $U = D^k_p\left (R\right )$
; note indeed that
$U = D^k_p\left (R\right )$
; note indeed that
![]() $z \in D^k_p\left (R\right )$
implies
$z \in D^k_p\left (R\right )$
implies
![]() $|z| \in D^k_p\left (R\right )$
, as required. Below, we denote this particular norm
$|z| \in D^k_p\left (R\right )$
, as required. Below, we denote this particular norm
![]() $\|\cdot \|_U$
by
$\|\cdot \|_U$
by
![]() $\|\cdot \|_{R,k,p}$
.
$\|\cdot \|_{R,k,p}$
.
Thus, let
![]() $f_p:S^{\tau }_p \longrightarrow \mathbb {C}$
be log-holomorphic and bounded, and assume that there is a natural set
$f_p:S^{\tau }_p \longrightarrow \mathbb {C}$
be log-holomorphic and bounded, and assume that there is a natural set
![]() $\Delta \subseteq [0,\infty )^m$
and, for each p, a convergent generalized power series
$\Delta \subseteq [0,\infty )^m$
and, for each p, a convergent generalized power series
![]() $T(f_p)(X) \in \mathbb {C}\left \{X^*\right \}$
with support contained in
$T(f_p)(X) \in \mathbb {C}\left \{X^*\right \}$
with support contained in
![]() $\Delta $
such that
$\Delta $
such that
![]() $\|T(f_p)\|_{R,k,p} < \infty $
and
$\|T(f_p)\|_{R,k,p} < \infty $
and
Assuming that
we have that
![]() $\sum _p f_p$
converges uniformly on
$\sum _p f_p$
converges uniformly on
![]() $S^{\tau }$
to a log-holomorphic function
$S^{\tau }$
to a log-holomorphic function
![]() $f:S^{\tau } \longrightarrow \mathbb {C}$
. As before, we abbreviate this situation by writing
$f:S^{\tau } \longrightarrow \mathbb {C}$
. As before, we abbreviate this situation by writing
and we set
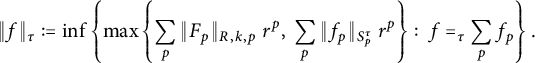 $$ \begin{align*}\|f\|_{\tau}:= \inf\left\{\max\left\{\sum_p \|F_p\|_{R,k,p}\ r^p,\ \sum_p \|f_p\|_{S^{\tau}_p}\ r^p\right\}:\ f =_{\tau} \sum_p f_p\right\}.\end{align*} $$
$$ \begin{align*}\|f\|_{\tau}:= \inf\left\{\max\left\{\sum_p \|F_p\|_{R,k,p}\ r^p,\ \sum_p \|f_p\|_{S^{\tau}_p}\ r^p\right\}:\ f =_{\tau} \sum_p f_p\right\}.\end{align*} $$
Thus, as in Section 2.4, we obtain a Banach algebra
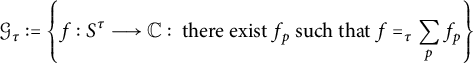 $$ \begin{align*}\mathcal{G}_{\tau}:= \left\{f: S^{\tau} \longrightarrow \mathbb{C}:\ \text{there exist } f_p \text{ such that } f =_{\tau} \sum_p f_p\right\}\end{align*} $$
$$ \begin{align*}\mathcal{G}_{\tau}:= \left\{f: S^{\tau} \longrightarrow \mathbb{C}:\ \text{there exist } f_p \text{ such that } f =_{\tau} \sum_p f_p\right\}\end{align*} $$
over
![]() $\mathbb {C}$
of functions in m variables with norm
$\mathbb {C}$
of functions in m variables with norm
![]() $\|\cdot \|_{\tau }$
. Note that if
$\|\cdot \|_{\tau }$
. Note that if
![]() $m=1$
,
$m=1$
,
![]() $\mathcal {G}_{\tau }$
as defined here is the same as
$\mathcal {G}_{\tau }$
as defined here is the same as
![]() $\mathcal {G}_{\tau '}$
defined in Section 2.4, where
$\mathcal {G}_{\tau '}$
defined in Section 2.4, where
![]() $\tau '=(K',R,r,\theta ,\Delta )$
with
$\tau '=(K',R,r,\theta ,\Delta )$
with
![]() $K'$
obtained from K by replacing all nonzero
$K'$
obtained from K by replacing all nonzero
![]() $k\in K$
by
$k\in K$
by
![]() $1/k$
(see the introductory remarks at the beginning of Section 3).
$1/k$
(see the introductory remarks at the beginning of Section 3).
Arguing as in the one-variable case, if
![]() $T(f_p)(X) = \sum a_{\alpha ,p} X^{\alpha }$
for each p, we obtain a generalized power series
$T(f_p)(X) = \sum a_{\alpha ,p} X^{\alpha }$
for each p, we obtain a generalized power series
![]() $Tf(X) = \sum a_{\alpha } X^{\alpha }$
, where
$Tf(X) = \sum a_{\alpha } X^{\alpha }$
, where
![]() $a_{\alpha } = \sum _p a_{\alpha ,p}$
for each
$a_{\alpha } = \sum _p a_{\alpha ,p}$
for each
![]() $\alpha $
.
$\alpha $
.
3.4 Quasianalyticity
In view of proving our o-minimality result in Section 5, we show in this section that the map
![]() $T:\mathcal {G}_{\tau } \longrightarrow \mathbb {C}\left [\!\left [X^*\right ]\!\right ]$
is injective. First, we explain the reason why we define the log-k-polysectors and the log-k-polydisks via scalar products rather than just taking Cartesian products of the corresponding objects in one variable. This is done because scalar product behaves well with respect to fibers, as shown in Remark 3.2.
$T:\mathcal {G}_{\tau } \longrightarrow \mathbb {C}\left [\!\left [X^*\right ]\!\right ]$
is injective. First, we explain the reason why we define the log-k-polysectors and the log-k-polydisks via scalar products rather than just taking Cartesian products of the corresponding objects in one variable. This is done because scalar product behaves well with respect to fibers, as shown in Remark 3.2.
We set
![]() $\mu _{K,i} := \min \left \{k_i:\ k \in K\right \}$
for
$\mu _{K,i} := \min \left \{k_i:\ k \in K\right \}$
for
![]() $i=1, \dots , m$
,
$i=1, \dots , m$
,
![]() $\mu _K:= (\mu _{K,1}, \dots , \mu _{K,m})$
and
$\mu _K:= (\mu _{K,1}, \dots , \mu _{K,m})$
and
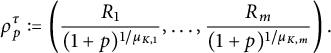 $$ \begin{align*}\rho^{\tau}_p := \left(\frac{R_1}{(1+p)^{1/\mu_{K,1}}}, \dots, \frac{R_m}{(1+p)^{1/\mu_{K,m}}}\right).\end{align*} $$
$$ \begin{align*}\rho^{\tau}_p := \left(\frac{R_1}{(1+p)^{1/\mu_{K,1}}}, \dots, \frac{R_m}{(1+p)^{1/\mu_{K,m}}}\right).\end{align*} $$
The next lemma shows that, although the log-k-polydisks are not themselves log-disks, the set
![]() $S^{\tau }_p$
contains a suitable log-disk.
$S^{\tau }_p$
contains a suitable log-disk.
Lemma 3.1 We have
![]() $H\left (\log \rho ^{\tau }_p\right ) \subseteq H^{\mu _K}_p(\log R) \subseteq \bigcap _{k \in K} H^k_p(\log R) \subseteq S^{\tau }_p$
.
$H\left (\log \rho ^{\tau }_p\right ) \subseteq H^{\mu _K}_p(\log R) \subseteq \bigcap _{k \in K} H^k_p(\log R) \subseteq S^{\tau }_p$
.
Proof The first and third inclusions are straightforward. For the second, let
![]() $k,l \in (0,\infty )^m$
be such that
$k,l \in (0,\infty )^m$
be such that
![]() $l \le k$
,
$l \le k$
,
![]() $p \in \mathbb {N}$
and
$p \in \mathbb {N}$
and
![]() $\rho \in \mathbb {R}$
; it suffices to show that
$\rho \in \mathbb {R}$
; it suffices to show that
![]() $H^k_p(\rho ) \subseteq H^k_p(\rho )$
. To see this, let
$H^k_p(\rho ) \subseteq H^k_p(\rho )$
. To see this, let
![]() $w \in H^k_p(\rho )$
. Then
$w \in H^k_p(\rho )$
. Then
Since
![]() $\operatorname {\mathrm {Re}} w < \rho $
as well, it follows that
$\operatorname {\mathrm {Re}} w < \rho $
as well, it follows that
![]() $k \cdot \operatorname {\mathrm {Re}} w < l \cdot \rho - \log (1+p)$
, as required.
$k \cdot \operatorname {\mathrm {Re}} w < l \cdot \rho - \log (1+p)$
, as required.
For the rest of this section, we set
![]() $x':= (x_1, \dots , x_{m-1})$
.
$x':= (x_1, \dots , x_{m-1})$
.
Remark 3.2 Let
![]() $a \in \overline {\mathbb {C}}^{m-1}$
. Set
$a \in \overline {\mathbb {C}}^{m-1}$
. Set
![]() $\theta (a):= \theta - \max \{k' \cdot \|\operatorname {\mathrm {Im}} a\|:\ k \in K\}$
and
$\theta (a):= \theta - \max \{k' \cdot \|\operatorname {\mathrm {Im}} a\|:\ k \in K\}$
and
where
![]() $\Pi _m:\mathbb {R}^m \longrightarrow \mathbb {R}$
is the projection on the last coordinate. Note that if
$\Pi _m:\mathbb {R}^m \longrightarrow \mathbb {R}$
is the projection on the last coordinate. Note that if
![]() $|\operatorname {\mathrm {Im}} a|$
is sufficiently small, then
$|\operatorname {\mathrm {Im}} a|$
is sufficiently small, then
![]() $\theta (a)> \pi /2$
.
$\theta (a)> \pi /2$
.
If
![]() $\theta (a)> 0$
, then
$\theta (a)> 0$
, then
![]() $S^{\tau (a)}$
is contained in the fiber
$S^{\tau (a)}$
is contained in the fiber
![]() $(S^{\tau })_a$
of
$(S^{\tau })_a$
of
![]() $S^{\tau }$
over a. Moreover, if
$S^{\tau }$
over a. Moreover, if
![]() $\operatorname {\mathrm {Re}} a < R'$
then, for each
$\operatorname {\mathrm {Re}} a < R'$
then, for each
![]() $p \in \mathbb {N}$
, the set
$p \in \mathbb {N}$
, the set
![]() $H^{k_m}_p\left (\log R_m\right )$
is contained in the fiber of the set
$H^{k_m}_p\left (\log R_m\right )$
is contained in the fiber of the set
![]() $H^k_p(\log R)$
over a. Therefore, if
$H^k_p(\log R)$
over a. Therefore, if
![]() $\theta (a)> 0$
and
$\theta (a)> 0$
and
![]() $\operatorname {\mathrm {Re}} a < \log R'$
, then
$\operatorname {\mathrm {Re}} a < \log R'$
, then
![]() $S^{\tau (a)}_p$
is contained in the fiber
$S^{\tau (a)}_p$
is contained in the fiber
![]() $\left (S^{\tau }_p\right )_a$
, for each p.
$\left (S^{\tau }_p\right )_a$
, for each p.
Lemma 3.3 Let
![]() $f \in \mathcal {G}_{\tau }$
and
$f \in \mathcal {G}_{\tau }$
and
![]() $a \in \overline {\mathbb {C}}^{m-1}$
be such that
$a \in \overline {\mathbb {C}}^{m-1}$
be such that
![]() $\theta (a)> 0$
and
$\theta (a)> 0$
and
![]() $\operatorname {\mathrm {Re}} a < \log R'$
. Then the function
$\operatorname {\mathrm {Re}} a < \log R'$
. Then the function
![]() $f_a: S^{\tau (a)} \longrightarrow \mathbb {C}$
, defined by
$f_a: S^{\tau (a)} \longrightarrow \mathbb {C}$
, defined by
![]() $f_a(w):= f(a,w)$
, belongs to
$f_a(w):= f(a,w)$
, belongs to
![]() $\mathcal {G}_{\tau (a)}$
and satisfies
$\mathcal {G}_{\tau (a)}$
and satisfies
![]() $\|f_a\|_{\tau (a)} \le \|f\|_{\tau }$
and
$\|f_a\|_{\tau (a)} \le \|f\|_{\tau }$
and
![]() $T(f_a)(X_m) = T(f)(e^a,X_m)$
.
$T(f_a)(X_m) = T(f)(e^a,X_m)$
.
Proof Choose
![]() $f_p$
, for
$f_p$
, for
![]() $p \in \mathbb {N}$
, such that
$p \in \mathbb {N}$
, such that
![]() $f =_{\tau } \sum f_p$
. For
$f =_{\tau } \sum f_p$
. For
![]() $p \in \mathbb {N}$
, let
$p \in \mathbb {N}$
, let
![]() $f_{a,p}:S^{\tau (a)}_p \longrightarrow \mathbb {C}$
be defined by
$f_{a,p}:S^{\tau (a)}_p \longrightarrow \mathbb {C}$
be defined by
![]() $f_{a,p}(w):= f_p(a,w)$
; these functions are well defined by Remark 3.2, and
$f_{a,p}(w):= f_p(a,w)$
; these functions are well defined by Remark 3.2, and
![]() $f_a(w) = \sum _p f_{a,p}(w)$
for every
$f_a(w) = \sum _p f_{a,p}(w)$
for every
![]() $w \in S^{\tau (a)}$
.
$w \in S^{\tau (a)}$
.
For each p, we set
![]() $F_{a,p}(X_m):= T(f_p)(e^a,X_m)$
, a generalized power series in the indeterminate
$F_{a,p}(X_m):= T(f_p)(e^a,X_m)$
, a generalized power series in the indeterminate
![]() $X_{m}$
. Since
$X_{m}$
. Since
![]() $\|T(f_p)\|_{R,k,p} < \infty $
and since, by Remark 3.2, the polyradius
$\|T(f_p)\|_{R,k,p} < \infty $
and since, by Remark 3.2, the polyradius
![]() $\rho (b):= \left ( |e^a|,b \right )$
belongs to
$\rho (b):= \left ( |e^a|,b \right )$
belongs to
![]() $\operatorname {\mathrm {cl}}\left (D^k_p\left (R\right )\right )$
for every
$\operatorname {\mathrm {cl}}\left (D^k_p\left (R\right )\right )$
for every
![]() $b \in \operatorname {\mathrm {cl}}\left (D^{k_m}_p\left ({R_m}\right )\right )$
, we have that
$b \in \operatorname {\mathrm {cl}}\left (D^{k_m}_p\left ({R_m}\right )\right )$
, we have that
in particular,
![]() $\|F_{a,p}\|_{R_m,k_m,p} \le \|T(f_p)\|_{R,k,p}$
and
$\|F_{a,p}\|_{R_m,k_m,p} \le \|T(f_p)\|_{R,k,p}$
and
![]() $f_{a,p} = \overline {F_{a,p}}$
, for each p. Therefore,
$f_{a,p} = \overline {F_{a,p}}$
, for each p. Therefore,
![]() $f_a =_{\tau (a)} \sum f_{a,p}$
, that is,
$f_a =_{\tau (a)} \sum f_{a,p}$
, that is,
![]() $f_a \in \mathcal {G}_{\tau (a)}$
. Since the inequality
$f_a \in \mathcal {G}_{\tau (a)}$
. Since the inequality
![]() $\sum \|F_{a,p}\|_{R_m,k_m,p}\ r^p \le \sum \|T(f_p)\|_{R,k,p}\ r^p$
holds for all choices of
$\sum \|F_{a,p}\|_{R_m,k_m,p}\ r^p \le \sum \|T(f_p)\|_{R,k,p}\ r^p$
holds for all choices of
![]() $\{f_p\}$
, we also get
$\{f_p\}$
, we also get
![]() $\|f_a\|_{\tau (a)} \le \|f\|_{\tau }$
.
$\|f_a\|_{\tau (a)} \le \|f\|_{\tau }$
.
Claim The series
![]() $T(f)(e^a,X_m)$
belongs to
$T(f)(e^a,X_m)$
belongs to
![]() $\mathbb {R}\left [\!\left [X_m^*\right ]\!\right ]$
and is equal to
$\mathbb {R}\left [\!\left [X_m^*\right ]\!\right ]$
and is equal to
![]() $T(f_a)(X_m)$
.
$T(f_a)(X_m)$
.
To see this claim, since
![]() $\sum \|T(f_p)\|_{R,k,p}\ r^p < \infty $
and
$\sum \|T(f_p)\|_{R,k,p}\ r^p < \infty $
and
![]() $\left (|e^a|,\rho ^{\tau (a)}_p\right ) \in \operatorname {\mathrm {cl}}\left (D^k_p\left (R\right )\right )$
for each p, it follows from Lemma 3.1 that for each
$\left (|e^a|,\rho ^{\tau (a)}_p\right ) \in \operatorname {\mathrm {cl}}\left (D^k_p\left (R\right )\right )$
for each p, it follows from Lemma 3.1 that for each
![]() $\alpha _m \in [0,\infty )$
and each p,
$\alpha _m \in [0,\infty )$
and each p,
 $$ \begin{align*} \sum_{\alpha' \in [0,\infty)^{m-1}} |a_{(\alpha',\alpha_m),p}|\ |e^{\alpha'\cdot a}| &\le \frac{\|Tf_p\|_{R,k,p}}{\left(\rho_p^{\tau(a)}\right)^{\alpha_m}} \\ &= \frac{\|Tf_p\|_{R,k,p}}{R_m^{\alpha_m}}\ (1+p)^{\alpha_m/k_m} \\ &\le \frac{\|Tf_p\|_{R,k,p}}{R_m^{\alpha_m}}\ s^p\ (1+p)^{\alpha_m/k_m}, \end{align*} $$
$$ \begin{align*} \sum_{\alpha' \in [0,\infty)^{m-1}} |a_{(\alpha',\alpha_m),p}|\ |e^{\alpha'\cdot a}| &\le \frac{\|Tf_p\|_{R,k,p}}{\left(\rho_p^{\tau(a)}\right)^{\alpha_m}} \\ &= \frac{\|Tf_p\|_{R,k,p}}{R_m^{\alpha_m}}\ (1+p)^{\alpha_m/k_m} \\ &\le \frac{\|Tf_p\|_{R,k,p}}{R_m^{\alpha_m}}\ s^p\ (1+p)^{\alpha_m/k_m}, \end{align*} $$
for any
![]() $s> 1$
. In particular, for
$s> 1$
. In particular, for
![]() $s \in (1,r)$
we have, for each
$s \in (1,r)$
we have, for each
![]() $\alpha _m \in [0,\infty )$
, that
$\alpha _m \in [0,\infty )$
, that
 $$ \begin{align} \qquad\sum_p \left(\sum_{\alpha'}|a_{(\alpha',\alpha_m),p}|\ |e^{\alpha'\cdot a}|\right) \le \frac1{R_m^{\alpha_m}} \sum_p \|Tf_p\|_{R,k,p}\ r^p \left(\frac sr\right)^p (1+p)^{\alpha_m/k_m} < \infty, \end{align} $$
$$ \begin{align} \qquad\sum_p \left(\sum_{\alpha'}|a_{(\alpha',\alpha_m),p}|\ |e^{\alpha'\cdot a}|\right) \le \frac1{R_m^{\alpha_m}} \sum_p \|Tf_p\|_{R,k,p}\ r^p \left(\frac sr\right)^p (1+p)^{\alpha_m/k_m} < \infty, \end{align} $$
which proves that
![]() $T(f)(e^a,X_m)$
belongs to
$T(f)(e^a,X_m)$
belongs to
![]() $\mathbb {R}\left [\!\left [X_m^*\right ]\!\right ]$
. Moreover, since
$\mathbb {R}\left [\!\left [X_m^*\right ]\!\right ]$
. Moreover, since
![]() $f_a \in \mathcal {G}_{\tau (a)}$
, we have
$f_a \in \mathcal {G}_{\tau (a)}$
, we have
It follows from (3.1) that for all
![]() $\alpha _m$
,
$\alpha _m$
,
 $$ \begin{align} \sum_{\alpha'}a_{(\alpha',\alpha_m)}e^{\alpha'\cdot a}=\sum_{\alpha'}\left(\sum_p a_{(\alpha',\alpha_m),p}\right)e^{\alpha'\cdot a}=\sum_p \sum_{\alpha'}a_{(\alpha',\alpha_m),p}e^{\alpha'\cdot a}. \end{align} $$
$$ \begin{align} \sum_{\alpha'}a_{(\alpha',\alpha_m)}e^{\alpha'\cdot a}=\sum_{\alpha'}\left(\sum_p a_{(\alpha',\alpha_m),p}\right)e^{\alpha'\cdot a}=\sum_p \sum_{\alpha'}a_{(\alpha',\alpha_m),p}e^{\alpha'\cdot a}. \end{align} $$
Hence,
![]() $T(f)(e^a,X_m) = \sum _p F_{a,p}(X_m) = T(f_a)(X_m)$
, as claimed.
$T(f)(e^a,X_m) = \sum _p F_{a,p}(X_m) = T(f_a)(X_m)$
, as claimed.
Proposition 3.4 (Quasianalyticity)
The map
![]() $T:\mathcal {G}_{\tau } \longrightarrow \mathbb {C}\left [\!\left [X^*\right ]\!\right ]$
is an injective
$T:\mathcal {G}_{\tau } \longrightarrow \mathbb {C}\left [\!\left [X^*\right ]\!\right ]$
is an injective
![]() $\mathbb {C}$
-algebra homomorphism.
$\mathbb {C}$
-algebra homomorphism.
Proof For the injectivity of T, let
![]() $f \in \mathcal {G}_{\tau }$
be such that
$f \in \mathcal {G}_{\tau }$
be such that
![]() $T(f) = 0$
; we need to show that
$T(f) = 0$
; we need to show that
![]() $f = 0$
. If
$f = 0$
. If
![]() $m=1$
, this is done in Proposition 2.27, so we assume
$m=1$
, this is done in Proposition 2.27, so we assume
![]() $m> 1$
. Let
$m> 1$
. Let
![]() $a \in \overline {\mathbb {C}}^{m-1}$
, and define
$a \in \overline {\mathbb {C}}^{m-1}$
, and define
![]() $\theta (a)$
and
$\theta (a)$
and
![]() $\tau (a)$
as in Remark 3.2. Assume that
$\tau (a)$
as in Remark 3.2. Assume that
![]() $\theta (a)> \pi /2$
and
$\theta (a)> \pi /2$
and
![]() $\operatorname {\mathrm {Re}} a < R'$
; by Lemma 3.3 and the assumption
$\operatorname {\mathrm {Re}} a < R'$
; by Lemma 3.3 and the assumption
![]() $Tf = 0$
, we obtain
$Tf = 0$
, we obtain
![]() $f_a \in \mathcal {G}_{\tau (a)}$
with
$f_a \in \mathcal {G}_{\tau (a)}$
with
![]() $T(f_a) = 0$
. It follows from quasianalyticity of
$T(f_a) = 0$
. It follows from quasianalyticity of
![]() $\mathcal {G}_{\tau (a)}$
that
$\mathcal {G}_{\tau (a)}$
that
![]() $f_a = 0$
. Since the set of
$f_a = 0$
. Since the set of
![]() $a \in \overline {\mathbb {C}}^{m-1}$
for which the latter holds contains an open set (by Lemma 3.3) and f is holomorphic on its (connected) domain, it follows that
$a \in \overline {\mathbb {C}}^{m-1}$
for which the latter holds contains an open set (by Lemma 3.3) and f is holomorphic on its (connected) domain, it follows that
![]() $f=0$
, as claimed.
$f=0$
, as claimed.
As in [Reference Van den Dries and Speissegger12, Corollary 2.19], we now obtain the following corollary.
Corollary 3.5 Let
![]() $f \in \mathcal {G}_{\tau }$
. Then
$f \in \mathcal {G}_{\tau }$
. Then
![]() $f(-\infty ,R) \subseteq \mathbb {R}$
if and only if
$f(-\infty ,R) \subseteq \mathbb {R}$
if and only if
![]() $Tf \in \mathbb {R}\left [\!\left [X^*\right ]\!\right ]$
.
$Tf \in \mathbb {R}\left [\!\left [X^*\right ]\!\right ]$
.
3.5 Monomial division
Let
![]() $F = \sum _{a \in [0,\infty )^m} a_{\alpha } X^{\alpha } \in \mathbb {C}\left [\!\left [X^*\right ]\!\right ]$
. Recall from [Reference Van den Dries and Speissegger11, Section 4] that
$F = \sum _{a \in [0,\infty )^m} a_{\alpha } X^{\alpha } \in \mathbb {C}\left [\!\left [X^*\right ]\!\right ]$
. Recall from [Reference Van den Dries and Speissegger11, Section 4] that
 $$ \begin{align*}\operatorname{\mathrm{ord}}(F)= \begin{cases} \min\{|\alpha|:\ a_{\alpha} \ne 0\}, &\text{if } f \ne 0, \\ \infty, &\text{if } f = 0. \end{cases}\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{ord}}(F)= \begin{cases} \min\{|\alpha|:\ a_{\alpha} \ne 0\}, &\text{if } f \ne 0, \\ \infty, &\text{if } f = 0. \end{cases}\end{align*} $$
For
![]() $i \in \{1, \dots , m\}$
, we also consider F as an element of
$i \in \{1, \dots , m\}$
, we also consider F as an element of
![]() $\mathbb {C}\left [\!\left [X_1^*, \dots , X_{i-1}^*, X_{i+1}^*, \dots , X_m^*\right ]\!\right ]\left [\!\left [X_i^*\right ]\!\right ]$
, and we denote by
$\mathbb {C}\left [\!\left [X_1^*, \dots , X_{i-1}^*, X_{i+1}^*, \dots , X_m^*\right ]\!\right ]\left [\!\left [X_i^*\right ]\!\right ]$
, and we denote by
![]() $\operatorname {\mathrm {ord}}_i(F)$
the corresponding order of F in the indeterminate
$\operatorname {\mathrm {ord}}_i(F)$
the corresponding order of F in the indeterminate
![]() $X_i$
. Note that
$X_i$
. Note that
![]() $\operatorname {\mathrm {ord}}_i(F)>0$
implies
$\operatorname {\mathrm {ord}}_i(F)>0$
implies
![]() $\operatorname {\mathrm {ord}}(F)>0$
, for each i.
$\operatorname {\mathrm {ord}}(F)>0$
, for each i.
Lemma 3.6 Let
![]() $f \in \mathcal {G}_{\tau }$
and assume that
$f \in \mathcal {G}_{\tau }$
and assume that
![]() $\gamma := \operatorname {\mathrm {ord}}_m(Tf)> 0$
. Let also
$\gamma := \operatorname {\mathrm {ord}}_m(Tf)> 0$
. Let also
![]() $s \in (1,r)$
and set
$s \in (1,r)$
and set
![]() $\tau ':= (K,R,s,\theta ,\Delta )$
. Then there exist
$\tau ':= (K,R,s,\theta ,\Delta )$
. Then there exist
![]() $g \in \mathcal {G}_{\tau '}$
and
$g \in \mathcal {G}_{\tau '}$
and
![]() $C = C(s/r)> 0$
depending only on
$C = C(s/r)> 0$
depending only on
![]() $\frac sr$
such that
$\frac sr$
such that
![]() $\|g\|_{\tau '} \le C \|f\|_{\tau '}$
and
$\|g\|_{\tau '} \le C \|f\|_{\tau '}$
and
Proof For simplicity, we write
![]() $\rho _p = \rho _p^{\tau } = \rho _p^{\tau '}$
and
$\rho _p = \rho _p^{\tau } = \rho _p^{\tau '}$
and
![]() $S_p = S_p^{\tau } = S_p^{\tau '}$
, for each p; recall that
$S_p = S_p^{\tau } = S_p^{\tau '}$
, for each p; recall that
![]() $\rho _p \in \operatorname {\mathrm {cl}}\left (D^k_p(R)\right )$
for each p. Say
$\rho _p \in \operatorname {\mathrm {cl}}\left (D^k_p(R)\right )$
for each p. Say
![]() $f =_{\tau } \sum _p f_p$
with
$f =_{\tau } \sum _p f_p$
with
![]() $\sum _p \|Tf_p\|_{R,k,p}\ r^p \le 2\|f\|_{\tau }$
and
$\sum _p \|Tf_p\|_{R,k,p}\ r^p \le 2\|f\|_{\tau }$
and
![]() $\sum _p \|f_p\|_{S_p}\ r^p \le 2\|f\|_{\tau }$
; since each
$\sum _p \|f_p\|_{S_p}\ r^p \le 2\|f\|_{\tau }$
; since each
![]() $Tf_p$
is convergent we may assume, after replacing each
$Tf_p$
is convergent we may assume, after replacing each
![]() $f_p$
by
$f_p$
by
![]() $f_p - \overline {(Tf_p)_{\gamma }}$
if necessary,Footnote
2
that
$f_p - \overline {(Tf_p)_{\gamma }}$
if necessary,Footnote
2
that
![]() $\operatorname {\mathrm {ord}}_m(Tf_p) \ge \gamma $
for each p. So there are
$\operatorname {\mathrm {ord}}_m(Tf_p) \ge \gamma $
for each p. So there are
![]() $G_p \in \mathbb {C}\left [\!\left [X^*\right ]\!\right ]$
with support contained in
$G_p \in \mathbb {C}\left [\!\left [X^*\right ]\!\right ]$
with support contained in
![]() $\operatorname {\mathrm {supp}}(Tf_p)$
(and hence natural) such that
$\operatorname {\mathrm {supp}}(Tf_p)$
(and hence natural) such that
![]() $Tf_p = X_m^{\gamma } G_p$
; since
$Tf_p = X_m^{\gamma } G_p$
; since
![]() $\|Tf_p\|_{\rho _p} = \rho _{p,m}^{\gamma } \|G_p\|_{\rho _p}$
, it follows that
$\|Tf_p\|_{\rho _p} = \rho _{p,m}^{\gamma } \|G_p\|_{\rho _p}$
, it follows that
![]() $G_p$
has radius of convergence at least
$G_p$
has radius of convergence at least
![]() $\rho _p$
, and that
$\rho _p$
, and that
where
![]() $g_p:= \overline {G_p}$
for each p. We extend
$g_p:= \overline {G_p}$
for each p. We extend
![]() $g_p$
to all of
$g_p$
to all of
![]() $S_p$
by setting
$S_p$
by setting
![]() $g_p(w):= f_p(w)/e^{\gamma w_m}$
for
$g_p(w):= f_p(w)/e^{\gamma w_m}$
for
![]() $w \in S_p\setminus H(\log \rho _p)$
.
$w \in S_p\setminus H(\log \rho _p)$
.
Since
![]() $\|Tf_p\|_{\rho _p} = \rho _{p,m}^{\gamma } \|Tg_p\|_{\rho _p}$
, for each p, we get
$\|Tf_p\|_{\rho _p} = \rho _{p,m}^{\gamma } \|Tg_p\|_{\rho _p}$
, for each p, we get
 $$ \begin{align*} \sum_p \|Tg_p\|_{\rho_p} s^p = \sum_p \frac{\|Tf_p\|_{\rho_p}}{\rho_{p,m}^{\gamma}} s^p \le \frac1{R_m^{\gamma}} \sum_p \|Tf_p\|_{\rho_p} r^p (1+p)^{k_m} \left(\frac sr\right)^p \le C \|g\|_{\tau} \end{align*} $$
$$ \begin{align*} \sum_p \|Tg_p\|_{\rho_p} s^p = \sum_p \frac{\|Tf_p\|_{\rho_p}}{\rho_{p,m}^{\gamma}} s^p \le \frac1{R_m^{\gamma}} \sum_p \|Tf_p\|_{\rho_p} r^p (1+p)^{k_m} \left(\frac sr\right)^p \le C \|g\|_{\tau} \end{align*} $$
for some
![]() $C = C(s/r)>0$
depending only on
$C = C(s/r)>0$
depending only on
![]() $\frac sr$
. It follows, on the one hand, that
$\frac sr$
. It follows, on the one hand, that
as well. On the other hand, since
![]() $\|Tg_p\|_{S_p \setminus H(\log \rho _p)} \le \rho _{p,m}^{-\gamma }\|Tf_p\|_{S_p\setminus H(\log \rho _p)}$
, the same argument as above also proves that
$\|Tg_p\|_{S_p \setminus H(\log \rho _p)} \le \rho _{p,m}^{-\gamma }\|Tf_p\|_{S_p\setminus H(\log \rho _p)}$
, the same argument as above also proves that
![]() $\sum _p \|g_p\|_{S_p \setminus H(\log \rho _p)} s^p \le C \|g\|_{\tau }$
. Therefore, the function
$\sum _p \|g_p\|_{S_p \setminus H(\log \rho _p)} s^p \le C \|g\|_{\tau }$
. Therefore, the function
![]() $g:S^{\tau '} \longrightarrow \mathbb {C}$
defined by
$g:S^{\tau '} \longrightarrow \mathbb {C}$
defined by
![]() $g:= \sum _p g_p$
belongs to
$g:= \sum _p g_p$
belongs to
![]() $\mathcal {G}_{\tau '}$
and satisfies
$\mathcal {G}_{\tau '}$
and satisfies
![]() $\|g\|_{\tau '} \le C \|g\|_{\tau }$
and
$\|g\|_{\tau '} \le C \|g\|_{\tau }$
and
![]() $f(w) = e^{\gamma w_m} g(w)$
for
$f(w) = e^{\gamma w_m} g(w)$
for
![]() $w \in S^{\tau '}$
, as claimed.
$w \in S^{\tau '}$
, as claimed.
3.6 Generalized multisummable germs
Similar to Section 2 of [Reference Van den Dries and Speissegger12], we let
![]() $(\mathcal {T}_m, \le )$
be the directed set of all tuples
$(\mathcal {T}_m, \le )$
be the directed set of all tuples
![]() $\tau = (K,R,r,\theta , \Delta )$
as above, where
$\tau = (K,R,r,\theta , \Delta )$
as above, where
![]() $\tau = (K,R,r,\theta ,\Delta ) \le \tau ' = (K',R',r',\theta ',\Delta ')$
if and only if
$\tau = (K,R,r,\theta ,\Delta ) \le \tau ' = (K',R',r',\theta ',\Delta ')$
if and only if
![]() $K \supseteq K'$
,
$K \supseteq K'$
,
![]() $R \le R'$
,
$R \le R'$
,
![]() $r \le r'$
,
$r \le r'$
,
![]() $\theta \le \theta '$
and
$\theta \le \theta '$
and
![]() $\Delta \supseteq \Delta '$
. Then
$\Delta \supseteq \Delta '$
. Then
![]() $S^{\tau '} \subseteq S^{\tau }$
whenever
$S^{\tau '} \subseteq S^{\tau }$
whenever
![]() $\tau ' \le \tau $
and in this situation, for
$\tau ' \le \tau $
and in this situation, for
![]() $f \in \mathcal {G}_{\tau }$
, the restriction
$f \in \mathcal {G}_{\tau }$
, the restriction
![]() $f\!\!\upharpoonright _{S^{\tau '}}$
belongs to
$f\!\!\upharpoonright _{S^{\tau '}}$
belongs to
![]() $\mathcal {G}_{\tau '}$
. The directed limit of the directed system
$\mathcal {G}_{\tau '}$
. The directed limit of the directed system
![]() $\left (\mathcal {G}_{\tau }:\ \tau \in \mathcal {T}_m\right )$
under these restrictions is the set
$\left (\mathcal {G}_{\tau }:\ \tau \in \mathcal {T}_m\right )$
under these restrictions is the set
![]() $\mathcal {G}_m$
of germs at
$\mathcal {G}_m$
of germs at
![]() $-\infty $
of functions in
$-\infty $
of functions in
![]() $\mathcal {G}_{\tau }$
, as
$\mathcal {G}_{\tau }$
, as
![]() $\tau $
ranges over
$\tau $
ranges over
![]() $\mathcal {T}_m$
. This
$\mathcal {T}_m$
. This
![]() $\mathcal {G}_m$
is a
$\mathcal {G}_m$
is a
![]() $\mathbb {C}$
-algebra containing the germs at
$\mathbb {C}$
-algebra containing the germs at
![]() $-\infty $
of the functions
$-\infty $
of the functions
![]() $e^{\gamma z_i}$
, for
$e^{\gamma z_i}$
, for
![]() $i=1, \dots , m$
and
$i=1, \dots , m$
and
![]() $\gamma \ge 0$
, and we extend each norm
$\gamma \ge 0$
, and we extend each norm
![]() $\|\cdot \|_{\tau }$
to all of
$\|\cdot \|_{\tau }$
to all of
![]() $\mathcal {G}_m$
by setting
$\mathcal {G}_m$
by setting
![]() $\|f\|_{\tau } := \infty $
whenever
$\|f\|_{\tau } := \infty $
whenever
![]() $g \notin \mathcal {G}_{\tau }$
.
$g \notin \mathcal {G}_{\tau }$
.
Below, we write
![]() $-\infty :=(-\infty , \dots , -\infty )$
. Note that
$-\infty :=(-\infty , \dots , -\infty )$
. Note that
![]() $f(-\infty ) = (Tf)(0)$
, since
$f(-\infty ) = (Tf)(0)$
, since
![]() $Tf$
is the asymptotic expansion of f at
$Tf$
is the asymptotic expansion of f at
![]() $-\infty $
; hence
$-\infty $
; hence
![]() $f(-\infty ) = 0$
if and only if
$f(-\infty ) = 0$
if and only if
![]() $\operatorname {\mathrm {ord}}(Tf)>0$
.
$\operatorname {\mathrm {ord}}(Tf)>0$
.
Lemma 3.7 Let
![]() $f \in \mathcal {G}_{m}$
.
$f \in \mathcal {G}_{m}$
.
-
(1) For
 $g \in \mathcal {G}_m$
and
$g \in \mathcal {G}_m$
and
 $\tau \in \mathcal {T}_m$
, we have
$\tau \in \mathcal {T}_m$
, we have
 $\|fg\|_{\tau } \le \|f\|_{\tau } \|g\|_{\tau }$
.
$\|fg\|_{\tau } \le \|f\|_{\tau } \|g\|_{\tau }$
. -
(2) If
 $f(-\infty ) = 0$
, then
$f(-\infty ) = 0$
, then
 $\,\lim _{\tau } \left \|f\right \|_{\tau } = 0$
, where the limit is taken over the downward directed set
$\,\lim _{\tau } \left \|f\right \|_{\tau } = 0$
, where the limit is taken over the downward directed set
 $\mathcal {T}_m$
.
$\mathcal {T}_m$
. -
(3) If
 $f(-\infty ) \neq 0$
, then f is a unit in
$f(-\infty ) \neq 0$
, then f is a unit in
 $\mathcal {G}_{m}$
.
$\mathcal {G}_{m}$
. -
(4) If
 $f(-\infty ) = 0$
, then there are
$f(-\infty ) = 0$
, then there are
 $\gamma _i> 0$
and
$\gamma _i> 0$
and
 $f_i \in \mathcal {G}_{m}$
for
$f_i \in \mathcal {G}_{m}$
for
 $i =1, \dots , m$
such that
$i =1, \dots , m$
such that
 $f = e^{\gamma _1 z_1} \cdot f_1 + \cdots + e^{\gamma _m z_m} \cdot f_m$
.
$f = e^{\gamma _1 z_1} \cdot f_1 + \cdots + e^{\gamma _m z_m} \cdot f_m$
. -
(5) If
 $m> 1$
, then the germ
$m> 1$
, then the germ
 $f(-\infty ,\cdot )$
belongs to
$f(-\infty ,\cdot )$
belongs to
 $\mathcal {G}_{m-1}$
.
$\mathcal {G}_{m-1}$
.
Proof Parts (2)–(4) are similar to Lemma 2.14 in [Reference Van den Dries and Speissegger12], using Lemma 3.6 for part (4). Part (5) follows from Lemma 3.3 with
![]() $\nu = 1$
.
$\nu = 1$
.
Similar to [Reference Van den Dries and Speissegger12, Section 3], we set
![]() $\mathbb {C}\left \{X^*\right \}_{\tau } := T(\mathcal {G}_{\tau })$
, for
$\mathbb {C}\left \{X^*\right \}_{\tau } := T(\mathcal {G}_{\tau })$
, for
![]() $\tau \in \mathcal {T}_m$
, and
$\tau \in \mathcal {T}_m$
, and
![]() $\mathbb {C}\left \{X^*\right \}_{\mathcal {G}} := T(\mathcal {G}_m)$
. We refer to the latter as the
$\mathbb {C}\left \{X^*\right \}_{\mathcal {G}} := T(\mathcal {G}_m)$
. We refer to the latter as the
![]() $\mathbb {C}$
-algebra of all generalized multisummable series in the indeterminates X; note that
$\mathbb {C}$
-algebra of all generalized multisummable series in the indeterminates X; note that
![]() $\mathbb {C}\left \{X^*\right \}_{\mathcal {G}} = \bigcup _{\tau \in \mathcal {T}_m} \mathbb {C}\left \{X^*\right \}_{\tau }$
. We make each
$\mathbb {C}\left \{X^*\right \}_{\mathcal {G}} = \bigcup _{\tau \in \mathcal {T}_m} \mathbb {C}\left \{X^*\right \}_{\tau }$
. We make each
![]() $\mathbb {C}\left \{X^*\right \}_{\tau }$
into an isomorphic copy of
$\mathbb {C}\left \{X^*\right \}_{\tau }$
into an isomorphic copy of
![]() $\mathcal {G}_{\tau }$
by setting
$\mathcal {G}_{\tau }$
by setting
![]() $\|Tf\|_{\tau } := \|f\|_{\tau }$
, for
$\|Tf\|_{\tau } := \|f\|_{\tau }$
, for
![]() $f \in \mathcal {G}_{\tau }$
; and we extend each norm
$f \in \mathcal {G}_{\tau }$
; and we extend each norm
![]() $\|\cdot \|_{\tau }$
to all of
$\|\cdot \|_{\tau }$
to all of
![]() $\mathbb {C}\left \{X^*\right \}_{\mathcal {G}}$
by setting
$\mathbb {C}\left \{X^*\right \}_{\mathcal {G}}$
by setting
![]() $\|F\|_{\tau }:= \infty $
for
$\|F\|_{\tau }:= \infty $
for
![]() $F \notin \mathbb {C}\left \{X^*\right \}_{\tau }$
.
$F \notin \mathbb {C}\left \{X^*\right \}_{\tau }$
.
Extending our notation of log-sum of convergent generalized power series, we also shall write
![]() $\overline F:= T^{-1}(F)$
, for
$\overline F:= T^{-1}(F)$
, for
![]() $F \in \mathbb {C}\left \{X^*\right \}_{\tau }$
.
$F \in \mathbb {C}\left \{X^*\right \}_{\tau }$
.
3.7 Mixed series
We now consider additional indeterminates
![]() $Y = (Y_1, \dots , Y_n)$
, and we defined mixed series similar to [Reference Van den Dries and Speissegger12, Section 3]. Thus, for
$Y = (Y_1, \dots , Y_n)$
, and we defined mixed series similar to [Reference Van den Dries and Speissegger12, Section 3]. Thus, for
![]() $\tau \in \mathcal {T}_m$
and
$\tau \in \mathcal {T}_m$
and
![]() $\rho \in (0,\infty )^n$
, and for
$\rho \in (0,\infty )^n$
, and for
![]() $F = \sum _{\beta \in \mathbb {N}^n} F_{\beta }(X) Y^{\beta } \in \mathbb {C}\left \{X^*\right \}_{\tau } [\![Y]\!]$
, we set
$F = \sum _{\beta \in \mathbb {N}^n} F_{\beta }(X) Y^{\beta } \in \mathbb {C}\left \{X^*\right \}_{\tau } [\![Y]\!]$
, we set
and
The latter is a Banach
![]() $\mathbb {C}$
-algebra with respect to the former norm. We sometimes refer to the indeterminates
$\mathbb {C}$
-algebra with respect to the former norm. We sometimes refer to the indeterminates
![]() $X_i$
as the generalized Gevrey variables and to the indeterminates
$X_i$
as the generalized Gevrey variables and to the indeterminates
![]() $Y_j$
as the convergent variables. Each
$Y_j$
as the convergent variables. Each
![]() $F = \sum _{\beta } F_{\beta }(X)Y^{\beta } \in \mathbb {C}\left \{X^*;Y\right \}_{\tau ,\rho }$
defines a log-holomorphic function
$F = \sum _{\beta } F_{\beta }(X)Y^{\beta } \in \mathbb {C}\left \{X^*;Y\right \}_{\tau ,\rho }$
defines a log-holomorphic function
![]() $\overline F:S^{\tau } \times D(\rho ) \longrightarrow \mathbb {C}$
by setting
$\overline F:S^{\tau } \times D(\rho ) \longrightarrow \mathbb {C}$
by setting
As in Section 3.6, we set
and we extend each norm
![]() $\|\cdot \|_{\tau ,\rho }$
to all of
$\|\cdot \|_{\tau ,\rho }$
to all of
![]() $\mathbb {C}\left \{X^*;Y\right \}_{\mathcal {G}}$
by setting
$\mathbb {C}\left \{X^*;Y\right \}_{\mathcal {G}}$
by setting
![]() $\|F\|_{\tau ,\rho }:= \infty $
whenever
$\|F\|_{\tau ,\rho }:= \infty $
whenever
![]() $F \notin \mathbb {C}\left \{X^*;Y\right \}_{\tau ,\rho }$
. Ordering the product
$F \notin \mathbb {C}\left \{X^*;Y\right \}_{\tau ,\rho }$
. Ordering the product
![]() $\mathcal {T}_m \times (0,\infty )^n$
by the product order, we obtain the following generalization of Lemma 3.7.
$\mathcal {T}_m \times (0,\infty )^n$
by the product order, we obtain the following generalization of Lemma 3.7.
Lemma 3.8 Let
![]() $F \in \mathbb {C}\left [\!\left [X^*;Y\right ]\!\right ]_{\mathcal {G}}$
.
$F \in \mathbb {C}\left [\!\left [X^*;Y\right ]\!\right ]_{\mathcal {G}}$
.
-
(1) For
 $G \in \mathbb {C}\left \{X^*;Y\right \}_{\mathcal {G}}$
,
$G \in \mathbb {C}\left \{X^*;Y\right \}_{\mathcal {G}}$
,
 $\tau \in \mathcal {T}_m$
and
$\tau \in \mathcal {T}_m$
and
 $\rho \in (0,\infty )^n$
, we have
$\rho \in (0,\infty )^n$
, we have
 $\|FG\|_{\tau ,\rho } \le \|F\|_{\tau ,\rho } \|G\|_{\tau ,\rho }$
.
$\|FG\|_{\tau ,\rho } \le \|F\|_{\tau ,\rho } \|G\|_{\tau ,\rho }$
. -
(2) If
 $\overline F(-\infty ,0) = 0$
, then
$\overline F(-\infty ,0) = 0$
, then
 $\,\lim _{(\tau ,\rho )} \left \|F\right \|_{\tau ,\rho } = 0$
, where the limit is taken over the downward directed set
$\,\lim _{(\tau ,\rho )} \left \|F\right \|_{\tau ,\rho } = 0$
, where the limit is taken over the downward directed set
 $\mathcal {T}_m \times (0,\infty )^n$
.
$\mathcal {T}_m \times (0,\infty )^n$
. -
(3) If
 $\overline F(-\infty ,0) \neq 0$
, then F is a unit in
$\overline F(-\infty ,0) \neq 0$
, then F is a unit in
 $\mathbb {C}\left \{X^*;Y\right \}_{\mathcal {G}}$
.
$\mathbb {C}\left \{X^*;Y\right \}_{\mathcal {G}}$
. -
(4) If
 $m> 1$
and
$m> 1$
and
 $X' = (X_2, \dots , X_m)$
, then
$X' = (X_2, \dots , X_m)$
, then
 $F(0,X',Y)$
belongs to
$F(0,X',Y)$
belongs to
 $\mathbb {C}\left \{(X')^*;Y\right \}_{\mathcal {G}}$
.
$\mathbb {C}\left \{(X')^*;Y\right \}_{\mathcal {G}}$
. -
(5)
 $\mathbb {C}\left \{X^*;Y\right \}_{\mathcal {G}}$
is complete in each norm
$\mathbb {C}\left \{X^*;Y\right \}_{\mathcal {G}}$
is complete in each norm
 $\|\cdot \|_{\tau ,\rho }$
.
$\|\cdot \|_{\tau ,\rho }$
. -
(6)
 $\mathbb {C}\left \{X^*;Y\right \}_{\mathcal {G}} \subseteq \mathbb {C}\left \{(X,Y)^*\right \}_{\mathcal {G}}$
.
$\mathbb {C}\left \{X^*;Y\right \}_{\mathcal {G}} \subseteq \mathbb {C}\left \{(X,Y)^*\right \}_{\mathcal {G}}$
.
Proof Parts (1)–(4) follow from Lemma 3.7. Part (5) is just a restatement of the fact that each
![]() $\mathbb {C}\left \{X^*;Y\right \}_{\tau ,\rho }$
is a Banach algebra. Part (6) is proved along the lines of [Reference Van den Dries and Speissegger12, Lemma 3.5].
$\mathbb {C}\left \{X^*;Y\right \}_{\tau ,\rho }$
is a Banach algebra. Part (6) is proved along the lines of [Reference Van den Dries and Speissegger12, Lemma 3.5].
Recall that
![]() $F \in \mathbb {C}\left [\!\left [X^*;Y\right ]\!\right ]$
is regular in
$F \in \mathbb {C}\left [\!\left [X^*;Y\right ]\!\right ]$
is regular in
![]() $Y_n$
of order d if
$Y_n$
of order d if
![]() $F(0,0,Y_n) = uY_n +$
terms in
$F(0,0,Y_n) = uY_n +$
terms in
![]() $Y_n$
of higher degree, with
$Y_n$
of higher degree, with
![]() $u \in \mathbb {C}$
nonzero. Using Lemma 3.8, the proof of [Reference Tougeron9, Proposition 4.1] now establishes the following proposition, where
$u \in \mathbb {C}$
nonzero. Using Lemma 3.8, the proof of [Reference Tougeron9, Proposition 4.1] now establishes the following proposition, where
![]() $Y' = (Y_1, \dots , Y_{n-1})$
.
$Y' = (Y_1, \dots , Y_{n-1})$
.
Proposition 3.9 Let
![]() $f \in \mathbb {C}\left \{X^*;Y\right \}_{\mathcal {G}}$
, and assume that
$f \in \mathbb {C}\left \{X^*;Y\right \}_{\mathcal {G}}$
, and assume that
![]() $n> 0$
and F is regular in
$n> 0$
and F is regular in
![]() $Y_n$
of order d. Then the series F factors uniquely as
$Y_n$
of order d. Then the series F factors uniquely as
![]() $F = GH$
, where
$F = GH$
, where
![]() $G \in \mathbb {C}\left \{X^*;Y\right \}_{\mathcal {G}}$
is a unit and
$G \in \mathbb {C}\left \{X^*;Y\right \}_{\mathcal {G}}$
is a unit and
![]() $H \in \mathbb {C}\left \{X^*;Y'\right \}_{\mathcal {G}} [Y_n]$
is monic in
$H \in \mathbb {C}\left \{X^*;Y'\right \}_{\mathcal {G}} [Y_n]$
is monic in
![]() $Y_n$
of degree d.
$Y_n$
of degree d.
4 Substitutions
In this section, we introduce the substitutions discussed in Sections 1.8 and 1.15 of [Reference Rolin and Servi7]. Let
![]() $m',n' \in \mathbb {N}$
and
$m',n' \in \mathbb {N}$
and
![]() $X' = (X^{\prime }_1, \dots , X^{\prime }_{m'})$
and
$X' = (X^{\prime }_1, \dots , X^{\prime }_{m'})$
and
![]() $Y' = (Y^{\prime }_1, \dots , Y^{\prime }_{n'})$
be indeterminates. Denote by
$Y' = (Y^{\prime }_1, \dots , Y^{\prime }_{n'})$
be indeterminates. Denote by
![]() $\{X,Y\}$
the set
$\{X,Y\}$
the set
![]() $\left \{ X_{1},\ldots ,X_{m},Y_{1},\ldots ,Y_{n}\right \}$
and let
$\left \{ X_{1},\ldots ,X_{m},Y_{1},\ldots ,Y_{n}\right \}$
and let
![]() $\sigma : \{X,Y\} \longrightarrow \mathbb {R}\left [\!\left [(X')^*,Y'\right ]\!\right ]$
be a map. We call
$\sigma : \{X,Y\} \longrightarrow \mathbb {R}\left [\!\left [(X')^*,Y'\right ]\!\right ]$
be a map. We call
![]() $\sigma $
a substitution if each
$\sigma $
a substitution if each
![]() $\sigma (X_i)$
is normal in the following sense:
$\sigma (X_i)$
is normal in the following sense:
-
(*) There exist
 $a_i \in [0,\infty )$
, nonzero
$a_i \in [0,\infty )$
, nonzero
 $\gamma _i \in [0,\infty )^{m'}$
,
$\gamma _i \in [0,\infty )^{m'}$
,
 $\lambda _i \in (0,\infty )$
, and
$\lambda _i \in (0,\infty )$
, and
 $H_i \in \mathbb {R}\left [\!\left [(X')^*,Y'\right ]\!\right ]$
such that
$H_i \in \mathbb {R}\left [\!\left [(X')^*,Y'\right ]\!\right ]$
such that
 $H_i(0) = 0$
and
$H_i(0) = 0$
and
 $\sigma (X_i) = a_i + (X')^{\gamma _i}(\lambda _{i} + H_i((X')^*,Y'))$
.
$\sigma (X_i) = a_i + (X')^{\gamma _i}(\lambda _{i} + H_i((X')^*,Y'))$
.
If
![]() $\sigma $
is a substitution such that
$\sigma $
is a substitution such that
![]() $\sigma (0) = 0$
(in particular,
$\sigma (0) = 0$
(in particular,
![]() $a_i = 0$
for each i), then
$a_i = 0$
for each i), then
![]() $\sigma $
extends to a unique
$\sigma $
extends to a unique
![]() $\mathbb {C}$
-algebra homomorphism
$\mathbb {C}$
-algebra homomorphism
![]() $\sigma :\mathbb {C}\left [\!\left [X^*, Y\right ]\!\right ] \longrightarrow \mathbb {C}\left [\!\left [(X')^*,Y'\right ]\!\right ]$
by using, for each
$\sigma :\mathbb {C}\left [\!\left [X^*, Y\right ]\!\right ] \longrightarrow \mathbb {C}\left [\!\left [(X')^*,Y'\right ]\!\right ]$
by using, for each
![]() $r>0$
and
$r>0$
and
![]() $\epsilon \in \mathbb {C}\left [\!\left [(X')^*,Y'\right ]\!\right ]$
with
$\epsilon \in \mathbb {C}\left [\!\left [(X')^*,Y'\right ]\!\right ]$
with
![]() $\epsilon (0) = 0$
, the binomial theorem
$\epsilon (0) = 0$
, the binomial theorem
In this situation, we write
![]() $\sigma F$
in place of
$\sigma F$
in place of
![]() $\sigma (F)$
for
$\sigma (F)$
for
![]() $F \in \mathbb {C}\left [\!\left [X^*, Y\right ]\!\right ]$
. If all
$F \in \mathbb {C}\left [\!\left [X^*, Y\right ]\!\right ]$
. If all
![]() $\sigma (X_i)$
and
$\sigma (X_i)$
and
![]() $\sigma (Y_j)$
lie in a subring A of
$\sigma (Y_j)$
lie in a subring A of
![]() $\mathbb {C}\left [\!\left [(X')^*,Y'\right ]\!\right ]$
, then we refer to
$\mathbb {C}\left [\!\left [(X')^*,Y'\right ]\!\right ]$
, then we refer to
![]() $\sigma $
also as a substitution
$\sigma $
also as a substitution
![]() $\sigma : \{X,Y\} \longrightarrow A$
. Note that, in this situation, we have
$\sigma : \{X,Y\} \longrightarrow A$
. Note that, in this situation, we have
![]() $\sigma (\mathbb {R}\left [\!\left [X^*,Y\right ]\!\right ]) \subseteq \mathbb {R}\left [\!\left [(X')^*,Y'\right ]\!\right ]$
.
$\sigma (\mathbb {R}\left [\!\left [X^*,Y\right ]\!\right ]) \subseteq \mathbb {R}\left [\!\left [(X')^*,Y'\right ]\!\right ]$
.
Remark While general substitutions do not extend to all of
![]() $\mathbb {C}\left [\!\left [X^*,Y\right ]\!\right ]$
, we describe particular substitutions below that do extend to certain subalgebras of
$\mathbb {C}\left [\!\left [X^*,Y\right ]\!\right ]$
, we describe particular substitutions below that do extend to certain subalgebras of
![]() $\mathbb {C}\left \{X^*,Y\right \}_{\mathcal {G}}$
.
$\mathbb {C}\left \{X^*,Y\right \}_{\mathcal {G}}$
.
Let
![]() $\sigma :\{X,Y\} \longrightarrow \mathbb {R}\left \{(X')^*,Y'\right \}_{\mathcal {G}}$
be a substitution. For each
$\sigma :\{X,Y\} \longrightarrow \mathbb {R}\left \{(X')^*,Y'\right \}_{\mathcal {G}}$
be a substitution. For each
![]() $\sigma (X_i)$
, we let
$\sigma (X_i)$
, we let
![]() $\gamma _i$
,
$\gamma _i$
,
![]() $\lambda _i$
and
$\lambda _i$
and
![]() $H_i$
be as in (
$H_i$
be as in (
![]() $\ast $
); by Lemma 3.8, we have
$\ast $
); by Lemma 3.8, we have
![]() $H_i \in \mathbb {R}\left \{(X')^*,Y'\right \}_{\mathcal {G}}$
as well. We call
$H_i \in \mathbb {R}\left \{(X')^*,Y'\right \}_{\mathcal {G}}$
as well. We call
![]() $\tau ' \in \mathcal {T}_{\mu }$
and
$\tau ' \in \mathcal {T}_{\mu }$
and
![]() $\rho ' \in (0,\infty )^{\nu } \ \sigma $
-admissible if each
$\rho ' \in (0,\infty )^{\nu } \ \sigma $
-admissible if each
![]() $\sigma (X_i)$
and
$\sigma (X_i)$
and
![]() $\sigma (Y_j)$
, as well as each
$\sigma (Y_j)$
, as well as each
![]() $H_i$
, belongs to
$H_i$
, belongs to
![]() $\mathbb {R}\left \{(X')^*,Y'\right \}_{\tau ',\rho '}$
, and we have
$\mathbb {R}\left \{(X')^*,Y'\right \}_{\tau ',\rho '}$
, and we have
![]() $\|H_i\|_{\tau ',\rho '} < |\lambda _i|$
for each i.
$\|H_i\|_{\tau ',\rho '} < |\lambda _i|$
for each i.
Let
![]() $\tau ' \in \mathcal {T}_{\mu }$
and
$\tau ' \in \mathcal {T}_{\mu }$
and
![]() $\rho ' \in (0,\infty )^{\nu }$
be
$\rho ' \in (0,\infty )^{\nu }$
be
![]() $\sigma $
-admissible. Then
$\sigma $
-admissible. Then
![]() $\sigma $
induces a log-holomorphic map
$\sigma $
induces a log-holomorphic map
![]() $\widetilde \sigma : S^{\tau '} \times D(\rho ') \longrightarrow \overline {\mathbb {C}}^{m+n}$
by setting
$\widetilde \sigma : S^{\tau '} \times D(\rho ') \longrightarrow \overline {\mathbb {C}}^{m+n}$
by setting
for
![]() $i = 1, \dots , m$
(where
$i = 1, \dots , m$
(where
![]() $\log $
denotes the standard branch of the logarithm), and
$\log $
denotes the standard branch of the logarithm), and
for
![]() $j=1, \dots , n$
. (Note that, for each i, we have
$j=1, \dots , n$
. (Note that, for each i, we have
![]() $\exp \circ \ \widetilde \sigma _i = \overline {\sigma (X_i)}$
.)
$\exp \circ \ \widetilde \sigma _i = \overline {\sigma (X_i)}$
.)
Example 4.1
-
(1) (Permutation of Gevrey variables) For a permutation
 $\pi \in \Sigma _m$
,
$\pi \in \Sigma _m$
,
 $\mu = m$
and
$\mu = m$
and
 $\nu = n$
, the substitution defined by
$\nu = n$
, the substitution defined by
 $\sigma (X_i):= X^{\prime }_{\pi (i)}$
and
$\sigma (X_i):= X^{\prime }_{\pi (i)}$
and
 $\sigma (Y_j):= Y_j$
.
$\sigma (Y_j):= Y_j$
. -
(2) (Blow-up chart in the Gevrey variables)
 $\sigma $
is any of the blow-up charts (1) or (2) found in [Reference Rolin and Servi7, Definition 1.13], also referred to as regular blow-up charts and singular blow-up charts, respectively.
$\sigma $
is any of the blow-up charts (1) or (2) found in [Reference Rolin and Servi7, Definition 1.13], also referred to as regular blow-up charts and singular blow-up charts, respectively. -
(3) (Ramification of a Gevrey variable) Here,
 $m'=m$
and
$m'=m$
and
 $n'=n$
, and we have
$n'=n$
, and we have
 $\sigma (X_{i_0}) = (X^{\prime }_{i_0})^{\alpha }$
for some
$\sigma (X_{i_0}) = (X^{\prime }_{i_0})^{\alpha }$
for some
 $\alpha \ge 0$
and
$\alpha \ge 0$
and
 $i_0 \in \{1, \dots , m\}$
,
$i_0 \in \{1, \dots , m\}$
,
 $\sigma (X_i) = X^{\prime }_i$
for each
$\sigma (X_i) = X^{\prime }_i$
for each
 $i \ne i_0$
, and
$i \ne i_0$
, and
 $\sigma (Y_j) = Y^{\prime }_j$
for each j.
$\sigma (Y_j) = Y^{\prime }_j$
for each j. -
(4) (Translation) For
 $(a,b)\in (0,\infty )^m \times \mathbb {R}^n$
, put
$(a,b)\in (0,\infty )^m \times \mathbb {R}^n$
, put
 $m':=|\{i:\ 1\le i\le m,\ a_i =0\}|$
and
$m':=|\{i:\ 1\le i\le m,\ a_i =0\}|$
and
 $n':= n+m-m'$
, and choose a permutation
$n':= n+m-m'$
, and choose a permutation
 $\pi \in \Sigma _m$
such that
$\pi \in \Sigma _m$
such that
 $\pi (\{i:\ 1 \le i \le m,\ a_i = 0\}) = \{1,\ldots ,m'\}$
. Then the translation by
$\pi (\{i:\ 1 \le i \le m,\ a_i = 0\}) = \{1,\ldots ,m'\}$
. Then the translation by
 $(a,b)$
is the substitution defined by
$(a,b)$
is the substitution defined by
 $\sigma (X_{\pi (i)}):= X^{\prime }_i$
for
$\sigma (X_{\pi (i)}):= X^{\prime }_i$
for
 $i = 1, \dots , m'$
,
$i = 1, \dots , m'$
,
 $\sigma (X_{\pi (m'+j)}):= a_{\pi (m'+j)} + Y^{\prime }_j$
for
$\sigma (X_{\pi (m'+j)}):= a_{\pi (m'+j)} + Y^{\prime }_j$
for
 $j = 1, \dots , m-m'$
, and
$j = 1, \dots , m-m'$
, and
 $\sigma (Y_j):= b_j + Y^{\prime }_{m-m'+j}$
for
$\sigma (Y_j):= b_j + Y^{\prime }_{m-m'+j}$
for
 $j=1, \dots , n$
.
$j=1, \dots , n$
. -
(5) (Infinitesimal substitution in the convergent variables) Here,
 $n>0$
,
$n>0$
,
 $\sigma (0) = 0$
,
$\sigma (0) = 0$
,
 $\sigma (X_i) = X_i$
for each i and
$\sigma (X_i) = X_i$
for each i and
 $\sigma (Y_j) \in \mathbb {R}\left \{(X')^*,Y'\right \}_{\mathcal {G}}$
for each j, where
$\sigma (Y_j) \in \mathbb {R}\left \{(X')^*,Y'\right \}_{\mathcal {G}}$
for each j, where
 $X' = (X^{\prime }_1, \dots , X^{\prime }_{m'})$
and
$X' = (X^{\prime }_1, \dots , X^{\prime }_{m'})$
and
 $Y' = (Y^{\prime }_1, \dots , Y^{\prime }_{n'})$
with
$Y' = (Y^{\prime }_1, \dots , Y^{\prime }_{n'})$
with
 $m'$
and
$m'$
and
 $n'$
arbitrary.
$n'$
arbitrary.
Note that for each of these substitutions
![]() $\sigma $
, every corresponding
$\sigma $
, every corresponding
![]() $\tau '$
and
$\tau '$
and
![]() $\rho '$
is
$\rho '$
is
![]() $\sigma $
-admissible. Also, while permutations and blow-up charts extend to all of
$\sigma $
-admissible. Also, while permutations and blow-up charts extend to all of
![]() $\mathbb {C}\left [\!\left [X^*,Y\right ]\!\right ]$
, translations do not in general do so.
$\mathbb {C}\left [\!\left [X^*,Y\right ]\!\right ]$
, translations do not in general do so.
We start with an elementary lemma similar to [Reference Van den Dries and Speissegger12, Lemma 4.3]. The essential difference between the proofs here and those in [Reference Van den Dries and Speissegger12, Section 4] is that we cannot use Taylor expansion to compute the series after substitution as in [Reference Van den Dries and Speissegger12, Lemma 4.2]; instead, we have to rely on our additional assumptions built into the norms
![]() $\|\cdot \|_{\tau }$
.
$\|\cdot \|_{\tau }$
.
Lemma 4.2 Let
![]() $X':= (X_1, \dots , X_{m-1})$
, and let
$X':= (X_1, \dots , X_{m-1})$
, and let
![]() $\sigma :\{X,Y\} \longrightarrow \mathbb {R}[X',Y]$
be the substitution given by
$\sigma :\{X,Y\} \longrightarrow \mathbb {R}[X',Y]$
be the substitution given by
![]() $\sigma (X_i) := X_i$
if
$\sigma (X_i) := X_i$
if
![]() $i < m$
,
$i < m$
,
![]() $\sigma (X_m):= X_{m-1}$
and
$\sigma (X_m):= X_{m-1}$
and
![]() $\sigma (Y_j):= Y_j$
for each j. Then for every
$\sigma (Y_j):= Y_j$
for each j. Then for every
![]() $F \in \mathbb {C}\left \{X^*,Y\right \}_{\mathcal {G}}$
, we have
$F \in \mathbb {C}\left \{X^*,Y\right \}_{\mathcal {G}}$
, we have
![]() $\sigma F \in \mathbb {C}\left \{(X')^*, Y\right \}_{\mathcal {G}}$
and
$\sigma F \in \mathbb {C}\left \{(X')^*, Y\right \}_{\mathcal {G}}$
and
![]() $\overline {\sigma F} = \overline F \circ \widetilde \sigma $
(as germs of functions).
$\overline {\sigma F} = \overline F \circ \widetilde \sigma $
(as germs of functions).
Proof Fix
![]() $\tau = (K,R,r,\theta ,\Delta ) \in \mathcal {T}_m$
and
$\tau = (K,R,r,\theta ,\Delta ) \in \mathcal {T}_m$
and
![]() $\rho \in (0,\infty )^n$
. Similar to [Reference Van den Dries and Speissegger12, Lemma 4.3], we set
$\rho \in (0,\infty )^n$
. Similar to [Reference Van den Dries and Speissegger12, Lemma 4.3], we set
Moreover, we set
since the projection of
![]() $\Delta '$
on each of the first
$\Delta '$
on each of the first
![]() $m-2$
coordinates is the same as of
$m-2$
coordinates is the same as of
![]() $\Delta $
, and since
$\Delta $
, and since
![]() $\Pi _{m-1}(\Delta ') \subseteq \Pi _{m-1}(\Delta ) + \Pi _m(\Delta )$
, this
$\Pi _{m-1}(\Delta ') \subseteq \Pi _{m-1}(\Delta ) + \Pi _m(\Delta )$
, this
![]() $\Delta '$
is natural. So we set
$\Delta '$
is natural. So we set
![]() $\tau ':= (K',R',r,\theta ,\Delta ') \in \mathcal {T}_{m-1}$
; we get from the proof of [Reference Van den Dries and Speissegger12, Lemma 4.3] that
$\tau ':= (K',R',r,\theta ,\Delta ') \in \mathcal {T}_{m-1}$
; we get from the proof of [Reference Van den Dries and Speissegger12, Lemma 4.3] that
![]() $\widetilde \sigma \left (S^{\tau '} \times D(\rho ')\right ) \subseteq S^{\tau } \times D(\rho )$
and, for each p, that
$\widetilde \sigma \left (S^{\tau '} \times D(\rho ')\right ) \subseteq S^{\tau } \times D(\rho )$
and, for each p, that
![]() $\widetilde \sigma \left (S^{\tau '}_p \times D(\rho ')\right ) \subseteq S^{\tau }_p \times D(\rho )$
. The lemma then follows from the following more precise statement:
$\widetilde \sigma \left (S^{\tau '}_p \times D(\rho ')\right ) \subseteq S^{\tau }_p \times D(\rho )$
. The lemma then follows from the following more precise statement:
Claim
For
![]() $F \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
, we have
$F \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
, we have
![]() $\sigma F \in \mathbb {C}\left \{(X')^*,Y\right \}_{\tau ',\rho }$
such that
$\sigma F \in \mathbb {C}\left \{(X')^*,Y\right \}_{\tau ',\rho }$
such that
![]() $\|\sigma F\|_{\tau '} \le \|F\|_{\tau }$
and
$\|\sigma F\|_{\tau '} \le \|F\|_{\tau }$
and
![]() $\overline {\sigma F} = \overline F \circ \widetilde \sigma $
.
$\overline {\sigma F} = \overline F \circ \widetilde \sigma $
.
To prove the claim, let
![]() $F \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
; we distinguish two cases.
$F \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
; we distinguish two cases.
Case 1:
![]() $n=0$
. Choose convergent
$n=0$
. Choose convergent
![]() $F_p \in \mathbb {C}\left \{X^*,Y\right \}$
such that
$F_p \in \mathbb {C}\left \{X^*,Y\right \}$
such that
![]() $\overline F =_{\tau } \sum _p \overline {F_p}$
; as in Case 1 of the proof of [Reference Van den Dries and Speissegger12, Lemma 4.3], it follows that
$\overline F =_{\tau } \sum _p \overline {F_p}$
; as in Case 1 of the proof of [Reference Van den Dries and Speissegger12, Lemma 4.3], it follows that
![]() $\sum _p \left \|\overline {F_p}\right \|_{S^{\tau '}_p} r^p \le \|F\|_{\tau }$
and
$\sum _p \left \|\overline {F_p}\right \|_{S^{\tau '}_p} r^p \le \|F\|_{\tau }$
and
![]() $\overline {\sigma F} = \overline F \circ \widetilde \sigma $
. Also, let
$\overline {\sigma F} = \overline F \circ \widetilde \sigma $
. Also, let
![]() $k'$
be defined for
$k'$
be defined for
![]() $K'$
as k is defined for K; it remains to show that
$K'$
as k is defined for K; it remains to show that
![]() $\sum _p \|\sigma F_p \|_{R',k',p}\ r^p < \infty $
. Let
$\sum _p \|\sigma F_p \|_{R',k',p}\ r^p < \infty $
. Let
![]() $s \in D^{k'}_p\left (e^{R'}\right )$
; then we have
$s \in D^{k'}_p\left (e^{R'}\right )$
; then we have
![]() $\|\sigma F_p\|_s = \|F_p\|_{\sigma (s)}$
, for each
$\|\sigma F_p\|_s = \|F_p\|_{\sigma (s)}$
, for each
![]() $p \in \mathbb {N}$
, by the definition of these norms. Since
$p \in \mathbb {N}$
, by the definition of these norms. Since
![]() $\sigma (s) \in D^k_p\left (e^R\right )$
, by the above, we obtain
$\sigma (s) \in D^k_p\left (e^R\right )$
, by the above, we obtain
Since
![]() $s \in D^{k'}_p\left (e^{R'}\right )$
was arbitrary, it follows that
$s \in D^{k'}_p\left (e^{R'}\right )$
was arbitrary, it follows that
![]() $\sum _p \|\sigma F_p \|_{R',k',p}\ r^p \le \sum _p \|F_p\|_{R,k,p}\ r^p$
, so that
$\sum _p \|\sigma F_p \|_{R',k',p}\ r^p \le \sum _p \|F_p\|_{R,k,p}\ r^p$
, so that
![]() $\sigma F \in \mathbb {C}\left \{(X')^*,Y\right \}_{\tau ',\rho }$
. Moreover, since this argument works for all sequences of convergent
$\sigma F \in \mathbb {C}\left \{(X')^*,Y\right \}_{\tau ',\rho }$
. Moreover, since this argument works for all sequences of convergent
![]() $F_p \in \mathbb {C}\left \{X^*,Y\right \}$
such that
$F_p \in \mathbb {C}\left \{X^*,Y\right \}$
such that
![]() $\overline F =_{\tau } \sum _p \overline {F_p}$
, we also get
$\overline F =_{\tau } \sum _p \overline {F_p}$
, we also get
![]() $\|\sigma F\|_{\tau '} \le \|F\|_{\tau }$
in this case.
$\|\sigma F\|_{\tau '} \le \|F\|_{\tau }$
in this case.
Case 2:
![]() $n>0$
. This case literally follows the proof of Case 2 of [Reference Van den Dries and Speissegger12, Lemma 4.3], which we reproduce here for the convenience of the reader. We let
$n>0$
. This case literally follows the proof of Case 2 of [Reference Van den Dries and Speissegger12, Lemma 4.3], which we reproduce here for the convenience of the reader. We let
![]() $F = \sum F_{\beta }(X) Y^{\beta }$
with each
$F = \sum F_{\beta }(X) Y^{\beta }$
with each
![]() $F_{\beta } \in \mathbb {C}\left \{X^*\right \}_{\tau }$
. By Case 1, each
$F_{\beta } \in \mathbb {C}\left \{X^*\right \}_{\tau }$
. By Case 1, each
![]() $\sigma F_{\beta }$
belongs to
$\sigma F_{\beta }$
belongs to
![]() $\mathbb {C}\left \{(X')^*\right \}_{\tau '}$
with
$\mathbb {C}\left \{(X')^*\right \}_{\tau '}$
with
![]() $\left \|\sigma F_{\beta }\right \|_{\tau '} \leq \left \|F_{\beta }\right \|_{\tau }$
. Hence,
$\left \|\sigma F_{\beta }\right \|_{\tau '} \leq \left \|F_{\beta }\right \|_{\tau }$
. Hence,
![]() $\sigma F$
belongs to
$\sigma F$
belongs to
![]() $\mathbb {C}\left \{(X')^*;Y\right \}_{\tau ',\rho }$
and satisfies
$\mathbb {C}\left \{(X')^*;Y\right \}_{\tau ',\rho }$
and satisfies
![]() $\left \|\sigma F\right \|_{\tau ',\rho } \leq \left \|F\right \|_{\tau ,\rho }$
, and it remains to show that
$\left \|\sigma F\right \|_{\tau ',\rho } \leq \left \|F\right \|_{\tau ,\rho }$
, and it remains to show that
![]() $\overline {\sigma F} = \overline F \circ \widetilde \sigma $
. For each
$\overline {\sigma F} = \overline F \circ \widetilde \sigma $
. For each
![]() $d \in \mathbb {N}$
, we put
$d \in \mathbb {N}$
, we put
By the same argument as before, each
![]() $\sigma F_d$
belongs to
$\sigma F_d$
belongs to
![]() $\mathbb {C}\left \{(X')^*, Y\right \}_{\tau ',\rho }$
, and since each
$\mathbb {C}\left \{(X')^*, Y\right \}_{\tau ',\rho }$
, and since each
![]() $F_d$
has finite support (as a series in Y), we get
$F_d$
has finite support (as a series in Y), we get
![]() $\overline {\sigma F_d} = \overline {F_d} \circ \widetilde \sigma $
. Clearly
$\overline {\sigma F_d} = \overline {F_d} \circ \widetilde \sigma $
. Clearly
![]() $\lim _{d \to \infty } \overline {F_d}(w,y) = \overline {F}(w,y)$
for all
$\lim _{d \to \infty } \overline {F_d}(w,y) = \overline {F}(w,y)$
for all
![]() $(w,y) \in S^{\tau } \times D(\rho )$
. Moreover, since
$(w,y) \in S^{\tau } \times D(\rho )$
. Moreover, since
![]() $\sigma :\mathbb {C}\left [\!\left [X;Y\right ]\!\right ] \longrightarrow \mathbb {C}\left [\!\left [X', Y\right ]\!\right ]$
is a homomorphism, we have
$\sigma :\mathbb {C}\left [\!\left [X;Y\right ]\!\right ] \longrightarrow \mathbb {C}\left [\!\left [X', Y\right ]\!\right ]$
is a homomorphism, we have
so that
![]() $\lim _{d \to \infty } \overline {\sigma F_d}(w',y) = \overline {\sigma F}(w',y)$
for all
$\lim _{d \to \infty } \overline {\sigma F_d}(w',y) = \overline {\sigma F}(w',y)$
for all
![]() $(w',y) \in S^{\tau '} \times D(\rho )$
. Hence,
$(w',y) \in S^{\tau '} \times D(\rho )$
. Hence,
for all
![]() $(w',y) \in S^{\tau '} \times D(\rho )$
, which finishes the proof.
$(w',y) \in S^{\tau '} \times D(\rho )$
, which finishes the proof.
We now proceed to proving closure under each of the substitutions in Example 4.1.
4.1 Permutations
Let
![]() $\sigma $
be a permutation of
$\sigma $
be a permutation of
![]() $\{1, \dots , m\}$
and, for
$\{1, \dots , m\}$
and, for
![]() $x \in \overline {\mathbb {C}}^m$
, we denote by
$x \in \overline {\mathbb {C}}^m$
, we denote by
![]() $\sigma (x)$
the tuple
$\sigma (x)$
the tuple
![]() $ \left (x_{\sigma (1)}, \dots , x_{\sigma (m)}\right )$
. For
$ \left (x_{\sigma (1)}, \dots , x_{\sigma (m)}\right )$
. For
![]() $\tau \in \mathcal {T}_m$
, we set
$\tau \in \mathcal {T}_m$
, we set
note that
![]() $\sigma :\mathcal {T}_m \longrightarrow \mathcal {T}_m$
is a bijection.
$\sigma :\mathcal {T}_m \longrightarrow \mathcal {T}_m$
is a bijection.
Lemma 4.3 For
![]() $\tau \in \mathcal {T}_m$
and
$\tau \in \mathcal {T}_m$
and
![]() $\rho \in (0,\infty )^n$
, we have
$\rho \in (0,\infty )^n$
, we have
![]() $F \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
if and only if
$F \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
if and only if
![]() $\sigma F \in \mathbb {C}\left \{X^*,Y\right \}_{\sigma ^{-1}(\tau ),\rho }$
, and for such F, we have
$\sigma F \in \mathbb {C}\left \{X^*,Y\right \}_{\sigma ^{-1}(\tau ),\rho }$
, and for such F, we have
![]() $\overline {\sigma F} = \overline F \circ \widetilde \sigma $
and
$\overline {\sigma F} = \overline F \circ \widetilde \sigma $
and
![]() $\|\sigma F\|_{\sigma ^{-1}(\tau ),\rho } = \|F\|_{\tau ,\rho }$
.
$\|\sigma F\|_{\sigma ^{-1}(\tau ),\rho } = \|F\|_{\tau ,\rho }$
.
Proof The proof follows the general strategy of the proof of Lemma 4.2, but is easier and left to the reader.
4.2 Blow-up charts
We let
![]() $1 \le j < i \le m$
and
$1 \le j < i \le m$
and
![]() $\lambda> 0$
and consider the regular blow-up chart
$\lambda> 0$
and consider the regular blow-up chart
![]() $\pi ^{\lambda }_{i,j}$
; the singular blow-up charts are handled similarly, but are actually easier to deal with and are left to the reader. Permuting the Gevrey variables if necessary, we assume that
$\pi ^{\lambda }_{i,j}$
; the singular blow-up charts are handled similarly, but are actually easier to deal with and are left to the reader. Permuting the Gevrey variables if necessary, we assume that
![]() $j = m-1$
and
$j = m-1$
and
![]() $i = m$
; to simplify notation, we write
$i = m$
; to simplify notation, we write
![]() $\sigma = \pi ^{\lambda }_{m,m-1}$
.
$\sigma = \pi ^{\lambda }_{m,m-1}$
.
Fix
![]() $\tau \in \mathcal {T}_m$
and
$\tau \in \mathcal {T}_m$
and
![]() $\rho \in (0,\infty )^n$
. Similar to [Reference Van den Dries and Speissegger12, Lemma 4.7], we now choose
$\rho \in (0,\infty )^n$
. Similar to [Reference Van den Dries and Speissegger12, Lemma 4.7], we now choose
![]() $\theta ' \in (\pi /2,\theta )$
and
$\theta ' \in (\pi /2,\theta )$
and
![]() $\rho _0> 0$
such that
$\rho _0> 0$
such that
![]() $k_m |\arg (\lambda + v)| < \theta - \theta '$
for all
$k_m |\arg (\lambda + v)| < \theta - \theta '$
for all
![]() $v \in D(2\rho _0)$
and all
$v \in D(2\rho _0)$
and all
![]() $k \in K$
. We set
$k \in K$
. We set
![]() $k':= (k_1, \dots , k_{m-2}, k_{m-1}+k_m)$
for
$k':= (k_1, \dots , k_{m-2}, k_{m-1}+k_m)$
for
![]() $k \in K$
,
$k \in K$
,
![]() $l:= \max \{k_m:\ k \in K\}$
and
$l:= \max \{k_m:\ k \in K\}$
and
![]() $R_{m-1}':= \min \left \{R_{m-1}, R_m, \frac {R_m}{(\lambda + 2\rho _0)^l}\right \}$
, as well as
$R_{m-1}':= \min \left \{R_{m-1}, R_m, \frac {R_m}{(\lambda + 2\rho _0)^l}\right \}$
, as well as
![]() $\Delta ':= \Pi _{m-1}(\Delta )$
and, finally,
$\Delta ':= \Pi _{m-1}(\Delta )$
and, finally,
![]() $\tau ':= (K',R',r,\theta ',\Delta ')$
and
$\tau ':= (K',R',r,\theta ',\Delta ')$
and
![]() $\rho ':= (\rho _0,\rho )$
. By Claims 1 and 2 in the proof of [Reference Van den Dries and Speissegger12, Lemma 4.7], we have
$\rho ':= (\rho _0,\rho )$
. By Claims 1 and 2 in the proof of [Reference Van den Dries and Speissegger12, Lemma 4.7], we have
![]() $\widetilde \sigma \left (S^{\tau '} \times D(\rho ')\right ) \subseteq S^{\tau } \times D(\rho )$
and, for each p, that
$\widetilde \sigma \left (S^{\tau '} \times D(\rho ')\right ) \subseteq S^{\tau } \times D(\rho )$
and, for each p, that
![]() $\widetilde \sigma \left (S^{\tau '}_p \times D(\rho ')\right ) \subseteq S^{\tau }_p \times D(\rho )$
.
$\widetilde \sigma \left (S^{\tau '}_p \times D(\rho ')\right ) \subseteq S^{\tau }_p \times D(\rho )$
.
Proposition 4.4 For
![]() $F \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
, we have
$F \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
, we have
![]() $\sigma F \in \mathbb {C}\left \{(X')^*,Y'\right \}_{\tau ',\rho '}$
such that
$\sigma F \in \mathbb {C}\left \{(X')^*,Y'\right \}_{\tau ',\rho '}$
such that
![]() $\overline {\sigma F} = \overline {F} \circ \widetilde \sigma $
and
$\overline {\sigma F} = \overline {F} \circ \widetilde \sigma $
and
![]() $\|\sigma F\|_{\tau ',\rho '} \le C \|F\|_{\tau ,\rho }$
, where
$\|\sigma F\|_{\tau ',\rho '} \le C \|F\|_{\tau ,\rho }$
, where
![]() $C \ge 1$
is independent of F.
$C \ge 1$
is independent of F.
Proof Let
![]() $F \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
; again, we distinguish two cases.
$F \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
; again, we distinguish two cases.
Case 1:
![]() $n=0$
. Then
$n=0$
. Then
![]() $F \in \mathbb {C}\left \{X^*\right \}_{\tau }$
, and we choose convergent
$F \in \mathbb {C}\left \{X^*\right \}_{\tau }$
, and we choose convergent
![]() $F_p \in \mathbb {C}\left \{X^*\right \}$
such that
$F_p \in \mathbb {C}\left \{X^*\right \}$
such that
![]() $\overline F =_{\tau } \sum _p \overline {F_p}$
. As in the proof of [Reference Van den Dries and Speissegger12, Lemma 4.7], for each
$\overline F =_{\tau } \sum _p \overline {F_p}$
. As in the proof of [Reference Van den Dries and Speissegger12, Lemma 4.7], for each
![]() $p, \nu \in \mathbb {N}$
, we define
$p, \nu \in \mathbb {N}$
, we define
![]() $f_{p,\nu }:S^{\tau '}_p \longrightarrow \mathbb {C}$
and
$f_{p,\nu }:S^{\tau '}_p \longrightarrow \mathbb {C}$
and
![]() $f_{\nu }:S^{\tau '} \longrightarrow \mathbb {C}$
by
$f_{\nu }:S^{\tau '} \longrightarrow \mathbb {C}$
by
 $$ \begin{align*}f_{p,\nu} (w') := \frac 1{\nu!} \frac {\partial^{\nu} \left(\overline{F_p} \circ \widetilde\sigma\right)} {\partial v^{\nu}} (w', 0) \quad\text{and}\quad f_{\nu} (w') := \frac 1{\nu!} \frac {\partial^{\nu} \left(\overline F \circ \widetilde\sigma\right)} {\partial v^{\nu}} (w', 0).\end{align*} $$
$$ \begin{align*}f_{p,\nu} (w') := \frac 1{\nu!} \frac {\partial^{\nu} \left(\overline{F_p} \circ \widetilde\sigma\right)} {\partial v^{\nu}} (w', 0) \quad\text{and}\quad f_{\nu} (w') := \frac 1{\nu!} \frac {\partial^{\nu} \left(\overline F \circ \widetilde\sigma\right)} {\partial v^{\nu}} (w', 0).\end{align*} $$
The argument there shows that, for each
![]() $\nu $
, we have
$\nu $
, we have
![]() $f_{\nu } = \sum _p f_{p,\nu }$
on
$f_{\nu } = \sum _p f_{p,\nu }$
on
![]() $S^{\tau '}$
with
$S^{\tau '}$
with
![]() $\|f_{\nu }\|_{S^{\tau '}} \le \left \|\overline F\right \|_{S^{\tau }}/(2\rho _0)^{\nu }$
. Hence,
$\|f_{\nu }\|_{S^{\tau '}} \le \left \|\overline F\right \|_{S^{\tau }}/(2\rho _0)^{\nu }$
. Hence,
![]() $\sum _{\nu } \|f_{\nu }\|_{S^{\tau '}} \rho _0^{\nu } \le \left \|\overline F\right \|_{S^{\tau }}$
, and it follows from Taylor’s theorem that
$\sum _{\nu } \|f_{\nu }\|_{S^{\tau '}} \rho _0^{\nu } \le \left \|\overline F\right \|_{S^{\tau }}$
, and it follows from Taylor’s theorem that
So it remains to show that each
![]() $f_{\nu }$
belongs to
$f_{\nu }$
belongs to
![]() $\mathcal {G}_{\tau '}$
; to do so, we define
$\mathcal {G}_{\tau '}$
; to do so, we define
![]() $k'$
for
$k'$
for
![]() $K'$
as k was defined for K, and we establish the following claim.
$K'$
as k was defined for K, and we establish the following claim.
Claim
Each
![]() $f_{p,\nu }$
is given by a generalized power series
$f_{p,\nu }$
is given by a generalized power series
![]() $F_{p,\nu }$
with support in
$F_{p,\nu }$
with support in
![]() $\Delta '$
such that
$\Delta '$
such that
![]() $\|F_{p,\nu }\|_{R',k',p} \le C \cdot \|F_p\|_{R,k,p}/(2\rho _0)^{\nu }$
, where
$\|F_{p,\nu }\|_{R',k',p} \le C \cdot \|F_p\|_{R,k,p}/(2\rho _0)^{\nu }$
, where
![]() $C>0$
is independent of F, p or
$C>0$
is independent of F, p or
![]() $\nu $
.
$\nu $
.
To see the claim, we use [Reference Van den Dries and Speissegger11, Lemma 6.5]—or more precisely, the following modification of it: the stated hypotheses there, namely, that
![]() $\tau \le \rho $
,
$\tau \le \rho $
,
![]() $\tau _m < \lambda $
and
$\tau _m < \lambda $
and
![]() $\tau _{m-1}^{\gamma }(\lambda + \tau _m) < \rho _m$
, were sufficient for the purposes of that paper, but not quite necessary to obtain the same conclusion from the proof of that lemma. Indeed, it suffices to assume that
$\tau _{m-1}^{\gamma }(\lambda + \tau _m) < \rho _m$
, were sufficient for the purposes of that paper, but not quite necessary to obtain the same conclusion from the proof of that lemma. Indeed, it suffices to assume that
![]() $\tau _i \le \rho _i$
for all
$\tau _i \le \rho _i$
for all
![]() $i \ne m$
, that
$i \ne m$
, that
![]() $\tau _m < \lambda $
and that
$\tau _m < \lambda $
and that
![]() $\tau _{m-1}^{\gamma }(\lambda + \tau _m) \le \rho _m$
to obtain the same conclusion, and we shall verify these weaker hypotheses below (with
$\tau _{m-1}^{\gamma }(\lambda + \tau _m) \le \rho _m$
to obtain the same conclusion, and we shall verify these weaker hypotheses below (with
![]() $\gamma = 1)$
in order to apply that lemma here, without further mention of this discrepancy.
$\gamma = 1)$
in order to apply that lemma here, without further mention of this discrepancy.
On the one hand, by Taylor’s theorem, we have for each p that
On the other hand, using the binomial formula, we have for each p that
 $$ \begin{align*}\sigma F_p = \sum_{\nu} F_{p,\nu}(X') \cdot X_m^{\nu} \quad\text{with}\quad F_{p,\nu}(X') = \frac1{\nu!} \frac{\partial^{\nu} (\sigma F_p)}{\partial X_m^{\nu}}(X',0);\end{align*} $$
$$ \begin{align*}\sigma F_p = \sum_{\nu} F_{p,\nu}(X') \cdot X_m^{\nu} \quad\text{with}\quad F_{p,\nu}(X') = \frac1{\nu!} \frac{\partial^{\nu} (\sigma F_p)}{\partial X_m^{\nu}}(X',0);\end{align*} $$
note that each
![]() $F_{p,\nu }$
has support contained in
$F_{p,\nu }$
has support contained in
![]() $\Delta '$
.
$\Delta '$
.
We now fix an arbitrary
![]() $s' \in \operatorname {\mathrm {cl}}\left (D^{k'}_p(\log R')\right ) \cap (0,\infty )^{m-1}$
and set
$s' \in \operatorname {\mathrm {cl}}\left (D^{k'}_p(\log R')\right ) \cap (0,\infty )^{m-1}$
and set
![]() $s:= (s',2\rho _0)$
and
$s:= (s',2\rho _0)$
and
![]() $t:= \sigma (s)$
. By Claim 2 of [Reference Van den Dries and Speissegger12, Lemma 4.7], we have
$t:= \sigma (s)$
. By Claim 2 of [Reference Van den Dries and Speissegger12, Lemma 4.7], we have
![]() $t \in \operatorname {\mathrm {cl}}\left (D^k_p(\log R)\right )$
. Since
$t \in \operatorname {\mathrm {cl}}\left (D^k_p(\log R)\right )$
. Since
![]() $s_i = t_i$
, for
$s_i = t_i$
, for
![]() $i=1, \dots , m-1$
,
$i=1, \dots , m-1$
,
![]() $s_m = 2\rho _0 < \lambda $
, and
$s_m = 2\rho _0 < \lambda $
, and
![]() $s_{m-1}(\lambda + s_m) = t_m$
, we get from [Reference Van den Dries and Speissegger11, Lemma 6.5] a constant
$s_{m-1}(\lambda + s_m) = t_m$
, we get from [Reference Van den Dries and Speissegger11, Lemma 6.5] a constant
![]() $C\ge 1$
, independent of F, p, or
$C\ge 1$
, independent of F, p, or
![]() $\nu $
, such that
$\nu $
, such that
Since
![]() $\|\sigma F_p\|_s = \sum _{\nu } \|F_{p,\nu }\|_{s'} s_m^{\nu }$
by definition of
$\|\sigma F_p\|_s = \sum _{\nu } \|F_{p,\nu }\|_{s'} s_m^{\nu }$
by definition of
![]() $\|\cdot \|_s$
, it follows that
$\|\cdot \|_s$
, it follows that
Since
![]() $s' \in \operatorname {\mathrm {cl}}\left (D^{k'}_p(\log R')\right ) \cap (0,\infty )^{m-1}$
was arbitrary, we finally get
$s' \in \operatorname {\mathrm {cl}}\left (D^{k'}_p(\log R')\right ) \cap (0,\infty )^{m-1}$
was arbitrary, we finally get
Finally, we get from [Reference Van den Dries and Speissegger11, Lemmas 5.9(2,3) and 6.3(4)] that
![]() $f_{p,\nu } = \overline {F_{p,\nu }}$
, for each p and
$f_{p,\nu } = \overline {F_{p,\nu }}$
, for each p and
![]() $\nu $
. This finishes the proof of the claim.
$\nu $
. This finishes the proof of the claim.
It follows from the claim that
![]() $f_{\nu } =_{\tau '} \sum _p f_{p,\nu }$
. Moreover, since the claim holds for all sequences
$f_{\nu } =_{\tau '} \sum _p f_{p,\nu }$
. Moreover, since the claim holds for all sequences
![]() $F_p$
such that
$F_p$
such that
![]() $\overline F =_{\tau } \sum _p \overline {F_p}$
, we also get that
$\overline F =_{\tau } \sum _p \overline {F_p}$
, we also get that
![]() $\|f_{\nu }\|_{\tau '} \le C \cdot \|F\|_{\tau }/(2\rho _0)^{\nu }$
for each
$\|f_{\nu }\|_{\tau '} \le C \cdot \|F\|_{\tau }/(2\rho _0)^{\nu }$
for each
![]() $\nu $
. It follows that
$\nu $
. It follows that
![]() $\|\sigma F\|_{\tau ',\rho _0} = \sum _{\nu } \|f_{\nu }\|_{\tau '} \rho _0^{\nu } \le C \|F\|_{\tau }$
, which finishes the proof of the proposition in Case 1.
$\|\sigma F\|_{\tau ',\rho _0} = \sum _{\nu } \|f_{\nu }\|_{\tau '} \rho _0^{\nu } \le C \|F\|_{\tau }$
, which finishes the proof of the proposition in Case 1.
Case 2:
![]() $n>0$
. Let
$n>0$
. Let
![]() $F = \sum _{\beta \in \mathbb {N}^n} F_{\beta }(X) Y^{\beta }$
. Then
$F = \sum _{\beta \in \mathbb {N}^n} F_{\beta }(X) Y^{\beta }$
. Then
![]() $\|\sigma F\|_{\tau ',\rho '} = \sum _{\beta \in \mathbb {N}^n} \|\sigma F_{\beta }\|_{\tau ',\rho _0}\ \rho ^{\beta }$
, so the proposition in Case 2 follows from Case 1 as in the proof of Lemma 4.2.
$\|\sigma F\|_{\tau ',\rho '} = \sum _{\beta \in \mathbb {N}^n} \|\sigma F_{\beta }\|_{\tau ',\rho _0}\ \rho ^{\beta }$
, so the proposition in Case 2 follows from Case 1 as in the proof of Lemma 4.2.
4.3 Ramifications
Let
![]() $\sigma $
be a ramification of the Gevrey variable
$\sigma $
be a ramification of the Gevrey variable
![]() $X_{i_0}$
as in Example 4.1(3). Permuting coordinates, we may assume that
$X_{i_0}$
as in Example 4.1(3). Permuting coordinates, we may assume that
![]() $i_0 = 1$
. Fix
$i_0 = 1$
. Fix
![]() $\tau \in \mathcal {T}_m$
and
$\tau \in \mathcal {T}_m$
and
![]() $\rho \in (0,\infty )^n$
. We define
$\rho \in (0,\infty )^n$
. We define
and
and we set
![]() $\tau ':= (K',R',r,\theta , \Delta ')$
; then
$\tau ':= (K',R',r,\theta , \Delta ')$
; then
![]() $\Delta '$
is natural, and we have
$\Delta '$
is natural, and we have
![]() $\widetilde \sigma \left (S^{\tau '} \times D(\rho )\right ) \subseteq S^{\tau } \times D(\rho )$
and
$\widetilde \sigma \left (S^{\tau '} \times D(\rho )\right ) \subseteq S^{\tau } \times D(\rho )$
and
![]() $\widetilde \sigma \left (S^{\tau '}_p \times D(\rho )\right ) \subseteq S^{\tau }_p \times D(\rho )$
for each p.
$\widetilde \sigma \left (S^{\tau '}_p \times D(\rho )\right ) \subseteq S^{\tau }_p \times D(\rho )$
for each p.
Proposition 4.5 For
![]() $F \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
, we have
$F \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
, we have
![]() $\sigma F \in \mathbb {C}\left \{(X')^*,Y'\right \}_{\tau ',\rho }$
such that
$\sigma F \in \mathbb {C}\left \{(X')^*,Y'\right \}_{\tau ',\rho }$
such that
![]() $\overline {\sigma F} = \overline {F} \circ \widetilde \sigma $
and
$\overline {\sigma F} = \overline {F} \circ \widetilde \sigma $
and
![]() $\|\sigma F\|_{\tau ',\rho } \le \|F\|_{\tau ,\rho }$
.
$\|\sigma F\|_{\tau ',\rho } \le \|F\|_{\tau ,\rho }$
.
Proof We let
![]() $F \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
, and we reduce to the case
$F \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
, and we reduce to the case
![]() $n=0$
as in the proof of Lemma 4.2. In this case, we let
$n=0$
as in the proof of Lemma 4.2. In this case, we let
![]() $k'$
be defined for
$k'$
be defined for
![]() $K'$
as k is defined for K, and we choose convergent
$K'$
as k is defined for K, and we choose convergent
![]() $F_p \in \mathbb {C}\left \{X^*\right \}$
such that
$F_p \in \mathbb {C}\left \{X^*\right \}$
such that
![]() $\overline F =_{\tau } \sum _p \overline {F_p}$
.
$\overline F =_{\tau } \sum _p \overline {F_p}$
.
Fix p and let
![]() $s \in D^{k'}_p(R') \cap (0,\infty )^m$
be a polyradius. Then
$s \in D^{k'}_p(R') \cap (0,\infty )^m$
be a polyradius. Then
![]() $\sigma (s) \in D^k_p(R)$
by the above and
$\sigma (s) \in D^k_p(R)$
by the above and
![]() $\|\sigma F_p\|_s = \|F_p\|_{\sigma (s)} \le \|F_p\|_{R,k,p}$
. Since
$\|\sigma F_p\|_s = \|F_p\|_{\sigma (s)} \le \|F_p\|_{R,k,p}$
. Since
![]() $s \in D^{k'}_p(R')$
was arbitrary, this shows that
$s \in D^{k'}_p(R')$
was arbitrary, this shows that
![]() $\|\sigma F_p\|_{R',k',p} \le \|F_p\|_{R,k,p}$
. Since we obviously have
$\|\sigma F_p\|_{R',k',p} \le \|F_p\|_{R,k,p}$
. Since we obviously have
![]() $\|\overline {\sigma F_p}\|_{S^{\tau '}_p} \le \|\overline {F_p}\|_{S^{\tau }_p}$
, it follows that
$\|\overline {\sigma F_p}\|_{S^{\tau '}_p} \le \|\overline {F_p}\|_{S^{\tau }_p}$
, it follows that
![]() $\sigma F \in \mathbb {C}\left \{(X')^*\right \}_{\tau '}$
and
$\sigma F \in \mathbb {C}\left \{(X')^*\right \}_{\tau '}$
and
![]() $\overline {\sigma F} = \overline F \circ \widetilde \sigma $
.
$\overline {\sigma F} = \overline F \circ \widetilde \sigma $
.
Moreover, since the above inequalities hold for all choices of
![]() $F_p$
such that
$F_p$
such that
![]() $\overline F =_{\tau } \sum _p F_p$
, it follows that
$\overline F =_{\tau } \sum _p F_p$
, it follows that
![]() $\|\sigma F\|_{\tau '} \le \|F\|_{\tau }$
.
$\|\sigma F\|_{\tau '} \le \|F\|_{\tau }$
.
4.4 Translations
Let
![]() $\sigma :\{X,Y\} \longrightarrow \mathbb {R}\left \{(X,X')^*,Y'\right \}_{\mathcal {G}}$
be the translation by a point
$\sigma :\{X,Y\} \longrightarrow \mathbb {R}\left \{(X,X')^*,Y'\right \}_{\mathcal {G}}$
be the translation by a point
![]() $(a,b) \in [0,\infty )^m \times \mathbb {R}^n$
.
$(a,b) \in [0,\infty )^m \times \mathbb {R}^n$
.
Proposition 4.6 Let
![]() $\tau \in \mathcal {T}_m$
and
$\tau \in \mathcal {T}_m$
and
![]() $\rho \in (0,\infty )^n$
be such that
$\rho \in (0,\infty )^n$
be such that
![]() $\|(a,b)\| \le (R,\rho )$
. Then, for every
$\|(a,b)\| \le (R,\rho )$
. Then, for every
![]() $F \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
, we have
$F \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
, we have
![]() $\sigma F \in \mathbb {C}\left \{(X')^*, Y'\right \}_{\mathcal {G}}$
and
$\sigma F \in \mathbb {C}\left \{(X')^*, Y'\right \}_{\mathcal {G}}$
and
![]() $\overline {\sigma F} = \overline F \circ \widetilde \sigma $
.
$\overline {\sigma F} = \overline F \circ \widetilde \sigma $
.
Proof We may assume that all but one of the coordinates of
![]() $(a,b)$
are zero. If
$(a,b)$
are zero. If
![]() $a_i \ne 0$
for some i, we may assume, after permuting the Gevrey variables if necessary, that
$a_i \ne 0$
for some i, we may assume, after permuting the Gevrey variables if necessary, that
![]() $i = m$
. This case is handled similarly to the proof of Proposition 4.4, except that we use [Reference Van den Dries and Speissegger11, Lemma 6.6] instead of [Reference Van den Dries and Speissegger11, Lemma 6.5] (with a similar weakening of hypotheses for the former as used above for the latter). So we assume that
$i = m$
. This case is handled similarly to the proof of Proposition 4.4, except that we use [Reference Van den Dries and Speissegger11, Lemma 6.6] instead of [Reference Van den Dries and Speissegger11, Lemma 6.5] (with a similar weakening of hypotheses for the former as used above for the latter). So we assume that
![]() $b_j \ne 0$
for some j; in this case, we adapt the usual Taylor expansion argument for convergent series to obtain the conclusion (details are left to the reader).
$b_j \ne 0$
for some j; in this case, we adapt the usual Taylor expansion argument for convergent series to obtain the conclusion (details are left to the reader).
4.5 Infinitesimal substitutions
We recall the following observations.
Lemma 4.7 Let
![]() $\tau = (K,R,r,\theta ,\Delta ) \in \mathcal {T}_m$
and
$\tau = (K,R,r,\theta ,\Delta ) \in \mathcal {T}_m$
and
![]() $X' = (X^{\prime }_1, \dots , X^{\prime }_n)$
, and let
$X' = (X^{\prime }_1, \dots , X^{\prime }_n)$
, and let
![]() $F \in \mathbb {C}\left \{X^*\right \}_{\tau }$
.
$F \in \mathbb {C}\left \{X^*\right \}_{\tau }$
.
-
(1) For any
 $\tau ' \geq \tau $
, we have
$\tau ' \geq \tau $
, we have
 $F \in \mathbb {C}\left \{X^*\right \}_{\tau '}$
with
$F \in \mathbb {C}\left \{X^*\right \}_{\tau '}$
with
 $\|F\|_{\tau '} \le \|F\|_{\tau }$
.
$\|F\|_{\tau '} \le \|F\|_{\tau }$
. -
(2) The series
 $G(X,X'):= F(X)$
belongs to
$G(X,X'):= F(X)$
belongs to
 $\mathbb {C}\left \{(X,X')^*\right \}_{\tau '}$
with
$\mathbb {C}\left \{(X,X')^*\right \}_{\tau '}$
with
 $\|G\|_{\tau '} = \|F\|_{\tau }$
, where
$\|G\|_{\tau '} = \|F\|_{\tau }$
, where
 $\tau ' = (K',R',r,\theta ,\Delta ')$
with
$\tau ' = (K',R',r,\theta ,\Delta ')$
with
 $K' := \left \{(k,0):\ k \in K\right \}$
,
$K' := \left \{(k,0):\ k \in K\right \}$
,
 $R' := (R,S)$
for any
$R' := (R,S)$
for any
 $S>0$
, and
$S>0$
, and
 $\Delta ':= \Delta \times \Gamma $
for any natural
$\Delta ':= \Delta \times \Gamma $
for any natural
 $\Gamma \subseteq [0,\infty )^n$
.
$\Gamma \subseteq [0,\infty )^n$
.
Proof Part (1) is a consequence of the discussion in Section 3.6. For part (2), note that
![]() $S^{\tau '} = S^{\tau } \times H(\log S)$
and
$S^{\tau '} = S^{\tau } \times H(\log S)$
and
![]() $S^{\tau '}_p = S^{\tau }_p \times H(\log S)$
, so that
$S^{\tau '}_p = S^{\tau }_p \times H(\log S)$
, so that
![]() $\|G\|_{\tau '} = \|F\|_{\tau }$
.
$\|G\|_{\tau '} = \|F\|_{\tau }$
.
Remark 4.8 We also need the following (crude) estimates from combinatorics. Let
![]() $n \in \mathbb {N}$
.
$n \in \mathbb {N}$
.
-
(1) Given
 $k \in \mathbb {N}$
, the number of elements
$k \in \mathbb {N}$
, the number of elements
 $\beta \in \mathbb {N}^n$
such that
$\beta \in \mathbb {N}^n$
such that
 $\sum \beta = k$
is bounded above by
$\sum \beta = k$
is bounded above by
 $k^n$
, because
$k^n$
, because
 $\{\beta \in \mathbb {N}^n:\ \sum \beta = k\} \subseteq \{1, \dots , k\}^n$
.
$\{\beta \in \mathbb {N}^n:\ \sum \beta = k\} \subseteq \{1, \dots , k\}^n$
. -
(2) For
 $\beta \in \mathbb {N}^n$
and
$\beta \in \mathbb {N}^n$
and
 $k \in \mathbb {N}$
, the number of ways to write
$k \in \mathbb {N}$
, the number of ways to write
 $\beta $
as the sum of at most
$\beta $
as the sum of at most
 $\sum \beta $
many nonzero elements in
$\sum \beta $
many nonzero elements in
 $\mathbb {N}^n$
is bounded above by
$\mathbb {N}^n$
is bounded above by
 $2^{n\sum \beta }$
. To see this, note that if
$2^{n\sum \beta }$
. To see this, note that if
 $n=1$
, then each such sum corresponds to a strictly increasing k-tuple
$n=1$
, then each such sum corresponds to a strictly increasing k-tuple
 $0 < a_1 < \cdots < a_k = \beta $
with
$0 < a_1 < \cdots < a_k = \beta $
with
 $k \le \beta = \sum \beta $
; so there are at most
$k \le \beta = \sum \beta $
; so there are at most
 $2^{\beta } = 1+ \sum _{k=1}^{\beta } \binom {\beta }{k}$
many ways to write
$2^{\beta } = 1+ \sum _{k=1}^{\beta } \binom {\beta }{k}$
many ways to write
 $\beta $
as the sum of at most
$\beta $
as the sum of at most
 $\beta $
many nonzero natural numbers. The claim for general n follows.
$\beta $
many nonzero natural numbers. The claim for general n follows. -
(3) For
 $\gamma \in \mathbb {N}^{n'}$
and
$\gamma \in \mathbb {N}^{n'}$
and
 $k \in \mathbb {N}$
, denote by
$k \in \mathbb {N}$
, denote by
 $N(\gamma ,k)$
the number of ways to write
$N(\gamma ,k)$
the number of ways to write
 $\gamma $
as the sum of exactly k many nonzero elements in
$\gamma $
as the sum of exactly k many nonzero elements in
 $\mathbb {N}^{n'}$
. Then, for any nonzero
$\mathbb {N}^{n'}$
. Then, for any nonzero
 $\beta \in \mathbb {N}^n$
, we have
$\beta \in \mathbb {N}^n$
, we have  $$ \begin{align*}N\left(\gamma,\sum\beta\right) = \sum_{\gamma^1 + \cdots + \gamma^n = \gamma} \left(\prod_{j=1}^n N\left(\gamma^j,\beta_j\right)\right).\end{align*} $$
$$ \begin{align*}N\left(\gamma,\sum\beta\right) = \sum_{\gamma^1 + \cdots + \gamma^n = \gamma} \left(\prod_{j=1}^n N\left(\gamma^j,\beta_j\right)\right).\end{align*} $$
Let
![]() $\sigma $
be an infinitesimal substitution as in Example 4.1(5); in particular, we may assume that
$\sigma $
be an infinitesimal substitution as in Example 4.1(5); in particular, we may assume that
![]() $n> 0$
. Let
$n> 0$
. Let
![]() $\tau = (K,R,r,\theta ,\Delta ) \in \mathcal {T}_m$
and
$\tau = (K,R,r,\theta ,\Delta ) \in \mathcal {T}_m$
and
![]() $\rho \in (0,\infty )^n$
, and let
$\rho \in (0,\infty )^n$
, and let
![]() $F = \sum _{\beta \in \mathbb {N}^n} F_{\beta } Y^{\beta } \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
. By Lemma 3.8(2), there exist
$F = \sum _{\beta \in \mathbb {N}^n} F_{\beta } Y^{\beta } \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
. By Lemma 3.8(2), there exist
![]() $\tau ' \in \mathcal {T}_{m'}$
and
$\tau ' \in \mathcal {T}_{m'}$
and
![]() $\rho ' \in (0,\infty )^{n'}$
such that
$\rho ' \in (0,\infty )^{n'}$
such that
in particular, we have
![]() $\widetilde {\sigma }\left (S^{\tau } \times S^{\tau '} \times D(\rho ')\right ) \subseteq S^{\tau } \times D(\rho )$
. For each j, we write
$\widetilde {\sigma }\left (S^{\tau } \times S^{\tau '} \times D(\rho ')\right ) \subseteq S^{\tau } \times D(\rho )$
. For each j, we write
![]() $\sigma (Y_j) = \sum _{\gamma \in \mathbb {N}^{n'}} G_{j,\gamma }(X') (Y')^{\gamma }$
with
$\sigma (Y_j) = \sum _{\gamma \in \mathbb {N}^{n'}} G_{j,\gamma }(X') (Y')^{\gamma }$
with
![]() $G_{j,\gamma } \in \mathbb {C}\left \{(X')^*\right \}_{\tau '}$
, and we write
$G_{j,\gamma } \in \mathbb {C}\left \{(X')^*\right \}_{\tau '}$
, and we write
![]() $\tau ' = (K',R',r,\theta ,\Delta ')$
(we can always reduce to the case where r and
$\tau ' = (K',R',r,\theta ,\Delta ')$
(we can always reduce to the case where r and
![]() $\theta $
are the same for both
$\theta $
are the same for both
![]() $\tau $
and
$\tau $
and
![]() $\tau '$
).
$\tau '$
).
By Lemma 4.7(2), we have
![]() $F_{\beta } \in \mathbb {C}\left \{(X,X')^*\right \}_{\eta _1}$
for each
$F_{\beta } \in \mathbb {C}\left \{(X,X')^*\right \}_{\eta _1}$
for each
![]() $\beta $
, where
$\beta $
, where
with
![]() $K_1 := \left \{(k,0):\ k \in K\right \}$
. Again by Lemma 4.7(2), and by Lemma 4.3, we have
$K_1 := \left \{(k,0):\ k \in K\right \}$
. Again by Lemma 4.7(2), and by Lemma 4.3, we have
![]() $G_{j,\gamma } \in \mathbb {C}\left \{(X,X')^*\right \}_{\eta _2}$
for each j and each
$G_{j,\gamma } \in \mathbb {C}\left \{(X,X')^*\right \}_{\eta _2}$
for each j and each
![]() $\gamma $
, where
$\gamma $
, where
with
![]() $K_1 := \left \{(0,k):\ k \in K'\right \}$
. So from Lemma 4.7(1), we get that each
$K_1 := \left \{(0,k):\ k \in K'\right \}$
. So from Lemma 4.7(1), we get that each
![]() $F_{\beta }$
and each
$F_{\beta }$
and each
![]() $G_{j,\gamma }$
belongs to
$G_{j,\gamma }$
belongs to
![]() $\mathbb {C}\left \{(X,X')^*\right \}_{\eta }$
, where
$\mathbb {C}\left \{(X,X')^*\right \}_{\eta }$
, where
![]() $\eta = (L,(R,R'),r,\theta , \Delta \times \Delta ')$
with
$\eta = (L,(R,R'),r,\theta , \Delta \times \Delta ')$
with
![]() $L:= K_1 \cup K_2$
. Moreover, Lemma 4.7 implies that
$L:= K_1 \cup K_2$
. Moreover, Lemma 4.7 implies that
![]() $\|F_{\beta }\|_{\eta } \le \|F_{\beta }\|_{\tau }$
and
$\|F_{\beta }\|_{\eta } \le \|F_{\beta }\|_{\tau }$
and
![]() $\|G_{j,\gamma }\|_{\eta } \le \|G_{j,\gamma }\|_{\tau '}$
for each
$\|G_{j,\gamma }\|_{\eta } \le \|G_{j,\gamma }\|_{\tau '}$
for each
![]() $\beta $
, j, and
$\beta $
, j, and
![]() $\gamma $
.
$\gamma $
.
Proposition 4.9 For
![]() $F \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
, we have
$F \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
, we have
![]() $\sigma F \in \mathbb {C}\left \{(X,X')^*,Y'\right \}_{\eta ,\rho '}$
such that
$\sigma F \in \mathbb {C}\left \{(X,X')^*,Y'\right \}_{\eta ,\rho '}$
such that
![]() $\overline {\sigma F} = \overline {F} \circ \widetilde \sigma $
and
$\overline {\sigma F} = \overline {F} \circ \widetilde \sigma $
and
![]() $\|\sigma F\|_{\eta ,\rho '} \le A\|F\|_{\tau ,\rho }$
, for some absolute constant
$\|\sigma F\|_{\eta ,\rho '} \le A\|F\|_{\tau ,\rho }$
, for some absolute constant
![]() $A>0$
.
$A>0$
.
Proof A first computation (left to the reader) shows that, for
![]() $\beta \in \mathbb {N}^{n}$
, we have
$\beta \in \mathbb {N}^{n}$
, we have
where
 $$ \begin{align*}H_{\beta,\gamma}(X') = \sum_{\gamma^1 + \cdots + \gamma^n = \gamma} \left(\prod_{j=1}^n \left(\sum_{\delta^1 + \cdots + \delta^{\beta_j} = \gamma^j} \left(\prod_{p=1}^{\beta_j} G_{j,\delta^p}(X')\right)\right)\right)\end{align*} $$
$$ \begin{align*}H_{\beta,\gamma}(X') = \sum_{\gamma^1 + \cdots + \gamma^n = \gamma} \left(\prod_{j=1}^n \left(\sum_{\delta^1 + \cdots + \delta^{\beta_j} = \gamma^j} \left(\prod_{p=1}^{\beta_j} G_{j,\delta^p}(X')\right)\right)\right)\end{align*} $$
and each
![]() $\gamma ^j$
and
$\gamma ^j$
and
![]() $\delta ^p$
belongs to
$\delta ^p$
belongs to
![]() $\mathbb {N}^{n'}$
and is nonzero. Therefore,
$\mathbb {N}^{n'}$
and is nonzero. Therefore,
 $$ \begin{align*}\sigma F(X,X',Y') = \sum_{\beta} F_{\beta}(X) \sigma(Y)^{\beta} = \sum_{\gamma} \left(\sum_{\beta} F_{\beta}(X) H_{\beta,\gamma}(X')\right) (Y')^{\gamma}.\end{align*} $$
$$ \begin{align*}\sigma F(X,X',Y') = \sum_{\beta} F_{\beta}(X) \sigma(Y)^{\beta} = \sum_{\gamma} \left(\sum_{\beta} F_{\beta}(X) H_{\beta,\gamma}(X')\right) (Y')^{\gamma}.\end{align*} $$
By the above, we have
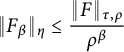 $$ \begin{align} \|F_{\beta}\|_{\eta} \le \frac{\|F\|_{\tau,\rho}}{\rho^{\beta}} \end{align} $$
$$ \begin{align} \|F_{\beta}\|_{\eta} \le \frac{\|F\|_{\tau,\rho}}{\rho^{\beta}} \end{align} $$
for each
![]() $\beta $
, and setting
$\beta $
, and setting
![]() $\widetilde \rho := 2^{n'+1}\rho '$
,
$\widetilde \rho := 2^{n'+1}\rho '$
,
 $$ \begin{align} \|G_{j,\gamma}\|_{\eta} \le \frac{\|\sigma(Y_j)\|_{\tau',\widetilde\rho}}{(\widetilde\rho)^{\gamma}} \le \frac{\rho_j/2}{(\widetilde\rho)^{\gamma}} \end{align} $$
$$ \begin{align} \|G_{j,\gamma}\|_{\eta} \le \frac{\|\sigma(Y_j)\|_{\tau',\widetilde\rho}}{(\widetilde\rho)^{\gamma}} \le \frac{\rho_j/2}{(\widetilde\rho)^{\gamma}} \end{align} $$
for each j and
![]() $\gamma $
. Therefore, denoting by
$\gamma $
. Therefore, denoting by
![]() $N(\gamma ,k)$
the number of ways to write
$N(\gamma ,k)$
the number of ways to write
![]() $\gamma $
as the sum of k many nonzero elements in
$\gamma $
as the sum of k many nonzero elements in
![]() $\mathbb {N}^{n'}$
, we get for each
$\mathbb {N}^{n'}$
, we get for each
![]() $\beta $
and
$\beta $
and
![]() $\gamma $
from Remark 4.8(3) that
$\gamma $
from Remark 4.8(3) that
 $$ \begin{align*} \|H_{\beta,\gamma}\|_{\eta} & \le \sum_{\gamma^1 + \cdots + \gamma^n = \gamma} \left(\prod_{j=1}^n \left(\sum_{\delta^1 + \cdots + \delta^{\beta_j} = \gamma^j} \left(\prod_{p=1}^{\beta_j} \frac{\rho_j/2}{(\widetilde\rho)^{\delta^p}}\right)\right)\right) \\ &= \sum_{\gamma^1 + \cdots + \gamma^n = \gamma} \left(\prod_{j=1}^n \left(\sum_{\delta^1 + \cdots + \delta^{\beta_j} = \gamma^j} \frac{(\rho_j/2)^{\beta_j}}{(\widetilde\rho)^{\gamma^j}}\right)\right) \\ &= \sum_{\gamma^1 + \cdots + \gamma^n = \gamma} \left(\prod_{j=1}^n \left( \frac{(\rho_j/2)^{\beta_j}}{(\widetilde\rho)^{\gamma^j}} N\left(\gamma^j,\beta_j\right) \right)\right) \\ &= \sum_{\gamma^1 + \cdots + \gamma^n = \gamma} \left(\frac{(\rho/2)^{\beta}}{(\widetilde\rho)^{\gamma}} \left(\prod_{j=1}^n N\left(\gamma^j,\beta_j\right)\right)\right) \\ &= \frac{(\rho/2)^{\beta}}{(\widetilde\rho)^{\gamma}} N\left(\gamma,\sum\beta\right). \\ \end{align*} $$
$$ \begin{align*} \|H_{\beta,\gamma}\|_{\eta} & \le \sum_{\gamma^1 + \cdots + \gamma^n = \gamma} \left(\prod_{j=1}^n \left(\sum_{\delta^1 + \cdots + \delta^{\beta_j} = \gamma^j} \left(\prod_{p=1}^{\beta_j} \frac{\rho_j/2}{(\widetilde\rho)^{\delta^p}}\right)\right)\right) \\ &= \sum_{\gamma^1 + \cdots + \gamma^n = \gamma} \left(\prod_{j=1}^n \left(\sum_{\delta^1 + \cdots + \delta^{\beta_j} = \gamma^j} \frac{(\rho_j/2)^{\beta_j}}{(\widetilde\rho)^{\gamma^j}}\right)\right) \\ &= \sum_{\gamma^1 + \cdots + \gamma^n = \gamma} \left(\prod_{j=1}^n \left( \frac{(\rho_j/2)^{\beta_j}}{(\widetilde\rho)^{\gamma^j}} N\left(\gamma^j,\beta_j\right) \right)\right) \\ &= \sum_{\gamma^1 + \cdots + \gamma^n = \gamma} \left(\frac{(\rho/2)^{\beta}}{(\widetilde\rho)^{\gamma}} \left(\prod_{j=1}^n N\left(\gamma^j,\beta_j\right)\right)\right) \\ &= \frac{(\rho/2)^{\beta}}{(\widetilde\rho)^{\gamma}} N\left(\gamma,\sum\beta\right). \\ \end{align*} $$
Also, since
![]() $N\left (\gamma , k\right ) = 0$
for
$N\left (\gamma , k\right ) = 0$
for
![]() $k> \sum \gamma $
, it follows from Remark 4.8(2) that
$k> \sum \gamma $
, it follows from Remark 4.8(2) that
 $$ \begin{align} \|H_{\beta,\gamma}\|_{\eta} \le 2^{n' \cdot \sum\gamma} \cdot \frac{(\rho/2)^{\beta}}{(\widetilde\rho)^{\gamma}}. \end{align} $$
$$ \begin{align} \|H_{\beta,\gamma}\|_{\eta} \le 2^{n' \cdot \sum\gamma} \cdot \frac{(\rho/2)^{\beta}}{(\widetilde\rho)^{\gamma}}. \end{align} $$
So for each
![]() $\gamma $
, we get
$\gamma $
, we get
 $$ \begin{align*} \left\|\sum_{\beta} (F_{\beta} H_{\beta,\gamma}) \right\|_{\eta} \le \|F\|_{\tau,\rho} \frac{2^{n'\cdot\sum\gamma}}{(\widetilde\rho)^{\gamma}} \cdot \sum_{\beta} \left(\frac12\right)^{\sum\beta}. \end{align*} $$
$$ \begin{align*} \left\|\sum_{\beta} (F_{\beta} H_{\beta,\gamma}) \right\|_{\eta} \le \|F\|_{\tau,\rho} \frac{2^{n'\cdot\sum\gamma}}{(\widetilde\rho)^{\gamma}} \cdot \sum_{\beta} \left(\frac12\right)^{\sum\beta}. \end{align*} $$
However, since
![]() $\sum _{\beta } \left (\frac 12\right )^{\sum \beta } = \sum _{k=0}^{\infty } \left (\sum _{\sum \beta = k} 1\right ) \left (\frac 12\right )^k \le C:= \sum _k \frac {k^n}{2^k}$
by Remark 4.8(1), we conclude that
$\sum _{\beta } \left (\frac 12\right )^{\sum \beta } = \sum _{k=0}^{\infty } \left (\sum _{\sum \beta = k} 1\right ) \left (\frac 12\right )^k \le C:= \sum _k \frac {k^n}{2^k}$
by Remark 4.8(1), we conclude that
 $$ \begin{align*} \left\|\sum_{\beta} (F_{\beta} H_{\beta,\gamma}) \right\|_{\eta} \le C \cdot \|F\|_{\tau,\rho} \frac{2^{n'\cdot\sum\gamma}}{(\widetilde\rho)^{\gamma}}, \end{align*} $$
$$ \begin{align*} \left\|\sum_{\beta} (F_{\beta} H_{\beta,\gamma}) \right\|_{\eta} \le C \cdot \|F\|_{\tau,\rho} \frac{2^{n'\cdot\sum\gamma}}{(\widetilde\rho)^{\gamma}}, \end{align*} $$
where
![]() $C>0$
is an absolute constant. Finally, since
$C>0$
is an absolute constant. Finally, since
![]() $(\widetilde \rho )^{\gamma } = 2^{(n'+1)\sum \gamma }\cdot (\rho ')^{\gamma }$
, we obtain
$(\widetilde \rho )^{\gamma } = 2^{(n'+1)\sum \gamma }\cdot (\rho ')^{\gamma }$
, we obtain
 $$ \begin{align} \left\|\sum_{\beta} (F_{\beta} H_{\beta,\gamma}) \right\|_{\eta} \le \frac{C \cdot \|F\|_{\tau,\rho}}{2^{\sum\gamma}\cdot (\rho')^{\gamma}}. \end{align} $$
$$ \begin{align} \left\|\sum_{\beta} (F_{\beta} H_{\beta,\gamma}) \right\|_{\eta} \le \frac{C \cdot \|F\|_{\tau,\rho}}{2^{\sum\gamma}\cdot (\rho')^{\gamma}}. \end{align} $$
Multiplying by
![]() $(\rho ')^{\gamma }$
and summing over
$(\rho ')^{\gamma }$
and summing over
![]() $\gamma $
, therefore, yields
$\gamma $
, therefore, yields
 $$ \begin{align*}\|\sigma F\|_{\eta,\rho'} \le C \cdot \|F\|_{\tau,\rho} \left(\sum_{\gamma} \left(\frac12\right)^{\sum\gamma}\right) \le C D \|F\|_{\tau,\rho}\end{align*} $$
$$ \begin{align*}\|\sigma F\|_{\eta,\rho'} \le C \cdot \|F\|_{\tau,\rho} \left(\sum_{\gamma} \left(\frac12\right)^{\sum\gamma}\right) \le C D \|F\|_{\tau,\rho}\end{align*} $$
for some absolute constant
![]() $D>0$
, as required.
$D>0$
, as required.
5 Closure properties and o-minimality
The goal of this section is to verify, for those mixed series of Section 3.7 with only real coefficients, the closure properties listed in Paragraphs 1.8 and 1.15 of [Reference Rolin and Servi7]. We will adopt the notations of the latter, and we need to define the real algebras
![]() $\mathcal {A}_{m,n,r}$
. So let
$\mathcal {A}_{m,n,r}$
. So let
![]() $m,n \in \mathbb {N}$
, and let
$m,n \in \mathbb {N}$
, and let
![]() $r = (s,t) = (s_1, \dots , s_m, t_1, \dots , t_n) \in (0,\infty )^{m+n}$
be a polyradius of type
$r = (s,t) = (s_1, \dots , s_m, t_1, \dots , t_n) \in (0,\infty )^{m+n}$
be a polyradius of type
![]() $(m,n)$
. (While we used the letter R for polyradii in the previous sections to mirror notations in [Reference Van den Dries and Speissegger12], we use the letters r, s, and t to mirror corresponding notations in [Reference Rolin and Servi7].) We set
$(m,n)$
. (While we used the letter R for polyradii in the previous sections to mirror notations in [Reference Van den Dries and Speissegger12], we use the letters r, s, and t to mirror corresponding notations in [Reference Rolin and Servi7].) We set
and define the
![]() $\mathbb {R}$
-algebras
$\mathbb {R}$
-algebras
and
Recall from [Reference Rolin and Servi7, Notation 1.7] the following definitions:
 $$ \begin{align*} I_{m,n,r} & :=(0,s_{1})\times\cdots\times(0,s_{m})\times(-t_{1},t_{1})\times\cdots\times(-t_{n},t_{n}),\\ \widehat{I}_{m,n,r} & :=[0,s_{1})\times\cdots\times[0,s_{m})\times\left(-t_{1},t_{1}\right)\times\cdots\times\left(-t_{n},t_{n}\right). \end{align*} $$
$$ \begin{align*} I_{m,n,r} & :=(0,s_{1})\times\cdots\times(0,s_{m})\times(-t_{1},t_{1})\times\cdots\times(-t_{n},t_{n}),\\ \widehat{I}_{m,n,r} & :=[0,s_{1})\times\cdots\times[0,s_{m})\times\left(-t_{1},t_{1}\right)\times\cdots\times\left(-t_{n},t_{n}\right). \end{align*} $$
In particular, each
![]() $\overline f \in \overline {\mathcal {A}}_{m,n,r}$
defines a continuous function
$\overline f \in \overline {\mathcal {A}}_{m,n,r}$
defines a continuous function
![]() $f:\widehat I_{m,n,r} \longrightarrow \mathbb {R}$
by setting
$f:\widehat I_{m,n,r} \longrightarrow \mathbb {R}$
by setting
this f is real analytic on
![]() $I_{m,n,r}$
. We let
$I_{m,n,r}$
. We let
![]() $\mathcal {A}_{m,n,r}$
be the
$\mathcal {A}_{m,n,r}$
be the
![]() $\mathbb {R}$
-algebra of all such functions obtained from
$\mathbb {R}$
-algebra of all such functions obtained from
![]() $\mathbb {R}\left \{X^*,Y\right \}_r$
, and we define the
$\mathbb {R}\left \{X^*,Y\right \}_r$
, and we define the
![]() $\mathbb {R}$
-algebra homomorphism
$\mathbb {R}$
-algebra homomorphism
![]() $T_{m,n,r}:\mathcal {A}_{m,n,r} \longrightarrow \mathbb {R}\left \{X^*,Y\right \}_r$
by letting
$T_{m,n,r}:\mathcal {A}_{m,n,r} \longrightarrow \mathbb {R}\left \{X^*,Y\right \}_r$
by letting
![]() $T_{m,n,r}f$
be the (by quasianalyticity) unique
$T_{m,n,r}f$
be the (by quasianalyticity) unique
![]() $F \in \mathbb {R}\left \{X^*,Y\right \}_r$
such that
$F \in \mathbb {R}\left \{X^*,Y\right \}_r$
such that
![]() $f(x,y) = \overline F(\log x,y)$
. We leave it to the reader to verify Properties (1)–(5) and (8) of [Reference Rolin and Servi7, Paragraph 1.8]. Properties (6) and (7) follow from Lemma 3.8(4,5).
$f(x,y) = \overline F(\log x,y)$
. We leave it to the reader to verify Properties (1)–(5) and (8) of [Reference Rolin and Servi7, Paragraph 1.8]. Properties (6) and (7) follow from Lemma 3.8(4,5).
Let
![]() $\{\mathcal {A}_{m,n}:\ m,n \in \mathbb {N}\}$
be the corresponding family of algebras of germs, as defined in [Reference Rolin and Servi7, Section 1.2]. By Proposition 4.6, every
$\{\mathcal {A}_{m,n}:\ m,n \in \mathbb {N}\}$
be the corresponding family of algebras of germs, as defined in [Reference Rolin and Servi7, Section 1.2]. By Proposition 4.6, every
![]() $f \in \mathcal {A}_{m,n,r}$
is
$f \in \mathcal {A}_{m,n,r}$
is
![]() $\mathcal {A}$
-analytic, as defined in [Reference Rolin and Servi7, Definition 1.10].
$\mathcal {A}$
-analytic, as defined in [Reference Rolin and Servi7, Definition 1.10].
It now remains to verify the properties listed in [Reference Rolin and Servi7, Paragraph 1.15] for the corresponding family
![]() $\mathcal {A}$
of algebras of germs. Property (1) there is obvious here; Property (3) follows from Lemma 4.3; Property (5) follows from Proposition 4.9; and Property (6) follows from Proposition 3.9. The remaining properties are handled below; we fix arbitrary
$\mathcal {A}$
of algebras of germs. Property (1) there is obvious here; Property (3) follows from Lemma 4.3; Property (5) follows from Proposition 4.9; and Property (6) follows from Proposition 3.9. The remaining properties are handled below; we fix arbitrary
![]() $\tau = (K,R,r,\theta ,\Delta ) \in \mathcal {T}_m$
and
$\tau = (K,R,r,\theta ,\Delta ) \in \mathcal {T}_m$
and
![]() $\rho \in (0,\infty )^n$
.
$\rho \in (0,\infty )^n$
.
5.1 Monomial division
Let
![]() $F \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
.
$F \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
.
First, we let
![]() $\alpha> 0$
and assume that
$\alpha> 0$
and assume that
![]() $F = X_1^{\alpha } G$
with
$F = X_1^{\alpha } G$
with
![]() $G \in \mathbb {C}\left [\!\left [X^*,Y\right ]\!\right ]$
. We write
$G \in \mathbb {C}\left [\!\left [X^*,Y\right ]\!\right ]$
. We write
![]() $F = \sum _{\beta \in \mathbb {N}^n} F_{\beta }(X) Y^n$
and
$F = \sum _{\beta \in \mathbb {N}^n} F_{\beta }(X) Y^n$
and
![]() $G = \sum _{\beta \in \mathbb {N}} G_{\beta }(X)Y^n$
with each
$G = \sum _{\beta \in \mathbb {N}} G_{\beta }(X)Y^n$
with each
![]() $F_{\beta } \in \mathbb {C}\left \{X^*\right \}_{\tau }$
and each
$F_{\beta } \in \mathbb {C}\left \{X^*\right \}_{\tau }$
and each
![]() $G_{\beta } \in \mathbb {C}\left [\!\left [X^*\right ]\!\right ]$
, and we set
$G_{\beta } \in \mathbb {C}\left [\!\left [X^*\right ]\!\right ]$
, and we set
![]() $\tau ':= (K,R,s,\theta ,\Delta )$
for some fixed (but arbitrary)
$\tau ':= (K,R,s,\theta ,\Delta )$
for some fixed (but arbitrary)
![]() $s \in (1,r)$
. Then, by Lemma 4.3 and Lemma 3.6, there exist
$s \in (1,r)$
. Then, by Lemma 4.3 and Lemma 3.6, there exist
![]() $C>0$
(depending only on
$C>0$
(depending only on
![]() $\frac sr$
) such that
$\frac sr$
) such that
![]() $\|G_{\beta }\|_{\tau }' \le C\|F_{\beta }\|_{\tau }$
, for each
$\|G_{\beta }\|_{\tau }' \le C\|F_{\beta }\|_{\tau }$
, for each
![]() $\beta $
. It follows that
$\beta $
. It follows that
![]() $\sum _{\beta } \|G_{\beta }\|_{\tau '} \rho ^n \le C \|F\|_{\tau ,\rho }$
, so that
$\sum _{\beta } \|G_{\beta }\|_{\tau '} \rho ^n \le C \|F\|_{\tau ,\rho }$
, so that
![]() $G \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ',\rho }$
.
$G \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ',\rho }$
.
Second, we let
![]() $n \in \mathbb {N}$
and assume that
$n \in \mathbb {N}$
and assume that
![]() $F = Y_1^n G$
with
$F = Y_1^n G$
with
![]() $G \in \mathbb {C}\left [\!\left [X^*,Y\right ]\!\right ]$
. Then by definition, we have
$G \in \mathbb {C}\left [\!\left [X^*,Y\right ]\!\right ]$
. Then by definition, we have
![]() $\|F\|_{\tau ,\rho } = \rho _1^n \|G\|_{\tau ,\rho }$
, so that
$\|F\|_{\tau ,\rho } = \rho _1^n \|G\|_{\tau ,\rho }$
, so that
![]() $G \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
.
$G \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
.
Putting together the two cases discussed here proves Property (2) of [Reference Rolin and Servi7, Paragraph 1.15].
5.2 Setting a variable equal to 0
Let
![]() $F \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
, and write
$F \in \mathbb {C}\left \{X^*,Y\right \}_{\tau ,\rho }$
, and write
![]() $F = \sum _{\beta \in \mathbb {N}^n} F_{\beta }(X) Y^n$
with each
$F = \sum _{\beta \in \mathbb {N}^n} F_{\beta }(X) Y^n$
with each
![]() $F_{\beta } \in \mathbb {C}\left \{X^*\right \}_{\tau }$
. Applying Lemma 3.3 with
$F_{\beta } \in \mathbb {C}\left \{X^*\right \}_{\tau }$
. Applying Lemma 3.3 with
![]() $\nu = 1$
and
$\nu = 1$
and
![]() $a = -\infty = \log 0$
followed by Lemma 4.3, we get that
$a = -\infty = \log 0$
followed by Lemma 4.3, we get that
![]() $F_{\beta ,0}:= F_{\beta }(X_1, \dots , X_{n-1},0) \in \mathbb {C}\left \{(X_1, \dots , X_{n-1})^*,Y\right \}_{\mu (a)}$
with
$F_{\beta ,0}:= F_{\beta }(X_1, \dots , X_{n-1},0) \in \mathbb {C}\left \{(X_1, \dots , X_{n-1})^*,Y\right \}_{\mu (a)}$
with
![]() $\|F_{\beta ,0}\|_{\mu (a)} \le \|F_{\beta }\|_{\tau }$
, for each
$\|F_{\beta ,0}\|_{\mu (a)} \le \|F_{\beta }\|_{\tau }$
, for each
![]() $\beta \in \mathbb {N}^n$
. Hence,
$\beta \in \mathbb {N}^n$
. Hence,
![]() $F_0:= F(X_1, \dots , X_{n-1},0,Y)$
belongs to
$F_0:= F(X_1, \dots , X_{n-1},0,Y)$
belongs to
![]() $\mathbb {C}\left \{(X_1, \dots , X_{n-1})^*,Y\right \}_{\mu (a),\rho }$
; this proves Property (4) of [Reference Rolin and Servi7, Paragraph 1.15].
$\mathbb {C}\left \{(X_1, \dots , X_{n-1})^*,Y\right \}_{\mu (a),\rho }$
; this proves Property (4) of [Reference Rolin and Servi7, Paragraph 1.15].
5.3 Blow-up charts
Here we refer to the blow-up charts (1)–(5) of [Reference Rolin and Servi7, Definition 1.13]. Closure under blow-up charts (1) (regular blow-ups) is proved by Proposition 4.4; closure under blow-up charts (2) (singular blow-ups) is similar, but easier and left to the reader. Blow-up charts (3) are infinitesimal substitutions and thus are handled by Proposition 4.9. For blow-up charts (4), note that
![]() $\mathbb {C}\left \{X^*,Y\right \}_{\mathcal {G}} \subseteq \mathbb {C}\left \{(X_1, \dots , X_{m+1})^*,Y\right \}_{\mathcal {G}}$
by Lemma 3.8(6); so closure under these blow-up charts follows from closure under blow-up charts (2) and Proposition 4.9. Closure under blow-up charts (5) follows again from Proposition 4.9. This proves Property (7) of [Reference Rolin and Servi7, Paragraph 1.15].
$\mathbb {C}\left \{X^*,Y\right \}_{\mathcal {G}} \subseteq \mathbb {C}\left \{(X_1, \dots , X_{m+1})^*,Y\right \}_{\mathcal {G}}$
by Lemma 3.8(6); so closure under these blow-up charts follows from closure under blow-up charts (2) and Proposition 4.9. Closure under blow-up charts (5) follows again from Proposition 4.9. This proves Property (7) of [Reference Rolin and Servi7, Paragraph 1.15].
As the results of [Reference Rolin and Servi7] do not make use of the Weierstrass Preparation Theorem (which is in general not available in the quasianalytic setting), we may dispense with proving this property here.
Proof of Main Theorem
The previous discussion implies that our system
![]() $\mathcal {A}$
of algebras satisfies Conditions (1) and (4) of [Reference Rolin and Servi7, Proviso 1.20]. Moreover, Condition (2) is implied by Proposition 4.6, while Condition (3) follows from Proposition 3.4. So the theorem follows from [Reference Rolin and Servi7, Theorems A and B]. Finally, note that it suffices to add the reciprocal function to obtain quantifier elimination, as all real powers with nonnegative exponents are already in the language
$\mathcal {A}$
of algebras satisfies Conditions (1) and (4) of [Reference Rolin and Servi7, Proviso 1.20]. Moreover, Condition (2) is implied by Proposition 4.6, while Condition (3) follows from Proposition 3.4. So the theorem follows from [Reference Rolin and Servi7, Theorems A and B]. Finally, note that it suffices to add the reciprocal function to obtain quantifier elimination, as all real powers with nonnegative exponents are already in the language
![]() $\mathcal {L}_{\mathcal {G}^*}$
.
$\mathcal {L}_{\mathcal {G}^*}$
.
Acknowledgment
The authors would like to thank the Fields Institute for Research in Mathematical Sciences for its hospitality and financial support, as part of this work was done while at its Thematic Program on Tame Geometry and Applications. They would also like to thank the referee for many useful remarks.