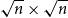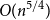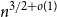1. Introduction
For graphs
![]() $G$
and
$G$
and
![]() $H$
, we say that
$H$
, we say that
![]() $G$
is Ramsey for
$G$
is Ramsey for
![]() $H$
, and write
$H$
, and write
![]() $G \rightarrow H$
, if every
$G \rightarrow H$
, if every
![]() $2$
-colouring of the edges of
$2$
-colouring of the edges of
![]() $G$
contains a monochromatic copy of
$G$
contains a monochromatic copy of
![]() $H$
. In 1978, Erdős, Faudree, Rousseau, and Schelp [Reference Erdős, Faudree, Rousseau and Schelp9] pioneered the study of the size-Ramsey number
$H$
. In 1978, Erdős, Faudree, Rousseau, and Schelp [Reference Erdős, Faudree, Rousseau and Schelp9] pioneered the study of the size-Ramsey number
![]() $\hat r(H)$
, defined as the smallest integer
$\hat r(H)$
, defined as the smallest integer
![]() $m$
for which there exists a graph
$m$
for which there exists a graph
![]() $G$
with
$G$
with
![]() $m$
edges such that
$m$
edges such that
![]() $G \rightarrow H$
. The existence of the usual Ramsey number
$G \rightarrow H$
. The existence of the usual Ramsey number
![]() $r(H)$
shows that this notion is sensible, since, for any
$r(H)$
shows that this notion is sensible, since, for any
![]() $H$
, it is easy to see that
$H$
, it is easy to see that
![]() $\hat r(H) \leqslant \binom{r(H)}{2}$
. When
$\hat r(H) \leqslant \binom{r(H)}{2}$
. When
![]() $H$
is a complete graph, this inequality is an equality, a simple fact first observed by Chvátal.
$H$
is a complete graph, this inequality is an equality, a simple fact first observed by Chvátal.
An early example showing that size-Ramsey numbers can exhibit interesting behaviour was found by Beck [Reference Beck1], who showed that
![]() $P_n$
, the path with
$P_n$
, the path with
![]() $n$
vertices, satisfies
$n$
vertices, satisfies
![]() $\hat r(P_n) = O(n)$
, which is significantly smaller than the
$\hat r(P_n) = O(n)$
, which is significantly smaller than the
![]() $O(n^2)$
bound that follows from applying the inequality above and the corresponding bound
$O(n^2)$
bound that follows from applying the inequality above and the corresponding bound
![]() $r(P_n) = O(n)$
for the usual Ramsey number of
$r(P_n) = O(n)$
for the usual Ramsey number of
![]() $P_n$
. In a follow-up paper, Beck [Reference Beck2] asked whether a similar phenomenon occurs for all bounded-degree graphs, that is, whether, for any integer
$P_n$
. In a follow-up paper, Beck [Reference Beck2] asked whether a similar phenomenon occurs for all bounded-degree graphs, that is, whether, for any integer
![]() $\Delta \geqslant 3$
, there exists a constant
$\Delta \geqslant 3$
, there exists a constant
![]() $c$
such that any graph
$c$
such that any graph
![]() $H$
with
$H$
with
![]() $n$
vertices and maximum degree
$n$
vertices and maximum degree
![]() $\Delta$
has size-Ramsey number at most
$\Delta$
has size-Ramsey number at most
![]() $cn$
. Although Rödl and Szemerédi [Reference Rödl and Szemerédi19] showed that this question has a negative answer already for
$cn$
. Although Rödl and Szemerédi [Reference Rödl and Szemerédi19] showed that this question has a negative answer already for
![]() $\Delta =3$
, much work has gone into extending Beck’s result to other natural families of graphs, including: cycles [Reference Haxell, Kohayakawa and Łuczak14], bounded-degree trees [Reference Friedman and Pippenger10], powers of paths and bounded-degree trees [Reference Berger, Kohayakawa and Maesaka3, Reference Clemens, Jenssen and Kohayakawa5, Reference Han, Jenssen, Kohayakawa, Mota and Roberts13], and more besides.
$\Delta =3$
, much work has gone into extending Beck’s result to other natural families of graphs, including: cycles [Reference Haxell, Kohayakawa and Łuczak14], bounded-degree trees [Reference Friedman and Pippenger10], powers of paths and bounded-degree trees [Reference Berger, Kohayakawa and Maesaka3, Reference Clemens, Jenssen and Kohayakawa5, Reference Han, Jenssen, Kohayakawa, Mota and Roberts13], and more besides.
Most of the known families with linear size-Ramsey numbers have a bounded structural parameter, such as bandwidth [Reference Clemens, Jenssen and Kohayakawa5] or, more generally, treewidth [Reference Kamčev, Liebenau, Wood and Yepremyan15] (though see the recent papers [Reference Draganić, Krivelevich and Nenadov8, Reference Letzter, Pokrovskiy and Yepremyan18] for examples with a somewhat different flavour). However, a fairly simple family of graphs which does not fall into any of these categories, but may still have linear size-Ramsey numbers, is the family of two-dimensional grid graphs. For
![]() $s \in{\mathbb{N}}$
, the
$s \in{\mathbb{N}}$
, the
![]() $s \times s$
grid is the graph with vertex set
$s \times s$
grid is the graph with vertex set
![]() $[s] \times [s]$
where two pairs are adjacent if and only if they differ by one in exactly one coordinate. Obviously, the maximum degree of the
$[s] \times [s]$
where two pairs are adjacent if and only if they differ by one in exactly one coordinate. Obviously, the maximum degree of the
![]() $s \times s$
grid is four, but its bandwidth and treewidth are both exactly
$s \times s$
grid is four, but its bandwidth and treewidth are both exactly
![]() $s$
(see, e.g., [Reference Chvátalová4]), so the problem of estimating the size-Ramsey number of this graph, and usually we will take
$s$
(see, e.g., [Reference Chvátalová4]), so the problem of estimating the size-Ramsey number of this graph, and usually we will take
![]() $s = \sqrt{n}$
so that the graph has
$s = \sqrt{n}$
so that the graph has
![]() $n$
vertices, provides an interesting test case for exploring new ideas and techniques.
$n$
vertices, provides an interesting test case for exploring new ideas and techniques.
Regarding upper bounds for the size-Ramsey number of the
![]() $\sqrt{n} \times \sqrt{n}$
grid, an important result of Kohayakawa, Rödl, Schacht, and Szemerédi [Reference Kohayakawa, Rödl, Schacht and Szemerédi17], which says that every graph
$\sqrt{n} \times \sqrt{n}$
grid, an important result of Kohayakawa, Rödl, Schacht, and Szemerédi [Reference Kohayakawa, Rödl, Schacht and Szemerédi17], which says that every graph
![]() $H$
with
$H$
with
![]() $n$
vertices and maximum degree
$n$
vertices and maximum degree
![]() $\Delta$
satisfies
$\Delta$
satisfies
![]() $\hat r(H) \leqslant n^{2-1/\Delta +o(1)}$
, immediately yields the bound
$\hat r(H) \leqslant n^{2-1/\Delta +o(1)}$
, immediately yields the bound
![]() $n^{7/4+o(1)}$
. This was recently improved by Clemens, Miralaei, Reding, Schacht, and Taraz [Reference Clemens, Miralaei, Reding, Schacht and Taraz6] to
$n^{7/4+o(1)}$
. This was recently improved by Clemens, Miralaei, Reding, Schacht, and Taraz [Reference Clemens, Miralaei, Reding, Schacht and Taraz6] to
![]() $n^{3/2+o(1)}$
(and an alternative proof of this bound was also noted in our recent paper [Reference Conlon, Nenadov and Trujić7]). The goal of this short note is to provide an elementary proof of an improved upper bound.
$n^{3/2+o(1)}$
(and an alternative proof of this bound was also noted in our recent paper [Reference Conlon, Nenadov and Trujić7]). The goal of this short note is to provide an elementary proof of an improved upper bound.
Theorem 1.1
There exists a constant
![]() $C \gt 0$
such that the size-Ramsey number of the
$C \gt 0$
such that the size-Ramsey number of the
![]() $\sqrt{n} \times \sqrt{n}$
grid graph is at most
$\sqrt{n} \times \sqrt{n}$
grid graph is at most
![]() $Cn^{5/4}$
.
$Cn^{5/4}$
.
Like much of the work on size-Ramsey numbers, the previous bounds for grids were obtained by applying the sparse regularity method to show that every
![]() $2$
-colouring of the edges of the Erdős–Rényi random graph
$2$
-colouring of the edges of the Erdős–Rényi random graph
![]() $G_{n, p}$
, for some appropriate density
$G_{n, p}$
, for some appropriate density
![]() $p$
, contains a monochromatic copy of the grid. However, it is a simple exercise in the first moment method to show that for
$p$
, contains a monochromatic copy of the grid. However, it is a simple exercise in the first moment method to show that for
![]() $p \ll n^{-1/2}$
the random graph
$p \ll n^{-1/2}$
the random graph
![]() $G_{n, p}$
with high probability does not contain the
$G_{n, p}$
with high probability does not contain the
![]() $s \times s$
grid graph as a subgraph if
$s \times s$
grid graph as a subgraph if
![]() $s = \Theta (\sqrt{n})$
, so the bound
$s = \Theta (\sqrt{n})$
, so the bound
![]() $O(n^{3/2})$
is the best that one can hope to achieve using this procedure.
$O(n^{3/2})$
is the best that one can hope to achieve using this procedure.
To see how it is that we gain on this bound, suppose that
![]() $s = \sqrt{n}$
. It is known [Reference Haxell, Kohayakawa and Łuczak14] that there are
$s = \sqrt{n}$
. It is known [Reference Haxell, Kohayakawa and Łuczak14] that there are
![]() $K, \Delta \gt 0$
and a graph
$K, \Delta \gt 0$
and a graph
![]() $H$
with
$H$
with
![]() $Ks$
vertices and maximum degree at most
$Ks$
vertices and maximum degree at most
![]() $\Delta$
which is Ramsey for
$\Delta$
which is Ramsey for
![]() $C_s$
, the cycle of length
$C_s$
, the cycle of length
![]() $s$
. Consider now a ‘blow-up’
$s$
. Consider now a ‘blow-up’
![]() $\Gamma$
of
$\Gamma$
of
![]() $H$
obtained by replacing every
$H$
obtained by replacing every
![]() $x \in V(H)$
by an independent set
$x \in V(H)$
by an independent set
![]() $V_x$
of order
$V_x$
of order
![]() $\Theta (s)$
and every
$\Theta (s)$
and every
![]() $xy \in H$
by a bipartite graph
$xy \in H$
by a bipartite graph
![]() $(V_x,V_y)$
in which every edge exists independently with probability
$(V_x,V_y)$
in which every edge exists independently with probability
![]() $p = \Theta (s^{-1/2})$
. With high probability, such a blow-up contains
$p = \Theta (s^{-1/2})$
. With high probability, such a blow-up contains
![]() $\Theta (s^{5/2}) = \Theta (n^{5/4})$
edges. That is, instead of revealing a random graph
$\Theta (s^{5/2}) = \Theta (n^{5/4})$
edges. That is, instead of revealing a random graph
![]() $G_{n, p}$
on all
$G_{n, p}$
on all
![]() $n = \Theta (s^2)$
vertices, we only reveal edges that lie within
$n = \Theta (s^2)$
vertices, we only reveal edges that lie within
![]() $\Theta (s)$
bipartite subgraphs, each with parts of order
$\Theta (s)$
bipartite subgraphs, each with parts of order
![]() $\Theta (s)$
. This salvages a significant number of edges which would otherwise go to waste.
$\Theta (s)$
. This salvages a significant number of edges which would otherwise go to waste.
Consider now a
![]() $2$
-colouring of
$2$
-colouring of
![]() $\Gamma$
and recall that
$\Gamma$
and recall that
![]() $H$
was chosen so that
$H$
was chosen so that
![]() $H \rightarrow C_s$
. A key lemma, Lemma 2.3 below, then allows us to conclude that there are sets
$H \rightarrow C_s$
. A key lemma, Lemma 2.3 below, then allows us to conclude that there are sets
![]() $V_1,\dotsc,V_s$
in
$V_1,\dotsc,V_s$
in
![]() $\Gamma$
and a collection
$\Gamma$
and a collection
![]() $U_i \subseteq V_i$
of large subsets such that all
$U_i \subseteq V_i$
of large subsets such that all
![]() $(U_i,U_{i+1})$
with
$(U_i,U_{i+1})$
with
![]() $i \in [s]$
, where addition is taken modulo
$i \in [s]$
, where addition is taken modulo
![]() $s$
, are ‘regular’ in the same colour. We may then sequentially embed the vertices of the grid so that the first row is embedded into
$s$
, are ‘regular’ in the same colour. We may then sequentially embed the vertices of the grid so that the first row is embedded into
![]() $U_1,\dotsc,U_s$
, the second into
$U_1,\dotsc,U_s$
, the second into
![]() $U_2,\dotsc,U_s,U_1$
, and so on.
$U_2,\dotsc,U_s,U_1$
, and so on.
2. Definitions and key lemmas
In this section, we recall several standard definitions and note two key lemmas that will be needed in the proof of Theorem 1.1. Most of these revolve around the concept of sparse regularity (for a thorough overview of which we refer the reader to the survey by Gerke and Steger [Reference Gerke and Steger12]).
For
![]() ${\varepsilon } \gt 0$
and
${\varepsilon } \gt 0$
and
![]() $p \in (0, 1]$
, a pair of sets
$p \in (0, 1]$
, a pair of sets
![]() $(V_1, V_2)$
is said to be
$(V_1, V_2)$
is said to be
![]() $({\varepsilon }, p)$
-lower-regular in a graph
$({\varepsilon }, p)$
-lower-regular in a graph
![]() $G$
if, for all
$G$
if, for all
![]() $U_i \subseteq V_i$
,
$U_i \subseteq V_i$
,
![]() $i \in \{1,2\}$
, with
$i \in \{1,2\}$
, with
![]() $|U_i| \geqslant{\varepsilon }|V_i|$
, the density
$|U_i| \geqslant{\varepsilon }|V_i|$
, the density
![]() $d_G(U_1, U_2) = e_G(U_1, U_2)/(|U_1||U_2|)$
of edges between
$d_G(U_1, U_2) = e_G(U_1, U_2)/(|U_1||U_2|)$
of edges between
![]() $U_1$
and
$U_1$
and
![]() $U_2$
satisfies
$U_2$
satisfies
Immediately from this definition, we get that in every
![]() $({\varepsilon },p)$
-lower-regular pair
$({\varepsilon },p)$
-lower-regular pair
![]() $(V_1, V_2)$
, for each
$(V_1, V_2)$
, for each
![]() $i \in \{1,2\}$
, all but at most
$i \in \{1,2\}$
, all but at most
![]() ${\varepsilon }|V_i|$
vertices in
${\varepsilon }|V_i|$
vertices in
![]() $V_i$
have degree at least
$V_i$
have degree at least
![]() $(1-{\varepsilon })p|V_{3-i}|$
into
$(1-{\varepsilon })p|V_{3-i}|$
into
![]() $V_{3-i}$
– a fact we will make use of in the proof of Theorem 1.1. Another useful and well-known property is that lower-regularity is inherited on large sets.
$V_{3-i}$
– a fact we will make use of in the proof of Theorem 1.1. Another useful and well-known property is that lower-regularity is inherited on large sets.
Lemma 2.1.
Let
![]() $0 \lt{\varepsilon } \lt \delta$
,
$0 \lt{\varepsilon } \lt \delta$
,
![]() $p \in (0, 1]$
, and let
$p \in (0, 1]$
, and let
![]() $(V_1, V_2)$
be an
$(V_1, V_2)$
be an
![]() $({\varepsilon }, p)$
-lower-regular pair. Then any pair of subsets
$({\varepsilon }, p)$
-lower-regular pair. Then any pair of subsets
![]() $V'_{\!\!i} \subseteq V_i$
,
$V'_{\!\!i} \subseteq V_i$
,
![]() $i \in \{1,2\}$
, with
$i \in \{1,2\}$
, with
![]() $|V'_{\!\!i}| \geqslant \delta |V_i|$
form an
$|V'_{\!\!i}| \geqslant \delta |V_i|$
form an
![]() $({\varepsilon }/\delta,p)$
-lower-regular pair.
$({\varepsilon }/\delta,p)$
-lower-regular pair.
For
![]() $\lambda \gt 0$
and
$\lambda \gt 0$
and
![]() $p \in (0, 1]$
, a graph
$p \in (0, 1]$
, a graph
![]() $G$
is said to be
$G$
is said to be
![]() $(\lambda,p)$
-uniform if, for all disjoint
$(\lambda,p)$
-uniform if, for all disjoint
![]() $X, Y \subseteq V(G)$
with
$X, Y \subseteq V(G)$
with
![]() $|X|, |Y| \geqslant \lambda |V(G)|$
, the density of edges between
$|X|, |Y| \geqslant \lambda |V(G)|$
, the density of edges between
![]() $X$
and
$X$
and
![]() $Y$
satisfies
$Y$
satisfies
![]() $d_G(X,Y) = (1\pm \lambda )p$
. If only the upper bound holds, the graph is said to be upper-uniform.Footnote 1 For example, it is easy to see that the random graph
$d_G(X,Y) = (1\pm \lambda )p$
. If only the upper bound holds, the graph is said to be upper-uniform.Footnote 1 For example, it is easy to see that the random graph
![]() $G_{n, p}$
is with high probability
$G_{n, p}$
is with high probability
![]() $(o(1),p)$
-uniform whenever
$(o(1),p)$
-uniform whenever
![]() $p \gg 1/n$
. If
$p \gg 1/n$
. If
![]() $G = (V_1, V_2;\; E)$
is bipartite, we say that
$G = (V_1, V_2;\; E)$
is bipartite, we say that
![]() $G$
is
$G$
is
![]() $(\lambda, p)$
-uniform or upper-uniform if the same conditions hold for all
$(\lambda, p)$
-uniform or upper-uniform if the same conditions hold for all
![]() $X \subseteq V_1$
and
$X \subseteq V_1$
and
![]() $Y \subseteq V_2$
with
$Y \subseteq V_2$
with
![]() $|X| \geqslant \lambda |V_1|$
and
$|X| \geqslant \lambda |V_1|$
and
![]() $|Y| \geqslant \lambda |V_2|$
. In order to prove our main technical lemma, we rely on the following result, a simple corollary of [Reference Kohayakawa, Konstadinidis and Mota16, Lemma 6], whose proof follows a density increment argument. The same conclusion can also be obtained by an application of the sparse regularity lemma.
$|Y| \geqslant \lambda |V_2|$
. In order to prove our main technical lemma, we rely on the following result, a simple corollary of [Reference Kohayakawa, Konstadinidis and Mota16, Lemma 6], whose proof follows a density increment argument. The same conclusion can also be obtained by an application of the sparse regularity lemma.
Lemma 2.2.
For all
![]() $0 \lt{\varepsilon } \lt 1/2$
and
$0 \lt{\varepsilon } \lt 1/2$
and
![]() $\alpha \in (0, 1)$
, there exists
$\alpha \in (0, 1)$
, there exists
![]() $\lambda \gt 0$
such that the following holds for every
$\lambda \gt 0$
such that the following holds for every
![]() $p \in (0, 1]$
. Let
$p \in (0, 1]$
. Let
![]() $G = (V_1, V_2;\; E)$
be a
$G = (V_1, V_2;\; E)$
be a
![]() $(\lambda, p)$
-upper-uniform bipartite graph with
$(\lambda, p)$
-upper-uniform bipartite graph with
![]() $|V_1| = |V_2|$
and
$|V_1| = |V_2|$
and
![]() $|E| \geqslant \alpha |V_1||V_2|p$
. Then there exist
$|E| \geqslant \alpha |V_1||V_2|p$
. Then there exist
![]() $U_i \subseteq V_i$
,
$U_i \subseteq V_i$
,
![]() $i \in \{1,2\}$
, with
$i \in \{1,2\}$
, with
![]() $|U_i| = \lambda |V_i|$
such that
$|U_i| = \lambda |V_i|$
such that
![]() $(U_1, U_2)$
is
$(U_1, U_2)$
is
![]() $({\varepsilon }, \alpha p)$
-lower-regular in
$({\varepsilon }, \alpha p)$
-lower-regular in
![]() $G$
.
$G$
.
The next lemma is the crux of our argument. Here and elsewhere, we say that
![]() $(X,Y;\; E)$
is lower-regular if
$(X,Y;\; E)$
is lower-regular if
![]() $(X,Y)$
is lower-regular with respect to the set of edges
$(X,Y)$
is lower-regular with respect to the set of edges
![]() $E$
.
$E$
.
Lemma 2.3.
For every
![]() $r, \Delta \geqslant 2$
and
$r, \Delta \geqslant 2$
and
![]() ${\varepsilon } \gt 0$
, there exists
${\varepsilon } \gt 0$
, there exists
![]() $\lambda \gt 0$
such that the following holds for every
$\lambda \gt 0$
such that the following holds for every
![]() $p \in (0, 1]$
. Let
$p \in (0, 1]$
. Let
![]() $H$
be a graph on at least two vertices with
$H$
be a graph on at least two vertices with
![]() $\Delta (H) \leqslant \Delta$
and let
$\Delta (H) \leqslant \Delta$
and let
![]() $\Gamma$
be obtained by replacing every
$\Gamma$
be obtained by replacing every
![]() $x \in V(H)$
with an independent set
$x \in V(H)$
with an independent set
![]() $V_x$
of sufficiently large order
$V_x$
of sufficiently large order
![]() $n$
and every
$n$
and every
![]() $xy \in H$
by a
$xy \in H$
by a
![]() $(\lambda,p)$
-uniform bipartite graph between
$(\lambda,p)$
-uniform bipartite graph between
![]() $V_x$
and
$V_x$
and
![]() $V_y$
. Then, for every
$V_y$
. Then, for every
![]() $r$
-colouring of the edges of
$r$
-colouring of the edges of
![]() $\Gamma$
, there exists an
$\Gamma$
, there exists an
![]() $r$
-colouring
$r$
-colouring
![]() $\varphi$
of the edges of
$\varphi$
of the edges of
![]() $H$
and, for every
$H$
and, for every
![]() $x \in V(H)$
, a subset
$x \in V(H)$
, a subset
![]() $U_x \subseteq V_x$
of order
$U_x \subseteq V_x$
of order
![]() $|U_x| = \lambda n$
such that
$|U_x| = \lambda n$
such that
![]() $(U_x, U_y;\; E_{\varphi (xy)})$
is
$(U_x, U_y;\; E_{\varphi (xy)})$
is
![]() $({\varepsilon },p/(2r))$
-lower-regular for each
$({\varepsilon },p/(2r))$
-lower-regular for each
![]() $xy \in H$
, where
$xy \in H$
, where
![]() $E_{\varphi (xy)} \subseteq E(\Gamma )$
stands for the edges in colour
$E_{\varphi (xy)} \subseteq E(\Gamma )$
stands for the edges in colour
![]() $\varphi (xy)$
.
$\varphi (xy)$
.
Proof. Given
![]() $\varepsilon$
,
$\varepsilon$
,
![]() $r$
, and
$r$
, and
![]() $\Delta$
, we let
$\Delta$
, we let
![]() $\alpha = 1/(2r)$
,
$\alpha = 1/(2r)$
,
![]() ${\varepsilon }_{\Delta +1} \;:\!=\;{\varepsilon }$
,
${\varepsilon }_{\Delta +1} \;:\!=\;{\varepsilon }$
,
![]() $\lambda _{\Delta +1} = \lambda _{2.2}({\varepsilon }_{\Delta +1},\alpha )$
, and, for every
$\lambda _{\Delta +1} = \lambda _{2.2}({\varepsilon }_{\Delta +1},\alpha )$
, and, for every
![]() $i = \Delta, \dotsc, 1$
, sequentially take
$i = \Delta, \dotsc, 1$
, sequentially take
![]() ${\varepsilon }_i ={\varepsilon }_{i+1}\lambda _{i+1}$
and
${\varepsilon }_i ={\varepsilon }_{i+1}\lambda _{i+1}$
and
![]() $\lambda _i = \lambda _{2.2}({\varepsilon }_i,\alpha )$
. Lastly, let
$\lambda _i = \lambda _{2.2}({\varepsilon }_i,\alpha )$
. Lastly, let
![]() $\lambda = \prod _{i \in [\Delta +1]} \lambda _i$
.
$\lambda = \prod _{i \in [\Delta +1]} \lambda _i$
.
Fix any
![]() $r$
-colouring of (the edges of)
$r$
-colouring of (the edges of)
![]() $\Gamma$
and, for every
$\Gamma$
and, for every
![]() $c \in [r]$
, let
$c \in [r]$
, let
![]() $\Gamma _c$
stand for the subgraph (in terms of edges) in colour
$\Gamma _c$
stand for the subgraph (in terms of edges) in colour
![]() $c$
. Note that
$c$
. Note that
![]() $H$
has edge-chromatic number at most
$H$
has edge-chromatic number at most
![]() $\Delta +1$
. In other words, there exists a partition of the edges of
$\Delta +1$
. In other words, there exists a partition of the edges of
![]() $H$
into
$H$
into
![]() $H_1,\dotsc,H_{\Delta +1}$
such that each
$H_1,\dotsc,H_{\Delta +1}$
such that each
![]() $H_i$
is a matching. We find the required collection
$H_i$
is a matching. We find the required collection
![]() $\{U_x\}_{x \in V(H)}$
by maintaining the following condition for every
$\{U_x\}_{x \in V(H)}$
by maintaining the following condition for every
![]() $i \in [\Delta +1]$
: for every
$i \in [\Delta +1]$
: for every
![]() $x \in V(H)$
, there exists a chain
$x \in V(H)$
, there exists a chain
![]() $V_x = U_x^0 \supseteq U_x^1 \supseteq U_x^2 \supseteq \dotsb \supseteq U_x^i$
such that
$V_x = U_x^0 \supseteq U_x^1 \supseteq U_x^2 \supseteq \dotsb \supseteq U_x^i$
such that
-
(i)
 $|U_x^j| = \lambda _j|U_x^{j-1}|$
for all
$|U_x^j| = \lambda _j|U_x^{j-1}|$
for all
 $j \in [i]$
and
$j \in [i]$
and -
(ii) for every
 $xy \in \bigcup _{j \leqslant i} H_j$
,
$xy \in \bigcup _{j \leqslant i} H_j$
,
 $(U_x^i, U_y^i)$
is
$(U_x^i, U_y^i)$
is
 $({\varepsilon }_i,\alpha p)$
-lower-regular in
$({\varepsilon }_i,\alpha p)$
-lower-regular in
 $\Gamma _c$
for some
$\Gamma _c$
for some
 $c \in [r]$
.
$c \in [r]$
.
Consequently, for
![]() $i = \Delta +1$
, we obtain sets
$i = \Delta +1$
, we obtain sets
![]() $U_x \subseteq V_x$
, for every
$U_x \subseteq V_x$
, for every
![]() $x \in V(H)$
, of order
$x \in V(H)$
, of order
![]() $|U_x| = \left(\prod _{i \in [\Delta +1]} \lambda _i\right)\! n = \lambda n$
such that
$|U_x| = \left(\prod _{i \in [\Delta +1]} \lambda _i\right)\! n = \lambda n$
such that
![]() $(U_x,U_y)$
is
$(U_x,U_y)$
is
![]() $({\varepsilon }_{\Delta +1},\alpha p)$
-lower-regular and, thus,
$({\varepsilon }_{\Delta +1},\alpha p)$
-lower-regular and, thus,
![]() $({\varepsilon },\alpha p)$
-lower-regular for every
$({\varepsilon },\alpha p)$
-lower-regular for every
![]() $xy \in H$
. It remains to show that we can indeed do this.
$xy \in H$
. It remains to show that we can indeed do this.
Consider first
![]() $i = 1$
. For each
$i = 1$
. For each
![]() $xy \in H_1$
, let
$xy \in H_1$
, let
![]() $c \in [r]$
be the majority colour in
$c \in [r]$
be the majority colour in
![]() $\Gamma [V_x,V_y]$
. As
$\Gamma [V_x,V_y]$
. As
![]() $e_{\Gamma _c}(V_x, V_y) \geqslant (1-\lambda )n^2p/r$
, we may apply Lemma 2.2 with
$e_{\Gamma _c}(V_x, V_y) \geqslant (1-\lambda )n^2p/r$
, we may apply Lemma 2.2 with
![]() ${\varepsilon }_1$
(as
${\varepsilon }_1$
(as
![]() $\varepsilon$
) and
$\varepsilon$
) and
![]() $\Gamma _c[V_x,V_y]$
(as
$\Gamma _c[V_x,V_y]$
(as
![]() $G$
) to obtain sets
$G$
) to obtain sets
![]() $U_x^1, U_y^1$
with the desired properties. For every
$U_x^1, U_y^1$
with the desired properties. For every
![]() $x \in V(H)$
which is isolated in
$x \in V(H)$
which is isolated in
![]() $H_1$
, we simply take an arbitrary subset
$H_1$
, we simply take an arbitrary subset
![]() $U_x^1 \subseteq V_x$
of order
$U_x^1 \subseteq V_x$
of order
![]() $\lambda _1|U_x^0|$
. Thus, the required condition holds for
$\lambda _1|U_x^0|$
. Thus, the required condition holds for
![]() $i=1$
.
$i=1$
.
Suppose now that the condition holds for some
![]() $i \geqslant 1$
and let us show that it also holds for
$i \geqslant 1$
and let us show that it also holds for
![]() $i+1$
. As above, for every
$i+1$
. As above, for every
![]() $xy \in H_{i+1}$
, let
$xy \in H_{i+1}$
, let
![]() $c \in [r]$
be the majority colour in
$c \in [r]$
be the majority colour in
![]() $\Gamma [V_x,V_y]$
. Since
$\Gamma [V_x,V_y]$
. Since
![]() $\Gamma [V_x, V_y]$
is
$\Gamma [V_x, V_y]$
is
![]() $(\lambda,p)$
-uniform and, by (i),
$(\lambda,p)$
-uniform and, by (i),
![]() $|U_x^i|, |U_y^i| \geqslant \lambda n$
, we have
$|U_x^i|, |U_y^i| \geqslant \lambda n$
, we have
![]() $e_\Gamma (U_x^i, U_y^i) = (1 \pm \lambda )|U_x^i||U_y^i|p$
and, hence,
$e_\Gamma (U_x^i, U_y^i) = (1 \pm \lambda )|U_x^i||U_y^i|p$
and, hence,
Lemma 2.2 applied to
![]() $\Gamma _c\!\left[U_x^i,U_y^i\right]$
with
$\Gamma _c\!\left[U_x^i,U_y^i\right]$
with
![]() ${\varepsilon }_{i+1}$
(as
${\varepsilon }_{i+1}$
(as
![]() $\varepsilon$
) gives sets
$\varepsilon$
) gives sets
![]() $U_x^{i+1} \subseteq U_x^i$
and
$U_x^{i+1} \subseteq U_x^i$
and
![]() $U_y^{i+1} \subseteq U_y^i$
of order
$U_y^{i+1} \subseteq U_y^i$
of order
for which
![]() $\left(U_x^{i+1},U_y^{i+1}\right)$
is
$\left(U_x^{i+1},U_y^{i+1}\right)$
is
![]() $({\varepsilon }_{i+1},\alpha p)$
-lower-regular in
$({\varepsilon }_{i+1},\alpha p)$
-lower-regular in
![]() $\Gamma _c$
. For every
$\Gamma _c$
. For every
![]() $x \in V(H)$
which is isolated in
$x \in V(H)$
which is isolated in
![]() $H_{i+1}$
, we again take an arbitrary subset
$H_{i+1}$
, we again take an arbitrary subset
![]() $U_x^{i+1} \subseteq U_x^i$
of order
$U_x^{i+1} \subseteq U_x^i$
of order
![]() $\lambda _{i+1}|U_x^i|$
. Observe also that, for every
$\lambda _{i+1}|U_x^i|$
. Observe also that, for every
![]() $xz \in \bigcup _{j \leqslant i} H_j$
, since
$xz \in \bigcup _{j \leqslant i} H_j$
, since
![]() $(U_x^i,U_z^i)$
was
$(U_x^i,U_z^i)$
was
![]() $({\varepsilon }_i,\alpha p)$
-lower-regular in
$({\varepsilon }_i,\alpha p)$
-lower-regular in
![]() $\Gamma_{c^{\prime}}$
for some
$\Gamma_{c^{\prime}}$
for some
![]() $c' \in [r]$
and
$c' \in [r]$
and
![]() $|U_x^{i+1}| = \lambda _{i+1}|U_x^i|$
, Lemma 2.1 and the fact that
$|U_x^{i+1}| = \lambda _{i+1}|U_x^i|$
, Lemma 2.1 and the fact that
![]() ${\varepsilon }_i/\lambda _{i+1} ={\varepsilon }_{i+1}$
imply that
${\varepsilon }_i/\lambda _{i+1} ={\varepsilon }_{i+1}$
imply that
![]() $\left(U_x^{i+1},U_z^{i+1}\right)$
is
$\left(U_x^{i+1},U_z^{i+1}\right)$
is
![]() $({\varepsilon }_{i+1},\alpha p)$
-lower-regular in
$({\varepsilon }_{i+1},\alpha p)$
-lower-regular in
![]() $\Gamma_{c^{\prime}}$
, as desired. This completes the proof.
$\Gamma_{c^{\prime}}$
, as desired. This completes the proof.
We also need a variant of a result from our previous paper [Reference Conlon, Nenadov and Trujić7, Lemma 3.5] about regularity inheritance. While that result was stated for the usual (full) notion of regularity, we only need lower-regularity here, allowing us to save a factor of
![]() $(\log n)^{1/2}$
.
$(\log n)^{1/2}$
.
Lemma 2.4.
For all
![]() ${\varepsilon }, \alpha, \lambda \gt 0$
, there exist positive constants
${\varepsilon }, \alpha, \lambda \gt 0$
, there exist positive constants
![]() ${\varepsilon }'({\varepsilon },\alpha )$
and
${\varepsilon }'({\varepsilon },\alpha )$
and
![]() $C({\varepsilon },\alpha,\lambda )$
such that for
$C({\varepsilon },\alpha,\lambda )$
such that for
![]() $p \geqslant Cn^{-1/2}$
, with probability at least
$p \geqslant Cn^{-1/2}$
, with probability at least
![]() $1 - o(n^{-5})$
, the random graph
$1 - o(n^{-5})$
, the random graph
![]() $\Gamma \sim G_{n, p}$
has the following property.
$\Gamma \sim G_{n, p}$
has the following property.
Suppose
![]() $G \subseteq \Gamma$
and
$G \subseteq \Gamma$
and
![]() $V_1, V_2 \subseteq V(\Gamma )$
are disjoint subsets of order
$V_1, V_2 \subseteq V(\Gamma )$
are disjoint subsets of order
![]() $\tilde n = \lambda n$
such that
$\tilde n = \lambda n$
such that
![]() $(V_1, V_2)$
is
$(V_1, V_2)$
is
![]() $({\varepsilon }',\alpha p)$
-lower-regular in
$({\varepsilon }',\alpha p)$
-lower-regular in
![]() $G$
. Then there exists
$G$
. Then there exists
![]() $B \subseteq V(\Gamma )$
of order
$B \subseteq V(\Gamma )$
of order
![]() $|B| \leqslant{\varepsilon }\tilde n$
such that, for each
$|B| \leqslant{\varepsilon }\tilde n$
such that, for each
![]() $v, w \in V(\Gamma ) \setminus (V_1 \cup V_2 \cup B)$
(not necessarily distinct), the following holds: for any two subsets
$v, w \in V(\Gamma ) \setminus (V_1 \cup V_2 \cup B)$
(not necessarily distinct), the following holds: for any two subsets
![]() $N_v \subseteq N_\Gamma (v, V_1)$
and
$N_v \subseteq N_\Gamma (v, V_1)$
and
![]() $N_w \subseteq N_\Gamma (w, V_2)$
of order
$N_w \subseteq N_\Gamma (w, V_2)$
of order
![]() $\alpha \tilde n p/4$
, both
$\alpha \tilde n p/4$
, both
![]() $(N_v, V_2)$
and
$(N_v, V_2)$
and
![]() $(N_v, N_w)$
are
$(N_v, N_w)$
are
![]() $({\varepsilon },\alpha p)$
-lower-regular in
$({\varepsilon },\alpha p)$
-lower-regular in
![]() $G$
.
$G$
.
Sketch of the proof. The proof proceeds along the same lines as the proof of [Reference Conlon, Nenadov and Trujić7, Lemma 3.5]. The only difference is that there we made use of an inheritance lemma for full regularity (namely, Corollary 3.5 in [Reference Škorić, Steger and Trujić20]), which requires the sets on which regularity is inherited to be of order at least
![]() $C\log n/p$
, resulting in the requirement that
$C\log n/p$
, resulting in the requirement that
![]() $p \geqslant C(\log n/n)^{1/2}$
. However, for lower-regularity, one can instead use the inheritance lemma of Gerke, Kohayakawa, Rödl, and Steger [Reference Gerke, Kohayakawa, Rödl and Steger11, Corollary 3.8], which only requires the sets to be of order at least
$p \geqslant C(\log n/n)^{1/2}$
. However, for lower-regularity, one can instead use the inheritance lemma of Gerke, Kohayakawa, Rödl, and Steger [Reference Gerke, Kohayakawa, Rödl and Steger11, Corollary 3.8], which only requires the sets to be of order at least
![]() $C/p$
, resulting in
$C/p$
, resulting in
![]() $p \geqslant Cn^{-1/2}$
. The rest of the proof remains exactly the same.
$p \geqslant Cn^{-1/2}$
. The rest of the proof remains exactly the same.
3. Proof of Theorem 1.1
Since it requires no additional work, we will actually prove the
![]() $r$
-colour analogue of Theorem 1.1. More precisely, we will show that for every integer
$r$
-colour analogue of Theorem 1.1. More precisely, we will show that for every integer
![]() $r \geqslant 2$
there exists a graph of order
$r \geqslant 2$
there exists a graph of order
![]() $n$
with
$n$
with
![]() $O(n^{5/4})$
edges for which every
$O(n^{5/4})$
edges for which every
![]() $r$
-colouring of the edges contains a monochromatic copy of the
$r$
-colouring of the edges contains a monochromatic copy of the
![]() $\delta \sqrt{n} \times \delta \sqrt{n}$
grid for some
$\delta \sqrt{n} \times \delta \sqrt{n}$
grid for some
![]() $\delta \gt 0$
.
$\delta \gt 0$
.
By a result of Haxell, Kohayakawa, and Łuczak [Reference Haxell, Kohayakawa and Łuczak14, Theorem 10], there exist constants
![]() $K, \Delta \gt 0$
, both depending only on
$K, \Delta \gt 0$
, both depending only on
![]() $r$
, such that, for every sufficiently large
$r$
, such that, for every sufficiently large
![]() $s \in{\mathbb{N}}$
, there is a graph
$s \in{\mathbb{N}}$
, there is a graph
![]() $H$
on
$H$
on
![]() $Ks$
vertices with maximum degree at most
$Ks$
vertices with maximum degree at most
![]() $\Delta$
which has the property that every
$\Delta$
which has the property that every
![]() $r$
-colouring of its edges contains a monochromatic copy of
$r$
-colouring of its edges contains a monochromatic copy of
![]() $C_\ell$
, the cycle of length
$C_\ell$
, the cycle of length
![]() $\ell$
, for every
$\ell$
, for every
![]() $\log s \ll \ell \leqslant s$
. Let
$\log s \ll \ell \leqslant s$
. Let
We show that the size-Ramsey number of the
![]() $\delta s \times \delta s$
grid is
$\delta s \times \delta s$
grid is
![]() $O(s^{5/2})$
, which, for
$O(s^{5/2})$
, which, for
![]() $s = \sqrt{n}$
, implies the desired statement.
$s = \sqrt{n}$
, implies the desired statement.
Let
![]() $\Gamma$
be a graph obtained by replacing every vertex
$\Gamma$
be a graph obtained by replacing every vertex
![]() $x \in V(H)$
by an independent set
$x \in V(H)$
by an independent set
![]() $V_x$
of order
$V_x$
of order
![]() $s$
and every edge
$s$
and every edge
![]() $xy \in H$
by a bipartite graph between
$xy \in H$
by a bipartite graph between
![]() $V_x$
and
$V_x$
and
![]() $V_y$
in which each edge exists independently with probability
$V_y$
in which each edge exists independently with probability
![]() $p = Cs^{-1/2}$
for some sufficiently large constant
$p = Cs^{-1/2}$
for some sufficiently large constant
![]() $C \gt 0$
. With high probability,
$C \gt 0$
. With high probability,
![]() $\Gamma$
has the following property:
$\Gamma$
has the following property:
-
(A1)
 $e_\Gamma (V'_{\!\!x}, V'_{\!\!y}) = (1\pm \lambda )|V'_{\!\!x}||V'_{\!\!y}| p$
for every
$e_\Gamma (V'_{\!\!x}, V'_{\!\!y}) = (1\pm \lambda )|V'_{\!\!x}||V'_{\!\!y}| p$
for every
 $xy \in H$
and
$xy \in H$
and
 $V'_{\!\!x} \subseteq V_x$
and
$V'_{\!\!x} \subseteq V_x$
and
 $V'_{\!\!y} \subseteq V_y$
with
$V'_{\!\!y} \subseteq V_y$
with
 $|V'_{\!\!x}||V'_{\!\!y}|p \geqslant 100s/\lambda ^2$
.
$|V'_{\!\!x}||V'_{\!\!y}|p \geqslant 100s/\lambda ^2$
.
This is a standard feature of random graphs and follows from the Chernoff bound together with an application of the union bound. In particular, it establishes that with high probability
![]() $\Gamma [V_x,V_y]$
is
$\Gamma [V_x,V_y]$
is
![]() $(\lambda,p)$
-uniform for every
$(\lambda,p)$
-uniform for every
![]() $xy \in H$
and, therefore,
$xy \in H$
and, therefore,
![]() $\Gamma$
has at most
$\Gamma$
has at most
edges. Additionally, with high probability,
![]() $\Gamma$
is such that every
$\Gamma$
is such that every
![]() $\Gamma [V_x \cup V_y \cup V_z]$
has the property of Lemma 2.4 (applied with
$\Gamma [V_x \cup V_y \cup V_z]$
has the property of Lemma 2.4 (applied with
![]() ${\varepsilon }/9$
as
${\varepsilon }/9$
as
![]() $\varepsilon$
,
$\varepsilon$
,
![]() $\lambda/3$
as
$\lambda/3$
as
![]() $\lambda$
, and
$\lambda$
, and
![]() $3s$
as
$3s$
as
![]() $n$
) for every path
$n$
) for every path
![]() $xyz$
of length two in
$xyz$
of length two in
![]() $H$
.Footnote 2 This again follows from the union bound, as there are
$H$
.Footnote 2 This again follows from the union bound, as there are
![]() $O(s)$
such paths in total and the conclusion of Lemma 2.4 holds with probability
$O(s)$
such paths in total and the conclusion of Lemma 2.4 holds with probability
![]() $1 - o(s^{-5})$
for every fixed path. We now fix an outcome of
$1 - o(s^{-5})$
for every fixed path. We now fix an outcome of
![]() $\Gamma$
which satisfies all of these properties.
$\Gamma$
which satisfies all of these properties.
Consider some
![]() $r$
-colouring of the edges of
$r$
-colouring of the edges of
![]() $\Gamma$
and let
$\Gamma$
and let
![]() $\varphi$
be the colouring of the edges of
$\varphi$
be the colouring of the edges of
![]() $H$
given by Lemma 2.3 (applied with
$H$
given by Lemma 2.3 (applied with
![]() $\varepsilon '$
as
$\varepsilon '$
as
![]() $\varepsilon$
). By the choice of
$\varepsilon$
). By the choice of
![]() $H$
, this colouring contains a monochromatic copy of
$H$
, this colouring contains a monochromatic copy of
![]() $C_{\delta s}$
, which, without loss of generality, we may assume has vertices
$C_{\delta s}$
, which, without loss of generality, we may assume has vertices
![]() $1,\dotsc,\delta s$
. Therefore, there is a colour
$1,\dotsc,\delta s$
. Therefore, there is a colour
![]() $c \in [r]$
and sets
$c \in [r]$
and sets
![]() $U_i$
of order
$U_i$
of order
![]() $\tilde s = \lambda s$
in
$\tilde s = \lambda s$
in
![]() $\Gamma$
such that, for every
$\Gamma$
such that, for every
![]() $i \in [\delta s]$
, the pair
$i \in [\delta s]$
, the pair
![]() $(U_i,U_{i+1})$
is
$(U_i,U_{i+1})$
is
![]() $({\varepsilon }',\alpha p)$
-lower-regular in the subgraph of
$({\varepsilon }',\alpha p)$
-lower-regular in the subgraph of
![]() $\Gamma$
induced by colour
$\Gamma$
induced by colour
![]() $c$
, where we identify
$c$
, where we identify
![]() $\delta s + i$
with
$\delta s + i$
with
![]() $i$
. Let
$i$
. Let
![]() $G$
be the graph induced by these sets whose edges are the edges of
$G$
be the graph induced by these sets whose edges are the edges of
![]() $\Gamma$
of colour
$\Gamma$
of colour
![]() $c$
. We will show that
$c$
. We will show that
![]() $G$
contains the
$G$
contains the
![]() $\delta s \times \delta s$
grid as a subgraph.
$\delta s \times \delta s$
grid as a subgraph.
For every
![]() $i \in [\delta s]$
, let
$i \in [\delta s]$
, let
![]() $B \subseteq U_i \cup U_{i+1} \cup U_{i+2}$
be the set given by Lemma 2.4 (which was applied with
$B \subseteq U_i \cup U_{i+1} \cup U_{i+2}$
be the set given by Lemma 2.4 (which was applied with
![]() ${\varepsilon }/9$
as
${\varepsilon }/9$
as
![]() $\varepsilon$
,
$\varepsilon$
,
![]() $\lambda/3$
as
$\lambda/3$
as
![]() $\lambda$
, and
$\lambda$
, and
![]() $3s$
as
$3s$
as
![]() $n$
) on
$n$
) on
![]() $\Gamma [U_i \cup U_{i+1} \cup U_{i+2}]$
, which is a set of ‘bad vertices’ for the pair
$\Gamma [U_i \cup U_{i+1} \cup U_{i+2}]$
, which is a set of ‘bad vertices’ for the pair
![]() $(U_{i+1}, U_{i+2})$
. As each
$(U_{i+1}, U_{i+2})$
. As each
![]() $U_i$
is a part of three such applications, by the chosen properties of
$U_i$
is a part of three such applications, by the chosen properties of
![]() $\Gamma$
, for every
$\Gamma$
, for every
![]() $i \in [\delta s]$
there exists a set
$i \in [\delta s]$
there exists a set
![]() $B_i \subseteq U_i$
of order
$B_i \subseteq U_i$
of order
![]() $|B_i| \leqslant{\varepsilon }\tilde s$
such that:
$|B_i| \leqslant{\varepsilon }\tilde s$
such that:
-
(B1)
 $(N_v, U_{i+2} \setminus B_{i+2})$
is
$(N_v, U_{i+2} \setminus B_{i+2})$
is
 $({\varepsilon }, \alpha p)$
-lower-regularFootnote 3 in
$({\varepsilon }, \alpha p)$
-lower-regularFootnote 3 in
 $G$
for every
$G$
for every
 $v \in U_i \setminus B_i$
and
$v \in U_i \setminus B_i$
and
 $N_v \subseteq N_G(v, U_{i+1})$
of order
$N_v \subseteq N_G(v, U_{i+1})$
of order
 $\alpha \tilde sp/4$
and
$\alpha \tilde sp/4$
and -
(B2)
 $(N_v, N_u)$
is
$(N_v, N_u)$
is
 $({\varepsilon }, \alpha p)$
-lower-regular in
$({\varepsilon }, \alpha p)$
-lower-regular in
 $G$
for every
$G$
for every
 $v \in U_i \setminus B_i$
,
$v \in U_i \setminus B_i$
,
 $u \in U_{i+1} \setminus B_{i+1}$
and
$u \in U_{i+1} \setminus B_{i+1}$
and
 $N_v \subseteq N_G(v, U_{i+1})$
,
$N_v \subseteq N_G(v, U_{i+1})$
,
 $N_u \subseteq N_G(u, U_{i+2})$
, each of order
$N_u \subseteq N_G(u, U_{i+2})$
, each of order
 $\alpha \tilde sp/4$
.
$\alpha \tilde sp/4$
.
Our plan is to embed the vertex
![]() $(i, j)$
of the
$(i, j)$
of the
![]() $\delta s \times \delta s$
grid into
$\delta s \times \delta s$
grid into
![]() $U_{i+j-1}$
. The next claim helps us achieve this.
$U_{i+j-1}$
. The next claim helps us achieve this.
Claim 3.1
Let
![]() $i \in [\delta s]$
. Suppose that sets
$i \in [\delta s]$
. Suppose that sets
![]() $S_{i+j-1} \subseteq U_{i+j-1} \setminus B_{i+j-1}$
of order
$S_{i+j-1} \subseteq U_{i+j-1} \setminus B_{i+j-1}$
of order
![]() $\alpha \tilde sp/4$
are given for each
$\alpha \tilde sp/4$
are given for each
![]() $j \in [\delta s]$
and that
$j \in [\delta s]$
and that
![]() $(S_{i+j-1}, S_{i+j})$
and
$(S_{i+j-1}, S_{i+j})$
and
![]() $(S_{i+j-1}, U_{i+j} \setminus B_{i+j})$
are
$(S_{i+j-1}, U_{i+j} \setminus B_{i+j})$
are
![]() $({\varepsilon }, \alpha p)$
-lower-regular. Then, for every
$({\varepsilon }, \alpha p)$
-lower-regular. Then, for every
![]() $Q_{i+j-1} \subseteq U_{i+j-1}$
,
$Q_{i+j-1} \subseteq U_{i+j-1}$
,
![]() $j \in [\delta s]$
, of order
$j \in [\delta s]$
, of order
![]() $|Q_{i+j-1}| \leqslant 2{\varepsilon } \tilde s$
, there exists a path
$|Q_{i+j-1}| \leqslant 2{\varepsilon } \tilde s$
, there exists a path
![]() $v_1,\dotsc,v_{\delta s}$
with each
$v_1,\dotsc,v_{\delta s}$
with each
![]() $v_j \in S_{i+j-1}$
such that
$v_j \in S_{i+j-1}$
such that
![]() $|N_G(v_j, U_{i+j} \setminus Q_{i+j})| \geqslant \alpha \tilde sp/4$
.
$|N_G(v_j, U_{i+j} \setminus Q_{i+j})| \geqslant \alpha \tilde sp/4$
.
Before proving the claim, we show how to complete the embedding of the grid assuming that it holds. We start by embedding the first row. Let
![]() $v_1 \in U_1 \setminus B_1$
be a vertex for which there is
$v_1 \in U_1 \setminus B_1$
be a vertex for which there is
![]() $S_2 \subseteq N_G(v_1, U_2 \setminus B_2)$
of order
$S_2 \subseteq N_G(v_1, U_2 \setminus B_2)$
of order
![]() $\alpha \tilde sp/4$
such that
$\alpha \tilde sp/4$
such that
![]() $(S_2, U_3 \setminus B_3)$
is
$(S_2, U_3 \setminus B_3)$
is
![]() $({\varepsilon }, \alpha p)$
-lower-regular. As
$({\varepsilon }, \alpha p)$
-lower-regular. As
![]() $(U_1 \setminus B_1, U_2 \setminus B_2)$
is
$(U_1 \setminus B_1, U_2 \setminus B_2)$
is
![]() $(2{\varepsilon }', \alpha p)$
-lower-regular, there are at least
$(2{\varepsilon }', \alpha p)$
-lower-regular, there are at least
![]() $(1-2{\varepsilon }')(1-{\varepsilon })\tilde s$
vertices
$(1-2{\varepsilon }')(1-{\varepsilon })\tilde s$
vertices
![]() $v \in U_1 \setminus B_1$
that satisfy
$v \in U_1 \setminus B_1$
that satisfy
by our choice of constants. Thus, by property () almost any choice of
![]() $v_1 \in U_1 \setminus B_1$
will do. Sequentially, for every
$v_1 \in U_1 \setminus B_1$
will do. Sequentially, for every
![]() $i \geqslant 2$
, let
$i \geqslant 2$
, let
![]() $v_i \in S_i$
be a vertex for which there is
$v_i \in S_i$
be a vertex for which there is
![]() $S_{i+1} \subseteq N_G(v_i, U_{i+1} \setminus B_{i+1})$
of order
$S_{i+1} \subseteq N_G(v_i, U_{i+1} \setminus B_{i+1})$
of order
![]() $\alpha \tilde sp/4$
and both
$\alpha \tilde sp/4$
and both
![]() $(S_{i+1}, U_{i+2} \setminus B_{i+2})$
and
$(S_{i+1}, U_{i+2} \setminus B_{i+2})$
and
![]() $(S_i, S_{i+1})$
are
$(S_i, S_{i+1})$
are
![]() $({\varepsilon }, \alpha p)$
-lower-regular. This is possible as
$({\varepsilon }, \alpha p)$
-lower-regular. This is possible as
![]() $(S_i, U_{i+1} \setminus B_{i+1})$
is
$(S_i, U_{i+1} \setminus B_{i+1})$
is
![]() $({\varepsilon }, \alpha p)$
-lower-regular and properties () and () hold. We continue until we have embedded the first row of the grid as
$({\varepsilon }, \alpha p)$
-lower-regular and properties () and () hold. We continue until we have embedded the first row of the grid as
![]() $v_1,\dotsc,v_{\delta s}$
, with
$v_1,\dotsc,v_{\delta s}$
, with
![]() $v_i \in U_i$
for every
$v_i \in U_i$
for every
![]() $i \in [\delta s]$
.
$i \in [\delta s]$
.
Consider now sets
![]() $S_2, \dotsc, S_{\delta s}, S_1$
which we previously chose, where we note that
$S_2, \dotsc, S_{\delta s}, S_1$
which we previously chose, where we note that
![]() $S_1$
was defined when we embedded
$S_1$
was defined when we embedded
![]() $v_{\delta s}$
. In particular,
$v_{\delta s}$
. In particular,
![]() $S_{1+j} \subseteq U_{1+j} \setminus B_{1+j}$
and
$S_{1+j} \subseteq U_{1+j} \setminus B_{1+j}$
and
![]() $(S_{1+j}, S_{2+j})$
and
$(S_{1+j}, S_{2+j})$
and
![]() $(S_{1+j}, U_{2+j} \setminus B_{2+j})$
are both
$(S_{1+j}, U_{2+j} \setminus B_{2+j})$
are both
![]() $({\varepsilon }, \alpha p)$
-regular for every
$({\varepsilon }, \alpha p)$
-regular for every
![]() $j \in [\delta s]$
. Then, by setting
$j \in [\delta s]$
. Then, by setting
![]() $Q_{1+j} \;:\!=\; B_{1+j} \cup \{v_{1+j}\}$
and invoking Claim 3.1 with
$Q_{1+j} \;:\!=\; B_{1+j} \cup \{v_{1+j}\}$
and invoking Claim 3.1 with
![]() $i = 2$
, we can embed the second row of the grid as
$i = 2$
, we can embed the second row of the grid as
![]() $u_1, \dotsc, u_{\delta s}$
, with
$u_1, \dotsc, u_{\delta s}$
, with
![]() $u_j \in S_{1+j}$
for every
$u_j \in S_{1+j}$
for every
![]() $j \in [\delta s]$
. By the conclusion of Claim 3.1 and a slight abuse of notation, there is a collection of sets
$j \in [\delta s]$
. By the conclusion of Claim 3.1 and a slight abuse of notation, there is a collection of sets
![]() $S_{2+j} \subseteq N_G(u_j, U_{2+j} \setminus Q_{2+j})$
for every
$S_{2+j} \subseteq N_G(u_j, U_{2+j} \setminus Q_{2+j})$
for every
![]() $j \in [\delta s]$
, each of order
$j \in [\delta s]$
, each of order
![]() $\alpha \tilde sp/4$
, which, by () and (), as
$\alpha \tilde sp/4$
, which, by () and (), as
![]() $u_j \in U_{1+j} \setminus B_{1+j}$
and
$u_j \in U_{1+j} \setminus B_{1+j}$
and
![]() $u_{j+1} \in U_{1+j+1} \setminus B_{1+j+1}$
, are such that
$u_{j+1} \in U_{1+j+1} \setminus B_{1+j+1}$
, are such that
![]() $(S_{2+j}, S_{2+j+1})$
and
$(S_{2+j}, S_{2+j+1})$
and
![]() $(S_{2+j}, U_{2+j+1} \setminus B_{2+j+1})$
are
$(S_{2+j}, U_{2+j+1} \setminus B_{2+j+1})$
are
![]() $({\varepsilon }, \alpha p)$
-lower-regular.
$({\varepsilon }, \alpha p)$
-lower-regular.
The same process can now be repeated for any
![]() $i \geqslant 3$
(see Figure 1) by setting the sets
$i \geqslant 3$
(see Figure 1) by setting the sets
![]() $Q_{i+j-1} \subseteq U_{i+j-1}$
for every
$Q_{i+j-1} \subseteq U_{i+j-1}$
for every
![]() $j \in [\delta s]$
to be the union of
$j \in [\delta s]$
to be the union of
![]() $B_{i+j-1}$
and the vertices of the grid that were previously embedded into
$B_{i+j-1}$
and the vertices of the grid that were previously embedded into
![]() $U_{i+j-1}$
, that is, the images of the vertices
$U_{i+j-1}$
, that is, the images of the vertices
![]() $(1,i+j-1), (2,i+j-2), \dotsc, (i-1,j+1)$
. Since
$(1,i+j-1), (2,i+j-2), \dotsc, (i-1,j+1)$
. Since
![]() $|B_{i+j-1}| \leqslant{\varepsilon }\tilde s$
,
$|B_{i+j-1}| \leqslant{\varepsilon }\tilde s$
,
![]() $\delta \lt{\varepsilon }\lambda$
, and the lower-regularity conditions hold by () and (), we may apply Claim 3.1 to embed the
$\delta \lt{\varepsilon }\lambda$
, and the lower-regularity conditions hold by () and (), we may apply Claim 3.1 to embed the
![]() $i$
th row. It only remains to prove this claim.
$i$
th row. It only remains to prove this claim.
Proof of Claim
3.1. Without loss of generality, we may assume that all the
![]() $Q_{i+j-1}$
are of order
$Q_{i+j-1}$
are of order
![]() $2{\varepsilon }\tilde s$
, as we can take arbitrary supersets if this is not the case. Let
$2{\varepsilon }\tilde s$
, as we can take arbitrary supersets if this is not the case. Let
![]() $S'_{\!\!i+j-1} \subseteq S_{i+j-1}$
be the set of all
$S'_{\!\!i+j-1} \subseteq S_{i+j-1}$
be the set of all
![]() $v \in S_{i+j-1}$
with at least
$v \in S_{i+j-1}$
with at least
![]() $\alpha \tilde sp/4$
neighbours in
$\alpha \tilde sp/4$
neighbours in
![]() $U_{i+j} \setminus Q_{i+j}$
. On the one hand, as
$U_{i+j} \setminus Q_{i+j}$
. On the one hand, as
![]() $(S_{i+j-1}, U_{i+j} \setminus B_{i+j})$
is
$(S_{i+j-1}, U_{i+j} \setminus B_{i+j})$
is
![]() $({\varepsilon },\alpha p)$
-lower-regular and, thus, there are fewer than
$({\varepsilon },\alpha p)$
-lower-regular and, thus, there are fewer than
![]() ${\varepsilon }|S_{i+j-1}|$
vertices in
${\varepsilon }|S_{i+j-1}|$
vertices in
![]() $S_{i+j-1}$
with degree less than
$S_{i+j-1}$
with degree less than
![]() $\alpha \tilde sp/2$
in
$\alpha \tilde sp/2$
in
![]() $U_{i+j} \setminus B_{i+j}$
, we have
$U_{i+j} \setminus B_{i+j}$
, we have
On the other hand, assuming
![]() $S_{i+j-1} \setminus S'_{\!\!i+j-1}$
is of order at least
$S_{i+j-1} \setminus S'_{\!\!i+j-1}$
is of order at least
![]() $\alpha \tilde sp/16$
and, hence,
$\alpha \tilde sp/16$
and, hence,
for
![]() $C \gt 0$
sufficiently large, property () implies that
$C \gt 0$
sufficiently large, property () implies that
Since
![]() ${\varepsilon } \lt \alpha/128$
, this is a contradiction. Therefore, there are sets
${\varepsilon } \lt \alpha/128$
, this is a contradiction. Therefore, there are sets
![]() $S'_{\!\!i+j-1} \subseteq S_{i+j-1}$
of order at least
$S'_{\!\!i+j-1} \subseteq S_{i+j-1}$
of order at least
![]() $|S_{i+j-1}| - \alpha \tilde sp/16$
for each
$|S_{i+j-1}| - \alpha \tilde sp/16$
for each
![]() $j \in [\delta s]$
such that every
$j \in [\delta s]$
such that every
![]() $v \in S'_{\!\!i+j-1}$
satisfies
$v \in S'_{\!\!i+j-1}$
satisfies
![]() $|N_G(v, U_{i+j} \setminus Q_{i+j})| \geqslant \alpha \tilde sp/4$
.
$|N_G(v, U_{i+j} \setminus Q_{i+j})| \geqslant \alpha \tilde sp/4$
.

Figure 1. A picture showing the first two rows of the grid already embedded (the thick black lines), the candidate sets for the third row (the grey blobs
![]() $S_3, S_4, \dotsc, S_{\delta s}, S_1, S_2$
), and (in red) the path
$S_3, S_4, \dotsc, S_{\delta s}, S_1, S_2$
), and (in red) the path
![]() $v_1, v_2, \dotsc, v_{\delta s}$
given by Claim 3.1, together with the corresponding neighbourhoods
$v_1, v_2, \dotsc, v_{\delta s}$
given by Claim 3.1, together with the corresponding neighbourhoods
![]() $N_G(v_j, U_{i+j} \setminus Q_{i+j})$
(the red blobs).
$N_G(v_j, U_{i+j} \setminus Q_{i+j})$
(the red blobs).
We will now find a collection of sets
![]() $S''_{\!\!\!i+j-1} \subseteq S'_{\!\!i+j-1}$
of order at least
$S''_{\!\!\!i+j-1} \subseteq S'_{\!\!i+j-1}$
of order at least
![]() $|S_{i+j-1}| - \alpha \tilde sp/8$
such that, for every
$|S_{i+j-1}| - \alpha \tilde sp/8$
such that, for every
![]() $2 \leqslant j \leqslant \delta s$
, every
$2 \leqslant j \leqslant \delta s$
, every
![]() $v \in S''_{\!\!\!i+j-2}$
has a non-empty
$v \in S''_{\!\!\!i+j-2}$
has a non-empty
![]() $N_G(v,S''_{\!\!\!i+j-1})$
. First, choose
$N_G(v,S''_{\!\!\!i+j-1})$
. First, choose
![]() $S''_{\!\!\!i+\delta s-1} \subseteq S'_{\!\!i+\delta s-1}$
of order
$S''_{\!\!\!i+\delta s-1} \subseteq S'_{\!\!i+\delta s-1}$
of order
![]() $|S_{i+\delta s-1}| - \alpha \tilde sp/8$
arbitrarily, noting that such a set exists by the bound on
$|S_{i+\delta s-1}| - \alpha \tilde sp/8$
arbitrarily, noting that such a set exists by the bound on
![]() $|S'_{\!\!i+\delta s-1}|$
. Having chosen
$|S'_{\!\!i+\delta s-1}|$
. Having chosen
![]() $S''_{\!\!\!i+j-1}$
for some
$S''_{\!\!\!i+j-1}$
for some
![]() $2 \leqslant j \leqslant \delta s$
, we choose
$2 \leqslant j \leqslant \delta s$
, we choose
![]() $S''_{\!\!\!i+j-2}$
as follows. Recall that
$S''_{\!\!\!i+j-2}$
as follows. Recall that
![]() $(S_{i+j-2},S_{i+j-1})$
is
$(S_{i+j-2},S_{i+j-1})$
is
![]() $({\varepsilon },\alpha p)$
-lower-regular and, thus, by Lemma 2.1 and the bounds on the orders of
$({\varepsilon },\alpha p)$
-lower-regular and, thus, by Lemma 2.1 and the bounds on the orders of
![]() $S'_{\!\!i+j-2}$
and
$S'_{\!\!i+j-2}$
and
![]() $S''_{\!\!\!i+j-1}$
,
$S''_{\!\!\!i+j-1}$
,
![]() $(S'_{\!\!i+j-2},S''_{\!\!\!i+j-1})$
is
$(S'_{\!\!i+j-2},S''_{\!\!\!i+j-1})$
is
![]() $(2{\varepsilon },\alpha p)$
-lower-regular. It follows that there are at least
$(2{\varepsilon },\alpha p)$
-lower-regular. It follows that there are at least
![]() $(1-2{\varepsilon })|S'_{\!\!i+j-2}| \geqslant |S_{i+j-2}| - \alpha \tilde sp/8$
vertices
$(1-2{\varepsilon })|S'_{\!\!i+j-2}| \geqslant |S_{i+j-2}| - \alpha \tilde sp/8$
vertices
![]() $v \in S'_{\!\!i+j-2}$
which satisfy
$v \in S'_{\!\!i+j-2}$
which satisfy
We declare the set of such vertices to be
![]() $S''_{\!\!\!i+j-2}$
and continue on to the next index
$S''_{\!\!\!i+j-2}$
and continue on to the next index
![]() $j$
.
$j$
.
Starting with an arbitrary
![]() $v_1 \in S''_{\!\!\!i}$
and sequentially choosing
$v_1 \in S''_{\!\!\!i}$
and sequentially choosing
![]() $v_j \in N_G(v_{j-1}, S''_{\!\!\!i+j-1})$
now completes the proof.
$v_j \in N_G(v_{j-1}, S''_{\!\!\!i+j-1})$
now completes the proof.