Anomalous reflection configuration

The chosen anomalous reflection configuration is the one depicted in Fig. 1.

Fig. 1.

Anomalous reflection of a TM plane wave occurring in the Oyz plane, with an ideal or a discretized linear phase gradient lying in the Oxy plane.

A plane wave coming from the direction θ _i impinges on a surface lying in a Oxy plane and is converted into an other plane wave reflected in the direction θ _r. Both waves are transverse magnetic polarized (TM, H⊥Oyz). The anomalous reflection is made possible by the presence of a linearly varying reflection phase distribution along u_y at the reflecting surface [Reference Yu, Genevet, Kats, Aieta, Tetienne, Capasso and Gaburro9].

A solution to synthesize such a phase gradient is to discretize it by using reflective cells. The discretization choice here is such that each gradient spatial period D _y is covered with a same periodically distributed supercell, composed itself of three cells of size d. The phase law can be written in three equivalent ways to express the useful dimensions:

(1)$$\sin( \theta_{r}) -\sin( \theta_{i}) = {1\over k}{{\rm d}\varphi\over {\rm d}y} = {1\over k}{2\pi\over D_y} = {\lambda\over 3 d}$$

where k and λ are the wave number and wavelength at a given frequency f, θ _i the direction of the incoming plane wave, and θ _r the direction of the reflected one. For f = 8 GHz, θ _i = 0°, and the anomalous reflection angle being set, for our example, to θ _r = 60°, the two other dimensions are deduced: D _y ≈ 43.3 mm and d ≈ 14.43 mm.

Phase law synthesis

To produce the desired phase law, H shape patch cells studied in [Reference Haddad, Loison, Gillard, Harmouch and Jrad17] are used. The cells consist of a perfect electric conductor (PEC) patch on top of a dielectric substrate of relative permittivity ${\epsilon _r = 2.17}$, backed by a PEC plane. Figure 2 presents the geometrical parameters of the cells as well as a phase response as a function of one parameter: the patch length L.

Fig. 2.

Variation of the phase response of the H cell versus L in infinite periodic environment for l = 3 mm. Fixed parameters are h = 1.6 mm, d = 14.43 mm, and W = 2 mm.

The three cells constituting the supercell must produce regularly spaced phase responses to create the linear phase variation. The needed geometrical parameters for each cell p ∈ {1,  2,  3}, highlighted on the trace of Fig. 2 by crosses, are listed in Table 1, as well as their phase response.

Table 1.

Geometrical parameters of the initial supercell

The supercell is then replicated nine times in the u_y direction to produce an approximate array length of 10 λ. The array is studied in full-wave simulation using HFSS with absorbing boundary conditions along u_y and a perfect magnetic conductor along u_x to ensure infinite periodicity along the u_x direction of TM polarization. The radiated fields are used to calculate a bistatic RCS pattern [Reference Knott, Shaeffer and Tuley18] that is shown in Fig. 3 in solid line.

Fig. 3.

Bistatic RCS for θ _i = 0° of the initial surface compared to the analytical one used to design the surface.

The structure mainly radiates in the desired direction θ = 60°, but also shows noticeable radiation levels in two other main directions : θ = 0° and θ = −60°.

Limitations of the approach

During the synthesis procedure the surface is considered as an array of cells only characterized by their reflection coefficients ${\Gamma _p = e^{j \varphi _p}}$, in such a way they are hosting a source field

(2)$${\bf E}_{s, p} = E_0 {\bf u}_y \Gamma_p = E_0 {\bf u}_y e^{\,j\varphi_p}$$

E ₀ being a unitary amplitude and φ_p taking only the three possible values presented in subsection “Phase law synthesis” with φ_p = φ_p+3. This source field can be converted into current densities and used in radiating integrals [Reference Balanis19] to calculate the field created by a vacuum-surrounded aperture hosting this source field. The obtained field is summed over all the 27 contributing cells to obtain a bistatic RCS diagram that is compared to the simulated one in Fig. 3.

This basic synthesis approach does not take into account the two parasitic radiation directions as only the main lobe at θ _r = 60° is predicted by the analytical model. It is worth mentioning that, despite the simplicity of this approach, the main lobe level is well estimated by the analytical model, with only 0.4 dB difference with respect to the full-wave HFSS simulation.

Expected behavior

The periodicity of the array, obtained by the replication of the supercell, is the cause of the parasitic reflections. To understand this phenomenon, we study the structure with the help of Floquet analysis. The total three main radiation directions are predicted by Floquet analysis [Reference Bhattacharyya20]. They correspond to every m that provides real solutions to the equation

(3)$$k_{zm}^2 = k^2 - k_{ym}^2$$

where

(4)$$k_{ym} = k_{y0} + {2\, m \pi\over D_y}$$

with k _y0 and k _ym the components along u_y of the k₀ and k_m wave vectors respectively. The first one is associated to the fundamental Floquet mode and the second one is associated to one harmonic Floquet mode. In the considered case, as the incoming and reflected waves propagate in the same medium, ${\lVert {\bf k}_0\rVert = \lVert {\bf k}_m\rVert = k}$. Writing down k _y0 = ksin (θ ₀) and k _ym = ksin (θ _m) in (4) leads to

(5)$$\sin( \theta_m) - \sin( \theta_0) = {1\over k}{2\pi\over D_y}$$

which is the generalized reflection law, written in (1), where θ _m is the intended reflection direction after an illumination in the θ ₀ direction. Performing anomalous reflection, with the help of the generalized reflection law, while setting the structure periodicity equal to the gradient periodicity is strictly equivalent to satisfy the m = 1 Floquet mode propagation condition. We also verify that in our case the modes m = −1 and m = 0 are propagative and correspond to the directions of the parasitic radiations observed in the previous section.

Usage of the Floquet-type simulation

In the light of the previous analysis, the anomalous reflection structure can be seen as a reflecting surface that has a conversion capability between the different propagative modes. To understand its behavior, the supercell can be simulated in a Floquet environment, as depicted in Fig. 4.

Fig. 4.

The supercell in Floquet-type simulation.

The supercell is infinitely replicated by the mean of master/slave pairs defined along the u_x and u_y directions. This allows to define a Floquet port that can be used to excite the structure.

Simulating such a structure gives access to a multimode coupling matrix whose elements are the S _m,n complex parameters defined as

(6)$$E_m = S_{m, n} E_n$$

where E _m is the complex field amplitude in a m reflected mode while the structure is studied under a n exciting mode of field amplitude E _n. The parameters of interest in our example are the S _m,0 because they correspond to an excitation with the n = 0 mode, which corresponds to an incidence of θ = 0°.

The S _m,0 parameters of the simulated supercell used to create the initial array are reported in Table 2. The S _−1,0 parameter is highlighted as it will be useful to be compared in the coming study of section “Metasurface optimization.”

Table 2.

S _m,0 parameters of the initial supercell

It can already be noticed that the weights in decibels attributed to each mode roughly follow the same hierarchy than the corresponding lobe levels observed on the RCS diagram.

Incorporation of S_m,0 parameters in the model

As described in subsection “Limitations of the approach,” a radiated field can be obtained considering source fields on the surface. This time, the surface is not seen as an array of cells any more, but in its entirety, hosting three different source fields for the three possible values of m

(7)$${\bf E}_{s, m} = E_0{\bf u}_y S_{m, 0} e^{-jk\sin( \theta_m) y}$$

Each source field is of unitary amplitude E ₀ with a weighting S _m,0, obtained from Table 2, and a phase variation corresponding to the considered Floquet mode. Source fields are again converted into current densities and used in radiation integrals. The three radiated fields are summed and give the bistatic RCS shown in Fig. 5 in dashed line.

Fig. 5.

Bistatic RCS for θ _i = 0° of the initial surface compared to the analytical one using S _m,0 simulation parameters.

The new source fields correctly reproduce the behavior of the simulated surface. Each main lobe level is well predicted, while the nine-supercell array is finite along u_y, in contrast with Floquet-type simulation. This conclusion gives credit toward a representation of the surface with using only the S parameters associated to the supercell, thus avoiding the burdensome simulation type required to solve the whole structure. Taking advantage of this situation, we propose to perform S parameter optimizations, obtained with effortless simulations, that are expected to have a quantitative repercussion on the bistatic RCS of the complete structure.

Process

The geometrical parameters of the cells (l _p,  L _p) are chosen to be the optimization input variables and the objective is to minimize the level of the S _−1,0 parameter. This definition is arbitrary and suits a particular application, the method is not restricted to it and can be used for other specifications. One may want to work for example with any S _−n,n parameter, corresponding to backscattering that is of specific interest for numerous RCS applications. Indices m and n can also be larger than 1, if the supercell length is set accordingly. Our proposed approach can theoretically be extended to the optimization of such supercells with more higher-order Floquet modes. The formalism using S parameters remains basically the same and so does the power-transfer mechanism between propagative modes. Of course, the optimization problem gets more complex and more degrees of freedom might be needed to solve it. The cost function to be minimized is then

(8)$$f_c( l_p,\; L_p) = -( \vert S_{1, 0} \vert - \vert S_{-1, 0} \vert) $$

The aim is then to increase the difference between the lobe levels associated to the modes m = −1 and m = 1, avoiding the solutions where both of them are low, and without having a particular interest in handling the mode m = 0.

Starting a gradient type optimization process from the first supercell dimensions as an initial guess, the solution is expected to be close to the initial one, as it is already shaped from the phase gradient. In the same spirit, the cells used in the array are obviously in a different environment than the infinite periodic one used to obtain their phase response. The proposed optimization process can thus be seen as a way to better take into account the neighborhood of each cell, as the whole supercell is simulated.

Finally, based on our observations, we experience that some parameters are more sensitive than others. For example, as the L dimension is oriented along E, it shows a greater influence on S parameters than l. Hence, the critical dimension L can be first used in a rough analysis and l can be used afterwards for a fine tuning. A similar reasoning process can be applied to deal with sensitive cells, that are close to resonance, before others.

Case of l = 8 mm

Since the complete procedure has already been discussed, we propose here to only give concluding results and to comment them. Tables 5 and 6 give the geometrical variations and S _m,0 parameter evolutions through the optimization process. Figure 9 shows the global bistatic RCS comparisons.

Fig. 9.

Bistatic RCS for θ _i = 0° of the optimized surface compared to the one of the initial surface, in rigorous simulation and by using S parameters. Case l = 8 mm.

Table 5.

Evolution of the supercell dimensions during the optimization process

Case l = 8 mm.

Table 6.

Evolution of the supercell S _m,0 parameters during the optimization process

Case l = 8 mm.

The $\vert S_{-1, 0} \vert$ level drastically decreases, but one should carefully keep in mind that the initial level was lower compared to the previous case. In contrast, the $\vert S_{0, 0} \vert$ level raises as the optimization process does not handle it. Geometrical variations of the supercell are smaller than in the first l = 3 mm case and so it is for phase response evolution. The largest geometrical variation for this case is 4% of the initial cell size and is in contrast about 32% for the first presented case. The optimized array performance is greatly improved, by an attenuation of 15 dB on the parasitic lobe level. Nevertheless, the model is less quantitative in this region where the RCS quantities are very low on the decibel scale.

Case of l = 12 mm

In the same way, concluding results for another case where the starting l value for optimization is 12 mm can be found in Tables 7 and 8 and in Fig. 10.

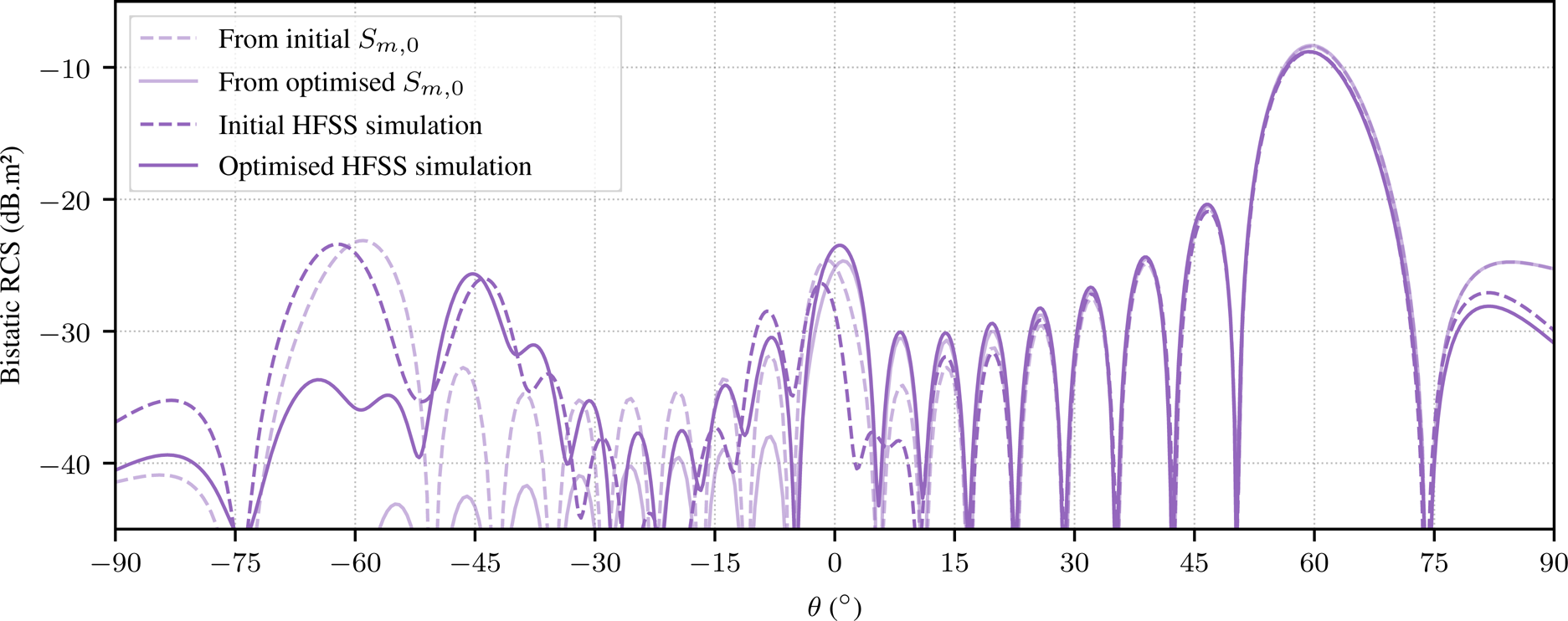
Fig. 10.

Bistatic RCS for θ _i = 0° of the optimized surface compared to the one of the initial surface, in rigorous simulation and by using S parameters. Case l = 12 mm.

Table 7.

Evolution of the supercell dimensions during the optimization process

Case l = 12 mm.

Table 8.

Evolution of the supercell S _m,0 parameters during the optimization process

Case l = 12 mm.

The $\vert S_{-1, 0} \vert$ value drops by a great amount as well and the expected RCS diagram shows very low lobe levels for the θ = −60° direction. Even if the bistatic RCS diagram shows a 10 dB reduction performance in the θ = −60° direction, the model is less accurate in this angular region, where RCS values are lower. Cell geometry variations are even smaller in this case, actually going under manufacturing precision. Still corroborating the viability of the used technique, this last example could however be unrealistic for practical implementation.

Global results commentary

The three pairs of presented structures exhibit a radiation peak around the −45° area. They also share a lot of their properties, such as array lengths, substrate thickness, cells, and patch shapes for example. It surely goes beyond the scope of the model presented in this publication, but exploring the shared properties of the surfaces should lead to discriminate the origin of this particular radiation.

All the presented structures use the same patch geometry and same degrees of freedom for optimization, but converge to different optimal values. This obviously proves that at least two of them are not global optimums. This is not a surprising conclusion since they all use an initial guess from which it is intended to not deviate too much. This is a way to keep the computing resources needed for optimization very low.

Figure 11 compares phase variations of the cells used in the three initial cases, with respect to L. Globally, the absolute value of the slope at resonance grows as l increases. This gives an explanation about the smaller geometrical variations observed through the three cases, as l is larger for each case.

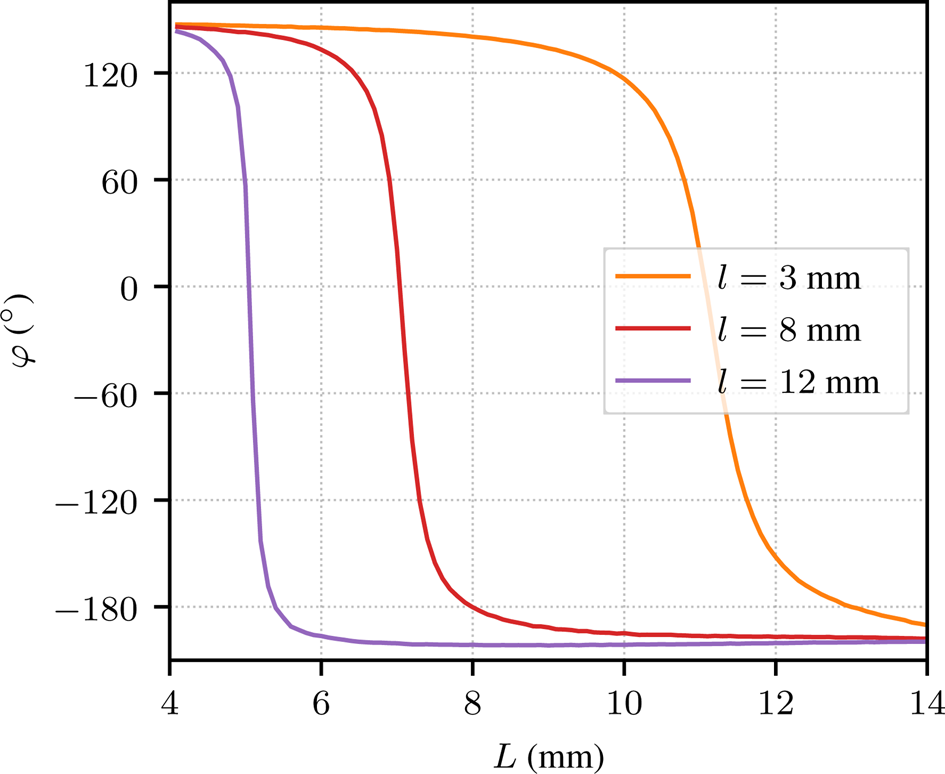
Fig. 11.

Phase response, in infinite periodic environment, of the H-shaped patch cells versus L for the three studied cases.

The case for which l = 3 mm shows a smoothly varying phase response with L, but the phase range being in greater L region the resulting cells are wider and then closer to their neighbor in array environment. This could expose them more to coupling effects. In a complementary way, the case for which l = 12 mm shows really sensitive phase response regarding L but giving huddled and then isolated cells once in an array. The Floquet-type simulation takes into account the coupling effects between cells in a supercell and between supercells in infinite array. Nevertheless, we may expect slight deviations in the case of a realistic finite array as we have here. The case for which l = 8 mm then results in a good trade-off for supercell stability. It is actually the case where the optimized array shows the best performance in attenuating the level of the S _−1,0 corresponding lobe.

Finally, applying the process to several cases showed the robustness of the proposed method while giving some synthesis advices for this kind of structures.