Methods

Between 21 February 1968 and 27 May 1969, the British Trans-Arctic Expedition (BTAE) crossed the Arctic Ocean between Barrow, Alaska, and a small island off the coast of Spitsbergen (Fig. 1).

Fig. 1. The Arctic Ocean showing the roule of the British Trans-Arctic Expedition. The broad arrows show the two main directions of ice drift. The Pacific Gyral lies between Point Barrow and the North Pole, and the Trans-Polar Drift Stream is on the Russian side of the Pole. The BTAE drifted from A to B between July 1968 and February 1969.

In order to study the regional variations of surface topography an ice log was kept during the journey. Between Barrow and the North Pole a summary of ice forms was made at the end of each day. Between the North Pole and Spitsbergen the estimated height of each ridge, the thickness of the ice slabs forming the ridge and the size and type of floes were recorded.

Over 250 holes were drilled through old and first-year ice to determine its thickness. Generally, one hole was drilled each day. 78% of the holes were drilled through old ice and the remainder through thick first-year ice. In addition, more than 100 thickness measurements were made through ice less than 0.5 m thick to estimate its load capacity. From these data the ice growth and overall ice thickness in winter have been calculated.

During July and August 1968 the expedition camped on a giant floe which drifted between lat. 81.5° N. and lat. 84.0° N. (Fig. 1). During this period, the ablation of the floe ice was studied. Ice ablation was measured at an ablatometer and two stakes, all on multi-year floes. The ablatometer consisted of two stakes frozen into the ice 2.5 m apart and joined by a cord. The mean height of the cord above the ice was measured daily. Bottom ice ablation was measured by repeated drilling at two sites. To relate these measurements to ablation over the entire surface, two sets of precise levelling traverses were made across 742 m of floes. The traverses included both new and old ridges. The first set was made on 17 and 18 July and the second on 28 August.

Accuracy

As the prime motive of the expedition was not a scientific one, the majority of the observations made during the travel periods were recorded while on the move. Due to the difficulty of distinguishing between first-year and second-year ice under a snow cover, any ice of indeterminate age was recorded as “old ice”. Because of this, the coverage of first-year ice has been underestimated by approximately 2%.

No device was used to measure distance while travelling so that all the ice-log observations are estimates. The total mileage travelled between the North Pole and Spitsbergen has been calculated from both the ice log and the astro-fixes. The ice-log mileage is 12% less than the true mileage. Part of this error is due to the fact that the estimated distance was often omitted from the ice log during periods when no observations were recorded. The ice-drift direction between the North Pole and Spitsbergen was favourable to the expedition and this may account for up to half of the distance error. The remaining error is believed to be evenly distributed throughout the data. To minimize the distance error, the relative and not the absolute cover of each ice type has been used.

The BTAE data were recorded from a single traverse and therefore may not be representative of the entire Arctic Ocean. It is impossible at the present time to determine the typicality of the data, but it will be seen later that they are, in many respects, in reasonable agreement with theoretical considerations of both the heat balance and the pattern of ice drift in the Arctic Ocean. The relative coverage of each ice type along the traverse route is believed correct to within ±5%. However, the final values for total accumulation, ablation and export, because some series of measurements are incomplete and unrepresentative, may be in error by as much as ±50%.

Relative coverage of deformed, old and young ice and ice-free areas (Table I; Fig. 2)

To compare the surface observations with those taken by nuclear submarine, the extent of ridges and hummocks below the water line (i.e keels and bummocks) has been calculated from a pressure-ridge model (paper in preparation by R. M. Koerner) similar to that of Reference Wittmann, Schule and FletcherWittmann and Schule (1966). From a study of under-ice profiles recorded by U.S. nuclear submarines, Reference Wittmann, Schule and FletcherWittmann and Schule (1966) found that 18% of the ice was ridged in the winter of 1960 and 13% in the summer of 1962. There is a difference of 3% between the BTAE and the submarine data. Old bummocks and ice keels have presumably been included in the calculation from the submarine profiles whereas, in the present data, ridges and hummocks more than 2 years old and smoothed by summer ablation, were recorded as unridged old ice. The difference in definition and a genuine annual variation may account for the 3% discrepancy between the BTAE and submarine data.

Table I. Ice Type, Expressed As A Percentage Of Distance Covered

Fig. 2. Distribution of ice types between lat. 89°N. and lat. 81° N. along approximately long. 30° E. expressed as a percentage of total area. 1. Mean value in the Pacific Gyral; 2. Mean value in the transition zone; A. Hummocks and ridges; B. Bummocks and keels.

In this paper, the term ice-free is used with reference both to areas where no sea ice is present and to areas where there is a cover of frazil ice or grease ice, as both of these ice types form in a few hours in mid-winter. Between the North Pole and Spitsbergen, only 0.6% of the area crossed by the expedition was ice-free (Table 1; Fig. 2). In March and early April, when the expedition was within a few degrees of the North Pole, only 0.2% of the area was ice-free. Badgley (1966), on theoretical grounds, considered that less than 1% of the Central Arctic Ocean should be ice-free in winter; Reference UntersteinerUntersteiner (1964) considered the coverage to be less than 0.5%. Profiles taken by U.S.S. Sargo in the winter of 1960 found an ice-free coverage of 1.8% (Reference Wittmann, Schule and FletcherWittmann and Schule, 1966). “Birds-eye” flight data give a mean winter ice-free coverage which is 11.0% of the total area (Reference Wittmann, Schule and FletcherWittmann and Schule, 1966); this percentage seems unreasonably high. The difference between the BTAE and submarine ice-free coverage values may in part be attributable to differences in time and place of observation. However, it is possible that the submarine-profiling system used in 1962 was unable to distinguish between an ice-free surface and very thin ice. It is interesting to note that 3.0% of the ice crossed in April 1969 was 0.3 m or less thick. This suggests the submarine profiler was at least capable of distinguishing between ice less than 0.3 m thick and ice-fřee areas. The high percentage of ice-free areas in the Gyral (Table I) is due to the lateness of the period of observation which extended into the summer months.

Nilas, young and first-year ice will be referred to collectively as first-year ice. The first-year ice coverage shown in Table I and Figure 2 is an underestimate by about 2% of the true value. Reference Wittmann, Schule and FletcherWittmann and Schule (1966, p. 237) calculated from “Birds-eye” flight data a 14% coverage for a similar ice type in the Trans-Polar Drift Stream. In the present data, the Gyral shows the smaller first-year ice coverage and this is in agreement with theoretical considerations of ice drift in the Arctic Ocean (e.g. Reference CampbellCampbell, 1965), which predict a higher occurrence of convergent ice flow in the Pacific Gyral than elsewhere. The most extensive coverage of first-year ice crossed by the BTAE was between lat. 85° N. and lat. 88° N. along long. 140° W. (Fig. 1). This indicates that there was considerable divergent movement in that area during the 1968–69 winter. The position of the area, on the edges of both the Gyral and Trans-Polar Drift Stream, may account for the scale of divergent movement. However, it is probably a transition zone that varies in position from year to year. For example, the Plaisted expedition approaching the North Pole from Ellesmere Island in April 1968, found large numbers of heavy old floes in the transition zone and at the North Pole (Reference Aufderheide and PitzlAufderheide and Pitzl, 1970). This suggests that in 1968 the Gyral extended its influence to at least the North Pole. A year later, the BTAE saw very few Gyral floes near the North Pole and, from a change in the topography, the northern edge of the Trans-Polar Drift Stream was estimated to be situated along lat. 88° N. on the Canadian–U.S.A. side of the North Pole.

Ice thickness (Fig. 3; Tables I and II)

Despite the fact that 75% of the thickness measurements were taken through old ice, there is a wide range of thicknesses (Fig. 3). Even when the first-year ice and hummock sites are excluded from the data, there is still no well-defined mode which can be identified as a steady-state thickness. The thickness of unhummocked ice can vary by more than 1.5 m on the same multi-year floe even though the floe may be several years old. A single steady-state thickness, therefore, seems to be theoretical. Instead, there is probably a separate steady-state thickness for each basic old-ice type. A mean multi-year floe thickness is more important for the purposes of the present study. This may be termed a mean steady-state thickness h _ss which is dependent on the relative coverage and thickness of hummocked, ponded and level, unpondcd ice. The relative coverages have been measured from a set of air photographs taken by the Polar Continental Shelf Project in the Lincoln Sea in July 1968, and from photographs taken by the BTAE. The mean thickness of undeformed old ice is taken from the ice-thickness data. A mean hummock thickness of 13 m has been estimated from a levelling profile across a multi-year floe and an above/below relationship of 1 : 7. (Density of old sea ice = 0.7 Mg m⁻³ (Reference Vowinckel, Weeks and LeeWeeks and Lee, 1958) and sea-water density = 1.025 Mg m⁻³ (Reference CabanissCabaniss, 1962), h _ss is calculated to be 3.5 m in the Pacific Gyral, 3.0 m in the Trans-Polar Drift Stream and 3.2 m in the transition zone between the two. The BTAE measurements showed no significant difference between the thickness of undeformed ice in the Pacific Gyral and the Trans-Polar Drift Stream so that the high h _ss value in the Pacific Gyral must be due to the larger number of hummocks on the relatively old multi-year floes there.

Fig. 3. Ice thickness (%) of floes more than 1.5 m and less than 4.5 m thick.

Table II. Annual Ice Export (G), Accumulation (C), Ablation (A), Balance (B) and Thickness In the Arctic Ocean ( M of Ice)

First-year ice covers a wide range of thicknesses (Table I). New ice beginning its growth in September can be identified by the fresh-water ice at its surface; seven measurements through this ice in late May gave a mean thickness of 2.04 m, which may be considered a season’s maximum growth from open water.

The mean thickness of the entire ice cover crossed by the expedition, ĥ _t , has been calculated from the extent and thickness of each ice type, including both undeformed and deformed ice. The three values for h _ss already calculated have been used in the computation of ĥ _t. The estimated or measured thickness of each area of undeformed first-year ice and the calculated thickness of deformed ice (based on the height of the feature above the water line) have been entered into the calculations separately. Two mean values are calculated. The first value ĥ_t(p) considers the cavities formed during the process of deformation as ice. The second value ĥ _t(e) is an equivalent ice thickness from which the cavities have been excluded. The latter is the more important of the two values in any consideration of the ice balance.

The results are shown in Table II. ĥ _t is greatest in the Pacific Gyral, again because of the larger number of old hummocks, but also due to the more massive nature of the ridges there; this is in accord with both the theoretical and observed patterns of ice drift in the Arctic Ocean.

Ice and Snow Accumulation (c) ( Tables II, III and. IV)

In this context, ice accumulation is the volume of ice forming in the Arctic Ocean in any one balance year. Although ice growth was measured at several sites on both new and old ice, the measurements do not cover a complete growth period. The results are shown in Table III and the high growth rate of first-year ice underlines the importance of fracturing in the process of ice accumulation.

Table III. Ice Growth (Mm D^{− 1}) In The Central Arctic Ocean, September 1968 To February 1969

Table IV. Ice Growth in a Small Area in the Central Arctic Ocean, 5 October 1968 to 22 February 1969. (mm of Ice a Day, Expressed as a Continuous Layer Covering the Entire Area Examined (i.e. ĉ)

First-year ice may be in either unridged or ridged forms. In the process of ridging of new ice, some old ice is often incorporated in the ridge. Between the North Pole and Spitsbergen, 16% of the new ridges contained some old ice. However, the total amount of old ice in first-year ridges is probably no more than 5% and the calculations of the amount of new ice in ridged form have been corrected by this amount.

The amount of new and first-year ice crossed by the expedition (i.e. the winter balance of ice less than 1 year old) is given in Table II. Errors are due to;

• i. An incorrect assessment of ice thickness.

• ii. Misidentification of some second-year ridges for first-year ridges.

• iii. Misidentification of first-year ice for old ice.

The errors under (i) are probably self-cancelling, and the errors under (iii) are believed to exceed those under (ii). The calculations therefore underestimate the amount of first-year ice.

Between 5 October 1968 and 23 February 1969, ice accumulation in fractures forming in an area approximately 5 km square was measured daily. The thickness of ice forming in new fractures was measured by drilling. The estimates of fracture width have an error of about 5% when made in periods of moonlight, but about 20% in periods of darkness when a battery spotlight was used. The total ice accumulation in fractures in the study area is shown in Table IV. Between 5 October 1968 and 2 January 1969, the figures refer essentially to three 400 m by 600 m floes and the fractures at their edges. After 2 January 1969, the study area included two large polynyas which opened at the edges of the floes. The polynyas increased the new-ice coverage in the study area to 70% which is clearly unrepresentative of the Pacific Gyral as a whole. If the growth rate of ice in fractures between 5 October 1968 and 2 January 1969 is extrapolated to cover a 1 September to mid-May growth period, the annual first-year ice accumulation (ĉ ₁) in the study area is an equivalent ice layer 0.3–0.6 m thick. A calculation from the ice-log data of first-year ice accumulation for the same growth period in the Pacific Gyral gives a comparable layer 0.5 m thick.

Ice growth under steady-state floes is well documented in the literature where values vary between 0.4 and 0.5 m of ice per year. However, the annual ice accumulation under old ice must be higher than this as it includes ice older than 1 year but of less than steady-state thickness. So that with a first-year annual ice accumulation (ĉ ₁) of about 0.5 m of ice and an old-ice annual accumulation slightly greater than o.4–0.5 m of ice, the contributions to the positive side of the ice balance of the two basic ice types are quite similar.

Snow accumulation was measured on the BTAE by probing to the ice surface in ten different places and taking one set of density measurements at each of 38 locations. The measurements were taken in the middle of large floes. The results are shown in Figure 4. Because snow is blown into open fractures and into hummock fields, the snow accumulation on the floes is less than the total precipation. There is a significant increase (at the <1% level) of snow accumulation towards each end of the traverse. The pattern is probably related to greater cyclonic activity round the periphery of the Arctic Ocean (Reference WilsonWilson, 1963, p. 268–69).

Fig. 4. Snow accumulation between Point Barrow (lat. 71° N.) and Spitsbergen (lat. 81° N.).

Superimposed ice forms in June at the base of the snowpack, particularly in depressions on the floes; 20–30 mm of this ice formed in June 1968.

Fresh-water ice forms at the interface between salt and fresh water in summer. In 1968, 20 mm of this ice formed in fractures at a depth of 1.5 m, equivalent to a continuous layer 2–4 mm thick.

Ablation ( Table II)

The measured ablation of a multi-year floe in 1968 was 500 kg m⁻² (i.e. a layer of ice 0.55 m thick). Precise levelling transects over the floe surface at the beginning and end of the melt season showed that the ablation of the surface ice is non-uniform (Table V). These observations indicated that hummocks, with an albedo about 10% higher than that of level ice (Reference KoernerKoerner, 1970), are self-perpetuating. The total ablation at the level site has been weighted according to the data in Table V to give a mean ablation ā _ss of 0.5 m of ice.

Table V. The Variation of Ablation on A Multi-Year Floe Expressed as A Percentage of the Ablation Measured at A Site on A Level. Area of That Floe (500 Kg M^{− 2} IΠ July And August 1968)

Because fracturing made first-year ablation sites inaccessible, a continuous record of the ablation of first-year ice, ā ₁, was not taken. However, Reference YanesYanes (1962), from measurements taken at U.S.S.R. floe stations, formulated the empirical relationship

(2)

Although Reference YanesYanes (1962) did not specify what type of multi-year ice surface ā _ss refers to, it is assumed to represent the ablation of level ice ā _ss(d); ā ₁, is then equal to an ice layer 0.8 m thick.

The ablation of new ridges ā _r and hummocks, ā _h is 2.6 times as great as that of undeformed multi-year ice ā _SS(d) (Table V). However, a ridge or hummock field contains about 15% cavities so that ablation there is:

(3)

Both the snow cover and superimposed ice layer ablated completely in the summer of 1968 in the vicinity of the camp (Fig. 1). The interface ice layer did not appear to ablate at all but was incorporated into the winter ice layers.

Balance (Table II)

The mass balance of first-year ice is positive (i.e. c ₁ > ā ₁), whereas the balance of steady-state Hoes is zero ( c _ss =ā _ss). However, the mass balance of old ice of less than steady-state thickness must be positive; as no separate study of floes of this age was made, the ice balance on them must be calculated.

To attain a mean steady-state thickness h _ss, a first-year floe of thickness h ₁ must have a total net balance, b _n(t), of h _ss— h ₁, over a period m— 1 years, where m is the age in years of a floe which has just attained steady-state thickness. The value for a full season’s growth quoted previously (2.04 m) can be used for h ₁, as ice thicker than this is in its second year of growth. Using the previously calculated values of h _ss in h _ss— h ₁, the value of b _n(t) where 1 < n < m years is 1.42 m in the Pacific Gyral, 1.19 m in the transition zone and 0.96 m in the Trans-Polar Drift Stream.

Ice drift in the Trans-Polar Drift Stream may be considered as stream flow where ice leaves the stream between Greenland and Spitsbergen. As a first approximation, therefore:

(4)

where S is the area of ice 1, 2, 3, and T years old. T is the age, in years, of the oldest ice commonly present and is given by:

(5)

where τ= 1 year. In this ease, S₁ includes areas of ridged and hummocked new and first-year ice. In the Trans-Polar Drift Stream S₁, is equal to 19.9% of S _t so that T is 5 years. However, hummocking annually reduces the area of old ice by an amount R which can be calculated from

(6)

where S _q is the area of hummock fields composed of old ice (6% of the total area in the Trans-Polar Drift Stream), h _q is the mean hummock field thickness (10 m, a figure based on a mean above-waterline height calculated from the BTAE ice log and an above : below relationship of 1 ; 7) and h _d is the thickness (in m) of the ice before hummocking (2.5 m from Figure 3). (S _q h _q)/ h _d in Equation (6) gives the original extent of undeformed ice that the hummock fields formed from; τ/T reduces the term to an annual value. In the Trans-Polar Drift Stream, R is equal to 3.6% of the total ice and ice-free area. The area of ice n years old (S _n) for n ⩾ 1 year is then given by:

(7)

where ϕ is R/S _t.

T can then be found from

(8)

Taking a representative area of 100 km² where S _t = 100 km², R = 3.5 km² and S ₁ = 19.9 km², T is still 5 years. 5 years is in fact similar to the drift period of several Russian floe stations in the Trans-Polar Drift Stream and to the combined drift period of Maud and Fram (Reference Dunbar and WittmannDunbar and Wittmann, 1963).

As, from thermodynamic considerations, there is no ice growth where h ⩾ h _SS, the area of hummock fields more than 1 year old must be subtracted from the total area of old ice so that

(9)

where S _n(d) is the area of undeformed old ice of less than steady-state thickness and S _ss(d) is the area of undeformed ice of steady-state thickness. Reference UntersteinerUntersteiner (1964) has calculated that h _ss is attained in 7–8 years from ice-free conditions. However, there is no significant difference between the set of old-ice thickness measurements from the Pacific Gyral and the set from the Trans-Polar Drift Stream despite the fact that ice may circulate for considerably longer periods in the Pacific Gyral. Similar old-ice thicknesses in each area, therefore, indicate that h _ss is attained in both, i.e. in less than 5 years. In Equation (10) it is assumed that h _ss is attained in 5 years so that S _ss(d) = 0; this assumption introduces a maximum error of 10% (i.e. h _ss is attained in 2 years). The annual balance, b _n , of old ice of less than steady-state thickness (i.e. where 1 ⩽ n ⩽ 5 years) is given by:

(10)

where m is the age in years of a floe which has just attained steady-state thickness. Again, taking a representative 100 km² area where S _n(d) = 74.4 km² and b _n(t) = 0.96 m, b _n is 17.8 m³ of ice. This may be represented as a layer of ice 0.2 m thick spread uniformly over the 100 km² area (i.e. b _n ).

The same arguments do not apply to the Pacific Gyral, where, due to the circulatory pattern of the drift (Fig. 1), ice of all ages may drift out of the Gyral in any one year. If there is a constant decrease in the area of any one year’s ice with time R′ (due to both ice export and ice deformation), then

(11)

as 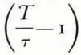R′ = S ¹– R ¹ this reduces to

(12)

In 1968, 11.5% of the ice crossed in the Gyral was in its first year. Substituting this value in Equation (12) gives T equal to 16 years. As there is an exponential rather than a linear decrease in area of any one year’s ice with time, 16 years must be regarded as a lower limit of T. There is insufficient ice-drift evidence from the Gyral at present with which to compare the calculated T value. Gyral floes have never been tracked from initial growth to export. However, it is known that Fletcher’s Ice Island (T-3) has drifted in the Pacific Gyral for over 20 years. Assuming again that h _SS is attained in 5 years, the area of undeformed old ice n years old (S _n(d)) where 1 ⩽n ⩽ 5 years is given by:

(13)

where R′ is S ₁τ/T. Taking a 100 km² representative area in the Pacific Gyral where S ₁ = 11.5 km² and T = 16 years, S _n(d) = 40.4 km². Then, putting S _n = 40.4 km² and b _n(t) = 1.42 m into Equation (10) we get b _n = 14.3 km³ or _n = 0.14 m of ice in the Pacific Gyral.

Using similar arguments in the transition zone, b _n there is 0.05 m of ice.

Ice export ( Table II)

If the ice balance in the Arctic Ocean is assumed to be in a steady-state condition, then ice export is equal to the sum of the balances of first-year ice and old ice of less than steady-state thickness. The calculated regional ice export values are shown in Table II. It should be noted that R′ in Equations (11) and (13) includes both the area of ice exported and the area reduced by the effect of ice deformation. However, even assuming the value R′ consists entirely of ice exported from the Pacific Gyral and the transition zone, the appropriate values for ĝ_t are not changed significantly.

The area of the Pacific Gyral, the Trans-Polar Drift Stream and the transition zone between has been estimated from the pattern of ice drift shown in Dunbar and Reference Dunbar and WittmannWittmann (1963, p. 92). The three regions cover 41, 55 and 4% of the Arctic Ocean, respectively (about to⁷ km²). If the ice-export values in Table II are representative, the total annual ice export from the Arctic Ocean is 5 580 km³, which is equivalent to a layer of ice 0.6 m thick spread over the entire Arctic Ocean. This means approximately 15% of the ice cover is exported each year. Gordiyenko and KarelinFootnote ^* estimated that an area of 1 036 000 km² of ice left the Arctic Ocean each year between 1933 and 1944. The mean annual thickness of the entire pack ice lies somewhere between the effective thickness (h _t(e)) at the end of winter (Table II)) and the effective thickness at the end of the melt season in August or September (i.e. h _t(e)−a _t). Using the values shown in Table II, we obtain a mean ice thickness of 3.7 m, which means Gordiyenko and Karelin’s ice-export value is equivalent to a continuous ice layer 0.4 m thick (3 800 km³). Reference Vowinckel, Weeks and LeeVowinckel (1964), from a study of wind and current drift into the Greenland Sea, calculated a similar value to that of Gordiycnko and Karelin. Because the BTAE data may not be representative of the whole Arctic Ocean, the value for ice export may be in error by as much as ±50%· However, it is believed that the data underestimate the first-year ice area in the Arctic Ocean and this leads to an underestimation of the ice export. In this case, it seems that even considering the errors in each of the three sets of calculations, the annual ice export for the period of the BTAE observations, i.e. 1967–69, exceeded that for the periods studied by Gordiyenko and Karelin, and Vowinckel (1964). This is in agreement with the records, showing an increasing severity of ice conditions off the north coast of Iceland in the 1960’s (Reference KristjannssonKristjannsson, 1969).