A group 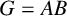G=AB$G=AB$ is the weakly mutually permutable product of the subgroups A and B, if A permutes with every subgroup of B containing 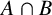A \cap B$A \cap B$ and B permutes with every subgroup of A containing 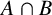A \cap B$A \cap B$. Weakly mutually permutable products were introduced by the first, second and fourth authors [‘Generalised mutually permutable products and saturated formations’, J. Algebra 595 (2022), 434–443] who showed that if 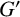G'$G'$ is nilpotent, A permutes with every Sylow subgroup of B and B permutes with every Sylow subgroup of A, then 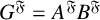G^{\mathfrak {F}}=A^{\mathfrak {F}}B^{\mathfrak {F}} $G^{\mathfrak {F}}=A^{\mathfrak {F}}B^{\mathfrak {F}}$, where 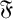\mathfrak {F} $\mathfrak {F}$ is a saturated formation containing 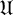\mathfrak {U} $\mathfrak {U}$, the class of supersoluble groups. In this article we prove results on weakly mutually permutable products concerning 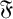\mathfrak {F} $\mathfrak {F}$-residuals, 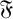\mathfrak {F} $\mathfrak {F}$-projectors and 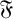\mathfrak {F}$\mathfrak {F}$-normalisers. As an application of some of our arguments, we unify some results on weakly mutually 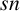sn$sn$-products.

In the setting of finite groups, suppose J$J$ acts on N$N$ via automorphisms so that the induced semidirect product N\rtimes J$N\rtimes J$ acts on some non-empty set \Omega$\Omega$, with N$N$ acting transitively. Glauberman proved that if the orders of J$J$ and N$N$ are coprime, then J$J$ fixes a point in \Omega$\Omega$. We consider the non-coprime case and show that if N$N$ is abelian and a Sylow p$p$-subgroup of J$J$ fixes a point in \Omega$\Omega$ for each prime p$p$, then J$J$ fixes a point in \Omega$\Omega$. We also show that if N$N$ is nilpotent, N\rtimes J$N\rtimes J$ is supersoluble, and a Sylow p$p$-subgroup of J$J$ fixes a point in \Omega$\Omega$ for each prime p$p$, then J$J$ fixes a point in \Omega$\Omega$.

A classical result of Baer states that a finite group G which is the product of two normal supersoluble subgroups is supersoluble if and only if Gʹ is nilpotent. In this article, we show that if G = AB is the product of supersoluble (respectively, w-supersoluble) subgroups A and B, A is normal in G and B permutes with every maximal subgroup of each Sylow subgroup of A, then G is supersoluble (respectively, w-supersoluble), provided that Gʹ is nilpotent. We also investigate products of subgroups defined above when A\cap B=1 $A\cap B=1$ and obtain more general results.

We demonstrate that two supersoluble complements of an abelian base in a finite split extension are conjugate if and only if, for each prime p$p$, a Sylow p$p$-subgroup of one complement is conjugate to a Sylow p$p$-subgroup of the other. As a corollary, we find that any two supersoluble complements of an abelian subgroup N$N$ in a finite split extension G$G$ are conjugate if and only if, for each prime p$p$, there exists a Sylow p$p$-subgroup S$S$ of G$G$ such that any two complements of S\cap N$S\cap N$ in S$S$ are conjugate in G$G$. In particular, restricting to supersoluble groups allows us to ease D. G. Higman's stipulation that the complements of S\cap N$S\cap N$ in S$S$ be conjugate within S$S$. We then consider group actions and obtain a fixed point result for non-coprime actions analogous to Glauberman's lemma.

In this note, we investigate some products of subgroups and vanishing conjugacy class sizes of finite groups. We prove some supersolubility criteria for groups with restrictions on the vanishing conjugacy class sizes of their subgroups.

In this paper, we study the structure of finite groups G=AB$G=AB$ which are a weakly mutually sn$sn$ -permutable product of the subgroups A and B, that is, A permutes with every subnormal subgroup of B containing A \cap B$A \cap B$ and B permutes with every subnormal subgroup of A containing A \cap B$A \cap B$ . We obtain generalisations of known results on mutually sn$sn$ -permutable products.

The first author [J. Brough, ‘On vanishing criteria that control finite group structure’, J. Algebra458 (2016), 207–215] has shown that for certain arithmetical results on conjugacy class sizes it is enough to consider only the vanishing conjugacy class sizes. In this paper we further weaken the conditions to consider only vanishing elements of prime power order.

We discuss some questions related to the generation of supersoluble groups. First we prove that the number of elements needed to generate a finite supersoluble group G with good probability can be quite a lot larger than the smallest cardinality d(G) of a generating set of G. Indeed, if G is the free prosupersoluble group of rank d ⩾ 2 and dP(G) is the minimum integer k such that the probability of generating G with k elements is positive, then dP(G) = 2d + 1. In contrast to this, if k – d(G) ⩾ 3, then the distribution of the first component in a k-tuple chosen uniformly in the set of all the k-tuples generating G is not too far from the uniform distribution.