Hostname: page-component-76fb5796d-vvkck Total loading time: 0 Render date: 2024-04-28T14:55:36.746Z Has data issue: false hasContentIssue false
  • English
  • Français

Antithetic multilevel particle filters

Part of: Probabilistic methods, simulation and stochastic differential equations Stochastic processes

Published online by Cambridge University Press:  16 April 2024

Ajay Jasra ,
Mohamed Maama  and
Hernando Ombao
Ajay Jasra*
Affiliation:
Chinese University of Hong Kong, Shenzhen
Mohamed Maama*
Affiliation:
King Abdullah University of Science and Technology
Hernando Ombao*
Affiliation:
King Abdullah University of Science and Technology
*
*Postal address: School of Data Science, Chinese University of Hong Kong, Shenzhen, China. Email address: ajayjasra@cuhk.edu.cn
**Postal address: King Abdullah University of Science and Technology, Computer, Electrical and Mathematical Sciences and Engineering, Thuwal 23955-6900, Saudi Arabia.
**Postal address: King Abdullah University of Science and Technology, Computer, Electrical and Mathematical Sciences and Engineering, Thuwal 23955-6900, Saudi Arabia.
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we consider the filtering of partially observed multidimensional diffusion processes that are observed regularly at discrete times. This is a challenging problem which requires the use of advanced numerical schemes based upon time-discretization of the diffusion process and then the application of particle filters. Perhaps the state-of-the-art method for moderate-dimensional problems is the multilevel particle filter of Jasra et al. (SIAM J. Numer. Anal. 55 (2017), 3068–3096). This is a method that combines multilevel Monte Carlo and particle filters. The approach in that article is based intrinsically upon an Euler discretization method. We develop a new particle filter based upon the antithetic truncated Milstein scheme of Giles and Szpruch (Ann. Appl. Prob. 24 (2014), 1585–1620). We show empirically for a class of diffusion problems that, for 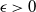$\epsilon>0$ given, the cost to produce a mean squared error (MSE) of 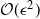$\mathcal{O}(\epsilon^2)$ in the estimation of the filter is 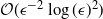$\mathcal{O}(\epsilon^{-2}\log(\epsilon)^2)$. In the case of multidimensional diffusions with non-constant diffusion coefficient, the method of Jasra et al. (2017) requires a cost of 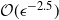$\mathcal{O}(\epsilon^{-2.5})$ to achieve the same MSE.

Keywords

Multilevel Monte Carloparticle filtersdiffusion processesfiltering

MSC classification

Primary: 65C05: Monte Carlo methods
Secondary: 60G05: Foundations of stochastic processes
Type
Original Article
Information
Advances in Applied Probability , First View , pp. 1 - 40
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beskos, A. and Roberts, G. (2005). Exact simulation of diffusions. Ann. Appl. Prob. 15, 2422–2444.CrossRefGoogle Scholar
Beskos, A. et al. (2017). Multilevel sequential Monte Carlo samplers. Stoch. Process. Appl. 127, 1417–1440.CrossRefGoogle Scholar
Beskos, A. et al. (2021). Score-based parameter estimation for a class of continuous-time state space models. SIAM J. Sci. Comput. 43, A2555–A2580.CrossRefGoogle Scholar
Blanchet, J. and Zhang, F. (2020). Exact simulation for multivariate Itô diffusions. Adv. Appl. Prob. 52, 1003–1034.CrossRefGoogle Scholar
Cappé, O., Moulines, E. and Rydén, T. (2005). Inference in Hidden Markov Models. Springer, New York.CrossRefGoogle Scholar
Del Moral, P. (2013). Mean Field Simulation for Monte Carlo Integration. Chapman and Hall, London.CrossRefGoogle Scholar
Del Moral, P., Jacod, J. and Protter, P. (2001). The Monte-Carlo method for filtering with discrete-time observations. Prob. Theory Relat. Fields 120, 346–368.CrossRefGoogle Scholar
Fearnhead, P., Papaspiliopoulos, O. and Roberts, G. O. (2008). Particle filters for partially observed diffusions. J. R. Statist. Soc. B [Statist. Methodology] 70, 755–777.CrossRefGoogle Scholar
Giles, M. B. (2008). Multilevel Monte Carlo path simulation. Operat. Res. 56, 607–617.CrossRefGoogle Scholar
Giles, M. B. (2015) Multilevel Monte Carlo methods. Acta Numerica 24, 259–328.CrossRefGoogle Scholar
Giles, M. B. and Szpruch, L. (2014). Antithetic multilevel Monte Carlo estimation for multi-dimensional SDEs without Lévy area simulation. Ann. Appl. Prob. 24, 1585–1620.CrossRefGoogle Scholar
Golightly, A. and Wilkinson, D. (2008). Bayesian inference for nonlinear multivariate diffusion models observed with error. Comput. Statist. Data Anal. 52, 1674–1693.CrossRefGoogle Scholar
Heinrich, S. (2001). Multilevel Monte Carlo methods. In LSSC ’01: Proceedings of the Third International Conference on Large-Scale Scientific Computing—Revised Papers, eds S. Margenov, J. Wasniewski and P. Yalamov, Springer, Berlin, Heidelberg, pp. 58–67.CrossRefGoogle Scholar
Jasra, A., Kamatani, K., Law, K. J. H. and Zhou, Y. (2017). Multilevel particle filters. SIAM J. Numer. Anal. 55, 3068–3096.CrossRefGoogle Scholar
Jasra, A., Kamatani, K., Osei, P. P. and Zhou, Y. (2018). Multilevel particle filters: normalizing constant estimation. Statist. Comput. 28, 47–60.CrossRefGoogle Scholar
Jasra, A., Law, K. J. H. and Osei, P. P. (2019). Multilevel particle filters for Lévy driven stochastic differential equations. Statist. Comput. 29, 775–789.CrossRefGoogle Scholar
Jasra, A., Law, K. J. H. and Suciu, C. (2020). Advanced multilevel Monte Carlo. Internat. Statist. Rev. 88, 548–579.CrossRefGoogle Scholar
Jasra, A., Law, K. J. H. and Yu, F. (2022). Unbiased filtering of a class of partially observed diffusions. Adv. Appl. Prob. 54, 661–687.CrossRefGoogle Scholar
Jasra, A. and Yu, F. (2020). Central limit theorems for coupled particle filters. Adv. Appl. Prob. 52, 942–1001.CrossRefGoogle Scholar
Rogers, L. C. G. and Williams, D. (2000). Diffusions, Markov Processes, and Martingales, Vol. 2. Cambridge University Press.Google Scholar
Ruzayqat, H. et al. (2023). Unbiased estimation using a class of diffusion processes. J. Comput. Phys. 472, article no. 111643.CrossRefGoogle Scholar
Ryder, T., Golightly, A., McGough, S. and Prangle, D. (2018). Black-box variational inference for stochastic differential equations. Internat. Conf. Mach. Learning 80, 4423–4432.Google Scholar
Stroock, D. W. (2008). Partial Differential Equations for Probabilists. Cambridge University Press.Google Scholar