Due to a wide variety of natural and economic factors, agriculture is a highly spatial industry. Existing analyses often reveal the presence of both spatial autocorrelation, which reflects the concept that agricultural processes are correlated over distance or across geographic boundaries, and hot spots, which are clustered areas with positively correlated high-attribute values (discussed further later). Roe, Irwin, and Sharp (Reference Roe, Irwin and Sharp2002) found that spatial lags were present in data relating to the hog production industry. Schmit and Hall (Reference Schmit and Hall2013) addressed the presence and impact of food industry clusters while Stewart et al. (Reference Stewart, Lambert, Wilcox and English2009) analyzed clusters specifically in Tennessee's agriculture industry. Grogan and Goodhue (Reference Grogan and Goodhue2012) used spatial analysis and found evidence that citrus producers chose pest control methods similar to those of nearby producers. Identification of hot spots or industry clusters is important because research often shows that they can be advantageous for economic development (Morrison Paul and Seigel Reference Morrison Paul and Seigel1999, Feser Reference Feser1998, Chevassus-Lozza and Galliano Reference Chevassus-Lozza and Galliano2003, Cainelli Reference Cainelli2008, Glaeser et al. Reference Glaeser, Kallal, Scheinkman and Shleifer1992, Greenstone, Hornbeck, and Moretti Reference Greenstone, Hornbeck and Moretti2010, Barkley and Henry Reference Barkley and Henry1997, Duranton and Puga Reference Duranton and Puga2004, Gibbs and Bernat Reference Gibbs and Bernat1997, Gabe Reference Gabe2004, Reference Gabe, Goetz, Deller and Harris2008, Graham and Kim Reference Graham and Kim2008, Rocha and Sternberg Reference Rocha and Sternberg2005, Feser, Renski, and Goldstein Reference Feser, Renski and Goldstein2008).
No theoretical reason has been found to suggest that hot spots and spatial correlation in organic agriculture, which we define as including organic production and handling, should be similar to agriculture in general. As a special case of agriculture, organic operations display different characteristics from those of conventional agricultural operations, including more restricted production methods (National Organic Program 2015), higher input costs (Economic Research Service 2012), need for more specialized labor (Klonsky and Tourte Reference Klonsky and Tourte1998), and more-frequent use of their own resources (Argiles and Brown Reference Argiles and Brown2010, Schmidtner et al. Reference Schmidtner, Lippert, Engler, Haring, Aurbacher and Dabbert2012). The demand side of the organic food market is different as well. Consumers of organic tend to have stronger concerns about healthiness, the environment, food safety, animal welfare, and local economies (Hughner et al. Reference Hughner, McDonagh, Prothero, Shultz and Stanton2007). These factors imply that the needs of organic operations are different and that such operations will not necessarily gravitate only to areas where agricultural establishments are prevalent.
The organic food industry is growing at a much faster rate than the conventional food industry; retail sales of organic food increased from $11 billion in 2004 to $27 billion in 2012 (Osteen, Gottlieb, and Vasavada Reference Osteen, Gottlieb and Vasavada2012, Onken, Bernard, and Pesek Reference Onken, Bernard and Pesek2011), and the amount of land devoted to organic food crops doubled between 1997 and 2005 (Dimitri and Oberholtzer Reference Dimitri and Oberholtzer2009). These trends have led to concern that some sectors of the organic food industry (particularly corn and soybeans, which are important inputs in production of organic milk and dairy products) may not be growing at a sufficiently fast pace to keep up with the increasing demand (Dimitri and Oberholtzer Reference Dimitri and Oberholtzer2009).
Because of the differences between organic and conventional agriculture and the growth of specific sectors of the organic industry, it is important to analyze and better understand where organic operations are thriving and where they are not. More specifically, understanding spatial relationships in the concentration of organic operations and how organic and nonorganic spatial relationships potentially differ may prove important as policymakers and industry participants plan for continued growth. This type of spatial analysis and identification of organic hot spots or cold spots is also an important first step in further research on the organic sector. Once the hot and cold spots are identified, that information can be used to answer follow-up questions relating to their formation and the economic impact of organic hot spots. This type of spatial analysis can therefore be valuable to governmental and private organizations that focus on development of the organic sector and on regional economic development.
Documenting spatially defined hot spots and spatial correlation in organic agriculture generally has not been done for U.S. organic agriculture, though Schmidtner et al. (Reference Schmidtner, Lippert, Engler, Haring, Aurbacher and Dabbert2012) did for German organic agriculture. A New York Times article (Fairfield Reference Fairfield2009) mentioned clustering in the U.S. organic sector but did not use spatial methods to identify the clusters, while Eades and Brown (Reference Eades and Brown2006) used spatial methods to identify clusters but did not identify cold spots. Neither of these sources analyzed the type of spatial autocorrelation. Furthermore, to our knowledge, prior research on organic clustering has not employed a bivariate analysis to compare types of organic operations or organic clusters to other types of clusters and has not examined whether (and if so, how) the size and location of organic clusters has changed over time.
This study systematically investigates clustering as it pertains to the U.S. organic agricultural sector. We first identify clusters of certified organic operations, analyze how they vary across primary scope (crops, handling, or livestock), and compare the locations to those of clusters of agricultural establishments and clusters of all establishments, including those not in agriculture. To assess if and how the clusters evolved over time, we compare organic clusters in 2009 and 2013. We then determine the form of spatial autocorrelation present in the distribution of organic operations by estimating spatial econometric models. In essence, we address the following questions: Where are county-level organic hot spots and cold spots? How might the hot spot and cold spot patterns differ if organic operations are defined more narrowly by primary scope or operation type? How have organic hot spots and cold spots evolved in recent years? How do the locations of organic hot spots and cold spots differ from those of conventional agriculture or establishments in general? What form does spatial autocorrelation take in the county-level distribution of certified organic operations?
Participants and observers may have speculated about hot spots, cold spots, or spatial autocorrelation, but our results provide one of the first efforts to document them using well-defined spatial statistical methods applied to the directory of certified organic operations collected by the U.S. Department of Agriculture's (USDA's) National Organic Program. Our cluster analysis of hot spots and cold spots is set apart from prior studies by its (i) use of a National Organic Program data set, (ii) analysis of different types of organic operations, including organic handlers, (iii) side-by-side comparisons and bivariate analyses of how different types of organic, agricultural, and general establishment clusters are related, and (iv) analysis of the evolution of organic clusters over time.
Our research identifies statistically significant hot spots for certified organic operations in parts of the West Coast, the Midwest, and the Northeast. The locations of these organic hot spots often do not coincide with hot spots of conventional agricultural establishments or general establishments. For example, some areas that contain a relatively small number of general and agricultural establishments are surrounded by areas with relatively high numbers of organic operations, and vice versa. We find that the overall clustering of organic operations remained stable between 2009Footnote 1 and 2013. Our results further suggest the presence of spatial autocorrelation and cross-county spillovers and that the type and level of spatial correlation and the geographic distribution of hot spots vary with the definition of organic operation used. The results generally are robust across different spatial econometric models.
Background on Cluster Identification and the Organic Food Sector
Much of the research on clusters (e.g., Porter Reference Porter2003, Goetz, Shields, and Wang Reference Goetz, Shields, Wang, Goetz, Deller and Harris2008) has focused on their identification and the definition of the term “cluster.” Some studies defined clusters based solely on geographic proximity of the industries or firms of interest (e.g., Lian et al. Reference Lian, Gong, Li, Sun, Zhao and Zhu2009, Banasick, Lin, and Hanham Reference Banasick, Lin and Hanham2009, Barkley and Henry Reference Barkley and Henry1997, Eades and Brown Reference Eades and Brown2006), some solely on economic interaction (e.g., Feser and Bergman Reference Feser and Bergman2000), and others on both geographic proximity and economic interaction (e.g., Greenstone, Hornbeck, and Moretti Reference Greenstone, Hornbeck and Moretti2010, Rocha and Sternberg Reference Rocha and Sternberg2005).
The studies that used geographic proximity employed various mathematical methods to test for and identify spatial autocorrelation, which measures the degree to which observations depend on the characteristics of neighbors (LeSage Reference LeSage1998, Anselin Reference Anselin1999). The Moran's I and local Moran's I (LMI) test statistics, which can both be used to test the null hypothesis of no spatial autocorrelation, are commonly used (e.g., Lian et al. Reference Lian, Gong, Li, Sun, Zhao and Zhu2009, Banasick, Lin, and Hanham Reference Banasick, Lin and Hanham2009, Moons, Brijs, and Wets Reference Moons, Brijs and Wets2008, Zhang and Lin Reference Zhang and Lin2008, Eades and Brown Reference Eades and Brown2006, Richards, Hamilton, and Patterson Reference Richards, Hamilton and Patterson2010, Hatzenbuehler, Gillespie, and O'Neil Reference Hatzenbuehler, Gillespie and O'Neil2012, Schmidtner et al. Reference Schmidtner, Lippert, Engler, Haring, Aurbacher and Dabbert2012). In a study of organic agriculture, Schmidtner et al. (Reference Schmidtner, Lippert, Engler, Haring, Aurbacher and Dabbert2012), for example, used the LMI to identify hot spots of organic farming in integrated counties in Germany.
In econometric models, spatial autocorrelation can be present in the dependent variables, the independent variables, and the residuals. Spatial autocorrelation in the dependent variable (spatial lag) implies that an observation at one location depends on observations at other locations and, thus, that variation in the dependent variable is due in part to differences at neighboring locations. In that case, the covariance of random variables at two locations is not zero. Spatial autocorrelation in the residuals of a regression (spatial error or heterogeneity) implies that the relationships vary over space, which further suggests nonconstant error variances and heteroskedasticity. Spatial autoregressive models are frequently used (e.g., Schmidtner et al. Reference Schmidtner, Lippert, Engler, Haring, Aurbacher and Dabbert2012) to account for the possibility of spatial lag and spatial error in regressions (LeSage Reference LeSage1998, Anselin Reference Anselin1999).
Other methods sometimes used to define geographic clusters include the location quotient, which is a measure of industry concentration (e.g., Greenstone, Hornbeck, and Moretti Reference Greenstone, Hornbeck and Moretti2010, Feser et al. Reference Feser, Renski and Goldstein2008, Eades and Brown Reference Eades and Brown2006, Rocha and Sternberg Reference Rocha and Sternberg2005); locational Gini coefficients, which are used to analyze the geographic distribution of employment for a specific industry in a region (e.g., Barkley and Henry Reference Barkley and Henry1997); and the Hirschman-Herfindahl Index (HHI), which is a general measure of concentration (Eades and Brown Reference Eades and Brown2006, Lopez et al. Reference Lopez, Azzam and Lirón-España2002). Studies that defined clusters using economic interaction have typically used data on input-output flows (e.g., Rocha and Sternberg Reference Rocha and Sternberg2005, Stewart et al. Reference Stewart, Lambert, Wilcox and English2009).
The definition chosen for a cluster is important. Jaenicke et al. (Reference Jaenicke, Goetz, Wu and Dimitri2009), for example, found that the impact of clustering on the output of organic handling firms varied as the number of firms necessary to constitute a cluster changed. Rocha and Sternberg (Reference Rocha and Sternberg2005) found that the effects of clusters defined by geographic proximity were different from the effects of clusters defined by economic interaction.
Some recent research on clustering in the food and agriculture industry has specifically looked at the organic food sector. Eades and Brown (Reference Eades and Brown2006), for example, found evidence of clustering in organic agriculture, and Schmidtner et al. (Reference Schmidtner, Lippert, Engler, Haring, Aurbacher and Dabbert2012) found that agglomeration influenced the spatial distribution of organic farms in Germany. Naik and Nagadevara (Reference Naik and Nagadevara2010), in a study of organic farming in Karnatka, India, identified economic benefits from clustering, and Jaenicke et al. (Reference Jaenicke, Goetz, Wu and Dimitri2009), in a study of the United States, found that clustering positively affected the output (in sales per employee) of organic handling firms. Using the location quotient to measure concentration, Taus, Ogneva-Himmelberger, and Rogan (Reference Taus, Ogneva-Himmelberger and Rogan2013) found that spatial dependence was a factor in the spatial distribution of farms in the United States being converted to organic agriculture. Hooker and Shanahan (Reference Hooker and Shanahan2012) used the Gini coefficient to measure concentration in the U.S. organic sector and a multiplicative model to analyze the impact that market access and input variables had on dispersion of organic producers.
Methodology: Identification of Hot Spots
To identify statistically significant hot spots (defined as counties with positively correlated, high values for attributes), cold spots (defined as counties with positively correlated, low values for attributes), and outliers (counties with negatively correlated attributes), we use the LMI test statistic. Anselin (Reference Anselin1995) provides a clear explanation of the LMI and how it is calculated, and the ArcGIS website (www.arcgis.com) explains the statistic in the context of the software. As previously noted, the LMI is used to test the null hypothesis of no spatial autocorrelation, and it allows one to divide the area of interest into smaller sections to test for the presence of local spatial autocorrelation. The LMI is calculated as
where x i represents the attribute level for section i, X avg is the mean attribute level for the entire area, and w ij is the weighting value between sections i and j. In our case, the sections are counties, the entire area is the United States, and the attribute level for county i is the number of organic operations (and, for comparison, the number of total agricultural farm establishments and total general establishments).
Spatial weighting matrices generally are based on contiguity or true distance. Two commonly used distance-based matrices are row-standardized distance bands and row-standardized inverse distances. A distance-band matrix assigns a weight of 1 for two counties that are within a specified threshold distance of each other and 0 otherwise (LeSage Reference LeSage1998, Anselin Reference Anselin1999). In a row-standardized matrix, the elements in each row are standardized to sum to 1. The distance threshold typically is defined as the minimum distance required for every section (county, in our case) to have at least one neighbor (GeoDa Center 2013). An inverse-distance matrix uses the inverse of the distance between two counties as their weight and can be constrained by a distance band (LeSage Reference LeSage1998, Anselin, Reference Anselin1999). To provide additional insight and check the robustness of the results, we compare the sets of clusters generated by using a contiguity weighting matrix and a distance-band weighting matrix.Footnote 2
To determine the significance of the LMI, we use a permutation method implemented in GeoDa software. The observation, or attribute level, in the county analyzed is held constant and all of the other observations are assigned a value from a vector of random numbers to relocate them in space, producing a random spatial distribution. The LMI for the county of interest is then calculated using the random spatial distribution, and the process is repeated multiple times using different random number seeds. The p-value is based on the probability that the actual LMI for the county is equal to the values calculated during the permutations (GeoDa Center 2013). Unlike z-score tests for significance (e.g., LeSage Reference LeSage1998, Anselin Reference Anselin1999), this method does not compute the significance of the LMI analytically, but it has the advantage of being able to test for the robustness of our results by comparing the results generated by different seeds and varying the number of permutations.Footnote 3
To better compare the distribution of organic operations to the distributions of agricultural farm establishments and general establishments, we also use the bivariate LMI test statistic (Anselin, Syabri, and Kho Reference Anselin, Syabri and Kho2006). It is similar to the univariate LMI but compares the level of an attribute in an area to the level of a different attribute in neighboring areas (e.g., comparing the number of organic operations in one area to the number of agricultural farm establishments in neighboring areas):
where x i is the level of attribute x for section i, X avg is the mean level of attribute x for the entire area, y i is the level of attribute y for section i, Y avg is the mean level of attribute y for the entire area, and w ij is the weighting value between sections i and j.
Under the bivariate LMI, interpretation of the hot spots, cold spots, and outliers changes slightly. A hot spot in this case indicates that a high level of an attribute in an area is positively correlated with high levels of another attribute in neighboring areas. Interpretation of the cold spots and outliers is similar. The procedure for determining the significance of the test statistic remains the same.
Our data on certified organic operations come from USDA's National Organic Program and are publicly available online. They consist of a list of all certified organic operations, along with information such as operation name, certifying agent, primary scope (i.e., handling, crops, and livestock), address, phone number, and products produced. Approximately 60 percent of the operations have crops as their primary scope while 28.5 percent have handling, 11.4 percent have livestock, and less than 1 percent have wild crops as their primary scopes. The data on agricultural operations come from the 2007 U.S. Census of Agriculture and includes information on agricultural farms. To facilitate the comparison between organic hot spots and general agricultural hot spots, we also create a variable for organic production operations (crops and livestock) only.
Hot Spot and Cold Spot Results
Figure 1 shows the clusters identified in our analysis for certified organic operations with separate maps of clusters for all organic operations and for organic production (crops and livestock), crops, handling, and livestock calculated using the univariate LMI statistic and a queen contiguity matrix (which considers both shared boundaries and shared points as contiguous).Footnote 4 We find that the clusters for all organic operations and organic production are very similar. The largest hot spot for both runs along nearly the entire West Coast. Another large hot spot is centered in part of Wisconsin and southeastern Minnesota, and others appear in Maine, New Hampshire, Vermont, Massachusetts, upstate New York, and southeastern Pennsylvania. Some relatively small hot spots are found in the Midwest and West. Cold spots, on the other hand, occur mainly in Southern states and cover many areas from Texas to Virginia. There are also relatively small cold spots in the West, Midwest, Alaska, and Hawaii. The outliers are scattered throughout the country.
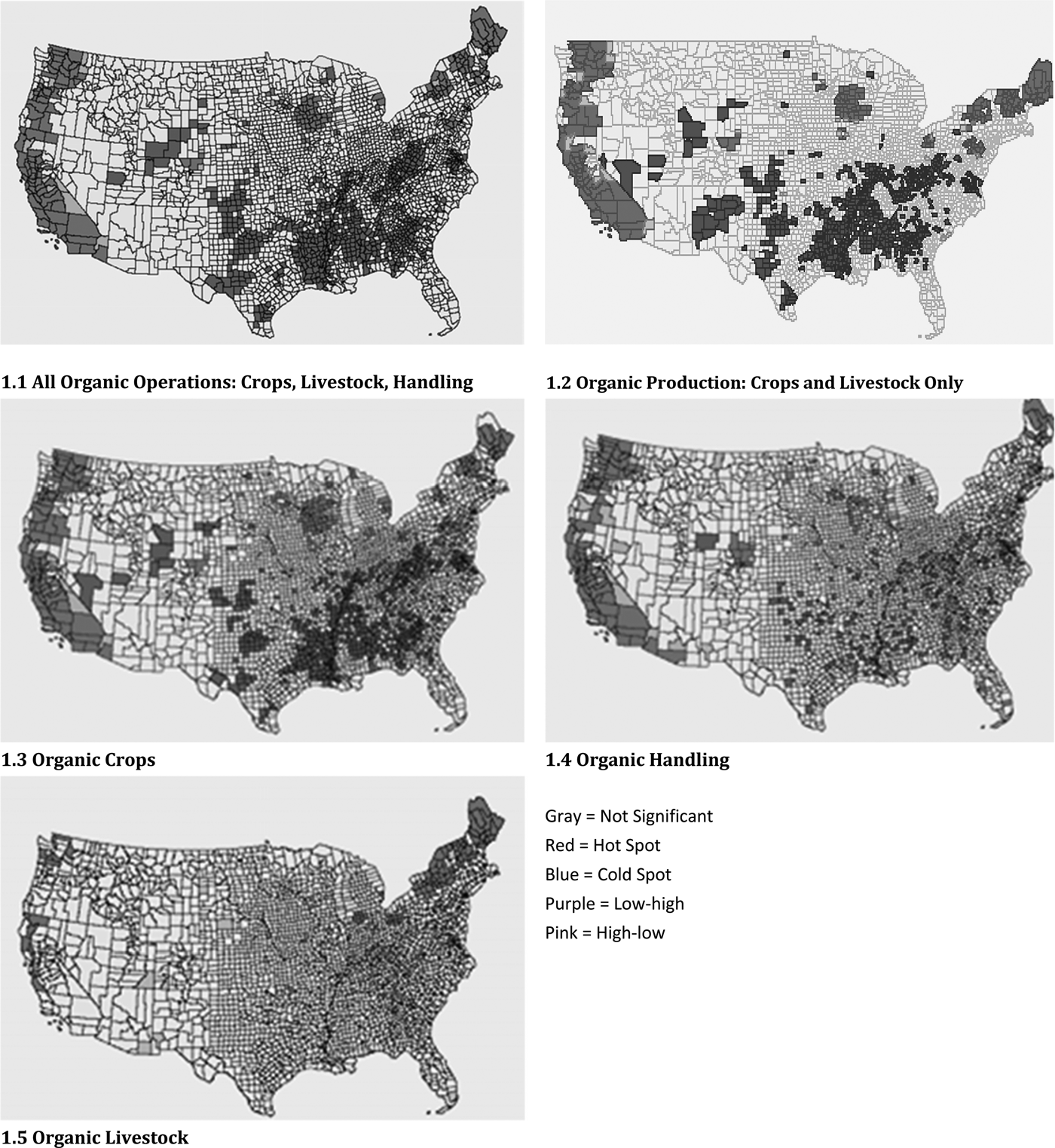
Figure 1. Organic Hot Spots, Cold Spots, and Outliers Based on Operation Counts
Hot spots for organic crops and handling are similarly situated, mostly along the West Coast and in the upper Midwest and parts of the Northeast and New England. Hot spots for organic livestock, on the other hand, are more isolated and scattered; the only concentrations are in northern New England and New York. We find numerous cold spots for organic crops throughout the South and in parts of the West, Appalachia, and the mid-Atlantic states; a smaller number of cold spots for organic handlers; and even fewer cold spots for livestock producers.
Figure 2 compares hot and cold spots for all organic operations in 2009 and 2013. We find that the distributions are generally the same, indicating that the organic industry remained relatively stable during those years. One notable difference is apparent growth of organic operations in southern Florida. Among all U.S. counties, 26 were hot spots in 2013 but not 2009 and 12 were hot spots in 2009 but not 2013. Similarly, 156 counties were cold spots in 2013 but not in 2009 and 145 were hot spots in 2009 but not 2013. It is important to note that some of this variation may be related to our use of a permutation method to identify hot spots. Because of a lack of data on organic operations prior to 2009, it is difficult to draw more-general conclusions about the distribution of organic operations over time.
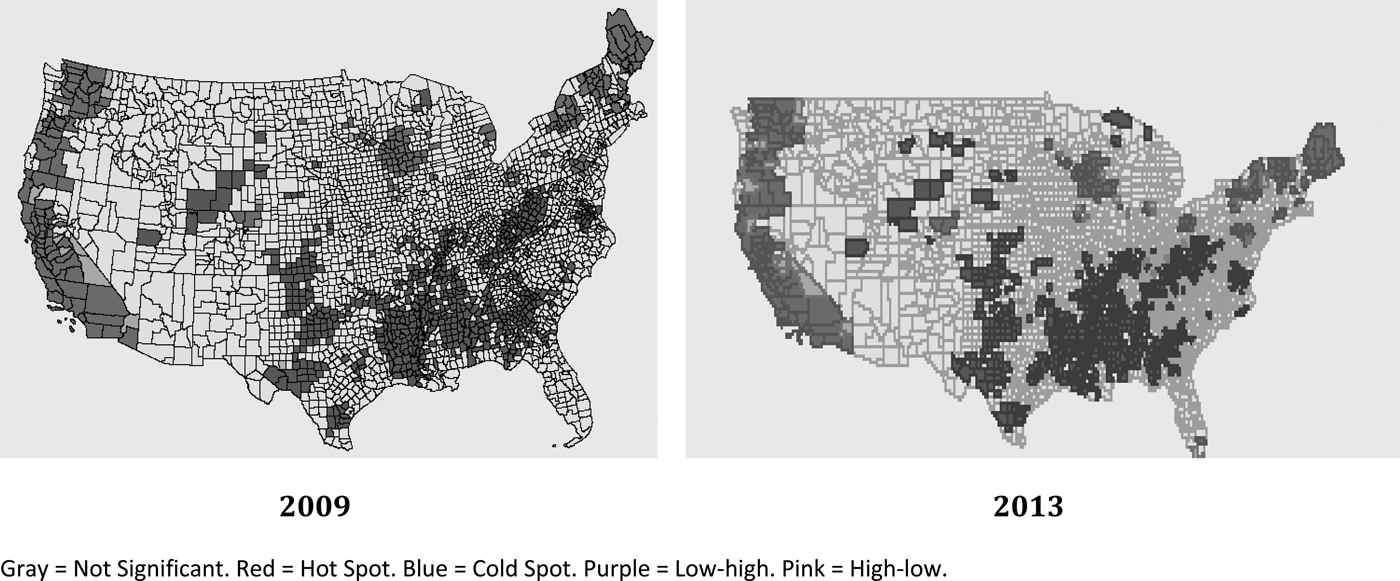
Figure 2. Organic Operation Hot Spots: 2009 and 2013
We next identified hot and cold spots for all agricultural establishments using U.S. Census of Agriculture data (2007) and the univariate LMI and then used a bivariate LMI statistic that uses both organic production and agricultural farms data to generate a different form of hot spots and cold spots. Figure 3.1 shows a map of clusters of agricultural production. When compared to Figure 1.2, Figure 3.1 shows that organic production hot spots and general agriculture hot spots match some but not most of the time, so that organic production does not necessarily follow the same pattern as conventional production. Both maps show hot spots along the West Coast and throughout the Midwest. However, many of the organic hot spots in the northeastern states are not present for agricultural farming. Some agricultural production hot spots now appear in Florida, Alabama, Louisiana, Texas, Oklahoma, and Arkansas.Footnote 5
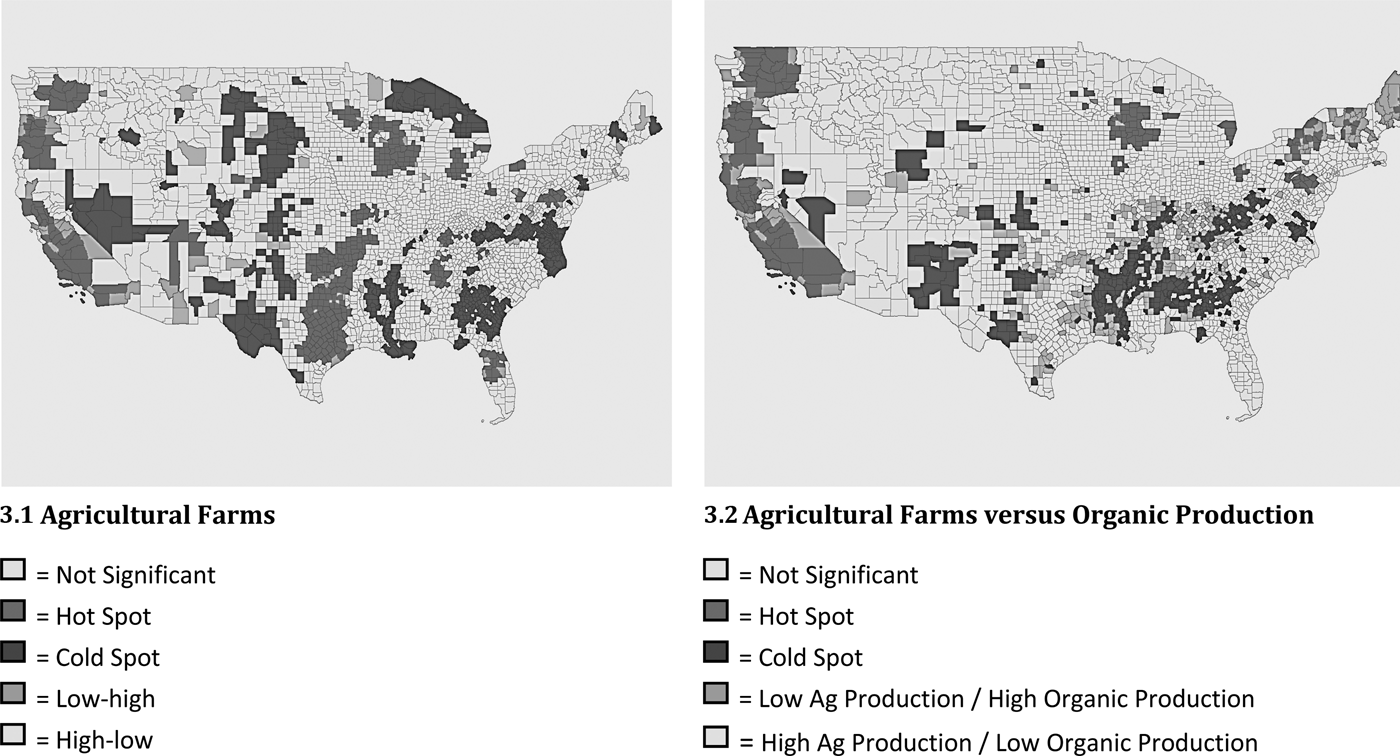
Figure 3. Hot Spots, Cold Spots, and Outliers of Agricultural Farms
Figure 3.2 provides a more formal comparison of organic production and general agricultural production. The definitions of hot spots, cold spots, and outliers are somewhat different because we use the bivariate LMI. We are particularly interested in areas with high-low spots—counties that have a relatively large number of general agricultural establishments surrounded by counties that have a relatively small number of organic production operations—and in areas with low-high spots—counties that have a relatively small number of agricultural production establishments surrounded by counties that have a relatively large number of organic production operations. Many of the high-low areas are in the South and Southeast with others scattered around the rest of the country. The low-high areas are in the Northeast and in the eastern portions of California, Oregon, and Washington. These results show that organic operations do not necessarily concentrate in primarily agricultural areas. In future research, it might be interesting to analyze the factors associated with these discrepancies.
Another aspect of growth in the organic sector is the concern that certain parts of this sector may not be growing at a sufficiently fast rate. To highlight this, Figure 4 looks at one specific type of agricultural crop, corn.Footnote 6 Figure 4.1 shows a map generated by the univariate LMI for operations that sell corn crops. It essentially shows that corn production was concentrated in the Midwest and almost nowhere else. More interesting, however, is Figure 4.2, which shows a bivariate analysis of corn to organic crops. Particularly relevant is the large area of low-high spots in the Midwest—counties that have a relatively low number of corn production operations but are surrounded by counties with high numbers of organic crop production operations. These low-high spots are consistent with concerns about insufficient expansion of organic corn crops discussed in Dimitri and Oberholtzer (Reference Dimitri and Oberholtzer2009).
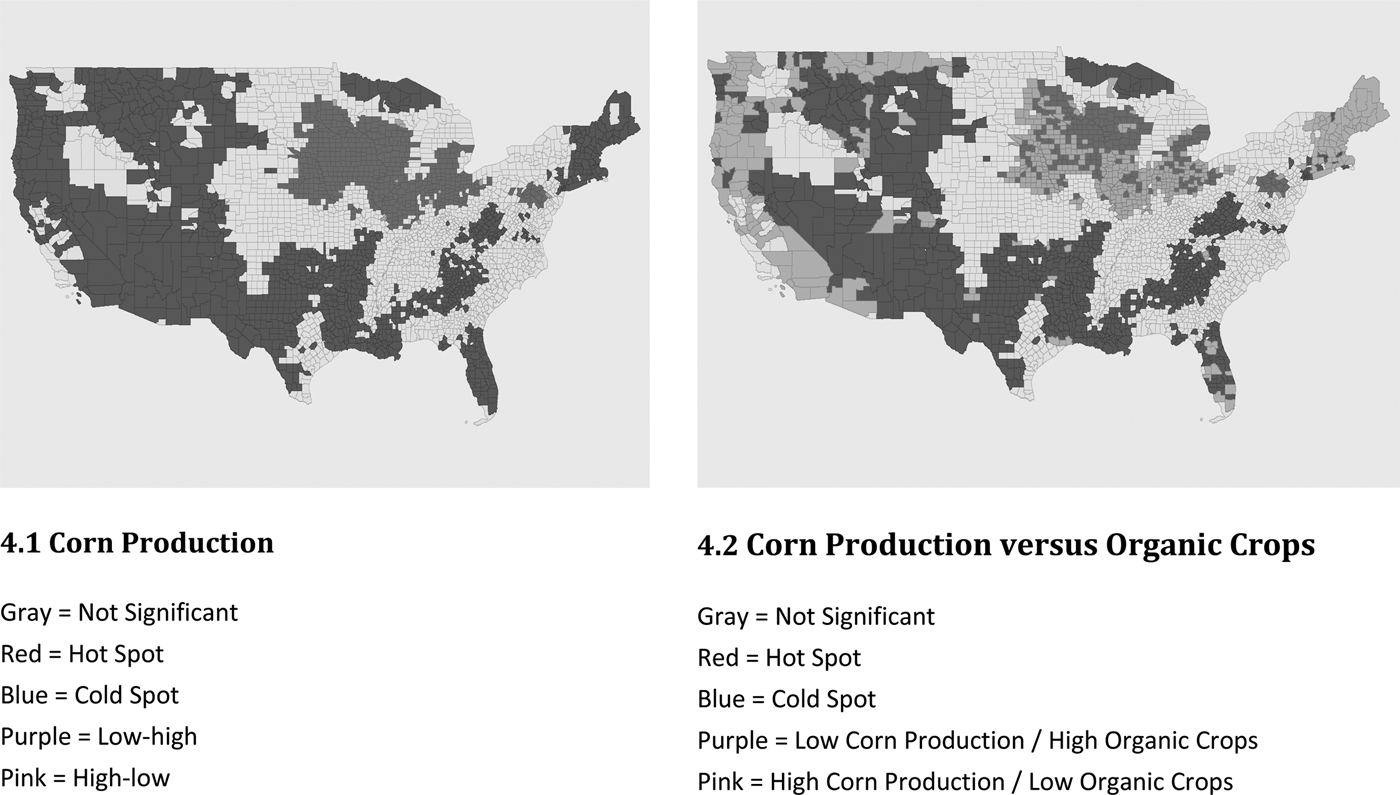
Figure 4. Hot Spots, Cold Spots, and Outliers of Corn Production
Figure 5 presents the results of a similar comparison of organic establishments versus establishments in general. We use business establishments in general as a proxy for density of economic activity and proximity to urban areas to determine whether organic agriculture thrives only in areas with high levels of economic activity. Comparing Figures 5.1 and 1.1, we find that hot spots of business establishments generally are less common than hot spots of organic operations. The largest concentrations of businesses in general are in northern and southern California, the Southwest, Florida, the Northeast corridor, and a multi-state area surrounding Chicago. The bivariate LMI analysis (Figure 5.2) identifies large areas of low-high spots along the West Coast, in parts of the Midwest, and in the Northeast. Interestingly, these same areas are organic hot spots (see Figure 1.1).
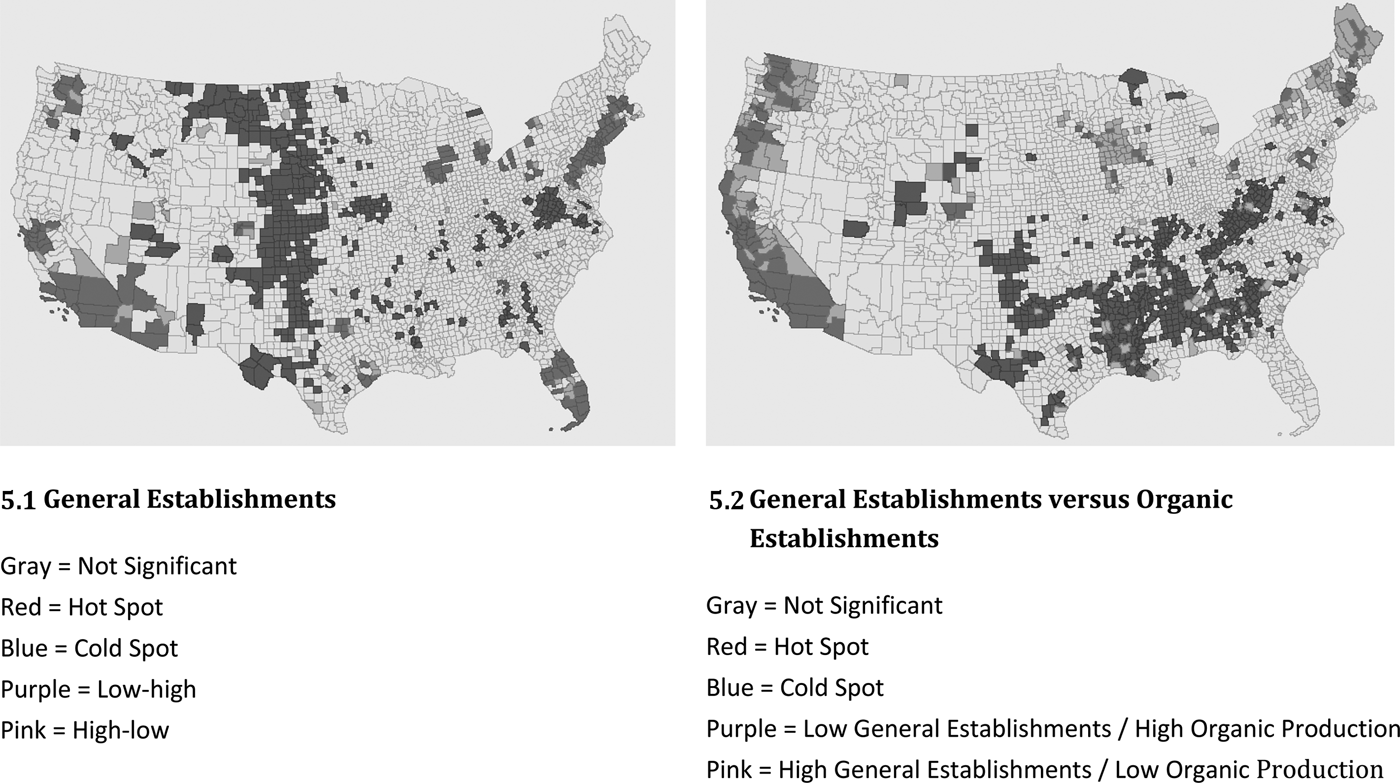
Figure 5. Hot Spots, Cold Spots, and Outliers of General Establishments
This result suggests that organic operations do not necessarily gravitate to areas that have a large number of establishments in general; on the contrary, we find that organic operations tend to concentrate in areas that have relatively few establishments and would not be characterized by sprawling development (Brown, Goetz, and Fleming Reference Brown, Goetz and Fleming2012). Some of these areas (parts of the Midwest and West Coast) coincide with hot spots of agriculture generally and thus may indicate the presence of large agricultural industries. Figure 5.2 also shows some isolated high-low spots scattered across the country, especially in the South.
Figure 6 shows the results of a bivariate LMI analysis for different types of organic operations. The first panel (6.1) shows the results of a comparison of handling versus production (crops and livestock) and identifies a number of areas in California and the Midwest in which there is a high level of organic production but relatively few handling operations. This pattern could reflect either a reliance on direct market sales in those areas or that organic production in those areas is transported to other areas for primary handling.Footnote 7 The second panel (6.2) compares production of organic crops with handling and suggests that their spatial distributions are similar with few high-low and low-high spots. The last two panels compare organic livestock production to organic crops (6.3) and organic handling (6.4). Many areas scattered throughout the country have a high level of organic crops or handling and few organic livestock operations. The only large area that has a high level of organic livestock and a low level of crops or handling is in the upper Northeast.
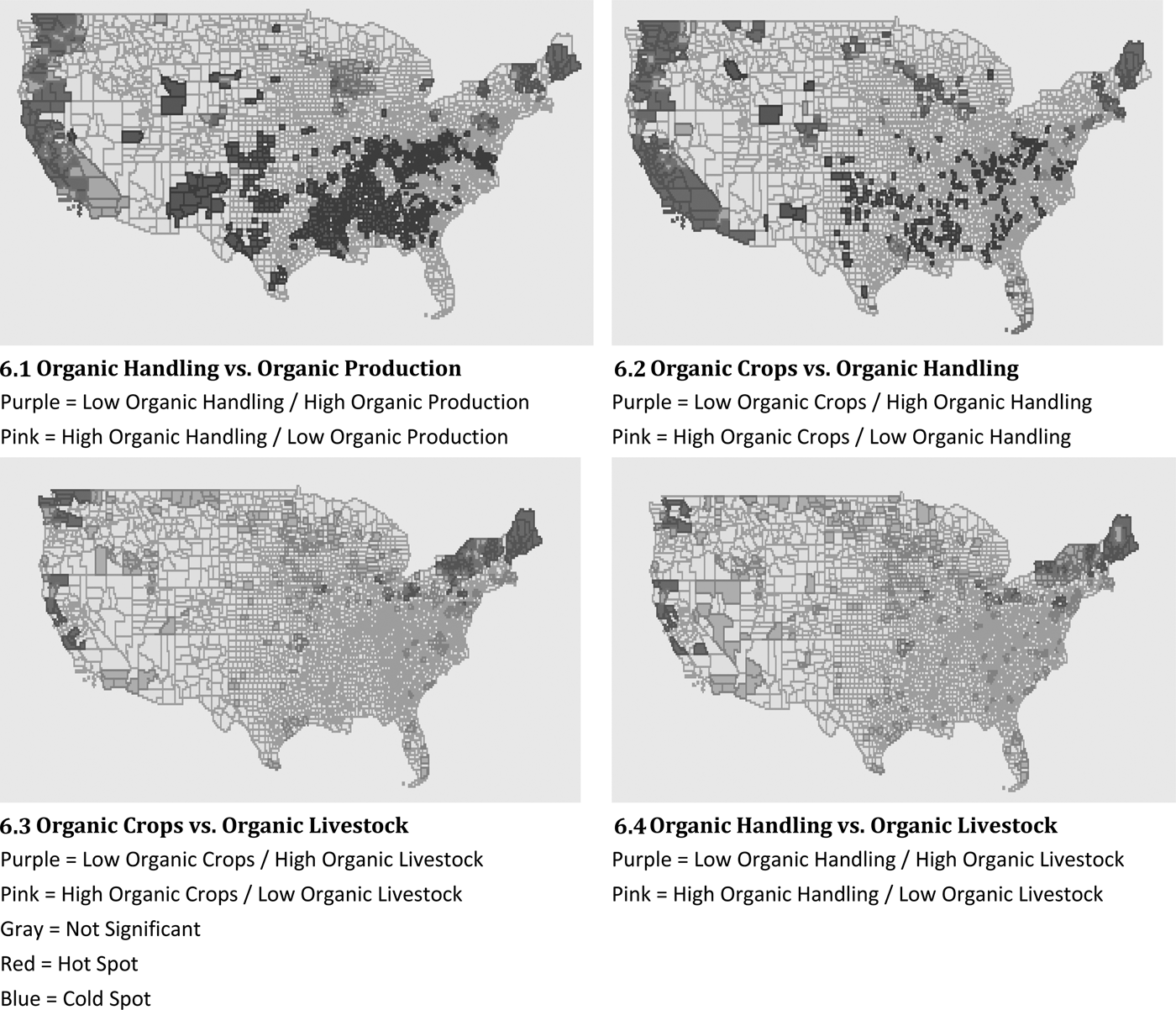
Figure 6. Comparison of Types of Hot Spots based on the Bivariate Local Moran's I
These results provide a starting point for further exploration of factors associated with the presence and formation of hot spots of organic operations. Several studies of the organic sector have addressed factors that promote or inhibit its growth. Farmer et al. (Reference Farmer, Peters, Hansen, Boettner and Betcher2013) and Farmer (Reference Farmer2014), for example, cited challenges and costs associated with sustaining organic growing methods, the cost of USDA certification and producers’ cynicism about it, concerns about a lack of benefit from certification (especially among operators of small farms), and producers’ and consumers’ lack of access to information as factors that inhibited the growth of organic agriculture in West Virginia. They also found that farmers who chose to pursue organic certification tended to be relatively young, had a higher level of education, split work evenly among men and women, operated relatively small farms, and had better access to the internet. On a more general scale, Marasteanu and Jaenicke (forthcoming) discuss several factors potentially leading to formation of hot spots of organic agricultural in the United States and find that population density, farm income, the presence of natural amenities, land values, proximity to urban areas, and support for the Green Party are significantly associated with the presence of hot spots.
To better place our findings within the context of existing literature and of future research, Figure 7 shows the relationships between the spatial distribution of organic operations and nine county-level variables that influence growth. Panels 7.1, 7.2, 7.4, 7.6, and 7.8 display many high-to-high and low-to-low areas and relatively few low-to-high and high-to-low areas, which indicates that organic operations tend to cluster in areas with a high average farm income, industry-entropy index, population density, value of land and buildings per acre, and receptiveness to organic (proxied by votes for the Green Party), respectively. On the other hand, panels 7.3 and 7.9 display many low-high and high-low areas and relatively few high-high and low-low areas, which suggests that organic operations tend to cluster in areas with shorter distances to highways and lower urban influence codes, respectively. The pattern is less clear for the score on the natural amenities scale (7.5) and property taxes (7.7). Further research is required to fully capture the effect of county-level characteristics on the spatial distribution of organic operations.
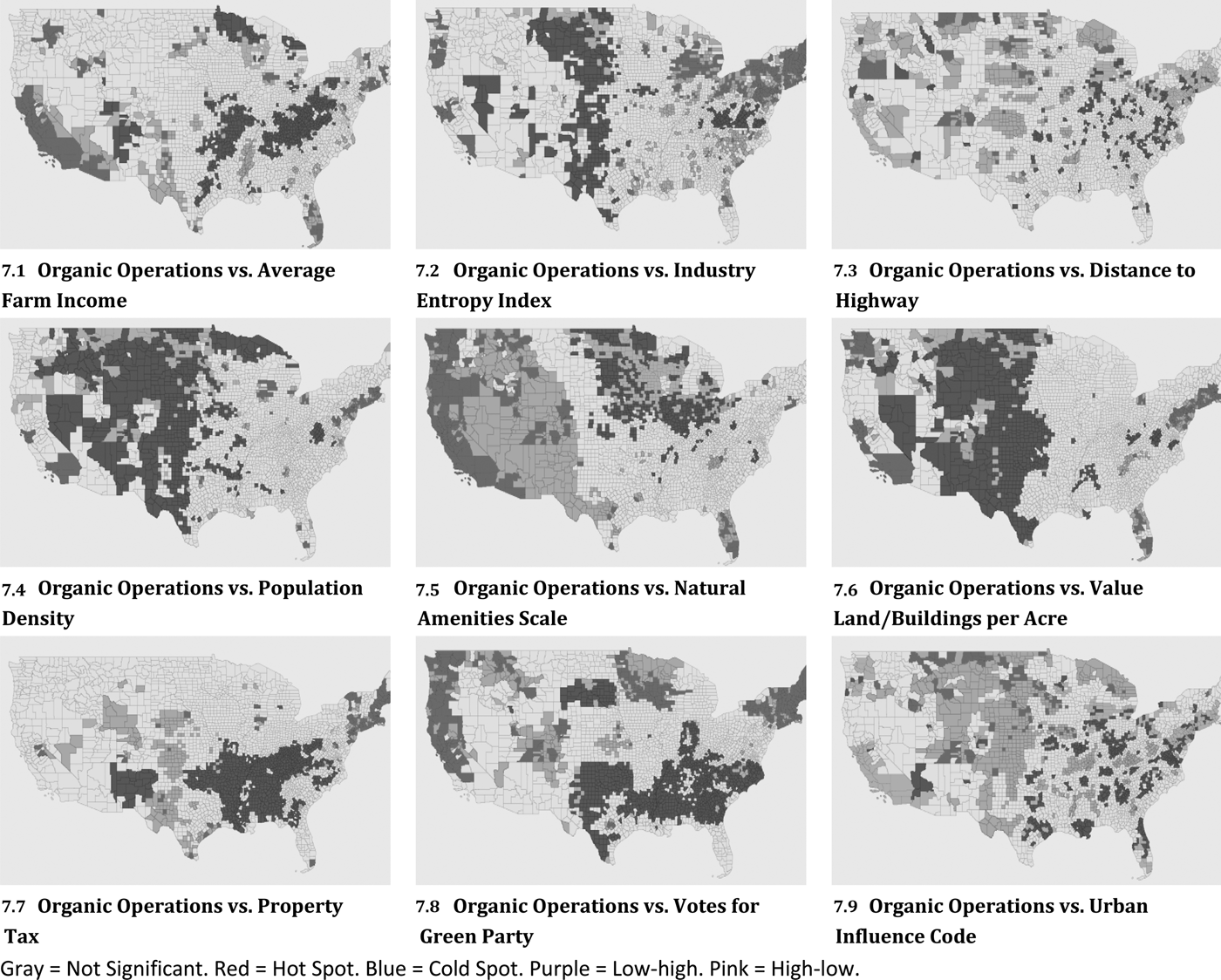
Figure 7. All Organic Operations versus County-level Characteristics
Methodology and Data: Identification of Spatial Autocorrelation by Type
In the second part of our analysis, we identify types of spatial autocorrelation present in the distribution of certified organic operations. In regressions, spatial autocorrelation typically takes two forms: spatial lag and spatial error. To illustrate this concept, we begin with the general spatial autoregressive model (LeSage Reference LeSage1998, Anselin Reference Anselin1999):
where μ = λW 2 μ + ε, ε is distributed N(0,σ2 I n ), and W 1 and W 2 are weighting matrices. As explained in Schmidtner et al. (Reference Schmidtner, Lippert, Engler, Haring, Aurbacher and Dabbert2012), the significance of λ implies that some spatially correlated explanatory variables are important in the error specification (spatial error/heterogeneity) and the significance of ρ implies that some explanatory variables that are correlated with the average of the dependent variable are important in the model specification (spatial lag).
In this case, y is a matrix of elements representing the number of certified organic operations as a share of total establishments in a particular county.Footnote 8 The elements in the x matrix represent county-level variables related to economic, demographic, climate, land, and political characteristics. To provide additional insight and check the robustness of our results, we also define alternative versions of y in which the elements represent the share of certified organic operations that have a specific primary scope (crops, handling, and livestock).Footnote 9
For the weighting matrices W 1 and W 2 , we use a row-standardized inverse-distance weighting matrix as we believe that is the most appropriate specification for our data. A common alternative is the contiguity-based weighting matrix, which would typically assign a weight of 1 to counties that are either adjacent to each other or have a shared corner and a weight of 0 otherwise (LeSage Reference LeSage1998, Anselin Reference Anselin1999). In our case, however, missing county-level data causes some observations to be dropped and a contiguity-based weighting matrix would create “islands” that do not exist. Distance-band weighting is another common alternative, but a brief analysis suggested that its results would not be significantly different from those of the inverse-distance weighting matrix. First, when comparing these two matrices, we find that they are correlated with a correlation coefficient of 0.6469. We also find that the correlation coefficient between the spatially lagged dependent variable with the inverse-distance matrix and the spatially lagged dependent variable with the distance-band matrix is 0.8688 and that the correlation coefficient between the spatially lagged matrix of independent variables with the inverse-distance matrix and the spatially lagged matrix of independent variables with the distance-band matrix is 0.7548. These results are consistent with LeSage and Pace (Reference LeSage and Pace2010), which noted that estimates from spatial models are not highly sensitive to the specification of the weighting matrix.
Although simple statistical tests are available for spatial lag and spatial error in a linear regression, we need to consider potential nonlinearity of our model. Close to half of the counties in our data set do not have any certified organic operations so our dependent variable is censored at 0. To account for this censoring, we consider a Tobit model (Sigelman and Zeng Reference Sigelman and Zeng1999) instead of a linear model when testing for spatial lags and errors. The Tobit model is defined as
where y i * is an unobserved latent variable (Greene Reference Greene2008). The observed variable, y i , is determined as follows.
Because we are aware of no established spatial autocorrelation tests for Tobit models, we estimate a Tobit spatial autoregressive model implemented in Matlab to determine whether our model exhibits a statistically significant spatial lag and to examine the statistical significance of the coefficient of the spatially lagged dependent variable. To test for the presence of spatial error, we estimate a Tobit spatial error model and look at the statistical significance of the coefficient for the spatially lagged error term (LeSage Reference LeSage2001).
When choosing an estimator for our spatial Tobit models, we need to take several details into account. First, according to literature addressing spatial autoregressive models (e.g., LeSage Reference LeSage1998, Kelejian and Prucha Reference Kelejian and Prucha1998, Fingleton and Le Gallo Reference Fingleton and Gallo2008), the spatial lag variable is endogenous because it captures simultaneous spatial interactions (Fingleton and Le Gallo Reference Fingleton and Gallo2008). Second, the estimator must account for the multivariate normal distribution of the dependent variable (LeSage and Pace Reference LeSage and Pace2009).Footnote 10 We therefore use a Gibbs sampling method to estimate a Bayesian spatial Tobit heteroskedastic model. This method appropriately defines the distributions of all of the parameters of interest and allows for sampling from multivariate and unknown distributions. The distribution of a parameter value of interest is calculated using an algorithm that starts with the initial values of the parameter and updates those values based on the other parameters and on draws from the appropriate distribution (formulas provided in LeSage (Reference LeSage1998, Reference LeSage1999b)). To implement this method, we use LeSage's (Reference LeSage2001) spatial econometric toolbox. To assess the accuracy and convergence of the Gibbs sampler, we follow LeSage (Reference LeSage1999b) and examine estimates of autocorrelation, Rafterty-Lewis Markov-chain Monte Carlo convergence diagnostics, and Geweke numerical standard errors, relative numerical efficiency estimates, and chi-squared tests.
The data on certified organic operations for this analysis again come from USDA's National Organic Program. Data for the county-level variables come from the U.S. Census Bureau (2010) and USDA's (2007) Census of Agriculture.
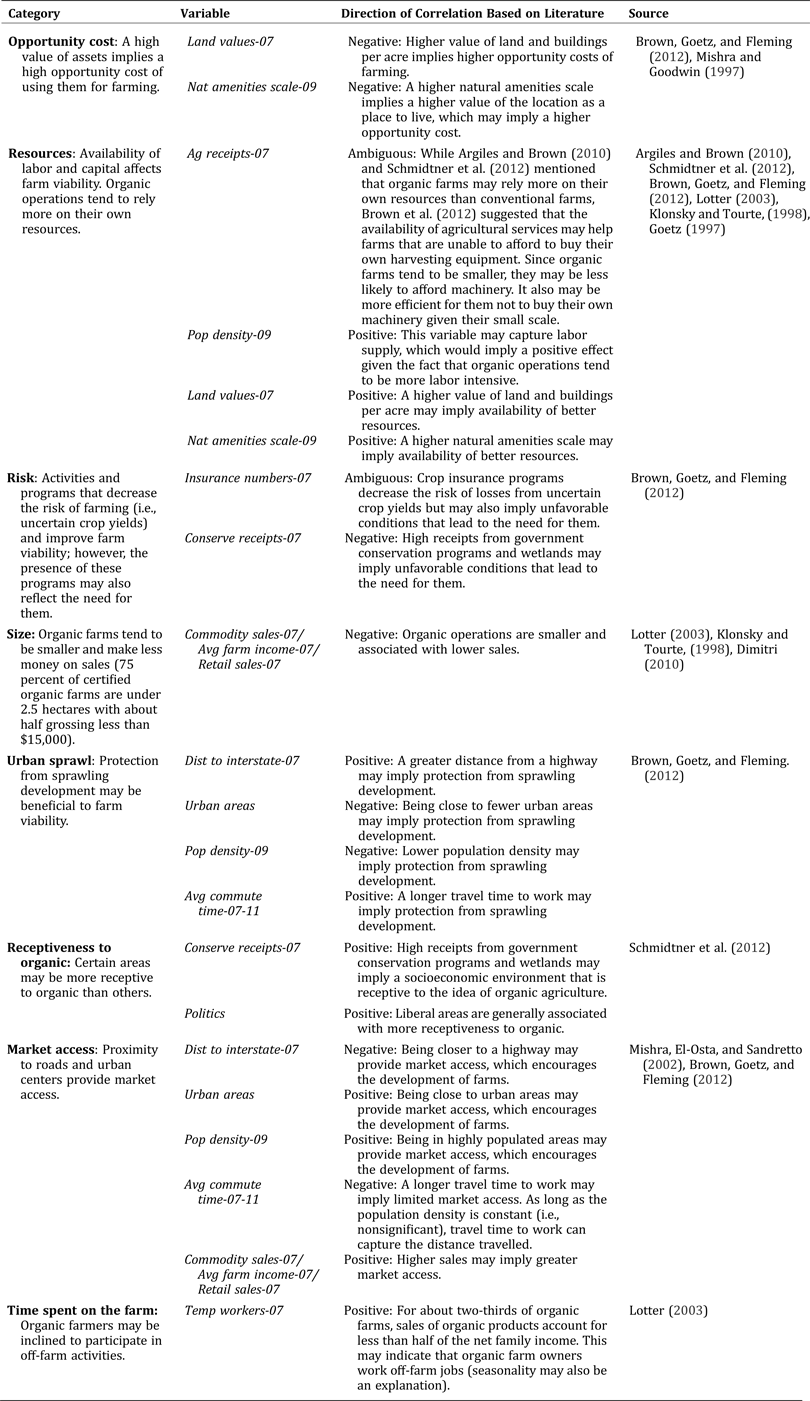
Economic theory provides little guidance regarding specific variables to include in x, which controls for factors other than the number of neighboring organic operations that may affect the spatial distribution of the organic operations, and we rely extensively on the current empirical literature to determine its specification. Table 1 provides descriptions and descriptive statistics for the variables chosen, and Table 2 presents our rationale for including each variable, assigns the variables to one of eight categories (opportunity cost, resources, risk, size, urban sprawl, receptiveness to organic, market access, and time spent on the farm), and cites the studies on which inclusion of the variables were based. We assigned the variables to categories solely to provide justification for their inclusion. We are mainly interested in testing for the presence of spatially lagged dependent variables and/or errors and do not attempt to test any hypotheses regarding the categories in which the independent variables fit. Because some of the studies of organic operations and clustering have yielded mixed results, variables sometimes fit into more than one category. For example, a negative coefficient for land values would fit into opportunity costs while a positive coefficient for the same variable would fit into resources.
Table 1. Summary Statistics and Description

a The maximum value corresponds with Kidder County, North Dakota, which is a sparsely populated, rural county (U.S. Census Bureau 2010). The second highest share is 0.341615.
Table 2. Independent Variables and Prior Studies by Category
To mitigate potential simultaneity and/or endogeneity, we add time lags for many of the variables in x. Specifically, we use data from 2009 for y and data from 2007 for many of the variables included in x, especially those that represent economic conditions and could affect the location of organic operations if concurrent data are used. Any other unaccounted-for factors are captured by the spatial error term, which captures spatial autocorrelation in the residuals.
Results of the Analysis of Spatial Autocorrelation
As shown in Table 3, all of the spatial autoregressive models (share of all organic operations and share of organic operations by primary scope) pass the accuracy and convergence tests and point to the presence of both spatial lags and spatial errorFootnote 11 (positive and significant spatial lag and spatial error terms). The positive spatial lag implies that organic operations in general and when broken down by primary scope tend to cluster near areas that have a high number of organic operations. The significant spatial error implies that variables that are not included in our model likely affect the spatial distribution of certified organic operations.
Table 3. Tests for Spatial Lag and Spatial Error in the Tobit Models

Note: * Significant at the 10 percent level. ** Significant at the 5 percent level. *** Significant at the 1 percent level.
Since we find that both spatial lag and spatial error are present, we cannot determine whether the spatial autoregressive or spatial error model is most appropriate. To our knowledge, there is no established method by which to compare the appropriateness of these two models, but LeSage and Pace (Reference LeSage and Pace2009) suggested an interesting solution: a spatial Durbin model is the proper specification when the probabilities of the correct model specification being a spatial autoregressive model and of being a spatial error model are both greater than zero. A spatial Durbin model (LeSage Reference LeSage1998) is defined as
According to LeSage (Reference LeSage1998), the results of this model take the possibility of spatial lag in both the dependent variable and in the independent variables into account. In our case, the coefficients in front of the spatially lagged independent variables show the effects of changes in the values of the independent variables in one county on the share of organic operations in neighboring counties. We therefore estimate spatial Durbin Tobit models.
The results of the spatial Durbin Tobit models, all of which pass the accuracy and convergence tests, suggest the presence of spatial autocorrelation and spillovers when analyzing the shares and counts of all organic operations and of the three types of organic operations (crops, handling, and livestock). Table 4 presents the results of the spatial Durbin Tobit model, which analyzes the share of all organic operations regressed against county-level factors. The positive significant coefficient ρ for the spatially lagged dependent variable implies that similar observations tend to be located close together; that is, counties that have a large share of organic operations tend to be relatively close to other counties that have large shares of organic operations.Footnote 12 As with hot spots, this result indicates that the intensity of organic operations of neighboring counties is positively related to a county's intensity of organic operations.
Table 4. Results: Share of Operation That Is Organic

Notes: A Bayesian spatial autoregressive Tobit heteroskedastic model yields similar estimates but with higher magnitudes and more significant variables. *Significant at the 10 percent level. ** Significant at the 5 percent level. *** Significant at the 1 percent level.
Seven of the fourteen spatially lagged independent variables are significant, suggesting the presence of cross-county spillover. For example, the positive significant coefficient for agricultural receipts (W-Ag receipts-07) indicates that availability of agricultural services in a county is positively related to the intensity of organic operations in neighboring counties. Simultaneously, there is a significant positive coefficient for land values (W-Land values-07) and a significant negative coefficient for the natural amenity score (W-Nat amenities scale-09). Considered together, these results point to cross-county spillovers for inputs and farm resources. The positive significant coefficient for support for the Democratic Party (W-Politics) suggests that political receptiveness to organic in one county may spill over into neighboring counties. Similarly, the negative coefficient for the number of organic operations participating in crop insurance programs (W-Insurance numbers-07) suggests that perceptions of risk associated with farming may also spill over into neighboring counties. The negative significant coefficient for average farm income (W-Avg farm income-07) indicates that the intensity of organic operations in a county is relatively high when the county is surrounded by counties that have a large number of small farms. The negative significant coefficient on travel time to work (W-traveltimetowork-07-11) suggests that a county's level of market access spills over to neighboring counties.
It is also interesting to examine the direct and indirect effects of the independent variables. The indirect effect of a variable represents the sum of its effects on observations outside of its area (∑(j≠i) ∂y j / ∂W x i ), and the direct effect represents the variable's effect on observations inside its area (∂y i / ∂x i ). The total effect is the sum of the direct and indirect effects (LeSage and Pace Reference LeSage and Pace2009). We find that the directions of the direct effects are consistent with the coefficients of the independent variables with no spatial lags and that the directions of the indirect effects are consistent with the coefficients of the spatially lagged independent variables.
Table 5 presents the results of the same analysis applied to the share of organic operations broken down by primary scope. As with the results for organic operations in general (crops, handling, and livestock), the coefficient for the spatially lagged dependent variable is positive and significant. Handling has the lowest coefficient and livestock has the highest.Footnote 13
Table 5. Results of Estimation by Primary Organic Scope

Notes: * Significant at the 10 percent level. ** Significant at the 5 percent level. *** Significant at the 1 percent level.
There are some differences, however, in the spatially lagged independent variables. For crop operations, the coefficients are negative and significant for average farm income, average commute time, and number of crop insurance participants and positive and significant for land values and political support for the Democratic Party. The coefficient for distance to the nearest interstate is positive and significant, indicating that the negative effects of urban sprawl may spill over county lines, and the positive significant coefficient for receipts from conservation programs (W-Conserve receipts-07) implies that the effects of receptiveness to organic may spill over county lines. The negative significant coefficient for retail sales suggests that the concentration of organic operations in a county is higher when the county is surrounded by counties with large numbers of small establishments.
The results for the share of organic operations with handling as the main scope are similar, except for the lack of significance for retail sales, land values, and number of participants in crop insurance programs and a positive significant coefficient for agricultural receipts. In the results for the share of organic operations with livestock as the main scope, the coefficient for support for the Democratic Party is significant and positive and the coefficients for average farm income and travel time to work are significant and negative, which is consistent with the results for crops and handling. However, the positive significant coefficient for retail sales (which fits into the market access category) and the negative significant coefficients for receipts from conservation programs (which fits into the risk category) and land values (which fits into the opportunity cost category) are not consistent with the results of the other groups.
The coefficients for the independent variables without spatial lags are less significant and are not necessarily consistent with the coefficients for the corresponding spatially lagged variables. Table 4 shows that the coefficients are significant for only five of the variables. The positive significant coefficient for agricultural receipts fits into the resource category and is in line with results of prior studies that showed that greater availability of agricultural services can be beneficial to organic farms. The positive significant coefficient on receipts from conservation programs fits into the category of receptiveness to organic, supporting the notion that organic operations are likely to be more prevalent in areas that are receptive to the idea of organic production. The positive significant coefficients for average commute time and distance to the nearest interstate and the negative coefficient for the number of urban areas all fit into the category of urban sprawl, in which organic farms tend to fare better when they are sheltered from urban development.
Table 5 shows that the results for the share of organic operations with crops and handling as the main scope are similar to those in Table 4, with the exception of the nonsignificant coefficient for distance to the nearest interstate and the negative significant coefficient for average farm income (crops only), which fits into the size category. For share of livestock operations, we find that the coefficient for the number of urban areas is negative and significant and the coefficients for average commute time and distance to the nearest interstate are positive and significant. The coefficient for commodity sales is also positive and significant, placing it in the market access category.
Conclusion
We document statistically significant hot spots and cold spots of certified organic operations under a broad definition and compare those results to organic hot spots and cold spots under three narrower definitions—crop producers, livestock producers, and handlers. We then compare all of those maps of distributions of organic hot spots and cold spots to those of agricultural farm establishments generally and of all business establishments.
We find that the largest hot spots for organic operations in general, crop operations, and handling operations occur along the West Coast of the United States from southern California to northern Washington. This extensive organic hot spot closely matches one of the hot spots for agricultural operations in general. However, many of the other organic hot spots do not match hot spots for general agriculture. This is particularly true for the Northeast, where we find numerous organic hot spots and almost no agricultural hot spots, and for the South and Southeast, where we find numerous agricultural hot spots and organic cold spots. Our spatial analysis thus demonstrates that organic operations follow a different geographic concentration pattern than agricultural operations generally and business establishments generally.
We also confirm the presence of spatial autocorrelation using various spatial autoregressive models that examine the shares or counts of certified organic operations. Spatial dependence is confirmed for a large number of variations in how organic operations are measured and for a number of spatial econometric models.
The results of this study clearly demonstrate the importance of spatial spillovers in organic agriculture. As a matter of policy, spatial dependence can be an important consideration for USDA and state governmental agencies that provide assistance to organic farmers. Our results suggest, for example, that public and private policies aimed at promoting organic agriculture might be most effective in areas where organic agriculture already has a foothold. In the future, a spatio-temporal analysis of organic operations over time could provide a fuller picture of the areas in the United States in which organic agriculture is prevalent and growing.
Our analysis of factors associated with the distribution of organic operations provides a starting point for further exploration of the formation of hot spots of organic operations. The results suggest, for example, that the degree of urban influence and distance to highways are negatively related to the formation of organic hot spots. We also find that the three types of organic operations—crop producers, livestock producers, and handlers—respond differently to these factors, potentially providing insight into their functions. One potentially interesting avenue for further study would be to analyze why receipts from agricultural services and custom work appear to have a significant association with organic crops and handling operations but not with organic livestock and why the distance to a highway appears to have a significant effect on organic livestock operations but not on crop and handling operations.
Our research also could be useful for understanding the consequences of the rapidly expanding demand for organic products and the potential for supply shortages. We find that areas of the United States known to be agricultural strongholds, such as the corn and soybean belts, are not hot spots of organic production. This research implicitly shows that some barriers exist in extending agricultural success in these prevalent and highly valued crops to similar success in their organic counterparts, which are known to be in great demand. Our results potentially provide a logical first step to a deeper investigation into organic agriculture's role as a rural development tool. Documenting hot spots and cold spots is a necessary starting point for investigating their potential economic impact on local economies.














