1. Introduction
The polar ice sheets are critical components of the Earth’s climate system. The volume of water confined in these regions represents roughly 7m and 73m global sea-level equivalent forGreenland and Antarctica, respectively (Reference Rignot and ThomasRignot and Thomas, 2002; Reference Alley, Clark, Huybrechts and JoughinAlley and others, 2005).
Just as physical oceanography has witnessed a paradigm shift from a passive, slowly changing, steady laminar fluid to a dynamically active fluid which is essentially turbulent (e.g.Reference Wunsch, Schmittner, Chiang and HemmingsWunsch, 2007), glaciologists are beginning to recognize that textbook accounts of ice sheets varying slowly over timescales of decades to millennia tell an oversimplified story. To demonstrate this point, compare the text by Reference Rignot and ThomasRignot and Thomas (2002):
As measurements become more precise and more widespread, it is becoming increasingly apparent that change on relatively short time-scales is commonplace: stoppage of huge glaciers, acceleration of others, appreciable thickening and far more rapid thinning of large sectors of ice sheet, rapid breakup of vast areas of ice shelf and acceleration of ice sheet flow..., and vigorous bottom melting near grounding lines. These observations run counter to much of the accepted wisdom regarding ice sheets, which, lacking modern observational capabilities, was largely based on ‘steady-state’ assumptions.
with that by Reference Wunsch, Schmittner, Chiang and HemmingsWunsch (2007):
Observational and computational progress in physical oceanography, however, over the last 30 years has rendered obsolete the old idea that the fluid ocean is a slowly changing, passive, almost geological system. Instead, it is a dynamically active, essentially turbulent fluid, inwhich large-scale tracer patterns arise fromactive turbulence and do not necessarily imply domination of the physics and climate system by large-scale flow fields. To the contrary, oceanic kinetic energy is dominated by the time and space-varying components. The complexity of the resulting fluid pathways is an essential part of any zero-order description of the system.
Recent observational studies have reported evidence of rapid changes in flow speed and mass balance in parts of Greenland and Antarctica (e.g. Reference KerrKerr, 2006; Reference Payne, Hunt and WinghamPayne and others, 2006; Reference Pennisi, Smith and StonePennisi and others, 2007). When trying to quantify short-term changes in the mass balance, however, these studies produce conflicting estimates depending on the choice of observing system (for recent reviews see Reference ZwallyZwally and others, 2005; Reference Bugnion, Hill and StoneCazenave, 2006; Reference Alley, Spencer and AnandakrishnanAlley and others, 2007; Reference Shepherd and WinghamShepherd and Wingham, 2007). Problems with mass-balance estimates relate to the size of the area covered, the limited time period spanned, instrumental uncertainties and sampling and interpolation issues. Inferred mass changes, which are translated into equivalent sea-level changes, therefore remain fragile. Reported changes are a significant contribution to observed sea-level changes (which are themselves fragile estimates (e.g.Reference Wunsch, Ponte and HeimbachWunsch and others, 2007)), but the associated uncertainties are so large that the sea-level change budget is far from closed.
Models complement data to assess the evolution of ice sheets. While sophisticated three-dimensional (3-D) ice-sheet models exist, they still suffer from serious limitations.
Some of the shortcomings are algorithmic in nature, failing for example to capture processes associated with abrupt, small-scale changes in the ice sheet such as melt-induced basal sliding or the effect of higher-order longitudinal stresses. These processes may well be crucial to instability mechanisms driving ice-sheet variations (Reference Truffer and FahnestockTruffer and Fahnestock, 2007; Reference Vaughan and ArthernVaughan and Arthern, 2007). Other limitations relate to poor understanding of the model’s internal dynamics and its built-in sensitivities.
This paper addresses the latter issue by providing a highly efficient method for calculating model sensitivities within a 3-D ice-sheet model. Traditional sensitivity analysis perturbs one parameter or one surface forcing variable at one point, and the ‘forward’ model calculates the impact of that change on all output variables and model diagnostics. The adjoint method, also widely known as the Lagrange multiplier method (LMM) (e.g. in classical mechanics and field theory) ‘inverts’ the problem by providing the partial derivatives or sensitivities of a single diagnostic to all model input variables (the controls) simultaneously. A very high-dimensional control space may have to be explored in models that are run from poorly known initial conditions and uncertain boundary forcings, using parameterizations with tuned (rather than known) parameters and where each of these variables may be spatially varying. Availability of the adjoint leads to a dramatic improvement in efficiency. As a result, we are able to build and display two-dimensional (2-D) and 3-D sensitivity maps of key ice-sheet diagnostics to ‘model controls’, allowing for rapid inspection and identification of areas and variables that might play an important role in influencing the ice-sheet dynamics.
At the heart of this study is the application of automatic differentiation (AD; Reference Griewank and WaltherGriewank and Walther, 2008) to derive Fortran code of an adjoint model (ADM) from the Fortran code of the 3-D thermomechanical ice-sheet model SICOPOLIS (SImulation COde for POLythermal Ice Sheets) (Reference GreveGreve, 1997). The automated construction of the ice-sheet model adjoint code ultimately opens doors to ice-sheet data assimilation. By combining the knowledge and skill present in the models with that existing in the data, better estimates can be provided of the state of the Greenland ice sheet than those derived from models or data in isolation.
Synthesizing the wealth of newly available observations and models via adjoint-based control methods was pioneered, in the context of ice streams, by Reference MacAyealMacAyeal (1992, Reference MacAyeal1993). (In the oceanographic context, among the earliest studies using control theory and the LMM were those of Reference WunschWunsch (1988), Reference Thacker and LongThacker and Long (1988) and Reference Tziperman and ThackerTziperman and Thacker (1989).) The main emphasis at the time was to elicit the main controls of ice-stream flows. The task was facilitated by the fact that the equations considered were mostly self-adjoint, rendering themethod comparatively easy to implement. Although the method was further developed by Reference Vieli and PayneVieli and Payne (2003), Reference Joughin, MacAyeal and TulaczykJoughin and others (2004, Reference Joughin, Bamber, Scambos, Tulaczyk, Fahnestock and MacAyeal2006), Reference Larour, Rignot, Joughin and AubryLarour and others (2005), Reference Vieli, Payne, Du and ShepherdVieli and others (2006) and Reference Khazendar, Rignot and LarourKhazendar and others (2007), no serious attempt has been made to extend it to comprehensive, 3-D ice-sheet models. Accomplishing this is the ultimate objective of adjoint code construction.
An important prerequisite for ice-sheet state estimation is a deep understanding of which control variables an ice-sheet model is most sensitive to. The choice of such controls remains a key scientific undertaking. Depending upon the problem investigated and the investigator’s insight, decisions are made on whether
1. the emphasis is only on observable quantities or on unknown key model parameters whose sensitivities (or tuning) provide critical insight into the model’s behavior; and
2. to explore a control space with the same gridpoint discretization as the model state space or with a reduced-order space through some meaningful basis functions.
This paper presents a range of sensitivity types:
1. sensitivity to internal model parameters such as the basal sliding coefficient: we transform model parameters into 2-D or 3-D fields in order to capture spatially varying sensitivities;
2. sensitivity to external forcing fields such as precipitation; and
3. sensitivity to the initial model state: this is particularly important in data assimilation when the ability to adjust the initial state of the system becomes an intrinsic part of minimizing the model-to-data misfit.
The range of diagnostic functions that can be used is endless and typically tailored to the research objective. Here we use the ice-sheet volume as a global diagnostic of evolution of the ice sheet. Other research objectives could use the total volume of meltwater, total calving volume or average ice-flow speed as sample diagnostics. Studies of ice-stream dynamics could use the ice velocity at a specific location as a diagnostic function. Data assimilation problems typically use the model-to-data misfit as the diagnostic function that is in turn minimized.
The objective of this paper is primarily a proof of concept. We realize that the underlying ice-sheet forward model will require a better representation of the stress tensor (e.g. through higher-order models) and a more refined sliding parameterization in order for the adjoint to portray more realistic sensitivities of the Greenland ice sheet, in particular in regions of fast ice flow. This proof of concept should, nevertheless, establish the viability of the approach in efficiently identifying the dominant processes and controls governing rapid ice-sheet variations.
2. Adjoint Modeling and Automatic Differentiation
Conventionally, sensitivities are assessed by perturbing a control variable of interest and investigating the ice-sheet response to the applied perturbation. For each quantity a separate run needs to be performed and, for quantities that vary spatially, assumptions need to be made about where to perturb. At one extreme, perturbations are spatially uniform (e.g. uniform air-temperature perturbation everywhere). At the other extreme, a separate perturbation at each gridpoint and a forward simulation for each such perturbation are performed in order to produce a full sensitivity map. For a model configuration withnx × ny × nz = 82× 140× 80 gridpoints, the initial value control problem spans a 918 400-dimensional control space.
Alternatively, the adjoint model is able to provide a complete set ormap of sensitivities in a single integration. For all its appeal, obtaining an adjoint model is not an easy task.
We attempt to provide a short self-contained introduction to adjoint modeling and automatic differentiation since no such description currently exists in the glaciological literature. We establish the connection between the tangent linear model (TLM), the ADM and Lagrange multipliers. We then show how to use AD to generate tangent linear and adjoint model code. Readers who wish to skip technical details should ignore sections 2.1–2.3 and resume reading at section 2.4.
2.1. The adjoint or Lagrange multiplier method
Our goal is to find sensitivities, i.e. partial derivatives of a scalar-valued objective or cost function J0[x] with respect to control variables u. The dependency ofJ 0 on u is usually indirect, i.e. through the dependency of elements of state variables x of a model on u. For simplicity, we focus on the case where u is the model’s initial state x(t 0 = 0). Following the notation of Reference WunschWunsch (2006), the time-dependent modelL has the general form
and is integrated from timet 0 = 0 tot =t f. (To simplify notation, we can formally extend the model state space x to include model prognostic variables as well as model parameters and boundary conditions.)
As an example, let the objective function consist of the time-mean volume over the lastn+1 time-stepst f −n,. . . ,t f − 1,t f of the ice sheet, expressed as the spatial, area-weighted sumV[x(t)] =Σ i,j H(i,j,t) dA(i,j) over the thickness field H(t) at timet, which is an element of the model prognostic state space x(t). We therefore have
The Lagrange multiplier method consists of rewriting the problem of finding derivatives ofJ 0, subject to the constraint of fulfilling Equation (1), into an extended and unconstrained problem:
For each element of the model state x(t) at timet, we have introduced a corresponding Lagrange multiplier μ(t).
The set of normal equations is obtained by requiring the partial derivatives of Equation (3) with respect to each variable for times t >t 0 to vanish independently (e.g. Reference WunschWunsch, 2006):
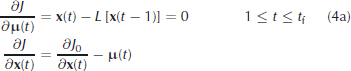
Equation (4a) simply recovers the model equations. The Lagrange multipliers μ(t) are found through successive evaluation of the normal equations backwards in time.
Starting att =t f we find (via Equation (4c) and using example cost Equation (2)),
n + 1 time-steps earlier att =t f − n. Using the results of μ(t f),. . . ,μ(t f − n + 1), we obtain (using Equation (4b)):
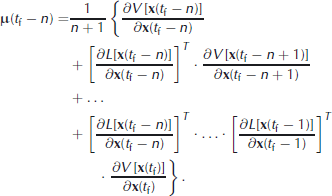
Finally, Equation (4d) provides the expression for the full gradient sought at timet 0 = 0.
We make the following interpretation. The Lagrange multiplier μ(t) provides the complete sensitivity ofJ 0 at timet by accumulating all partial derivatives ofJ 0 with respect to x from each time-stept f ,t f −1,. . . ,t. Those partial derivatives taken at later timest +1,. . . ,t f are propagated to timet via the ADM, which is the transpose
of the model Jacobian or tangent linear model (TLM)
with contributions from different times linearly superimposed. Further simplifying the example objective function (2) to the special case where instead of the time-mean only the volume at the last time-stept f is chosen, i.e.n = 0, Equation (5) simplifies in that all terms vanish except for that containing
2.2. The tangent linear and adjoint models
All relevant aspects of the LMM have now been derived, but we wish to make plain the duality between the TLM and the ADM. We restate our problem in a slightly different but equivalent framework which provides a natural basis for introducing the concept of AD. The non-linear model (NLM)L of Equation (1) may be viewed as a mapping of the state space (again incorporating all parameters and initial and boundary conditions into an extended state space) from timet = 0 tot =t f. The cost functionJ 0 (Equation (2)) is then a composite mapping from the state space att 0 = 0 tot =t f, and from there to the real numbers. To simplify notation, let y = x(t f) and consider the special casen = 0, i.e.J 0 =V[x(t f)] =V[y]. Then,
The composite nature of the mapping ofJ 0 is readily apparent:
A perturbation of the initial state x(0) is linked to a perturbation ofJ 0 by applying the chain rule to Equation (7):
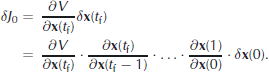
Recognizing thatδJ0 is simply the scalar product of andδy, we can use the formal definition of an adjoint operator (x | Ay)= (ATx|y) to rewrite this equation:
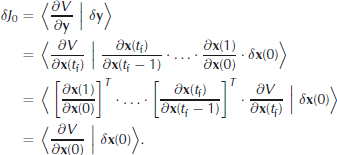
Alternatively, by denoting the tangent linear and adjoint matrices asTLM andADM, respectively, we have:
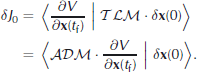
Equations (5), (9) and (10) highlight various features:
1. the equivalence between Lagrange multipliers and the adjoint operator;
2. the fact that the TLM runs forward in time, propagating the effect of a perturbationδx(0) to all model outputs, while the ADM runs backward, accumulating sensitivities ofδJ0 to all model inputs; and
3. the advantage of the ADM, which provides the full gradient of a model-constrained objective function∂V/∂x(0) over the TLM which only provides the projection of∂V/∂y onto the perturbed vectorδy from initial perturbationδx(0).
2.3. Derivative code generation via automatic differentiation
Although we have demonstrated the power of the adjoint method, we have not yet discussed how to obtain it. In general, the complexity and effort involved in developing an adjoint model matches that in its parent NLM development and frequently prohibits adjoint model applications. An alternative to hand-coding the adjoint (i.e. coding the discretized adjoint equations) and a major step forward is the use of AD compared to derivative (e.g. ADM or TLM) code generation (Reference Griewank and WaltherGriewank and Walther, 2008). The advent of AD source-to-source transformation tools such as the commercial tool ‘Transformation of Algorithms in Fortran’ (TAF) (Reference Giering, Kaminski and SlawigGiering and others, 2005) or the open-source tool OpenAD (Reference UtkeUtke and others, 2008) has enabled the development of exact adjoint models from complex, nonlinear forward models. In the oceanographic context, there is now a decade of experience in applying this method to a state-of-the-art ocean general circulation model (e.g. Reference Marotzke, Giering, Zhang, Stammer, Hill and LeeMarotzke and others, 1999; Reference Galanti, Tziperman, Harrison, Rosati, Giering and SirkesGalanti and others, 2002; Reference Heimbach, Hill, Giering, Dongarra, Sloot and TanHeimbach and others, 2002; Reference StammerStammer and others, 2003; Reference HeimbachHeimbach, 2008) which encourages us to apply such tools to state-of-the-art ice-sheet models.
The composite nature of the mappingJ 0 is that of a large number of elementary operations; Equation (6) reflects this at the time-stepping level. Carrying the concept of composition to its extreme, ultimately each line of code can be viewed as an elementary operation. At the elementary level, the AD tool knows the complete set of derivatives (i.e. the elementary Jacobians)√ for each intrinsic arithmetic function (+, –, *,/,√., sin(.), etc.), as well as logical/conditional instructions.
Here, we demonstrate how the AD tool generates line-byline elementary Jacobians (TLM code) and their transpose (ADM code). The full model Jacobian is recovered by composition of each elementary Jacobian according to the chain and product rule. A very simple example is given in Figure 1, demonstrating the relationship between the NLM, TLM and ADM. The full derivative is readily calculated (line TLM), and the adjoint model easily derived by taking the transposes of dJ0 and dL. It is readily apparent that while the TLM only provides a projection of the gradient onto the directional perturbation vectorδx, the ADM provides the full gradient vector.

Fig. 1. Example of the relationship between the NLM, the TLM and the ADM. The general formalism is summarized in the upper table for a squared-valued cost functionJ 0 =|y| 2. The lower table provides a written example for a simple 2-D vector modelL, one time-step of which consists of a rotation and stretching followed by evaluation of the squared costJ 0.
In the context of a more complex model, we chose as an example the advection problem arising from solving the continuity equation for the ice-sheet volume, expressed in terms of ice-sheet elevationH. The velocityU b at which basal sliding-related advection takes place is inferred from a Weertman-type sliding law. Part of the time-stepping loop at timem might look like the chart in Figure 2.

Fig. 2. Upper box shows a simplified time-stepping loop of the nonlinear forward model; lower box shows the time-reversed adjoint time-stepping. Note the reversal of the order of sub-routine calls.
At the elementary level, the full derivative of the code line forU b can be written (dropping superscriptm):
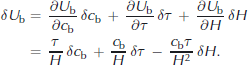
This can be rearranged in matrix form (Reference Giering and KaminskiGiering and Kaminski, 1998):

where the variablesδc b,δτ,δH andδU b are perturbations, i.e. elements of the TLM state space. Expressing the model in such a manner enables straightforward access to the transpose
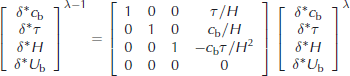
where the variablesδ∗c b,δ∗τ,δ∗H and δ∗U b are now sensitivities, i.e. elements of the adjoint model state space.
(Strictly, adjoint variables are co-vectors and are elements of the dual or co-tangent space to the tangent space of the model.) From Equation (13), we can readily calculate the following lines which represent the adjoint code:
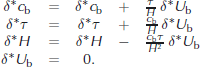
The result can be interpreted in the following way.
1. From Equation (11) we infer how perturbations to the inputs affect the outputδU b,whereas Equation (14) shows how the output sensitivityδ∗U b has been influenced by each input sensitivity.
2. The aspect oftangent linear (and adjoint) is clear: knowledge of thecurrent state at timem of τm,Hm is necessary to evaluate either Equation (11) or Equation (14).
3. The TLM is evaluated in the same order as the non-linear parent modelL and evaluating both can be combined. The ADM is evaluated in reverse order, and making the required state variables accessible becomes a major problem in evaluating the adjoint model exactly.
Requiring the model state in reverse order is at the heart of the technical difficulties and one of the main hurdles in generating efficient and exact adjoint code for large-scale transient non-linear applications.
For the present study we have chosen the AD tool TAF. It solves the problem of requiring model state variables in reverse temporal order through a hierarchical ‘checkpointing’ and targeted ‘taping’ algorithm which provides a computationally efficient mix between saving and recomputing required variables. To achieve this, the user has to guide TAF through insertion of directives into the parent model to trigger storing of specific variables. A description is beyond the scope of this paper. Further details of the oceanographic context, as well as other topics (e.g. treatment of conditional (IF-) statements, (massive) parallel adjoint-code generation in the context of domain decomposition and treatment of implicit elliptic solvers) are given in Reference Heimbach, Hill and GieringHeimbach and others (2005).
As a final note of caution, because of thetangent linearity of the adjoint sensitivity, a limitation is that sensitivities are valid with respect to the reference model state for which they are computed. For purely linear problems they are independent of the reference state, but with increasing nonlinearity. Knowledge of the forward state becomes essential when interpreting such sensitivities; re-running the adjoint for different reference states may prove necessary. The implications are readily apparent from the example of a quadratic cost function provided in Figure 1. Nevertheless, since the same considerations apply to forward perturbation or TLM simulations, this does not constitute a disadvantage of the adjoint compared with forward methods.
2.4. Choice of control variables
Successful modeling requires relevant internal physics as well as appropriate representation of surface and basal boundary conditions. It is often the prescription of these which leads to significant differences in simulations.
At the surface of the ice sheet, interaction with the atmosphere is achieved through the prescription of meteorological and climatic inputs, consisting of surface mass-balance (accumulation minus ablation), precipitation, surface air temperature and refreezing and meltwater runoff parameterization (from positive degree-day method). Boundary conditions at the base of the ice sheet must account for interaction with the bedrock and the ocean, including basal sliding parameter, basal shear stress, basal melt/freeze rate, bed topography and geothermal heat flux. Finally, initial conditions are required for an ice sheet whose full 3-D state is usually poorly known and difficult to observe. The adjoint model provides sensitivities to each of these processes.
Boundary conditions are often heavily parameterized, and the sensitivity of the solution to the parameter choice can be substantial. Ultimately, all model ingredients that have associated uncertainties are relevant control variables.
Even quantities which are supposedly well determined, such as the precipitation products from the US National Centers for Environmental Prediction/US National Center for Atmospheric Research (NCEP/NCAR) (Reference KalnayKalnay and others, 1996) or the European Centre for Medium-Range Weather Forecasts (ECMWF) ERA-40 (Reference UppalaUppala and others, 2005) so-called ‘re-analyses’, have major uncertainties or biases, as discussed by Reference Bèranger, Barnier, Gulev and CrèponBèranger and others (2006). Their primary goal is to provide the best initial conditions for a subsequent forecast, but no requirements are imposed to preserve longterm global budgets. Furthermore, there is limited data coverage in polar regions, and they may be poorly constrained there. The finding by Reference Wingham, Shepherd, Muir and MarshallWingham and others (2006) that these fields ‘are not able to characterize the contemporary snowfall fluctuation with useful accuracy’ is therefore unsurprising.
3. A Sensitivity Study of Greenland Ice Volume
Important factors in the choice of the 3-D ice-sheet model SICOPOLIS were
1. sufficient model complexity and size of the model state and control spaces to provide a convincing, non-trivial application of AD; and
2. that it is written in Fortran, the only language which most source-to-source AD tools to date can handle for fairly complex codes.
SICOPOLIS (Reference GreveGreve, 1997, Reference Greve2000) was the first model to resolve explicitly both the cold and polythermal regions of the ice sheet. The shallow-ice approximation (SIA) is used to simplify the stress tensor by neglecting the longitudinal stress gradients. The ice dynamics are solved on a staggered grid. The rheological behavior is assumed to be that of an incompressible, non-linear viscous and heat-conducting fluid. SICOPOLIS has been used successfully to simulate the variation of the Greenland ice sheet between ice ages and interglacial periods and in climate-change simulations (Reference Bugnion and HillBugnion and Stone, 2002). SICOPOLIS also participated in the European Ice Sheet Modeling Initiative (EISMINT) project (Reference PaynePayne and others, 2000) and in the ongoing Ice-Sheet Model Intercomparison Project (ISMIP).
The models, both forward and adjoint, are solved on a 20km× 20 km horizontal grid with 80 vertical layers and a 5 year time-step. The model was spun up over a 60 000 year period, using as forcing fields constant present-day precipitation, a degree-day model formulation based on current average temperature over the ice sheet and a constant geothermal heat flux. The equilibrium topography shown in Figure 3 differs little from current conditions, which is to a large extent determined by the prescribed accumulation field. Individual drainage basins are well delineated, although the model resolution and model physics are insufficient to resolve fast-moving ice streams such as Jakobshavn Isbræ, Greenland, or the ‘Northeast Greenland Ice Stream’. Associated basal temperature and basal melt-rate maps are shown in Figure 4. The model state at the end of the spin-up was saved and used as a starting point for the adjoint runs.

Fig. 3. Simulated surface elevation or ice thickness in meters (using the terminology of Reference GreveGreve, 1997) of the Greenland ice sheet from a 60 000 year spin-up integration. Region indices refer to various perturbation experiments (Table 1).

Fig. 4. Basal properties at equilibrium of the Greenland ice sheet from a 60 000 year spin-up: (a) temperature and (b) melt rate. These properties are useful in interpreting elements of the adjoint sensitivities.
Our analysis focuses on total ice volume of the Greenland ice sheet as objective function (Equation (2)). The adjoint integration is performed over a 100 year period with a 5 year time-step. The integration picks up from an equilibrated state which has been spun up for 60 000 years. The computed reference total ice volume isV ref =3.248×1015 m 3 . The adjoint is exact in the sense oftangent linearity, i.e. all derivatives are evaluated with respect to the exact instantaneous forward model state.
We investigate three types of sensitivities:
1. model parameter sensitivities;
2. model forcing sensitivities; and
3. initial value sensitivities.
3.1. Sensitivity to model parameters: the case of basal sliding and basal melt rate
Boundary conditions at the base of the ice sheet have an important, yet poorly understood, control on the evolution of the ice sheet. It is clear that the underlying model cannot simulate fast, realistic ice-stream flows, both because of the grid resolution and because of the use of the SIA. Nevertheless, even for long-term integrations for which this model seems more appropriate, the effect is relevant as it may provide a crucial mechanism for millennial-scale ice-sheet disintegration.
We investigate the effect of the sliding law with a Weertman-type parameterization ofU b, which is a function of the (uncertain) sliding coefficientc b (Reference GreveGreve, 1997, equation 5). The reference value used in the model is a spatially uniformc b = 11.2ma− 1 Pa− 1. We makec b a spatially dependent control variable, i.e.c b =c b(i,j). To put these sensitivities into context, we also derive sensitivities to basal melt rateq bm. Equation (4.143) of Reference GreveGreve (1997) shows that this quantity is dependent on several factors. It is a function of vertical ice and lithosphere temperature gradients (with corresponding conductivity coefficients), as well as horizontal gradients of sliding velocityU b times the vertical shear stress components in each direction. We only consider their cumulative effect here and represent the sensitivity by a spatially varying control variablea 0 =q bm L, basal melt rate times latent heatL = 3.35× 105 J kg− 1 .
Figure 5a and b depict∂V/∂c b and∂V/∂a 0, respectively, the sensitivities of total ice volume to basal sliding and basal melt rates. The main features of sensitivity patterns can be summarized as follows.

Fig. 5. Adjoint sensitivity maps related to (a) basal sliding and (b) basal melt rate. A unit perturbationδc b toc b location (i,j) will change the cost functionV by the amountδV = (∂V/∂c b)δc b. To infer useful quantities forδV, we consider physically reasonable perturbations ofδc b (e.g. representing typical standard deviations at this location, measurement uncertainties or model uncertainties). Qualitatively, melt-rate sensitivities (b) are fairly uniform where they do not vanish, whereas sliding sensitivities (a) exhibit significant regional variations.
1. The geographical variation of the sensitivities is readily apparent. Patterns of significant sensitivities are broadly similar. They are very small in the ice-sheet interior, but differ in detail where sensitivities are larger. Patterns of significanta 0 sensitivities coincide with bottom-ice temperatures near the melting point and essentially vanish where temperatures fall below∼–3◦C. Largestc b sensitivities are more concentrated near the margins of the ice sheet.
2. As expected, bothc b anda 0 sensitivities are mostly negative, i.e. increasing the basal sliding coefficient or the basal melt rate in most locations will reduce the total ice volume.
3. In contrast to the fairly uniform basal melt-rate sensitivities, those for basal sliding show conspicuous positive regions (region 2 in Fig. 3 and Table 1), implying that increasing the basal sliding coefficient increases the ice volume.
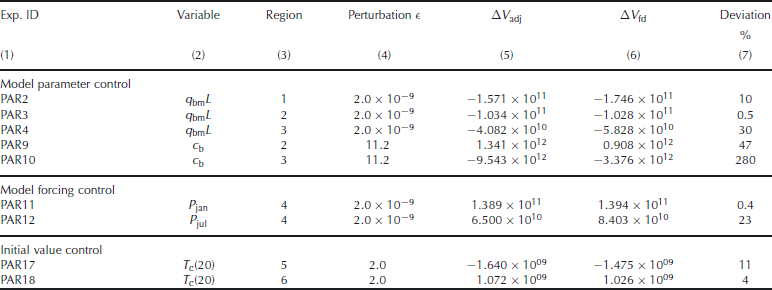
Table 1. Ice-volume changes inferred from adjoint sensitivities (column 5) and corresponding finite-difference perturbations (column 6) for various control variables (column 2) and perturbation regions (column 3). Perturbations 𝜖 are chosen to be 100% of base values (column 4) or assumed uncertainties (the former choice usually has a fairly large value compared to the latter). Reference total ice volume is V ref = 3.248 × 1015 m3. The reasons for such large deviations are large perturbation values 𝜖 compared to mean; associated gradients are small and therefore noisy; or the presence of significant non-linearities, for which either the magnitude of 𝜖 or integration period (or both) are beyond the validity range of the assumption of linearity
3.2. Testing the adjoint sensitivities
Before proceeding, we make an important step in testing whether the computed adjoint sensitivities are reliable. We do so by performing a series of finite-perturbation simulations which we compare to adjoint-based perturbations. Table 1 summarizes the results. In particular, columns 5 and 6 represent values of total ice volume perturbations, which are computed as follows (e.g. fora 0 as control):
Column 5: The value ΔV adj at position (i,j) inferred from the adjoint sensitivity field∂V/∂a 0 (i,j) is obtained by integrating the sensitivities multiplied by a typical perturbationδ a0 =є (column 4) over the region of interest (column 3) that is being perturbed, i.e.
Column 6: The value ΔV fd is inferred by applying a uniform perturbationδ a0 =є toa 0 over the identical region (column 3) and performing a forward model simulation to compute the modifiedV(a 0 +δ a0). We therefore have:
We performed perturbation comparisons ofq bm in four different regions (Table 1, experiments PAR2–PAR4). Given the localized nature of the perturbations, the smallness ofє (in most cases) and the shortness of the integration, the perturbed total ice volume remains comparatively small. Ice-volume changes computed from adjoint sensitivities deviate from finite-difference perturbations by 10%, 0.5% and 30% for regions 1–3 (cf.Fig. 1 and Table 1), respectively. The large deviation for PAR4 is associated with comparatively small perturbed values ofV (a factor of two smaller than for PAR2 and PAR3), indicating that the adjoint and finite-difference values are likely noisy in these cases. In contrast, for larger perturbedV there is good agreement between adjoint-derived and finite-difference perturbations (PAR2 and PAR3).
We have ascertained the validity of the gradient via finite-difference perturbations. Table 1 confirms both the positive gradient in region 2 (PAR9) and the negative gradient in nearby region 3 (PAR10). The changes in ice thicknessH c incurred by the perturbation are plotted in Figure 6. Thec b perturbations over region 2 lead to a dipole-like response inH c (Fig. 6a), i.e. a decrease to the east of the perturbation and an increase over (and to the west of) the perturbation. The western thickness increase dominates the eastern decrease, leading to an overall positive ΔV as predicted by the adjoint. Region 3 just west of region 2 has a negative sensitivity and a mostly negative response pattern inH c (Fig. 6b), again consistent with the adjoint inference.

Fig. 6. Response of ice-sheet elevation to perturbation in sliding coefficientc b (Table 1, PAR9, PAR10). The differences between perturbed and unperturbed ice thicknesses (m) are depicted. The applied perturbation was fairly large (δc b = 11.2ma− 1 Pa− 1, which is 100% of the mean value). The aim is twofold: (1) to ascertain the sign and magnitude of the adjoint sensitivities and (2) to investigate the structure of the response to the perturbations and its physical causes. An upstream/downstream dipole pattern is apparent for the region 2 perturbation, with a dominating increase downstream of the perturbation. The region 3 perturbation (b) results mainly in a decrease in ice thickness.
Table 1. Ice-volume changes inferred from adjoint sensitivities (column 5) and corresponding finite-difference perturbations (column 6) for various control variables (column 2) and perturbation regions (column 3). Perturbationsє are chosen to be 100% of base values (column 4) or assumed uncertainties (the former choice usually has a fairly large value compared to the latter). Reference total ice volume isV ref = 3.248× 10 15 m3. The reasons for such large deviations are large perturbation valuesє compared to mean; associated gradients are small and therefore noisy; or the presence of significant non-linearities, for which either the magnitude ofє or integration period (or both) are beyond the validity range of the assumption of linearity
By increasing the sliding coefficient in region 3, it appears that while the ice thickness decreases upstream of the test region (relative to the flow direction), the rate of ice melt of the displaced ice just downstream of the perturbation is lower than for the unperturbed run. This may be due to ice emanating from further inland being further away from melting, thus temporarily reducing basal melt compared to the equilibrium case. The reduction of melt of the displaced ice therefore leads to overall increased ice volumes and the observed positive sensitivities.
3.3. Sensitivity to model forcing: the case of precipitation
A second important class of control variables is model forcings. The same adjoint calculation that provided the parameter sensitivity fields also furnishes sensitivities to various forcings, one of which we investigate in some detail (Fig. 7).

Fig. 7. Adjoint sensitivity maps of ice volume to precipitation for mean January (a) and July (b) conditions (10− 18 m3 (ms− 1)− 1). The interpretation is similar to that of Figure 5. Interior ice-sheet sensitivities are equal for summer and winter months, but values near the margins deviate strongly. An interpretation in terms of the seasonal snow-to-rain conversion function is given in the text.
The model uses an annual mean precipitation field as input. This field is first modified to account for elevation desertification with a threshold ice thickness of 2000 m. The resulting field is used to compute a mean annual snowfall, taking into account an annual cycle in surface air temperature. Accordingly, the snowfall for monthi is computed from the given annual mean precipitation, precip, and monthly mean surface air temperature fieldT air(i) as

Here,T rain= 7◦C andT snow =−10◦C are threshold temperatures for precipitation which is equivalent to 100% rain and snow, respectively, andf (0, 1) is a function between 0 and 1. From this we can interpret the qualitative structure of the main differences between the adjoint sensitivity maps of January vs July precipitation (Fig. 7). We do so with the help of the adjoint statement of Equation (17), which we derive in the same way as for the adjoint code (Equation (14)):
In certain regions, and for months where fact(T air(i)) = 1, January and July sensitivities coincide. In regions where the annual cycle in temperature exceeds the snow or even the rain threshold, the difference in sensitivities is greater. These regions are concentrated at low altitudes and near the coast. As a consequence, the ice volume sensitivities exhibit a seasonal dependence on precipitation induced by air temperature, and the equilibrium line is clearly visible. Sensitivities at the margins are significantly enhanced (large snow accumulation) during winter. During summer, however, they are strongly reduced if not reversed in sign due to melting.
Note that this example demonstrates that conditional statements (IF-statements) as represented by the function fact(T air(i)) can be readily dealt with in the context of AD and adjoint code generation. They are best viewed as implementations of piecewise differentiable expressions. In fact, exact adjoint code relies on the availability of the exact branch of a condition when evaluating the adjoint.
3.4. Sensitivity to initial state
A third class of control variables concerns the initial conditions of the model. The main quantity of interest here is the 3-D ice temperature distribution. Its uncertainties are considerable: observations of the interior of the ice sheets, or even near the base, are almost entirely lacking. Assessing sensitivities of ice volume to changes in ice temperature anywhere in the ice sheet is therefore of considerable significance. In data assimilation, where initial conditions are sought from the model run to produce a best fit to observations (state estimation mode) or to produce an ‘optimal forecast’ (forecast mode), the initial condition control problem is essential. We therefore include a a brief discussion here.
Figure 8 depicts a sensitivity map at a randomly chosen vertical level of the ice sheet (note that because of the use of rescaled vertical coordinates, i.e. scaled thickness from 0 to 1, the ordinate does not reflect thickness itself but a level index). A complementary view is obtained by considering zonal or meridional cross-sections. Here we choose a north–south section ati = 32 (Fig. 9). Considerable regional variations are evident (both positive and negative areas exist), as are dependencies with respect to vertical position. Sensitivities are much larger near the base where temperatures are closer to the melting point, and are mostly negative (i.e. increasing the temperature will decrease the ice volume). Towards the surface the ice sheet seems insulated against significant ice-sheet volume sensitivities. As was the case for basal sliding, the temperature sensitivity maps contain evidence of the main drainage systems of the ice sheet, albeit coarsely represented at this resolution.

Fig. 8. Adjoint sensitivity of ice volume to ice temperature variations; vertical levelk = 20 (of 80, counted from ice-sheet base) (10− 6 m3 ◦C− 1). Significant spatial variations are apparent, with conspicuous regions of positive sensitivities. A hint of drainage basins near the coast is evident. Maps similar to this would be used in data assimilation to infer model initial condition changes that lead to an improved model simulation vs observation misfit.

Fig. 9. Meridional section ati = 32 vs vertical level of adjoint ice temperature sensitivities across the ice sheet (10− 7 m3 ◦C− 1). The plot complements Figure 8 in resolving the dependency of ice temperature sensitivities. Main features are insulation of sensitivities toward the ice sheet’s upper boundary; dominance of negative sensitivities, increasing in magnitude towards the ice-sheet base; and confirmation of the positive sensitivity band near, but not immediately adjacent to, the ice-sheet base.
Of particular interest is a significant band of positive sensitivities extending mostly in the north–south direction in the southwest sector of the ice sheet. This band is near the coast yet separated from it by a band of negative sensitivities. They seem to coincide with regions of positive sensitivities to changes in the basal sliding coefficientc b (Fig. 5) which were attributed to the interaction between enhanced sliding and coastal ice melt rates. These patterns show that warming the ice will not necessarily have the uniform consequence of shrinking the ice sheet. They are unexpected, but confirmed by finite-difference perturbations (Fig. 3, regions 5 and 6; Table 1, PAR17, PAR18).
4. Discussion and Outlook
We have presented a method of extending the application of control methods, pioneered by Reference MacAyealMacAyeal (1992, Reference MacAyeal1993) in the context of ice-stream models, to comprehensive 3-D thermomechanical ice-sheet models. We demonstrate that efficient, reliable Lagrange multipliers (i.e. adjoint sensitivities) can be computed from an adjoint model generated from its original parent model by rigorous application of automatic differentiation. This method is extremely powerful in the context of large model codes (in the present context of the order of 10 000 lines of code), which are undergoing continued model development and improvement.
To illustrate the approach, we choose the problem of determining the sensitivity of Greenland ice volume over a 100 year time horizon. The control space consisted of three types of variables (only some of which were analyzed here in detail):
1. model parameters (basal melt rates, basal sliding coefficient);
2. model forcing (air temperature, precipitation, geothermal heat flux); and
3. model initial conditions (3-D initial ice distribution).
Taken together, the control space has of the order of 1.2×106 elements. The adjoint model permits the spatially varying gradients of all control variables to be calculated in a single simulation.
To ensure reliability of the computed gradients, a number of finite-difference perturbation simulations were performed for the same 100 year time horizon and for various control variables, and were then applied to various regions. Where the perturbations have a substantial impact on the ice volume, there was very good quantitative agreement with the adjoint prediction, lending credence to the adjoint model.
The results demonstrate that various aspects of the spatial patterns of sensitivities can be assessed qualitatively and quantitatively from adjoint fields. While many features follow conventional wisdom (‘increasing temperatures lead to decreasing ice volume’), the adjoint solution allows the detection of regions where model sensitivities are unexpected or seemingly counter-intuitive (although ‘real’ in the sense of actual model behavior). Examples in the present context include positive basal sliding coefficient sensitivities, as well as positive ice temperature sensitivities in certain parts of the ice sheet.
Given the large uncertainties that exist in the prescription of model parameters, in the variability of forcing fields and in the knowledge of the detailed interior temperature distribution of an ice sheet, comprehensive sensitivity information provides crucial information to guide model improvement and the need for more observations (e.g. Reference Gudmundsson and RaymondGudmundsson and Raymond, 2008).
For climate-related studies which target century to millenial timescales, the adjoint code developed will be a very useful tool for sensitivity studies (an ocean analogue is the series of studies by Reference Bugnion and StoneBugnion and Hill (2006) and Reference Bugnion, Hill and StoneBugnion and others (2006a,Reference Bugnion, Hill and Stoneb)). We do not attempt to provide a hierarchy of most important variables in terms of ice volume sensitivities; this is left for future studies.
4.1. Extension to state estimation
The SICOPOLIS code was originally written for zero-order flow regimes (SIA), and extensions have subsequently been made to incorporate first-order physics (e.g. Reference BlatterBlatter, 1995). Our proof-of-concept study may only partially address the fast-flow regimes; an extension should include more comprehensive higher-order dynamics. The next major step, therefore, is to derive an adjoint of a 3-D model which captures fast ice streams by incorporating higher-order stresses in the momentum balance. This is indispensable for our longterm goal of applying the adjoint method for 3-D ice-sheet state estimation over the period of satellite observations.
Available adjoint code generation tools which require certain coding standards to be maintained open up a variety of novel applications, notably with regard to sensitivity and uncertainty analyses and ice-sheet state estimation or data assimilation. Another advantage is the ability to include comprehensive sensitivity norms in model intercomparison projects.
Hurdles anticipated during the development of a real-world estimation system (and close analogues encountered and addressed with some success in the ocean state estimation context) include:
1. model errors for an incomplete flow model, leading to insufficient representation of fast ice streams;
2. small-scale processes that are not captured even by higher-order models, but may be significant in abrupt flow behavior (e.g. role of subglacial lakes, moulins and sediment feedback);
3. highly non-linear processes, jumps and their representation in the adjoint;
4. timescales of relevant processes and observational record; and
5. prior uncertainties, error covariances, data sampling, lack of observation time series of the ice-sheet interior and details of the bedrock.
Viewed in a different way, most of these problems arise from implicit or explicit hypotheses (model assumptions, retrieval algorithms, sampling limitations and error propagation). Formalizing, quantifying and testing these hypotheses through a rigorous estimation system should help to improve our understanding of the evolution of ice sheets.
4.2. An approach in support of IPCC
At the time of writing, the Intergovernmental Panel on Climate Change (IPCC) is preparing model configurations for its fifth assessment report (AR5) due in 2013. IPCC AR4 has identified the Greenland and Antarctic ice sheets as major sources of uncertainties in terms of projecting global sea-level changes (Reference Lemke and SolomonLemke and others, 2007). As a consequence, several climate-modeling groups are now coupling ice-sheet models to existing climate models (Reference LittleLittle and others, 2007; Reference Lipscomb, Bindschadler, Bueler, Holland, Johnson and PriceLipscomb and others, 2009). In order to be available for analysis by 2010, calculations need to begin by mid-2009, which limits development to successful coupling of existing ice-sheet models. It is likely that the complexity of ice-sheet models employed for AR5 is very similar to that investigated here. This prompts us to sketch a complementary route to assess the effect of the ice sheets on sea level using the adjoint technique. A road map might take the following form.
1. Derive the adjoint of a suitable ice-sheet model.
2. Identify relevant control variables whose changes are expected to have a significant impact on ice-sheet mass over the integration period (100+ years). These include surface boundary conditions such as atmospheric forcings, possibly lateral boundary conditions around Antarctica such as ocean temperatures and model parameters such as basal sliding and basal melt rate. Effects not represented by the model, such as basal lubrication from surface melting, loss of buttressing through calving or grounding line retreat, may remain inaccessible for study (in the same way as for coupled climate simulations).
3. An initial assessment of which controls have the strongest impact on ice-sheet mass loss may help to sharpen the focus on adjoint calculations.
4. Adjoint calculations should be performed for various IPCC forcing scenarios, and sensitivity maps similar to those presented here should be provided.
5. Sea-level changes can then be inferred from adjoint sensitivity maps by applying expected perturbations to the control variables for different scenarios along the lines of the perturbation calculation Equation (15), which yield ice-sheet mass changes in global sea-level equivalent.
One advantage of this approach is that calculations are much cheaper, and calculating large ensembles may enable quantification of uncertainties.
Another approach could be to use the derived sensitivity maps as Green’s or response functions for coupled models. Under the assumption of linearity (probably useful for the timescale investigated and the model approximations employed), the ice-sheet model may then be replaced by a suitable set of such response functions. Although this method does not allow for two-way coupling, the results may provide useful order-of-magnitude estimates.
Given the current inability of ice-sheet models to capture fast processes and their limited predictive power, assessment of useful bounds of uncertainty of their impact on sea-level change will likely remain the focus for the foreseeable future. Methods which can provide quantitative descriptions of the response of ice sheets under climate-change scenarios, and which are also efficient in exploring large parameter spaces, seem well suited for the task.
Acknowledgements
Work on the SICOPOLIS adjoint was initiated during a stay by V.B. and P.H. at Bjerknes Centre for Climate Research. We are very grateful to our host, K.H. Nisancioglu. Further motivation to pursue the idea came from an invitation by J. Zwally to NASA’s Goddard Space Flight Center, as well as encouragement by C. Wunsch and J. Marshall at the Massachusetts Institute of Technology. The original SICOPOLIS code was kindly provided by R. Greve. The adjoint was generated using the AD tool TAF by FastOpt. Comments by G.K.C. Clarke, D. MacAyeal, M. Truffer and G. Forget were very helpful. P.H. is partly supported through the US National Ocean Partnership Program’s ‘Estimating the Circulation and Climate of the Ocean: Global Ocean Data Assimilation Experiment’ (ECCO-GODAE) project with funding from NASA and through the US National Science Foundation’s Collaboration in Mathematical Geosciences (CMG) ‘Uncertainty Quantification inGeophysical State Estimation’.



