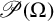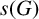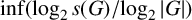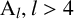1 Introduction
Let G be a permutation group acting on a finite set
![]() $\Omega $
of size n. Then G induces a natural action on the power set
$\Omega $
of size n. Then G induces a natural action on the power set
![]() $\mathscr{P}(\Omega )$
. The orbits of this action are called set orbits and we let
$\mathscr{P}(\Omega )$
. The orbits of this action are called set orbits and we let
![]() $s(G)$
denote the total number of set orbits in this action. This number was studied by Babai and Pyber in [Reference Babai and Pyber1]; in particular, they proved that if G is a permutation group of degree n with no composition factor isomorphic to
$s(G)$
denote the total number of set orbits in this action. This number was studied by Babai and Pyber in [Reference Babai and Pyber1]; in particular, they proved that if G is a permutation group of degree n with no composition factor isomorphic to
![]() ${ {\textrm {A}}}_k$
for
${ {\textrm {A}}}_k$
for
![]() $k>t$
(where
$k>t$
(where
![]() $t\geq 4$
) then
$t\geq 4$
) then
![]() $s(G)\geq 2^{c_1n/t}$
for some absolute constant
$s(G)\geq 2^{c_1n/t}$
for some absolute constant
![]() $c_1>0$
. Clearly
$c_1>0$
. Clearly
![]() $c_1$
depends on t, but no value or bound for
$c_1$
depends on t, but no value or bound for
![]() $c_1$
was given. As a corollary, they obtained
$c_1$
was given. As a corollary, they obtained
![]() $s(G)\geq |G|^{c_2/(t \log _2 t)}$
for a constant
$s(G)\geq |G|^{c_2/(t \log _2 t)}$
for a constant
![]() $c_2$
which depends only on t but was also unspecified. This latter bound plays a crucial role in finding lower bounds for the number of conjugacy classes of finite groups. The best such bounds are currently obtained via Pyber’s approach [Reference Maróti6], which relies on the bound on set orbits. It is therefore desirable to have an idea of the size of
$c_2$
which depends only on t but was also unspecified. This latter bound plays a crucial role in finding lower bounds for the number of conjugacy classes of finite groups. The best such bounds are currently obtained via Pyber’s approach [Reference Maróti6], which relies on the bound on set orbits. It is therefore desirable to have an idea of the size of
![]() $c_2$
, or even its exact value. It turns out that with today’s computational power, it is possible to determine
$c_2$
, or even its exact value. It turns out that with today’s computational power, it is possible to determine
![]() $c_2$
in some situations. We focus on the important case when
$c_2$
in some situations. We focus on the important case when
![]() $t=4$
, that is, avoiding any simple alternating composition factor. For
$t=4$
, that is, avoiding any simple alternating composition factor. For
![]() $t=4$
we can restate the above bound by saying that there is an absolute positive constant
$t=4$
we can restate the above bound by saying that there is an absolute positive constant
![]() $c_3$
such that for any permutation group G with no simple alternating composition factor we have
$c_3$
such that for any permutation group G with no simple alternating composition factor we have
![]() $s(G)\geq |G|^{c_3}$
and the best possible value for
$s(G)\geq |G|^{c_3}$
and the best possible value for
![]() $c_3$
is
$c_3$
is
![]() $\inf ({\log _2 s(G)}/{\log _2 |G|})$
. We determine this value and also the corresponding permutation groups that attain it. Our main result is the following theorem.
$\inf ({\log _2 s(G)}/{\log _2 |G|})$
. We determine this value and also the corresponding permutation groups that attain it. Our main result is the following theorem.
Theorem 1.1. We have
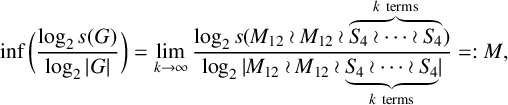 $$ \begin{align*}\inf\bigg( \frac{\log_2 s(G)}{\log_2 |G|} \bigg) = \lim_{k\to \infty} \frac{\log_2 s(M_{12}\wr M_{12} \wr \overset{k \ \mbox{terms}}{\overbrace{S_4\wr \cdots \wr S_4}})}{\log_2 |M_{12}\wr M_{12} \wr \underset{k \ \mbox{terms}}{\underbrace{S_4\wr \cdots \wr S_4}}|}=:M,\end{align*} $$
$$ \begin{align*}\inf\bigg( \frac{\log_2 s(G)}{\log_2 |G|} \bigg) = \lim_{k\to \infty} \frac{\log_2 s(M_{12}\wr M_{12} \wr \overset{k \ \mbox{terms}}{\overbrace{S_4\wr \cdots \wr S_4}})}{\log_2 |M_{12}\wr M_{12} \wr \underset{k \ \mbox{terms}}{\underbrace{S_4\wr \cdots \wr S_4}}|}=:M,\end{align*} $$
where the infimum is taken over all permutation groups G not containing any
![]() ${ {\textrm {A}}}_l, l> 4$
, as a composition factor. (Here
${ {\textrm {A}}}_l, l> 4$
, as a composition factor. (Here
![]() $M_{12}$
acts naturally on
$M_{12}$
acts naturally on
![]() $12$
elements.)
$12$
elements.)
We will give a good estimate for the value M in Theorem 2.11.
While we believe that the result is nice, its proof, admittedly, is not. By its nature the proof requires some subtle, but tedious, estimates and lots of calculations, The clean end result justifies the effort.
For solvable groups,
![]() $\inf ({\log _2 s(G)}/{\log _2 |G|})$
has already been determined in [Reference Gao and Yang3] to be
$\inf ({\log _2 s(G)}/{\log _2 |G|})$
has already been determined in [Reference Gao and Yang3] to be
![]() $\approx 0.18939$
, which is obtained by the group
$\approx 0.18939$
, which is obtained by the group
![]() $G = S_4 \wr \cdots \wr S_4$
. The value of
$G = S_4 \wr \cdots \wr S_4$
. The value of
![]() $c_1$
has also been studied. In [Reference Yang9], the ratio
$c_1$
has also been studied. In [Reference Yang9], the ratio
![]() ${\log _2 s(G)}/{n}$
was considered for solvable G; here
${\log _2 s(G)}/{n}$
was considered for solvable G; here
![]() $G = A\Gamma (2^3) \wr S_4 \wr \cdots \wr S_4$
gave the minimum. In [Reference Yang10], the same ratio for arbitrary G with no simple alternating composition factors was determined and the group that yields the minimum is
$G = A\Gamma (2^3) \wr S_4 \wr \cdots \wr S_4$
gave the minimum. In [Reference Yang10], the same ratio for arbitrary G with no simple alternating composition factors was determined and the group that yields the minimum is
![]() $G = M_{24} \wr M_{12} \wr S_4 \wr \cdots \wr S_4$
. Some more general situations have recently been studied in [Reference Yan and Yang8].
$G = M_{24} \wr M_{12} \wr S_4 \wr \cdots \wr S_4$
. Some more general situations have recently been studied in [Reference Yan and Yang8].
The main difficulty of this and the previous papers is to determine a sequence of groups that achieves the infimum. The experience gained in the previous work allows us to narrow this down to a few candidates with some thorough calculations. The other major challenge of this paper is that much tighter estimates than before are needed to eliminate candidate groups that give sequences very close to the one we ultimately prove to yield the infimum.
2 Main results
We use
![]() $H\wr S$
to denote the wreath product of H with S where H is a group and S is a permutation group.
$H\wr S$
to denote the wreath product of H with S where H is a group and S is a permutation group.
Let G be a permutation group and
![]() $s(G)$
denote the number of set orbits of G. Following the notation in [Reference Gao and Yang3], we let
$s(G)$
denote the number of set orbits of G. Following the notation in [Reference Gao and Yang3], we let
![]() $\textit {ds}(G) = {\log _2 s(G)}/{\log _2 |G|}$
.
$\textit {ds}(G) = {\log _2 s(G)}/{\log _2 |G|}$
.
We provide some preliminary facts about transitive groups. Let G be a transitive permutation group on a set
![]() $\Omega $
where
$\Omega $
where
![]() $|\Omega | = n$
. A system of imprimitivity is a partition of
$|\Omega | = n$
. A system of imprimitivity is a partition of
![]() $\Omega $
which is invariant under the action of G. A transitive group is primitive if the only systems of imprimitivity are
$\Omega $
which is invariant under the action of G. A transitive group is primitive if the only systems of imprimitivity are
![]() $1$
-sets and
$1$
-sets and
![]() $\Omega $
itself. Let
$\Omega $
itself. Let
![]() $(\Omega _1, \ldots , \Omega _m)$
denote a system of imprimitivity with maximal block-size b (where
$(\Omega _1, \ldots , \Omega _m)$
denote a system of imprimitivity with maximal block-size b (where
![]() $1\leq b < n, bm = n$
and
$1\leq b < n, bm = n$
and
![]() $b=1$
if and only if G is primitive). Let N be the intersection of the stabilisers of the blocks. Then
$b=1$
if and only if G is primitive). Let N be the intersection of the stabilisers of the blocks. Then
![]() $G/N$
is a primitive group acting on the set of blocks
$G/N$
is a primitive group acting on the set of blocks
![]() $\Omega _i$
.
$\Omega _i$
.
Let G be a transitive permutation group of degree n that is not primitive. If we have a system of imprimitivity with
![]() $m \geq 2$
blocks of size b with b maximal, then
$m \geq 2$
blocks of size b with b maximal, then
![]() $G\lesssim K\wr P_1$
where K is a permutation group of degree
$G\lesssim K\wr P_1$
where K is a permutation group of degree
![]() $n/m$
and
$n/m$
and
![]() $P_1$
is the primitive group acting on the m blocks. We may keep doing this and, after reindexing for convenience, we have
$P_1$
is the primitive group acting on the m blocks. We may keep doing this and, after reindexing for convenience, we have
![]() $G\lesssim H\wr P_1 \wr \cdots \wr P_j$
where each
$G\lesssim H\wr P_1 \wr \cdots \wr P_j$
where each
![]() $P_i$
is primitive and H is a permutation group. In this case, we say that G is induced from H.
$P_i$
is primitive and H is a permutation group. In this case, we say that G is induced from H.
The following two results are from [Reference Babai and Pyber1].
Lemma 2.1. If
![]() $L\leq G\leq \mbox {Sym}(\Omega )$
, then
$L\leq G\leq \mbox {Sym}(\Omega )$
, then
![]() $s(G)\leq s(L)\leq s(G)\cdot |G:L|$
.
$s(G)\leq s(L)\leq s(G)\cdot |G:L|$
.
Lemma 2.2. Assume that G is intransitive on
![]() $\Omega $
and has orbits
$\Omega $
and has orbits
![]() $\Omega _1, \ldots , \Omega _m$
. Let
$\Omega _1, \ldots , \Omega _m$
. Let
![]() $G_i$
be the restriction of G to
$G_i$
be the restriction of G to
![]() $\Omega _i$
. Then
$\Omega _i$
. Then
![]() $s(G) \geq s(G_1)\times \cdots \times s(G_m).$
$s(G) \geq s(G_1)\times \cdots \times s(G_m).$
Suppose the action of G on
![]() $\Omega $
is not transitive. Since the number of set orbits will increase with the number of orbits on
$\Omega $
is not transitive. Since the number of set orbits will increase with the number of orbits on
![]() $\Omega $
, we may assume that G has two orbits
$\Omega $
, we may assume that G has two orbits
![]() $\Omega _1$
and
$\Omega _1$
and
![]() $\Omega _2$
. Let
$\Omega _2$
. Let
![]() $G_i$
denote the restriction of G to
$G_i$
denote the restriction of G to
![]() $\Omega _i$
. Then
$\Omega _i$
. Then
![]() $G\leq G_1\times G_2$
and
$G\leq G_1\times G_2$
and
![]() $|G| \leq |G_1|\cdot |G_2|$
. By Lemma 2.2,
$|G| \leq |G_1|\cdot |G_2|$
. By Lemma 2.2,
![]() $s(G) \geq s(G_1)\cdot s(G_2)$
. Then
$s(G) \geq s(G_1)\cdot s(G_2)$
. Then
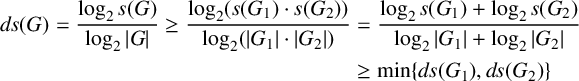 $$ \begin{align*} \textit{ds}(G) =\frac{\log_2 s(G)}{\log_2 |G|} \geq \frac{\log_2 (s(G_1)\cdot s(G_2))}{\log_2 (|G_1|\cdot |G_2|)} & = \frac{\log_2 s(G_1) + \log_2 s(G_2)}{\log_2 |G_1| +\log_2 |G_2|} \\ & \geq \min\{\textit{ds}(G_1), \textit{ds}(G_2) \} \end{align*} $$
$$ \begin{align*} \textit{ds}(G) =\frac{\log_2 s(G)}{\log_2 |G|} \geq \frac{\log_2 (s(G_1)\cdot s(G_2))}{\log_2 (|G_1|\cdot |G_2|)} & = \frac{\log_2 s(G_1) + \log_2 s(G_2)}{\log_2 |G_1| +\log_2 |G_2|} \\ & \geq \min\{\textit{ds}(G_1), \textit{ds}(G_2) \} \end{align*} $$
(since
![]() ${(a+b)}/{(c+d)} \geq \min \{{a}/{c}, {b}/{d}\}$
for positive numbers
${(a+b)}/{(c+d)} \geq \min \{{a}/{c}, {b}/{d}\}$
for positive numbers
![]() $a, b, c$
and d). Thus, in order to prove Theorem 1.1, we need only consider transitive groups.
$a, b, c$
and d). Thus, in order to prove Theorem 1.1, we need only consider transitive groups.
Lemma 2.3. Let
![]() $G = H \wr P$
be a permutation group of degree
$G = H \wr P$
be a permutation group of degree
![]() $nm$
where H is a permutation group of degree n and P has degree m. Then
$nm$
where H is a permutation group of degree n and P has degree m. Then
![]() $\textit {ds}(H) \geq \textit {ds}(G)$
.
$\textit {ds}(H) \geq \textit {ds}(G)$
.
Proof. Let
![]() $F = H\times H\times \cdots \times H$
with m terms. Note that
$F = H\times H\times \cdots \times H$
with m terms. Note that
![]() $F \unlhd G$
and
$F \unlhd G$
and
![]() $s(F) = s(H)^m$
by Lemma 2.2. Also
$s(F) = s(H)^m$
by Lemma 2.2. Also
![]() $s(F) \geq s(G)$
by Lemma 2.1 and
$s(F) \geq s(G)$
by Lemma 2.1 and
![]() $|H|^m = |F| \leq |G|$
. Then
$|H|^m = |F| \leq |G|$
. Then
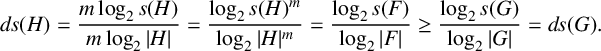 $$ \begin{align*} \textit{ds}(H) = \frac{m\log_2 s(H)}{m\log_2 |H|} = \frac{\log_2 s(H)^m}{\log_2 |H|^m} = \frac{\log_2 s(F)}{\log_2 |F|} \geq \frac{\log_2 s(G)}{\log_2 |G|} = \textit{ds}(G).\\[-42pt] \end{align*} $$
$$ \begin{align*} \textit{ds}(H) = \frac{m\log_2 s(H)}{m\log_2 |H|} = \frac{\log_2 s(H)^m}{\log_2 |H|^m} = \frac{\log_2 s(F)}{\log_2 |F|} \geq \frac{\log_2 s(G)}{\log_2 |G|} = \textit{ds}(G).\\[-42pt] \end{align*} $$
We also make use of Tables 1 and 2 in [Reference Yang10]. Table 1 provides lower bounds for the number of set orbits of a primitive group and Table 2 provides upper bounds on the orders of primitive groups not containing
![]() ${ {\textrm {A}}}_l, l>4$
, as a composition factor.
${ {\textrm {A}}}_l, l>4$
, as a composition factor.
We introduce several sequences to assist with our proof. Define
![]() $\{a_k\}_{k \geq -1}$
by
$\{a_k\}_{k \geq -1}$
by
![]() $a_{-1} = s(M_{12}) = 14$
and
$a_{-1} = s(M_{12}) = 14$
and
![]() $a_{0} = s(M_{12} \wr M_{12}) = 604576714$
. Let
$a_{0} = s(M_{12} \wr M_{12}) = 604576714$
. Let
![]() $a_k = {a_{k - 1} + 3 \choose 4}$
for
$a_k = {a_{k - 1} + 3 \choose 4}$
for
![]() $k\geq 1$
. The value of
$k\geq 1$
. The value of
![]() $a_{-1}$
may be easily verified in GAP [Reference Pyber7], and we explain
$a_{-1}$
may be easily verified in GAP [Reference Pyber7], and we explain
![]() $a_{0}$
shortly. Define the sequence
$a_{0}$
shortly. Define the sequence
![]() $\{b_k\}_{k \geq 0}$
by
$\{b_k\}_{k \geq 0}$
by
![]() $b_0 = 0$
and
$b_0 = 0$
and
![]() $b_{k+1} = 4\cdot b_k + 1$
. The explicit formula is
$b_{k+1} = 4\cdot b_k + 1$
. The explicit formula is
![]() $b_k = {(4^k - 1)}/{3}$
, which may be easily checked by induction. Lastly, define
$b_k = {(4^k - 1)}/{3}$
, which may be easily checked by induction. Lastly, define
 $$\begin{align*}c_k = \frac{\log_2(a_k)}{\log_2(95040^{13\cdot 4^k} \cdot 24^{b_k})}=\frac{\log_2(a_k)}{13\cdot 4^k \cdot \log_2 95040 + b_k\cdot \log_2 24}.\end{align*}$$
$$\begin{align*}c_k = \frac{\log_2(a_k)}{\log_2(95040^{13\cdot 4^k} \cdot 24^{b_k})}=\frac{\log_2(a_k)}{13\cdot 4^k \cdot \log_2 95040 + b_k\cdot \log_2 24}.\end{align*}$$
The following calculation shows that
![]() $c_k$
is decreasing:
$c_k$
is decreasing:
 $$ \begin{align*} c_{k+1} &= \frac{\log_2(a_{k + 1})}{\log_2(95040^{13\cdot 4^{k + 1}} \cdot 24^{b_{k + 1}})} = \frac{\log_2{a_k+3 \choose 4}}{4^{k+1}\log_295040^{13} + (4b_k + 1) \cdot \log_2 24} \\ &\leq \frac{4 \log_2 a_k}{4^{k+1}\cdot \log_2 95040^{13} + 4\cdot b_k \cdot \log_2 24 + \log_2 24} \\ &< \frac{\log_2 a_k}{4^k \cdot \log_2 95040^{13} + b_k\cdot \log_2 24} = c_k. \end{align*} $$
$$ \begin{align*} c_{k+1} &= \frac{\log_2(a_{k + 1})}{\log_2(95040^{13\cdot 4^{k + 1}} \cdot 24^{b_{k + 1}})} = \frac{\log_2{a_k+3 \choose 4}}{4^{k+1}\log_295040^{13} + (4b_k + 1) \cdot \log_2 24} \\ &\leq \frac{4 \log_2 a_k}{4^{k+1}\cdot \log_2 95040^{13} + 4\cdot b_k \cdot \log_2 24 + \log_2 24} \\ &< \frac{\log_2 a_k}{4^k \cdot \log_2 95040^{13} + b_k\cdot \log_2 24} = c_k. \end{align*} $$
We may obtain using Maple that
![]() $c_1 \approx 0.129675$
,
$c_1 \approx 0.129675$
,
![]() $c_2 \approx 0.128179$
,
$c_2 \approx 0.128179$
,
![]() $c_3 \approx 0.127806$
and
$c_3 \approx 0.127806$
and
![]() $c_4\approx 0.127712$
. Also
$c_4\approx 0.127712$
. Also
![]() $c_8 < 0.1276818245$
.
$c_8 < 0.1276818245$
.
To calculate
![]() $s(M_{12} \wr M_{12})$
, we consider the structure of the group action of
$s(M_{12} \wr M_{12})$
, we consider the structure of the group action of
![]() $M_{12}$
and provide a method for calculating
$M_{12}$
and provide a method for calculating
![]() $s(G \wr M_{12})$
in general. A partition of a positive integer n expresses n as the sum of a sequence of strictly positive integers. Let
$s(G \wr M_{12})$
in general. A partition of a positive integer n expresses n as the sum of a sequence of strictly positive integers. Let
![]() $\Pi $
denote the set of all partitions of
$\Pi $
denote the set of all partitions of
![]() $12$
and suppose that
$12$
and suppose that
![]() $\pi \in \Pi $
is a partition of
$\pi \in \Pi $
is a partition of
![]() $12$
. Let
$12$
. Let
![]() $B(\pi )$
denote the number of terms in the partition, say
$B(\pi )$
denote the number of terms in the partition, say
![]() $B(\pi ) = n_1 + n_2+ \cdots + n_j$
, where
$B(\pi ) = n_1 + n_2+ \cdots + n_j$
, where
![]() $n_1$
is the number of occurrences of the largest term in the partition,
$n_1$
is the number of occurrences of the largest term in the partition,
![]() $n_2$
is the number of occurrences of the second largest term and so on. Define
$n_2$
is the number of occurrences of the second largest term and so on. Define
![]() $F(\pi ) = n_1! n_2! \cdots n_j!$
. For example, if
$F(\pi ) = n_1! n_2! \cdots n_j!$
. For example, if
![]() $\pi = (4, 2, 2, 1, 1, 1, 1)$
, then
$\pi = (4, 2, 2, 1, 1, 1, 1)$
, then
![]() $n_1 = 1$
,
$n_1 = 1$
,
![]() $n_2 = 2$
and
$n_2 = 2$
and
![]() $n_3 = 4$
, which gives
$n_3 = 4$
, which gives
![]() $B(\pi ) = 7$
and
$B(\pi ) = 7$
and
![]() $F(\pi ) = 1!2!4!$
. Let
$F(\pi ) = 1!2!4!$
. Let
![]() $P(n,k)$
denote the number of ways to permute k objects out of n, so
$P(n,k)$
denote the number of ways to permute k objects out of n, so
![]() ${P(s(G), B(\pi ))}/{F(\pi )}$
gives the number of ways of choosing
${P(s(G), B(\pi ))}/{F(\pi )}$
gives the number of ways of choosing
![]() $B(\pi )$
orbits from the set orbits of G with repetitions described by
$B(\pi )$
orbits from the set orbits of G with repetitions described by
![]() $n_1, n_2, \dots , n_k$
. Finally, we define
$n_1, n_2, \dots , n_k$
. Finally, we define
![]() $N(\pi )$
to be the number of orbits of
$N(\pi )$
to be the number of orbits of
![]() $M_{12}$
on all the multiset permutations (permutations with repetitions) of a set of
$M_{12}$
on all the multiset permutations (permutations with repetitions) of a set of
![]() $12$
elements with the partition
$12$
elements with the partition
![]() $\pi $
as multiset structure. Table 3 in [Reference Yang10] provides a summary of this information. Thus we can calculate
$\pi $
as multiset structure. Table 3 in [Reference Yang10] provides a summary of this information. Thus we can calculate
![]() $s(G \wr M_{12})$
using
$s(G \wr M_{12})$
using
 $$ \begin{align*}s(G \wr M_{12}) = \sum_{\pi \in \Pi}N(\pi) \cdot \frac{P(s(G), B(\pi))}{F(\pi)}\end{align*} $$
$$ \begin{align*}s(G \wr M_{12}) = \sum_{\pi \in \Pi}N(\pi) \cdot \frac{P(s(G), B(\pi))}{F(\pi)}\end{align*} $$
and Table 3 in [Reference Yang10] and verify that
![]() $a_0 = 604576714$
. The GAP code for these calculations is available at https://www.math.txstate.edu/research-conferences/summerreu/ yang_documents.html.
$a_0 = 604576714$
. The GAP code for these calculations is available at https://www.math.txstate.edu/research-conferences/summerreu/ yang_documents.html.
Lemma 2.4 [Reference Yang10, Lemma 2.3]
Let G be a transitive permutation group acting on a set
![]() $\Omega $
, where
$\Omega $
, where
![]() $|\Omega | = n$
. Let
$|\Omega | = n$
. Let
![]() $(\Omega _1, \ldots , \Omega _m)$
denote a system of imprimitivity of maximal block-size b. Let N denote the normal subgroup of G stabilising each of the blocks
$(\Omega _1, \ldots , \Omega _m)$
denote a system of imprimitivity of maximal block-size b. Let N denote the normal subgroup of G stabilising each of the blocks
![]() $\Omega _i$
. Let
$\Omega _i$
. Let
![]() $G_i = {\operatorname {Stab}}_G(\Omega _i)$
and
$G_i = {\operatorname {Stab}}_G(\Omega _i)$
and
![]() $s = s(G_1)$
. Then
$s = s(G_1)$
. Then
-
(1)
 $s(G) \geq s^m / |G/N|$
,
$s(G) \geq s^m / |G/N|$
, -
(2)
 $s(G) \geq {s + m -1 \choose s - 1}$
and equality holds if
$s(G) \geq {s + m -1 \choose s - 1}$
and equality holds if
 $G/N \cong S_m$
.
$G/N \cong S_m$
.
Lemma 2.5. Let G be a permutation group that does not contain any alternating group
![]() ${ {\textrm {A}}}_l$
with
${ {\textrm {A}}}_l$
with
![]() $l> 4$
as a composition factor and suppose G is induced from H. If
$l> 4$
as a composition factor and suppose G is induced from H. If
 $$ \begin{align} \frac{\log_2(s(H))}{\log_2|H|} -\frac{\log_2(24^{\alpha})}{\log_2|H|} \geq \beta, \end{align} $$
$$ \begin{align} \frac{\log_2(s(H))}{\log_2|H|} -\frac{\log_2(24^{\alpha})}{\log_2|H|} \geq \beta, \end{align} $$
where
![]() $\alpha = {23}/{60}$
and
$\alpha = {23}/{60}$
and
![]() $0\leq \beta \leq {3}/{20}$
, then
$0\leq \beta \leq {3}/{20}$
, then
![]() ${\log _2(s(G))}/{\log _2|G|}\geq \beta $
.
${\log _2(s(G))}/{\log _2|G|}\geq \beta $
.
Proof. We may assume
![]() $G\lesssim H \wr P_1 \wr \cdots \wr P_j$
where each
$G\lesssim H \wr P_1 \wr \cdots \wr P_j$
where each
![]() $P_i$
is primitive and deg
$P_i$
is primitive and deg
![]() $(P_i) = m_i$
. By (2.1),
$(P_i) = m_i$
. By (2.1),
![]() $s(H) \geq 24^{\alpha } \cdot |H|^{\beta }$
. Also
$s(H) \geq 24^{\alpha } \cdot |H|^{\beta }$
. Also
![]() $|P_1| \leq (24^{1/3})^{m_1 - 1}$
by [Reference Keller5, Corollary 1.5]. By Lemma 2.4,
$|P_1| \leq (24^{1/3})^{m_1 - 1}$
by [Reference Keller5, Corollary 1.5]. By Lemma 2.4,
 $$ \begin{align*} s(H\wr P_1) \geq s(H)^{m_1} / |P_1| &\geq \frac{24^{\alpha m_1} \cdot |H|^{\beta m_1}}{24^{(m_1-1)/3}} = 24^{\alpha} \cdot |H|^{\beta \cdot m_1} \cdot (24^{{({1}/{3})} (m_1-1)})^{{3}/{20}} \\ &\geq 24^{\alpha} \cdot |H|^{\beta \cdot m_1} \cdot (24^{{({1}/{3})} (m_1-1)})^{\beta} \geq 24^{\alpha} \cdot |H|^{\beta \cdot m_1} \cdot |P_1|^{\beta}. \end{align*} $$
$$ \begin{align*} s(H\wr P_1) \geq s(H)^{m_1} / |P_1| &\geq \frac{24^{\alpha m_1} \cdot |H|^{\beta m_1}}{24^{(m_1-1)/3}} = 24^{\alpha} \cdot |H|^{\beta \cdot m_1} \cdot (24^{{({1}/{3})} (m_1-1)})^{{3}/{20}} \\ &\geq 24^{\alpha} \cdot |H|^{\beta \cdot m_1} \cdot (24^{{({1}/{3})} (m_1-1)})^{\beta} \geq 24^{\alpha} \cdot |H|^{\beta \cdot m_1} \cdot |P_1|^{\beta}. \end{align*} $$
Thus
 $$ \begin{align*}\frac{\log_2 s(H\wr P_1)}{\log_2 |H\wr P_1|} - \frac{\log_2 24^{\alpha}}{\log_2 |H\wr P_1|} \geq \beta.\end{align*} $$
$$ \begin{align*}\frac{\log_2 s(H\wr P_1)}{\log_2 |H\wr P_1|} - \frac{\log_2 24^{\alpha}}{\log_2 |H\wr P_1|} \geq \beta.\end{align*} $$
By induction,
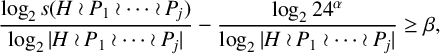 $$ \begin{align*}\frac{\log_2 s(H\wr P_1\wr \cdots \wr P_j)}{\log_2 |H\wr P_1\wr \cdots \wr P_j|} - \frac{\log_2 24^{\alpha}}{\log_2 |H\wr P_1\wr \cdots \wr P_j|} \geq \beta,\end{align*} $$
$$ \begin{align*}\frac{\log_2 s(H\wr P_1\wr \cdots \wr P_j)}{\log_2 |H\wr P_1\wr \cdots \wr P_j|} - \frac{\log_2 24^{\alpha}}{\log_2 |H\wr P_1\wr \cdots \wr P_j|} \geq \beta,\end{align*} $$
from which
![]() $\textit {ds}(G) \geq {\log _2 s(H\wr P_1\wr \cdots \wr P_j)}/{\log _2 |H\wr P_1\wr \cdots \wr P_j|}$
by Lemma 2.1.
$\textit {ds}(G) \geq {\log _2 s(H\wr P_1\wr \cdots \wr P_j)}/{\log _2 |H\wr P_1\wr \cdots \wr P_j|}$
by Lemma 2.1.
Lemma 2.6 [Reference Keller5]
If H be a primitive group of degree n where H does not contain
![]() ${ {\textrm {A}}}_n$
, then:
${ {\textrm {A}}}_n$
, then:
-
(1)
 $|H| < 50 \cdot n^{\sqrt {n}}$
;
$|H| < 50 \cdot n^{\sqrt {n}}$
; -
(2)
 $|H| < 3^n$
and
$|H| < 3^n$
and
 $|H| < 2^n$
if
$|H| < 2^n$
if
 $n> 24$
;
$n> 24$
; -
(3)
 $|H| < 2^{0.76n}$
when
$|H| < 2^{0.76n}$
when
 $n \geq 25$
and
$n \geq 25$
and
 $n \neq 32$
.
$n \neq 32$
.
Proposition 2.7. Let G be a primitive permutation group of degree n, not containing
![]() ${ {\textrm {A}}}_l$
with
${ {\textrm {A}}}_l$
with
![]() $l> 4$
as a composition factor. Then
$l> 4$
as a composition factor. Then
![]() $\textit {ds}(G)> c_8$
.
$\textit {ds}(G)> c_8$
.
Proof. Let G be a primitive permutation group of degree n not containing
![]() ${ {\textrm {A}}}_l,\ \mathrm{for} l> 4$
, as a composition factor. If
${ {\textrm {A}}}_l,\ \mathrm{for} l> 4$
, as a composition factor. If
![]() $n \geq 25$
and
$n \geq 25$
and
![]() $n\neq 32$
, then
$n\neq 32$
, then
![]() $|G| \leq 2^{0.76n}$
by Lemma 2.6, so
$|G| \leq 2^{0.76n}$
by Lemma 2.6, so
![]() $s(G)\geq {2^n}/{|G|} \geq 2^{0.24n}$
and
$s(G)\geq {2^n}/{|G|} \geq 2^{0.24n}$
and
 $$ \begin{align*}\textit{ds}(G) = \frac{\log_2 s(G)}{\log_2 |G|} \geq \frac{\log_2 2^{0.24n}}{\log_2 2^{0.76n}} = \frac{24}{76}> 0.3157 > c_8.\end{align*} $$
$$ \begin{align*}\textit{ds}(G) = \frac{\log_2 s(G)}{\log_2 |G|} \geq \frac{\log_2 2^{0.24n}}{\log_2 2^{0.76n}} = \frac{24}{76}> 0.3157 > c_8.\end{align*} $$
If
![]() $n=32$
, then
$n=32$
, then
![]() $s(G) \geq 361$
by Table 2 of [Reference Yang10]. Also
$s(G) \geq 361$
by Table 2 of [Reference Yang10]. Also
![]() $|G|< 2^{32}$
by Lemma 2.6. So
$|G|< 2^{32}$
by Lemma 2.6. So
 $$ \begin{align*}\textit{ds}(G) = \frac{\log_2 s(G)}{\log_2 |G|}> \frac{\log_2 361}{32\cdot \log_2 2} > 0.2654 > c_8.\end{align*} $$
$$ \begin{align*}\textit{ds}(G) = \frac{\log_2 s(G)}{\log_2 |G|}> \frac{\log_2 361}{32\cdot \log_2 2} > 0.2654 > c_8.\end{align*} $$
If
![]() $n < 25$
, we note that
$n < 25$
, we note that
![]() $s(G) \geq n + 1$
and
$s(G) \geq n + 1$
and
![]() $|G| < 3^n$
by Lemma 2.6. For
$|G| < 3^n$
by Lemma 2.6. For
![]() $2\leq n \leq 20$
, direct calculation shows that
$2\leq n \leq 20$
, direct calculation shows that
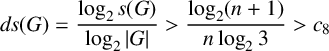 $$ \begin{align*} \textit{ds}(G) = \frac{\log_2 s(G)}{\log_2 |G|}> \frac{\log_2 (n+1)}{n\log_2 3} > c_8 \end{align*} $$
$$ \begin{align*} \textit{ds}(G) = \frac{\log_2 s(G)}{\log_2 |G|}> \frac{\log_2 (n+1)}{n\log_2 3} > c_8 \end{align*} $$
for each n. For
![]() $n = 21, 22, 23$
and
$n = 21, 22, 23$
and
![]() $24$
, we use the upper bounds for
$24$
, we use the upper bounds for
![]() $|G|$
in Table 2 of [Reference Yang10]. In all cases,
$|G|$
in Table 2 of [Reference Yang10]. In all cases,
![]() $\textit {ds}(G)> 1.66 > c_8$
.
$\textit {ds}(G)> 1.66 > c_8$
.
Theorem 2.8. Let G be a transitive permutation group not containing any composition factors
![]() ${ {\textrm {A}}}_l, l> 4$
. Let G be induced from H where H is a primitive permutation group of degree n. If H is different from
${ {\textrm {A}}}_l, l> 4$
. Let G be induced from H where H is a primitive permutation group of degree n. If H is different from
![]() $M_{12}$
, then
$M_{12}$
, then
![]() $\textit {ds}(G)> c_8$
.
$\textit {ds}(G)> c_8$
.
Proof. By Lemma 2.5, it suffices to show that
 $$ \begin{align*}\frac{\log_2 s(H)}{\log_2 |H|}-\frac{\frac{23}{60} \log_2 (24)}{\log_2 |H|}> c_8\end{align*} $$
$$ \begin{align*}\frac{\log_2 s(H)}{\log_2 |H|}-\frac{\frac{23}{60} \log_2 (24)}{\log_2 |H|}> c_8\end{align*} $$
for all n. Suppose
![]() $n\geq 25$
and
$n\geq 25$
and
![]() $n\neq 32$
. Then
$n\neq 32$
. Then
![]() $|H| \leq 2^{0.76n}$
and
$|H| \leq 2^{0.76n}$
and
![]() $s(H) \geq {2^n}/{|H|} \geq 2^{0.24n}$
by Lemma 2.6. Then
$s(H) \geq {2^n}/{|H|} \geq 2^{0.24n}$
by Lemma 2.6. Then
 $$ \begin{align*}\frac{\log_2 s(H) -\frac{23}{60} \log_2 24}{\log_2 |H|} \geq \frac{0.24n - \log_2 (24^{{23}/{60}})}{0.76n} = \frac{24}{76} - \frac{\frac{23}{60} \log_2 24}{ 0.76 \cdot 25}> 0.223 > c_8.\end{align*} $$
$$ \begin{align*}\frac{\log_2 s(H) -\frac{23}{60} \log_2 24}{\log_2 |H|} \geq \frac{0.24n - \log_2 (24^{{23}/{60}})}{0.76n} = \frac{24}{76} - \frac{\frac{23}{60} \log_2 24}{ 0.76 \cdot 25}> 0.223 > c_8.\end{align*} $$
Suppose
![]() $n = 32$
. Then
$n = 32$
. Then
![]() $s(H)\geq 361$
and
$s(H)\geq 361$
and
![]() $|H| \leq 2^{32}$
by Table 2 of [Reference Yang10] and Lemma 2.6 and so
$|H| \leq 2^{32}$
by Table 2 of [Reference Yang10] and Lemma 2.6 and so
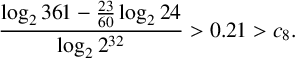 $$ \begin{align*}\frac{\log_2 361 - \frac{23}{60} \log_2 24}{\log_2 2^{32}}> 0.21 > c_8.\end{align*} $$
$$ \begin{align*}\frac{\log_2 361 - \frac{23}{60} \log_2 24}{\log_2 2^{32}}> 0.21 > c_8.\end{align*} $$
For
![]() $21\leq n \leq 24$
and
$21\leq n \leq 24$
and
![]() $n = 14, 15, 16$
and
$n = 14, 15, 16$
and
![]() $17$
we refer to Tables 1 and 2 in [Reference Yang10] to find bounds for
$17$
we refer to Tables 1 and 2 in [Reference Yang10] to find bounds for
![]() $s(H)$
and
$s(H)$
and
![]() $|P_1|$
. Direct calculation shows that the inequality holds.
$|P_1|$
. Direct calculation shows that the inequality holds.
For
![]() $3\leq n \leq 13$
and
$3\leq n \leq 13$
and
![]() $n = 18, 19$
and
$n = 18, 19$
and
![]() $20$
, we note that
$20$
, we note that
![]() $s(H) \geq n + 1$
. We use the upper bounds for
$s(H) \geq n + 1$
. We use the upper bounds for
![]() $|P_1|$
from [Reference Yang10] and direct calculation shows that the inequality holds in all cases excluding
$|P_1|$
from [Reference Yang10] and direct calculation shows that the inequality holds in all cases excluding
![]() $M_{12}$
.
$M_{12}$
.
We need to consider
![]() $n= 2, 3$
and
$n= 2, 3$
and
![]() $4$
differently. We note that by Lemma 2.7, G is not primitive and so we may assume that
$4$
differently. We note that by Lemma 2.7, G is not primitive and so we may assume that
![]() $G\lesssim H\wr P_1 \wr \cdots \wr P_j$
where each
$G\lesssim H\wr P_1 \wr \cdots \wr P_j$
where each
![]() $P_i$
is primitive of degree
$P_i$
is primitive of degree
![]() $m_1$
. Let
$m_1$
. Let
![]() $K = H\wr P_1$
. We show that
$K = H\wr P_1$
. We show that
 $$ \begin{align} \frac{\log_2 s(K) }{\log_2 |K| } -\frac{\frac{23}{60} \log_2 24}{\log_2 |K|}> c_8. \end{align} $$
$$ \begin{align} \frac{\log_2 s(K) }{\log_2 |K| } -\frac{\frac{23}{60} \log_2 24}{\log_2 |K|}> c_8. \end{align} $$
Suppose that
![]() $n = 4$
. Then
$n = 4$
. Then
![]() $s(H) \geq 5$
and
$s(H) \geq 5$
and
![]() $s(K) \geq 5^{m_1} / |P_1|$
by Lemma 2.4. Also
$s(K) \geq 5^{m_1} / |P_1|$
by Lemma 2.4. Also
![]() $|H| \leq 24$
. If
$|H| \leq 24$
. If
![]() $m_1 \geq 25$
and
$m_1 \geq 25$
and
![]() $m_1\neq 32$
, then
$m_1\neq 32$
, then
![]() $|P_1| \leq 2^{0.76 m_1}$
by Lemma 2.6. Then
$|P_1| \leq 2^{0.76 m_1}$
by Lemma 2.6. Then
 $$ \begin{align*}\frac{\log_2 ({5^{m_1}}/{2^{0.76m_1})}}{\log_2 (24^{m_1} \cdot 2^{0.76m_1})}-\frac{\frac{23}{60}\log_2 24}{25\cdot \log_2 24\cdot 2^{0.76}}> 0.279 > c_8.\end{align*} $$
$$ \begin{align*}\frac{\log_2 ({5^{m_1}}/{2^{0.76m_1})}}{\log_2 (24^{m_1} \cdot 2^{0.76m_1})}-\frac{\frac{23}{60}\log_2 24}{25\cdot \log_2 24\cdot 2^{0.76}}> 0.279 > c_8.\end{align*} $$
If
![]() $m_1 = 32$
, then
$m_1 = 32$
, then
![]() $|P_1| \leq 319979520$
by [Reference Yang10]. So
$|P_1| \leq 319979520$
by [Reference Yang10]. So
![]() $s(K) \geq 5^{32}/319979520$
. We verify that (⋆) is satisfied.
$s(K) \geq 5^{32}/319979520$
. We verify that (⋆) is satisfied.
For
![]() $5 \leq m_1 \leq 24$
we use the bounds for
$5 \leq m_1 \leq 24$
we use the bounds for
![]() $|P_1|$
in [Reference Yang10] and the estimate
$|P_1|$
in [Reference Yang10] and the estimate
![]() $s(K) \geq 5^{m_1} / |P_1|$
and direct calculation shows that (⋆) is satisfied in all cases except when
$s(K) \geq 5^{m_1} / |P_1|$
and direct calculation shows that (⋆) is satisfied in all cases except when
![]() $P_1 \cong M_{12}$
. If
$P_1 \cong M_{12}$
. If
![]() $P_1\cong M_{12}$
, we calculate
$P_1\cong M_{12}$
, we calculate
![]() $s(S_4\wr M_{12}) = 5825$
by the method outlined above. Since
$s(S_4\wr M_{12}) = 5825$
by the method outlined above. Since
![]() $|M_{12}| = 95040$
, direct calculation shows that (⋆) is satisfied.
$|M_{12}| = 95040$
, direct calculation shows that (⋆) is satisfied.
For
![]() $2\leq m_1 \leq 4$
, we note that
$2\leq m_1 \leq 4$
, we note that
![]() $s(K) \geq {s(H) - 1 + m_1 \choose s(H) - 1} = {4 + m_1 \choose 4}$
by Lemma 2.6. If
$s(K) \geq {s(H) - 1 + m_1 \choose s(H) - 1} = {4 + m_1 \choose 4}$
by Lemma 2.6. If
![]() $m_1 = 4$
, then
$m_1 = 4$
, then
![]() $|P_1| \leq 24$
and
$|P_1| \leq 24$
and
![]() $s(K) \geq {8\choose 4} = 70$
. It is easy to see that (⋆) is satisfied. Similarly, direct calculation shows that (⋆) is satisfied when
$s(K) \geq {8\choose 4} = 70$
. It is easy to see that (⋆) is satisfied. Similarly, direct calculation shows that (⋆) is satisfied when
![]() $m_1 = 2$
or
$m_1 = 2$
or
![]() $3$
.
$3$
.
If
![]() $n = 3$
, then
$n = 3$
, then
![]() $s(H) \geq 4$
and
$s(H) \geq 4$
and
![]() $s(K) \geq 4^{m_1}/ |P_1|$
by Lemma 2.4. If
$s(K) \geq 4^{m_1}/ |P_1|$
by Lemma 2.4. If
![]() $m_1 \geq 25$
and
$m_1 \geq 25$
and
![]() $m_1 \neq 32$
, then
$m_1 \neq 32$
, then
![]() $|P_1| \leq 2^{0.76m_1}$
by Lemma 2.6 and
$|P_1| \leq 2^{0.76m_1}$
by Lemma 2.6 and
![]() $|K| = |H|^{m_1}|P_1| \leq 6^{m_1}\cdot 2^{0.76m_1}$
since
$|K| = |H|^{m_1}|P_1| \leq 6^{m_1}\cdot 2^{0.76m_1}$
since
![]() $|H| \leq 6$
. Thus, we see that
$|H| \leq 6$
. Thus, we see that
 $$ \begin{align*}\frac{\log_2 s(K) }{\log_2 |K| } -\frac{\frac{23}{60} \log_2 24}{\log_2 |K|} \geq \frac{\log_2 ({4^{m_1}}/{2^{0.76m_1}}) }{\log_2 6^{m_1}\cdot2^{0.76m_1}} -\frac{\frac{23}{60} \log_2 24}{\log_2 6^{25}\cdot2^{0.76\cdot25}} = 0.349> c_8.\end{align*} $$
$$ \begin{align*}\frac{\log_2 s(K) }{\log_2 |K| } -\frac{\frac{23}{60} \log_2 24}{\log_2 |K|} \geq \frac{\log_2 ({4^{m_1}}/{2^{0.76m_1}}) }{\log_2 6^{m_1}\cdot2^{0.76m_1}} -\frac{\frac{23}{60} \log_2 24}{\log_2 6^{25}\cdot2^{0.76\cdot25}} = 0.349> c_8.\end{align*} $$
For
![]() $m_1 = 32$
and
$m_1 = 32$
and
![]() $5 \leq m_1 \leq 24$
with
$5 \leq m_1 \leq 24$
with
![]() $P_1\not \cong M_{12}$
and
$P_1\not \cong M_{12}$
and
![]() $m_1 \neq 8$
, the bounds in [Reference Yang10] and
$m_1 \neq 8$
, the bounds in [Reference Yang10] and
![]() $s(K) \geq 4^{m_1} / |P_1|$
show that (⋆) is satisfied. If
$s(K) \geq 4^{m_1} / |P_1|$
show that (⋆) is satisfied. If
![]() $P_1 \cong M_{12}$
, then
$P_1 \cong M_{12}$
, then
![]() $s(S_3\wr M_{12}) = 862$
by the method outlined above. Direct calculation shows that (⋆) is satisfied.
$s(S_3\wr M_{12}) = 862$
by the method outlined above. Direct calculation shows that (⋆) is satisfied.
For
![]() $2\leq m_1 \leq 4$
and
$2\leq m_1 \leq 4$
and
![]() $m_1 = 8$
, the bounds
$m_1 = 8$
, the bounds
![]() $s(K) \geq {s(H) - 1 + m_1\choose s(H) -1 } = {3 + m_1 \choose 3}$
and the bounds for
$s(K) \geq {s(H) - 1 + m_1\choose s(H) -1 } = {3 + m_1 \choose 3}$
and the bounds for
![]() $|P_1|$
in [Reference Yang10] show that (⋆) is satisfied by direct computation.
$|P_1|$
in [Reference Yang10] show that (⋆) is satisfied by direct computation.
Suppose that
![]() $n = 2$
. Then
$n = 2$
. Then
![]() $|H| = 2$
and
$|H| = 2$
and
![]() $s(H) \geq 3$
. If
$s(H) \geq 3$
. If
![]() $m_1 \geq 25$
and
$m_1 \geq 25$
and
![]() $m_1 \neq 32$
, then
$m_1 \neq 32$
, then
![]() $|P_1| \leq 2^{0.76m_1}$
. Also
$|P_1| \leq 2^{0.76m_1}$
. Also
![]() $s(H\wr P_1) \geq 3^{m_1}/|P_1|$
. Then
$s(H\wr P_1) \geq 3^{m_1}/|P_1|$
. Then
 $$ \begin{align*}\frac{\log_2 s(K) }{\log_2 |K| } -\frac{\frac{23}{60} \log_2 24}{\log_2 |K|} \geq \frac{\log_2 ({3^{m_1}}/{2^{0.76m_1}}) }{\log_2 2^{m_1}\cdot2^{0.76m_1}} -\frac{\frac{23}{60} \log_2 24}{\log_2 2^{25}\cdot2^{0.76\cdot25}} = 0.664> c_8.\end{align*} $$
$$ \begin{align*}\frac{\log_2 s(K) }{\log_2 |K| } -\frac{\frac{23}{60} \log_2 24}{\log_2 |K|} \geq \frac{\log_2 ({3^{m_1}}/{2^{0.76m_1}}) }{\log_2 2^{m_1}\cdot2^{0.76m_1}} -\frac{\frac{23}{60} \log_2 24}{\log_2 2^{25}\cdot2^{0.76\cdot25}} = 0.664> c_8.\end{align*} $$
For
![]() $m_1 = 32$
and
$m_1 = 32$
and
![]() $12 \leq m_1 \leq 24$
and
$12 \leq m_1 \leq 24$
and
![]() $P_1 \not \cong M_{12}$
, we use the bound
$P_1 \not \cong M_{12}$
, we use the bound
![]() $s(K) \geq 3^{m_1} / |P_1|$
and the bounds in [Reference Yang10]. Direct calculation shows that (⋆) is satisfied. If
$s(K) \geq 3^{m_1} / |P_1|$
and the bounds in [Reference Yang10]. Direct calculation shows that (⋆) is satisfied. If
![]() $P_1\cong M_{12}$
, then
$P_1\cong M_{12}$
, then
![]() $s(S_2\wr M_{12}) = 120$
by the method described above. We verify that (⋆) is satisfied.
$s(S_2\wr M_{12}) = 120$
by the method described above. We verify that (⋆) is satisfied.
For
![]() $2\leq m_1 \leq 11$
, we use
$2\leq m_1 \leq 11$
, we use
![]() $s(K) \geq {s(H) - 1 + m_1 \choose s(H) -1} = {2 + m_1 \choose 2}$
. Direct calculation shows that (⋆) is satisfied.
$s(K) \geq {s(H) - 1 + m_1 \choose s(H) -1} = {2 + m_1 \choose 2}$
. Direct calculation shows that (⋆) is satisfied.
Therefore,
![]() $\textit {ds}(G)> c_8$
provided H is different from
$\textit {ds}(G)> c_8$
provided H is different from
![]() $M_{12}$
.
$M_{12}$
.
Theorem 2.9. Let G be a transitive permutation group where G does not contain any alternating group
![]() ${ {\textrm {A}}}_l$
,
${ {\textrm {A}}}_l$
,
![]() $l> 4$
, as a composition factor. Let
$l> 4$
, as a composition factor. Let
![]() $G\cong M_{12} \wr P_1 \wr \cdots \wr P_j$
where each
$G\cong M_{12} \wr P_1 \wr \cdots \wr P_j$
where each
![]() $P_i$
is a primitive group. If
$P_i$
is a primitive group. If
![]() $P_1$
is different from
$P_1$
is different from
![]() $M_{12}$
, then
$M_{12}$
, then
![]() $\textit {ds}(G)> c_8$
.
$\textit {ds}(G)> c_8$
.
Proof. Note that
![]() $s(M_{12}) = 14$
and
$s(M_{12}) = 14$
and
![]() $|M_{12}| = 95040$
. Let
$|M_{12}| = 95040$
. Let
![]() $L = M_{12} \wr P_1$
, where deg
$L = M_{12} \wr P_1$
, where deg
![]() $(P_1) = m_1 \geq 2$
. By Lemma 2.4,
$(P_1) = m_1 \geq 2$
. By Lemma 2.4,
![]() $s(L) \geq 14^{m_1}/ |P_1|$
. Also
$s(L) \geq 14^{m_1}/ |P_1|$
. Also
![]() $|L| = 95040^{m_1} \cdot |P_1|$
. By Lemma 2.5, it suffices to show that for all
$|L| = 95040^{m_1} \cdot |P_1|$
. By Lemma 2.5, it suffices to show that for all
![]() $m_1 \geq 2$
,
$m_1 \geq 2$
,
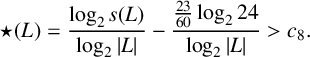 $$ \begin{align*}\star(L) = \frac{\log_2 s(L)}{\log_2 |L|} - \frac{\frac{23}{60} \log_2 24}{\log_2 |L|}> c_8.\end{align*} $$
$$ \begin{align*}\star(L) = \frac{\log_2 s(L)}{\log_2 |L|} - \frac{\frac{23}{60} \log_2 24}{\log_2 |L|}> c_8.\end{align*} $$
If
![]() $m_1 \geq 25$
and
$m_1 \geq 25$
and
![]() $m_1 \neq 32$
, then
$m_1 \neq 32$
, then
![]() $|P_1| \leq 2^{0.76 m_1}$
by Lemma 2.6. Then
$|P_1| \leq 2^{0.76 m_1}$
by Lemma 2.6. Then
![]() $s(L) \geq 14^{m_1}/ 2^{0.76m_1}$
and
$s(L) \geq 14^{m_1}/ 2^{0.76m_1}$
and
 $$ \begin{align*}\star(L) \geq \frac{ \log_2 ({14}/{2^{0.76}})}{\log_2 (95040\cdot 2^{0.76})} - \frac{\frac{23}{60} \log_2 24}{25\cdot \log_2 (95040\cdot 2^{0.76})}> 0.172 > c_8.\end{align*} $$
$$ \begin{align*}\star(L) \geq \frac{ \log_2 ({14}/{2^{0.76}})}{\log_2 (95040\cdot 2^{0.76})} - \frac{\frac{23}{60} \log_2 24}{25\cdot \log_2 (95040\cdot 2^{0.76})}> 0.172 > c_8.\end{align*} $$
If
![]() $m_1 = 32$
, then
$m_1 = 32$
, then
![]() $|P_1| \leq 319979520$
and so
$|P_1| \leq 319979520$
and so
![]() $s(L) \geq 14^{32}/ 319979520$
. Thus we see that
$s(L) \geq 14^{32}/ 319979520$
. Thus we see that
![]() $\star (L)> 0.164 > c_8$
.
$\star (L)> 0.164 > c_8$
.
For
![]() $5 \leq m_1 \leq 24$
, bounds for
$5 \leq m_1 \leq 24$
, bounds for
![]() $|P_1|$
are obtained from [Reference Yang10] and
$|P_1|$
are obtained from [Reference Yang10] and
![]() $\star (L)> c_8$
is verified by direct computation.
$\star (L)> c_8$
is verified by direct computation.
For the remaining computations, we use Lemma 2.4 to get a better bound:
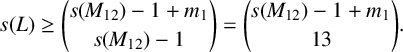 $$ \begin{align*}s(L) \geq {s(M_{12})-1+m_1 \choose s(M_{12}) - 1} = {s(M_{12})-1+m_1 \choose 13}.\end{align*} $$
$$ \begin{align*}s(L) \geq {s(M_{12})-1+m_1 \choose s(M_{12}) - 1} = {s(M_{12})-1+m_1 \choose 13}.\end{align*} $$
If
![]() $m_1 = 4$
, then
$m_1 = 4$
, then
![]() $|P_1| \leq 24$
and
$|P_1| \leq 24$
and
![]() $s(L) \geq {17 \choose 13} = 2380$
, so
$s(L) \geq {17 \choose 13} = 2380$
, so
![]() $\star (L)> 0.133 > c_8$
. If
$\star (L)> 0.133 > c_8$
. If
![]() $m_1 = 3$
, then
$m_1 = 3$
, then
![]() $|P_1| \leq 6$
and
$|P_1| \leq 6$
and
![]() $s(L) \geq {16 \choose 13} = 560$
, so
$s(L) \geq {16 \choose 13} = 560$
, so
![]() $\star (L)> 0.141 > c_8$
. If
$\star (L)> 0.141 > c_8$
. If
![]() $m_1 = 2$
, then
$m_1 = 2$
, then
![]() $|P_1| \leq 2$
and
$|P_1| \leq 2$
and
![]() $s(L) \geq {15 \choose 13} = 105$
, so
$s(L) \geq {15 \choose 13} = 105$
, so
![]() $\star (L)> 0.145 > c_8$
.
$\star (L)> 0.145 > c_8$
.
Therefore, deg
![]() $(P_1) = 12$
and
$(P_1) = 12$
and
![]() $P_1\cong M_{12}$
.
$P_1\cong M_{12}$
.
Theorem 2.10. Let H be a transitive permutation group where H does not contain any alternating group
![]() ${ {\textrm {A}}}_l$
,
${ {\textrm {A}}}_l$
,
![]() $l> 4$
, as a composition factor. Let
$l> 4$
, as a composition factor. Let
![]() $H \cong M_{12} \wr M_{12} \wr \underset {t \ \mbox {terms}}{\underbrace {S_4\wr \cdots \wr S_4}}$
, where
$H \cong M_{12} \wr M_{12} \wr \underset {t \ \mbox {terms}}{\underbrace {S_4\wr \cdots \wr S_4}}$
, where
![]() $t \ge 0$
. Then
$t \ge 0$
. Then
![]() $\textit {ds}(H\wr S_4\wr S_4\wr S_4\wr S_4 \wr S_4) \leq \textit {ds}(H\wr P_1 \wr \cdots \wr P_j)$
where each
$\textit {ds}(H\wr S_4\wr S_4\wr S_4\wr S_4 \wr S_4) \leq \textit {ds}(H\wr P_1 \wr \cdots \wr P_j)$
where each
![]() $P_i$
is a primitive group if
$P_i$
is a primitive group if
![]() $\mathrm {deg}(P_1) \neq 4$
.
$\mathrm {deg}(P_1) \neq 4$
.
Proof. As calculated before,
![]() $s(M_{12} \wr M_{12}) = 604576714$
and
$s(M_{12} \wr M_{12}) = 604576714$
and
![]() $|M_{12} \wr M_{12}| = 95040^{13}$
. If K is an arbitrary group,
$|M_{12} \wr M_{12}| = 95040^{13}$
. If K is an arbitrary group,
![]() $|K \wr S_4| = |K|^4 \cdot 24$
, and so one can easily verify by induction that
$|K \wr S_4| = |K|^4 \cdot 24$
, and so one can easily verify by induction that
![]() $|H| = 95040^{13\cdot 4^t} \cdot 24^{b_t} = 95040^{13\cdot 4^t} \cdot 24^{{(4^t - 1)}/{3}}$
.
$|H| = 95040^{13\cdot 4^t} \cdot 24^{b_t} = 95040^{13\cdot 4^t} \cdot 24^{{(4^t - 1)}/{3}}$
.
Next we need some bounds on
![]() $s(H\wr S_4\wr S_4\wr S_4\wr S_4 \wr S_4)$
and
$s(H\wr S_4\wr S_4\wr S_4\wr S_4 \wr S_4)$
and
![]() $s(H\wr P_1 \wr \cdots \wr P_j)$
. We handle the first group by defining the sequence
$s(H\wr P_1 \wr \cdots \wr P_j)$
. We handle the first group by defining the sequence
![]() $A_0 = s(H)$
,
$A_0 = s(H)$
,
![]() $A_1 = s(H \wr S_4)$
,
$A_1 = s(H \wr S_4)$
,
![]() $A_2 = s(H \wr S_4 \wr S_4)$
,
$A_2 = s(H \wr S_4 \wr S_4)$
,
![]() $A_3 =s(H \wr S_4 \wr S_4 \wr S_4)$
,
$A_3 =s(H \wr S_4 \wr S_4 \wr S_4)$
,
![]() $A_4 = s(H \wr S_4 \wr S_4 \wr S_4 \wr S_4)$
and
$A_4 = s(H \wr S_4 \wr S_4 \wr S_4 \wr S_4)$
and
![]() $A_5 = s(H \wr S_4 \wr S_4 \wr S_4 \wr S_4 \wr S_4)$
. By Lemma 2.4(2),
$A_5 = s(H \wr S_4 \wr S_4 \wr S_4 \wr S_4 \wr S_4)$
. By Lemma 2.4(2),
![]() $A_{i+1} = {A_i + 3 \choose 4}$
for
$A_{i+1} = {A_i + 3 \choose 4}$
for
![]() $0 \leq i \leq 4$
. Hence
$0 \leq i \leq 4$
. Hence
![]() $A_{i+1} = {(A_i+3)(A_i+2)(A_i+1)(A_i)}/{24}$
and
$A_{i+1} = {(A_i+3)(A_i+2)(A_i+1)(A_i)}/{24}$
and
![]() $A_{i+1}+3 \leq {(A_i+3)^4}/{24}$
since
$A_{i+1}+3 \leq {(A_i+3)^4}/{24}$
since
![]() $A_0 \geq a_0 = 604576714$
. For simplicity, we set
$A_0 \geq a_0 = 604576714$
. For simplicity, we set
![]() $A_0 = A$
. Then
$A_0 = A$
. Then
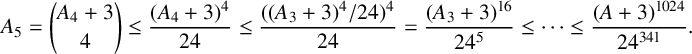 $$ \begin{align*}A_5 = {A_4 + 3 \choose 4} \leq \frac{(A_4+3)^4}{24} \leq \frac{({(A_3+3)^4}/{24})^4}{24} = \frac{(A_3 + 3)^{16}}{24^5} \leq \cdots \leq \frac{(A+3)^{1024}}{24^{341}}.\end{align*} $$
$$ \begin{align*}A_5 = {A_4 + 3 \choose 4} \leq \frac{(A_4+3)^4}{24} \leq \frac{({(A_3+3)^4}/{24})^4}{24} = \frac{(A_3 + 3)^{16}}{24^5} \leq \cdots \leq \frac{(A+3)^{1024}}{24^{341}}.\end{align*} $$
Also
![]() $|H \wr S_4 \wr S_4 \wr S_4 \wr S_4 \wr S_4| = |H|^{1024}\cdot 24^{341}> |H|^{1024}\cdot 2.88^{1024}$
. Consequently,
$|H \wr S_4 \wr S_4 \wr S_4 \wr S_4 \wr S_4| = |H|^{1024}\cdot 24^{341}> |H|^{1024}\cdot 2.88^{1024}$
. Consequently,
 $$ \begin{align*} \textit{ds}(H\wr S_4\wr S_4 \wr S_4\wr S_4 \wr S_4) &\leq \frac{\log_2 ( {(A+3)^{1024}}/{24^{341}})}{\log_2 |H|^{1024}\cdot 24^{341}} \\ &\leq \frac{\log_2 (A+3)^{1024} - \log_2 24^{341}}{ \log_2 |H|^{1024} \cdot 2.88^{1024}} \\ &= \frac{\log_2 (A+3) }{\log_2 2.88|H|} - \frac{ 341 \cdot \log_2 24}{1024 \log_2 2.88|H|}. \end{align*} $$
$$ \begin{align*} \textit{ds}(H\wr S_4\wr S_4 \wr S_4\wr S_4 \wr S_4) &\leq \frac{\log_2 ( {(A+3)^{1024}}/{24^{341}})}{\log_2 |H|^{1024}\cdot 24^{341}} \\ &\leq \frac{\log_2 (A+3)^{1024} - \log_2 24^{341}}{ \log_2 |H|^{1024} \cdot 2.88^{1024}} \\ &= \frac{\log_2 (A+3) }{\log_2 2.88|H|} - \frac{ 341 \cdot \log_2 24}{1024 \log_2 2.88|H|}. \end{align*} $$
Next we obtain a similar bound for
![]() $s(H\wr P_1 \wr \cdots \wr P_j)$
. Consider
$s(H\wr P_1 \wr \cdots \wr P_j)$
. Consider
![]() $s(H\wr P_1)$
where deg
$s(H\wr P_1)$
where deg
![]() $(P_1)=m_1 \neq 4$
. Note that
$(P_1)=m_1 \neq 4$
. Note that
![]() $s(H\wr P_1) \geq A^{m_1}/ |P_1|$
by Lemma 2.4(1). From the proof of Lemma 2.5,
$s(H\wr P_1) \geq A^{m_1}/ |P_1|$
by Lemma 2.4(1). From the proof of Lemma 2.5,
 $$ \begin{align*}\textit{ds}(H\wr P_1\wr \cdots \wr P_j) \geq \frac{\log_2 A^{m_1}/|P_1|}{\log_2 |H|^{m_1}\cdot |P_1|} - \frac{\frac{23}{60} \log_2 24}{\log_2 |H|^{m_1}\cdot |P_1|}.\end{align*} $$
$$ \begin{align*}\textit{ds}(H\wr P_1\wr \cdots \wr P_j) \geq \frac{\log_2 A^{m_1}/|P_1|}{\log_2 |H|^{m_1}\cdot |P_1|} - \frac{\frac{23}{60} \log_2 24}{\log_2 |H|^{m_1}\cdot |P_1|}.\end{align*} $$
Since
![]() $|P_1| < 3^{m_1}$
by Lemma 2.6, we have
$|P_1| < 3^{m_1}$
by Lemma 2.6, we have
 $$ \begin{align*} \textit{ds}(H\wr P_1\wr \cdots \wr P_j) &> \frac{\log_2 A}{\log_2 3|H|} - \frac{\log_2 |P_1|}{m_1 \log_2 3|H|} - \frac{\frac{23}{60} \log_2 24}{m_1 \log_2 3|H|} \\ &> \frac{\log_2 A}{\log_2 3|H|} - \frac{\log_2 |P_1|}{m_1 \log_2 2|H|} - \frac{\frac{23}{60} \log_2 24}{m_1 \log_2 2|H|}. \end{align*} $$
$$ \begin{align*} \textit{ds}(H\wr P_1\wr \cdots \wr P_j) &> \frac{\log_2 A}{\log_2 3|H|} - \frac{\log_2 |P_1|}{m_1 \log_2 3|H|} - \frac{\frac{23}{60} \log_2 24}{m_1 \log_2 3|H|} \\ &> \frac{\log_2 A}{\log_2 3|H|} - \frac{\log_2 |P_1|}{m_1 \log_2 2|H|} - \frac{\frac{23}{60} \log_2 24}{m_1 \log_2 2|H|}. \end{align*} $$
It suffices to show that
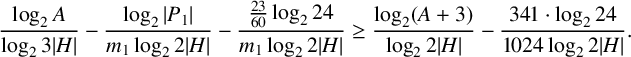 $$ \begin{align*} \frac{\log_2 A}{\log_2 3|H|} - \frac{\log_2 |P_1|}{m_1 \log_2 2|H|} - \frac{\frac{23}{60} \log_2 24}{m_1 \log_2 2|H|} & \geq \frac{\log_2 (A+3) }{\log_2 2|H|} - \frac{ 341 \cdot \log_2 24}{1024 \log_2 2|H|}. \end{align*} $$
$$ \begin{align*} \frac{\log_2 A}{\log_2 3|H|} - \frac{\log_2 |P_1|}{m_1 \log_2 2|H|} - \frac{\frac{23}{60} \log_2 24}{m_1 \log_2 2|H|} & \geq \frac{\log_2 (A+3) }{\log_2 2|H|} - \frac{ 341 \cdot \log_2 24}{1024 \log_2 2|H|}. \end{align*} $$
By rearranging these terms, we can write this inequality as
 $$ \begin{align*} \frac{\log_2 2|H|}{\log_2 3|H|} \cdot \log_2 A - \log_2 (A+3) &\geq \frac{\log_2 |P_1|}{m_1} + \frac{23 \cdot \log_2 24}{60 m_1} - \frac{341 \cdot \log_2 24 }{1024}. \end{align*} $$
$$ \begin{align*} \frac{\log_2 2|H|}{\log_2 3|H|} \cdot \log_2 A - \log_2 (A+3) &\geq \frac{\log_2 |P_1|}{m_1} + \frac{23 \cdot \log_2 24}{60 m_1} - \frac{341 \cdot \log_2 24 }{1024}. \end{align*} $$
Note that
![]() $|H| \geq 95040^{13}$
, so
$|H| \geq 95040^{13}$
, so
![]() ${\log _2 2|H|}/{\log _2 3|H|} \geq 0.99729879$
. Further, we have
${\log _2 2|H|}/{\log _2 3|H|} \geq 0.99729879$
. Further, we have
![]() $A \geq 604576714$
, so
$A \geq 604576714$
, so
 $$ \begin{align*} & \frac{\log_2 2|H|}{\log_2 3|H|} \cdot \log_2 A - \log_2 (A+3) + \frac{341 \cdot \log_2 24}{1024} \\ &\quad \geq 0.99729879\cdot \log_2 A - \log_2(A+3) + \frac{341 \cdot \log_2 24}{1024} \geq 1.4480303828. \end{align*} $$
$$ \begin{align*} & \frac{\log_2 2|H|}{\log_2 3|H|} \cdot \log_2 A - \log_2 (A+3) + \frac{341 \cdot \log_2 24}{1024} \\ &\quad \geq 0.99729879\cdot \log_2 A - \log_2(A+3) + \frac{341 \cdot \log_2 24}{1024} \geq 1.4480303828. \end{align*} $$
Thus it suffices to show that
If
![]() $m_1 \geq 25$
, then
$m_1 \geq 25$
, then
![]() $|P_1| \leq 2^{m_1}$
by Lemma 2.6 and
$|P_1| \leq 2^{m_1}$
by Lemma 2.6 and
![]() $\star (P_1) \leq 1.08 < \gamma .$
Similar computations hold for
$\star (P_1) \leq 1.08 < \gamma .$
Similar computations hold for
![]() $2 \leq m_1 \leq 24$
by reading off the bounds for
$2 \leq m_1 \leq 24$
by reading off the bounds for
![]() $|P_1|$
from Table 2 of [Reference Yang10], and one obtains
$|P_1|$
from Table 2 of [Reference Yang10], and one obtains
![]() $\star (P_1) < \gamma $
in all cases except when
$\star (P_1) < \gamma $
in all cases except when
![]() $P_1 \cong M_{12}$
and
$P_1 \cong M_{12}$
and
![]() $P_1 \cong \rm ASL(3,2)$
, a primitive group of degree
$P_1 \cong \rm ASL(3,2)$
, a primitive group of degree
![]() $8$
. We now take care of these two cases.
$8$
. We now take care of these two cases.
Suppose
![]() $P_1 \cong M_{12}$
. Since
$P_1 \cong M_{12}$
. Since
![]() $|M_{12}| = 95040 < 2.6^{12}$
,
$|M_{12}| = 95040 < 2.6^{12}$
,
 $$ \begin{align*} \textit{ds}(H \wr P_1 \wr \cdots \wr P_j) &\geq \frac{\log_2(A^{12}) - \log_2 95040 - \frac{23}{60}\log_2 24}{\log_2(95040|H|^{12})} \\ &> \frac{12\cdot \log_2(A) - \log_2 95040 - \frac{23}{60}\log_2 24}{12\cdot \log_2(2.6|H|)} \\ &= \frac{\log_2(A)}{\log_2(2.6|H|)} - \frac{\log_2 95040}{12 \cdot \log_2(2.6|H|)} - \frac{\frac{23}{60}\log_2 24}{12 \cdot \log_2(2.6|H|)}. \end{align*} $$
$$ \begin{align*} \textit{ds}(H \wr P_1 \wr \cdots \wr P_j) &\geq \frac{\log_2(A^{12}) - \log_2 95040 - \frac{23}{60}\log_2 24}{\log_2(95040|H|^{12})} \\ &> \frac{12\cdot \log_2(A) - \log_2 95040 - \frac{23}{60}\log_2 24}{12\cdot \log_2(2.6|H|)} \\ &= \frac{\log_2(A)}{\log_2(2.6|H|)} - \frac{\log_2 95040}{12 \cdot \log_2(2.6|H|)} - \frac{\frac{23}{60}\log_2 24}{12 \cdot \log_2(2.6|H|)}. \end{align*} $$
Given that
![]() $A \geq 604576714$
, it suffices to show that,
$A \geq 604576714$
, it suffices to show that,
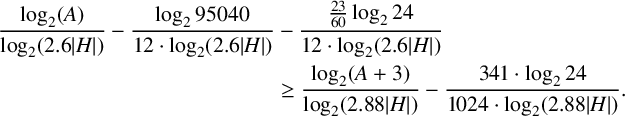 $$ \begin{align*} \frac{\log_2(A)}{\log_2(2.6|H|)} - \frac{\log_2 95040}{12\cdot \log_2(2.6|H|)} &- \frac{\frac{23}{60}\log_2 24}{12\cdot \log_2(2.6|H|)} \\ &\geq \frac{\log_2(A+3)}{\log_2 (2.88|H|)} - \frac{341\cdot \log_224}{1024\cdot \log_2(2.88|H|)}.\\[-14pt] \end{align*} $$
$$ \begin{align*} \frac{\log_2(A)}{\log_2(2.6|H|)} - \frac{\log_2 95040}{12\cdot \log_2(2.6|H|)} &- \frac{\frac{23}{60}\log_2 24}{12\cdot \log_2(2.6|H|)} \\ &\geq \frac{\log_2(A+3)}{\log_2 (2.88|H|)} - \frac{341\cdot \log_224}{1024\cdot \log_2(2.88|H|)}.\\[-14pt] \end{align*} $$
By rearranging these terms, we can write this inequality as
 $$ \begin{align*} \frac{\log_2(2.88|H|) \cdot \log_2(A)}{\log_2(2.6|H|)} & - \log_2(A+3) + \frac{341 \cdot \log_224}{1024} \\ &\geq \frac{\log_2(2.88|H|)}{\log_2(2.6|H|)} \bigg( \frac{\log_2 95040}{12} + \frac{\frac{23}{60} \log_224}{12} \bigg). \end{align*} $$
$$ \begin{align*} \frac{\log_2(2.88|H|) \cdot \log_2(A)}{\log_2(2.6|H|)} & - \log_2(A+3) + \frac{341 \cdot \log_224}{1024} \\ &\geq \frac{\log_2(2.88|H|)}{\log_2(2.6|H|)} \bigg( \frac{\log_2 95040}{12} + \frac{\frac{23}{60} \log_224}{12} \bigg). \end{align*} $$
Here
![]() $|H| = 95040^{13\cdot 4^t} \cdot 24^{{(4^t - 1)}/{3}}$
, where t is the number of terms of
$|H| = 95040^{13\cdot 4^t} \cdot 24^{{(4^t - 1)}/{3}}$
, where t is the number of terms of
![]() $S_4$
in H. Define
$S_4$
in H. Define
 $$ \begin{align*} h_1(t) = \frac{\log_2(2.88|H|)}{\log_2(2.6|H|)} & = \frac{\log_2 2.88 + 13\cdot4^t\cdot\log_2 95040 + ({(4^t - 1)}/{3})\log_2 24}{\log_2 2.6 + 13\cdot4^t\cdot\log_2 95040 + ({(4^t - 1)}/{3})\log_2 24}, \\ a_1(x,t) & = h_1(t) \cdot \log_2 x - \log_2 (x+3) +\frac{341 \cdot \log_2 24}{1024}, \\ s_1(t) & = h_1(t) \cdot \bigg( \frac{\log_2 95040 + \frac{23}{60} \log_2 24}{12} \bigg). \end{align*} $$
$$ \begin{align*} h_1(t) = \frac{\log_2(2.88|H|)}{\log_2(2.6|H|)} & = \frac{\log_2 2.88 + 13\cdot4^t\cdot\log_2 95040 + ({(4^t - 1)}/{3})\log_2 24}{\log_2 2.6 + 13\cdot4^t\cdot\log_2 95040 + ({(4^t - 1)}/{3})\log_2 24}, \\ a_1(x,t) & = h_1(t) \cdot \log_2 x - \log_2 (x+3) +\frac{341 \cdot \log_2 24}{1024}, \\ s_1(t) & = h_1(t) \cdot \bigg( \frac{\log_2 95040 + \frac{23}{60} \log_2 24}{12} \bigg). \end{align*} $$
It suffices to show that the inequality above, now translated as
![]() $a_1(x,t)> s_1(t)$
, holds for all
$a_1(x,t)> s_1(t)$
, holds for all
![]() $x \geq A=604576714$
and
$x \geq A=604576714$
and
![]() $t \geq 0$
.
$t \geq 0$
.
Clearly
![]() $h_1(t)$
is a decreasing function and
$h_1(t)$
is a decreasing function and
![]() $h_1(t) \to 1$
as
$h_1(t) \to 1$
as
![]() $t \to \infty $
. The function
$t \to \infty $
. The function
![]() $a_1(x,t)$
is increasing for a fixed value of
$a_1(x,t)$
is increasing for a fixed value of
![]() $t \geq 0$
, and achieves a minimum when
$t \geq 0$
, and achieves a minimum when
![]() $t\to \infty $
and
$t\to \infty $
and
![]() $x = 604576714$
. Thus,
$x = 604576714$
. Thus,
![]() $a_1(x,t) \geq 1.5268$
. Since
$a_1(x,t) \geq 1.5268$
. Since
![]() $h_1(t)$
is decreasing,
$h_1(t)$
is decreasing,
![]() $s_1(t)$
is decreasing. So
$s_1(t)$
is decreasing. So
![]() $s_1(t)$
achieves its maximum value for
$s_1(t)$
achieves its maximum value for
![]() $t=1$
and
$t=1$
and
![]() $s_1(1) < 1.5248$
. Thus,
$s_1(1) < 1.5248$
. Thus,
![]() $a_1(x,t)> s_1(t)$
for all x and t.
$a_1(x,t)> s_1(t)$
for all x and t.
Finally, consider
![]() $P_1 \cong \rm ASL(3,2)$
, where
$P_1 \cong \rm ASL(3,2)$
, where
![]() $|\rm ASL(3,2)| = 1344 < 2.47^8$
. Thus,
$|\rm ASL(3,2)| = 1344 < 2.47^8$
. Thus,
 $$ \begin{align*} \textit{ds}(H\wr P_1 \wr \cdots \wr P_j) &\geq \frac{\log_2 (A^8) - \log_2 1344 - \frac{23}{60} \log_2 24 }{\log_2 (|H|^8 \cdot 1344)} \\ &> \frac{ 8\cdot \log_2 (A) - \log_2 1344 - \frac{23}{60} \log_2 24 }{ 8\cdot \log_2 (2.47\cdot |H|)} \\ &= \frac{\log_2 A}{\log_2(2.47 |H|)} - \frac{\log_2 1344}{8\cdot \log_2 (2.47 |H|)} - \frac{\frac{23}{60} \log_2 24}{8 \cdot \log_2 (2.47 |H|)}. \end{align*} $$
$$ \begin{align*} \textit{ds}(H\wr P_1 \wr \cdots \wr P_j) &\geq \frac{\log_2 (A^8) - \log_2 1344 - \frac{23}{60} \log_2 24 }{\log_2 (|H|^8 \cdot 1344)} \\ &> \frac{ 8\cdot \log_2 (A) - \log_2 1344 - \frac{23}{60} \log_2 24 }{ 8\cdot \log_2 (2.47\cdot |H|)} \\ &= \frac{\log_2 A}{\log_2(2.47 |H|)} - \frac{\log_2 1344}{8\cdot \log_2 (2.47 |H|)} - \frac{\frac{23}{60} \log_2 24}{8 \cdot \log_2 (2.47 |H|)}. \end{align*} $$
It suffices to show that
 $$ \begin{align*} \frac{\log_2 A}{\log_2(2.47 |H|)} - \frac{\log_2 1344}{8\cdot \log_2 (2.47 |H|)} & - \frac{\frac{23}{60} \log_2 24}{8\cdot \log_2 (2.47 |H|)} \\ &\geq \frac{\log_2(A+3)}{\log_2 (2.88|H|)} - \frac{341\cdot \log_224}{1024\cdot \log_2(2.88|H|)}. \end{align*} $$
$$ \begin{align*} \frac{\log_2 A}{\log_2(2.47 |H|)} - \frac{\log_2 1344}{8\cdot \log_2 (2.47 |H|)} & - \frac{\frac{23}{60} \log_2 24}{8\cdot \log_2 (2.47 |H|)} \\ &\geq \frac{\log_2(A+3)}{\log_2 (2.88|H|)} - \frac{341\cdot \log_224}{1024\cdot \log_2(2.88|H|)}. \end{align*} $$
By rearranging the terms, we can write this inequality as
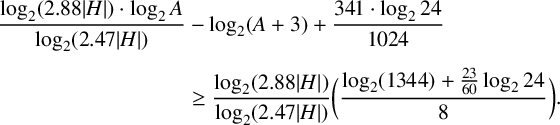 $$ \begin{align*} \frac{\log_2 (2.88|H|) \cdot \log_2 A}{\log_2 (2.47|H|)} & - \log_2 (A+3) + \frac{341 \cdot \log_2 24}{1024} \\[4pt] &\geq \frac{\log_2 (2.88|H|)}{\log_2 (2.47|H|)} \bigg(\frac{\log_2 (1344) + \frac{23}{60} \log_2 24}{8} \bigg). \end{align*} $$
$$ \begin{align*} \frac{\log_2 (2.88|H|) \cdot \log_2 A}{\log_2 (2.47|H|)} & - \log_2 (A+3) + \frac{341 \cdot \log_2 24}{1024} \\[4pt] &\geq \frac{\log_2 (2.88|H|)}{\log_2 (2.47|H|)} \bigg(\frac{\log_2 (1344) + \frac{23}{60} \log_2 24}{8} \bigg). \end{align*} $$
As before,
![]() $|H| = 95040^{13\cdot 4^t} \cdot 24^{{(4^t - 1)}/{3}}$
, where t is the number of terms of
$|H| = 95040^{13\cdot 4^t} \cdot 24^{{(4^t - 1)}/{3}}$
, where t is the number of terms of
![]() $S_4$
in H. Define
$S_4$
in H. Define
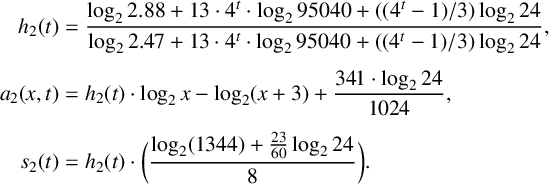 $$ \begin{align*} h_2(t) & = \frac{\log_2 2.88 + 13\cdot4^t\cdot\log_2 95040 + ({(4^t - 1)}/{3})\log_2 24}{\log_2 2.47 + 13\cdot4^t\cdot\log_2 95040 + ({(4^t - 1)}/{3})\log_2 24}, \\[4pt] a_2(x, t) & = h_2(t) \cdot \log_2 x - \log_2 (x+3) + \frac{341 \cdot \log_2 24}{1024}, \\[4pt] s_2(t) & = h_2(t) \cdot \bigg(\frac{\log_2 (1344) + \frac{23}{60} \log_2 24}{8} \bigg). \end{align*} $$
$$ \begin{align*} h_2(t) & = \frac{\log_2 2.88 + 13\cdot4^t\cdot\log_2 95040 + ({(4^t - 1)}/{3})\log_2 24}{\log_2 2.47 + 13\cdot4^t\cdot\log_2 95040 + ({(4^t - 1)}/{3})\log_2 24}, \\[4pt] a_2(x, t) & = h_2(t) \cdot \log_2 x - \log_2 (x+3) + \frac{341 \cdot \log_2 24}{1024}, \\[4pt] s_2(t) & = h_2(t) \cdot \bigg(\frac{\log_2 (1344) + \frac{23}{60} \log_2 24}{8} \bigg). \end{align*} $$
Again,
![]() $h_2(t)$
is a decreasing function with
$h_2(t)$
is a decreasing function with
![]() $h_2(t) \to 1$
as
$h_2(t) \to 1$
as
![]() $t \to \infty $
and
$t \to \infty $
and
![]() $a_2(x,t)$
is increasing for a fixed value of t. We still have
$a_2(x,t)$
is increasing for a fixed value of t. We still have
![]() $a_2(x, t) \geq 1.526$
and
$a_2(x, t) \geq 1.526$
and
![]() $s_2(t)$
achieves its maximum value for
$s_2(t)$
achieves its maximum value for
![]() $t = 1$
and
$t = 1$
and
![]() $s_2(1) < 1.520$
. Thus,
$s_2(1) < 1.520$
. Thus,
![]() $a_2(x,t)> s_2(t)$
for all x and t.
$a_2(x,t)> s_2(t)$
for all x and t.
Theorem 2.11. We have
 $$ \begin{align*}\inf\bigg( \frac{\log_2 s(G)}{\log_2 |G|} \bigg) = \lim_{k\to \infty} \frac{\log_2 s(M_{12}\wr M_{12} \wr \overset{k \ \mbox{terms}}{\overbrace{S_4\wr \cdots \wr S_4}})}{\log_2 |M_{12}\wr M_{12} \wr \underset{k \ \mbox{terms}}{\underbrace{S_4\wr \cdots \wr S_4}}|} = \lim_{k\to \infty} c_k,\end{align*} $$
$$ \begin{align*}\inf\bigg( \frac{\log_2 s(G)}{\log_2 |G|} \bigg) = \lim_{k\to \infty} \frac{\log_2 s(M_{12}\wr M_{12} \wr \overset{k \ \mbox{terms}}{\overbrace{S_4\wr \cdots \wr S_4}})}{\log_2 |M_{12}\wr M_{12} \wr \underset{k \ \mbox{terms}}{\underbrace{S_4\wr \cdots \wr S_4}}|} = \lim_{k\to \infty} c_k,\end{align*} $$
where the infimum is taken over all permutation groups G not containing any
![]() ${ {\textrm {A}}}_l, l> 4$
, as a composition factor.
${ {\textrm {A}}}_l, l> 4$
, as a composition factor.
Proof. Let G be a permutation group. Let
![]() $M = \lim _{k\to \infty } c_k$
so that
$M = \lim _{k\to \infty } c_k$
so that
![]() $M < c_8$
. By our earlier remarks, G is transitive. By Proposition 2.7, if G is primitive,
$M < c_8$
. By our earlier remarks, G is transitive. By Proposition 2.7, if G is primitive,
![]() $\textit {ds}(G)> c_8 > M$
. So we assume that G is imprimitive.
$\textit {ds}(G)> c_8 > M$
. So we assume that G is imprimitive.
By Theorem 2.8, G is induced from
![]() $M_{12}$
and, by Theorem 2.9, G is induced from
$M_{12}$
and, by Theorem 2.9, G is induced from
![]() ${M_{12} \wr M_{12}}$
. By Theorem 2.10,
${M_{12} \wr M_{12}}$
. By Theorem 2.10,
![]() $\inf ( {\log _2 s(G)}/{\log _2 |G|} ) = \lim _{k\to \infty } c_k$
.
$\inf ( {\log _2 s(G)}/{\log _2 |G|} ) = \lim _{k\to \infty } c_k$
.
Remark 2.12. Again we set
![]() $M = \lim _{k \to \infty } c_k$
. By Lemma 2.5,
$M = \lim _{k \to \infty } c_k$
. By Lemma 2.5,
 $$ \begin{align*}M> c_8 - \frac{\frac{23}{60}\log_2(24)}{(13\cdot4^8)\log_2(95040) + ({(4^8 - 1)}/{3})\log_2(24)} \approx 0.1276817008.\end{align*} $$
$$ \begin{align*}M> c_8 - \frac{\frac{23}{60}\log_2(24)}{(13\cdot4^8)\log_2(95040) + ({(4^8 - 1)}/{3})\log_2(24)} \approx 0.1276817008.\end{align*} $$
Since
![]() $c_k$
is a strictly decreasing sequence with
$c_k$
is a strictly decreasing sequence with
![]() $c_8\, {<}\, 0.1276818247$
, this gives
$c_8\, {<}\, 0.1276818247$
, this gives
This estimate will give an explicit bound for [Reference Babai and Pyber1, Corollary 1] when
![]() $t=4$
. Since [Reference Babai and Pyber1, Corollary 1] is an important ingredient in Pyber’s proof of a lower bound for the number of conjugacy classes
$t=4$
. Since [Reference Babai and Pyber1, Corollary 1] is an important ingredient in Pyber’s proof of a lower bound for the number of conjugacy classes
![]() $k(G)$
of a finite group G in terms of its order [Reference Maróti6] (which has undetermined constants in it), it is likely that our result will help to find an explicit scalar constant in this result. We note that Pyber’s result has been improved in [Reference Baumeister, Maróti and Tong-Viet2, 4]. We also note that [4, Theorem 3.1] now has an (albeit extremely small) bound thanks to the main result of [Reference Gao and Yang3] (which is generalised by our result here). In particular, the currently best lower bound for
$k(G)$
of a finite group G in terms of its order [Reference Maróti6] (which has undetermined constants in it), it is likely that our result will help to find an explicit scalar constant in this result. We note that Pyber’s result has been improved in [Reference Baumeister, Maróti and Tong-Viet2, 4]. We also note that [4, Theorem 3.1] now has an (albeit extremely small) bound thanks to the main result of [Reference Gao and Yang3] (which is generalised by our result here). In particular, the currently best lower bound for
![]() $k(G)$
in terms of
$k(G)$
in terms of
![]() $|G|$
for solvable groups, as stated in [4, Corollary 3.2], is explicit.
$|G|$
for solvable groups, as stated in [4, Corollary 3.2], is explicit.
Acknowledgements
This research was conducted by Gintz, Kortje and Wang during the summer of 2021 under the supervision of Keller and Yang. The authors thank Texas State University for providing a great working environment and support. The authors are grateful to the referee for the valuable suggestions which greatly improved the manuscript.