Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Girela, Daniel
1992.
Mean growth of the derivative of certain classes of analytic functions.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 112,
Issue. 2,
p.
335.
Miao, Jie
1992.
A property of analytic functions with Hadamard gaps.
Bulletin of the Australian Mathematical Society,
Vol. 45,
Issue. 1,
p.
105.
Miao, Jie
1992.
Characterisations for analytic functions of bounded mean oscillation.
Bulletin of the Australian Mathematical Society,
Vol. 46,
Issue. 1,
p.
115.
Jevtić, Miroljub
and
Pavlović, Miroslav
1995.
On ℳ-harmonic Bloch space.
Proceedings of the American Mathematical Society,
Vol. 123,
Issue. 5,
p.
1385.
Aulaskari, Rauno
and
Zhao, Ruhan
1995.
Some Characterizations of Normal and Little Normal Functions.
Complex Variables, Theory and Application: An International Journal,
Vol. 28,
Issue. 2,
p.
135.
Zengjian, Lou
1996.
Carleson measure characterization of Bloch functions.
Acta Mathematica Sinica,
Vol. 12,
Issue. 2,
p.
175.
Choa, Jun Soo
1996.
Some properties of analytic functions on the unit ball with hadamard gaps.
Complex Variables, Theory and Application: An International Journal,
Vol. 29,
Issue. 3,
p.
277.
Stroethoff, Karel
1996.
The Bloch space and Besov spaces of analytic functions.
Bulletin of the Australian Mathematical Society,
Vol. 54,
Issue. 2,
p.
211.
Aulaskari, R.
Stegenga, David A.
and
Xiao, Jie
1996.
Some Subclasses of BMOA and their Characterization in Terms of Carleson Measures.
Rocky Mountain Journal of Mathematics,
Vol. 26,
Issue. 2,
Zhao, Ruhan
1996.
ON α-BLOCH FUNCTIONS AND VMOA.
Acta Mathematica Scientia,
Vol. 16,
Issue. 3,
p.
349.
Choe, Boo Rim
and
Rim, Kyung Soo
1996.
Fractional derivatives of Bloch functions, growth rate, and interpolation.
Acta Mathematica Hungarica,
Vol. 72,
Issue. 1-2,
p.
67.
Aulaskari, Rauno
Lappan, Peter
Xiao, Jie
and
Zhao, Ruhan
1997.
On α-Bloch Spaces and Multipliers of Dirichlet Spaces.
Journal of Mathematical Analysis and Applications,
Vol. 209,
Issue. 1,
p.
103.
Choe, Boo Rim
and
Lee, Young Joo
1998.
On M-harmonic Bloch functions and their Carleson measures.
Glasgow Mathematical Journal,
Vol. 40,
Issue. 2,
p.
273.
Aulaskari, Rauno
Nowak, Maria
and
Zhao, Ruhan
1998.
The n-th derivative characterisation of Möbius invariant Dirichlet space.
Bulletin of the Australian Mathematical Society,
Vol. 58,
Issue. 1,
p.
43.
Gürlebeck, K.
Kähler, U.
Shapiro, M.V.
and
Tovar, L.M.
1999.
On Qp-spaces of quaternion-valued functions.
Complex Variables, Theory and Application: An International Journal,
Vol. 39,
Issue. 2,
p.
115.
Gürlebeck, K.
2000.
Proceedings of the Second ISAAC Congress.
Vol. 8,
Issue. ,
p.
1387.
Nowak, Maria
2001.
Bloch space and möbius invariant besov spaces on the unit ball of .
Complex Variables, Theory and Application: An International Journal,
Vol. 44,
Issue. 1,
p.
1.
Gürlebeck, Klaus
2001.
Clifford Analysis and Its Applications.
p.
81.
Gürlebeck, K.
and
Malonek, H. R.
2001.
On strict inclusions of weighted dirichlet spaces of monogenic functions.
Bulletin of the Australian Mathematical Society,
Vol. 64,
Issue. 1,
p.
33.
Ren, Guangbin
and
Kähler, Uwe
2003.
Weighted Harmonic Bloch Spaces and Gleason's Problem.
Complex Variables, Theory and Application: An International Journal,
Vol. 48,
Issue. 3,
p.
235.
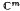 . Finally we discuss the related spaces BMOA and VMOA.
. Finally we discuss the related spaces BMOA and VMOA.

