Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-29T08:28:52.771Z Has data issue: false hasContentIssue false
  • English
  • Français

A MODIFIED FR CONJUGATE GRADIENT METHOD FOR COMPUTING 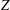$Z$-EIGENPAIRS OF SYMMETRIC TENSORS

Part of: Basic linear algebra Nonlinear algebraic or transcendental equations

Published online by Cambridge University Press:  26 July 2016

MEILAN ZENG  and
GUANGHUI ZHOU
MEILAN ZENG
Affiliation:
Nanjing University of Aeronautics and Astronautics, Nanjing, Jiangsu 210016, China Hubei Engineering University, Xiaogan, Hubei 432000, China email zml571@126.com
GUANGHUI ZHOU*
Affiliation:
Nanjing University of Aeronautics and Astronautics, Nanjing, Jiangsu 210016, China School of Mathematical Sciences, Information College, Huaibei Normal University, Huaibei, Anhui 235000, China email 163zgh@163.com
*
✉163zgh@163.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper proposes improvements to the modified Fletcher–Reeves conjugate gradient method (FR-CGM) for computing 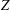$Z$-eigenpairs of symmetric tensors. The FR-CGM does not need to compute the exact gradient and Jacobian. The global convergence of this method is established. We also test other conjugate gradient methods such as the modified Polak–Ribière–Polyak conjugate gradient method (PRP-CGM) and shifted power method (SS-HOPM). Numerical experiments of FR-CGM, PRP-CGM and SS-HOPM show the efficiency of the proposed method for finding 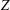$Z$-eigenpairs of symmetric tensors.

Keywords

conjugate gradient methodZ-eigenpairsymmetric tensor

MSC classification

Primary: 15A18: Eigenvalues, singular values, and eigenvectors
Secondary: 65H10: Systems of equations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 3 , December 2016 , pp. 411 - 420
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Chang, K.-C. and Zhang, T., ‘On the uniqueness and non-uniqueness of the positive z-eigenvector for transition probability tensors’, J. Math. Anal. Appl. 408(2) (2013), 525–540.Google Scholar
Cooper, J. and Dutle, A., ‘Spectra of uniform hypergraphs’, Linear Algebra Appl. 436(9) (2012), 3268–3292.Google Scholar
Cui, C., Dai, Y. and Nie, J., ‘All real eigenvalues of symmetric tensors’, SIAM J. Matrix Anal. Appl. 35(4) (2014), 1582–1601.Google Scholar
Gu, G., Li, D., Qi, L. and Zhou, S., ‘Descent directions of quasi-Newton methods for symmetric nonlinear equations’, SIAM J. Numer. Anal. 40(5) (2002), 1763–1774.Google Scholar
Han, L., ‘An unconstrained optimization approach for finding real eigenvalues of even order symmetric tensors’, Numer. Algebra Control Optim. 3(3) (2012), 583–599.Google Scholar
Henrion, D., Lasserre, J.-B. and Lofberg, J., ‘Gloptipoly 3: moments, optimization and semidefinite programming’, Optim. Methods Softw. 24(4–5) (2009), 761–779.Google Scholar
Hu, S., Huang, Z. and Qi, L., ‘Finding the extreme z-eigenvalues of tensors via a sequential semidefinite programming method’, Numer. Linear Algebra Appl. 20(6) (2013), 972–984.Google Scholar
Hu, S., Li, G., Qi, L. and Song, Y., ‘Finding the maximum eigenvalue of essentially nonnegative symmetric tensors via sum of squares programming’, J. Optim. Theory Appl. 158(3) (2013), 717–738.Google Scholar
Hu, S. and Qi, L., ‘Algebraic connectivity of an even uniform hypergraph’, J. Comb. Optim. 24(4) (2012), 564–579.CrossRefGoogle Scholar
Kofidis, E. and Regalia, P. A., ‘On the best rank-1 approximation of higher-order supersymmetric tensors’, SIAM J. Matrix Anal. Appl. 23(3) (2002), 863–884.CrossRefGoogle Scholar
Kolda, T. G. and Mayo., J. R., ‘Shifted power method for computing tensor eigenpairs’, SIAM J. Matrix Anal. Appl. 32(4) (2011), 1095–1124.CrossRefGoogle Scholar
Kolda, T. G. and Mayo, J. R., ‘An adaptive shifted power method for computing generalized tensor eigenpairs’, SIAM J. Matrix Anal. Appl. 35(4) (2014), 1563–1581.Google Scholar
Li, D. and Fukushima, M., ‘A globally and superlinearly convergent Gauss–Newton-based BFGS method for symmetric nonlinear equations’, SIAM J. Numer. Anal. 37(1) (1999), 152–172.CrossRefGoogle Scholar
Li, D. and Wang, X., ‘A modified Fletcher–Reeves-type derivative-free method for symmetric nonlinear equations’, Numer. Algebra Control Optim. 1(1) (2011), 71–82.CrossRefGoogle Scholar
Li, X., Ng, M. and Ye, Y., ‘Finding stationary probability vector of a transition probability tensor arising from a higher-order Markov chain’, Matrix 1 (2011), 1.Google Scholar
Li, G., Qi, L. and Yu, Y., ‘The z-eigenvalues of a symmetric tensor and its application to spectral hypergraph theory’, Numer. Linear Algebra Appl. 20(6) (2013), 1001–1029.CrossRefGoogle Scholar
Ni, Q. and Qi, L., ‘A quadratically convergent algorithm for finding the largest eigenvalue of a nonnegative homogeneous polynomial map’, J. Global Optim. 61(4) (2015), 627–641.Google Scholar
Ni, Q., Qi, L. and Wang, F., ‘An eigenvalue method for the positive definiteness identification problem’, IEEE Trans. Automat. Control 53 (2008), 1096–1107.Google Scholar
Qi, L., ‘Eigenvalues of a real supersymmetric tensor’, J. Symbolic Comput. 40(6) (2005), 1302–1324.CrossRefGoogle Scholar
Qi, L., ‘Rank and eigenvalues of a supersymmetric tensor, the multivariate homogeneous polynomial and the algebraic hypersurface it defines’, J. Symbolic Comput. 41(12) (2006), 1309–1327.Google Scholar
Qi, L., Wang, F. and Wang, Y., ‘Z-eigenvalue methods for a global polynomial optimization problem’, Math. Program. 118(2) (2009), 301–316.Google Scholar
Qi, L., Wang, Y. and Wu, E. X., ‘D-eigenvalues of diffusion kurtosis tensors’, J. Comput. Appl. Math. 221(1) (2008), 150–157.Google Scholar
Qi, L., Yu, G. and Wu, E. X., ‘Higher order positive semidefinite diffusion tensor imaging’, SIAM J. Imaging Sci. 3(3) (2010), 416–433.Google Scholar
Zeng, M. and Ni, Q., ‘Quasi-Newton method for computing z-eigenpairs of a symmetric tensor’, Pac. J. Optim. 11(2) (2015), 279–290.Google Scholar
Zhou, W. and Shen, D., ‘An inexact PRP conjugate gradient method for symmetric nonlinear equations’, Numer. Funct. Anal. Optim. 35(3) (2014), 370–388.Google Scholar