A simple graph 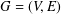 $G=(V,E)$ admits an
$G=(V,E)$ admits an 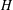 $H$ -covering if every edge in
$H$ -covering if every edge in 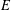 $E$ belongs to at least one subgraph of
$E$ belongs to at least one subgraph of 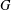 $G$ isomorphic to a given graph
$G$ isomorphic to a given graph 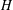 $H$ . Then the graph
$H$ . Then the graph 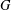 $G$ is
$G$ is 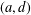 $(a,d)$ -
$(a,d)$ - 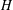 $H$ -antimagic if there exists a bijection
$H$ -antimagic if there exists a bijection 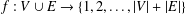 $f:V\cup E\rightarrow \{1,2,\ldots ,|V|+|E|\}$ such that, for all subgraphs
$f:V\cup E\rightarrow \{1,2,\ldots ,|V|+|E|\}$ such that, for all subgraphs 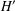 $H^{\prime }$ of
$H^{\prime }$ of 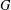 $G$ isomorphic to
$G$ isomorphic to 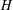 $H$ , the
$H$ , the 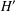 $H^{\prime }$ -weights,
$H^{\prime }$ -weights, 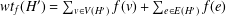 $wt_{f}(H^{\prime })=\sum _{v\in V(H^{\prime })}f(v)+\sum _{e\in E(H^{\prime })}f(e)$ , form an arithmetic progression with the initial term
$wt_{f}(H^{\prime })=\sum _{v\in V(H^{\prime })}f(v)+\sum _{e\in E(H^{\prime })}f(e)$ , form an arithmetic progression with the initial term  $a$ and the common difference
$a$ and the common difference 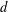 $d$ . When
$d$ . When 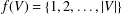 $f(V)=\{1,2,\ldots ,|V|\}$ , then
$f(V)=\{1,2,\ldots ,|V|\}$ , then  $G$ is said to be super
$G$ is said to be super 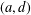 $(a,d)$ -
$(a,d)$ -  $H$ -antimagic. In this paper, we study super
$H$ -antimagic. In this paper, we study super 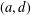 $(a,d)$ -
$(a,d)$ - 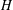 $H$ -antimagic labellings of a disjoint union of graphs for
$H$ -antimagic labellings of a disjoint union of graphs for 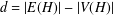 $d=|E(H)|-|V(H)|$ .
$d=|E(H)|-|V(H)|$ .
 $n$
$n$
 $H$ -ANTIMAGICNESS OF DISCONNECTED GRAPHS
$H$ -ANTIMAGICNESS OF DISCONNECTED GRAPHS
 $p$ -ADIC HYPERGEOMETRIC FUNCTIONS
$p$ -ADIC HYPERGEOMETRIC FUNCTIONS
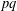 $pq$
$pq$
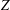 $Z$ -EIGENPAIRS OF SYMMETRIC TENSORS
$Z$ -EIGENPAIRS OF SYMMETRIC TENSORS