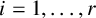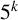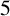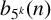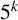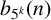Refine listing
Actions for selected content:
317 results in 05-XX
Self-avoiding walk is ballistic on graphs with more than one end
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 October 2025, e179
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Inequality arising from the iterated Laguerre operator for various partitions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 23 October 2025, pp. 1-22
-
- Article
- Export citation
Some algebraic properties of ASM varieties
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 22 October 2025, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE NUMBER OF PARTS IN A RANDOM t-REGULAR PARTITION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 16 October 2025, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Revisiting sums and products in countable and finite fields
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 13 October 2025, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Alternating sign matrices with reflective symmetry and plane partitions:
 $n+3$ pairs of equivalent statistics and a Cauchy-type identity
$n+3$ pairs of equivalent statistics and a Cauchy-type identity
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 08 October 2025, e168
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The algebraic structure of Dyson–Schwinger equations with multiple insertion places
- Part of
-
- Journal:
- Canadian Mathematical Communications / Volume 1 / 2025
- Published online by Cambridge University Press:
- 29 August 2025, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modified ascent sequences avoiding a pattern of length 4
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1390-1418
-
- Article
- Export citation
ENUMERATION AND DIVISIBILITY OF HIGHER DIMENSIONAL KING WALKS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 28 July 2025, pp. 1-12
-
- Article
- Export citation
Hook length inequalities for t-regular partitions in the t-aspect
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 24 July 2025, pp. 1-12
-
- Article
- Export citation
Zero-one dual characters of flagged Weyl modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 08 July 2025, pp. 1-23
-
- Article
- Export citation
K-Orbit closures and Hessenberg varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 30 June 2025, e103
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integration on complex Grassmannians, deformed monotone Hurwitz numbers, and interlacing phenomena
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 30 June 2025, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Congruences modulo powers of 5 for partition k-tuples with 5-cores
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 17 June 2025, pp. 1245-1261
-
- Article
- Export citation
Exact solution to the Chow–Robbins game for almost all n, by using a catalan triangle
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 16 May 2025, pp. 1-36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A REMARK ON GENERALISED CUBIC PARTITIONS MODULO
 $5$
$5$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 07 May 2025, pp. 1-5
-
- Article
- Export citation
ON
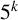 $5^k$-REGULAR PARTITIONS MODULO POWERS OF
$5^k$-REGULAR PARTITIONS MODULO POWERS OF 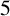 $5$
$5$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 14 April 2025, pp. 1-9
-
- Article
- Export citation
COMBINATORIAL PROOFS FOR TWO-COLOUR PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1-5
-
- Article
- Export citation
A combinatorial formula for the nabla operator
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 17 September 2025, pp. 800-830
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWO NEW TRUNCATED IDENTITIES AND PARTITION THEOREMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 21 March 2025, pp. 1-8
-
- Article
- Export citation