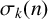FirstView articles
Contents
Research Article
GALOIS GROUPS OF APÉRY-LIKE SERIES MODULO PRIMES
- Part of:
-
- Published online by Cambridge University Press:
- 13 February 2026, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE KNOT QUANDLES OF SUCIU’S RIBBON n-KNOTS AND AUTOMORPHISMS ON THE FREE GROUP OF RANK TWO
- Part of:
-
- Published online by Cambridge University Press:
- 13 February 2026, pp. 1-6
-
- Article
- Export citation
ON PROPERLY
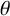 $\theta $-CONGRUENT NUMBERS OVER REAL NUMBER FIELDS
$\theta $-CONGRUENT NUMBERS OVER REAL NUMBER FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 13 February 2026, pp. 1-6
-
- Article
- Export citation
SOME MONOCHROMATIC PATTERNS IN NATURAL NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 13 February 2026, pp. 1-13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON THE PLANAR SKOROKHOD EMBEDDING PROBLEM
- Part of:
-
- Published online by Cambridge University Press:
- 12 February 2026, pp. 1-7
-
- Article
- Export citation
ON MAXIMAL CYCLIC SUBGROUPS OF FINITE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 12 February 2026, pp. 1-9
-
- Article
- Export citation
PARTITIONS OF NATURAL NUMBERS AND THEIR ORDERED REPRESENTATION FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 12 February 2026, pp. 1-8
-
- Article
- Export citation
MINIMALLY IRREDUCIBLE FAMILIES OF COMPLEX MATRICES
- Part of:
-
- Published online by Cambridge University Press:
- 06 February 2026, pp. 1-12
-
- Article
- Export citation
PhD Abstract
(WEAK) COMPACTNESS CRITERIA IN NONCOMMUTATIVE SYMMETRIC SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 05 February 2026, pp. 1-2
-
- Article
-
- You have access
- HTML
- Export citation
Research Article
GROUPS WITH AT MOST 13 NONPOWER SUBGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 30 January 2026, pp. 1-14
-
- Article
- Export citation
GROUPS WITH ONLY NEARLY NORMAL OR CONTRANORMAL SUBGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 30 January 2026, pp. 1-10
-
- Article
- Export citation
PhD Abstract
NEW EXPLICIT AND ASYMPTOTIC RESULTS IN SIEVE THEORY
- Part of:
-
- Published online by Cambridge University Press:
- 30 January 2026, pp. 1-3
-
- Article
-
- You have access
- HTML
- Export citation
Research Article
FIXED-ROTATION MINKOWSKI AVERAGING: CLASSIFICATION AND SHARP RATES
- Part of:
-
- Published online by Cambridge University Press:
- 29 January 2026, pp. 1-12
-
- Article
- Export citation
MODULAR ELEMENTS IN THE LATTICE OF MONOID VARIETIES
- Part of:
-
- Published online by Cambridge University Press:
- 29 January 2026, pp. 1-11
-
- Article
- Export citation
SIMULTANEOUS BOUNDING OF
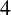 $4$-RANKS IN NARROW CLASS GROUPS OF QUADRATIC FIELDS
$4$-RANKS IN NARROW CLASS GROUPS OF QUADRATIC FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 29 January 2026, pp. 1-7
-
- Article
- Export citation
LINEAR INDEPENDENCE OF QUANTUM TRANSLATES
- Part of:
-
- Published online by Cambridge University Press:
- 26 January 2026, pp. 1-7
-
- Article
- Export citation
MULTIPLE SOLUTIONS FOR QUASILINEAR SCHRÖDINGER EQUATIONS WITH NONLINEARITY SUBLINEAR AT ZERO
- Part of:
-
- Published online by Cambridge University Press:
- 26 January 2026, pp. 1-13
-
- Article
- Export citation
p-ADIC VALUATION OF
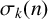 $\sigma _k(n)$
$\sigma _k(n)$
- Part of:
-
- Published online by Cambridge University Press:
- 26 January 2026, pp. 1-5
-
- Article
- Export citation
COMBINATORIAL PROOFS OF CERTAIN RESULTS OF CHEN AND ZOU ON TWO-COLOUR PARTITIONS
- Part of:
-
- Published online by Cambridge University Press:
- 12 January 2026, pp. 1-7
-
- Article
- Export citation
THE REIDEMEISTER SPECTRUM OF ZM-GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 12 January 2026, pp. 1-6
-
- Article
- Export citation