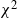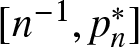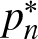Refine listing
Actions for selected content:
423 results in 60Dxx
Limit theorems for the number of crossings and stress in projections of a random geometric graph
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 01 October 2025, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Large and moderate deviations in Poisson navigations
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 10 September 2025, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounds on some geometric functionals of high dimensional Brownian convex hulls and their inverse processes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 27 August 2025, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Couplings and Poisson approximation for stabilising functionals of determinantal point processes
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 11 July 2025, pp. 635-648
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Extremal behavior of stationary marked point processes
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 18 June 2025, pp. 1-42
-
- Article
- Export citation
Sojourn functionals of time-dependent
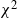 $\chi^2$-random fields on two-point homogeneous spaces
$\chi^2$-random fields on two-point homogeneous spaces
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 13 June 2025, pp. 1-20
-
- Article
- Export citation
Moderate deviations for weight-dependent random connection models
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 04 June 2025, pp. 1-23
-
- Article
- Export citation
Estranged facets and k-facets of Gaussian random point sets
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 02 April 2025, pp. 859-875
- Print publication:
- September 2025
-
- Article
- Export citation
GAUSSIAN HOLOMORPHIC SECTIONS ON NONCOMPACT COMPLEX MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 12 March 2025, pp. 1197-1262
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Graph connectivity with fixed endpoints in the random-connection model
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 39 / Issue 3 / July 2025
- Published online by Cambridge University Press:
- 21 February 2025, pp. 370-396
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Probability that n points are in convex position in a regular κ-gon: Asymptotic results
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 17 January 2025, pp. 811-870
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the asymptotic normality of persistent Betti numbers
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 03 December 2024, pp. 492-523
- Print publication:
- June 2025
-
- Article
- Export citation
Non-hyperuniformity of Gibbs point processes with short-range interactions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 02 August 2024, pp. 1380-1406
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the probability of a Pareto record
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 04 June 2024, pp. 752-764
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Depths in random recursive metric spaces
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1448-1462
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Series expansions for random disc-polygons in smooth plane convex bodies
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 16 May 2024, pp. 1407-1423
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Buffon’s problem determines Gaussian curvature in three geometries
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 08 April 2024, pp. 1127-1138
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Central limit theorem for a birth–growth model with poisson arrivals and random growth speed
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 19 January 2024, pp. 1004-1032
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On minimum spanning trees for random Euclidean bipartite graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 30 November 2023, pp. 319-350
-
- Article
- Export citation
Almost sure convergence and second moments of geometric functionals of fractal percolation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 927-959
- Print publication:
- September 2024
-
- Article
- Export citation