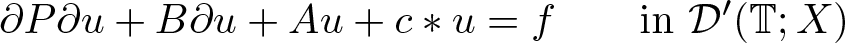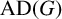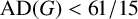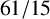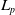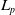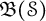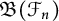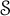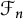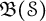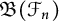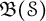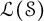Refine listing
Actions for selected content:
261 results in 43Axx
Non-uniqueness phase in hyperbolic marked random connection models using the spherical transform
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 03 October 2025, pp. 1-48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Green’s relations and left amenable semigroups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 15 September 2025, pp. 1-14
-
- Article
- Export citation
Lorentz boundedness and compactness of Riesz transform commutator on stratified Lie groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 15 September 2025, pp. 1-28
-
- Article
- Export citation
Characterisation of Locally Compact Abelian Groups Having Spectral Synthesis
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 15 September 2025, e145
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The invariant subspaces of periodic Fourier multipliers with application to abstract evolution equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 June 2025, pp. 1-47
-
- Article
- Export citation
SMALL VALUES AND FORBIDDEN VALUES FOR THE FOURIER ANTI-DIAGONAL CONSTANT OF A FINITE GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 07 April 2025, pp. 297-316
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MULTIPLICATIVE (IN)STABILITY OF BANACH ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 17 March 2025, pp. 194-200
- Print publication:
- August 2025
-
- Article
- Export citation
Non-commutative skew-product extension dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 2672-2694
- Print publication:
- September 2025
-
- Article
- Export citation
Hardy spaces and Riesz transforms on a Lie group of exponential growth
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 17 February 2025, pp. 731-762
-
- Article
- Export citation
Absolute dilations of UCP self-adjoint Fourier multipliers: the nonunimodular case
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 14 February 2025, pp. 307-324
- Print publication:
- September 2025
-
- Article
- Export citation
An endpoint estimate for product singular integral operators on stratified Lie groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWISTED RUELLE ZETA FUNCTION ON HYPERBOLIC MANIFOLDS AND COMPLEX-VALUED ANALYTIC TORSION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 22 January 2025, pp. 813-845
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transference of multilinear Fourier and Schur multipliers acting on noncommutative
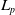 $L_p$-spaces for non-unimodular groups
$L_p$-spaces for non-unimodular groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 197-223
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Entropy of group actions beyond uniform lattices
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 21 November 2024, pp. 1461-1502
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE WEYL TRANSFORM OF A SMOOTH MEASURE ON A REAL-ANALYTIC SUBMANIFOLD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 11 October 2024, pp. 184-193
- Print publication:
- August 2025
-
- Article
- Export citation
Bounds on multiplicities of symmetric pairs of finite groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 09 September 2024, e73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weak amenability for dual Banach algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 29 April 2024, pp. 740-748
-
- Article
- Export citation
Thompson’s semigroup and the first Hochschild cohomology
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 07 March 2024, pp. 842-862
- Print publication:
- June 2025
-
- Article
- Export citation
Bohr chaoticity of principal algebraic actions and Riesz product measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 2933-2959
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Arens regularity of ideals of the group algebra of a compact Abelian group
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 27 October 2023, pp. 718-734
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation