Hostname: page-component-5b777bbd6c-w9n4q Total loading time: 0 Render date: 2025-06-24T23:40:14.516Z Has data issue: false hasContentIssue false
  • English
  • Français

The invariant subspaces of periodic Fourier multipliers with application to abstract evolution equations

Part of: Miscellaneous applications of functional analysis Abstract harmonic analysis Abstract integral equations, integral equations in abstract spaces Harmonic analysis in several variables Harmonic analysis in one variable

Published online by Cambridge University Press:  24 June 2025

Sebastian Król  and
Jarosław Sarnowski
Sebastian Król*
Affiliation:
Faculty of Mathematics and Computer Science, Adam Mickiewicz University in Poznań, ul. Uniwersytetu Poznańskiego 4, Poznań, Poland (sebastian.krol@amu.edu.pl) (corresponding author)
Jarosław Sarnowski
Affiliation:
Faculty of Mathematics and Computer Science, Nicolaus Copernicus University in Toruń, ul. Chopina 12/18, Toruń, Poland (jsarnowski@doktorant.umk.pl)
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

By methods of harmonic analysis, we identify large classes of Banach spaces invariant of periodic Fourier multipliers with symbols satisfying the classical Marcinkiewicz type conditions. Such classes include general (vector-valued) Banach function spaces Φ and/or the scales of Besov and Triebel–Lizorkin spaces defined on the basis of Φ.

We apply these results to the study of the well-posedness and maximal regularity property of an abstract second-order integro-differential equation, which models various types of elliptic and parabolic problems arising in different areas of applied mathematics. In particular, under suitable conditions imposed on a convolutor c and the geometry of an underlying Banach space X, we characterize the conditions on the operators A, B, and P on X such that the following periodic problem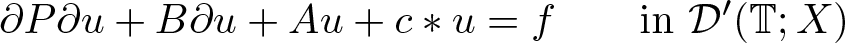

\begin{equation*}\partial P \partial u + B \partial u + {A} u + c \ast u = f \qquad \textrm{in } {\mathcal D}'({\mathbb{T}}; X)\end{equation*}

is well-posed with respect to large classes of function spaces. The obtained results extend the known theory on the maximal regularity of such problem.

Keywords

Besov spacesHardy–Littlewood maximal operatorintegro-differential equationsmaximal regularityperiodic Fourier multipliersRubio de Francia iteration algorithmTriebel–Lizorkin spaceswell-posedness

MSC classification

Primary: 42B37: Harmonic analysis and PDE
Secondary: 42A45: Multipliers 45N05: Abstract integral equations, integral equations in abstract spaces 46N20: Applications to differential and integral equations 43A15: $L^p$-spaces and other function spaces on groups, semigroups, etc.
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 47
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Amann, H.. Linear and quasilinear parabolic problems: Abstract linear theory, Monographs in Mathematics, Vol. 89 (Birkhäuser, Basel, 1995).Google Scholar
Amann, H.. Operator-valued Fourier multipliers, vector-valued Besov spaces, and applications. Math. Nachr. 186 (1997), 5–56.CrossRefGoogle Scholar
Andersen, K. F. and Mohanty, P.. Restriction and extension of Fourier multipliers between weighted Lp spaces on $\Bbb{R}^n$ and $\Bbb{T}^n$. Proc. Amer. Math. Soc. 137 (2009), 1689–1697.CrossRefGoogle Scholar
Aparicio, R. and Keyantuo, V.. Besov maximal regularity for a class of degenerate integro-differential equations with infinite delay in Banach spaces. Math. Methods Appl. Sci. 43 (2020), 7239–7268.CrossRefGoogle Scholar
Aparicio, R. and Keyantuo, V.. Lp-maximal regularity for a class of degenerate integro-differential equations with infinite delay in Banach spaces. J. Fourier Anal. Appl. 26 (2020), 39.CrossRefGoogle Scholar
Arendt, W., Batty, C. and Bu, S.. Fourier multipliers for Hölder continuous functions and maximal regularity. Studia Math. 160 (2004), 23–51.CrossRefGoogle Scholar
Arendt, W. and Bu, S.. The operator-valued Marcinkiewicz multiplier theorem and maximal regularity. Math. Z. 240 (2002), 311–343.CrossRefGoogle Scholar
Arendt, W. and Bu, S.. Operator-valued Fourier multipliers on periodic Besov spaces and applications. Proc. Edinb. Math. Soc. (2) 47 (2004), 15–33.CrossRefGoogle Scholar
Arendt, W. and Bu, S.. Operator-valued multiplier theorems characterizing Hilbert spaces. J. Aust. Math. Soc. 77 (2004), 175–184.CrossRefGoogle Scholar
Asmar, N., Berkson, E. and Gillespie, T. A.. On Jodeit’s multiplier extension theorems. J. Anal. Math. 64 (1994), 337–345.CrossRefGoogle Scholar
Auscher, P. and Axelsson, A.. Remarks on maximal regularity, Parabolic problems, Progr. Nonlinear Differential Equations Appl., Vol. 80, (Birkhäuser/Springer Basel AG, Basel, 2011).Google Scholar
Auscher, P. and Axelsson, A.. Weighted maximal regularity estimates and solvability of non-smooth elliptic systems I. Invent. Math. 184 (2011), 47–115.CrossRefGoogle Scholar
Böttcher, A. and Karlovich, Y.I.. Carleson curves, Muckenhoupt weights, and Toeplitz operators, Progress in Mathematics, Vol. 154 (Birkhäuser, Basel, 1997).Google Scholar
Bennett, C. and Sharpley, R.. Interpolation of operators, Pure and Applied Mathematics, Vol. 129 (Academic Press, Inc., Boston, MA, 1988).Google Scholar
Berkson, E. and Gillespie, T. A.. On restrictions of multipliers in weighted settings. Indiana Univ. Math. J. 52 (2003), 927–961.CrossRefGoogle Scholar
Blasco, O. and Villarroya, P.. Transference of vector-valued multipliers on weighted Lp-spaces. Canad. J. Math. 65 (2013), 510–543.CrossRefGoogle Scholar
Bourgain, J.. Some remarks on Banach spaces in which martingale difference sequences are unconditional. Ark. Math. 21 (1983), 163–168.CrossRefGoogle Scholar
Bu, S.. Well-posedness of second order degenerate differential equations in vector-valued function spaces. Studia Math. 214 (2013), 1–16.CrossRefGoogle Scholar
Bu, S. and Cai, G.. Well-posedness of second-order degenerate differential equations with finite delay in vector-valued function spaces. Pacific J. Math. 288 (2017), 27–46.CrossRefGoogle Scholar
Bu, S. and Cai, G.. Periodic solutions of second order degenerate differential equations with delay in Banach spaces. Canad. Math. Bull. 61 (2018), 717–737.CrossRefGoogle Scholar
Bu, S. and Cai, G.. Periodic solutions of second order degenerate differential equations with finite delay in Banach spaces. J. Fourier Anal. Appl. 25 (2019), 32–50.CrossRefGoogle Scholar
Bu, S. and Fang, Y.. Maximal regularity for integro-differential equation on periodic Triebel-Lizorkin spaces. Taiwanese J. Math. 12 (2008), 281–292.CrossRefGoogle Scholar
Bu, S. and Fang, Y.. Periodic solutions of delay equations in Besov spaces and Triebel-Lizorkin spaces. Taiwanese J. Math. 13 (2009), 1063–1076.CrossRefGoogle Scholar
Bu, S. and Kim, J. M.. Operator-valued Fourier multiplier theorems on Lp-spaces on $\Bbb{T}^d$. Arch. Math. (Basel) 82 (2004), 404–414.CrossRefGoogle Scholar
Bu, S. and Kim, J. M.. Operator-valued Fourier multiplier theorems on periodic Triebel spaces. Acta Mathematica Sinica 21 (2005), 1049–1056.CrossRefGoogle Scholar
Burkholder, D. L.. A geometrical characterization of Banach spaces in which martingale difference sequences are unconditional. Ann. Probab. 9 (1981), 997–1011.CrossRefGoogle Scholar
Chill, R., and Fiorenza, A.. Singular integral operators with operator-valued kernels, and extrapolation of maximal regularity into rearrangement invariant Banach function spaces. J. Evol. Eq 14 (2014), 795–828.CrossRefGoogle Scholar
Chill, R. and Król, S.. Weighted inequalities for singular integral operators on the half-line. Studia Math. 243 (2018), 171–206.CrossRefGoogle Scholar
Chill, R. and Srivastava, S.. Lp-maximal regularity for second order Cauchy problems. Math. Z. 251 (2005), 751–781.CrossRefGoogle Scholar
Clément, P., de Pagter, B., Sukochev, F. A. and Witvliet, H.. Schauder decomposition and multiplier theorems. Studia Math. 138 (2000), 135–163.Google Scholar
Clément, P. and Prüss, J.. Lecture Notes in Pure and Appl. Math., Vol. 215, (Dekker, New York, 2001).Google Scholar
de Leeuw, K.. On Lp multipliers. Ann. of Math. (2) 81 (1965), 364–379.CrossRefGoogle Scholar
Denk, R., Hieber, M. and Prüss, J.. Optimal $L_p-L_q$-regularity estimates for parabolic boundary value problems with inhomogeneous data. Math. Z. 257 (2007), 193–224.CrossRefGoogle Scholar
Edwards, R. E.. Fourier series: A modern introduction. Vol. II (Holt, Rinehart and Winston, Inc., New York-Montreal, Que.-London, 1967).Google Scholar
Edwards, R. E.. Fourier series. A modern introduction. Vol. 1, Graduate Texts in Mathematics, 2nd ed., Vol. 64 (Springer, New York-Berlin, 1979).Google Scholar
Fackler, S.. Maximal regularity: Positive counterexamples on UMD-Banach lattices and exact intervals for the negative solution of the extrapolation problem. Proc. Amer. Math. Soc. 144 (2016), 2015–2028.CrossRefGoogle Scholar
Fackler, S., Hytönen, T. and Lindemulder, N.. Weighted estimates for operator-valued Fourier multipliers. Collect. Math. 71 (2020), 511–548.CrossRefGoogle Scholar
Fu, X. and Li, M.. Maximal regularity of second-order evolution equations with infinite delay in Banach spaces. Studia Math. 224 (2014), 199–219.CrossRefGoogle Scholar
Girardi, M. and Weis, L.. Operator-valued Fourier multiplier theorems on Besov spaces. Math. Nachr. 251 (2003), 34–51.CrossRefGoogle Scholar
, H. Triebel. Spaces of Besov-Hardy-Sobolev type, Teubner-Texte Math., Vol. 15 (Teubner, Leipzig, 1978).Google Scholar
Henríquez, H. R. and Lizama, C.. Periodic solutions of abstract functional differential equations with infinite delay. Nonlinear Anal. 75 (2012), 2016–2023.CrossRefGoogle Scholar
Hytönen, T.. The sharp weighted bound for general Calderón-Zygmund operators. Ann. of Math. (2) 175 (2012), 1473–1506.CrossRefGoogle Scholar
Hytönen, T., van Neerven, J., Veraar, M. and Weis, L.. Analysis in Banach spaces. Vol. I. Martingales and Littlewood-Paley theory, Ergebnisse der Mathematik und Ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], Vol. 63 (Springer, Cham, 2016).Google Scholar
Hytönen, T., van Neerven, J., Veraar, M. and Weis, L.. Analysis in Banach spaces. Vol. II. Probabilistic methods and operator theory, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], Vol. 67 (Springer, Cham, 2017).Google Scholar
Hytönen, T. and Weis, L.. Singular integrals on Besov spaces. Math. Nachr. 279 (2006), 581–598.CrossRefGoogle Scholar
Hytönen, T. and Weis, L.. Singular convolution integrals with operator-valued kernel. Math. Z. 255 (2007), 393–425.CrossRefGoogle Scholar
Jodeit, M.. Restrictions and extensions of Fourier multipliers. Studia Math. 34 (1970), 215–226.CrossRefGoogle Scholar
Kalton, N. J. and Lancien, G.. A solution to the problem of Lp-maximal regularity. Math. Z. 235 (2000), 559–568.CrossRefGoogle Scholar
Keyantuo, V. and Lizama, C.. Fourier multipliers and integro-differential equations in Banach spaces. J. London Math. Soc. 69 (2004), 737–750.CrossRefGoogle Scholar
Keyantuo, V. and Lizama, C.. Maximal regularity for a class of integro-differential equations with infinite delay in Banach spaces. Studia Math. 168 (2005), 25–50.CrossRefGoogle Scholar
Keyantuo, V., Lizama, C. and Poblete, V.. Periodic solutions of integro-differential equations in vector-valued function spaces. J. Differential Equations 246 (2009), 1007–1037.CrossRefGoogle Scholar
Knese, G., McCarthy, J. E. and Moen, K.. Unions of Lebesgue spaces and A 1 majorants. Pacific J. Math. 280 (2016), 411–432.CrossRefGoogle Scholar
Król, S.. The maximal regularity property of abstract integro-differential equations. J. Evol. Equ. 23 (2023), 38.CrossRefGoogle Scholar
Kunstmann, P. C. and Weis, L.. Maximal Lp regularity for parabolic equations, Fourier multiplier theorems and $H^\infty$ functional calculus, Levico Lectures, Proceedings of the Autumn School on Evolution Equations and Semigroups (Iannelli, M., Nagel, R. and Piazzera, S., eds.), (Springer Verlag, 2004), , Vol. 69, Heidelberg, Berlin.CrossRefGoogle Scholar
Lizama, C.. Fourier multipliers and periodic solutions of delay equations in Banach spaces. J. Math. Anal. Appl. 324 (2006), 921–933.CrossRefGoogle Scholar
Lizama, C. and Poblete, V.. Maximal regularity for perturbed integral equations on periodic Lebesgue spaces. J. Math. Anal. Appl. 348 (2008), 775–786.CrossRefGoogle Scholar
Lizama, C. and Ponce, R.. Periodic solutions of degenerate differential equations in vector-valued function spaces. Studia Math. 202 (2011), 49–63.CrossRefGoogle Scholar
Lizama, C. and Ponce, R.. Maximal regularity for degenerate differential equations with infinite delay in periodic vector-valued function spaces. Proc. Edinb. Math. Soc. 56 (2013), 853–871.CrossRefGoogle Scholar
Poblete, V.. Maximal regularity of second-order equations with delay. J. Differential Equations 246 (2009), 261–276.CrossRefGoogle Scholar
Prüss, J.. Evolutionary integral equations and applications, Monographs in Mathematics, Vol. 87 (Birkhäuser Verlag, Basel, 1993).Google Scholar
Prüss, J. and Simonett, G.. Maximal regularity for evolution equations in weighted $L\ p$-spaces. Arch. Math. (Basel) 82 (2004), 415–431.CrossRefGoogle Scholar
Prüss, J. and Simonett, G.. $H^\infty$ calculus for the sum of non-commuting operators. Trans. Amer. Math. Soc. 359 (2007), 3549–3565.CrossRefGoogle Scholar
Da Prato, G., and Lunardi, A.. Periodic solutions for linear integro-differential equations with infinite delay in Banach spaces, Differential Equations in Banach Spaces (Bologna, 1985), Lecture Notes in Math., Vol. 1223, (Springer, Berlin, 1986).Google Scholar
Rubio de Francia, J. L.. Martingale and integral transforms of Banach space valued functions, Probability and Banach Spaces (Zaragoza, 1985), Lecture Notes in Math., Vol. 1221, (Springer, Berlin, 1986).Google Scholar
Rubio de Francia, J. L., Ruiz, F. J. and Torrea, J. L.. Calderón-Zygmund theory for operator-valued kernels. Adv. in Math. 62 (1986), 7–48.CrossRefGoogle Scholar
Schmeisser, H. J. and Triebel, H.. Topics in Fourier Analysis and Function Spaces (A Wiley-Interscience Publication, John Wiley & Sons, Ltd, Chichester, 1987).Google Scholar
Stein, E. M.. Harmonic analysis: Real-variable methods, orthogonality, and oscillatory integrals, With the assistance of Timothy S. Murphy, Monographs in Harmonic Analysis, III, Princeton Mathematical Series, Vol. 43 (Princeton University Press, Princeton, NJ, 1993).Google Scholar
Strkalj, Z. and Weis, L.. On operator-valued Fourier multiplier theorems. Trans. Amer. Math. Soc. 359 (2007), 3529–3547.CrossRefGoogle Scholar
Weis, L.. Operator-valued Fourier multiplier theorems and maximal Lp-regularity. Math. Ann. 319 (2001), 735–758.CrossRefGoogle Scholar