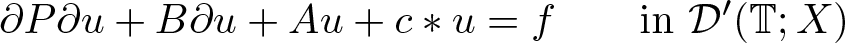Refine listing
Actions for selected content:
270 results in 42Bxx
Weak porosity on metric measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 17 November 2025, pp. 1-48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Localization operators on discrete Orlicz modulation spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 14 November 2025, pp. 1-21
-
- Article
- Export citation
A phase-space approach to weighted Fourier extension inequalities
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 03 November 2025, e181
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Variation of the one-dimensional centered maximal operator on simple functions with gaps between pieces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ANALYSIS OF THE LAPLACIAN ON A CLASS OF NONDOUBLING CONNECTED SUMS AND MANIFOLDS WITH QUADRATICALLY DECAYING RICCI CURVATURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 17 October 2025, pp. 1-2
-
- Article
-
- You have access
- HTML
- Export citation
Weighted decoupling estimates and the Bochner-Riesz means
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 06 October 2025, e167
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lorentz boundedness and compactness of Riesz transform commutator on stratified Lie groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 15 September 2025, pp. 1-28
-
- Article
- Export citation
A note on the best constant for uncentered maximal functions with measure on ℝ
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 12 September 2025, pp. 1-9
-
- Article
- Export citation
Quantitative ergodic theorems for actions of groups of polynomial growth
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 04 September 2025, pp. 1-54
-
- Article
- Export citation
An extension-restriction theorem for weighted Besov spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 26 August 2025, pp. 1-48
-
- Article
- Export citation
The boundedness of the bilinear fractional integrals along curves
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 22 August 2025, pp. 1-31
-
- Article
- Export citation
Well-posedness of Naiver–Stokes equations in logarithmic Q spaces covering
 $BMO^{-1}$ and its fractional counterpart
$BMO^{-1}$ and its fractional counterpart
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 11 August 2025, pp. 1-64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On decoupling and restriction estimates
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 07 August 2025, pp. 731-736
- Print publication:
- November 2025
-
- Article
- Export citation
Hardy-type inequalities for the drifting p-Laplace operator and applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 06 August 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On global fractional Calderón–Zygmund regularity for the fractional Dirichlet problem on Lipschitz domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 August 2025, pp. 1-31
-
- Article
- Export citation
The invariant subspaces of periodic Fourier multipliers with application to abstract evolution equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 June 2025, pp. 1-47
-
- Article
- Export citation
The local geometry of idempotent Schur multipliers
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 March 2025, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some remarks on Riesz transforms on exterior Lipschitz domains
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 March 2025, e58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Parabolic Muckenhoupt weights characterized by parabolic fractional maximal and integral operators with time lag
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 17 March 2025, pp. 1-54
-
- Article
- Export citation
Boundedness on Triebel–Lizorkin spaces for the Calderón commutator with rough kernel
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 12 March 2025, pp. 1069-1081
- Print publication:
- December 2025
-
- Article
- Export citation