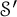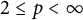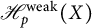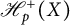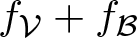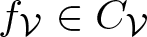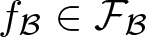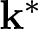Refine listing
Actions for selected content:
218 results in 46Exx
Banach lattices of positively homogeneous functions induced by a Banach space
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 27 October 2025, pp. 1-37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ANALYSIS OF THE LAPLACIAN ON A CLASS OF NONDOUBLING CONNECTED SUMS AND MANIFOLDS WITH QUADRATICALLY DECAYING RICCI CURVATURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 17 October 2025, pp. 1-2
-
- Article
-
- You have access
- HTML
- Export citation
A unified topological analysis of variable growth Kirchhoff-type equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Continuity and realization of multiplicative maps between RKHS and their cyclicity preserving properties
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 08 September 2025, pp. 1-14
-
- Article
- Export citation
On the Assouad spectrum of Hölder and Sobolev graphs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An extension-restriction theorem for weighted Besov spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 26 August 2025, pp. 1-48
-
- Article
- Export citation
Well-posedness of Naiver–Stokes equations in logarithmic Q spaces covering
 $BMO^{-1}$ and its fractional counterpart
$BMO^{-1}$ and its fractional counterpart
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 11 August 2025, pp. 1-64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Schur–Agler class in infinitely many variables
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 14 July 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Isometric rigidity of the Wasserstein space over the plane with the maximum metric
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 June 2025, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A logarithmic uncertainty principle for functions with radial symmetry
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 31 March 2025, pp. 811-824
-
- Article
- Export citation
Trudinger-type inequalities in Musielak–Orlicz spaces and double phase functionals
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 27 March 2025, pp. 1-18
-
- Article
- Export citation
New aspects of Bargmann transform using Touchard polynomials and hypergeometric functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-46
-
- Article
- Export citation
Volterra operators between Hardy spaces of vector-valued Dirichlet series
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 286-300
- Print publication:
- March 2025
-
- Article
- Export citation
Functions with small BMO norm
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 08 January 2025, pp. 1-15
-
- Article
- Export citation
Beurling type invariant subspaces on Hardy and Bergman spaces of the unit ball or polydisk
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 232-245
- Print publication:
- March 2025
-
- Article
- Export citation
Finely quasiconformal mappings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 23 December 2024, pp. 1-25
-
- Article
- Export citation
Fractal interpolant curve fitting and reproducing kernel Hilbert spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 247-267
-
- Article
- Export citation
Tilings of the hyperbolic space and Lipschitz functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 18 November 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maximal noncompactness of limiting Sobolev embeddings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 November 2024, pp. 1-19
-
- Article
- Export citation
A note on the space of all Toeplitz operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 12 November 2024, pp. 1123-1140
- Print publication:
- December 2024
-
- Article
- Export citation