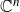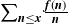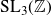FirstView articles
Contents
Research Article
Some uniform effective results on André–Oort for sums of powers in
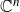 ${\mathbb{C}}^n$
${\mathbb{C}}^n$
- Part of:
-
- Published online by Cambridge University Press:
- 13 January 2026, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
How negative can
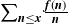 $\boldsymbol{\sum}_{\textbf{n}\le \textbf{x}}\frac{\textbf{f}(\textbf{n})}{\textbf{n}}$ be?
$\boldsymbol{\sum}_{\textbf{n}\le \textbf{x}}\frac{\textbf{f}(\textbf{n})}{\textbf{n}}$ be?
- Part of:
-
- Published online by Cambridge University Press:
- 05 January 2026, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $\Omega$-results for exponential sums related to Maass cusp forms for
$\Omega$-results for exponential sums related to Maass cusp forms for 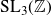 $\mathrm{SL}_3(\mathbb Z)$
$\mathrm{SL}_3(\mathbb Z)$
- Part of:
-
- Published online by Cambridge University Press:
- 29 December 2025, pp. 1-54
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A construction of minimal coherent filling pairs
- Part of:
-
- Published online by Cambridge University Press:
- 16 December 2025, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The rational (non-)formality of the non-3-equal manifolds
- Part of:
-
- Published online by Cambridge University Press:
- 08 December 2025, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on transverse sets and bilinear varieties
- Part of:
-
- Published online by Cambridge University Press:
- 27 November 2025, pp. 1-13
-
- Article
- Export citation
Local central limit theorem for triangle counts in sparse random graphs
- Part of:
-
- Published online by Cambridge University Press:
- 14 November 2025, pp. 1-17
-
- Article
- Export citation
Quantization dimensions of negative order
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Initial degenerations of flag varieties
- Part of:
-
- Published online by Cambridge University Press:
- 10 November 2025, pp. 1-29
-
- Article
- Export citation
On The Schinzel–Wójcik Problem Under Hypothesis H
- Part of:
-
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-13
-
- Article
- Export citation
Silting, cosilting and extensions of commutative rings
- Part of:
-
- Published online by Cambridge University Press:
- 27 October 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The structure of Lonely Runner spectra
- Part of:
-
- Published online by Cambridge University Press:
- 24 October 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the degree-two part of the associated graded of the lower central series of the Torelli group
- Part of:
-
- Published online by Cambridge University Press:
- 20 October 2025, pp. 1-39
-
- Article
- Export citation
Infinitely many standard trisection diagrams for Gluck twisting
- Part of:
-
- Published online by Cambridge University Press:
- 16 October 2025, pp. 1-27
-
- Article
- Export citation
A note on morphisms to wreath products
- Part of:
-
- Published online by Cambridge University Press:
- 08 October 2025, pp. 1-28
-
- Article
- Export citation
Combinatorial cusp count and clover invariants
- Part of:
-
- Published online by Cambridge University Press:
- 03 October 2025, pp. 1-9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation