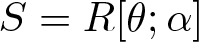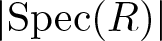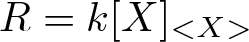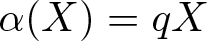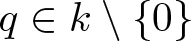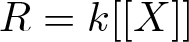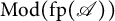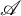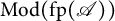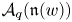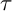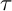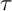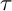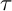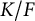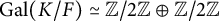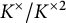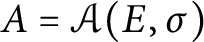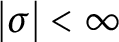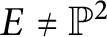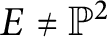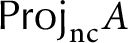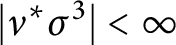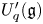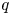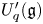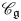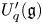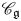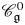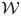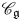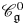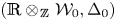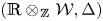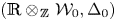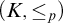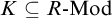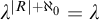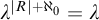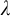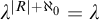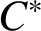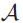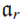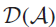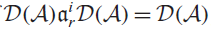Refine listing
Actions for selected content:
106 results in 16Dxx
Silting, cosilting and extensions of commutative rings
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 27 October 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Property (◇) for Ore extensions of small Krull dimension
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 21 May 2025, pp. 1169-1187
-
- Article
- Export citation
Noetherianity of twisted Zhu’s algebras and bimodules
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 675-704
-
- Article
- Export citation
Drinfeld centers and Morita equivalence classes of fusion 2-categories
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 17 June 2025, pp. 305-340
- Print publication:
- February 2025
-
- Article
- Export citation
Locally finitely presented Grothendieck categories and the pure semisimplicity conjecture
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-27
-
- Article
- Export citation
Enlargements and Morita contexts for rings with involution
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 131-162
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Laurent family of simple modules over quiver Hecke algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 September 2024, pp. 1916-1940
- Print publication:
- August 2024
-
- Article
- Export citation
Skew group categories, algebras associated to Cartan matrices and folding of root lattices
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1-45
-
- Article
- Export citation
GRAPH CHARACTERISATION OF THE ANNIHILATOR IDEALS OF LEAVITT PATH ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 498-507
- Print publication:
- December 2024
-
- Article
- Export citation
Boolean algebras, Morita invariance and the algebraic K-theory of Lawvere theories
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 27 February 2023, pp. 253-270
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MINIMAL (
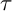 $\tau $-)TILTING INFINITE ALGEBRAS
$\tau $-)TILTING INFINITE ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 249 / March 2023
- Published online by Cambridge University Press:
- 11 October 2022, pp. 221-238
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Galois module structure of square power classes for biquadratic extensions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 25 April 2022, pp. 804-827
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The generalized auslander–reiten duality on a module category
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 19 January 2022, pp. 167-181
-
- Article
- Export citation
Quantum projective planes finite over their centers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 10 January 2022, pp. 53-67
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Simply laced root systems arising from quantum affine algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 168-210
- Print publication:
- January 2022
-
- Article
- Export citation
SOME STABLE NON-ELEMENTARY CLASSES OF MODULES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 13 September 2021, pp. 93-117
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EVERY GRADED IDEAL OF A LEAVITT PATH ALGEBRA IS GRADED ISOMORPHIC TO A LEAVITT PATH ALGEBRA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 23 August 2021, pp. 248-256
- Print publication:
- April 2022
-
- Article
- Export citation
AS-REGULARITY OF GEOMETRIC ALGEBRAS OF PLANE CUBIC CURVES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 22 June 2021, pp. 193-217
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- Export citation
SIMPLICITY CRITERIA FOR RINGS OF DIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 347-351
- Print publication:
- May 2022
-
- Article
- Export citation
On certain Tannakian categories of integrable connections over Kähler manifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 21 April 2021, pp. 1034-1061
- Print publication:
- August 2022
-
- Article
- Export citation