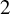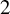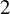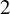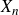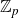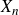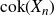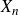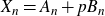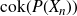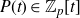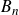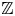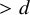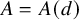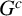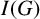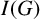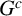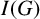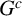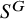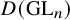Refine listing
Actions for selected content:
103 results in 13Fxx
ON THE TRIVIALITY OF AN
 $\mathbb A^2$-FIBRATION OVER A DVR
$\mathbb A^2$-FIBRATION OVER A DVR
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 260 / December 2025
- Published online by Cambridge University Press:
- 12 September 2025, pp. 826-832
- Print publication:
- December 2025
-
- Article
- Export citation
Regularity and multiplicity of Veronese type algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 08 August 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Consistent dimer models on surfaces with boundary
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 July 2025, e114
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An analogue of the Milnor conjecture for the de Rham-Witt complex in characteristic 2
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e87
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Koszul homomorphisms and universal resolutions in local algebra
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 March 2025, e63
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The cokernel of a polynomial push-forward of a random integral matrix with concentrated residue
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. 229-257
- Print publication:
- March 2025
-
- Article
- Export citation
TENSOR PRODUCTS OF d-FOLD MATRIX FACTORIZATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE DENSE REGION IN SCATTERING DIAGRAMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 290-302
- Print publication:
- October 2025
-
- Article
- Export citation
On class groups of upper cluster algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 January 2025, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FORMAL LIFTING OF DUALIZING COMPLEXES AND CONSEQUENCES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 219-236
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Classification of multiplication modules over multiplication rings with finitely many minimal primes
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 03 October 2024, pp. 67-71
- Print publication:
- January 2025
-
- Article
- Export citation
Laurent family of simple modules over quiver Hecke algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 September 2024, pp. 1916-1940
- Print publication:
- August 2024
-
- Article
- Export citation
CONSTANCY OF THE HILBERT–SAMUEL FUNCTION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 256 / December 2024
- Published online by Cambridge University Press:
- 24 May 2024, pp. 938-952
- Print publication:
- December 2024
-
- Article
- Export citation
ON THE SET OF BETTI ELEMENTS OF A PUISEUX MONOID
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 20 May 2024, pp. 80-92
- Print publication:
- February 2025
-
- Article
- Export citation
Relative rank and regularization
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 March 2024, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HOMOLOGICAL LINEAR QUOTIENTS AND EDGE IDEALS OF GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 29 January 2024, pp. 291-302
- Print publication:
- October 2024
-
- Article
- Export citation
DILOGARITHM IDENTITIES IN CLUSTER SCATTERING DIAGRAMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 21 December 2023, pp. 1-22
- Print publication:
- March 2024
-
- Article
- Export citation
When are the natural embeddings of classical invariant rings pure?
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 03 August 2023, e67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiple generalized cluster structures on
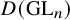 $D(\mathrm {GL}_n)$
$D(\mathrm {GL}_n)$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 09 June 2023, e46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Product decompositions of moment-angle manifolds and B-rigidity
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1313-1325
- Print publication:
- December 2023
-
- Article
- Export citation