1 Introduction
Dimer models were introduced as a model to study phase transitions in solid state physics. In this setting, a dimer model is a bicolored graph embedded into a surface, representing a configuration of particles which may bond to one another. The physics of this system is described by perfect matchings of the graph; see the survey [Reference Kenyon38] and references therein. Moreover, to a dimer model one may associate a dimer algebra, which is the Jacobian algebra of a certain quiver with potential, whose combinatorics and representation theory relate to the physics of the dimer model. In the physics literature, dimer models on tori have seen the most study, especially those satisfying certain consistency conditions [Reference Hanany and Vegh32]. Under these conditions, several authors including Mozgovoy and Reineke [Reference Mozgovoy and Reineke43], Davison [Reference Davison15] and Broomhead [Reference Broomhead11], showed that the dimer algebra is 3-Calabi-Yau. Ishii and Ueda [Reference Ishii and Ueda33] showed that the moduli space
![]() $\mathcal M_\theta $
of stable representations of the dimer algebra with dimension vector
$\mathcal M_\theta $
of stable representations of the dimer algebra with dimension vector
![]() $(1,\dots ,1)$
and a generic stability condition
$(1,\dots ,1)$
and a generic stability condition
![]() $\theta $
in the sense of King [Reference King40] is a smooth toric Calabi-Yau 3-fold. Moreover, the center Z of the dimer algebra
$\theta $
in the sense of King [Reference King40] is a smooth toric Calabi-Yau 3-fold. Moreover, the center Z of the dimer algebra
![]() $A_Q$
is a Gorenstein affine 3-fold, the dimer algebra
$A_Q$
is a Gorenstein affine 3-fold, the dimer algebra
![]() $A_Q$
is a non-commutative crepant resolution of Z, and
$A_Q$
is a non-commutative crepant resolution of Z, and
![]() $\mathcal M_\theta $
is a crepant resolution of Z [Reference Ishii and Ueda33]. Properties of the category of coherent sheaves over
$\mathcal M_\theta $
is a crepant resolution of Z [Reference Ishii and Ueda33]. Properties of the category of coherent sheaves over
![]() $\mathcal M_\theta $
may be understood through the combinatorics of the dimer model, opening a rich connection to mirror symmetry [Reference Bocklandt8, Reference Bocklandt9, Reference Franco, Hanany, Vegh, Wecht and Kennaway23, Reference Futaki and Ueda29].
$\mathcal M_\theta $
may be understood through the combinatorics of the dimer model, opening a rich connection to mirror symmetry [Reference Bocklandt8, Reference Bocklandt9, Reference Franco, Hanany, Vegh, Wecht and Kennaway23, Reference Futaki and Ueda29].
Many equivalent definitions of consistency have been introduced for torus dimer models. See, for example, [Reference Bocklandt6, Theorem 10.2], [Reference Bocklandt7, Reference Broomhead11, Reference Kennaway37, Reference Mozgovoy and Reineke43]. In particular, consistency of a dimer model is equivalent to the absence of certain bad configurations in the strand diagram of the dimer model [Reference Bocklandt8, Theorem 1.37].
Dimer models on disks have been studied separately, and are of particular interest to the theory of cluster algebras. Postnikov introduced plabic graphs and strand diagrams in [Reference Postnikov44]. Scott [Reference Scott50] showed that the homogeneous coordinate ring of the Grassmannian
![]() $\text {Gr}(k,n)$
is a cluster algebra, in which certain seeds are indexed by
$\text {Gr}(k,n)$
is a cluster algebra, in which certain seeds are indexed by
![]() $(k,n)$
-Postnikov diagrams. Jensen-King-Su [Reference Tore Jensen, King and Su36] gave an additive categorification for this cluster structure, and Baur-King-Marsh [Reference Baur, King and Marsh4] interpreted this categorification as the Gorenstein-projective module category over the completed boundary algebra of the associated dimer model. Pressland extended these results to arbitrary Postnikov diagrams in [Reference Pressland48] and observed that a dimer model coming from a Postnikov diagram satisfies a thinness condition, which is analogous to the algebraic consistency conditions in the torus literature.
$(k,n)$
-Postnikov diagrams. Jensen-King-Su [Reference Tore Jensen, King and Su36] gave an additive categorification for this cluster structure, and Baur-King-Marsh [Reference Baur, King and Marsh4] interpreted this categorification as the Gorenstein-projective module category over the completed boundary algebra of the associated dimer model. Pressland extended these results to arbitrary Postnikov diagrams in [Reference Pressland48] and observed that a dimer model coming from a Postnikov diagram satisfies a thinness condition, which is analogous to the algebraic consistency conditions in the torus literature.
A systematic study on dimer models on more general surfaces was initiated by Franco in [Reference Franco16]. This study is largely concerned with the master and mesonic moduli spaces on dimer models, which may be computed using the combinatorics of perfect matchings. Operations such as removing an edge and the dual untwisting map were investigated in [Reference Franco16, Reference Franco, Galloni and Seong21, Reference Franco and Uranga27]. Quiver mutation and square moves were connected with cluster mutation in [Reference Franco17], and further connected with combinatorial mutation of polytopes in [Reference Franco and Seong26]. Dimer models on general surfaces were connected with matroid polytopes and used to obtain a partial matroid stratification of the Grassmannian, generalizing the place of dimer models in disks in the matroid stratification of the Grassmannian [Reference Franco, Galloni and Mariotti19, Reference Franco, Galloni and Mariotti18, Reference Franco, Galloni, Penante and Wen20, Reference Bourjaily, Franco, Galloni and Wen10, Reference Franco and Musiker25]. Various generalizations of the notions of consistency in the disk and torus case have been considered in this body of work.
We define a new notion of consistency for dimer models on compact orientable surfaces with or without boundary. We call a dimer model path-consistent if, for any fixed vertices
![]() $v_1$
and
$v_1$
and
![]() $v_2$
and a fixed homotopy class C of paths from
$v_2$
and a fixed homotopy class C of paths from
![]() $v_1$
to
$v_1$
to
![]() $v_2$
, there is a unique (up to path-equivalence) minimal path r from
$v_2$
, there is a unique (up to path-equivalence) minimal path r from
![]() $v_1$
to
$v_1$
to
![]() $v_2$
in C such that any path from
$v_2$
in C such that any path from
![]() $v_1$
to
$v_1$
to
![]() $v_2$
in C is equivalent to r composed with some number face-paths. When Q is a dimer model on a torus, path-consistency is equivalent to the many consistency conditions in the literature. When Q is a dimer model on a higher genus surface without boundary, path-consistency is equivalent to the weaker notions of consistency rather than the stronger algebraic consistency. See [Reference Bocklandt6, Theorem 10.2]. When Q is on a disk, path-consistency is the thinness condition appearing in Pressland [Reference Pressland48].
$v_2$
in C is equivalent to r composed with some number face-paths. When Q is a dimer model on a torus, path-consistency is equivalent to the many consistency conditions in the literature. When Q is a dimer model on a higher genus surface without boundary, path-consistency is equivalent to the weaker notions of consistency rather than the stronger algebraic consistency. See [Reference Bocklandt6, Theorem 10.2]. When Q is on a disk, path-consistency is the thinness condition appearing in Pressland [Reference Pressland48].
We associate a strand diagram to a dimer model and define bad configurations. We say that a dimer model is strand-consistent if it has no bad configurations. This matches the notion of zigzag consistency of general dimer models on surfaces with boundary briefly considered in the first section of [Reference Bocklandt8]. In particular, it agrees with the well-studied notions of consistency in the torus case.
Our first main theorem is as follows, where we exclude the case of a sphere without boundary, as such a dimer model is never strand-consistent. A key idea of the proof is to observe that either notion of consistency of a dimer model is equivalent to consistency of its (possibly infinite) universal cover model, which enables the assumption of simple connectedness.
Theorem A (Theorem 4.13).
Let Q be a dimer model not on a sphere. The following are equivalent:
-
1. The dimer model Q is path-consistent.
-
2. The dimer model Q is strand-consistent.
-
3. The dimer algebra
 $A_Q$
is cancellative.
$A_Q$
is cancellative.
We may thus say that a weakly consistent dimer model is a model not on a sphere satisfying any of the above equivalent conditions. This generalizes results in the case of the torus [Reference Bocklandt6, Theorem 10.1], [Reference Ishii and Ueda34]. This was also shown for dimer models on the disk corresponding to
![]() $(k,n)$
-diagrams in [Reference Baur, King and Marsh4]. The implication (2)
$(k,n)$
-diagrams in [Reference Baur, King and Marsh4]. The implication (2)
![]() $\implies $
(1) for general dimer models on disks appears in [Reference Pressland48, Proposition 2.11]. A corollary of our result is the reverse direction in the disk case (Corollary 4.14).
$\implies $
(1) for general dimer models on disks appears in [Reference Pressland48, Proposition 2.11]. A corollary of our result is the reverse direction in the disk case (Corollary 4.14).
As an application, we use the strand diagram characterization of consistency to prove that dimer submodels of weakly consistent dimer models are weakly consistent (Corollary 5.1). This gives us practical ways to get new weakly consistent models from old and to understand equivalence classes of minimal paths.
Next, we study perfect matchings of weakly consistent dimer models. In the torus case, perfect matchings of the dimer model feature prominently [Reference Ishii and Ueda34, Reference Broomhead11, Reference Bocklandt6]. Perfect matchings of a torus dimer model generate the cone of R-symmetries, which have applications in physics. Perfect matchings may be used to calculate the perfect matching polygon of the dimer model, which is related to the center of the dimer algebra. Perfect matchings of a dimer model on a disk [Reference Çanakç, King and Pressland13, Reference Lam41] are the natural analog and may be connected with certain perfect matching modules of the completed dimer algebra to understand the categorification given by the boundary algebra of a dimer model on a disk [Reference Çanakç, King and Pressland13]. Over arbitrary compact surfaces with boundary, perfect matchings may be used to describe the master and mesonic moduli spaces associated to the dimer model. Moreover, perfect matchings of a dimer model on a general surface may be calculated by taking determinants of Kasteleyn matrices [Reference Hanany and Kennaway31], [Reference Franco16, §5]. In Theorem 6.7, we show that any (possibly infinite) simply connected weakly consistent dimer model has a perfect matching. This means that the universal cover model of any weakly consistent dimer model has a perfect matching. However, we give an example of a (non-simply-connected) weakly consistent dimer model which has no perfect matching (Example 6.8). One important notion for dimer models in the disk and torus is nondegeneracy, which requires that all arrows are contained in a perfect matching. We extend this definition to general surfaces and show that nondegeneracy gives a positive grading to the dimer algebra. We define a strongly consistent dimer model as one which is weakly consistent and nondegenerate. In the disk and torus case, weak and strong consistency are equivalent, but this is not true for more general surfaces. We then use [Reference Pressland48] to prove the following result.
Theorem B (Theorem 7.7).
Let Q be a finite strongly consistent dimer model. Then the dimer algebra
![]() $A_Q$
and the completed dimer algebra
$A_Q$
and the completed dimer algebra
![]() $\widehat A_Q$
are bimodule internally 3-Calabi-Yau with respect to their boundary idempotents.
$\widehat A_Q$
are bimodule internally 3-Calabi-Yau with respect to their boundary idempotents.
When Q is a dimer model on a disk, we recover [Reference Pressland48, Theorem 3.7]. When Q has no boundary, this translates to the algebra being 3-Calabi-Yau [Reference Pressland46, Remark 2.2]. Hence, we recover the statement in the torus (and closed surface of higher genus) literature that consistent dimer models are 3-Calabi-Yau proven in [Reference Davison15, Corollary 4.4]. Using [Reference Amiot, Iyama and Reiten2, Theorem 4.1 and Theorem 4.10], Theorem B immediately implies the following.
Corollary C (Corollary 7.9).
Let Q be a strongly consistent, Noetherian, and boundary-finite (Definition 7.11) dimer model with no 1-cycles or 2-cycles. Then the Gorenstein-projective module category of the completed boundary algebra of Q categorifies the cluster algebra given by the ice quiver of Q.
We use the term ‘categorification’ for brevity during the introduction; see Corollary 7.9 for a more rigorous statement. We give some examples of strongly consistent dimer models on annuli satisfying the requirements of Corollary C.
Next, we use the theory of dimer submodels to get some interesting results about equivalence classes of minimal paths in (weakly and strongly) consistent dimer models. We prove that in a weakly consistent dimer model, minimal leftmost and rightmost paths in a given homotopy class between two vertices are unique when they exist. If we further assume nondegeneracy, then they always exist.
Finally, we study the reduction of dimer models. In the disk case, consistent dimer models with at least three boundary vertices may be reduced in order to obtain a dimer model with no 2-cycles and an isomorphic dimer algebra [Reference Pressland48, §2]. We show in Proposition 9.1 that a similar process may be used to remove certain, but not all, digons in the non-simply-connected case. Figure 21 gives a weakly (but not strongly) consistent dimer model with a digon which may not be removed in this way. However, Corollary 9.3 states that if we require strong consistency, then we may remove all digons from a dimer model.
The article is organized as follows. In Section 2, we define dimer models and prove that path-consistency is equivalent to cancellativity. We also show that these notions behave well when passing to the universal cover of a dimer model. In Section 3, we develop some technical theory of basic and cycle-removing morphs in order to prove that a path-consistent and simply connected dimer model has no irreducible pairs (Theorem 3.19). This result is used in Section 4 to complete the proof of Theorem A by showing that path-consistency and strand-consistency are equivalent. Next, in Section 5, we introduce dimer submodels and prove that dimer submodels of weakly consistent dimer models are weakly consistent (Corollary 5.1). This gives us practical ways to get new weakly consistent models from old and to understand equivalence classes of minimal paths. Section 6 is dedicated to perfect matchings of weakly consistent dimer models. In Section 7, we prove that the noncompleted and completed dimer algebras of a strongly consistent dimer model are bimodule internally 3-Calabi-Yau with respect to their boundary idempotents (Theorem B). As a result, we obtain our categorification result in Corollary C. In Section 8, we use the results of Section 5 to understand the equivalence classes of minimal paths in (weakly and/or strongly) consistent dimer models. Lastly, in Section 9, we discuss the process of reducing a dimer model by removing digons. We prove that if Q is strongly consistent, then all digons may be removed.
2 Covers and consistency
In this section, we define a dimer model on an arbitrary surface with boundary. We introduce path-consistency, which generalizes notions of consistency of dimer models on the disk and torus. We show that path-consistency is equivalent to cancellativity. Moreover, we prove that these notions work well with taking the universal cover of a dimer model.
2.1 Dimer models
We begin by defining dimer models, following [Reference Baur, King and Marsh4, §3]. A quiver is a directed graph. A cycle of Q is a nonconstant oriented path of Q which starts and ends at the same vertex. A cycle of length a is called an a-cycle. Two cycles
![]() $\alpha _1\dots \alpha _a$
and
$\alpha _1\dots \alpha _a$
and
![]() $\beta _1\dots \beta _b$
are cyclically equivalent if
$\beta _1\dots \beta _b$
are cyclically equivalent if
![]() $a=b$
and there is some
$a=b$
and there is some
![]() $j\in \mathbb Z$
such that
$j\in \mathbb Z$
such that
![]() $\alpha _i=\beta _{i+j}$
(where the subscript addition is calculated modulo a) for all
$\alpha _i=\beta _{i+j}$
(where the subscript addition is calculated modulo a) for all
![]() $i\in [a]$
. If Q is a quiver, we write
$i\in [a]$
. If Q is a quiver, we write
![]() $Q_{\text {cyc}}$
for the set of cycles in Q of length at least two up to cyclic equivalence.
$Q_{\text {cyc}}$
for the set of cycles in Q of length at least two up to cyclic equivalence.
Definition 2.1. A quiver with faces is a triple
![]() $Q=(Q_0,Q_1,Q_2)$
, where
$Q=(Q_0,Q_1,Q_2)$
, where
![]() $(Q_0,Q_1)$
are the vertices and arrows of a quiver and
$(Q_0,Q_1)$
are the vertices and arrows of a quiver and
![]() $Q_2\subseteq Q_{\text {cyc}}$
is a set of faces of Q.
$Q_2\subseteq Q_{\text {cyc}}$
is a set of faces of Q.
A digon of Q is a face in
![]() $Q_2$
consisting of two arrows. Given a vertex
$Q_2$
consisting of two arrows. Given a vertex
![]() $i\in Q_0$
, we define the incidence graph of Q at i to be the graph whose vertices are given by the arrows incident to i and whose arrows
$i\in Q_0$
, we define the incidence graph of Q at i to be the graph whose vertices are given by the arrows incident to i and whose arrows
![]() $\alpha \to \beta $
correspond to paths
$\alpha \to \beta $
correspond to paths
which occur in faces of Q.
Definition 2.2. A (locally finite, oriented) dimer model with boundary is given by a quiver with faces
![]() $Q=(Q_0,Q_1,Q_2)$
, where
$Q=(Q_0,Q_1,Q_2)$
, where
![]() $Q_2$
is written as a disjoint union
$Q_2$
is written as a disjoint union
![]() $Q_2=Q_2^{cc}\cup Q_2^{cl}$
, satisfying the following properties:
$Q_2=Q_2^{cc}\cup Q_2^{cl}$
, satisfying the following properties:
-
1. Each arrow of
 $Q_1$
is in either one face or two faces of Q. An arrow which is in one face is called a boundary arrow, and an arrow which is in two faces is called an internal arrow.
$Q_1$
is in either one face or two faces of Q. An arrow which is in one face is called a boundary arrow, and an arrow which is in two faces is called an internal arrow. -
2. Each internal arrow appears once in one cycle bounding a face in
 $Q_2^{cc}$
and once in one cycle bounding a face in
$Q_2^{cc}$
and once in one cycle bounding a face in
 $Q_2^{cl}$
.
$Q_2^{cl}$
. -
3. The incidence graph of Q at each vertex is connected.
-
4. Any vertex of Q is incident with a finite number of arrows.
A vertex of Q is called boundary if it is adjacent to a boundary arrow, and otherwise it is called internal.
Given a dimer model with boundary Q, we may associate each face F of Q with a polygon whose edges are labeled by the arrows in F and glue the edges of these polygons together as indicated by the directions of the arrows to form a surface with boundary
![]() $S(Q)$
into which Q may be embedded [Reference Bocklandt7, Lemma 6.4]. The surface
$S(Q)$
into which Q may be embedded [Reference Bocklandt7, Lemma 6.4]. The surface
![]() $S(Q)$
is oriented such that the cycles of faces in
$S(Q)$
is oriented such that the cycles of faces in
![]() $Q_2^{cc}$
are oriented positive (or counter-clockwise) and the cycles of faces in
$Q_2^{cc}$
are oriented positive (or counter-clockwise) and the cycles of faces in
![]() $Q_2^{cl}$
are oriented negative (or clockwise). The boundary of
$Q_2^{cl}$
are oriented negative (or clockwise). The boundary of
![]() $S(Q)$
runs along the boundary arrows of Q. If
$S(Q)$
runs along the boundary arrows of Q. If
![]() $S(Q)$
is a disk, then we say that Q is a dimer model on a disk. If
$S(Q)$
is a disk, then we say that Q is a dimer model on a disk. If
![]() $S(Q)$
is simply connected, then we say that Q is a simply connected dimer model.
$S(Q)$
is simply connected, then we say that Q is a simply connected dimer model.
A dimer model Q is finite if its vertex set is finite. Note that Q is finite if and only if
![]() $S(Q)$
is compact.
$S(Q)$
is compact.
Suppose that Q is a finite quiver such that every vertex has finite degree. Suppose further that Q has an embedding into an oriented surface
![]() $\Sigma $
with boundary such that the complement of Q in
$\Sigma $
with boundary such that the complement of Q in
![]() $\Sigma $
is a disjoint union of discs, each of which is bounded by a cycle of Q. We may then view Q as a dimer model with boundary by declaring
$\Sigma $
is a disjoint union of discs, each of which is bounded by a cycle of Q. We may then view Q as a dimer model with boundary by declaring
![]() $Q_2^{cc}$
(respectively
$Q_2^{cc}$
(respectively
![]() $Q_2^{cl}$
) to be the set of positively (respectively, negatively) oriented cycles of Q which bound a connected component of the complement of Q in
$Q_2^{cl}$
) to be the set of positively (respectively, negatively) oriented cycles of Q which bound a connected component of the complement of Q in
![]() $\Sigma $
. All dimer models may be obtained in this way.
$\Sigma $
. All dimer models may be obtained in this way.
Let Q be a dimer model and let p be a path in Q. We write
![]() $t(p)$
and
$t(p)$
and
![]() $h(p)$
for the start and end vertex of p, respectively. If a path q can be factored in the form
$h(p)$
for the start and end vertex of p, respectively. If a path q can be factored in the form
![]() $q=q_2pq_1$
, where
$q=q_2pq_1$
, where
![]() $h(q_1)=t(p)$
and
$h(q_1)=t(p)$
and
![]() $t(q_2)=h(p)$
, we say that p is in q or that q contains p as a subpath and we write
$t(q_2)=h(p)$
, we say that p is in q or that q contains p as a subpath and we write
![]() $p\in q$
. Corresponding to any vertex v is a constant path
$p\in q$
. Corresponding to any vertex v is a constant path
![]() $e_v$
from v to itself which has no arrows.
$e_v$
from v to itself which has no arrows.
Any arrow
![]() $\alpha $
in Q is associated with at most one clockwise and one counter-clockwise face of the dimer model. We refer to these faces as
$\alpha $
in Q is associated with at most one clockwise and one counter-clockwise face of the dimer model. We refer to these faces as
![]() $F_\alpha ^{cl}$
and
$F_\alpha ^{cl}$
and
![]() $F_\alpha ^{cc}$
, respectively, when they exist. Let
$F_\alpha ^{cc}$
, respectively, when they exist. Let
![]() $R_\alpha ^{cl}$
(respectively
$R_\alpha ^{cl}$
(respectively
![]() $R_\alpha ^{cc}$
) be the subpath of
$R_\alpha ^{cc}$
) be the subpath of
![]() $F_\alpha ^{cl}$
(respectively
$F_\alpha ^{cl}$
(respectively
![]() $F_\alpha ^{cc}$
) beginning at
$F_\alpha ^{cc}$
) beginning at
![]() $h(\alpha )$
and ending at
$h(\alpha )$
and ending at
![]() $t(\alpha )$
, and consisting of all arrows in
$t(\alpha )$
, and consisting of all arrows in
![]() $F_\alpha ^{cl}$
(respectively
$F_\alpha ^{cl}$
(respectively
![]() $R_\alpha ^{cc}$
) except for
$R_\alpha ^{cc}$
) except for
![]() $\alpha $
. A path in Q of the form
$\alpha $
. A path in Q of the form
![]() $R_\alpha ^{cl}$
(respectively
$R_\alpha ^{cl}$
(respectively
![]() $R_\alpha ^{cc}$
) for some
$R_\alpha ^{cc}$
) for some
![]() $\alpha $
is called a clockwise return path (respectively a counter-clockwise return path) of
$\alpha $
is called a clockwise return path (respectively a counter-clockwise return path) of
![]() $\alpha $
.
$\alpha $
.
Definition 2.3. Given a dimer model with boundary Q, the dimer algebra
![]() $A_Q$
is defined as the quotient of the path algebra
$A_Q$
is defined as the quotient of the path algebra
![]() $\mathbb CQ$
by the relations
$\mathbb CQ$
by the relations
for every internal arrow
![]() $\alpha \in Q_1$
.
$\alpha \in Q_1$
.
We now make more definitions. We say that two paths p and q in Q are path-equivalent if their associated elements in the dimer algebra
![]() $A_Q$
are equal. If p is a path in Q, we write
$A_Q$
are equal. If p is a path in Q, we write
![]() $[p]$
for the path-equivalence class of p under these relations.
$[p]$
for the path-equivalence class of p under these relations.
The set of left-morphable (respectively right-morphable) arrows for p is the set of internal arrows
![]() $\alpha \in Q_1$
such that
$\alpha \in Q_1$
such that
![]() $R_\alpha ^{cc}$
(respectively
$R_\alpha ^{cc}$
(respectively
![]() $R_\alpha ^{cl}$
) is in p. The set of morphable arrows for p is the set of arrows which are left-morphable or right-morphable for p. Let
$R_\alpha ^{cl}$
) is in p. The set of morphable arrows for p is the set of arrows which are left-morphable or right-morphable for p. Let
![]() $\alpha $
be a morphable arrow for p. We also say that p has the morphable arrow
$\alpha $
be a morphable arrow for p. We also say that p has the morphable arrow
![]() $\alpha $
. Then p contains
$\alpha $
. Then p contains
![]() $R_\alpha ^{cl}$
or
$R_\alpha ^{cl}$
or
![]() $R_\alpha ^{cc}$
as a subpath and may possibly contain multiple such subpaths. If
$R_\alpha ^{cc}$
as a subpath and may possibly contain multiple such subpaths. If
![]() $p'$
is a path obtained from p by replacing a single subpath
$p'$
is a path obtained from p by replacing a single subpath
![]() $R_\alpha ^{cl}$
with
$R_\alpha ^{cl}$
with
![]() $R_\alpha ^{cc}$
(
$R_\alpha ^{cc}$
(
![]() $R_\alpha ^{cc}$
with
$R_\alpha ^{cc}$
with
![]() $R_\alpha ^{cl}$
, respectively), then we say that
$R_\alpha ^{cl}$
, respectively), then we say that
![]() $p'$
is a basic right-morph (respectively, basic left-morph) of p. We omit the word ‘basic’ when the context is clear. If p only has one subpath which is a copy of
$p'$
is a basic right-morph (respectively, basic left-morph) of p. We omit the word ‘basic’ when the context is clear. If p only has one subpath which is a copy of
![]() $R_\alpha ^{cl}$
or
$R_\alpha ^{cl}$
or
![]() $R_\alpha ^{cc}$
, then we say that
$R_\alpha ^{cc}$
, then we say that
![]() $p'$
is an unambiguous basic (right or left) morph of p and we write
$p'$
is an unambiguous basic (right or left) morph of p and we write
![]() $p'=m_\alpha (p)$
. We say that
$p'=m_\alpha (p)$
. We say that
![]() $\alpha $
is an unambiguous morphable arrow for p in this case. Since the relations of
$\alpha $
is an unambiguous morphable arrow for p in this case. Since the relations of
![]() $A_Q$
are generated by the relations
$A_Q$
are generated by the relations
![]() $\{R_\alpha ^{cc}-R_\alpha ^{cl}\ :\ \alpha \text { is an internal arrow of }Q\}$
, two paths p and q are path-equivalent if and only if there is a sequence of paths
$\{R_\alpha ^{cc}-R_\alpha ^{cl}\ :\ \alpha \text { is an internal arrow of }Q\}$
, two paths p and q are path-equivalent if and only if there is a sequence of paths
![]() $p=r_1,\dots ,r_m=q$
such that
$p=r_1,\dots ,r_m=q$
such that
![]() $r_{i+1}$
is a basic morph of
$r_{i+1}$
is a basic morph of
![]() $r_i$
for
$r_i$
for
![]() $i\in [m-1]$
.
$i\in [m-1]$
.
Suppose p is a cycle in Q which starts and ends at some vertex v and travels around a face of Q once. Then we say that p is a face-path of Q starting at v. The terminology is justified by the following observation, which follows from the defining relations.
Remark 2.4. Any two face-paths of Q starting at v are path-equivalent.
Definition 2.5. For all
![]() $v\in Q_0$
, fix some face-path
$v\in Q_0$
, fix some face-path
![]() $f_v$
at v. Then define
$f_v$
at v. Then define
If
![]() $|Q_0|$
is finite, then
$|Q_0|$
is finite, then
![]() $[f]$
is an element of
$[f]$
is an element of
![]() $A_Q$
. It follows from Remark 2.4 that the path-equivalence class
$A_Q$
. It follows from Remark 2.4 that the path-equivalence class
![]() $[f]$
is independent of the choice of
$[f]$
is independent of the choice of
![]() $f_v$
for all
$f_v$
for all
![]() $v\in Q_0$
. Moreover, the dimer algebra relations imply that
$v\in Q_0$
. Moreover, the dimer algebra relations imply that
![]() $[f]$
commutes with every arrow. Hence, if
$[f]$
commutes with every arrow. Hence, if
![]() $|Q_0|$
is finite, then
$|Q_0|$
is finite, then
![]() $[f]$
is in the center of
$[f]$
is in the center of
![]() $A_Q$
. If
$A_Q$
. If
![]() $|Q_0|$
is not finite, then
$|Q_0|$
is not finite, then
![]() $[f]$
is not an element of the dimer model
$[f]$
is not an element of the dimer model
![]() $A_Q$
. However, every element x of
$A_Q$
. However, every element x of
![]() $A_Q$
has a well-defined product with f, so we use notation such as
$A_Q$
has a well-defined product with f, so we use notation such as
![]() $[xf^m]$
in this case as well.
$[xf^m]$
in this case as well.
The completed path algebra
![]() $\langle \langle \mathbb CQ\rangle \rangle $
is the completion of
$\langle \langle \mathbb CQ\rangle \rangle $
is the completion of
![]() $\mathbb CQ$
with respect to the arrow ideal. The completed path algebra has as its underlying vector space the possibly infinite linear combinations of (distinct) finite paths in Q. Multiplication in
$\mathbb CQ$
with respect to the arrow ideal. The completed path algebra has as its underlying vector space the possibly infinite linear combinations of (distinct) finite paths in Q. Multiplication in
![]() $\langle \langle \mathbb CQ\rangle \rangle $
is induced by composition. See [Reference Pressland47, Definition 2.6].
$\langle \langle \mathbb CQ\rangle \rangle $
is induced by composition. See [Reference Pressland47, Definition 2.6].
Definition 2.6. The completed dimer algebra
![]() $\widehat A_Q$
is the quotient of the completed path algebra
$\widehat A_Q$
is the quotient of the completed path algebra
![]() $\mathbb C\langle \langle Q\rangle \rangle $
by the closure
$\mathbb C\langle \langle Q\rangle \rangle $
by the closure
![]() $\widehat I_Q$
of the ideal generated by the relations
$\widehat I_Q$
of the ideal generated by the relations
![]() $R_\alpha ^{cc}-R_\alpha ^{cl}$
for each internal arrow
$R_\alpha ^{cc}-R_\alpha ^{cl}$
for each internal arrow
![]() $\alpha $
with respect to the arrow ideal.
$\alpha $
with respect to the arrow ideal.
Elements of
![]() $\widehat A_Q$
are possibly infinite linear combinations of (finite) paths of Q, with multiplication induced by composition.
$\widehat A_Q$
are possibly infinite linear combinations of (finite) paths of Q, with multiplication induced by composition.
2.2 Path-consistency
We now define path-consistency, which is a nice condition on the equivalence classes of paths between two vertices. We prove some short lemmas about path-consistent models.
A path p in Q is also a path in the surface
![]() $S(Q)$
. We thus say that paths p and q of Q are homotopic if they are homotopic as paths in
$S(Q)$
. We thus say that paths p and q of Q are homotopic if they are homotopic as paths in
![]() $S(Q)$
.
$S(Q)$
.
Definition 2.7. A path p in a dimer model Q is minimal if we may not write
![]() $[p]=[qf^m]$
for any
$[p]=[qf^m]$
for any
![]() $m\geq 1$
.
$m\geq 1$
.
Definition 2.8. A dimer model
![]() $Q=(Q_0,Q_1,Q_2)$
is path-consistent if it satisfies the following path-consistency condition:
$Q=(Q_0,Q_1,Q_2)$
is path-consistent if it satisfies the following path-consistency condition:
Fix vertices
![]() $v_1$
and
$v_1$
and
![]() $v_2$
of Q. For any homotopy class C of paths in
$v_2$
of Q. For any homotopy class C of paths in
![]() $S(Q)$
from
$S(Q)$
from
![]() $v_1$
to
$v_1$
to
![]() $v_2$
, there is a minimal path
$v_2$
, there is a minimal path
![]() $p_{v_2v_1}^C$
, unique up to path-equivalence, with the property that any path p from
$p_{v_2v_1}^C$
, unique up to path-equivalence, with the property that any path p from
![]() $v_1$
to
$v_1$
to
![]() $v_2$
in Q in the homotopy class C satisfies
$v_2$
in Q in the homotopy class C satisfies
![]() $[p]=[f^mp_{v_2v_1}^C]$
for a unique nonnegative integer m. We call m the c-value of p.
$[p]=[f^mp_{v_2v_1}^C]$
for a unique nonnegative integer m. We call m the c-value of p.
We remark that equivalent paths of a general dimer model must be homotopic, so in some sense, this is the ‘lowest number of path equivalence classes’ that one could hope for in a dimer model.
Lemma 2.9. If p and q are paths in a path-consistent dimer model Q with
![]() $h(p)=t(q)$
, then the c-value of the composition
$h(p)=t(q)$
, then the c-value of the composition
![]() $qp$
is greater than or equal to the c-value of p plus the c-value of q.
$qp$
is greater than or equal to the c-value of p plus the c-value of q.
Proof. If p and q are paths in a path-consistent dimer model Q with
![]() $h(p)=t(q)$
, then we may write
$h(p)=t(q)$
, then we may write
![]() $[p]=[f^{m_p}r_p]$
and
$[p]=[f^{m_p}r_p]$
and
![]() $[q]=[f^{m_q}r_q]$
for some minimal paths
$[q]=[f^{m_q}r_q]$
for some minimal paths
![]() $r_p$
and
$r_p$
and
![]() $r_q$
. Then
$r_q$
. Then
![]() $m_p$
is the c-value of p and
$m_p$
is the c-value of p and
![]() $m_q$
is the c-value of q. Then, using the fact that
$m_q$
is the c-value of q. Then, using the fact that
![]() $[f]$
is central, we calculate
$[f]$
is central, we calculate
We have shown that
![]() $[f^{m_q+m_p}]$
may be factored out of
$[f^{m_q+m_p}]$
may be factored out of
![]() $[qp]$
; hence, the c-value of
$[qp]$
; hence, the c-value of
![]() $[qp]$
is greater than or equal to
$[qp]$
is greater than or equal to
![]() $m_q+m_p$
.
$m_q+m_p$
.
Two paths are equivalent if and only if there is a sequence of basic morphs taking one to the other. Since a basic morph cannot remove some arrows without replacing them with other arrows, the constant path is the unique minimal path from a vertex to itself. This leads to the following remark.
Remark 2.10. If Q is path-consistent and p is a nonconstant null-homotopic cycle, then the c-value of p is positive.
It is an important fact that all face-paths of a dimer model are null-homotopic. This lets us show the following.
Lemma 2.11. Let Q be a path-consistent dimer model. Any proper subpath of a face-path of Q is minimal.
Proof. Suppose p is a proper subpath of a face-path
![]() $f_v$
starting at
$f_v$
starting at
![]() $v:=t(p)$
. Let
$v:=t(p)$
. Let
![]() $p'$
be the subpath of
$p'$
be the subpath of
![]() $f_v$
such that
$f_v$
such that
![]() $p'p=f_v$
. If p is not minimal, then by definition of path-consistency,
$p'p=f_v$
. If p is not minimal, then by definition of path-consistency,
![]() $[p]=[rf^m]$
for some positive integer m and some minimal path r from v to
$[p]=[rf^m]$
for some positive integer m and some minimal path r from v to
![]() $h(p)$
homotopic to p. Then
$h(p)$
homotopic to p. Then
![]() $[p'p]=[p'rf^m]=[p'rf_v^m]$
. Moreover, r is homotopic to p, and hence,
$[p'p]=[p'rf^m]=[p'rf_v^m]$
. Moreover, r is homotopic to p, and hence,
![]() $p'r$
is homotopic to the face-path
$p'r$
is homotopic to the face-path
![]() $p'p$
and hence is null-homotopic. Then by Remark 2.10, it has some positive c-value of
$p'p$
and hence is null-homotopic. Then by Remark 2.10, it has some positive c-value of
![]() $m'$
. By definition of path-consistency,
$m'$
. By definition of path-consistency,
![]() $[p'r]=[f_v^{m'}]$
. It follows that
$[p'r]=[f_v^{m'}]$
. It follows that
which is a contradiction since
![]() $m+m'\geq 1+1=2$
but all face-paths trivially have a c-value of 1. It follows that p is minimal.
$m+m'\geq 1+1=2$
but all face-paths trivially have a c-value of 1. It follows that p is minimal.
Lemma 2.12. Let Q be a simply connected path-consistent dimer model. No proper subpath of a face-path of Q is a cycle.
Proof. Suppose p is a proper subpath of a face-path of Q which is a cycle. By Lemma 2.11, the path p is minimal. Since Q is simply-connected, p is null-homotopic. The only minimal null-homotopic path from a vertex to itself is the constant path, so this is a contradiction.
2.3 Universal covers
We define the notion of a universal cover dimer model and show that it behaves well with respect to path-consistency and the cancellation property.
Let Q be a dimer model. We construct a dimer model
![]() $\widetilde Q$
over the universal cover
$\widetilde Q$
over the universal cover
![]() $\widetilde {S(Q)}$
of
$\widetilde {S(Q)}$
of
![]() $S(Q)$
. We consider Q to be embedded into
$S(Q)$
. We consider Q to be embedded into
![]() $S(Q)$
, so that a vertex
$S(Q)$
, so that a vertex
![]() $v\in Q$
may be considered as a point of
$v\in Q$
may be considered as a point of
![]() $S(Q)$
. Similarly, we describe
$S(Q)$
. Similarly, we describe
![]() $\widetilde Q$
embedded into
$\widetilde Q$
embedded into
![]() $\widetilde {S(Q)}$
.
$\widetilde {S(Q)}$
.
The vertices of
![]() $\widetilde Q$
are the points
$\widetilde Q$
are the points
![]() $\tilde v\in \widetilde {S(Q)}$
which descend to vertices v of
$\tilde v\in \widetilde {S(Q)}$
which descend to vertices v of
![]() $S(Q)$
. For any arrow
$S(Q)$
. For any arrow
![]() $\alpha $
from v to w in Q and any
$\alpha $
from v to w in Q and any
![]() $\tilde v\in \widetilde Q_0$
, there is an arrow
$\tilde v\in \widetilde Q_0$
, there is an arrow
![]() $\alpha _{\tilde v}$
obtained by lifting
$\alpha _{\tilde v}$
obtained by lifting
![]() $\alpha $
as a path in Q up to a path in
$\alpha $
as a path in Q up to a path in
![]() $\widetilde Q$
starting at
$\widetilde Q$
starting at
![]() $\tilde v$
. The face-paths of
$\tilde v$
. The face-paths of
![]() $\widetilde Q$
are similarly induced by lifting the face-paths of Q. It is not hard to see that
$\widetilde Q$
are similarly induced by lifting the face-paths of Q. It is not hard to see that
![]() $\widetilde Q$
is a (locally finite) dimer model. The following facts follow by universal cover theory.
$\widetilde Q$
is a (locally finite) dimer model. The following facts follow by universal cover theory.
-
1. If
 $S(Q)$
is not a sphere, then
$S(Q)$
is not a sphere, then
 $\widetilde {S(Q)}$
is not a sphere.
$\widetilde {S(Q)}$
is not a sphere. -
2. The surface
 $\widetilde {S(Q)}$
is simply connected.
$\widetilde {S(Q)}$
is simply connected. -
3. Let
 $\tilde p$
and
$\tilde p$
and
 $\tilde q$
be paths in
$\tilde q$
be paths in
 $\widetilde Q$
with the same start and end vertices which are lifts of paths p and q of Q, respectively. Then
$\widetilde Q$
with the same start and end vertices which are lifts of paths p and q of Q, respectively. Then
 $[p]=[q]$
in
$[p]=[q]$
in
 $A_Q$
if and only if
$A_Q$
if and only if
 $[\tilde p]=[\tilde q]$
in
$[\tilde p]=[\tilde q]$
in
 $A_{\widetilde Q}$
.
$A_{\widetilde Q}$
.
Universal covers are useful to consider because simple cycles on the universal cover have well-defined interiors. The following remark gives another advantage of universal covers.
Remark 2.13. Choose vertices
![]() $\tilde v_1$
and
$\tilde v_1$
and
![]() $\tilde v_2$
of
$\tilde v_2$
of
![]() $\widetilde Q$
. Any two paths from
$\widetilde Q$
. Any two paths from
![]() $\tilde v_1$
to
$\tilde v_1$
to
![]() $\tilde v_2$
are homotopic and hence descend to homotopic paths in Q. Then this choice of vertices gives a homotopy class C of paths between the corresponding vertices
$\tilde v_2$
are homotopic and hence descend to homotopic paths in Q. Then this choice of vertices gives a homotopy class C of paths between the corresponding vertices
![]() $v_1$
and
$v_1$
and
![]() $v_2$
of Q. The paths from
$v_2$
of Q. The paths from
![]() $\tilde v_1$
to
$\tilde v_1$
to
![]() $\tilde v_2$
in
$\tilde v_2$
in
![]() $\widetilde Q$
correspond precisely to the paths from
$\widetilde Q$
correspond precisely to the paths from
![]() $v_1$
to
$v_1$
to
![]() $v_2$
in the homotopy class C. Equivalence classes of paths in the dimer algebra are respected by this correspondence.
$v_2$
in the homotopy class C. Equivalence classes of paths in the dimer algebra are respected by this correspondence.
Remark 2.13 relates Q and
![]() $\widetilde Q$
in a useful way. Many of our technical results require simple connectedness. Passing to the universal cover model allows us to prove things about general dimer models Q by considering their simply connected universal cover models. In particular, we may study path-consistency of Q by studying path-consistency of
$\widetilde Q$
in a useful way. Many of our technical results require simple connectedness. Passing to the universal cover model allows us to prove things about general dimer models Q by considering their simply connected universal cover models. In particular, we may study path-consistency of Q by studying path-consistency of
![]() $\widetilde Q$
.
$\widetilde Q$
.
Proposition 2.14. A dimer model Q is path-consistent if and only if
![]() $\widetilde Q$
is path-consistent.
$\widetilde Q$
is path-consistent.
Proof. Suppose Q is path-consistent. Choose vertices
![]() $\tilde v_1$
and
$\tilde v_1$
and
![]() $\tilde v_2$
of
$\tilde v_2$
of
![]() $\widetilde Q$
; these correspond to vertices
$\widetilde Q$
; these correspond to vertices
![]() $v_1$
and
$v_1$
and
![]() $v_2$
of Q and induce a homotopy class C of paths between them. By Remark 2.13, the paths in
$v_2$
of Q and induce a homotopy class C of paths between them. By Remark 2.13, the paths in
![]() $\widetilde Q$
from
$\widetilde Q$
from
![]() $\tilde v_1$
to
$\tilde v_1$
to
![]() $\tilde v_2$
correspond to the paths in Q from
$\tilde v_2$
correspond to the paths in Q from
![]() $v_1$
to
$v_1$
to
![]() $v_2$
in C. By path-consistency of Q, each such path in Q is equivalent to
$v_2$
in C. By path-consistency of Q, each such path in Q is equivalent to
![]() $p_{v_2v_1}^C$
composed with some power of a face-path, hence
$p_{v_2v_1}^C$
composed with some power of a face-path, hence
![]() $\widetilde Q$
is path-consistent.
$\widetilde Q$
is path-consistent.
The other direction is similar.
It follows from Lemma 2.12 and Proposition 2.14 that a path-consistent dimer model cannot have contractible loops.
Definition 2.15. A dimer algebra
![]() $A_Q=\mathbb C Q/I$
is called a cancellation algebra (or cancellative) if for paths
$A_Q=\mathbb C Q/I$
is called a cancellation algebra (or cancellative) if for paths
![]() $p,q,a,b$
of Q with
$p,q,a,b$
of Q with
![]() $h(a)=t(p)=t(q)$
and
$h(a)=t(p)=t(q)$
and
![]() $t(b)=h(p)=h(q)$
, we have
$t(b)=h(p)=h(q)$
, we have
![]() $[pa]=[qa]\iff [p]=[q]$
and
$[pa]=[qa]\iff [p]=[q]$
and
![]() $[bp]=[bq]\iff [p]=[q]$
. We call this the cancellation property.
$[bp]=[bq]\iff [p]=[q]$
. We call this the cancellation property.
Lemma 2.16.
![]() $A_Q$
is a cancellation algebra if and only if
$A_Q$
is a cancellation algebra if and only if
![]() $A_{\widetilde Q}$
is a cancellation algebra.
$A_{\widetilde Q}$
is a cancellation algebra.
Proof. This follows because
![]() $[p]=[q]$
in
$[p]=[q]$
in
![]() $A_Q$
if and only if
$A_Q$
if and only if
![]() $[\tilde p]=[\tilde q]$
in
$[\tilde p]=[\tilde q]$
in
![]() $A_{\widetilde Q}$
, where
$A_{\widetilde Q}$
, where
![]() $\tilde p$
and
$\tilde p$
and
![]() $\tilde q$
are any lifts of p and q to
$\tilde q$
are any lifts of p and q to
![]() $\widetilde Q$
with
$\widetilde Q$
with
![]() $t(\tilde p)=t(\tilde q)$
.
$t(\tilde p)=t(\tilde q)$
.
Lemma 2.17. Let p be a path in Q of length m. Then the composition of face-paths
![]() $f^m_{t(p)}$
is equivalent to a path beginning with p.
$f^m_{t(p)}$
is equivalent to a path beginning with p.
Proof. Let
![]() $p=\gamma _m\dots \gamma _1$
be a product of arrows. For each
$p=\gamma _m\dots \gamma _1$
be a product of arrows. For each
![]() $\gamma _i$
, let
$\gamma _i$
, let
![]() $R_{\gamma _i}$
be a return path of
$R_{\gamma _i}$
be a return path of
![]() $\gamma _i$
. The path
$\gamma _i$
. The path
![]() $R_{\gamma _1}\dots R_{\gamma _m}\gamma _m\dots \gamma _1$
is equivalent to
$R_{\gamma _1}\dots R_{\gamma _m}\gamma _m\dots \gamma _1$
is equivalent to
![]() $f^m_{t(p)}$
and begins with p.
$f^m_{t(p)}$
and begins with p.
We now show that the notions of path-consistency and cancellativity coincide.
Theorem 2.18. A dimer model Q is path-consistent if and only if
![]() $A_Q$
is a cancellation algebra.
$A_Q$
is a cancellation algebra.
Proof. By Lemma 2.16 and Proposition 2.14, it suffices to show the result on the universal cover
![]() $\widetilde Q$
.
$\widetilde Q$
.
Suppose that
![]() $\widetilde Q$
is path-consistent. We prove that
$\widetilde Q$
is path-consistent. We prove that
![]() $A_{\widetilde Q}$
is a cancellation algebra. Accordingly, take paths
$A_{\widetilde Q}$
is a cancellation algebra. Accordingly, take paths
![]() $p,q,a$
of
$p,q,a$
of
![]() ${\widetilde Q}$
with
${\widetilde Q}$
with
![]() $h(a)=t(p)=t(q)$
and
$h(a)=t(p)=t(q)$
and
![]() $h(p)=h(q)$
. We show that
$h(p)=h(q)$
. We show that
![]() $[pa]=[qa]\implies [p]=[q]$
. The case of left composition is symmetric. By path-consistency, we may write
$[pa]=[qa]\implies [p]=[q]$
. The case of left composition is symmetric. By path-consistency, we may write
![]() $[p]=[rf^{m_p}]$
and
$[p]=[rf^{m_p}]$
and
![]() $[q]=[rf^{m_q}]$
, where r is a minimal path from
$[q]=[rf^{m_q}]$
, where r is a minimal path from
![]() $t(p)$
to
$t(p)$
to
![]() $h(p)$
, necessarily homotopic to p and q by simple connectedness. Given
$h(p)$
, necessarily homotopic to p and q by simple connectedness. Given
![]() $[pa]=[qa]$
, we have
$[pa]=[qa]$
, we have
![]() $[f^{m_p}ra]=[f^{m_q}ra]$
. Then
$[f^{m_p}ra]=[f^{m_q}ra]$
. Then
![]() $m_p=m_q$
by path-consistency. We have shown that
$m_p=m_q$
by path-consistency. We have shown that
and the proof of this direction is complete.
Suppose now that
![]() $A_{\widetilde Q}$
is a cancellation algebra. We first show that only a finite number of face-paths may be factored out of any path p, and that this number is bounded by the number of arrows in p. Suppose to the contrary that there is some path p of Q with m arrows such that we may write
$A_{\widetilde Q}$
is a cancellation algebra. We first show that only a finite number of face-paths may be factored out of any path p, and that this number is bounded by the number of arrows in p. Suppose to the contrary that there is some path p of Q with m arrows such that we may write
![]() $[p]=[p'f^{m'}]$
for some
$[p]=[p'f^{m'}]$
for some
![]() $m'>m$
. By Lemma 2.17,
$m'>m$
. By Lemma 2.17,
![]() $[p'f^{m'}]=[lp]$
for some nonconstant cycle l at
$[p'f^{m'}]=[lp]$
for some nonconstant cycle l at
![]() $h(p)$
. Applying the cancellation property to the equation
$h(p)$
. Applying the cancellation property to the equation
![]() $[p]=[p'f^{m'}]=[lp]$
gives that l is equivalent to the constant path, which is a contradiction. This shows that only a finite number of face-paths may be factored out of any path of
$[p]=[p'f^{m'}]=[lp]$
gives that l is equivalent to the constant path, which is a contradiction. This shows that only a finite number of face-paths may be factored out of any path of
![]() ${\widetilde Q}$
.
${\widetilde Q}$
.
Then any path p of
![]() ${\widetilde Q}$
is equivalent to
${\widetilde Q}$
is equivalent to
![]() $rf^m$
for a minimal path r and a nonnegative integer m. Suppose
$rf^m$
for a minimal path r and a nonnegative integer m. Suppose
![]() $[p]=[rf^m]=[r'f^{m'}]$
for some nonnegative integers m and
$[p]=[rf^m]=[r'f^{m'}]$
for some nonnegative integers m and
![]() $m'$
and minimal paths r and
$m'$
and minimal paths r and
![]() $r'$
. Without loss of generality, suppose
$r'$
. Without loss of generality, suppose
![]() $m\leq m'$
. By the cancellation property,
$m\leq m'$
. By the cancellation property,
![]() $[r]=[r'f^{m'-m}]$
. Then if
$[r]=[r'f^{m'-m}]$
. Then if
![]() $m'>m$
, we have factored a face-path out of r, contradicting minimality of r; hence,
$m'>m$
, we have factored a face-path out of r, contradicting minimality of r; hence,
![]() $m'=m$
and
$m'=m$
and
![]() $[r]=[r']$
.
$[r]=[r']$
.
Then if
![]() ${\widetilde Q}$
is not path-consistent, there must be minimal paths p and q between the same vertices which are not equivalent. Take m which is greater than the length of p and the length of q. By Lemma 2.17,
${\widetilde Q}$
is not path-consistent, there must be minimal paths p and q between the same vertices which are not equivalent. Take m which is greater than the length of p and the length of q. By Lemma 2.17,
![]() $[pf^m]=[pq'q]$
for some path
$[pf^m]=[pq'q]$
for some path
![]() $q'$
from
$q'$
from
![]() $h(q)$
to
$h(q)$
to
![]() $t(q)$
. Suppose we have shown that
$t(q)$
. Suppose we have shown that
![]() $pq'$
is equivalent to
$pq'$
is equivalent to
![]() $f^{m'}$
for some
$f^{m'}$
for some
![]() $m'$
. Then
$m'$
. Then
By the cancellation property, we get either
![]() $[p]=[qf^{m'-m}]$
or
$[p]=[qf^{m'-m}]$
or
![]() $[q]=[pf^{m-m'}]$
. Since p and q are minimal, we have
$[q]=[pf^{m-m'}]$
. Since p and q are minimal, we have
![]() $m=m'$
and
$m=m'$
and
![]() $[p]=[q]$
, contradicting our initial assumption. The proof is then complete if we show that any cycle is equivalent to a composition of face-paths. We do so now.
$[p]=[q]$
, contradicting our initial assumption. The proof is then complete if we show that any cycle is equivalent to a composition of face-paths. We do so now.
Suppose to the contrary and take a simple cycle
![]() $l=\gamma _{s'}\dots \gamma _1$
which is not equivalent to a composition of face-paths and such that every simple cycle inside the disk bounded by l is equivalent to a composition of face-paths. Note that if
$l=\gamma _{s'}\dots \gamma _1$
which is not equivalent to a composition of face-paths and such that every simple cycle inside the disk bounded by l is equivalent to a composition of face-paths. Note that if
![]() $\widetilde {S(Q)}$
is a sphere, then choose one of the two regions that l bounds as being the disk. For any arrow
$\widetilde {S(Q)}$
is a sphere, then choose one of the two regions that l bounds as being the disk. For any arrow
![]() $\gamma _i\in l$
, let
$\gamma _i\in l$
, let
![]() $R_{\gamma _i}$
be the return path of
$R_{\gamma _i}$
be the return path of
![]() $\gamma _i$
inside of the disk bounded by l. As in Lemma 2.17, set
$\gamma _i$
inside of the disk bounded by l. As in Lemma 2.17, set
![]() $l':=R_1\dots R_{s'}$
. Then
$l':=R_1\dots R_{s'}$
. Then
![]() $l'l=R_1\dots R_{s'}\gamma _{{s'}}\dots \gamma _1$
is equivalent to
$l'l=R_1\dots R_{s'}\gamma _{{s'}}\dots \gamma _1$
is equivalent to
![]() $f_{t(l)}^{s'}$
. Moreover,
$f_{t(l)}^{s'}$
. Moreover,
![]() $l'$
is a cycle lying in the area bounded by l. If
$l'$
is a cycle lying in the area bounded by l. If
![]() $l'$
is a simple cycle strictly contained in l, then
$l'$
is a simple cycle strictly contained in l, then
![]() $l'$
is equivalent to a composition of face-paths by choice of l. If
$l'$
is equivalent to a composition of face-paths by choice of l. If
![]() $l'$
is not a simple cycle, then one-by-one we remove simple proper subcycles of
$l'$
is not a simple cycle, then one-by-one we remove simple proper subcycles of
![]() $l'$
, each of which is strictly contained in the area defined by l and hence is equivalent to a composition of face-paths. Then we replace them with a composition of face-paths until we get
$l'$
, each of which is strictly contained in the area defined by l and hence is equivalent to a composition of face-paths. Then we replace them with a composition of face-paths until we get
![]() $[l']=[f_{t(p)}^{s}]$
for some s.
$[l']=[f_{t(p)}^{s}]$
for some s.
Either way,
![]() $l'$
is equivalent to some composition of face-paths
$l'$
is equivalent to some composition of face-paths
![]() $f_{t(p)}^s$
. Then
$f_{t(p)}^s$
. Then
![]() $[f_{t(p)}^{s'}]=[l'l]=[f_{t(p)}^sl]$
. Since
$[f_{t(p)}^{s'}]=[l'l]=[f_{t(p)}^sl]$
. Since
![]() $l'$
is a subpath of
$l'$
is a subpath of
![]() $l'l$
, we must have that
$l'l$
, we must have that
![]() ${s'}\geq s$
. Then the cancellation property gives
${s'}\geq s$
. Then the cancellation property gives
![]() $[f_{t(p)}^{{s'}-s}]=[l]$
and l is equivalent to a composition of face-paths, contradicting the choice of l. This completes the proof that all cycles are equivalent to a composition of face-paths and yields the theorem.
$[f_{t(p)}^{{s'}-s}]=[l]$
and l is equivalent to a composition of face-paths, contradicting the choice of l. This completes the proof that all cycles are equivalent to a composition of face-paths and yields the theorem.
2.4 Winding numbers
In later sections, we will make use of the winding number of an (undirected) cycle around a point in a simply connected dimer model. We now set up notation and prove a lemma.
A signed arrow
![]() $\alpha ^{\varepsilon }$
of Q is an arrow
$\alpha ^{\varepsilon }$
of Q is an arrow
![]() $\alpha $
along with a sign
$\alpha $
along with a sign
![]() $\varepsilon \in \{1,-1\}$
. We consider
$\varepsilon \in \{1,-1\}$
. We consider
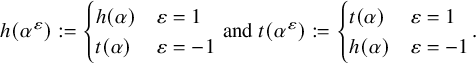 $$\begin{align*}h(\alpha^\varepsilon):=\begin{cases} h(\alpha)&\varepsilon=1\\t(\alpha)&\varepsilon=-1\end{cases} \text{ and } t(\alpha^\varepsilon):=\begin{cases} t(\alpha)&\varepsilon=1\\h(\alpha)&\varepsilon=-1\end{cases}.\end{align*}$$
$$\begin{align*}h(\alpha^\varepsilon):=\begin{cases} h(\alpha)&\varepsilon=1\\t(\alpha)&\varepsilon=-1\end{cases} \text{ and } t(\alpha^\varepsilon):=\begin{cases} t(\alpha)&\varepsilon=1\\h(\alpha)&\varepsilon=-1\end{cases}.\end{align*}$$
A walk on Q is a string of signed arrows
![]() $p:=\alpha _m^{\varepsilon _m}\dots \alpha _1^{\varepsilon _1}$
of Q such that
$p:=\alpha _m^{\varepsilon _m}\dots \alpha _1^{\varepsilon _1}$
of Q such that
![]() $h(\alpha _j^{\varepsilon _j})=t(\alpha _{j+1}^{\varepsilon _{j+1}})$
for all
$h(\alpha _j^{\varepsilon _j})=t(\alpha _{j+1}^{\varepsilon _{j+1}})$
for all
![]() $j\in [m-1]$
. The walk p is a cycle-walk if
$j\in [m-1]$
. The walk p is a cycle-walk if
![]() $h(\alpha _m^{\varepsilon _m})=t(\alpha _1^{\varepsilon _1})$
. Furthermore, we write
$h(\alpha _m^{\varepsilon _m})=t(\alpha _1^{\varepsilon _1})$
. Furthermore, we write
![]() $p^{-1}=\alpha _1^{-\varepsilon _1}\dots \alpha _m^{-\varepsilon _m}$
.
$p^{-1}=\alpha _1^{-\varepsilon _1}\dots \alpha _m^{-\varepsilon _m}$
.
Definition 2.19. Let p be a path in
![]() $\widetilde Q$
and let F be a face of
$\widetilde Q$
and let F be a face of
![]() $\widetilde Q$
. Let q be a walk on
$\widetilde Q$
. Let q be a walk on
![]() $\widetilde Q$
from
$\widetilde Q$
from
![]() $h(p)$
to
$h(p)$
to
![]() $t(p)$
. We write
$t(p)$
. We write
![]() $\text {Wind}(qp,F)$
for the winding number of the path
$\text {Wind}(qp,F)$
for the winding number of the path
![]() $qp$
, considered as a path on the surface
$qp$
, considered as a path on the surface
![]() $\widetilde {S(Q)}$
, around some point in the interior of F.
$\widetilde {S(Q)}$
, around some point in the interior of F.
Lemma 2.20. Let p be a path in
![]() $\widetilde Q$
and let q be a walk on
$\widetilde Q$
and let q be a walk on
![]() $\widetilde Q$
such that
$\widetilde Q$
such that
![]() $qp$
is a cycle-walk. Let
$qp$
is a cycle-walk. Let
![]() $\alpha $
be a left-morphable arrow for p. Then for any face F of
$\alpha $
be a left-morphable arrow for p. Then for any face F of
![]() $\widetilde Q$
,
$\widetilde Q$
,
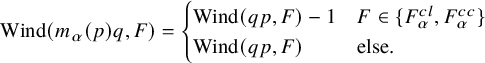 $$ \begin{align} \text{Wind}(m_\alpha(p)q,F)= \begin{cases} \text{Wind}(qp,F)-1 & F\in\{F_\alpha^{cl},F_\alpha^{cc}\}\\ \text{Wind}(qp,F) & \text{else}. \end{cases} \end{align} $$
$$ \begin{align} \text{Wind}(m_\alpha(p)q,F)= \begin{cases} \text{Wind}(qp,F)-1 & F\in\{F_\alpha^{cl},F_\alpha^{cc}\}\\ \text{Wind}(qp,F) & \text{else}. \end{cases} \end{align} $$
Proof. If
![]() $F=F_\alpha ^{cc}$
or
$F=F_\alpha ^{cc}$
or
![]() $F=F_\alpha ^{cl}$
, then
$F=F_\alpha ^{cl}$
, then
![]() $R_\alpha ^{cc}$
winds around F for some positive angle
$R_\alpha ^{cc}$
winds around F for some positive angle
![]() $0\leq \theta \leq 2\pi $
, while
$0\leq \theta \leq 2\pi $
, while
![]() $R_\alpha ^{cl}$
winds around F for an angle of
$R_\alpha ^{cl}$
winds around F for an angle of
![]() $\theta -2\pi $
. Left-morphing at
$\theta -2\pi $
. Left-morphing at
![]() $\alpha $
switches the former for the latter, leading to a net decrease of
$\alpha $
switches the former for the latter, leading to a net decrease of
![]() $2\pi $
radians. Then
$2\pi $
radians. Then
![]() $\text {Wind}(m_\alpha (p)q,F)=\text {Wind}(qp,F)-1$
in this case. If F is any other face, then
$\text {Wind}(m_\alpha (p)q,F)=\text {Wind}(qp,F)-1$
in this case. If F is any other face, then
![]() $R_\alpha ^{cl}$
and
$R_\alpha ^{cl}$
and
![]() $R_\alpha ^{cc}$
do not wind differently around F and the winding number does not change.
$R_\alpha ^{cc}$
do not wind differently around F and the winding number does not change.
3 Morphs and chains
In this section, we prove some technical results about basic morphs with the goal of proving that a path-consistent and simply connected dimer model has no irreducible pairs (Theorem 3.19). This result will be used in Section 4 to characterize path-consistency in terms of the strand diagram of a dimer model. We start with a definition.
In the preceding, we have used the fact that two paths p and q are equivalent if and only if there is a sequence of basic morphs taking p to q. We introduce the idea of a chain of morphable arrows that allows us to talk about sequences of morphs applied to a path in special cases.
Recall that a morphable arrow
![]() $\alpha $
for p is unambiguous if p only has one subpath which is a copy of
$\alpha $
for p is unambiguous if p only has one subpath which is a copy of
![]() $R_\alpha ^{cl}$
or
$R_\alpha ^{cl}$
or
![]() $R_\alpha ^{cc}$
. In this case, there is a unique path
$R_\alpha ^{cc}$
. In this case, there is a unique path
![]() $p'=m_\alpha (p)$
obtained by replacing the subpath
$p'=m_\alpha (p)$
obtained by replacing the subpath
![]() $R_\alpha ^{cl}$
with
$R_\alpha ^{cl}$
with
![]() $R_\alpha ^{cc}$
, or vice versa. If
$R_\alpha ^{cc}$
, or vice versa. If
![]() $\alpha _1,\dots ,\alpha _r\in Q_1$
with each
$\alpha _1,\dots ,\alpha _r\in Q_1$
with each
![]() $\alpha _i$
an unambiguous morphable arrow for
$\alpha _i$
an unambiguous morphable arrow for
![]() $m_{\alpha _{i-1}}\circ \dots \circ m_{\alpha _1}(p)$
for all
$m_{\alpha _{i-1}}\circ \dots \circ m_{\alpha _1}(p)$
for all
![]() $i\leq r$
, we call the sequence
$i\leq r$
, we call the sequence
![]() $a=\alpha _r\dots \alpha _1$
a morphable chain, or simply a chain, for p. We introduce the notation
$a=\alpha _r\dots \alpha _1$
a morphable chain, or simply a chain, for p. We introduce the notation
![]() $m_{a}(p):=m_{\alpha _r}\circ \dots \circ m_{\alpha _1}(p)$
, and we say that a is a chain from p to
$m_{a}(p):=m_{\alpha _r}\circ \dots \circ m_{\alpha _1}(p)$
, and we say that a is a chain from p to
![]() $m_a(p)$
. For some
$m_a(p)$
. For some
![]() $i\in [r]$
, we say that
$i\in [r]$
, we say that
![]() $\alpha _i$
is a left-morph (respectively right-morph) of a if
$\alpha _i$
is a left-morph (respectively right-morph) of a if
![]() $\alpha _i$
is left-morphable (respectively right-morphable) for
$\alpha _i$
is left-morphable (respectively right-morphable) for
![]() $m_{\alpha _{i-1}\dots \alpha _{1}}(p)$
. Note that since
$m_{\alpha _{i-1}\dots \alpha _{1}}(p)$
. Note that since
![]() $\alpha _i$
is an unambiguous morphable arrow for this path,
$\alpha _i$
is an unambiguous morphable arrow for this path,
![]() $\alpha _i$
is either a left-morph or a right-morph of a, but not both. If
$\alpha _i$
is either a left-morph or a right-morph of a, but not both. If
![]() $\alpha _i$
is a left-morph (respectively right-morph) for all i, we say that a is a left-chain (respectively right-chain). Two chains a and b of p are equivalent if
$\alpha _i$
is a left-morph (respectively right-morph) for all i, we say that a is a left-chain (respectively right-chain). Two chains a and b of p are equivalent if
![]() $m_a(p)=m_b(p)$
.
$m_a(p)=m_b(p)$
.
Since we require morphable arrows of a chain to be unambiguous, it may be the case that paths p and q are equivalent despite there being no chain from p to q. For example, this is true if p and q are equivalent but distinct and every morphable arrow for p is ambiguous. In reasonable circumstances; however, the notion of a chain is often sufficient. For example, minimal paths (in path-consistent dimer models) have no unambiguous morphs, so two minimal paths are equivalent if and only if there is a chain from one to the other.
3.1 Cycle-removing morphs
In this subsection, we let
![]() $\widetilde Q$
be a path-consistent and simply connected dimer model, and we define a new type of morph which weakly decreases the c-value of a path and preserves the property of being an elementary path, which we define now.
$\widetilde Q$
be a path-consistent and simply connected dimer model, and we define a new type of morph which weakly decreases the c-value of a path and preserves the property of being an elementary path, which we define now.
Definition 3.1. A elementary path in a dimer model Q is a (possibly constant) path which is not a face-path and which contains no cycles as proper subpaths.
Note that an elementary path may never contain all arrows in a given face-path. Then if p is elementary, no morphable arrow for p is in p. Moreover, every morphable arrow for p is unambiguous. We also have the following.
Definition 3.2. Let p be an elementary path in a path-consistent dimer model
![]() ${\widetilde Q}$
. Let
${\widetilde Q}$
. Let
![]() $\alpha $
be a right-morphable arrow for p. If
$\alpha $
be a right-morphable arrow for p. If
![]() $m_\alpha (p)$
is elementary, we define the cycle-removing right-morph
$m_\alpha (p)$
is elementary, we define the cycle-removing right-morph
![]() $\omega _\alpha (p)$
to be
$\omega _\alpha (p)$
to be
![]() $m_\alpha (p)$
.
$m_\alpha (p)$
.
If not, write
![]() $p=p"R_\alpha ^{cl}p'$
for subpaths
$p=p"R_\alpha ^{cl}p'$
for subpaths
![]() $p'$
and
$p'$
and
![]() $p"$
of p. This decomposition is unique because morphable arrows for elementary paths are unambiguous. Let
$p"$
of p. This decomposition is unique because morphable arrows for elementary paths are unambiguous. Let
![]() $v_0:=h(\alpha )$
and number the vertices of
$v_0:=h(\alpha )$
and number the vertices of
![]() $F_\alpha ^{cc}$
counter-clockwise as
$F_\alpha ^{cc}$
counter-clockwise as
![]() $h(\alpha )=v_0,v_1,\dots ,v_m=t(\alpha )$
. Let a be the largest integer less than m such that
$h(\alpha )=v_0,v_1,\dots ,v_m=t(\alpha )$
. Let a be the largest integer less than m such that
![]() $v_a\in p'$
. Note that if
$v_a\in p'$
. Note that if
![]() $v_m\in p'$
, then
$v_m\in p'$
, then
![]() $p"$
is constant by elementariness. Let b be the smallest integer greater than 0 such that
$p"$
is constant by elementariness. Let b be the smallest integer greater than 0 such that
![]() $v_b\in p"$
.
$v_b\in p"$
.
Since
![]() $p=p"R_\alpha ^{cl}p'$
is elementary,
$p=p"R_\alpha ^{cl}p'$
is elementary,
![]() $p'$
and
$p'$
and
![]() $p"$
do not intersect except for possibly at the endpoints
$p"$
do not intersect except for possibly at the endpoints
![]() $t(p'),h(p")$
if they coincide. Then any proper subcycle of
$t(p'),h(p")$
if they coincide. Then any proper subcycle of
![]() $m_\alpha (p)=p"R_\alpha ^{cc}p'$
must involve some
$m_\alpha (p)=p"R_\alpha ^{cc}p'$
must involve some
![]() $v_i$
for
$v_i$
for
![]() $i\in \{1,\dots ,m-1\}$
; hence, either
$i\in \{1,\dots ,m-1\}$
; hence, either
![]() $a>0$
or
$a>0$
or
![]() $b<m$
or both. Moreover,
$b<m$
or both. Moreover,
![]() $a\leq b$
.
$a\leq b$
.
Let
![]() $q'$
be the subpath of
$q'$
be the subpath of
![]() $p'$
from
$p'$
from
![]() $t(p')$
to
$t(p')$
to
![]() $v_a$
. Let
$v_a$
. Let
![]() $R'$
be the subpath of
$R'$
be the subpath of
![]() $R_\alpha ^{cc}$
from
$R_\alpha ^{cc}$
from
![]() $v_a$
to
$v_a$
to
![]() $v_b$
. Let
$v_b$
. Let
![]() $q"$
be the subpath of
$q"$
be the subpath of
![]() $p"$
from
$p"$
from
![]() $v_b$
to
$v_b$
to
![]() $h(p")$
. If
$h(p")$
. If
![]() $q"R'q'$
is not a face-path, define the cycle-removing right-morph
$q"R'q'$
is not a face-path, define the cycle-removing right-morph
![]() $\omega _\alpha (p)$
to be
$\omega _\alpha (p)$
to be
![]() $q"R'q'$
. Otherwise, define
$q"R'q'$
. Otherwise, define
![]() $\omega _\alpha (p)$
to be the constant path. For example, see Figures 1 and 2.
$\omega _\alpha (p)$
to be the constant path. For example, see Figures 1 and 2.
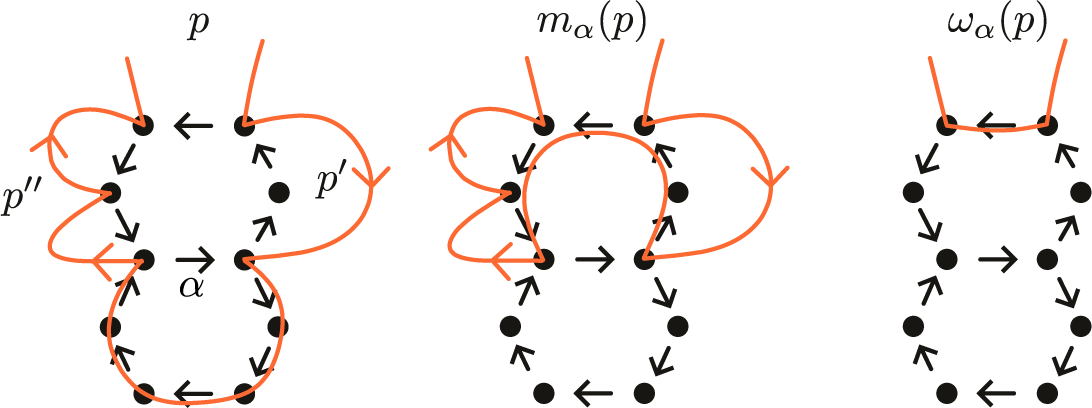
Figure 1 An example of a cycle-removing morph.
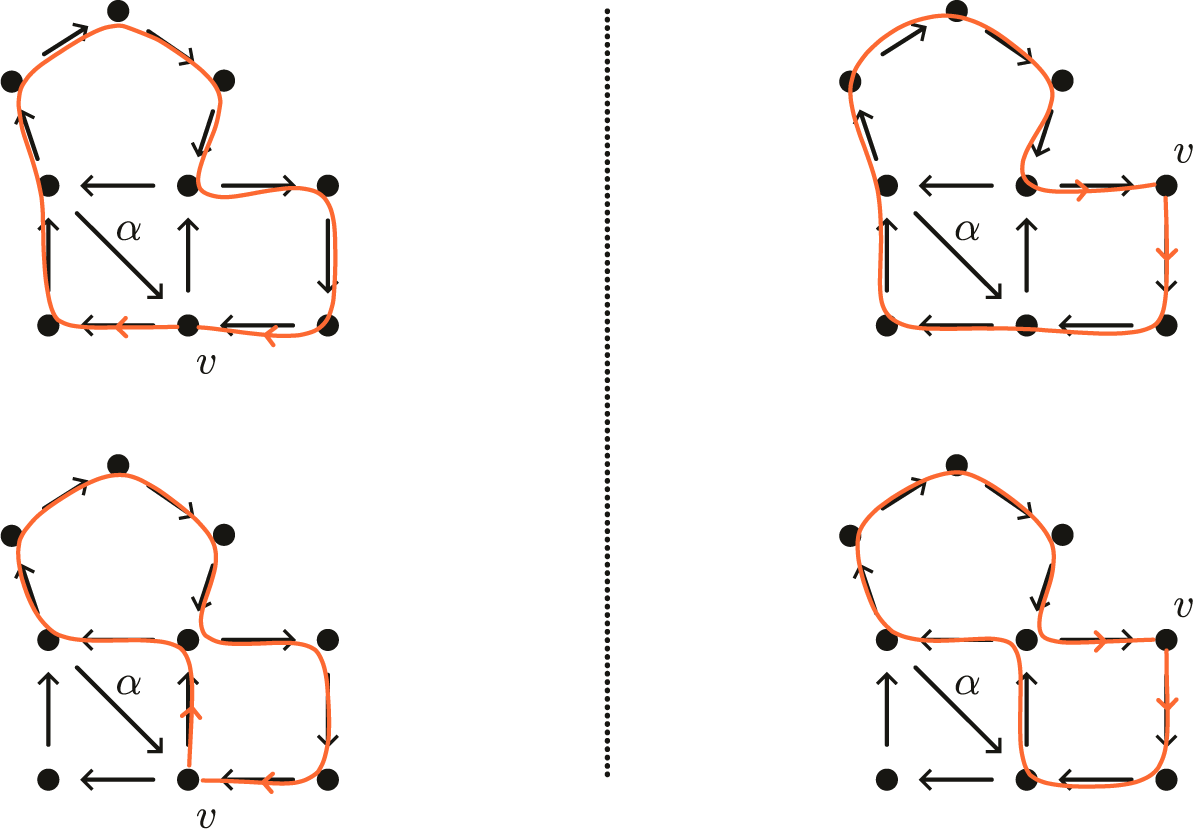
Figure 2 The top left shows a clockwise cycle p at v. The bottom left shows
![]() $m_\alpha (p)$
. In the notation of Definition 3.2,
$m_\alpha (p)$
. In the notation of Definition 3.2,
![]() $a=b$
and the paths
$a=b$
and the paths
![]() $p',q',R',q"$
are all constant paths at v; hence,
$p',q',R',q"$
are all constant paths at v; hence,
![]() $\omega _\alpha (p)$
is constant. The top right shows a clockwise cycle q at a different v, and the bottom right shows
$\omega _\alpha (p)$
is constant. The top right shows a clockwise cycle q at a different v, and the bottom right shows
![]() $m_\alpha (q)$
. In this case,
$m_\alpha (q)$
. In this case,
![]() $q"R'q'$
is the clockwise square face containing v, so
$q"R'q'$
is the clockwise square face containing v, so
![]() $\omega _\alpha (q)$
is defined to be constant.
$\omega _\alpha (q)$
is defined to be constant.
We similarly define cycle-removing left-morphs.
Intuitively, the cycle-removing right-morph
![]() $\omega _\alpha (p)$
is obtained by removing the proper subcycles from
$\omega _\alpha (p)$
is obtained by removing the proper subcycles from
![]() $m_\alpha (p)$
to get an elementary path. Since
$m_\alpha (p)$
to get an elementary path. Since
![]() $\widetilde Q$
is path-consistent, any cycle is equivalent to a composition of face-paths; hence,
$\widetilde Q$
is path-consistent, any cycle is equivalent to a composition of face-paths; hence,
![]() $m_\alpha (p)$
is equivalent to
$m_\alpha (p)$
is equivalent to
![]() $\omega _\alpha (p)f^m$
for some
$\omega _\alpha (p)f^m$
for some
![]() $m\geq 0$
.
$m\geq 0$
.
We define cycle-removing morphs only for simply connected and path-consistent dimer models because without these hypotheses, there may be cycles which are not equivalent to a composition of face-paths. Hence, we may have that
![]() $m_\alpha (p)$
is not equivalent to
$m_\alpha (p)$
is not equivalent to
![]() $\omega _\alpha (p)f^m$
for any
$\omega _\alpha (p)f^m$
for any
![]() $m\geq 0$
. If Q is path-consistent but not simply connected, we can pass to
$m\geq 0$
. If Q is path-consistent but not simply connected, we can pass to
![]() $\widetilde Q$
, do a cycle-removing morph, and pass back to Q. The result is that we do the corresponding basic morph and remove null-homotopic cycles of Q.
$\widetilde Q$
, do a cycle-removing morph, and pass back to Q. The result is that we do the corresponding basic morph and remove null-homotopic cycles of Q.
If p is elementary and
![]() $m_\alpha (p)$
contains a proper subcycle, we say that
$m_\alpha (p)$
contains a proper subcycle, we say that
![]() $\alpha $
creates a proper subcycle of p. Observe that
$\alpha $
creates a proper subcycle of p. Observe that
![]() $\alpha $
creates a proper subcycle if and only if
$\alpha $
creates a proper subcycle if and only if
![]() $\omega _\alpha (p)\neq m_\alpha (p)$
.
$\omega _\alpha (p)\neq m_\alpha (p)$
.
Lemma 3.3. Let p be an elementary path in a path-consistent quiver
![]() ${\widetilde Q}$
and let
${\widetilde Q}$
and let
![]() $\alpha $
be a right-morphable arrow for p. Then we have the following:
$\alpha $
be a right-morphable arrow for p. Then we have the following:
-
1. The cycle-removing right-morph
 $\omega _\alpha (p)$
is elementary.
$\omega _\alpha (p)$
is elementary. -
2. The cycle-removing right-morph
 $\omega _\alpha (p)$
contains some arrow of
$\omega _\alpha (p)$
contains some arrow of
 $R_\alpha ^{cc}$
if and only if
$R_\alpha ^{cc}$
if and only if
 $\omega _\alpha (p)$
is nonconstant.
$\omega _\alpha (p)$
is nonconstant. -
3. The arrow
 $\alpha $
creates a proper subcycle if and only if
$\alpha $
creates a proper subcycle if and only if
 $\omega _\alpha (p)$
does not contain all of
$\omega _\alpha (p)$
does not contain all of
 $R_\alpha ^{cc}$
.
$R_\alpha ^{cc}$
.
Proof. Parts (1) and (3) follow from the definitions. We prove (2). Certainly, if
![]() $\omega _\alpha (p)$
is constant, then it contains no arrow of
$\omega _\alpha (p)$
is constant, then it contains no arrow of
![]() $R_\alpha ^{cc}$
. However, if
$R_\alpha ^{cc}$
. However, if
![]() $\omega _\alpha (p)$
is nonconstant, then in the notation of Definition 3.2, we must have
$\omega _\alpha (p)$
is nonconstant, then in the notation of Definition 3.2, we must have
![]() $a<b$
. Then some arrow of
$a<b$
. Then some arrow of
![]() $R_\alpha ^{cc}$
is contained in
$R_\alpha ^{cc}$
is contained in
![]() $R'$
and hence is contained in
$R'$
and hence is contained in
![]() $\omega _\alpha (p)=q"R'q'$
.
$\omega _\alpha (p)=q"R'q'$
.
Remark 3.4. Many of the definitions and results appearing above as well as later in the text are symmetric. If one switches ‘left’ for ‘right’ and ‘clockwise’ for ‘counter-clockwise’ in the statements and proofs, the analogous arguments and results hold. We will refer to these as dual results without stating them separately.
3.2 Left, right, good and bad
For the remainder of Section 3, we assume that
![]() $\widetilde {S(Q)}$
is not a sphere. We now define a notion of one path being to the right of another. We obtain some conditions under which cycle-removing morphs behave well with respect to this concept of left and right.
$\widetilde {S(Q)}$
is not a sphere. We now define a notion of one path being to the right of another. We obtain some conditions under which cycle-removing morphs behave well with respect to this concept of left and right.
Definition 3.5. Suppose p and q are elementary paths in a simply connected dimer model
![]() ${\widetilde Q}$
which is not on a sphere with
${\widetilde Q}$
which is not on a sphere with
![]() $t(p)=t(q)$
and
$t(p)=t(q)$
and
![]() $h(p)=h(q)$
. We say that p is to the right of q if the following conditions are satisfied.
$h(p)=h(q)$
. We say that p is to the right of q if the following conditions are satisfied.
-
1. The shared vertices of p and q may be ordered
 $v_1,\dots ,v_m$
such that
$v_1,\dots ,v_m$
such that
 $v_i$
is the ith vertex among
$v_i$
is the ith vertex among
 $\{v_1,\dots ,v_m\}$
to appear in p and is the ith such vertex to appear in q. We remark that if p is an elementary cycle and q is trivial, then
$\{v_1,\dots ,v_m\}$
to appear in p and is the ith such vertex to appear in q. We remark that if p is an elementary cycle and q is trivial, then
 $m=2$
and
$m=2$
and
 $v_1=v_2$
.
$v_1=v_2$
. -
2. For all
 $i\in [m-1]$
, if
$i\in [m-1]$
, if
 $p_i$
(respectively
$p_i$
(respectively
 $q_i$
) is the subpath of p (respectively q) from
$q_i$
) is the subpath of p (respectively q) from
 $v_i$
to
$v_i$
to
 $v_{i+1}$
, then either
$v_{i+1}$
, then either
 $p_i$
and
$p_i$
and
 $q_i$
are the same arrow or
$q_i$
are the same arrow or
 $q_i^{-1}p_i$
is a counter-clockwise (necessarily simple) cycle-walk. In the latter case, we say that p and q bound the disk
$q_i^{-1}p_i$
is a counter-clockwise (necessarily simple) cycle-walk. In the latter case, we say that p and q bound the disk
 $q_i^{-1}p_i$
.
$q_i^{-1}p_i$
.
See Figure 3. We remark that if q is constant and p is an elementary counter-clockwise cycle, then p is to the right of q with
![]() $m=2$
and
$m=2$
and
![]() $v_1=v_2$
. Similarly, an elementary clockwise cycle at v is to the left of the constant path at v.
$v_1=v_2$
. Similarly, an elementary clockwise cycle at v is to the left of the constant path at v.
Figure 3 The paths p and q bound two disks and p is to the right of q.
We warn the reader that Definition 3.5 does not form a partial order on paths in
![]() $\widetilde Q$
with the same start and end vertices as the relation is not transitive. See Figure 4 for an example.
$\widetilde Q$
with the same start and end vertices as the relation is not transitive. See Figure 4 for an example.
Figure 4 The path q is to the right of p and r is to the right of q, but r is not to the right of p.
Remark 3.6. Definition 3.5 relies on the notion of a simple cycle-walk being clockwise or counter-clockwise. This is only well defined when the surface is not a sphere. In the following, we will prove that path-consistency implies strand-consistency while making heavy use of the notions of left and right as well as those of clockwise and counter-clockwise, culminating in the proof of Proposition 4.12. These arguments require
![]() $\widetilde Q$
not to be on a sphere, and indeed dimer models on spheres may not be strand-consistent but may be cancellative, so Proposition 4.12 does not hold in this case.
$\widetilde Q$
not to be on a sphere, and indeed dimer models on spheres may not be strand-consistent but may be cancellative, so Proposition 4.12 does not hold in this case.
Definition 3.7. A path p is a rightmost path (respectively leftmost path); there are no right-morphable (respectively left-morphable) arrows for p.
Definition 3.8. An irreducible pair is a pair of paths
![]() $(p,q)$
in
$(p,q)$
in
![]() $\widetilde Q$
such that
$\widetilde Q$
such that
![]() $q^{-1}p$
is a simple counter-clockwise cycle-walk, p is leftmost, and q is rightmost.
$q^{-1}p$
is a simple counter-clockwise cycle-walk, p is leftmost, and q is rightmost.
If
![]() $(p,q)$
is an irreducible pair, then p is to the right of q. Note that p or q may be constant. If this is true, then the other path in the pair cannot be a face-path by elementariness. The notion of an irreducible pair appears in [Reference Bocklandt6] when Q is a dimer model on a torus. We now make preparations to prove that irreducible pairs may not occur in path-consistent dimer models.
$(p,q)$
is an irreducible pair, then p is to the right of q. Note that p or q may be constant. If this is true, then the other path in the pair cannot be a face-path by elementariness. The notion of an irreducible pair appears in [Reference Bocklandt6] when Q is a dimer model on a torus. We now make preparations to prove that irreducible pairs may not occur in path-consistent dimer models.
Definition 3.9. Let p be an elementary path of
![]() $\widetilde Q$
and let
$\widetilde Q$
and let
![]() $\alpha $
be a morphable arrow for p. We say that
$\alpha $
be a morphable arrow for p. We say that
![]() $\alpha $
is good if
$\alpha $
is good if
![]() $\alpha $
is a left-morphable arrow or if
$\alpha $
is a left-morphable arrow or if
![]() $\alpha $
is a right-morphable arrow such that
$\alpha $
is a right-morphable arrow such that
![]() $m_\alpha (p)$
does not contain a proper counter-clockwise subcycle. If
$m_\alpha (p)$
does not contain a proper counter-clockwise subcycle. If
![]() $\alpha $
is a right-morphable arrow for p such that
$\alpha $
is a right-morphable arrow for p such that
![]() $m_\alpha (p)$
contains a proper counter-clockwise subcycle, then we say that
$m_\alpha (p)$
contains a proper counter-clockwise subcycle, then we say that
![]() $\alpha $
is bad. A cycle-removing chain
$\alpha $
is bad. A cycle-removing chain
![]() $a=\alpha _r\dots \alpha _1$
of p is good if each
$a=\alpha _r\dots \alpha _1$
of p is good if each
![]() $\alpha _i$
is a good morphable arrow for
$\alpha _i$
is a good morphable arrow for
![]() $\omega _{\alpha _{i-1}\dots \alpha _{1}}(p)$
. Otherwise, a is bad.
$\omega _{\alpha _{i-1}\dots \alpha _{1}}(p)$
. Otherwise, a is bad.
There is an asymmetry to our definitions of good and bad cycle-removing morphs. This is because we intend to apply them only to the leftmost path p in an irreducible pair
![]() $(p,q)$
. Our strategy will be to obtain a good cycle-removing chain taking p to a minimal path
$(p,q)$
. Our strategy will be to obtain a good cycle-removing chain taking p to a minimal path
![]() $p'$
, where
$p'$
, where
![]() $q^{-1}p$
is contained in the area enclosed by the simple counter-clockwise cycle-walk
$q^{-1}p$
is contained in the area enclosed by the simple counter-clockwise cycle-walk
![]() $q^{-1}p'$
. Dually, one obtains a minimal path
$q^{-1}p'$
. Dually, one obtains a minimal path
![]() $q'$
so that
$q'$
so that
![]() $(q')^{-1}p'$
is a simple counter-clockwise cycle-walk, which we show to be impossible in the path-consistent case.
$(q')^{-1}p'$
is a simple counter-clockwise cycle-walk, which we show to be impossible in the path-consistent case.
Good morphs are useful because a good cycle-removing morph behaves reasonably well with respect to the notion of one path being to the left or right of another. Consider the following.
Lemma 3.10.
-
(1) Let q be an elementary path in
 $\widetilde Q$
and let p be any elementary path to the right of q. Let
$\widetilde Q$
and let p be any elementary path to the right of q. Let
 $\beta $
be a left-morphable arrow for p which is not a left-morphable arrow for q. Then
$\beta $
be a left-morphable arrow for p which is not a left-morphable arrow for q. Then
 $\omega _\beta (p)$
is to the right of q.
$\omega _\beta (p)$
is to the right of q. -
(2) Let p be an elementary counter-clockwise cycle in
 $\widetilde Q$
and let
$\widetilde Q$
and let
 $\alpha $
be a right-morphable arrow for p such that
$\alpha $
be a right-morphable arrow for p such that
 $m_\alpha (p)$
has no proper counter-clockwise subcycle. Then p is contained in the area enclosed by
$m_\alpha (p)$
has no proper counter-clockwise subcycle. Then p is contained in the area enclosed by
 $\omega _\alpha (p)$
.
$\omega _\alpha (p)$
.
Proof. To see (1), it suffices to reduce to the case where p and q share only their start and end vertices. In this case, they bound one disk
![]() $q^{-1}p$
and a left-morph of p at
$q^{-1}p$
and a left-morph of p at
![]() $\beta $
results in a path contained in the area enclosed by
$\beta $
results in a path contained in the area enclosed by
![]() $q^{-1}p$
.
$q^{-1}p$
.
We now prove (2). We show that
![]() $\text {Wind}(\omega _\alpha (p),F)\geq \text {Wind}(p,F)$
for any face F. It follows that
$\text {Wind}(\omega _\alpha (p),F)\geq \text {Wind}(p,F)$
for any face F. It follows that
![]() $\omega _\alpha (p)$
is also an elementary counter-clockwise cycle. Since any face F is in the interior of p (respectively
$\omega _\alpha (p)$
is also an elementary counter-clockwise cycle. Since any face F is in the interior of p (respectively
![]() $\omega _\alpha (p)$
) if and only if
$\omega _\alpha (p)$
) if and only if
![]() $\text {Wind}(p,F)>0$
(respectively
$\text {Wind}(p,F)>0$
(respectively
![]() $\text {Wind}(\omega _\alpha (p),F)>0$
), it further follows that if F is in the interior of p, then F is in the interior of
$\text {Wind}(\omega _\alpha (p),F)>0$
), it further follows that if F is in the interior of p, then F is in the interior of
![]() $\omega _\alpha (p)$
and the statement is proven.
$\omega _\alpha (p)$
and the statement is proven.
Let p be an elementary counter-clockwise cycle in
![]() $\widetilde Q$
and let
$\widetilde Q$
and let
![]() $\alpha $
be a right-morphable arrow for p such that
$\alpha $
be a right-morphable arrow for p such that
![]() $m_\alpha (p)$
has no proper counter-clockwise subcycle. By Lemma 2.20,
$m_\alpha (p)$
has no proper counter-clockwise subcycle. By Lemma 2.20,
![]() $\text {Wind}(m_\alpha (p),F)\geq \text {Wind}(p,F)$
. The path
$\text {Wind}(m_\alpha (p),F)\geq \text {Wind}(p,F)$
. The path
![]() $\omega _\alpha (p)$
is obtained from
$\omega _\alpha (p)$
is obtained from
![]() $m_\alpha (p)$
by deleting some number of proper elementary subcycles. All of these are clockwise and hence have a winding number less than or equal to zero around F, by assumption. It follows that their deletion can only increase the winding number around F, and we have
$m_\alpha (p)$
by deleting some number of proper elementary subcycles. All of these are clockwise and hence have a winding number less than or equal to zero around F, by assumption. It follows that their deletion can only increase the winding number around F, and we have
If F is enclosed within p, then
![]() $\text {Wind}(p,F)=1$
, and the above inequality forces
$\text {Wind}(p,F)=1$
, and the above inequality forces
![]() $\text {Wind}(\omega _\alpha (p),F)=1$
. It follows that F is enclosed within
$\text {Wind}(\omega _\alpha (p),F)=1$
. It follows that F is enclosed within
![]() $\omega _\alpha (p)$
. This ends the proof.
$\omega _\alpha (p)$
. This ends the proof.
Note that the conditions of (1) and (2) of Lemma 3.10 necessitate that the morphable arrows considered are good. Some caution must be shown when considering whether cycle-removing morphs move paths to the right or left, particularly when the morphs are bad. For example, see the bad right-morph of Figure 5. On the left is a path p with a right-morphable arrow
![]() $\alpha $
, and on the right is the path
$\alpha $
, and on the right is the path
![]() $\omega _\alpha (p)$
. Note that p is not contained in the area enclosed by
$\omega _\alpha (p)$
. Note that p is not contained in the area enclosed by
![]() $\omega _\alpha (p)$
, justifying the limited scope of Lemma 3.10 (2).
$\omega _\alpha (p)$
, justifying the limited scope of Lemma 3.10 (2).
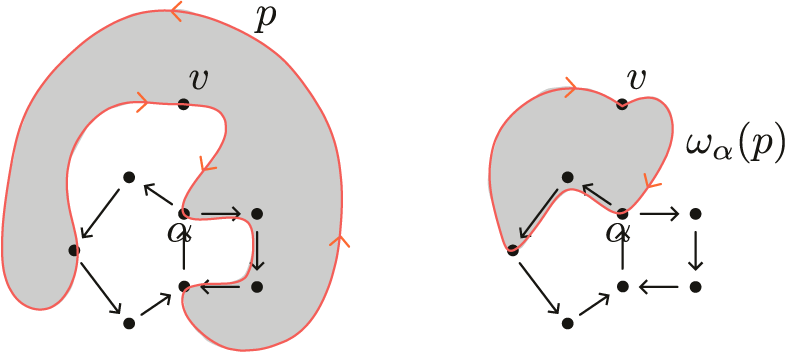
Figure 5 On the left is a counter-clockwise cycle p at v. Cycle-removing right-morphing p at the arrow
![]() $\alpha $
results in a clockwise cycle which does not enclose p.
$\alpha $
results in a clockwise cycle which does not enclose p.
3.3 Irreducible pairs
The goal of this section is to show that irreducible pairs (Definition 3.8) cannot appear in simply connected path-consistent dimer models. We begin with some technical lemmas about cycle-removing morphs.
Lemma 3.11. Let p be an elementary path in a path-consistent quiver
![]() $\widetilde Q$
. Let
$\widetilde Q$
. Let
![]() $\alpha $
be a right-morphable arrow for p and let
$\alpha $
be a right-morphable arrow for p and let
![]() $\beta $
be a left-morphable arrow for
$\beta $
be a left-morphable arrow for
![]() $\omega _\alpha (p)$
distinct from
$\omega _\alpha (p)$
distinct from
![]() $\alpha $
. Then
$\alpha $
. Then
![]() $\beta $
is a left-morphable arrow for p.
$\beta $
is a left-morphable arrow for p.
Proof. Any subpath of
![]() $\omega _\alpha (p)$
which is not a subpath of p must contain some arrow
$\omega _\alpha (p)$
which is not a subpath of p must contain some arrow
![]() $\gamma $
of
$\gamma $
of
![]() $R_\alpha ^{cc}$
. Since
$R_\alpha ^{cc}$
. Since
![]() $\omega _\alpha (p)$
does not contain
$\omega _\alpha (p)$
does not contain
![]() $\alpha $
, the only counter-clockwise return path which
$\alpha $
, the only counter-clockwise return path which
![]() $\gamma $
could be a part of is
$\gamma $
could be a part of is
![]() $R_\alpha ^{cc}$
. This shows that
$R_\alpha ^{cc}$
. This shows that
![]() $\omega _\alpha (p)$
contains no counter-clockwise return paths which are not in p, other than possibly
$\omega _\alpha (p)$
contains no counter-clockwise return paths which are not in p, other than possibly
![]() $R_\alpha ^{cc}$
. The result follows.
$R_\alpha ^{cc}$
. The result follows.
Definition 3.12. We say that a (cycle-removing) chain
![]() $a=\alpha _r\dots \alpha _1$
of an elementary path p is crossing-creating if
$a=\alpha _r\dots \alpha _1$
of an elementary path p is crossing-creating if
![]() $m_{\alpha _i\dots \alpha _1}(p)$
is elementary for
$m_{\alpha _i\dots \alpha _1}(p)$
is elementary for
![]() $i<r$
but
$i<r$
but
![]() $m_a(p)$
is not elementary.
$m_a(p)$
is not elementary.
If a path p of a path-consistent dimer model is not minimal, then there must be a crossing-creating chain of p. Our goal is now to show that there must be a good crossing-creating chain of p (Proposition 3.17). Our first step is Lemmas 3.13 and 3.14. These show that an elementary path must have a crossing-creating left-chain under certain technical conditions.
Lemma 3.13. Let p be an elementary counter-clockwise cycle in
![]() $\widetilde Q$
. Let
$\widetilde Q$
. Let
![]() $\alpha $
be a right-morphable arrow for p such that
$\alpha $
be a right-morphable arrow for p such that
![]() $m_\alpha (p)$
has no proper counter-clockwise subcycle. Suppose there is a crossing-creating left-chain of
$m_\alpha (p)$
has no proper counter-clockwise subcycle. Suppose there is a crossing-creating left-chain of
![]() $\omega _\alpha (p)$
. Then there is a crossing-creating left-chain of p.
$\omega _\alpha (p)$
. Then there is a crossing-creating left-chain of p.
Proof. Let
![]() $b=\beta _s\dots \beta _1$
be a crossing-creating left-chain of
$b=\beta _s\dots \beta _1$
be a crossing-creating left-chain of
![]() $\omega _\alpha (p)$
. Let j be maximal such that
$\omega _\alpha (p)$
. Let j be maximal such that
![]() $b':=\beta _j\dots \beta _1$
is a left-chain of p as well as
$b':=\beta _j\dots \beta _1$
is a left-chain of p as well as
![]() $\omega _\alpha (p)$
. If
$\omega _\alpha (p)$
. If
![]() $b'$
is crossing-creating for p, then we are done, so suppose
$b'$
is crossing-creating for p, then we are done, so suppose
![]() $b'$
is not a crossing-creating chain of p.
$b'$
is not a crossing-creating chain of p.
Suppose first that b is a left-chain of p, and hence that
![]() $j=s$
and
$j=s$
and
![]() $b'=b$
. Since b creates a crossing of
$b'=b$
. Since b creates a crossing of
![]() $\omega _\alpha (p)$
but not of p, there must be a proper subcycle of
$\omega _\alpha (p)$
but not of p, there must be a proper subcycle of
![]() $m_{b}(\omega _\alpha (p))$
starting at a vertex v of
$m_{b}(\omega _\alpha (p))$
starting at a vertex v of
![]() $\omega _\alpha (p)$
which is not a vertex of p. Then left-morphing
$\omega _\alpha (p)$
which is not a vertex of p. Then left-morphing
![]() $m_{\beta _{s-1}\dots \beta _{1}}(p)$
at
$m_{\beta _{s-1}\dots \beta _{1}}(p)$
at
![]() $\beta _s$
must add v to p. By Lemma 3.10 (2), the area bounded by p is contained in the area bounded by
$\beta _s$
must add v to p. By Lemma 3.10 (2), the area bounded by p is contained in the area bounded by
![]() $\omega _\alpha (p)$
. In particular, vertices of
$\omega _\alpha (p)$
. In particular, vertices of
![]() $\omega _\alpha (p)$
which are not vertices of p are not in the area bounded by p. Since left-morphing p at b does not create any crossings,
$\omega _\alpha (p)$
which are not vertices of p are not in the area bounded by p. Since left-morphing p at b does not create any crossings,
![]() $p=\omega _b(\omega _b(p))$
is obtained by applying the (cycle-removing) right-chain b to
$p=\omega _b(\omega _b(p))$
is obtained by applying the (cycle-removing) right-chain b to
![]() $\omega _b(p)$
. Then Lemma 3.10 (2) applied to
$\omega _b(p)$
. Then Lemma 3.10 (2) applied to
![]() $\omega _b(p)$
shows that
$\omega _b(p)$
shows that
![]() $\omega _b(p)$
is strictly contained in the area bounded by p. Since v is not in the area bounded by p, the vertex v cannot be in
$\omega _b(p)$
is strictly contained in the area bounded by p. Since v is not in the area bounded by p, the vertex v cannot be in
![]() $\omega _b(p)$
. This is a contradiction.
$\omega _b(p)$
. This is a contradiction.
It follows that b is not a left-chain of p and hence that
![]() $j<s$
. We claim that
$j<s$
. We claim that
![]() $R_\alpha ^{cl}\in m_{\beta _{j'}\dots \beta _{1}}(p)$
and that no arrow of
$R_\alpha ^{cl}\in m_{\beta _{j'}\dots \beta _{1}}(p)$
and that no arrow of
![]() $F_\alpha ^{cl}$
is in
$F_\alpha ^{cl}$
is in
![]() $m_{\beta _{j'}\dots \beta _{1}}(\omega _\alpha (p))$
for any
$m_{\beta _{j'}\dots \beta _{1}}(\omega _\alpha (p))$
for any
![]() $1\leq j'\leq j$
. Since
$1\leq j'\leq j$
. Since
![]() $R_\alpha ^{cl}\in p$
and
$R_\alpha ^{cl}\in p$
and
![]() $\beta _1$
does not create a crossing of p, we must have
$\beta _1$
does not create a crossing of p, we must have
![]() $\beta _1\not \in F_\alpha ^{cl}$
. Since no arrow of
$\beta _1\not \in F_\alpha ^{cl}$
. Since no arrow of
![]() $F_\alpha ^{cl}$
is in
$F_\alpha ^{cl}$
is in
![]() $\omega _\alpha (p)$
and
$\omega _\alpha (p)$
and
![]() $R_{\beta _1}^{cc}\in \omega _\alpha (p)$
, for any
$R_{\beta _1}^{cc}\in \omega _\alpha (p)$
, for any
![]() $\alpha '\in F_\alpha ^{cl}$
we must have
$\alpha '\in F_\alpha ^{cl}$
we must have
![]() $\beta _1\not \in F_{\alpha '}^{cc}$
. It follows that
$\beta _1\not \in F_{\alpha '}^{cc}$
. It follows that
![]() $R_\alpha ^{cl}$
is in
$R_\alpha ^{cl}$
is in
![]() $m_{\beta _1}(p)$
and that no arrow of
$m_{\beta _1}(p)$
and that no arrow of
![]() $F_\alpha ^{cl}$
is in
$F_\alpha ^{cl}$
is in
![]() $m_{\beta _1}(\omega _\alpha (p))$
. We repeat this argument to see that
$m_{\beta _1}(\omega _\alpha (p))$
. We repeat this argument to see that
![]() $R_\alpha ^{cl}\in m_{\beta {j'}\dots \beta _{1}}(p)$
and that no arrow of
$R_\alpha ^{cl}\in m_{\beta {j'}\dots \beta _{1}}(p)$
and that no arrow of
![]() $F_\alpha ^{cl}$
is in
$F_\alpha ^{cl}$
is in
![]() $m_{\beta {j'}\dots \beta _{1}}(\omega _\alpha (p))$
for any
$m_{\beta {j'}\dots \beta _{1}}(\omega _\alpha (p))$
for any
![]() $1\leq j'\leq j$
, proving the claim.
$1\leq j'\leq j$
, proving the claim.
First, we suppose that
![]() $m_\alpha (p)$
is not elementary and hence that
$m_\alpha (p)$
is not elementary and hence that
![]() $\omega _\alpha (p)$
does not contain all of
$\omega _\alpha (p)$
does not contain all of
![]() $R_\alpha ^{cc}$
. In particular, either the arrow
$R_\alpha ^{cc}$
. In particular, either the arrow
![]() $\alpha '$
following
$\alpha '$
following
![]() $\alpha $
in
$\alpha $
in
![]() $R_\alpha ^{cc}$
or the arrow
$R_\alpha ^{cc}$
or the arrow
![]() $\alpha "$
preceding
$\alpha "$
preceding
![]() $\alpha $
in
$\alpha $
in
![]() $R_\alpha ^{cc}$
(or both) are absent from
$R_\alpha ^{cc}$
(or both) are absent from
![]() $\omega _\alpha (p)$
. Suppose that
$\omega _\alpha (p)$
. Suppose that
![]() $\alpha '$
is not in
$\alpha '$
is not in
![]() $\omega _\alpha (p)$
; the
$\omega _\alpha (p)$
; the
![]() $\alpha "$
case is the same. Since
$\alpha "$
case is the same. Since
![]() $b'$
is a left-chain of p and
$b'$
is a left-chain of p and
![]() $R_\alpha ^{cl}$
is in
$R_\alpha ^{cl}$
is in
![]() $m_{\beta _{j'}\dots \beta _{1}}(p)$
by the claim above, the arrows
$m_{\beta _{j'}\dots \beta _{1}}(p)$
by the claim above, the arrows
![]() $\alpha '$
and
$\alpha '$
and
![]() $\alpha $
may not be added by any morph in
$\alpha $
may not be added by any morph in
![]() $b'$
without creating a crossing in p, which would contradict our choice of
$b'$
without creating a crossing in p, which would contradict our choice of
![]() $b'$
. Hence, neither
$b'$
. Hence, neither
![]() $\alpha '$
nor
$\alpha '$
nor
![]() $\alpha $
is in
$\alpha $
is in
![]() $m_{\beta _j\dots \beta _1}(\omega _\alpha (p))$
. In particular, no return path of an arrow in
$m_{\beta _j\dots \beta _1}(\omega _\alpha (p))$
. In particular, no return path of an arrow in
![]() $F_\alpha ^{cc}$
is a subpath of
$F_\alpha ^{cc}$
is a subpath of
![]() $m_{\beta _j\dots \beta _1}(\omega _\alpha (p))$
. Since
$m_{\beta _j\dots \beta _1}(\omega _\alpha (p))$
. Since
![]() $\beta _{j+1}$
is a left-morphable arrow for
$\beta _{j+1}$
is a left-morphable arrow for
![]() $m_{b'}(\omega _\alpha (p))$
but not of
$m_{b'}(\omega _\alpha (p))$
but not of
![]() $m_{b'}(p)$
, it must be the case that
$m_{b'}(p)$
, it must be the case that
![]() $R_{\beta _{j+1}}^{cc}$
is a subpath of
$R_{\beta _{j+1}}^{cc}$
is a subpath of
![]() $m_{b'}(\omega _\alpha (p))$
but not of
$m_{b'}(\omega _\alpha (p))$
but not of
![]() $m_{b'}(p)$
. Since the only such subpaths contain some arrow of
$m_{b'}(p)$
. Since the only such subpaths contain some arrow of
![]() $R_\alpha ^{cc}$
, we must have that
$R_\alpha ^{cc}$
, we must have that
![]() $\beta _{j+1}\in F_\alpha ^{cc}$
. This contradicts the fact that no return path in
$\beta _{j+1}\in F_\alpha ^{cc}$
. This contradicts the fact that no return path in
![]() $F_\alpha ^{cc}$
is a subpath of
$F_\alpha ^{cc}$
is a subpath of
![]() $m_{\beta _j\dots \beta _1}(\omega _\alpha (p))$
.
$m_{\beta _j\dots \beta _1}(\omega _\alpha (p))$
.
However, suppose that
![]() $m_\alpha (p)$
is elementary, and hence that
$m_\alpha (p)$
is elementary, and hence that
![]() $\omega _\alpha (p)=m_\alpha (p)$
. As above, the arrow
$\omega _\alpha (p)=m_\alpha (p)$
. As above, the arrow
![]() $\beta _{j+1}$
must be in
$\beta _{j+1}$
must be in
![]() $F_\alpha ^{cc}$
. If
$F_\alpha ^{cc}$
. If
![]() $\beta _{j+1}\neq \alpha $
, then
$\beta _{j+1}\neq \alpha $
, then
![]() $\alpha \in m_{\beta _j\dots \beta _1}(\omega _\alpha (p))$
, contradicting the claim in the third paragraph, so
$\alpha \in m_{\beta _j\dots \beta _1}(\omega _\alpha (p))$
, contradicting the claim in the third paragraph, so
![]() $\beta _{j+1}=\alpha $
. Consider the chain
$\beta _{j+1}=\alpha $
. Consider the chain
![]() $\beta _{j+1}\beta _j\dots \beta _1\alpha $
of p. The left-morph
$\beta _{j+1}\beta _j\dots \beta _1\alpha $
of p. The left-morph
![]() $\beta _{j+1}$
cancels out the right-morph
$\beta _{j+1}$
cancels out the right-morph
![]() $\alpha $
in this chain; hence, the left-chain
$\alpha $
in this chain; hence, the left-chain
![]() $\beta _{j+2}\beta _j\dots \beta _1$
of p is equivalent to
$\beta _{j+2}\beta _j\dots \beta _1$
of p is equivalent to
![]() $\beta _{j+2}\dots \beta _2\beta _1\alpha $
. Then
$\beta _{j+2}\dots \beta _2\beta _1\alpha $
. Then
![]() $\beta _s\dots \beta _{j+2}\beta _j\dots \beta _1$
is a crossing-creating left-chain of p. This completes the proof.
$\beta _s\dots \beta _{j+2}\beta _j\dots \beta _1$
is a crossing-creating left-chain of p. This completes the proof.
Lemma 3.14. Let p be an elementary path in
![]() $\widetilde Q$
. Let
$\widetilde Q$
. Let
![]() $\alpha $
be a right-morphable arrow for p and let l be a proper elementary counter-clockwise subcycle of
$\alpha $
be a right-morphable arrow for p and let l be a proper elementary counter-clockwise subcycle of
![]() $m_\alpha (p)$
. Suppose there is a crossing-creating left-chain of l. Then there is a crossing-creating left-chain of p.
$m_\alpha (p)$
. Suppose there is a crossing-creating left-chain of l. Then there is a crossing-creating left-chain of p.
Proof. The proof is the same as that of Lemma 3.13, with l taking the place of
![]() $\omega _\alpha (p)$
.
$\omega _\alpha (p)$
.
Lemma 3.15. Let p be an elementary path and let
![]() $\alpha $
be a right-morphable arrow for p. Then
$\alpha $
be a right-morphable arrow for p. Then
![]() $m_\alpha (p)$
does not contain a counter-clockwise face-path.
$m_\alpha (p)$
does not contain a counter-clockwise face-path.
Proof. Any arrow added by right-morphing at
![]() $\alpha $
is only a part of one counter-clockwise face, which is
$\alpha $
is only a part of one counter-clockwise face, which is
![]() $F_\alpha ^{cc}$
. Since p is elementary,
$F_\alpha ^{cc}$
. Since p is elementary,
![]() $\alpha $
is not in p and hence is not in
$\alpha $
is not in p and hence is not in
![]() $m_\alpha (p)$
. The result follows.
$m_\alpha (p)$
. The result follows.
Before finally proving that any elementary path has a good crossing-creating chain (Proposition 3.17), we first prove the special case that any counter-clockwise elementary cycle has a good crossing-creating chain.
Proposition 3.16. Let p be a counter-clockwise elementary cycle in a path-consistent dimer model
![]() $\widetilde Q$
. Then p has a crossing-creating left-chain.
$\widetilde Q$
. Then p has a crossing-creating left-chain.
Proof. We induct on the c-value of p. For the base case, let p be an elementary counter-clockwise cycle with a minimal c-value among elementary counter-clockwise cycles. By path-consistency, p must be equivalent to a composition of face-paths and hence must have a crossing-creating chain. If p has a good crossing-creating chain
![]() $a=\alpha _r\dots \alpha _1$
such that
$a=\alpha _r\dots \alpha _1$
such that
![]() $\alpha _r$
is a right-morph, then
$\alpha _r$
is a right-morph, then
![]() $\omega _a(p)$
is an elementary counter-clockwise cycle by Lemma 3.10 (2), and necessarily has a lower c-value than p, contradicting our choice of p. Suppose p has a good crossing-creating chain
$\omega _a(p)$
is an elementary counter-clockwise cycle by Lemma 3.10 (2), and necessarily has a lower c-value than p, contradicting our choice of p. Suppose p has a good crossing-creating chain
![]() $a=\alpha _r\dots \alpha _1$
such that
$a=\alpha _r\dots \alpha _1$
such that
![]() $\alpha _r$
is a left-morph. If a is a left-chain, then there is nothing to show; otherwise, let j be maximal such that
$\alpha _r$
is a left-morph. If a is a left-chain, then there is nothing to show; otherwise, let j be maximal such that
![]() $\alpha _j$
is a right-morph. Applying Lemma 3.13 to
$\alpha _j$
is a right-morph. Applying Lemma 3.13 to
![]() $m_{\alpha _1\dots \alpha _{j-1}}(p)$
shows that there is a crossing-creating left-chain of
$m_{\alpha _1\dots \alpha _{j-1}}(p)$
shows that there is a crossing-creating left-chain of
![]() $m_{\alpha _1\dots \alpha _{j-1}}(p)$
. Repeating this process for each right-morph of a gives that there is a crossing-creating left-chain of p. If p has a bad crossing-creating chain
$m_{\alpha _1\dots \alpha _{j-1}}(p)$
. Repeating this process for each right-morph of a gives that there is a crossing-creating left-chain of p. If p has a bad crossing-creating chain
![]() $a=\alpha _r\dots \alpha _1$
, then
$a=\alpha _r\dots \alpha _1$
, then
![]() $\alpha _r$
is a right-morph and
$\alpha _r$
is a right-morph and
![]() $m_a(p)$
contains a proper subpath l which is a simple counter-clockwise cycle. By Lemma 3.15, l is not a face-path and hence is elementary. This contradicts our choice of p, since l has a strictly lower c-value than p. This completes the proof of the base case.
$m_a(p)$
contains a proper subpath l which is a simple counter-clockwise cycle. By Lemma 3.15, l is not a face-path and hence is elementary. This contradicts our choice of p, since l has a strictly lower c-value than p. This completes the proof of the base case.
Now suppose that p is an elementary counter-clockwise cycle which does not have a minimal c-value. There must be a crossing-creating chain
![]() $c=\gamma _r\dots \gamma _1$
of p. We first show that there must be a crossing-creating chain
$c=\gamma _r\dots \gamma _1$
of p. We first show that there must be a crossing-creating chain
![]() $ab$
of p where b is a left-chain of p and a is a (possibly empty) right-chain of
$ab$
of p where b is a left-chain of p and a is a (possibly empty) right-chain of
![]() $m_b(p)$
. Suppose c is not already of this form and let j be minimal such that
$m_b(p)$
. Suppose c is not already of this form and let j be minimal such that
![]() $\gamma _{j-1}$
is a right-morph in c and
$\gamma _{j-1}$
is a right-morph in c and
![]() $\gamma _j$
is a left-morph in c.
$\gamma _j$
is a left-morph in c.
If
![]() $\gamma _{j-1}$
and
$\gamma _{j-1}$
and
![]() $\gamma _j$
are the same arrow, then
$\gamma _j$
are the same arrow, then
![]() $\gamma _j$
cannot create a crossing, and the term
$\gamma _j$
cannot create a crossing, and the term
![]() $\gamma _{j}\gamma _{j-1}$
may be removed from c to get an equivalent chain
$\gamma _{j}\gamma _{j-1}$
may be removed from c to get an equivalent chain
![]() $\gamma _r\dots \gamma _{j+1}\gamma _{j-2}\dots \gamma _1$
. If
$\gamma _r\dots \gamma _{j+1}\gamma _{j-2}\dots \gamma _1$
. If
![]() $\gamma _{j-1}$
and
$\gamma _{j-1}$
and
![]() $\gamma _j$
are not the same arrow, then by Lemma 3.11,
$\gamma _j$
are not the same arrow, then by Lemma 3.11,
![]() $\gamma _j$
is a left-morphable arrow for
$\gamma _j$
is a left-morphable arrow for
![]() $m_{\gamma _{j-2}\dots \gamma _1}(p)=\omega _{\gamma _{j-2}\dots \gamma _1}(p)$
. If this left-morph creates a crossing, then let
$m_{\gamma _{j-2}\dots \gamma _1}(p)=\omega _{\gamma _{j-2}\dots \gamma _1}(p)$
. If this left-morph creates a crossing, then let
![]() $c_1:=\gamma _j\gamma _{j-2}\dots \gamma _1$
. Otherwise, note that
$c_1:=\gamma _j\gamma _{j-2}\dots \gamma _1$
. Otherwise, note that
![]() $\gamma _j\gamma _{j-1}$
and
$\gamma _j\gamma _{j-1}$
and
![]() $\gamma _{j-1}\gamma _{j}$
are equivalent chains of
$\gamma _{j-1}\gamma _{j}$
are equivalent chains of
![]() $m_{\gamma _{j-2}\dots \gamma _1}(p)$
; hence,
$m_{\gamma _{j-2}\dots \gamma _1}(p)$
; hence,
is a crossing-creating chain of p equivalent to c. We apply the above logic repeatedly to move all left-morphs in c to the front. We end up with some crossing-creating chain
![]() $c_m=ab$
, where b is a left-chain of p and a is a right-chain of
$c_m=ab$
, where b is a left-chain of p and a is a right-chain of
![]() $m_b(p)$
. If a is trivial, then b is a crossing-creating left-chain and we are done. Otherwise, let
$m_b(p)$
. If a is trivial, then b is a crossing-creating left-chain and we are done. Otherwise, let
![]() $a=\alpha _r\dots \alpha _1$
. Lemma 3.14 or Lemma 3.13 (depending on whether
$a=\alpha _r\dots \alpha _1$
. Lemma 3.14 or Lemma 3.13 (depending on whether
![]() $m_{ba}(p)$
contains a proper counter-clockwise subcycle) along with the induction hypothesis shows that
$m_{ba}(p)$
contains a proper counter-clockwise subcycle) along with the induction hypothesis shows that
![]() $m_{\alpha _{r-1}\dots \alpha _1b}(p)$
has a crossing-creating left-chain. We now repeatedly apply Lemma 3.13 to see that
$m_{\alpha _{r-1}\dots \alpha _1b}(p)$
has a crossing-creating left-chain. We now repeatedly apply Lemma 3.13 to see that
![]() $m_b(p)$
has a crossing-creating left-chain
$m_b(p)$
has a crossing-creating left-chain
![]() $b'$
. Then
$b'$
. Then
![]() $b'b$
is a crossing-creating left-chain of p.
$b'b$
is a crossing-creating left-chain of p.
Proposition 3.17. Let p be an elementary path in a path-consistent dimer model
![]() $\widetilde Q$
. Then there exists a good cycle-removing chain from p to a minimal path.
$\widetilde Q$
. Then there exists a good cycle-removing chain from p to a minimal path.
Proof. We prove by induction on the c-value of p. The base case when p is minimal is trivial. Suppose the result has been shown for paths with a strictly lower c-value than that of some non-minimal path p. We first show that p has a good crossing-creating chain. Since p is not minimal, there is some crossing-creating chain
![]() $a=\alpha _r\dots \alpha _1$
of p. If
$a=\alpha _r\dots \alpha _1$
of p. If
![]() $\alpha _r$
is a left-morph or if
$\alpha _r$
is a left-morph or if
![]() $m_a(p)$
contains no proper counter-clockwise subcycle, then a is a good crossing-creating chain of p. If not, then
$m_a(p)$
contains no proper counter-clockwise subcycle, then a is a good crossing-creating chain of p. If not, then
![]() $m_a(p)$
contains a proper counter-clockwise simple subcycle l, which is not a face-path by Lemma 3.15. By Proposition 3.16, l has a crossing-creating left-chain. By Lemma 3.14,
$m_a(p)$
contains a proper counter-clockwise simple subcycle l, which is not a face-path by Lemma 3.15. By Proposition 3.16, l has a crossing-creating left-chain. By Lemma 3.14,
![]() $m_{\alpha _{r-1}\dots \alpha _{1}}(p)$
has a crossing-creating left-chain
$m_{\alpha _{r-1}\dots \alpha _{1}}(p)$
has a crossing-creating left-chain
![]() $a'$
. Then
$a'$
. Then
![]() $a'\alpha _{r-1}\dots \alpha _1$
is a good crossing-creating chain of p. Then we may suppose that p has a good crossing-creating chain a. Since
$a'\alpha _{r-1}\dots \alpha _1$
is a good crossing-creating chain of p. Then we may suppose that p has a good crossing-creating chain a. Since
![]() $\omega _a(p)$
is an elementary path with a lower c-value than p, by the induction hypothesis there is a good cycle-removing chain
$\omega _a(p)$
is an elementary path with a lower c-value than p, by the induction hypothesis there is a good cycle-removing chain
![]() $a"$
from
$a"$
from
![]() $\omega _a(p)$
to a minimal path. Then
$\omega _a(p)$
to a minimal path. Then
![]() $a"a$
is a good cycle-removing chain from p to a minimal path.
$a"a$
is a good cycle-removing chain from p to a minimal path.
We are now ready to prove the main result of this section.
Lemma 3.18. Let
![]() $(p,q)$
be an irreducible pair of a path-consistent dimer model
$(p,q)$
be an irreducible pair of a path-consistent dimer model
![]() $\widetilde Q$
. Let r be an elementary path from
$\widetilde Q$
. Let r be an elementary path from
![]() $t(p)$
to
$t(p)$
to
![]() $h(p)$
which does not enter the interior of
$h(p)$
which does not enter the interior of
![]() $q^{-1}p$
and let
$q^{-1}p$
and let
![]() $\alpha $
be a morphable arrow for r. Then
$\alpha $
be a morphable arrow for r. Then
![]() $m_\alpha (r)$
does not enter the interior of
$m_\alpha (r)$
does not enter the interior of
![]() $q^{-1}p$
.
$q^{-1}p$
.
Figure 6 On the left, r winds to the right from
![]() $t(p)$
to
$t(p)$
to
![]() $t(\alpha )$
. On the left, r winds to the left from
$t(\alpha )$
. On the left, r winds to the left from
![]() $t(p)$
to
$t(p)$
to
![]() $h(\alpha )$
. In both cases, there is no way to complete the beginning of r (pictured) to a path from
$h(\alpha )$
. In both cases, there is no way to complete the beginning of r (pictured) to a path from
![]() $t(p)$
to
$t(p)$
to
![]() $h(p)$
without breaking elementariness or entering
$h(p)$
without breaking elementariness or entering
![]() $q^{-1}p$
.
$q^{-1}p$
.
Proof. Suppose to the contrary that
![]() $m_\alpha (r)$
enters the interior of
$m_\alpha (r)$
enters the interior of
![]() $q^{-1}p$
. Since p is leftmost and q is rightmost, it must be the case that
$q^{-1}p$
. Since p is leftmost and q is rightmost, it must be the case that
![]() $\alpha $
is a right-morph at an arrow of p or a left-morph at an arrow of q. Suppose the former is true; the latter case is symmetric. The segment
$\alpha $
is a right-morph at an arrow of p or a left-morph at an arrow of q. Suppose the former is true; the latter case is symmetric. The segment
![]() $r'$
of r from
$r'$
of r from
![]() $t(p)$
to
$t(p)$
to
![]() $h(\alpha )$
either winds right or left around
$h(\alpha )$
either winds right or left around
![]() $q^{-1}p$
. See Figure 6. In either case, as can be seen from Figure 6, the path
$q^{-1}p$
. See Figure 6. In either case, as can be seen from Figure 6, the path
![]() $R_\alpha ^{cl}r'$
may not be completed to a path from
$R_\alpha ^{cl}r'$
may not be completed to a path from
![]() $t(p)$
to
$t(p)$
to
![]() $h(p)$
without entering the interior of
$h(p)$
without entering the interior of
![]() $q^{-1}p$
or causing a self-intersection.
$q^{-1}p$
or causing a self-intersection.
Theorem 3.19. A simply connected path-consistent dimer model, that is not on a sphere, has no irreducible pairs.
Proof. Let
![]() $\widetilde Q$
be path-consistent and simply connected dimer model that is not on a sphere. Take a pair
$\widetilde Q$
be path-consistent and simply connected dimer model that is not on a sphere. Take a pair
![]() $(p,q)$
of paths such that
$(p,q)$
of paths such that
![]() $q^{-1}p$
is an elementary counter-clockwise cycle-walk. We show that p has a left-morphable arrow or q has a right-morphable arrow. If p is a cycle and q is trivial, then Proposition 3.16 shows the desired result. If p is trivial and q is a cycle, the dual of Proposition 3.16 shows the desired result. We may now assume that p and q are not cycles. Suppose for the sake of contradiction that
$q^{-1}p$
is an elementary counter-clockwise cycle-walk. We show that p has a left-morphable arrow or q has a right-morphable arrow. If p is a cycle and q is trivial, then Proposition 3.16 shows the desired result. If p is trivial and q is a cycle, the dual of Proposition 3.16 shows the desired result. We may now assume that p and q are not cycles. Suppose for the sake of contradiction that
![]() $(p,q)$
is an irreducible pair.
$(p,q)$
is an irreducible pair.
Choose a face F in the interior of
![]() $q^{-1}p$
. By Proposition 3.17, there is a good cycle-removing chain
$q^{-1}p$
. By Proposition 3.17, there is a good cycle-removing chain
![]() $a=\alpha _r\dots \alpha _1$
from p to some minimal path
$a=\alpha _r\dots \alpha _1$
from p to some minimal path
![]() $\omega _a(p)$
. By repeated application of Lemma 3.18, no intermediate path of this chain enters the interior of
$\omega _a(p)$
. By repeated application of Lemma 3.18, no intermediate path of this chain enters the interior of
![]() $q^{-1}p$
. In particular, no arrow
$q^{-1}p$
. In particular, no arrow
![]() $\alpha _i$
is an arrow of F. Then Lemma 2.20 tells us that
$\alpha _i$
is an arrow of F. Then Lemma 2.20 tells us that
![]() $\text {Wind}\big (q^{-1}m_{\alpha _i}(\omega _{\alpha _{i-1}\dots \alpha _{1}}(p)),F\big )=\text {Wind}\big (q^{-1}\omega _{\alpha _{i-1}\dots \alpha _{1}}(p),F\big )$
for each i. There may be some clockwise cycles removed from
$\text {Wind}\big (q^{-1}m_{\alpha _i}(\omega _{\alpha _{i-1}\dots \alpha _{1}}(p)),F\big )=\text {Wind}\big (q^{-1}\omega _{\alpha _{i-1}\dots \alpha _{1}}(p),F\big )$
for each i. There may be some clockwise cycles removed from
![]() $m_{\alpha _i}(\omega _{\alpha _{i-1}\dots \alpha _{1}}(p))$
to get
$m_{\alpha _i}(\omega _{\alpha _{i-1}\dots \alpha _{1}}(p))$
to get
![]() $\omega _{\alpha _i\dots \alpha _1}(p)$
, but since a is good, no counter-clockwise cycles are removed. Hence,
$\omega _{\alpha _i\dots \alpha _1}(p)$
, but since a is good, no counter-clockwise cycles are removed. Hence,
 $$ \begin{align*} \text{Wind}\big(q^{-1}\omega_{\alpha_i\dots\alpha_1}(p),F\big) &\geq\text{Wind}\big(q^{-1}m_{\alpha_i}(\omega_{\alpha_{i-1}\dots\alpha_1}(p)),F\big)\\ &=\text{Wind}(\omega_{\alpha_{i-1}\dots\alpha_1}(p),F). \end{align*} $$
$$ \begin{align*} \text{Wind}\big(q^{-1}\omega_{\alpha_i\dots\alpha_1}(p),F\big) &\geq\text{Wind}\big(q^{-1}m_{\alpha_i}(\omega_{\alpha_{i-1}\dots\alpha_1}(p)),F\big)\\ &=\text{Wind}(\omega_{\alpha_{i-1}\dots\alpha_1}(p),F). \end{align*} $$
By applying this result for each i, we see that
Dually, there is a cycle-removing chain
![]() $b=\beta _s\dots \beta _1$
of q removing only counter-clockwise cycles such that
$b=\beta _s\dots \beta _1$
of q removing only counter-clockwise cycles such that
![]() $\omega _b(q)$
is minimal and
$\omega _b(q)$
is minimal and
By path-consistency,
![]() $\omega _a(p)$
and
$\omega _a(p)$
and
![]() $\omega _b(q)$
are equivalent. Then there is a chain
$\omega _b(q)$
are equivalent. Then there is a chain
![]() $c=\gamma _t\dots \gamma _1$
such that
$c=\gamma _t\dots \gamma _1$
such that
![]() $m_c(\omega _a(p))=\omega _b(q)$
. As above, Lemma 3.18 shows that no arrow
$m_c(\omega _a(p))=\omega _b(q)$
. As above, Lemma 3.18 shows that no arrow
![]() $\gamma _i$
of c is an arrow of F; hence, repeated application of Lemma 2.20 gives that
$\gamma _i$
of c is an arrow of F; hence, repeated application of Lemma 2.20 gives that
![]() $1\leq \text {Wind}(q^{-1}\omega _a(p),F)=\text {Wind}(q^{-1}\omega _b(p),F)\leq 0$
, a contradiction.
$1\leq \text {Wind}(q^{-1}\omega _a(p),F)=\text {Wind}(q^{-1}\omega _b(p),F)\leq 0$
, a contradiction.
4 Strand diagrams and strand-consistency
In this section, we use zigzag paths to associate a dimer model to a strand diagram on its surface. Our goal is to prove that, excluding the case of a sphere, a finite dimer model is path-consistent if and only if there are no bad configurations in its strand diagram. This generalizes ideas of Bocklandt [Reference Bocklandt6] and Ishii and Ueda [Reference Ishii and Ueda34]. The theory of cycle-removing morphs developed in Section 3, in particular Theorem 3.19, is necessary to prove this result.
4.1 Strand diagrams
We define strand diagrams and connect them to dimer models. The below definition is a reformulation of [Reference Bocklandt8, Definition 1.10].
Definition 4.1. Let
![]() $\Sigma $
be an oriented surface with or without boundary with a discrete set of marked points on its boundary. A (connected) strand diagram D in
$\Sigma $
be an oriented surface with or without boundary with a discrete set of marked points on its boundary. A (connected) strand diagram D in
![]() $\Sigma $
consists of a collection of smooth directed curves drawn on the surface
$\Sigma $
consists of a collection of smooth directed curves drawn on the surface
![]() $\Sigma $
, called strands, each of which is either an interior cycle contained entirely in the interior of D or starts and ends at marked boundary points, subject to the following conditions.
$\Sigma $
, called strands, each of which is either an interior cycle contained entirely in the interior of D or starts and ends at marked boundary points, subject to the following conditions.
-
1. Each boundary marked point is the start point of exactly one strand, and the end point of exactly one strand.
-
2. Any two strands intersect in finitely many points, and each intersection involves only two strands. Each intersection not at a marked boundary point is transversal.
-
3. Moving along a strand, the signs of its crossings with other strands alternate. This includes intersections at a marked boundary point. See the figure below, where the bold segment is boundary.

-
4. Any connected component C of the complement of D in the interior of
 $\Sigma $
is an open disk. The boundary of C may contain either zero or one one-dimensional ‘boundary segment’ of the boundary of
$\Sigma $
is an open disk. The boundary of C may contain either zero or one one-dimensional ‘boundary segment’ of the boundary of
 $\Sigma $
. In the former case, C is an internal region. In the latter, C is a boundary region. It follows from (3) that C is either an oriented region (i.e., all strands on the boundary of the component are oriented in the same direction) or an alternating region (i.e., the strands on the boundary of the component alternate directions). See the left and right sides of Figure 7, respectively. Note that by (3), any boundary region with multiple strands must be alternating. We consider a boundary region with a single strand to be alternating.
$\Sigma $
. In the former case, C is an internal region. In the latter, C is a boundary region. It follows from (3) that C is either an oriented region (i.e., all strands on the boundary of the component are oriented in the same direction) or an alternating region (i.e., the strands on the boundary of the component alternate directions). See the left and right sides of Figure 7, respectively. Note that by (3), any boundary region with multiple strands must be alternating. We consider a boundary region with a single strand to be alternating.
Figure 7 One oriented (left) and two alternating (right) regions. The bold segment is boundary.
-
5. The union of the strands is connected.
The diagram D is called a Postnikov diagram if, in addition, it satisfies the following conditions
-
1. No subpath of a strand is a null-homotopic interior cycle.
-
2. If two strand segments intersect twice and are oriented in the same direction between these intersection points, then they must not be homotopic.
In other words, bad configurations shown in Figure 8 and described below must not appear in order for D to be a Postnikov diagram:
Figure 8 The three bad configurations. The shaded areas are contractible.
-
1. A strand which intersects itself through a null-homotopic cycle as forbidden in (1), called a null-homotopic self-intersecting strand.
-
2. A null-homotopic strand in the interior as forbidden in (1), called a null-homotopic interior cycle.
-
3. Two strand segments which intersect in the same order null-homotopically as forbidden in (2), called a bad lens.
When
![]() $Q=\widetilde Q$
is simply connected, any cycle is null-homotopic and we often omit “null-homotopic” from (1) and (2).
$Q=\widetilde Q$
is simply connected, any cycle is null-homotopic and we often omit “null-homotopic” from (1) and (2).
Remark 4.2. In fact, if
![]() $\Sigma $
is simply connected then conditions (5) and (3) of a strand diagram along with the lack of bad lenses imply that if there are multiple strands, then there is no strand which starts and ends at the same marked boundary point, and hence no strand contains a cycle. To see this, suppose there is a strand z which starts and ends at the same marked boundary point. Consider the first time this strand intersects with another strand w. Then by connectedness (3), w must enter the area defined by z at this intersection. Then w must eventually leave the area bounded by z, creating a bad lens.
$\Sigma $
is simply connected then conditions (5) and (3) of a strand diagram along with the lack of bad lenses imply that if there are multiple strands, then there is no strand which starts and ends at the same marked boundary point, and hence no strand contains a cycle. To see this, suppose there is a strand z which starts and ends at the same marked boundary point. Consider the first time this strand intersects with another strand w. Then by connectedness (3), w must enter the area defined by z at this intersection. Then w must eventually leave the area bounded by z, creating a bad lens.
Definition 4.3. Let D be a strand diagram in a surface. We associate to D a dimer model
![]() $Q_D$
as follows. The vertices of
$Q_D$
as follows. The vertices of
![]() $Q_D$
are the alternating regions of D. When the closures of two different alternating regions
$Q_D$
are the alternating regions of D. When the closures of two different alternating regions
![]() $v_1$
and
$v_1$
and
![]() $v_2$
meet in a crossing point between strands of D, or at one of the marked boundary points, we draw an arrow between
$v_2$
meet in a crossing point between strands of D, or at one of the marked boundary points, we draw an arrow between
![]() $v_1$
and
$v_1$
and
![]() $v_2$
, oriented in a way consistent with these strands, as shown in Figure 9. The counter-clockwise (respectively clockwise) faces of
$v_2$
, oriented in a way consistent with these strands, as shown in Figure 9. The counter-clockwise (respectively clockwise) faces of
![]() $Q_D$
are the arrows around a counter-clockwise (respectively clockwise) region of D.
$Q_D$
are the arrows around a counter-clockwise (respectively clockwise) region of D.
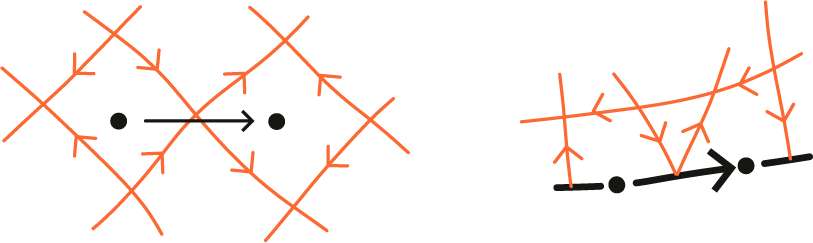
Figure 9 The arrows between two alternating faces. The bold arrow is a boundary arrow.
We may also go in the other direction.
Definition 4.4. Let Q be a dimer model. We associate a strand diagram
![]() $D_Q$
to Q embedded in the surface
$D_Q$
to Q embedded in the surface
![]() $S(Q)$
as follows. To any arrow
$S(Q)$
as follows. To any arrow
![]() $\alpha $
of Q, let
$\alpha $
of Q, let
![]() $v_\alpha $
be the point in the center of
$v_\alpha $
be the point in the center of
![]() $\alpha $
in the embedding of Q into
$\alpha $
in the embedding of Q into
![]() $S(Q)$
.
$S(Q)$
.
For any two arrows
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
of Q such that
$\beta $
of Q such that
![]() $\beta \alpha $
is a subpath of a face-path, we draw a path from
$\beta \alpha $
is a subpath of a face-path, we draw a path from
![]() $v_\alpha $
to
$v_\alpha $
to
![]() $v_\beta $
along the interior of the face containing
$v_\beta $
along the interior of the face containing
![]() $\beta \alpha $
. The union of these strand segments forms a connected strand diagram
$\beta \alpha $
. The union of these strand segments forms a connected strand diagram
![]() $D_Q$
[Reference Bocklandt8, §0.4 – 0.5]. See Figure 11 for an example on the disk and annulus.
$D_Q$
[Reference Bocklandt8, §0.4 – 0.5]. See Figure 11 for an example on the disk and annulus.
The above constructions are mutual inverses, and hence establish a correspondence between strand diagrams and dimer models. This is implicit in the work of Bocklandt [Reference Bocklandt8].
Definition 4.5. A dimer model Q is strand-consistent if its strand diagram
![]() $D_Q$
does not have any bad configurations. In other words, Q is strand-consistent if
$D_Q$
does not have any bad configurations. In other words, Q is strand-consistent if
![]() $D_Q$
is a Postnikov diagram.
$D_Q$
is a Postnikov diagram.
Remark 4.6. A dimer model on a sphere is never strand-consistent since there must be a null-homotopic interior cycle. However, a dimer model on a sphere can still satisfy the path-consistency condition of Definition 2.8. Hence, in order to prove that the notions of path-consistency and strand-consistency are equivalent (Theorem 4.13), it is necessary to throw out the case where
![]() $S(Q)$
is a sphere.
$S(Q)$
is a sphere.
Since a cycle on a surface
![]() $\Sigma $
lifts to a cycle on the universal cover if and only if it is null-homotopic in
$\Sigma $
lifts to a cycle on the universal cover if and only if it is null-homotopic in
![]() $\Sigma $
, bad configurations in Q correspond precisely to bad configurations in
$\Sigma $
, bad configurations in Q correspond precisely to bad configurations in
![]() $\widetilde Q$
. The following result is a consequence of this observation.
$\widetilde Q$
. The following result is a consequence of this observation.
Proposition 4.7.
Q is strand-consistent if and only if
![]() $\widetilde Q$
is strand-consistent.
$\widetilde Q$
is strand-consistent.
Proposition 4.7 is useful because bad configurations are easier to work with on the simply connected dimer model
![]() $\widetilde Q$
. In particular, the null-homotopic conditions appearing in each of the three bad configurations may be ignored in the simply connected case. As such, we often pass to the universal cover models when working with strand diagrams.
$\widetilde Q$
. In particular, the null-homotopic conditions appearing in each of the three bad configurations may be ignored in the simply connected case. As such, we often pass to the universal cover models when working with strand diagrams.
4.2 Path-consistency implies strand-consistency
We now prove that path-consistency implies strand-consistency for finite dimer models. We must first define zigzag paths and their return paths. The notion of a zigzag path is based on work by Kenyon in [Reference Kenyon38] and Kenyon and Schlenker in [Reference Kenyon and Schlenker39].
Definition 4.8. Let Q be a dimer model. A zigzag path of Q is a maximal (possibly infinite) path
![]() $z=\dots \gamma _{i+1}\gamma _{i}\dots $
such that one of the following holds.
$z=\dots \gamma _{i+1}\gamma _{i}\dots $
such that one of the following holds.
-
1.
 $\gamma _{i+1}\gamma _{i}$
is part of a counter-clockwise face if i is odd and a clockwise face if i is even. In the former case,
$\gamma _{i+1}\gamma _{i}$
is part of a counter-clockwise face if i is odd and a clockwise face if i is even. In the former case,
 $\gamma _{i+1}\gamma _{i}$
is called a zig and
$\gamma _{i+1}\gamma _{i}$
is called a zig and
 $h(\gamma _i)$
is a zig vertex. In the latter,
$h(\gamma _i)$
is a zig vertex. In the latter,
 $\gamma _{i+1}\gamma _{i}$
is a zag and
$\gamma _{i+1}\gamma _{i}$
is a zag and
 $h(\gamma _i)$
is a zag vertex.
$h(\gamma _i)$
is a zag vertex. -
2.
 $\gamma _{i+1}\gamma _i$
is part of a clockwise face if i is odd and a counter-clockwise face if i is even. In the former case,
$\gamma _{i+1}\gamma _i$
is part of a clockwise face if i is odd and a counter-clockwise face if i is even. In the former case,
 $\gamma _{i+1}\gamma _i$
is called a zag and
$\gamma _{i+1}\gamma _i$
is called a zag and
 $h(\gamma _i)$
is a zag vertex. In the latter,
$h(\gamma _i)$
is a zag vertex. In the latter,
 $\gamma _{i+1}\gamma _i$
is a zig and
$\gamma _{i+1}\gamma _i$
is a zig and
 $h(\gamma _i)$
is a zig vertex.
$h(\gamma _i)$
is a zig vertex.
If z is a finite path, then we write
![]() $z=\gamma _t\dots \gamma _0$
, and we note that
$z=\gamma _t\dots \gamma _0$
, and we note that
![]() $\gamma _0$
and
$\gamma _0$
and
![]() $\gamma _t$
must be boundary arrows. we similarly may have infinite zigzag paths
$\gamma _t$
must be boundary arrows. we similarly may have infinite zigzag paths
![]() $\gamma _0\gamma _{-1}\dots $
or
$\gamma _0\gamma _{-1}\dots $
or
![]() $\dots \gamma _{1}\gamma _0$
ending or starting at boundary vertices, respectively.
$\dots \gamma _{1}\gamma _0$
ending or starting at boundary vertices, respectively.
It is immediate by the constructions of Definitions 4.4 and 4.3 that zigzag paths of Q correspond to strands of
![]() $D_Q$
. Intersections of strands in
$D_Q$
. Intersections of strands in
![]() $D_Q$
correspond to shared arrows of zigzag paths in the quiver. We may thus view the bad configurations of Definition 4.1 as bad configurations of zigzag paths.
$D_Q$
correspond to shared arrows of zigzag paths in the quiver. We may thus view the bad configurations of Definition 4.1 as bad configurations of zigzag paths.
-
1. A zigzag path has a null-homotopic self-intersection if it passes through the same arrow twice, first as the start of a zig and then as the start of a zag (or vice versa), and the segment between these occurrences is null-homotopic.
-
2. A zigzag path is a null-homotopic interior cycle if it is cyclic, infinitely repeating and null-homotopic.
-
3. Two homotopic segments of (possibly the same) zigzag paths
 $z'$
and
$z'$
and
 $w'$
form a bad lens if
$w'$
form a bad lens if
 $z'=\beta z_s\dots z_0\alpha $
and
$z'=\beta z_s\dots z_0\alpha $
and
 $w'=\beta w_t\dots w_0 \alpha $
and
$w'=\beta w_t\dots w_0 \alpha $
and
 $z_i\neq w_j$
for all i and j.
$z_i\neq w_j$
for all i and j.
The following definition appears in the literature on dimer models in tori. See, for example, [Reference Bocklandt6] and [Reference Broomhead11].
Definition 4.9. Take a subpath
![]() $z':=\gamma _t\dots \gamma _1$
of a zigzag path z such that
$z':=\gamma _t\dots \gamma _1$
of a zigzag path z such that
![]() $\gamma _i\neq \gamma _j$
for
$\gamma _i\neq \gamma _j$
for
![]() $i\neq j$
. Suppose that
$i\neq j$
. Suppose that
![]() $t(z')$
and
$t(z')$
and
![]() $h(z')$
are both zag vertices of z. For each zig
$h(z')$
are both zag vertices of z. For each zig
![]() $\gamma _{j+1}\gamma _j$
(for
$\gamma _{j+1}\gamma _j$
(for
![]() $j<t$
odd), let
$j<t$
odd), let
![]() $p_j$
be the subpath of
$p_j$
be the subpath of
![]() $F_{\gamma _j}^{cc}$
from
$F_{\gamma _j}^{cc}$
from
![]() $h(\gamma _{j+1})$
to
$h(\gamma _{j+1})$
to
![]() $t(\gamma _j)$
. Then
$t(\gamma _j)$
. Then
![]() $p_j$
consists of all arrows in
$p_j$
consists of all arrows in
![]() $F_{\gamma _j}^{cc}$
except for
$F_{\gamma _j}^{cc}$
except for
![]() $\gamma _{j+1}$
and
$\gamma _{j+1}$
and
![]() $\gamma _j$
.
$\gamma _j$
.
The right return path is the composition
![]() $p_{j_{t-1}}\dots p_{j_1}$
of all such
$p_{j_{t-1}}\dots p_{j_1}$
of all such
![]() $p_j$
’s. The elementary right return path is the path obtained by removing all proper elementary subcycles of the right return path in order of their appearance. If the result is a face-path, then the elementary right return path is constant. We dually define (elementary) left return paths.
$p_j$
’s. The elementary right return path is the path obtained by removing all proper elementary subcycles of the right return path in order of their appearance. If the result is a face-path, then the elementary right return path is constant. We dually define (elementary) left return paths.
For examples, see Figure 10. In particular, the left of this figure gives an example where the right return path and the elementary right return path differ. It is immediate that right return paths are leftmost and left return paths are rightmost.
Figure 10 An example of a self-intersection (left), interior cycle (middle), and bad lens (right). All of these give rise to irreducible pairs.
Theorem 4.10. A path-consistent dimer model not on a sphere is strand-consistent.
Proof. Given a path-consistent dimer model Q, Proposition 2.14 implies that
![]() $\widetilde Q$
is path-consistent. By Proposition 4.7, it suffices to show that
$\widetilde Q$
is path-consistent. By Proposition 4.7, it suffices to show that
![]() $\widetilde Q$
is strand-consistent. We will do this by showing that self-intersecting strands, interior cycles and bad lenses in the strand diagram give rise to irreducible pairs, which cannot occur in strand-consistent models by Theorem 3.19, since
$\widetilde Q$
is strand-consistent. We will do this by showing that self-intersecting strands, interior cycles and bad lenses in the strand diagram give rise to irreducible pairs, which cannot occur in strand-consistent models by Theorem 3.19, since
![]() $\widetilde Q$
is not a sphere. See Figure 10.
$\widetilde Q$
is not a sphere. See Figure 10.
First, suppose there is some self-intersecting strand z of
![]() $D_{\widetilde Q}$
. Recall from the discussion following Definition 4.8 that intersections of the strand z correspond to multiple incidences of an arrow in its associated zigzag path in
$D_{\widetilde Q}$
. Recall from the discussion following Definition 4.8 that intersections of the strand z correspond to multiple incidences of an arrow in its associated zigzag path in
![]() ${\widetilde Q}$
. Then there is some segment
${\widetilde Q}$
. Then there is some segment
![]() $C=\gamma _0\gamma _t\dots \gamma _1\gamma _0$
of the zigzag path associated to z such that
$C=\gamma _0\gamma _t\dots \gamma _1\gamma _0$
of the zigzag path associated to z such that
![]() $\gamma _i\neq \gamma _j$
for
$\gamma _i\neq \gamma _j$
for
![]() $i\neq j$
. Suppose that the segment of the strand z corresponding to
$i\neq j$
. Suppose that the segment of the strand z corresponding to
![]() $\gamma _t\dots \gamma _0$
is a clockwise cycle; the counter-clockwise case is symmetric. See the left of Figure 10. Let
$\gamma _t\dots \gamma _0$
is a clockwise cycle; the counter-clockwise case is symmetric. See the left of Figure 10. Let
![]() $v_1:=h(\gamma _0)$
and
$v_1:=h(\gamma _0)$
and
![]() $v_2:=t(\gamma _0)$
. Since the cycle runs clockwise,
$v_2:=t(\gamma _0)$
. Since the cycle runs clockwise,
![]() $v_1$
and
$v_1$
and
![]() $v_2$
are both zag vertices of z. Let
$v_2$
are both zag vertices of z. Let
![]() $z':=\gamma _t\dots \gamma _1$
and let p be the elementary right return path of
$z':=\gamma _t\dots \gamma _1$
and let p be the elementary right return path of
![]() $z'$
. Then p is a leftmost path from
$z'$
. Then p is a leftmost path from
![]() $v_2$
to
$v_2$
to
![]() $v_1$
, and
$v_1$
, and
![]() $\gamma _0^{-1}p$
is an elementary counter-clockwise cycle-path winding counter-clockwise around
$\gamma _0^{-1}p$
is an elementary counter-clockwise cycle-path winding counter-clockwise around
![]() $z'$
; hence,
$z'$
; hence,
![]() $(p,\gamma _0)$
is an irreducible pair. This contradicts Theorem 3.19.
$(p,\gamma _0)$
is an irreducible pair. This contradicts Theorem 3.19.
Now suppose there is a strand z of
![]() $D_{\widetilde Q}$
which is an interior cycle. By the above, we may suppose that z contains no self-intersections. Then we may realize z as a path
$D_{\widetilde Q}$
which is an interior cycle. By the above, we may suppose that z contains no self-intersections. Then we may realize z as a path
![]() $z':=\gamma _t\dots \gamma _0$
of
$z':=\gamma _t\dots \gamma _0$
of
![]() ${\widetilde Q}$
such that
${\widetilde Q}$
such that
![]() $t(\gamma _t)=h(\gamma _0)$
is a zag vertex of z and
$t(\gamma _t)=h(\gamma _0)$
is a zag vertex of z and
![]() $\gamma _i\neq \gamma _j$
for
$\gamma _i\neq \gamma _j$
for
![]() $i\neq j$
. See the middle of Figure 10. As above, we assume that
$i\neq j$
. See the middle of Figure 10. As above, we assume that
![]() $z'$
winds clockwise. Let p be the elementary right return path of
$z'$
winds clockwise. Let p be the elementary right return path of
![]() $z'$
. Then p winds counter-clockwise around
$z'$
. Then p winds counter-clockwise around
![]() $z'$
and thus is a nontrivial counter-clockwise path which is leftmost, contradicting Theorem 3.19.
$z'$
and thus is a nontrivial counter-clockwise path which is leftmost, contradicting Theorem 3.19.
Now, suppose there is a bad lens in
![]() $D_{\widetilde Q}$
. Accordingly, we may take subpaths of zigzag paths
$D_{\widetilde Q}$
. Accordingly, we may take subpaths of zigzag paths
![]() $z':=\beta \gamma _t\dots \gamma _1\alpha $
and
$z':=\beta \gamma _t\dots \gamma _1\alpha $
and
![]() $w':=\beta \delta _s\dots \delta _1\alpha $
such that
$w':=\beta \delta _s\dots \delta _1\alpha $
such that
![]() $\gamma _i\neq \delta _j$
for
$\gamma _i\neq \delta _j$
for
![]() $i\neq j$
. By the above, the strands have no self-intersections, and hence,
$i\neq j$
. By the above, the strands have no self-intersections, and hence,
![]() $z'$
and
$z'$
and
![]() $w'$
have no repeated arrows. Suppose without loss of generality that
$w'$
have no repeated arrows. Suppose without loss of generality that
![]() $z'$
is to the left of
$z'$
is to the left of
![]() $w'$
. Then
$w'$
. Then
![]() $t(\alpha )$
and
$t(\alpha )$
and
![]() $h(\beta )$
are zig vertices of w and zag vertices of z. See the right of Figure 10. Let p be the right elementary return path of
$h(\beta )$
are zig vertices of w and zag vertices of z. See the right of Figure 10. Let p be the right elementary return path of
![]() $z'$
and let q be the left elementary return path of
$z'$
and let q be the left elementary return path of
![]() $w'$
.
$w'$
.
Let
![]() $p_0:=p$
and
$p_0:=p$
and
![]() $q_0:=q$
. Choose a face F in the interior of the bad lens. Then
$q_0:=q$
. Choose a face F in the interior of the bad lens. Then
![]() $p_0$
is a leftmost elementary path and
$p_0$
is a leftmost elementary path and
![]() $q_0$
is a rightmost elementary path such that
$q_0$
is a rightmost elementary path such that
![]() $\text {Wind}(q_0^{-1}p_0,F)=1>0$
, since
$\text {Wind}(q_0^{-1}p_0,F)=1>0$
, since
![]() $q^{-1}p$
winds counter-clockwise around the lens. If
$q^{-1}p$
winds counter-clockwise around the lens. If
![]() $q_0^{-1}p_0$
is simple, then
$q_0^{-1}p_0$
is simple, then
![]() $(p_0,q_0)$
is an irreducible pair and we are done. If not, then
$(p_0,q_0)$
is an irreducible pair and we are done. If not, then
![]() $q_0^{-1}p_0$
has some simple proper subcycle-walk l. The paths
$q_0^{-1}p_0$
has some simple proper subcycle-walk l. The paths
![]() $p_0$
and
$p_0$
and
![]() $q_0$
are elementary, so l must be of the form
$q_0$
are elementary, so l must be of the form
![]() $(q^{\prime }_0)^{-1}p^{\prime }_0$
, where
$(q^{\prime }_0)^{-1}p^{\prime }_0$
, where
![]() $p^{\prime }_0,q^{\prime }_0,p_1,q_1$
are paths such that
$p^{\prime }_0,q^{\prime }_0,p_1,q_1$
are paths such that
![]() $p_0=p^{\prime }_0p_1$
and
$p_0=p^{\prime }_0p_1$
and
![]() $q_0=q_1q^{\prime }_0$
. If
$q_0=q_1q^{\prime }_0$
. If
![]() $(q^{\prime }_0)^{-1}p^{\prime }_0$
is counter-clockwise, then
$(q^{\prime }_0)^{-1}p^{\prime }_0$
is counter-clockwise, then
![]() $(p^{\prime }_0,q^{\prime }_0)$
forms an irreducible pair, since any subpath of p is leftmost and any subpath of q is rightmost. If not, then the removal of
$(p^{\prime }_0,q^{\prime }_0)$
forms an irreducible pair, since any subpath of p is leftmost and any subpath of q is rightmost. If not, then the removal of
![]() $(q^{\prime }_0)^{-1}p^{\prime }_0$
from
$(q^{\prime }_0)^{-1}p^{\prime }_0$
from
![]() $q_0^{-1}p_0$
may only increase the winding number around F; hence,
$q_0^{-1}p_0$
may only increase the winding number around F; hence,
![]() $\text {Wind}(q_1^{-1}p_1,F)\geq \text {Wind}(q_0^{-1}p_0,F)>0$
. We now start the process over with
$\text {Wind}(q_1^{-1}p_1,F)\geq \text {Wind}(q_0^{-1}p_0,F)>0$
. We now start the process over with
![]() $p_1$
and
$p_1$
and
![]() $q_1$
in place of
$q_1$
in place of
![]() $p_0$
and
$p_0$
and
![]() $q_0$
. This process must eventually terminate when some
$q_0$
. This process must eventually terminate when some
![]() $(p^{\prime }_i,q^{\prime }_i)$
forms an irreducible pair, contradicting Theorem 3.19.
$(p^{\prime }_i,q^{\prime }_i)$
forms an irreducible pair, contradicting Theorem 3.19.
4.3 Strand-consistency implies path-consistency
We now prove the converse of Theorem 4.10, completing the proof that the notions of path-consistency and strand-consistency are equivalent for finite dimer models on surfaces which are not spheres. In the case where Q is a dimer model on a disk, this is proven in [Reference Çanakç, King and Pressland13, Proposition 2.15]. In the case where Q is a dimer model on a compact surface without boundary, it appears in [Reference Bocklandt6, Theorem 10.1, Theorem 10.2]. First, we need the following definition.
Definition 4.11. Let
![]() $Q=(Q_0,Q_1,Q_2)$
be a dimer model. Let
$Q=(Q_0,Q_1,Q_2)$
be a dimer model. Let
![]() $\mathcal F\subseteq Q_2$
be a set of faces of
$\mathcal F\subseteq Q_2$
be a set of faces of
![]() $Q_2$
which form a connected surface with boundary which is a subspace of the surface
$Q_2$
which form a connected surface with boundary which is a subspace of the surface
![]() $S(Q)$
of Q.
$S(Q)$
of Q.
We define the dimer submodel
![]() $Q^{\mathcal F}$
of Q induced by
$Q^{\mathcal F}$
of Q induced by
![]() $\mathcal F$
as the dimer model
$\mathcal F$
as the dimer model
![]() $Q^{\mathcal F}=(Q^{\mathcal F}_0,Q^{\mathcal F}_1,\mathcal F)$
, where
$Q^{\mathcal F}=(Q^{\mathcal F}_0,Q^{\mathcal F}_1,\mathcal F)$
, where
![]() $Q^{\mathcal F}_0$
and
$Q^{\mathcal F}_0$
and
![]() $Q^{\mathcal F}_1$
are the sets of vertices and edges of Q appearing in some face of
$Q^{\mathcal F}_1$
are the sets of vertices and edges of Q appearing in some face of
![]() $\mathcal F$
.
$\mathcal F$
.
Intuitively,
![]() $Q^{\mathcal F}$
is obtained by deleting all faces of Q which are not in
$Q^{\mathcal F}$
is obtained by deleting all faces of Q which are not in
![]() $\mathcal F$
. See Figure 11. It is immediate that if
$\mathcal F$
. See Figure 11. It is immediate that if
![]() $\mathcal G\subseteq \mathcal F\subseteq Q_2$
induce dimer submodels, then
$\mathcal G\subseteq \mathcal F\subseteq Q_2$
induce dimer submodels, then
![]() $Q^{\mathcal G}=(Q^{\mathcal F})^{\mathcal G}$
. A disk submodel is a dimer submodel which is a dimer model on a disk.
$Q^{\mathcal G}=(Q^{\mathcal F})^{\mathcal G}$
. A disk submodel is a dimer submodel which is a dimer model on a disk.
Figure 11 The disk model on the left is not weakly consistent, since it has a homologically trivial interior cycle. When we delete the center face by taking the submodel induced by all other faces, this cycle still exists but is no longer homologically trivial. The result is a weakly consistent dimer model on an annulus.
Proposition 4.12. A strand-consistent dimer model is path-consistent.
Proof. By Theorem 2.18, Q is path-consistent if and only if
![]() $A_Q$
is cancellative. By Lemma 2.16, this is true if and only if
$A_Q$
is cancellative. By Lemma 2.16, this is true if and only if
![]() $A_{\widetilde Q}$
is cancellative. Hence, it suffices to show that
$A_{\widetilde Q}$
is cancellative. Hence, it suffices to show that
![]() $A_{\widetilde Q}$
is a cancellation algebra. Accordingly, suppose
$A_{\widetilde Q}$
is a cancellation algebra. Accordingly, suppose
![]() $p,q,a$
are paths of
$p,q,a$
are paths of
![]() $\widetilde Q$
such that
$\widetilde Q$
such that
![]() $h(a)=t(p)=t(q)$
and
$h(a)=t(p)=t(q)$
and
![]() $h(p)=h(q)$
and
$h(p)=h(q)$
and
![]() $[pa]=[qa]$
. Then there is a finite sequence of morphs taking
$[pa]=[qa]$
. Then there is a finite sequence of morphs taking
![]() $pa$
to
$pa$
to
![]() $qa$
in
$qa$
in
![]() $\widetilde Q$
. Let
$\widetilde Q$
. Let
![]() $Q'$
be a disk submodel of
$Q'$
be a disk submodel of
![]() $\widetilde Q$
containing every intermediate path in this sequence. Since
$\widetilde Q$
containing every intermediate path in this sequence. Since
![]() $D_{Q'}$
is a restriction of
$D_{Q'}$
is a restriction of
![]() $D_{\widetilde Q}$
, which has no bad configurations, the former also has no bad configurations. By [Reference Çanakç, King and Pressland13, Proposition 2.15],
$D_{\widetilde Q}$
, which has no bad configurations, the former also has no bad configurations. By [Reference Çanakç, King and Pressland13, Proposition 2.15],
![]() $Q'$
is path-consistent. By Theorem 2.18,
$Q'$
is path-consistent. By Theorem 2.18,
![]() $A_{Q'}$
is cancellative; hence,
$A_{Q'}$
is cancellative; hence,
![]() $[p]=[q]$
in
$[p]=[q]$
in
![]() $Q'$
. Then there is a sequence of morphs taking p to q in
$Q'$
. Then there is a sequence of morphs taking p to q in
![]() $Q'$
; this is necessarily a sequence of morphs in
$Q'$
; this is necessarily a sequence of morphs in
![]() $\widetilde Q$
, so
$\widetilde Q$
, so
![]() $[p]=[q]$
in
$[p]=[q]$
in
![]() $\widetilde Q$
.
$\widetilde Q$
.
It may similarly be shown that if
![]() $p,q,b$
are paths of
$p,q,b$
are paths of
![]() $\widetilde Q$
such that
$\widetilde Q$
such that
![]() $t(b)=h(p)=h(q)$
and
$t(b)=h(p)=h(q)$
and
![]() $t(p)=t(q)$
, then
$t(p)=t(q)$
, then
![]() $[bp]=[bq]$
implies
$[bp]=[bq]$
implies
![]() $[p]=[q]$
. This completes the proof that
$[p]=[q]$
. This completes the proof that
![]() $A_{\widetilde Q}$
is cancellation, and thus that Q is path-consistent.
$A_{\widetilde Q}$
is cancellation, and thus that Q is path-consistent.
Theorem 4.13. Let Q be a dimer model not on a sphere. The following are equivalent:
-
1. Q is path-consistent,
-
2. Q is strand-consistent,
-
3. The dimer algebra
 $A_Q$
is cancellative.
$A_Q$
is cancellative.
Proof. Path-consistency implies strand-consistency by Theorem 4.10. Strand-consistency implies path-consistency by Proposition 4.12. Path-consistency is equivalent to cancellativity by Theorem 2.18.
Theorem 4.13 is known for dimer models on tori; for example, see [Reference Bocklandt6] and references therein. It was shown for dimer models on the disk corresponding to
![]() $(k,n)$
-diagrams in [Reference Baur, King and Marsh4]. The implication (2)
$(k,n)$
-diagrams in [Reference Baur, King and Marsh4]. The implication (2)
![]() $\implies $
(1) for general dimer models on disks appears in [Reference Pressland48, Proposition 2.11]. The authors are not aware of a proof in the other implication in the case of the disk; hence, we include this corollary.
$\implies $
(1) for general dimer models on disks appears in [Reference Pressland48, Proposition 2.11]. The authors are not aware of a proof in the other implication in the case of the disk; hence, we include this corollary.
Corollary 4.14. Let Q be a dimer model in a disk. Then Q is path-consistent if and only if Q is strand-consistent.
In light of Theorem 4.13, we use the word weakly consistent to refer to both path-consistent and strand-consistent dimer models that are not on a sphere. We will define strong consistency in Section 6.
5 Dimer submodels
Recall the definition of a dimer submodel in Definition 4.11. We now show that the dimer submodel of a weakly consistent model is weakly consistent, and moreover that the path equivalence classes of a dimer submodel may be understood in terms of the original dimer model. This is a useful result that will lead to some nice corollaries in Section 8.
Corollary 5.1. Let Q be a dimer model. Let
![]() $\mathcal F$
be a set of faces of Q forming a surface S such that the restriction of the strand diagram
$\mathcal F$
be a set of faces of Q forming a surface S such that the restriction of the strand diagram
![]() $D_Q$
to S has no bad configurations. Then
$D_Q$
to S has no bad configurations. Then
![]() $Q^{\mathcal F}$
is weakly consistent. In particular, if Q is weakly consistent, then any dimer submodel of Q is weakly consistent.
$Q^{\mathcal F}$
is weakly consistent. In particular, if Q is weakly consistent, then any dimer submodel of Q is weakly consistent.
Proof. Since weak consistency is characterized by the absence of bad configurations by Theorem 4.13, the first statement is trivial. Passing from Q to a dimer submodel
![]() $Q^{\mathcal F}$
corresponds to restricting the strand diagram of Q to the surface given by the union of the faces in
$Q^{\mathcal F}$
corresponds to restricting the strand diagram of Q to the surface given by the union of the faces in
![]() $\mathcal F$
. This cannot create any bad configurations, so the second statement follows.
$\mathcal F$
. This cannot create any bad configurations, so the second statement follows.
See Figure 11 for an example of how Corollary 5.1 may be used in practice to obtain weakly consistent dimer models from existing (not necessarily weakly consistent) models.
Theorem 5.2. Let Q be a weakly consistent dimer model and let
![]() $Q^{\mathcal F}$
be a (necessarily weakly consistent) dimer submodel of Q. Then two paths in
$Q^{\mathcal F}$
be a (necessarily weakly consistent) dimer submodel of Q. Then two paths in
![]() $Q^{\mathcal F}$
are equivalent in
$Q^{\mathcal F}$
are equivalent in
![]() $Q^{\mathcal F}$
if and only if they are equivalent in Q and homotopic in
$Q^{\mathcal F}$
if and only if they are equivalent in Q and homotopic in
![]() $S(Q^{\mathcal F})$
.
$S(Q^{\mathcal F})$
.
Proof. If
![]() $[p]=[q]$
in
$[p]=[q]$
in
![]() $Q^{\mathcal F}$
, then certainly
$Q^{\mathcal F}$
, then certainly
![]() $[p]=[q]$
in Q. Moreover, in this case, p is homotopic to q in
$[p]=[q]$
in Q. Moreover, in this case, p is homotopic to q in
![]() $S(Q^{\mathcal F})$
, and hence in Q. However, suppose that
$S(Q^{\mathcal F})$
, and hence in Q. However, suppose that
![]() $[p]=[q]$
in Q and that p is homotopic to q in
$[p]=[q]$
in Q and that p is homotopic to q in
![]() $S(Q^{\mathcal F})$
. By path-consistency of
$S(Q^{\mathcal F})$
. By path-consistency of
![]() $Q^{\mathcal F}$
, without loss of generality, we have
$Q^{\mathcal F}$
, without loss of generality, we have
![]() $[p]=[qf^m]$
in
$[p]=[qf^m]$
in
![]() $Q^{\mathcal F}$
for some nonnegative integer m. Then we have
$Q^{\mathcal F}$
for some nonnegative integer m. Then we have
![]() $[p]=[qf^m]$
in Q. By path-consistency of Q, since
$[p]=[qf^m]$
in Q. By path-consistency of Q, since
![]() $[p]=[q]$
in Q, we must have
$[p]=[q]$
in Q, we must have
![]() $m=0$
, and hence,
$m=0$
, and hence,
![]() $[p]=[q]$
in
$[p]=[q]$
in
![]() $Q^{\mathcal F}$
.
$Q^{\mathcal F}$
.
Remark 5.3. Theorem 5.2 could be stated more generally without changing the proof. We do not need Q to be weakly consistent; we merely need to be able to ‘cancel face-paths’ in Q. In other words, we require that
![]() $[pf^m]=[p]$
cannot hold for positive m. This is a weaker condition than cancellativity (and hence weak consistency) and is satisfied – for example, if Q has a perfect matching. See Section 6 and Lemma 6.1.
$[pf^m]=[p]$
cannot hold for positive m. This is a weaker condition than cancellativity (and hence weak consistency) and is satisfied – for example, if Q has a perfect matching. See Section 6 and Lemma 6.1.
6 Perfect matchings
A perfect matching of a dimer model Q is a collection of arrows
![]() $\mathcal M$
of Q such that every face of Q contains exactly one arrow in
$\mathcal M$
of Q such that every face of Q contains exactly one arrow in
![]() $\mathcal M$
. See Figure 12 for two examples.
$\mathcal M$
. See Figure 12 for two examples.
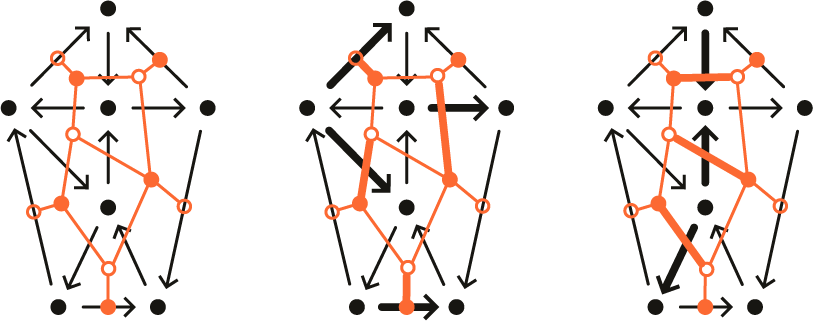
Figure 12 On the left, a dimer model on a disk with its plabic graph overlayed is pictured. The two pictures on the right show two different perfect matchings, both as collections of arrows of the quiver and as collections of edges of the plabic graph.
Dimer models on the torus with perfect matchings have been studied in, for example, [Reference Ishii and Ueda34], [Reference Broomhead11], [Reference Bocklandt6] and are often called dimer configurations. The Gorenstein affine toric threefold obtained by putting the perfect matching polygon at height one is the center of the dimer algebra, and the dimer algebra is viewed as a non-commutative crepant resolution of this variety; for example, see [Reference Bocklandt8, Reference Broomhead11, Reference Ishii and Ueda35, Reference Mozgovoy42]. Perfect matchings of dimer models on a more general surface, often called almost perfect matchings, are a natural generalization. Perfect matching polygons may be extended to dimer models over arbitrary compact surfaces with boundary, and capture the data of the master and mesonic moduli spaces [Reference Franco16]. Perfect matchings may be calculated by taking determinants of Kasteleyn matrices; see [Reference Hanany and Kennaway31] and [Reference Franco16, §5].
In the present paper, we give some basic results, prove existence of perfect matchings in weakly consistent simply connected dimer models, and give a counterexample to the existence of perfect matchings in arbitrary weakly consistent dimer models.
We use combinatorial theory of matchings of (undirected) graphs in order to prove the main result of this section. In order to do so, we associate to Q a bipartite plabic graph
![]() $\mathcal G=(\mathcal G_0^b,\mathcal G_0^w,\mathcal G_1)$
embedded into
$\mathcal G=(\mathcal G_0^b,\mathcal G_0^w,\mathcal G_1)$
embedded into
![]() $S(Q)$
as follows. To each face F of Q, we associate an internal vertex
$S(Q)$
as follows. To each face F of Q, we associate an internal vertex
![]() $v_F$
embedded in the interior of F. If F is a clockwise face, we say that
$v_F$
embedded in the interior of F. If F is a clockwise face, we say that
![]() $v_F$
is a black vertex and we write
$v_F$
is a black vertex and we write
![]() $v_F\in \mathcal G_0^b$
. If F is a counter-clockwise face, we say that
$v_F\in \mathcal G_0^b$
. If F is a counter-clockwise face, we say that
![]() $v_F$
is a white vertex and we write
$v_F$
is a white vertex and we write
![]() $v_F\in \mathcal G_0^w$
. For any boundary arrow
$v_F\in \mathcal G_0^w$
. For any boundary arrow
![]() $\alpha $
of Q, we draw a boundary vertex
$\alpha $
of Q, we draw a boundary vertex
![]() $v_\alpha $
embedded in the middle of
$v_\alpha $
embedded in the middle of
![]() $\alpha $
. We consider
$\alpha $
. We consider
![]() $v_\alpha $
to be a white vertex if
$v_\alpha $
to be a white vertex if
![]() $\alpha $
is part of a clockwise face, and a black vertex if
$\alpha $
is part of a clockwise face, and a black vertex if
![]() $\alpha $
is part of a counter-clockwise face. For each internal arrow
$\alpha $
is part of a counter-clockwise face. For each internal arrow
![]() $\alpha $
of Q, we draw an edge between
$\alpha $
of Q, we draw an edge between
![]() $v_{F_\alpha ^{cl}}$
and
$v_{F_\alpha ^{cl}}$
and
![]() $v_{F_\alpha ^{cc}}$
. For each boundary arrow
$v_{F_\alpha ^{cc}}$
. For each boundary arrow
![]() $\alpha $
of Q, we draw an edge between
$\alpha $
of Q, we draw an edge between
![]() $v_\alpha $
and the vertex corresponding to the unique face incident to
$v_\alpha $
and the vertex corresponding to the unique face incident to
![]() $\alpha $
. See Figure 12.
$\alpha $
. See Figure 12.
A perfect matching
![]() $\mathcal M$
of Q is dual to a collection of edges
$\mathcal M$
of Q is dual to a collection of edges
![]() $\mathcal N$
of the plabic graph
$\mathcal N$
of the plabic graph
![]() $\mathcal G$
of Q such that every internal vertex of
$\mathcal G$
of Q such that every internal vertex of
![]() $\mathcal G$
is contained in exactly one edge of
$\mathcal G$
is contained in exactly one edge of
![]() $\mathcal N$
. We refer to both
$\mathcal N$
. We refer to both
![]() $\mathcal M$
and
$\mathcal M$
and
![]() $\mathcal N$
as perfect matching of Q. If Q has no boundary, then a perfect matching is dual to a perfect matching of the dual (plabic) graph of Q in the usual sense. See Figure 12.
$\mathcal N$
as perfect matching of Q. If Q has no boundary, then a perfect matching is dual to a perfect matching of the dual (plabic) graph of Q in the usual sense. See Figure 12.
If
![]() $\mathcal M$
is a perfect matching of Q, we say that the intersections of a path p with
$\mathcal M$
is a perfect matching of Q, we say that the intersections of a path p with
![]() $\mathcal M$
are the arrows of p which are in
$\mathcal M$
are the arrows of p which are in
![]() $\mathcal M$
. The intersection number
$\mathcal M$
. The intersection number
![]() $\mathcal M(p)$
of p with
$\mathcal M(p)$
of p with
![]() $\mathcal M$
is the number of intersections of p with
$\mathcal M$
is the number of intersections of p with
![]() $\mathcal M$
(counting ‘multiplicities’ if p has multiple instances of the same arrow).
$\mathcal M$
(counting ‘multiplicities’ if p has multiple instances of the same arrow).
Lemma 6.1. Suppose Q has a perfect matching
![]() $\mathcal M$
. If
$\mathcal M$
. If
![]() $[p]=[q]$
, then
$[p]=[q]$
, then
![]() $\mathcal M(p)=\mathcal M(q)$
.
$\mathcal M(p)=\mathcal M(q)$
.
Proof. Since
![]() $R_\alpha ^{cl}$
contains an arrow of
$R_\alpha ^{cl}$
contains an arrow of
![]() $\mathcal M$
if and only if
$\mathcal M$
if and only if
![]() $R_\alpha ^{cc}$
does, it follows that basic morphs preserve intersection number. The result follows.
$R_\alpha ^{cc}$
does, it follows that basic morphs preserve intersection number. The result follows.
Proposition 6.2. Suppose Q is weakly consistent and that Q has a perfect matching
![]() $\mathcal M$
. Let p and q be paths of Q with the same start vertex, end vertex and homotopy class. Then
$\mathcal M$
. Let p and q be paths of Q with the same start vertex, end vertex and homotopy class. Then
![]() $[p]=[q]$
if and only if
$[p]=[q]$
if and only if
![]() $\mathcal M(p)=\mathcal M(q)$
.
$\mathcal M(p)=\mathcal M(q)$
.
Proof. Lemma 6.1 shows that if
![]() $[p]=[q]$
then
$[p]=[q]$
then
![]() $\mathcal M(p)=\mathcal M(q)$
. However, if
$\mathcal M(p)=\mathcal M(q)$
. However, if
![]() $[p]\neq [q]$
, then without loss of generality,
$[p]\neq [q]$
, then without loss of generality,
![]() $[p]=[qf^m]$
for some
$[p]=[qf^m]$
for some
![]() $m>0$
. Since any face-path contains exactly one arrow of
$m>0$
. Since any face-path contains exactly one arrow of
![]() $\mathcal M$
, we have
$\mathcal M$
, we have
![]() $\mathcal M(p)=m+\mathcal M(q)$
, ending the proof.
$\mathcal M(p)=m+\mathcal M(q)$
, ending the proof.
Lemma 6.3. Suppose Q has a perfect matching
![]() $\mathcal M$
and let p be a path in Q. The set
$\mathcal M$
and let p be a path in Q. The set
is bounded above by
![]() $\mathcal M(p)$
. In particular, only a finite number of face-paths can be factored out of p.
$\mathcal M(p)$
. In particular, only a finite number of face-paths can be factored out of p.
Proof. Any face-path has an intersection number of one with any perfect matching. Hence, if
![]() $[p]=[f^mq]$
, then by Lemma 6.1,
$[p]=[f^mq]$
, then by Lemma 6.1,
![]() $\mathcal M(p)$
must be at least m.
$\mathcal M(p)$
must be at least m.
The condition that only a finite number of face-paths can be factored out of any path p is implied by path-consistency. In fact, it is a strictly weaker property than weak consistency.
We show the stronger statement that the existence of a perfect matching does not imply weak consistency. Indeed, Figure 13, which shows a dimer model which has a perfect matching but is not weakly consistent. More generally, if Q is a weakly consistent dimer model, then let
![]() $Q'$
be the dimer model obtained by replacing some internal arrow
$Q'$
be the dimer model obtained by replacing some internal arrow
![]() $\alpha $
of Q with two consecutive arrows
$\alpha $
of Q with two consecutive arrows
![]() $\gamma \beta $
such that
$\gamma \beta $
such that
![]() $h(\gamma )=h(\alpha )$
and
$h(\gamma )=h(\alpha )$
and
![]() $t(\beta )=t(\alpha )$
and
$t(\beta )=t(\alpha )$
and
![]() $h(\beta )=t(\gamma )$
is a new vertex of
$h(\beta )=t(\gamma )$
is a new vertex of
![]() $Q'$
. Then the strand diagram of
$Q'$
. Then the strand diagram of
![]() $Q'$
has a bad digon, and hence is not weakly consistent. However, Q has a perfect matching by Theorem 6.7; hence,
$Q'$
has a bad digon, and hence is not weakly consistent. However, Q has a perfect matching by Theorem 6.7; hence,
![]() $Q'$
has a perfect matching.
$Q'$
has a perfect matching.
Figure 13 A dimer model on a disk which is not weakly consistent but has a perfect matching.
6.1 Consistency and existence of perfect matchings
We have seen that the existence of a perfect matching does not guarantee weak consistency. We now investigate whether weak consistency guarantees the existence of a perfect matching. We show in Theorem 6.7 that perfect matchings exist in simply connected weakly consistent dimer models. However, we see in Example 6.8 that perfect matchings need not exist in arbitrary weakly consistent dimer models.
Definition 6.4. Let
![]() $(V_1,V_2,E)$
be a possibly infinite bipartite graph. Let
$(V_1,V_2,E)$
be a possibly infinite bipartite graph. Let
![]() $\{i,j\}=\{1,2\}$
. Let
$\{i,j\}=\{1,2\}$
. Let
![]() $S\subseteq V_i$
. A matching from S into
$S\subseteq V_i$
. A matching from S into
![]() $V_j$
is a set
$V_j$
is a set
![]() $\mathcal N$
of disjoint edges in E such that every vertex of S is incident to precisely one edge in
$\mathcal N$
of disjoint edges in E such that every vertex of S is incident to precisely one edge in
![]() $\mathcal N$
.
$\mathcal N$
.
A perfect matching of a dimer model, then, is a matching onto some full subgraph of the plabic graph
![]() $\mathcal G$
of Q induced by all of the internal vertices and some subset of the boundary vertices. We use the following formulation of Hall’s marriage theorem for locally finite graphs.
$\mathcal G$
of Q induced by all of the internal vertices and some subset of the boundary vertices. We use the following formulation of Hall’s marriage theorem for locally finite graphs.
Theorem 6.5 [Reference Clark14, Theorem 6].
Let
![]() $(V_1,V_2,E)$
be a bipartite graph in which every vertex has finite degree. The following are equivalent.
$(V_1,V_2,E)$
be a bipartite graph in which every vertex has finite degree. The following are equivalent.
-
1. There is a matching from
 $V_1$
into
$V_1$
into
 $V_2$
.
$V_2$
. -
2. Any m vertices of
 $V_1$
have at least m distinct neighbors in
$V_1$
have at least m distinct neighbors in
 $V_2$
.
$V_2$
.
Theorem 6.6 [Reference Aharoni1, Theorem 1.1].
Let
![]() $(V_1,V_2,E)$
be a bipartite graph. Let
$(V_1,V_2,E)$
be a bipartite graph. Let
![]() $A\subseteq V_1$
and
$A\subseteq V_1$
and
![]() $B\subseteq V_2$
. If there exists a matching from A into
$B\subseteq V_2$
. If there exists a matching from A into
![]() $V_2$
and a matching from B into
$V_2$
and a matching from B into
![]() $V_1$
, then there exists a disjoint set of edges
$V_1$
, then there exists a disjoint set of edges
![]() $\mathcal N$
in E such that each vertex in
$\mathcal N$
in E such that each vertex in
![]() $A\cup B$
is incident to precisely one edge in
$A\cup B$
is incident to precisely one edge in
![]() $\mathcal N$
.
$\mathcal N$
.
Theorem 6.7. If a simply connected dimer model
![]() $\widetilde Q$
is weakly consistent, then it has a perfect matching.
$\widetilde Q$
is weakly consistent, then it has a perfect matching.
Proof. We will use the dual definition of a perfect matching. We must then show that there is a set
![]() $\mathcal N$
of edges of the plabic graph
$\mathcal N$
of edges of the plabic graph
![]() $\mathcal G$
of
$\mathcal G$
of
![]() $\widetilde Q$
such that every vertex of
$\widetilde Q$
such that every vertex of
![]() $\mathcal G$
is incident to exactly one edge of
$\mathcal G$
is incident to exactly one edge of
![]() $\mathcal N$
.
$\mathcal N$
.
We first claim that it suffices to show that any collection of m internal black vertices is connected to at least m white vertices and that any collection of m internal white vertices is connected to at least m black vertices. Suppose this is true. By applying Theorem 6.5 to the internal black vertices, we see that there is a matching from the set of internal black vertices into the white vertices. Symmetrically, we get a matching from the set of internal white vertices into the black vertices. Then Theorem 6.6 shows that there exists a perfect matching. This ends the proof of the claim.
We show that any collection of m internal white vertices is connected to at least m black vertices. The remaining case is symmetric. Take a set S of m internal white vertices of
![]() $\mathcal G_{\widetilde Q}$
. These correspond to m internal faces of
$\mathcal G_{\widetilde Q}$
. These correspond to m internal faces of
![]() $\widetilde Q$
. Let
$\widetilde Q$
. Let
![]() $Q'$
be a disk submodel of
$Q'$
be a disk submodel of
![]() $\widetilde Q$
containing all faces of S. Such a disk submodel must exist since
$\widetilde Q$
containing all faces of S. Such a disk submodel must exist since
![]() $\widetilde Q$
is simply connected. Since
$\widetilde Q$
is simply connected. Since
![]() $D_{\widetilde Q}$
has no bad configurations and
$D_{\widetilde Q}$
has no bad configurations and
![]() $D_{Q'}$
is a restriction of
$D_{Q'}$
is a restriction of
![]() $D_{\widetilde Q}$
, the latter also has no bad configurations. By [Reference Çanakç, King and Pressland13, Proposition 2.15],
$D_{\widetilde Q}$
, the latter also has no bad configurations. By [Reference Çanakç, King and Pressland13, Proposition 2.15],
![]() $Q'$
is a path-consistent dimer model. By [Reference Çanakç, King and Pressland13, Corollary 4.6],
$Q'$
is a path-consistent dimer model. By [Reference Çanakç, King and Pressland13, Corollary 4.6],
![]() $\mathcal G_{Q'}$
has a perfect matching. In particular, by Hall’s marriage theorem (Theorem 6.5), the set S of white vertices considered as vertices of
$\mathcal G_{Q'}$
has a perfect matching. In particular, by Hall’s marriage theorem (Theorem 6.5), the set S of white vertices considered as vertices of
![]() $\mathcal G_{Q'}$
has at least m neighbors in
$\mathcal G_{Q'}$
has at least m neighbors in
![]() $\mathcal G_{Q'}$
; hence, S has at least m neighbors in
$\mathcal G_{Q'}$
; hence, S has at least m neighbors in
![]() $\mathcal G_{\widetilde Q}$
. This completes the proof.
$\mathcal G_{\widetilde Q}$
. This completes the proof.
Example 6.8 shows that Theorem 6.7 does not work for dimer models which are not simply connected.
Example 6.8. Consider the dimer model on a torus pictured in Figure 14. It is immediate that any perfect matching of this dimer model must contain one of the arrows of its digon. A short check verifies that a perfect matching must also contain the arrows
![]() $\{\alpha , \beta \}$
or the arrows
$\{\alpha , \beta \}$
or the arrows
![]() $\{\gamma , \delta \}$
. However, this prevents any arrow of the face appearing in a corner of the diagram from being in a perfect matching. Hence, this dimer model has no perfect matching. We remark that this dimer model is obtained by taking a weakly consistent dimer model on a torus, and replacing a counter-clockwise square with a variant of the dimer model of Figure 21.
$\{\gamma , \delta \}$
. However, this prevents any arrow of the face appearing in a corner of the diagram from being in a perfect matching. Hence, this dimer model has no perfect matching. We remark that this dimer model is obtained by taking a weakly consistent dimer model on a torus, and replacing a counter-clockwise square with a variant of the dimer model of Figure 21.
Figure 14 A weakly consistent dimer model on a torus with a disk taken out which has no perfect matching. Opposite dashed edges are identified.
Example 6.8 raises a question: What sort of conditions may we impose on a weakly consistent dimer model to necessitate the existence of some perfect matching? In particular, does any weakly consistent dimer model with no digons have a perfect matching?
6.2 Nondegeneracy
In the disk and torus case, an important idea is nondegeneracy of dimer models. We will define nondegeneracy and prove a simple result which will be used in Section 7.
Definition 6.9. A dimer model Q is nondegenerate if every arrow is contained in a perfect matching. Otherwise, it is degenerate.
In the disk and torus case, nondegeneracy is implied by weak consistency [Reference Ishii and Ueda35, Proposition 6.2] [Reference Çanakç, King and Pressland13]. In the general case, this is not true. For example, the weakly consistent dimer model in Figure 14 has no perfect matchings, and hence is certainly degenerate. The middle of Figure 15 shows a weakly consistent dimer model which has a perfect matching but is still degenerate. Nondegeneracy will feature prominently in Section 7 and Section 9. Figure 13 gives an example of a disk model which is nondegenerate but not weakly consistent. See Example 7.16 for multiple examples of nondegenerate weakly consistent dimer models on annuli. In the rest of this paper, we will see that nondegeneracy is a useful condition that allows us to generalize results from the disk and torus case, motivating the following definition.
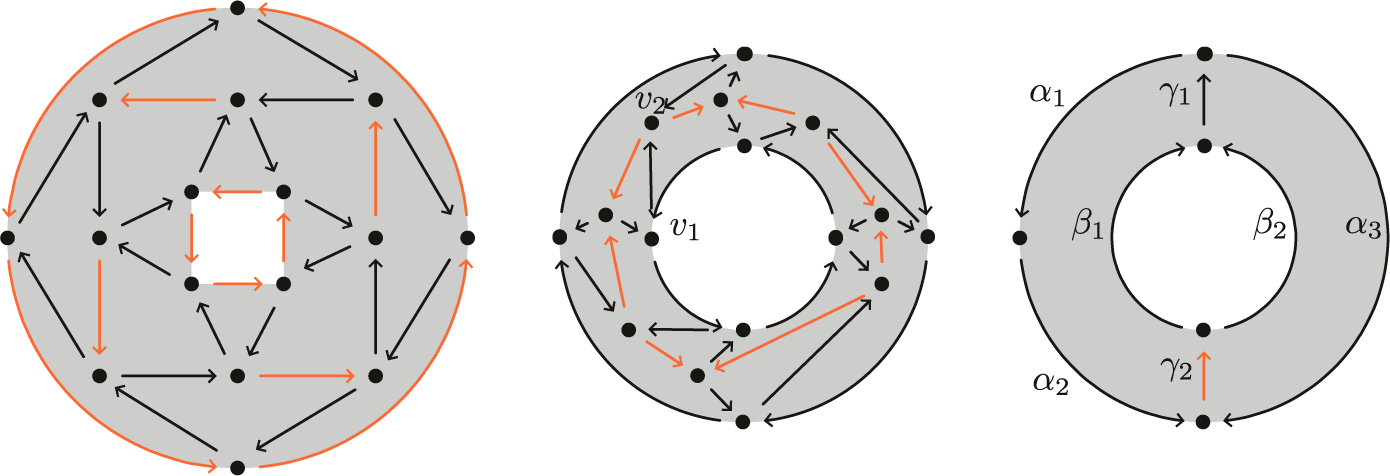
Figure 15 On the left is a strongly consistent dimer model on an annulus which is Noetherian but not boundary-finite. In the middle is a weakly consistent dimer model on an annulus which is boundary-finite but not Noetherian. On the right is a strongly consistent dimer model on an annulus which is boundary-finite but not Noetherian.
Definition 6.10. A dimer model is strongly consistent if it is weakly consistent and nondegenerate.
The following lemma generalizes the well-known situation in the torus and disk literature. See, for example, [Reference Broomhead11, §2.3] in the torus case and [Reference Pressland48, Proposition 3.1] in the disk case.
Lemma 6.11. If Q is finite and strongly consistent, then
![]() $A_Q$
(and hence
$A_Q$
(and hence
![]() $\widehat A_Q$
) admits a
$\widehat A_Q$
) admits a
![]() $\mathbb Z$
-grading such that
$\mathbb Z$
-grading such that
-
1. Every nonconstant path has a positive degree, and
-
2. Every face-path has the same degree.
Proof. Let C be a collection of all perfect matchings on Q. Since Q is finite, C has finite cardinality. Given a path p of Q, we give p the grading
where
![]() $\mathcal M(p)$
is the number of arrows of p which are in
$\mathcal M(p)$
is the number of arrows of p which are in
![]() $\mathcal M$
. Note that, for any perfect matching
$\mathcal M$
. Note that, for any perfect matching
![]() $\mathcal M$
, the quantity
$\mathcal M$
, the quantity
![]() $\mathcal M(p)$
is unchanged by applying a basic morph to p. This means that the quantity
$\mathcal M(p)$
is unchanged by applying a basic morph to p. This means that the quantity
![]() $G(p)$
is a well-defined number of the equivalence class of p. It is clear that if p, q, and
$G(p)$
is a well-defined number of the equivalence class of p. It is clear that if p, q, and
![]() $qp$
are paths, then
$qp$
are paths, then
![]() $G(p)+G(q)=G(qp)$
. It follows that G gives a positive
$G(p)+G(q)=G(qp)$
. It follows that G gives a positive
![]() $\mathbb Z$
-grading on A through which every arrow is given a positive degree. The second statement follows because the degree of any face-path is equal to the number of perfect matchings on Q.
$\mathbb Z$
-grading on A through which every arrow is given a positive degree. The second statement follows because the degree of any face-path is equal to the number of perfect matchings on Q.
Lemma 6.12. Let Q be finite and strongly consistent. Then an arbitrary element x of the completed dimer algebra
![]() $\widehat A_Q$
may be represented as
$\widehat A_Q$
may be represented as
where the second sum iterates over all homotopy classes of paths from v to w, and
![]() $a_{C,m}\in \mathbb {C}$
. Moreover, this element is zero if and only if all coefficients
$a_{C,m}\in \mathbb {C}$
. Moreover, this element is zero if and only if all coefficients
![]() $a_{C,m}$
are zero.
$a_{C,m}$
are zero.
Proof. Since Q is strongly consistent, we may fix a positive
![]() $\mathbb Z$
-grading G of the completed dimer algebra
$\mathbb Z$
-grading G of the completed dimer algebra
![]() $\widehat A_Q$
as in Lemma 6.11. We first show that an arbitrary
$\widehat A_Q$
as in Lemma 6.11. We first show that an arbitrary
![]() $x\in \widehat A_Q$
is of the desired form. By definition, an element
$x\in \widehat A_Q$
is of the desired form. By definition, an element
![]() $x\in \widehat A_Q$
is of the form
$x\in \widehat A_Q$
is of the form
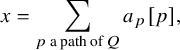 $$ \begin{align}x=\sum_{p\text{ a path of }Q}a_p[p],\end{align} $$
$$ \begin{align}x=\sum_{p\text{ a path of }Q}a_p[p],\end{align} $$
for some coefficients
![]() $a_p\in \mathbb C$
. Define
$a_p\in \mathbb C$
. Define
![]() $G_{\min }:=\text {min}\{G(\alpha )\ :\ \alpha \in Q_1\}$
.
$G_{\min }:=\text {min}\{G(\alpha )\ :\ \alpha \in Q_1\}$
.
Let p be any path of Q. Let C be the homotopy class of p. By path-consistency, write
![]() $[p]=[r_Cf^{m}]$
for some value m and a minimal path
$[p]=[r_Cf^{m}]$
for some value m and a minimal path
![]() $r_C$
in homotopy class C. Let
$r_C$
in homotopy class C. Let
![]() $M_{C,m}$
be an integer greater than
$M_{C,m}$
be an integer greater than
![]() $\frac {G(p)}{G_{\min }}$
. Then any path of Q with at least
$\frac {G(p)}{G_{\min }}$
. Then any path of Q with at least
![]() $M_{C,m}$
arrows must have a grading greater than
$M_{C,m}$
arrows must have a grading greater than
![]() $G(p)$
; hence, every path equivalent to p must have less than
$G(p)$
; hence, every path equivalent to p must have less than
![]() $M_{C,m}$
arrows. Such paths are finite in number, and hence, the path equivalence class of p is finite. Then we may define
$M_{C,m}$
arrows. Such paths are finite in number, and hence, the path equivalence class of p is finite. Then we may define
![]() $a_{C,m}:=\sum _{q\text { equivalent to }p}a_q$
. The desired
$a_{C,m}:=\sum _{q\text { equivalent to }p}a_q$
. The desired
now follows from rearranging the terms of equation (3).
Now suppose that some
![]() $a_{C',m'}$
is nonzero. Define a real number
$a_{C',m'}$
is nonzero. Define a real number
![]() $G'>G(r_C'f^{m'})$
. We show that the graded part of x below
$G'>G(r_C'f^{m'})$
. We show that the graded part of x below
![]() $G'$
must be nonzero, and hence that x itself is nonzero. Define for any homotopy class C and
$G'$
must be nonzero, and hence that x itself is nonzero. Define for any homotopy class C and
![]() $m\geq 0$
$m\geq 0$
 $$\begin{align*}a^{\prime}_{C,m}:=\begin{cases} a_{C,m}&G(r_Cf^m)<G' \\ 0&\text{else.} \end{cases}\end{align*}$$
$$\begin{align*}a^{\prime}_{C,m}:=\begin{cases} a_{C,m}&G(r_Cf^m)<G' \\ 0&\text{else.} \end{cases}\end{align*}$$
Then the sum
gives the graded part of x below
![]() $G'$
.
$G'$
.
Set
![]() $M'>\frac {G'}{G_{\min }}$
. Then any path of Q with grading less than
$M'>\frac {G'}{G_{\min }}$
. Then any path of Q with grading less than
![]() $G'$
has less than
$G'$
has less than
![]() $M'$
arrows. So, the sum (4) has a finite number of nonzero summands. Then the sum (4) is in the noncompleted path algebra of Q. Since
$M'$
arrows. So, the sum (4) has a finite number of nonzero summands. Then the sum (4) is in the noncompleted path algebra of Q. Since
![]() $a_{C',m'}$
is nonzero and in this sum, then
$a_{C',m'}$
is nonzero and in this sum, then
![]() $x_{G'}$
is not in the ideal
$x_{G'}$
is not in the ideal
![]() $I_Q$
of the noncompleted dimer algebra. Moreover, since every path with at least
$I_Q$
of the noncompleted dimer algebra. Moreover, since every path with at least
![]() $M'$
arrows has a grading greater than
$M'$
arrows has a grading greater than
![]() $G'$
, the sum
$G'$
, the sum
![]() $x_{G'}$
cannot be in the completion of
$x_{G'}$
cannot be in the completion of
![]() $I_Q$
with respect to the arrow ideal. This shows that
$I_Q$
with respect to the arrow ideal. This shows that
![]() $x_{G'}$
is nonzero in the completed dimer algebra; hence, x is nonzero in the completed dimer algebra.
$x_{G'}$
is nonzero in the completed dimer algebra; hence, x is nonzero in the completed dimer algebra.
7 Bimodule internal 3-Calabi-Yau property
We show that finite strongly consistent (completed or noncompleted) dimer models are bimodule internally 3-Calabi-Yau with respect to their boundary idempotent in the sense of [Reference Pressland46]. As an application, we use a result from [Reference Amiot, Iyama and Reiten2] to show that the Gorenstein-projective module category over the completed boundary algebra of a finite strongly consistent dimer model Q satisfying some extra conditions categorifies the cluster algebra given by the ice quiver of Q. We give new examples of suitable dimer models.
The technical part of this section follows [Reference Pressland48, §3] (in the disk case) and [Reference Broomhead11, §7] (in the torus case). Note that the former writes A for the completed dimer algebra (or Jacobian algebra)
![]() $\widehat A_Q$
, and the latter deals only with the noncompleted dimer algebra.
$\widehat A_Q$
, and the latter deals only with the noncompleted dimer algebra.
Throughout this section, let Q be a finite weakly consistent dimer model. We will eventually pass to the case when Q is in addition nondegenerate. We write
![]() ${\mathcal A}$
to denote simultaneously the noncompleted dimer algebra
${\mathcal A}$
to denote simultaneously the noncompleted dimer algebra
![]() $A_Q$
and the completed dimer algebra
$A_Q$
and the completed dimer algebra
![]() $\widehat A_Q$
, since the arguments are the same.
$\widehat A_Q$
, since the arguments are the same.
7.1 One-sided and two-sided complexes
We begin by defining some
![]() $({\mathcal A},{\mathcal A})$
-bimodules. If v is a vertex of Q, define
$({\mathcal A},{\mathcal A})$
-bimodules. If v is a vertex of Q, define
![]() $T_v$
(respectively
$T_v$
(respectively
![]() $H_v$
) to be the set of all arrows with tail (respectively head) v. Define
$H_v$
) to be the set of all arrows with tail (respectively head) v. Define
![]() $Q_0^m$
to be the set of internal vertices of Q. Let
$Q_0^m$
to be the set of internal vertices of Q. Let
![]() $Q_1^m$
be the set of internal arrows of Q. Define
$Q_1^m$
be the set of internal arrows of Q. Define
![]() $T_v^m$
and
$T_v^m$
and
![]() $H_v^m$
to be the internal arrows of
$H_v^m$
to be the internal arrows of
![]() $T_v$
and
$T_v$
and
![]() $H_v$
, respectively. We define vector spaces
$H_v$
, respectively. We define vector spaces
The
![]() $({\mathcal A},{\mathcal A})$
-bimodule structures are given by
$({\mathcal A},{\mathcal A})$
-bimodule structures are given by
All other products with the generators of
![]() $T_i$
are zero. In this section, all tensor products are over
$T_i$
are zero. In this section, all tensor products are over
![]() $T_0$
unless otherwise specified. We consider the following complex, which we will call the two-sided complex.
$T_0$
unless otherwise specified. We consider the following complex, which we will call the two-sided complex.
We consider
![]() ${\mathcal A}\otimes T_0\otimes {\mathcal A}$
to be the degree-zero term of the complex, and we define the maps
${\mathcal A}\otimes T_0\otimes {\mathcal A}$
to be the degree-zero term of the complex, and we define the maps
![]() $\mu _i$
as follows. First, define a function
$\mu _i$
as follows. First, define a function
![]() $\partial $
on the arrows of Q by
$\partial $
on the arrows of Q by
 $$\begin{align*}\partial(\alpha)=\begin{cases}R_\alpha^{cc}-R_\alpha^{cl}&\alpha\text{ is an internal arrow}\\ R_\alpha^{cc}&\alpha\text{ is a boundary arrow in a counter-clockwise face}\\ -R_\alpha^{cl}&\alpha\text{ is a boundary arrow in a clockwise face}.\end{cases}\end{align*}$$
$$\begin{align*}\partial(\alpha)=\begin{cases}R_\alpha^{cc}-R_\alpha^{cl}&\alpha\text{ is an internal arrow}\\ R_\alpha^{cc}&\alpha\text{ is a boundary arrow in a counter-clockwise face}\\ -R_\alpha^{cl}&\alpha\text{ is a boundary arrow in a clockwise face}.\end{cases}\end{align*}$$
For a path
![]() $p=\alpha _m\dots \alpha _1$
, we define
$p=\alpha _m\dots \alpha _1$
, we define
and extend by linearity and continuity to obtain a map
![]() $\Delta _\alpha :\mathbb C\langle \langle Q\rangle \rangle \to {\mathcal A}\otimes T_1\otimes {\mathcal A}$
. Then we define
$\Delta _\alpha :\mathbb C\langle \langle Q\rangle \rangle \to {\mathcal A}\otimes T_1\otimes {\mathcal A}$
. Then we define
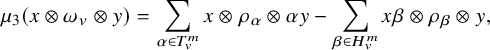 $$\begin{align*}\mu_3(x\otimes\omega_v\otimes y)=\sum_{\alpha\in T_v^{m}}x\otimes\rho_\alpha\otimes \alpha y-\sum_{\beta\in H_v^{m}}x\beta\otimes\rho_\beta\otimes y,\end{align*}$$
$$\begin{align*}\mu_3(x\otimes\omega_v\otimes y)=\sum_{\alpha\in T_v^{m}}x\otimes\rho_\alpha\otimes \alpha y-\sum_{\beta\in H_v^{m}}x\beta\otimes\rho_\beta\otimes y,\end{align*}$$
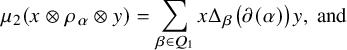 $$\begin{align*}\mu_2(x\otimes\rho_\alpha\otimes y)=\sum_{\beta\in Q_1}x\Delta_\beta\big(\partial(\alpha)\big)y,\text{ and }\end{align*}$$
$$\begin{align*}\mu_2(x\otimes\rho_\alpha\otimes y)=\sum_{\beta\in Q_1}x\Delta_\beta\big(\partial(\alpha)\big)y,\text{ and }\end{align*}$$
Since the tensor products are over
![]() $T_0$
, there is a natural isomorphism
$T_0$
, there is a natural isomorphism
![]() ${\mathcal A}\otimes T_0\otimes {\mathcal A}\cong {\mathcal A}\otimes {\mathcal A}$
. This may be composed with the multiplication map to obtain
${\mathcal A}\otimes T_0\otimes {\mathcal A}\cong {\mathcal A}\otimes {\mathcal A}$
. This may be composed with the multiplication map to obtain
![]() $\mu _0$
.
$\mu _0$
.
The following was shown for Jacobian ice quivers, and completed dimer algebras are special case of these. Nevertheless, the same proof applies in the noncompleted case, so we cite it here without this limitation.
Theorem 7.1 [Reference Pressland46, Theorem 5.6].
If the complex (5) is exact, then
![]() ${\mathcal A}$
is bimodule internally 3-Calabi-Yau with respect to the idempotent given by the sum of all frozen vertex simples.
${\mathcal A}$
is bimodule internally 3-Calabi-Yau with respect to the idempotent given by the sum of all frozen vertex simples.
Our goal is to show that when Q is strongly consistent, the complex (5) is exact. To do this, we will first define a version of (5) which is merely a complex of modules, rather than bimodules, and prove that exactness of this one-sided complex is equivalent to exactness of the two-sided complex (5) in the nondegenerate case. We will then show that the one-sided complex is exact to finish the proof.
Use the quotient map
![]() ${\mathcal A}\to {\mathcal A}/\text {rad}\ {\mathcal A}\cong T_0$
to consider
${\mathcal A}\to {\mathcal A}/\text {rad}\ {\mathcal A}\cong T_0$
to consider
![]() $T_0$
as an
$T_0$
as an
![]() $({\mathcal A},{\mathcal A})$
-bimodule. Using this bimodule structure, we consider the functor
$({\mathcal A},{\mathcal A})$
-bimodule. Using this bimodule structure, we consider the functor
![]() $\mathcal F=-\otimes _{\mathcal A} T_0$
from the category of
$\mathcal F=-\otimes _{\mathcal A} T_0$
from the category of
![]() $({\mathcal A},{\mathcal A})$
-bimodules to itself. We apply this to the complex (5) and note that
$({\mathcal A},{\mathcal A})$
-bimodules to itself. We apply this to the complex (5) and note that
![]() $T_i\otimes {\mathcal A}\otimes _{\mathcal A} T_0\cong T_i$
and
$T_i\otimes {\mathcal A}\otimes _{\mathcal A} T_0\cong T_i$
and
![]() ${\mathcal A}\otimes _{T_0}T_0\cong {\mathcal A}$
to get the complex
${\mathcal A}\otimes _{T_0}T_0\cong {\mathcal A}$
to get the complex
We forget the right
![]() ${\mathcal A}$
-module structure and treat this as a complex of left
${\mathcal A}$
-module structure and treat this as a complex of left
![]() ${\mathcal A}$
-modules, which we refer to as the one-sided complex.
${\mathcal A}$
-modules, which we refer to as the one-sided complex.
Remark 7.2. The two-sided sequence (5) is indeed a complex of
![]() ${\mathcal A}$
-modules, which is exact in degrees 1, 0, -1. This can be seen as follows. In the noncompleted case
${\mathcal A}$
-modules, which is exact in degrees 1, 0, -1. This can be seen as follows. In the noncompleted case
![]() ${\mathcal A} = {\mathcal A}_Q$
, this follows by the work of Ginzburg [Reference Ginzburg30, Proposition 5.1.9 and Theorem 5.3.1]; see also the exposition in [Reference Broomhead11, Section 7.1]. In the completed case
${\mathcal A} = {\mathcal A}_Q$
, this follows by the work of Ginzburg [Reference Ginzburg30, Proposition 5.1.9 and Theorem 5.3.1]; see also the exposition in [Reference Broomhead11, Section 7.1]. In the completed case
![]() ${\mathcal A} = \widehat {\mathcal A}_Q$
, this statement appears in [Reference Pressland46, Lemma 5.5]; however, as noted by Pressland [Reference Pressland45], there is a gap in the proof. Namely, the citation of the results by Butler and King for the exactness in degrees 1, 0, -1 applies only for the noncompleted algebra. Instead, following Pressland [Reference Pressland45], we can deduce exactness of the one-sided sequence (6) from [Reference Bakke Buan, Iyama, Reiten and Smith12, Proposition 3.3] in degrees 1, 0, -1. Then the same holds for the two-sided complex by taking inverse limits as in the proof of [Reference Pressland49, Lemma 4.7], which works degree by degree.
${\mathcal A} = \widehat {\mathcal A}_Q$
, this statement appears in [Reference Pressland46, Lemma 5.5]; however, as noted by Pressland [Reference Pressland45], there is a gap in the proof. Namely, the citation of the results by Butler and King for the exactness in degrees 1, 0, -1 applies only for the noncompleted algebra. Instead, following Pressland [Reference Pressland45], we can deduce exactness of the one-sided sequence (6) from [Reference Bakke Buan, Iyama, Reiten and Smith12, Proposition 3.3] in degrees 1, 0, -1. Then the same holds for the two-sided complex by taking inverse limits as in the proof of [Reference Pressland49, Lemma 4.7], which works degree by degree.
We would like to show exactness of the one-sided complex in degrees
![]() $-3$
and
$-3$
and
![]() $-2$
, so we explicitly write the maps
$-2$
, so we explicitly write the maps
![]() $\mathcal F(\mu _3)$
and
$\mathcal F(\mu _3)$
and
![]() $\mathcal F(\mu _2)$
.
$\mathcal F(\mu _2)$
.
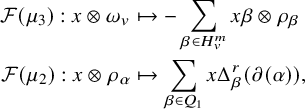 $$ \begin{align*} \mathcal F(\mu_3):x\otimes\omega_v&\mapsto -\sum_{\beta\in H_v^m}x\beta\otimes\rho_\beta\\ \mathcal F(\mu_2):x\otimes\rho_\alpha&\mapsto\sum_{\beta\in Q_1}x\Delta_\beta^r(\partial(\alpha)), \end{align*} $$
$$ \begin{align*} \mathcal F(\mu_3):x\otimes\omega_v&\mapsto -\sum_{\beta\in H_v^m}x\beta\otimes\rho_\beta\\ \mathcal F(\mu_2):x\otimes\rho_\alpha&\mapsto\sum_{\beta\in Q_1}x\Delta_\beta^r(\partial(\alpha)), \end{align*} $$
where, for
![]() $p=\alpha _m\dots \alpha _1$
,
$p=\alpha _m\dots \alpha _1$
,
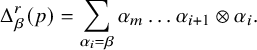 $$\begin{align*}\Delta_\beta^r(p)=\sum_{\alpha_i=\beta}\alpha_m\dots\alpha_{i+1}\otimes\alpha_i.\end{align*}$$
$$\begin{align*}\Delta_\beta^r(p)=\sum_{\alpha_i=\beta}\alpha_m\dots\alpha_{i+1}\otimes\alpha_i.\end{align*}$$
We now do some calculations for
![]() $\mu _3$
.
$\mu _3$
.
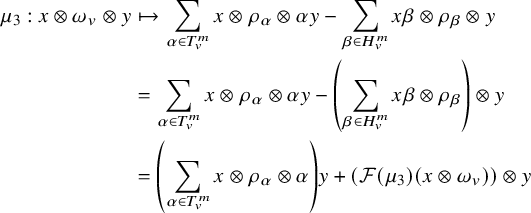 $$ \begin{align*} \mu_3:x\otimes\omega_v\otimes y&\mapsto \sum_{\alpha\in T_v^{m}}x\otimes\rho_\alpha\otimes\alpha y-\sum_{\beta\in H_v^{m}}x\beta\otimes\rho_\beta\otimes y\\ &=\sum_{\alpha\in T_v^{m}}x\otimes\rho_\alpha\otimes\alpha y-\left(\sum_{\beta\in H_v^m}x\beta\otimes\rho_\beta\right)\otimes y\\ &=\left(\sum_{\alpha\in T_v^{m}}x\otimes\rho_\alpha\otimes\alpha\right)y+(\mathcal F(\mu_3)(x\otimes\omega_v))\otimes y \end{align*} $$
$$ \begin{align*} \mu_3:x\otimes\omega_v\otimes y&\mapsto \sum_{\alpha\in T_v^{m}}x\otimes\rho_\alpha\otimes\alpha y-\sum_{\beta\in H_v^{m}}x\beta\otimes\rho_\beta\otimes y\\ &=\sum_{\alpha\in T_v^{m}}x\otimes\rho_\alpha\otimes\alpha y-\left(\sum_{\beta\in H_v^m}x\beta\otimes\rho_\beta\right)\otimes y\\ &=\left(\sum_{\alpha\in T_v^{m}}x\otimes\rho_\alpha\otimes\alpha\right)y+(\mathcal F(\mu_3)(x\otimes\omega_v))\otimes y \end{align*} $$
We perform a similar calculation for
![]() $\mu _2$
.
$\mu _2$
.
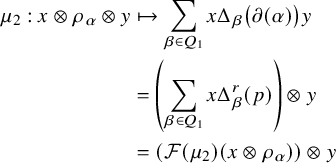 $$ \begin{align*} \mu_2:x\otimes\rho_\alpha\otimes y&\mapsto\sum_{\beta\in Q_1}x\Delta_\beta\big(\partial(\alpha)\big)y\\ &=\left(\sum_{\beta\in Q_1}x\Delta_\beta^r(p)\right)\otimes y\\ &=(\mathcal F(\mu_2)(x\otimes\rho_\alpha))\otimes y \end{align*} $$
$$ \begin{align*} \mu_2:x\otimes\rho_\alpha\otimes y&\mapsto\sum_{\beta\in Q_1}x\Delta_\beta\big(\partial(\alpha)\big)y\\ &=\left(\sum_{\beta\in Q_1}x\Delta_\beta^r(p)\right)\otimes y\\ &=(\mathcal F(\mu_2)(x\otimes\rho_\alpha))\otimes y \end{align*} $$
We have shown that, for
![]() $j\in \{2,3\}$
, we have
$j\in \{2,3\}$
, we have
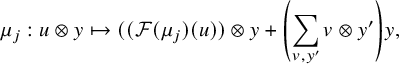 $$ \begin{align}\mu_j:u\otimes y\mapsto((\mathcal F(\mu_j)(u))\otimes y+\left(\sum_{v,y'}v\otimes y'\right)y,\end{align} $$
$$ \begin{align}\mu_j:u\otimes y\mapsto((\mathcal F(\mu_j)(u))\otimes y+\left(\sum_{v,y'}v\otimes y'\right)y,\end{align} $$
where
-
• u is in either
 ${\mathcal A}\otimes T_3$
(if
${\mathcal A}\otimes T_3$
(if
 $j=3$
) or
$j=3$
) or
 ${\mathcal A}\otimes T_2$
(if
${\mathcal A}\otimes T_2$
(if
 $j=2$
),
$j=2$
), -
• v ranges across some elements of
 ${\mathcal A}\otimes T_2$
(if
${\mathcal A}\otimes T_2$
(if
 $j=3$
) or
$j=3$
) or
 ${\mathcal A}\otimes T_1$
(if
${\mathcal A}\otimes T_1$
(if
 $j=2$
), and
$j=2$
), and -
•
 $y'$
ranges across some arrows of
$y'$
ranges across some arrows of
 ${\mathcal A}$
.
${\mathcal A}$
.
7.2 Proving 3-Calabi-Yau property for strongly consistent models
We now show that exactness of the bimodule complex (5) is equivalent to exactness of the one-sided complex (6) when Q is strongly consistent. We will then show that the one-sided complex is exact, and hence that the completed dimer algebra is bimodule internally 3-Calabi-Yau with respect to its boundary idempotent.
We consider the bimodules
![]() $T_i$
to be
$T_i$
to be
![]() $\mathbb Z$
-graded as follows. All elements of
$\mathbb Z$
-graded as follows. All elements of
![]() $T_3$
and
$T_3$
and
![]() $T_0$
have degree 0. An element
$T_0$
have degree 0. An element
![]() $\rho _\alpha $
in
$\rho _\alpha $
in
![]() $T_2$
corresponding to an arrow
$T_2$
corresponding to an arrow
![]() $\alpha \in Q$
is given the negative of the grading of
$\alpha \in Q$
is given the negative of the grading of
![]() $\alpha $
in Q. An element
$\alpha $
in Q. An element
![]() $\alpha $
in
$\alpha $
in
![]() $T_1$
corresponding to an arrow
$T_1$
corresponding to an arrow
![]() $\alpha \in Q$
is given the grading of
$\alpha \in Q$
is given the grading of
![]() $\alpha $
in Q.
$\alpha $
in Q.
We extend the grading on
![]() ${\mathcal A}$
given by Lemma 6.11 with the gradings on
${\mathcal A}$
given by Lemma 6.11 with the gradings on
![]() $T_i$
described above to a
$T_i$
described above to a
![]() $\mathbb Z$
-grading on the bimodule complex
$\mathbb Z$
-grading on the bimodule complex
![]() ${\mathcal A}\otimes T_*\otimes {\mathcal A}$
by adding the grading in each of the three positions.
${\mathcal A}\otimes T_*\otimes {\mathcal A}$
by adding the grading in each of the three positions.
We remark that the grading on
![]() ${\mathcal A}\otimes T_2\otimes {\mathcal A}$
is not positive. The minimum possible degree of an element of
${\mathcal A}\otimes T_2\otimes {\mathcal A}$
is not positive. The minimum possible degree of an element of
![]() ${\mathcal A}\otimes T_2\otimes {\mathcal A}$
is
${\mathcal A}\otimes T_2\otimes {\mathcal A}$
is
![]() $-m$
, where m is the maximum possible degree of an arrow of
$-m$
, where m is the maximum possible degree of an arrow of
![]() ${\mathcal A}$
. Moreover, every face-path has degree equal to the number of perfect matchings on Q.
${\mathcal A}$
. Moreover, every face-path has degree equal to the number of perfect matchings on Q.
Lemma 7.3. The maps
![]() $\mu _3$
and
$\mu _3$
and
![]() $\mu _2$
are maps of graded bimodules. In other words, they map homogeneous elements to homogeneous elements.
$\mu _2$
are maps of graded bimodules. In other words, they map homogeneous elements to homogeneous elements.
Proof. First, we consider
![]() $\mu _3$
. Any summand of
$\mu _3$
. Any summand of
![]() $\mu _3(x\otimes \omega _v\otimes y)$
is of the form
$\mu _3(x\otimes \omega _v\otimes y)$
is of the form
![]() $x\otimes \rho _\alpha \otimes \alpha y$
or
$x\otimes \rho _\alpha \otimes \alpha y$
or
![]() $x\alpha \otimes \rho _\alpha \otimes y$
for some arrow
$x\alpha \otimes \rho _\alpha \otimes y$
for some arrow
![]() $\alpha $
. The
$\alpha $
. The
![]() $\alpha $
on the left or right summands adds some number m to the degree, and the
$\alpha $
on the left or right summands adds some number m to the degree, and the
![]() $\rho _\alpha $
in the middle subtracts that same degree, so the degree of
$\rho _\alpha $
in the middle subtracts that same degree, so the degree of
![]() $\mu _3(x\otimes \omega _v\otimes y)$
is the same as the degree of
$\mu _3(x\otimes \omega _v\otimes y)$
is the same as the degree of
![]() $x\otimes \omega _v\otimes y$
.
$x\otimes \omega _v\otimes y$
.
We now consider
![]() $\mu _2$
. Any summand of
$\mu _2$
. Any summand of
![]() $\mu _2(x\otimes \rho _\alpha \otimes y)$
is of the form
$\mu _2(x\otimes \rho _\alpha \otimes y)$
is of the form
![]() $xR"\otimes \beta \otimes R'y$
for some arrow
$xR"\otimes \beta \otimes R'y$
for some arrow
![]() $\beta $
and some paths
$\beta $
and some paths
![]() $R'$
and
$R'$
and
![]() $R"$
such that
$R"$
such that
![]() $R"\beta R'$
is some return path
$R"\beta R'$
is some return path
![]() $R_\alpha $
of
$R_\alpha $
of
![]() $\alpha $
. Compared to
$\alpha $
. Compared to
![]() $x\otimes \rho _\alpha \otimes y$
, we are replacing the (negative) grading of middle term
$x\otimes \rho _\alpha \otimes y$
, we are replacing the (negative) grading of middle term
![]() $\rho _\alpha $
with the (positive) grading of the path
$\rho _\alpha $
with the (positive) grading of the path
![]() $R_\alpha =R"\beta R'$
. The result is that the grading has increased by the grading of
$R_\alpha =R"\beta R'$
. The result is that the grading has increased by the grading of
![]() $\alpha R_\alpha $
in
$\alpha R_\alpha $
in
![]() ${\mathcal A}$
. This is a face-path, and all face-paths have the same grading. It follows that
${\mathcal A}$
. This is a face-path, and all face-paths have the same grading. It follows that
![]() $\mu _2$
has the effect of increasing the grading of a homogeneous element by the grading of a face-path in
$\mu _2$
has the effect of increasing the grading of a homogeneous element by the grading of a face-path in
![]() ${\mathcal A}$
.
${\mathcal A}$
.
Theorem 7.4 [Reference Pressland49, Lemma 4.7].
If the one-sided complex (6) is exact for
![]() ${\mathcal A}=\widehat A_Q$
, then the two-sided complex (5) is exact for
${\mathcal A}=\widehat A_Q$
, then the two-sided complex (5) is exact for
![]() ${\mathcal A}=\widehat A_Q$
.
${\mathcal A}=\widehat A_Q$
.
To show a version of Theorem 7.4 when
![]() ${\mathcal A}$
is the noncompleted dimer algebra
${\mathcal A}$
is the noncompleted dimer algebra
![]() $A_Q$
, we assume in addition nondegeneracy.
$A_Q$
, we assume in addition nondegeneracy.
Proposition 7.5. Suppose Q is strongly consistent. If the one-sided complex (6) is exact, then the two-sided complex (5) is exact.
Proof. We follow the proof of [Reference Broomhead11, Proposition 7.5]. Suppose the one-sided complex (6) is exact. We know by Remark 7.2 that the bimodule complex (5) is exact in every degree except for, possibly,
![]() $-3$
and
$-3$
and
![]() $-2$
. It remains to show that
$-2$
. It remains to show that
![]() $\ker \mu _2\subseteq \text {im}\mu _3$
and
$\ker \mu _2\subseteq \text {im}\mu _3$
and
![]() $\ker \mu _3\subseteq \text {im}\mu _4=0$
, where
$\ker \mu _3\subseteq \text {im}\mu _4=0$
, where
![]() $T_4:=0$
and
$T_4:=0$
and
![]() $\mu _4:T_4\to {\mathcal A}\otimes T_3\otimes {\mathcal A}$
is the zero map.
$\mu _4:T_4\to {\mathcal A}\otimes T_3\otimes {\mathcal A}$
is the zero map.
Let
![]() $j\in \{3,2\}$
. Let
$j\in \{3,2\}$
. Let
![]() $\phi _0$
be a nonzero element of
$\phi _0$
be a nonzero element of
![]() ${\mathcal A}\otimes T_j\otimes {\mathcal A}$
which is in the kernel of
${\mathcal A}\otimes T_j\otimes {\mathcal A}$
which is in the kernel of
![]() $\mu _j$
. We show that
$\mu _j$
. We show that
![]() $\phi _0$
is in the image of
$\phi _0$
is in the image of
![]() $\mu _{j+1}$
. Since the grading is respected by the map
$\mu _{j+1}$
. Since the grading is respected by the map
![]() $\mu _j$
(Lemma 7.3), we may assume that
$\mu _j$
(Lemma 7.3), we may assume that
![]() $\phi _0$
is homogeneous of some grade d. We may organize the terms of
$\phi _0$
is homogeneous of some grade d. We may organize the terms of
![]() $\phi _0$
by the degree of the term in third position.
$\phi _0$
by the degree of the term in third position.
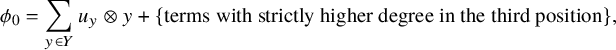 $$\begin{align*}\phi_0=\sum_{y\in Y}u_y\otimes y+\{\text{terms with strictly higher degree in the third position}\},\end{align*}$$
$$\begin{align*}\phi_0=\sum_{y\in Y}u_y\otimes y+\{\text{terms with strictly higher degree in the third position}\},\end{align*}$$
where Y is a nonempty linearly independent set of monomials in the graded piece
![]() ${\mathcal A}^{(d_0)}$
with least possible degree, and
${\mathcal A}^{(d_0)}$
with least possible degree, and
![]() $u_y\in ({\mathcal A}\otimes T_j)^{(d-d_0)}$
. Applying the map
$u_y\in ({\mathcal A}\otimes T_j)^{(d-d_0)}$
. Applying the map
![]() $\mu _j$
and using (7) and Lemma 6.11, we see that
$\mu _j$
and using (7) and Lemma 6.11, we see that
![]() $\mu _j(\phi _0)=0$
is equivalent to the condition
$\mu _j(\phi _0)=0$
is equivalent to the condition
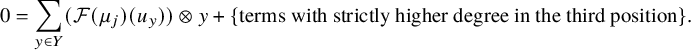 $$\begin{align*}0=\sum_{y\in Y}(\mathcal F(\mu_j)(u_y))\otimes y+\{\text{terms with strictly higher degree in the third position}\}. \end{align*}$$
$$\begin{align*}0=\sum_{y\in Y}(\mathcal F(\mu_j)(u_y))\otimes y+\{\text{terms with strictly higher degree in the third position}\}. \end{align*}$$
Since the monomials
![]() $y\in Y$
are linearly independent, this implies that for all
$y\in Y$
are linearly independent, this implies that for all
![]() $y\in Y$
, we have
$y\in Y$
, we have
![]() ${\mathcal F(\mu _j)(u_y)=0}$
. Using the exactness of the one-sided complex, we conclude that there exist elements
${\mathcal F(\mu _j)(u_y)=0}$
. Using the exactness of the one-sided complex, we conclude that there exist elements
![]() $v_y\in ({\mathcal A}\otimes T_{j+1})^{(d-d_0)}$
such that
$v_y\in ({\mathcal A}\otimes T_{j+1})^{(d-d_0)}$
such that
![]() $\mathcal F(\mu _j)(v_y)=u_y$
for each
$\mathcal F(\mu _j)(v_y)=u_y$
for each
![]() $y\in Y$
. We construct an element
$y\in Y$
. We construct an element
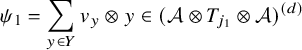 $$\begin{align*}\psi_1=\sum_{y\in Y}v_y\otimes y\in({\mathcal A}\otimes T_{j_1}\otimes{\mathcal A})^{(d)}\end{align*}$$
$$\begin{align*}\psi_1=\sum_{y\in Y}v_y\otimes y\in({\mathcal A}\otimes T_{j_1}\otimes{\mathcal A})^{(d)}\end{align*}$$
and apply
![]() $\mu _{j+1}$
to get
$\mu _{j+1}$
to get
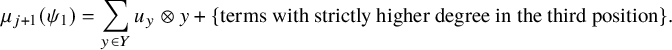 $$\begin{align*}\mu_{j+1}(\psi_1)=\sum_{y\in Y}u_y\otimes y+\{\text{terms with strictly higher degree in the third position}\}.\end{align*}$$
$$\begin{align*}\mu_{j+1}(\psi_1)=\sum_{y\in Y}u_y\otimes y+\{\text{terms with strictly higher degree in the third position}\}.\end{align*}$$
We observe that
![]() $\phi _1:=\phi _0-\mu _{j+1}(\psi _1)$
is in the kernel of
$\phi _1:=\phi _0-\mu _{j+1}(\psi _1)$
is in the kernel of
![]() $\mu _{j}$
and that its terms have strictly higher degree in the third position than
$\mu _{j}$
and that its terms have strictly higher degree in the third position than
![]() $\phi _0$
. We iterate the procedure, noting that the degree in the third position is strictly increasing but is bounded above by the total degree d if
$\phi _0$
. We iterate the procedure, noting that the degree in the third position is strictly increasing but is bounded above by the total degree d if
![]() $j=3$
, and by d plus the maximum degree of an arrow of
$j=3$
, and by d plus the maximum degree of an arrow of
![]() ${\mathcal A}$
if
${\mathcal A}$
if
![]() $j=2$
. Hence, after a finite number of iterations, we get
$j=2$
. Hence, after a finite number of iterations, we get
![]() $\phi _r=\phi _0-\sum _{i=1}^r\mu _{j+1}(\psi _i)=0$
. We conclude that
$\phi _r=\phi _0-\sum _{i=1}^r\mu _{j+1}(\psi _i)=0$
. We conclude that
![]() $\phi _0=\mu _{j+1}(\sum _{i=1}^r\psi _i)$
and that the complex (5) is exact at
$\phi _0=\mu _{j+1}(\sum _{i=1}^r\psi _i)$
and that the complex (5) is exact at
![]() ${\mathcal A}\otimes T_j\otimes {\mathcal A}$
.
${\mathcal A}\otimes T_j\otimes {\mathcal A}$
.
We now know that in order to show exactness of the bimodule complex (5), it suffices to show exactness of the one-sided complex (6). We follow [Reference Pressland48, §3] and consider exactness of (6) vertex by vertex. If v is a vertex, let
![]() $S_v:=e_vT_0e_v$
be the simple module at v.
$S_v:=e_vT_0e_v$
be the simple module at v.
We may consider the complex (6) as a complex of
![]() $({\mathcal A},T_0)$
-bimodules, which we denote by
$({\mathcal A},T_0)$
-bimodules, which we denote by
![]() $\mathbf P^1$
. Since
$\mathbf P^1$
. Since
![]() $T_0=\oplus _{v\in Q_0}S_v$
, we have
$T_0=\oplus _{v\in Q_0}S_v$
, we have
as a complex of left
![]() ${\mathcal A}$
-modules. Hence, in order to show exactness of the complex of left
${\mathcal A}$
-modules. Hence, in order to show exactness of the complex of left
![]() ${\mathcal A}$
-modules (6), it suffices to show that for any vertex v of Q, the complex of left
${\mathcal A}$
-modules (6), it suffices to show that for any vertex v of Q, the complex of left
![]() ${\mathcal A}$
-modules
${\mathcal A}$
-modules
![]() $\mathbf P^1e_v$
is exact. We rewrite this complex
$\mathbf P^1e_v$
is exact. We rewrite this complex
![]() $\mathbf P^1e_v$
as
$\mathbf P^1e_v$
as
where the spaces
![]() $X_i$
are defined as
$X_i$
are defined as
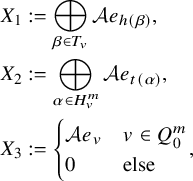 $$ \begin{align*} X_1&:=\bigoplus_{\beta\in T_v}{\mathcal A} e_{h(\beta)},\\ X_2&:=\bigoplus_{\alpha\in H_v^m}{\mathcal A} e_{t(\alpha)},\\ X_3&:=\begin{cases} {\mathcal A} e_v&v\in Q_0^m\\ 0&\text{else}\end{cases}, \end{align*} $$
$$ \begin{align*} X_1&:=\bigoplus_{\beta\in T_v}{\mathcal A} e_{h(\beta)},\\ X_2&:=\bigoplus_{\alpha\in H_v^m}{\mathcal A} e_{t(\alpha)},\\ X_3&:=\begin{cases} {\mathcal A} e_v&v\in Q_0^m\\ 0&\text{else}\end{cases}, \end{align*} $$
and the maps
![]() $\bar \mu _j$
are induced by
$\bar \mu _j$
are induced by
![]() $\mathcal F(\mu _j)$
under the relevant isomorphisms. We will make explicit the maps
$\mathcal F(\mu _j)$
under the relevant isomorphisms. We will make explicit the maps
![]() $\bar \mu _3$
and
$\bar \mu _3$
and
![]() $\bar \mu _2$
after introducing some notation. We write a general element x of
$\bar \mu _2$
after introducing some notation. We write a general element x of
![]() $\oplus _{\alpha \in H_v^{m}}{\mathcal A} e_{t(\alpha )}$
as
$\oplus _{\alpha \in H_v^{m}}{\mathcal A} e_{t(\alpha )}$
as
![]() $x=\sum _{\alpha \in H_v^{m}}x_\alpha \otimes [\alpha ]$
, where for any
$x=\sum _{\alpha \in H_v^{m}}x_\alpha \otimes [\alpha ]$
, where for any
![]() $\alpha \in H_v^{m}$
, the summand
$\alpha \in H_v^{m}$
, the summand
![]() $x_\alpha \otimes [\alpha ]$
refers to the element
$x_\alpha \otimes [\alpha ]$
refers to the element
![]() $x_\alpha \in {\mathcal A} e_{t(\alpha )}$
in the summand of
$x_\alpha \in {\mathcal A} e_{t(\alpha )}$
in the summand of
![]() $\oplus _{\alpha \in H_v^{m}}{\mathcal A} e_{t(\alpha )}$
indexed by
$\oplus _{\alpha \in H_v^{m}}{\mathcal A} e_{t(\alpha )}$
indexed by
![]() $\alpha $
. Similarly, a general element of
$\alpha $
. Similarly, a general element of
![]() $\oplus _{\beta \in T_v}{\mathcal A} e_{h(\beta )}$
will be written as
$\oplus _{\beta \in T_v}{\mathcal A} e_{h(\beta )}$
will be written as
![]() $y=\sum _{\beta \in T_v}y_\beta \otimes [\beta ]$
.
$y=\sum _{\beta \in T_v}y_\beta \otimes [\beta ]$
.
We define the right derivative
![]() $\partial _\beta ^r$
with respect to
$\partial _\beta ^r$
with respect to
![]() $\beta $
on a path
$\beta $
on a path
![]() $\gamma _k\dots \gamma _1$
by
$\gamma _k\dots \gamma _1$
by
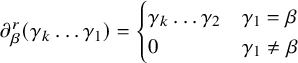 $$\begin{align*}\partial_\beta^r(\gamma_k\dots\gamma_1)=\begin{cases}\gamma_k\dots\gamma_2&\gamma_1=\beta\\ 0&\gamma_1\neq\beta\end{cases}\end{align*}$$
$$\begin{align*}\partial_\beta^r(\gamma_k\dots\gamma_1)=\begin{cases}\gamma_k\dots\gamma_2&\gamma_1=\beta\\ 0&\gamma_1\neq\beta\end{cases}\end{align*}$$
and extend linearly and continuously. Similarly, there is a left derivative, defined on paths by
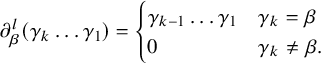 $$\begin{align*}\partial_\beta^l(\gamma_k\dots\gamma_1)= \begin{cases}\gamma_{k-1}\dots\gamma_1&\gamma_k=\beta\\0&\gamma_k\neq\beta.\end{cases}\end{align*}$$
$$\begin{align*}\partial_\beta^l(\gamma_k\dots\gamma_1)= \begin{cases}\gamma_{k-1}\dots\gamma_1&\gamma_k=\beta\\0&\gamma_k\neq\beta.\end{cases}\end{align*}$$
Given two arrows
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
of Q, we observe that
$\beta $
of Q, we observe that
We now calculate:
 $$ \begin{align*} \bar\mu_2(x)&=\sum_{\beta\in T_v}\left(\sum_{\alpha\in H_v^m}x_\alpha\partial_\beta^r(\partial(\alpha))\right)\otimes[\beta]\\ \bar\mu_3(x)&=\sum_{\alpha\in H_v^{m}}x\alpha\otimes[\alpha]. \end{align*} $$
$$ \begin{align*} \bar\mu_2(x)&=\sum_{\beta\in T_v}\left(\sum_{\alpha\in H_v^m}x_\alpha\partial_\beta^r(\partial(\alpha))\right)\otimes[\beta]\\ \bar\mu_3(x)&=\sum_{\alpha\in H_v^{m}}x\alpha\otimes[\alpha]. \end{align*} $$
We now finally prove the main result of this section after citing the disk version proven by Pressland. Note that in [Reference Pressland48], dimer models on a disk are required to have at least three boundary vertices to avoid degenerate cases. This condition is not used in the cited result (see [Reference Pressland48, Remark 2.2]), so we cite it without this limitation. The results and proofs of [Reference Pressland46, Theorem 5.6] and [Reference Pressland48, Theorem 3.7] are stated only for completed Jacobian algebras, but work also for their noncompleted variants. Hence, we cite this result for the completed and noncompleted algebras simultaneously.
Theorem 7.6 [Reference Pressland48, Theorem 3.7], [Reference Pressland46, Theorem 5.6].
If Q is a path-consistent dimer model on a disk, then the sequence (8) is exact for all v, and hence,
![]() ${\mathcal A}$
is bimodule internally 3-Calabi-Yau with respect to its boundary idempotent.
${\mathcal A}$
is bimodule internally 3-Calabi-Yau with respect to its boundary idempotent.
In fact, Pressland’s proof of Theorem 7.6 works in the general setting, with the stipulation that all computations must be performed as a sum over homotopy classes. We give a shorter proof here, which uses Pressland’s result for disk models as well as the theory of dimer submodels developed in Section 5.
Theorem 7.7. Let Q be a strongly consistent finite dimer model. Then
![]() $A_Q$
and
$A_Q$
and
![]() $\widehat A_Q$
are bimodule internally 3-Calabi-Yau with respect to their boundary idempotents.
$\widehat A_Q$
are bimodule internally 3-Calabi-Yau with respect to their boundary idempotents.
Proof. By Theorem 7.1, it suffices to prove exactness of the two-sided complex (5). By Proposition 7.5 or Theorem 7.4 (depending on whether
![]() ${\mathcal A}=A_Q$
or
${\mathcal A}=A_Q$
or
![]() ${\mathcal A}=\widehat A_Q$
), it suffices to prove exactness of the one-sided complex (6). As argued in the text following Proposition 7.5, we may prove this by showing that the complex (8) is exact for any choice of
${\mathcal A}=\widehat A_Q$
), it suffices to prove exactness of the one-sided complex (6). As argued in the text following Proposition 7.5, we may prove this by showing that the complex (8) is exact for any choice of
![]() $v\in Q_0$
. We need only show that
$v\in Q_0$
. We need only show that
![]() $\bar \mu _3$
is injective and that
$\bar \mu _3$
is injective and that
![]() $\ker \bar \mu _2\subseteq \text {im}\ \bar \mu _3$
.
$\ker \bar \mu _2\subseteq \text {im}\ \bar \mu _3$
.
First, we show injectivity of
![]() $\bar \mu _3$
. If v is boundary, then this is trivial, so suppose
$\bar \mu _3$
. If v is boundary, then this is trivial, so suppose
![]() $v\in Q_0^{m}$
. Suppose there is some nonzero
$v\in Q_0^{m}$
. Suppose there is some nonzero
![]() $x\in {\mathcal A} e_v$
with
$x\in {\mathcal A} e_v$
with
![]() $0=\bar \mu _3(x)=\sum _{\alpha \in H_v^{m}}x\alpha \otimes [\alpha ]$
. Write
$0=\bar \mu _3(x)=\sum _{\alpha \in H_v^{m}}x\alpha \otimes [\alpha ]$
. Write
![]() $x=\sum _Cx_C$
, where the sum is over homotopy classes of paths in Q starting at v and
$x=\sum _Cx_C$
, where the sum is over homotopy classes of paths in Q starting at v and
![]() $x_C=\sum _{m=0}^\infty a_{C,m}r_Cf^m$
, where
$x_C=\sum _{m=0}^\infty a_{C,m}r_Cf^m$
, where
![]() $r_C$
is a minimal path in the homotopy class C and
$r_C$
is a minimal path in the homotopy class C and
![]() $a_{C,m}\in \mathbb C$
.
$a_{C,m}\in \mathbb C$
.
If C and
![]() $C'$
are different homotopy classes, then
$C'$
are different homotopy classes, then
![]() $C\alpha $
and
$C\alpha $
and
![]() $C'\alpha $
are different homotopy classes for any arrow
$C'\alpha $
are different homotopy classes for any arrow
![]() $\alpha $
. In particular, the summands of
$\alpha $
. In particular, the summands of
![]() $\bar \mu _3(x_C)$
and
$\bar \mu _3(x_C)$
and
![]() $\bar \mu _3(x_{C'})$
corresponding to each arrow
$\bar \mu _3(x_{C'})$
corresponding to each arrow
![]() $\alpha \in H_v^{m}$
are in different homotopy classes. Since
$\alpha \in H_v^{m}$
are in different homotopy classes. Since
![]() $\bar \mu _3(x)=0$
, this means that
$\bar \mu _3(x)=0$
, this means that
![]() $\bar \mu _3(x_C)=0$
for all homotopy classes C. Since
$\bar \mu _3(x_C)=0$
for all homotopy classes C. Since
![]() $x\neq 0$
, we may choose a homotopy class C and
$x\neq 0$
, we may choose a homotopy class C and
![]() $m\geq 0$
such that
$m\geq 0$
such that
![]() $a_{C,m}\neq 0$
. Then
$a_{C,m}\neq 0$
. Then
![]() $0=\bar \mu _3(x_C)=\sum _{\alpha \in H_v^{m}}x_C\alpha \otimes [\alpha ]$
. Then
$0=\bar \mu _3(x_C)=\sum _{\alpha \in H_v^{m}}x_C\alpha \otimes [\alpha ]$
. Then
![]() $0=x_C\alpha =\sum _{m=0}^\infty a_{C,m}r_C\alpha f^m$
for all
$0=x_C\alpha =\sum _{m=0}^\infty a_{C,m}r_C\alpha f^m$
for all
![]() $\alpha \in H_v^{m}$
. Hence,
$\alpha \in H_v^{m}$
. Hence,
![]() $a_{C,m}=0$
for all
$a_{C,m}=0$
for all
![]() $m\geq 0$
(if
$m\geq 0$
(if
![]() ${\mathcal A}=A_Q$
, this is immediate by cancellativity, and if
${\mathcal A}=A_Q$
, this is immediate by cancellativity, and if
![]() ${\mathcal A}=\widehat A_Q$
, this follows from Lemma 6.12) and we have
${\mathcal A}=\widehat A_Q$
, this follows from Lemma 6.12) and we have
![]() $x_C=0$
. This contradicts our choice of C and completes the proof of injectivity of
$x_C=0$
. This contradicts our choice of C and completes the proof of injectivity of
![]() $\bar \mu _3$
.
$\bar \mu _3$
.
We now prove that the image of
![]() $\bar \mu _3$
contains the kernel of
$\bar \mu _3$
contains the kernel of
![]() $\bar \mu _2$
. Take a nonzero element
$\bar \mu _2$
. Take a nonzero element
![]() $x=\sum _Cx_C$
of
$x=\sum _Cx_C$
of
![]() $\ker \bar \mu _2$
, where the sum is over homotopy classes of paths in Q starting at the tail of some arrow
$\ker \bar \mu _2$
, where the sum is over homotopy classes of paths in Q starting at the tail of some arrow
![]() $\alpha \in H_v^{m}$
and
$\alpha \in H_v^{m}$
and
![]() $x_C=\sum _{\alpha \in H_v^{m}}\left (a_{C,\alpha ,m}r_Cf^m\otimes [\alpha ]\right )$
, where
$x_C=\sum _{\alpha \in H_v^{m}}\left (a_{C,\alpha ,m}r_Cf^m\otimes [\alpha ]\right )$
, where
![]() $r_C$
is a minimal path in Q homotopic to C and
$r_C$
is a minimal path in Q homotopic to C and
![]() $a_{C,\alpha ,m}$
are some coefficients in
$a_{C,\alpha ,m}$
are some coefficients in
![]() $\mathbb C$
. We wish to find
$\mathbb C$
. We wish to find
![]() $y\in X_3$
such that
$y\in X_3$
such that
![]() $\bar \mu _3(y)=x$
. It suffices to find
$\bar \mu _3(y)=x$
. It suffices to find
![]() $y_C$
for each homotopy class C with
$y_C$
for each homotopy class C with
![]() $\bar \mu _3(y_C)=x_C$
(note that paths in
$\bar \mu _3(y_C)=x_C$
(note that paths in
![]() $y_C$
will not be in the homotopy class C), so fix a homotopy class C. Pick a vertex
$y_C$
will not be in the homotopy class C), so fix a homotopy class C. Pick a vertex
![]() $\tilde v$
of
$\tilde v$
of
![]() $\widetilde Q$
corresponding to v. For
$\widetilde Q$
corresponding to v. For
![]() $\alpha \in H_v^{m}$
, let
$\alpha \in H_v^{m}$
, let
![]() $\tilde \alpha $
be the corresponding arrow of
$\tilde \alpha $
be the corresponding arrow of
![]() $\widetilde Q$
ending at
$\widetilde Q$
ending at
![]() $\tilde v$
. Choose a (finite) disk submodel
$\tilde v$
. Choose a (finite) disk submodel
![]() $Q^C$
of
$Q^C$
of
![]() $\widetilde Q$
containing
$\widetilde Q$
containing
![]() $\tilde v$
and a minimal path
$\tilde v$
and a minimal path
![]() $r_{C\alpha }$
in Q homotopic to
$r_{C\alpha }$
in Q homotopic to
![]() $C\alpha $
for each
$C\alpha $
for each
![]() $\alpha \in H_v^{m}$
. Lift each
$\alpha \in H_v^{m}$
. Lift each
![]() $r_{C\alpha }$
to a minimal path
$r_{C\alpha }$
to a minimal path
![]() $\tilde r_{C\alpha }$
beginning at
$\tilde r_{C\alpha }$
beginning at
![]() $t(\tilde \alpha )$
.
$t(\tilde \alpha )$
.
Similarly, lift
![]() $x_C$
to
$x_C$
to
![]() $\tilde x_C:=\sum _{\alpha \in H_v^{m}}(a_{C,\alpha ,m}\tilde r_Cf^m\otimes [\alpha ])$
, where
$\tilde x_C:=\sum _{\alpha \in H_v^{m}}(a_{C,\alpha ,m}\tilde r_Cf^m\otimes [\alpha ])$
, where
![]() $\tilde r_C$
is the lift of
$\tilde r_C$
is the lift of
![]() $r_C$
to
$r_C$
to
![]() $\widetilde Q$
beginning at
$\widetilde Q$
beginning at
![]() $\tilde v$
. We claim that
$\tilde v$
. We claim that
![]() $\tilde x_C$
is in the kernel of the lift
$\tilde x_C$
is in the kernel of the lift
![]() $\widetilde {\bar \mu _2}$
.
$\widetilde {\bar \mu _2}$
.
Choose coefficients
![]() $b_{\beta ,D,m}$
such that
$b_{\beta ,D,m}$
such that
![]() $\bar \mu _2(x_C)=\sum _{\beta \in T_v}\sum _{D:h(\beta )\to ?}\sum _{m\geq 0}b_{\beta ,D,m}[r_Df^m]\otimes [\beta ]$
, where the second sum iterates over homotopy classes of paths of Q starting at
$\bar \mu _2(x_C)=\sum _{\beta \in T_v}\sum _{D:h(\beta )\to ?}\sum _{m\geq 0}b_{\beta ,D,m}[r_Df^m]\otimes [\beta ]$
, where the second sum iterates over homotopy classes of paths of Q starting at
![]() $h(\beta )$
. For
$h(\beta )$
. For
![]() $\beta \in T_v$
, let
$\beta \in T_v$
, let
![]() $\tilde \beta \in T_{\tilde v}\subseteq \widetilde Q_1$
be the corresponding arrow of
$\tilde \beta \in T_{\tilde v}\subseteq \widetilde Q_1$
be the corresponding arrow of
![]() $\widetilde Q_1$
starting at
$\widetilde Q_1$
starting at
![]() $\tilde v$
. Similarly, for any
$\tilde v$
. Similarly, for any
![]() $r_D$
starting at some
$r_D$
starting at some
![]() $h(\beta )$
, lift it to
$h(\beta )$
, lift it to
![]() $\tilde r_D$
starting at
$\tilde r_D$
starting at
![]() $h(\tilde \beta )$
. It follows from the definition of
$h(\tilde \beta )$
. It follows from the definition of
![]() $\bar \mu _2$
and
$\bar \mu _2$
and
![]() $\widetilde {\bar \mu _2}$
, then, that
$\widetilde {\bar \mu _2}$
, then, that
 $$\begin{align*}\widetilde{\bar\mu_2}(\tilde x_C)=\sum_{\beta\in T_{\tilde v}}\sum_{D:h(\tilde\beta)\to?}\sum_{m\geq0}b_{\beta,D,m}[\tilde r_Df^m]\otimes[\tilde\beta].\end{align*}$$
$$\begin{align*}\widetilde{\bar\mu_2}(\tilde x_C)=\sum_{\beta\in T_{\tilde v}}\sum_{D:h(\tilde\beta)\to?}\sum_{m\geq0}b_{\beta,D,m}[\tilde r_Df^m]\otimes[\tilde\beta].\end{align*}$$
But
![]() $\bar \mu _2(x_C)=0$
, so for each
$\bar \mu _2(x_C)=0$
, so for each
![]() $\beta \in T_v$
, we have
$\beta \in T_v$
, we have
![]() $\sum _{D:h(\beta )\to ?}\sum _{m\geq 0}b_{\beta ,D,m}[r_Df^m]=0$
. Then each coefficient
$\sum _{D:h(\beta )\to ?}\sum _{m\geq 0}b_{\beta ,D,m}[r_Df^m]=0$
. Then each coefficient
![]() $b_{\beta ,D,m}=0$
(again this is immediate if
$b_{\beta ,D,m}=0$
(again this is immediate if
![]() ${\mathcal A}=A_Q$
and follows from Lemma 6.12 if
${\mathcal A}=A_Q$
and follows from Lemma 6.12 if
![]() ${\mathcal A}=\widehat A_Q$
). Then the above formula shows that
${\mathcal A}=\widehat A_Q$
). Then the above formula shows that
![]() $\widetilde {\bar \mu _2}(\tilde x_C)=0$
. Then
$\widetilde {\bar \mu _2}(\tilde x_C)=0$
. Then
![]() $\tilde x_C$
is in the kernel of
$\tilde x_C$
is in the kernel of
![]() $\widetilde {\bar \mu _2}$
.
$\widetilde {\bar \mu _2}$
.
By Corollary 5.1,
![]() $Q^C$
is weakly consistent. By Theorem 5.2, two paths of
$Q^C$
is weakly consistent. By Theorem 5.2, two paths of
![]() $Q^C$
are equivalent in
$Q^C$
are equivalent in
![]() $Q^C$
if and only if they are equivalent as paths of
$Q^C$
if and only if they are equivalent as paths of
![]() $\widetilde Q$
. By Theorem 7.6, the exact sequence corresponding to (8) of
$\widetilde Q$
. By Theorem 7.6, the exact sequence corresponding to (8) of
![]() $Q^C$
must be exact. In particular, we get some
$Q^C$
must be exact. In particular, we get some
![]() $\tilde y_C$
in
$\tilde y_C$
in
![]() $\tilde X_3$
which maps to
$\tilde X_3$
which maps to
![]() $\tilde x_C$
through
$\tilde x_C$
through
![]() $\widetilde {\bar \mu _3}$
. Then
$\widetilde {\bar \mu _3}$
. Then
![]() $\tilde y_C$
considered as a sum of paths in
$\tilde y_C$
considered as a sum of paths in
![]() $\widetilde Q$
descends to some
$\widetilde Q$
descends to some
![]() $y_C$
in
$y_C$
in
![]() $X_3$
with
$X_3$
with
![]() $\bar \mu _3(y_C)=x_C$
, and the proof is complete.
$\bar \mu _3(y_C)=x_C$
, and the proof is complete.
7.3 Categorification
In certain special cases, Theorem 7.7 provides examples of categorifications of cluster algebras. We loosely model this section after [Reference Pressland48, §4]. We avoid defining technical terms used in this subsection, and instead refer to [Reference Pressland48] for more information.
Theorem 7.8 [Reference Amiot, Iyama and Reiten2, Theorem 4.1 and Theorem 4.10].
Let A be an algebra and
![]() $e\in A$
an idempotent. If A is Noetherian,
$e\in A$
an idempotent. If A is Noetherian,
![]() $\underline A=A/\langle e\rangle $
is finite-dimensional, and A is bimodule 3-Calabi-Yau with respect to e, then
$\underline A=A/\langle e\rangle $
is finite-dimensional, and A is bimodule 3-Calabi-Yau with respect to e, then
-
1.
 $B=eAe$
is Iwanaga-Gorenstein with Gorenstein dimension at most 3,
$B=eAe$
is Iwanaga-Gorenstein with Gorenstein dimension at most 3, -
2.
 $eA$
is a cluster-tilting object in the Frobenius category of Gorenstein projective modules
$eA$
is a cluster-tilting object in the Frobenius category of Gorenstein projective modules
 $\text {GP}(B)$
,
$\text {GP}(B)$
, -
3. The stable category
 $\underline {\text {GP}}(B)$
is a 2-Calabi-Yau triangulated category, and
$\underline {\text {GP}}(B)$
is a 2-Calabi-Yau triangulated category, and -
4. The natural maps
 $A\to \text {End}_B(eA)^{op}$
and
$A\to \text {End}_B(eA)^{op}$
and
 $\underline {A}\to \underline {\text {End}}_B(eA)^{op}$
are isomorphisms.
$\underline {A}\to \underline {\text {End}}_B(eA)^{op}$
are isomorphisms.
If Q is a strongly consistent dimer model and e is its boundary idempotent, then
![]() $\widehat A_Q$
is bimodule internally 3-Calabi-Yau with respect to e by Theorem 7.7. Hence, in order to apply Theorem 7.8, it suffices to check that
$\widehat A_Q$
is bimodule internally 3-Calabi-Yau with respect to e by Theorem 7.7. Hence, in order to apply Theorem 7.8, it suffices to check that
![]() $\widehat A_Q$
is Noetherian and that
$\widehat A_Q$
is Noetherian and that
![]() $\widehat A/\langle e\rangle $
is finite-dimensional as a vector space.
$\widehat A/\langle e\rangle $
is finite-dimensional as a vector space.
Corollary 7.9. Let Q be a finite strongly consistent dimer model with boundary idempotent e. Suppose that
![]() $\widehat A_Q/\langle e\rangle $
is finite-dimensional (hence that
$\widehat A_Q/\langle e\rangle $
is finite-dimensional (hence that
![]() $\widehat A_Q/\langle e\rangle \cong A_Q/\langle e\rangle $
) and that
$\widehat A_Q/\langle e\rangle \cong A_Q/\langle e\rangle $
) and that
![]() $\widehat A_Q$
is Noetherian. Write
$\widehat A_Q$
is Noetherian. Write
![]() $\widehat B_Q:=e\widehat A_Qe$
for the completed boundary algebra of Q.
$\widehat B_Q:=e\widehat A_Qe$
for the completed boundary algebra of Q.
-
1.
 $\widehat B_Q$
is Iwanaga-Gorenstein with Gorenstein dimension at most 3,
$\widehat B_Q$
is Iwanaga-Gorenstein with Gorenstein dimension at most 3, -
2.
 $e\widehat A_Q$
is a cluster-tilting object in the Frobenius category of Gorenstein projective modules
$e\widehat A_Q$
is a cluster-tilting object in the Frobenius category of Gorenstein projective modules
 $\text {GP}(\widehat B_Q)$
,
$\text {GP}(\widehat B_Q)$
, -
3. The stable category
 $\underline {\text {GP}}(B_Q)$
is a 2-Calabi-Yau triangulated category, and
$\underline {\text {GP}}(B_Q)$
is a 2-Calabi-Yau triangulated category, and -
4. The natural maps
 $\widehat A_Q\to \text {End}_{\widehat B_Q}(e\widehat A_Q)^{op}$
and
$\widehat A_Q\to \text {End}_{\widehat B_Q}(e\widehat A_Q)^{op}$
and
 $A_Q/\langle e\rangle \to \widehat A_Q/\langle e\rangle \cong \underline {\text {End}}_{\widehat B_Q}(e\widehat A_Q)^{op}$
are isomorphisms.
$A_Q/\langle e\rangle \to \widehat A_Q/\langle e\rangle \cong \underline {\text {End}}_{\widehat B_Q}(e\widehat A_Q)^{op}$
are isomorphisms.
If Q has no 1-cycles or 2-cycles, then it follows from Corollary 7.9 (4) that
![]() ${\text {GP}}(\widehat B_Q)$
is a categorification of the cluster algebra whose seed is given by the underlying ice quiver of Q. Section 9 gives us tools to reduce a dimer model by removing digons while preserving the dimer algebra.
${\text {GP}}(\widehat B_Q)$
is a categorification of the cluster algebra whose seed is given by the underlying ice quiver of Q. Section 9 gives us tools to reduce a dimer model by removing digons while preserving the dimer algebra.
Remark 7.10. In the setting of Theorem 7.8, if
![]() $e"$
is an idempotent orthogonal to e, then
$e"$
is an idempotent orthogonal to e, then
![]() $\widehat A$
is 3-Calabi-Yau with respect to
$\widehat A$
is 3-Calabi-Yau with respect to
![]() $e':=e+e"$
by [Reference Pressland46, Remark 2.2]. This means that if Q is a strongly consistent dimer model and
$e':=e+e"$
by [Reference Pressland46, Remark 2.2]. This means that if Q is a strongly consistent dimer model and
![]() $\widehat A_Q$
is Noetherian, then even if
$\widehat A_Q$
is Noetherian, then even if
![]() $\widehat A_Q/\langle e\rangle $
is not Noetherian, we may use a larger idempotent
$\widehat A_Q/\langle e\rangle $
is not Noetherian, we may use a larger idempotent
![]() $e'$
, where some of the internal vertices are seen to be frozen, in order to apply Theorem 7.8. In this way, we can get categorifications even from, for example, a consistent dimer model on a torus. See [Reference Amiot, Iyama and Reiten2, §6].
$e'$
, where some of the internal vertices are seen to be frozen, in order to apply Theorem 7.8. In this way, we can get categorifications even from, for example, a consistent dimer model on a torus. See [Reference Amiot, Iyama and Reiten2, §6].
Definition 7.11. We say that a dimer model Q is boundary-finite if
![]() $\widehat A_Q/\langle e\rangle $
is finite-dimensional. We say that Q is Noetherian if
$\widehat A_Q/\langle e\rangle $
is finite-dimensional. We say that Q is Noetherian if
![]() $\widehat A_Q$
is Noetherian.
$\widehat A_Q$
is Noetherian.
Hence, if Q is a finite strongly consistent dimer model, then in order to apply Corollary 7.9, we must only check Noetherianness and boundary-finiteness of Q. The authors are not aware of an example of a (weakly or strongly) consistent Noetherian dimer model on a surface other than a disk, annulus or torus. Dimer models on tori and disks have been studied extensively.
-
• Any consistent dimer model on a torus is Noetherian [Reference Beil5], but since the boundary idempotent is zero, such a dimer model is never boundary-finite. However, as in Remark 7.10, we may use a larger idempotent to apply Theorem 7.8.
-
• If Q is a consistent dimer model on a disk with no digons, Pressland showed in [Reference Pressland48, Proposition 4.4] that Q is Noetherian and boundary-finite. Hence, Corollary 7.9 can be applied to any consistent dimer model on a disk. Moreover, in the same paper, it is shown that
 $(\text {GP}(\widehat B_Q),e\widehat A_Q)$
is a Frobenius 2-Calabi-Yau realization of the cluster algebra
$(\text {GP}(\widehat B_Q),e\widehat A_Q)$
is a Frobenius 2-Calabi-Yau realization of the cluster algebra
 $\mathscr A_Q$
given by the ice quiver Q.
$\mathscr A_Q$
given by the ice quiver Q.
However, dimer models on annuli have seen comparatively little attention. We give some examples pertaining to Corollary 7.9 in the following subsection.
7.4 Examples on the annulus
We first prove a technical lemma which we will use to verify Noetherianness of some examples from this section. Recall that
![]() $r_C$
denotes a minimal path in the homotopy class C of paths on the surface of Q.
$r_C$
denotes a minimal path in the homotopy class C of paths on the surface of Q.
Lemma 7.12. Let Q be a strongly consistent dimer model on an annulus. Pick a vertex v of the dimer model and a generator of the homotopy group of cycles on the annulus at v. Let
![]() $C_v$
be the homotopy class of this generator. For any vertex w of Q, pick a path
$C_v$
be the homotopy class of this generator. For any vertex w of Q, pick a path
![]() $p:w\to v$
and let
$p:w\to v$
and let
![]() $C_w$
be the homotopy class of
$C_w$
be the homotopy class of
![]() $p^{-1}C_vp$
(note this does not depend on the choice of p). Suppose there exists a perfect matching
$p^{-1}C_vp$
(note this does not depend on the choice of p). Suppose there exists a perfect matching
![]() $\mathcal M$
of Q such that, for any vertex w of Q, we have
$\mathcal M$
of Q such that, for any vertex w of Q, we have
![]() $\mathcal M(r_{C_v})=\mathcal M(r_{C_w})$
and
$\mathcal M(r_{C_v})=\mathcal M(r_{C_w})$
and
![]() $\mathcal M(r_{C_v^{-1}})=\mathcal M(r_{C_w^{-1}})$
. Then
$\mathcal M(r_{C_v^{-1}})=\mathcal M(r_{C_w^{-1}})$
. Then
![]() $A_Q$
and
$A_Q$
and
![]() $\widehat A_Q$
are Noetherian.
$\widehat A_Q$
are Noetherian.
Proof. Define
![]() ${\mathcal A}$
to be either
${\mathcal A}$
to be either
![]() $A_Q$
or
$A_Q$
or
![]() $\widehat A_Q$
. We must show that
$\widehat A_Q$
. We must show that
![]() ${\mathcal A}$
is Noetherian.
${\mathcal A}$
is Noetherian.
We first claim that for any vertex w and any
![]() $m\geq 1$
, the path
$m\geq 1$
, the path
![]() $(r_{C_w})^m$
is the minimal path in the homotopy class
$(r_{C_w})^m$
is the minimal path in the homotopy class
![]() $C_w^m$
. We show this by induction on m. The base case is true by hypothesis. Now choose minimal cycle p in some homotopy class
$C_w^m$
. We show this by induction on m. The base case is true by hypothesis. Now choose minimal cycle p in some homotopy class
![]() $C_w^m$
(for
$C_w^m$
(for
![]() $m\in \mathbb N_{>1}$
) and suppose we have shown the claim for smaller values of m. Since
$m\in \mathbb N_{>1}$
) and suppose we have shown the claim for smaller values of m. Since
![]() $S(Q)$
is an annulus and
$S(Q)$
is an annulus and
![]() $m>1$
, we must be able to factor
$m>1$
, we must be able to factor
![]() $p=p_2 q p_1$
, where q is a cycle and either
$p=p_2 q p_1$
, where q is a cycle and either
![]() $p_1$
or
$p_1$
or
![]() $p_2$
(or both) is nonconstant. Since p is minimal, the paths
$p_2$
(or both) is nonconstant. Since p is minimal, the paths
![]() $p_1,q,p_2$
must be minimal, so by the induction hypothesis, we know that
$p_1,q,p_2$
must be minimal, so by the induction hypothesis, we know that
![]() $[q]=[r_{C_{t(q)}}^a]$
and
$[q]=[r_{C_{t(q)}}^a]$
and
![]() $[p_2p_1]=[r_{C_w}^b]$
for some
$[p_2p_1]=[r_{C_w}^b]$
for some
![]() $a,b\in \mathbb N_{\geq 1}$
such that
$a,b\in \mathbb N_{\geq 1}$
such that
![]() $a+b=m$
. Then
$a+b=m$
. Then
![]() $\mathcal M(p)=\mathcal M(p_2 qp_1)=\mathcal M(r_{C_{t(q)}}^a)+\mathcal M(r_{C_{w}}^b)=\mathcal M(r_{C_w}^m)$
, and hence,
$\mathcal M(p)=\mathcal M(p_2 qp_1)=\mathcal M(r_{C_{t(q)}}^a)+\mathcal M(r_{C_{w}}^b)=\mathcal M(r_{C_w}^m)$
, and hence,
![]() $[p]=[p_2qp_1]=[r_{C_w}^m]$
by Proposition 6.2.
$[p]=[p_2qp_1]=[r_{C_w}^m]$
by Proposition 6.2.
Symmetrically, for any vertex w and
![]() $m\geq 1$
, we have that
$m\geq 1$
, we have that
![]() $(r_{C_w})^{-m}$
is the minimal path in the homotopy class
$(r_{C_w})^{-m}$
is the minimal path in the homotopy class
![]() $C_w^{-m}$
.
$C_w^{-m}$
.
Define
![]() $M:=\mathcal M(r_{C_v}r_{C_v^{-1}})$
. Note that by assumption for any
$M:=\mathcal M(r_{C_v}r_{C_v^{-1}})$
. Note that by assumption for any
![]() $w\in Q_0$
, we have
$w\in Q_0$
, we have
![]() $\mathcal M(r_{C_w}r_{C_{w}^{-1}})=\mathcal M(r_{C_v}r_{C_{v}^{-1}})=M$
. Then for any
$\mathcal M(r_{C_w}r_{C_{w}^{-1}})=\mathcal M(r_{C_v}r_{C_{v}^{-1}})=M$
. Then for any
![]() $w\in Q_0$
, we have
$w\in Q_0$
, we have
![]() $r_{C_w}r_{C_w^{-1}}=f_w^M$
, and hence,
$r_{C_w}r_{C_w^{-1}}=f_w^M$
, and hence,
![]() $\left (\sum _{w\in Q_0}r_{C_w}\right )\left (\sum _{w\in Q_0}r_{C_w^{-1}}\right )=f^M$
.
$\left (\sum _{w\in Q_0}r_{C_w}\right )\left (\sum _{w\in Q_0}r_{C_w^{-1}}\right )=f^M$
.
Define the subalgebra
![]() $\mathcal Z$
of
$\mathcal Z$
of
![]() $\mathcal A$
as the set of (possibly infinite if
$\mathcal A$
as the set of (possibly infinite if
![]() $\mathcal A=\widehat A_Q$
) linear combinations of elements of the form
$\mathcal A=\widehat A_Q$
) linear combinations of elements of the form
![]() $\sum _{w\in Q_0}f^ar_{C_w}^b$
or
$\sum _{w\in Q_0}f^ar_{C_w}^b$
or
![]() $\sum _{w\in Q_0}f^ar_{C_w^{-1}}^b$
, for
$\sum _{w\in Q_0}f^ar_{C_w^{-1}}^b$
, for
![]() $a,b\in \mathbb N_{\geq 0}$
. Then
$a,b\in \mathbb N_{\geq 0}$
. Then
![]() $\mathcal Z$
is the polynomial ring (if
$\mathcal Z$
is the polynomial ring (if
![]() $\mathcal A=A_Q$
) or ring of formal power series (if
$\mathcal A=A_Q$
) or ring of formal power series (if
![]() $\mathcal A=\widehat A_Q$
) in three variables f and
$\mathcal A=\widehat A_Q$
) in three variables f and
![]() $\sum _{w\in Q_0}r_{C_w}$
and
$\sum _{w\in Q_0}r_{C_w}$
and
![]() $\sum _{w\in Q_0}r_{C_w^{-1}}$
, modulo the relation
$\sum _{w\in Q_0}r_{C_w^{-1}}$
, modulo the relation
![]() $\left (\sum _{w\in Q_0}r_{C_w}\right )\left (\sum _{w\in Q_0}r_{C_w^{-1}}\right )=f^M$
. In either case,
$\left (\sum _{w\in Q_0}r_{C_w}\right )\left (\sum _{w\in Q_0}r_{C_w^{-1}}\right )=f^M$
. In either case,
![]() $\mathcal A$
is Noetherian by standard results.
$\mathcal A$
is Noetherian by standard results.
Let S be the set of paths of Q containing no cycles. Since Q is finite, S is also finite. We claim that
![]() $\mathcal A$
is generated as a
$\mathcal A$
is generated as a
![]() $\mathcal Z$
-algebra by S.
$\mathcal Z$
-algebra by S.
Indeed, take any path p of Q. We may write p in the form
![]() $p_m l_m \dots l_2p_2l_1p_1$
for some
$p_m l_m \dots l_2p_2l_1p_1$
for some
![]() $m\in \mathbb N_{\geq 0}$
and paths
$m\in \mathbb N_{\geq 0}$
and paths
![]() $p_i$
and
$p_i$
and
![]() $l_j$
such that each
$l_j$
such that each
![]() $l_j$
is a cycle and
$l_j$
is a cycle and
![]() $p_m\dots p_2p_1$
is a path which contains no cycles. This expression is not unique. By the claim, each
$p_m\dots p_2p_1$
is a path which contains no cycles. This expression is not unique. By the claim, each
![]() $l_j$
is equivalent to
$l_j$
is equivalent to
![]() $r_{C_{t(l_j)}^{\varepsilon _j}}^{a_j}f^{b_j}$
for some
$r_{C_{t(l_j)}^{\varepsilon _j}}^{a_j}f^{b_j}$
for some
![]() $a_j,b_j\in \mathbb N_{\geq 0}$
and
$a_j,b_j\in \mathbb N_{\geq 0}$
and
![]() $\varepsilon _j\in \{1,-1\}$
. Then
$\varepsilon _j\in \{1,-1\}$
. Then
 $$ \begin{align*} [p]&=[p_ml_m\dots l_2p_2l_1p_1] \\ &=\left[p_m\left( r_{C_{t(l_m)}^{\varepsilon_m}}^{a_m}f^{b_m}\right)\dots p_2 \left(r_{C_{t(l_1)}^{\varepsilon_1}}^{a_1}f^{b_1}\right)p_1\right]\\ &=\left[ \left(\sum_{j\in[m] :\ \varepsilon_j=1}r_{C_{h(p_m)}}^{a_j}f^{b_j}\right) \left(\sum_{j\in[m] :\ \varepsilon_j=-1}r_{C_{h(p_m)}^{-1}}^{a_j}f^{b_j}\right)\right][p_m\dots p_1]. \end{align*} $$
$$ \begin{align*} [p]&=[p_ml_m\dots l_2p_2l_1p_1] \\ &=\left[p_m\left( r_{C_{t(l_m)}^{\varepsilon_m}}^{a_m}f^{b_m}\right)\dots p_2 \left(r_{C_{t(l_1)}^{\varepsilon_1}}^{a_1}f^{b_1}\right)p_1\right]\\ &=\left[ \left(\sum_{j\in[m] :\ \varepsilon_j=1}r_{C_{h(p_m)}}^{a_j}f^{b_j}\right) \left(\sum_{j\in[m] :\ \varepsilon_j=-1}r_{C_{h(p_m)}^{-1}}^{a_j}f^{b_j}\right)\right][p_m\dots p_1]. \end{align*} $$
Note that
![]() $p_m\dots p_1\in S$
and
$p_m\dots p_1\in S$
and
 $$\begin{align*}\left[ \left(\sum_{j\in[m] :\ \varepsilon_j=1}r_{C_{h(p_m)}}^{a_j}f^{b_j}\right) \left(\sum_{j\in[m] :\ \varepsilon_j=-1}r_{C_{h(p_m)}^{-1}}^{a_j}f^{b_j}\right)\right]\end{align*}$$
$$\begin{align*}\left[ \left(\sum_{j\in[m] :\ \varepsilon_j=1}r_{C_{h(p_m)}}^{a_j}f^{b_j}\right) \left(\sum_{j\in[m] :\ \varepsilon_j=-1}r_{C_{h(p_m)}^{-1}}^{a_j}f^{b_j}\right)\right]\end{align*}$$
is in
![]() $\mathcal Z$
. Since every path is of this form, it follows that
$\mathcal Z$
. Since every path is of this form, it follows that
![]() $\mathcal A$
is generated by the finite set of paths S as a
$\mathcal A$
is generated by the finite set of paths S as a
![]() $\mathcal Z$
-module. Since
$\mathcal Z$
-module. Since
![]() $\mathcal Z$
is Noetherian, the algebra
$\mathcal Z$
is Noetherian, the algebra
![]() $\mathcal A$
is also Noetherian, completing the proof.
$\mathcal A$
is also Noetherian, completing the proof.
Before giving positive examples, we give three examples to which Corollary 7.9 may not be applied in Figure 15, explained in the following two example environments. These examples show that neither the assumption of Noetherianness nor boundary-finiteness is vacuous in Corollary 7.9.
Example 7.13. Consider the dimer model Q on the left of Figure 15. It may be checked using the strand diagram that Q is weakly consistent, and it is not hard to see that Q is in addition nondegenerate. Let
![]() $\mathcal M$
be the perfect matching consisting of the arrows drawn in red. For any vertex
$\mathcal M$
be the perfect matching consisting of the arrows drawn in red. For any vertex
![]() $w\in Q_0$
, let
$w\in Q_0$
, let
![]() $C_w$
be the homotopy class of cycles at w winding once counter-clockwise around the annulus as embedded in Figure 15. Then it may be checked that, for any w, we have
$C_w$
be the homotopy class of cycles at w winding once counter-clockwise around the annulus as embedded in Figure 15. Then it may be checked that, for any w, we have
![]() $\mathcal M(r_{C_w})=0$
and
$\mathcal M(r_{C_w})=0$
and
![]() $\mathcal M(r_{C_w^{-1}})=4$
. Then Lemma 7.12 shows that
$\mathcal M(r_{C_w^{-1}})=4$
. Then Lemma 7.12 shows that
![]() $A_Q$
and
$A_Q$
and
![]() $\widehat A_Q$
are Noetherian. However, if w is an internal vertex, then any power of
$\widehat A_Q$
are Noetherian. However, if w is an internal vertex, then any power of
![]() $r_{C_w}$
is the only path in its equivalence class, showing that Q is not boundary-finite. Then Q satisfies all requirements for Corollary 7.9 except for boundary-finiteness.
$r_{C_w}$
is the only path in its equivalence class, showing that Q is not boundary-finite. Then Q satisfies all requirements for Corollary 7.9 except for boundary-finiteness.
Example 7.14. Consider the dimer model Q in the middle of Figure 15. As in Lemma 7.12, let
![]() $\mathcal A$
be
$\mathcal A$
be
![]() $A_Q$
or
$A_Q$
or
![]() $\widehat A_Q$
. It may be verified using the strand diagram that Q is weakly consistent, though Q is not strongly consistent because no perfect matching contains any of its outer boundary arrows. Since every path with at least two arrows passes through a boundary vertex, the model Q is boundary-finite.
$\widehat A_Q$
. It may be verified using the strand diagram that Q is weakly consistent, though Q is not strongly consistent because no perfect matching contains any of its outer boundary arrows. Since every path with at least two arrows passes through a boundary vertex, the model Q is boundary-finite.
Let
![]() $\mathcal M$
be the perfect matching consisting of the arrows drawn in red. We have
$\mathcal M$
be the perfect matching consisting of the arrows drawn in red. We have
![]() $\mathcal M(r_{C_{v_1}})=0$
but
$\mathcal M(r_{C_{v_1}})=0$
but
![]() $\mathcal M(r_{C_{v_2}})=1$
. Now for any
$\mathcal M(r_{C_{v_2}})=1$
. Now for any
![]() $j\in \mathbb N_{\geq 0}$
, define
$j\in \mathbb N_{\geq 0}$
, define
![]() $I_j$
to be the left ideal of
$I_j$
to be the left ideal of
![]() $\mathcal A$
generated by
$\mathcal A$
generated by
![]() $\{\alpha r_{C_{v_1}}^{i}\ :\ i\in [j]\}$
, where
$\{\alpha r_{C_{v_1}}^{i}\ :\ i\in [j]\}$
, where
![]() $\alpha $
denotes the arrow
$\alpha $
denotes the arrow
![]() $v_1\to v_2$
. For any j, we have
$v_1\to v_2$
. For any j, we have
![]() $\mathcal M(\alpha r_{C_{v_1}}^j)=0$
, and hence,
$\mathcal M(\alpha r_{C_{v_1}}^j)=0$
, and hence,
![]() $\alpha r_{C_{v_1}}^j$
is minimal. Since this path has no morphable arrows, it is the only minimal path in its homotopy class. This shows that
$\alpha r_{C_{v_1}}^j$
is minimal. Since this path has no morphable arrows, it is the only minimal path in its homotopy class. This shows that
![]() $[\alpha r_{C_{v_1}}^j]$
is nonzero in
$[\alpha r_{C_{v_1}}^j]$
is nonzero in
![]() $\widehat A_Q$
and that, moreover, if
$\widehat A_Q$
and that, moreover, if
![]() $j>0$
, then
$j>0$
, then
![]() $\alpha r_{C_{v_1}}^j$
is not in the left ideal
$\alpha r_{C_{v_1}}^j$
is not in the left ideal
![]() $I_{j-1}$
. Then
$I_{j-1}$
. Then
![]() $I_0\subsetneq I_1\subsetneq I_2\subsetneq \dots $
is an infinite increasing chain of left ideals of
$I_0\subsetneq I_1\subsetneq I_2\subsetneq \dots $
is an infinite increasing chain of left ideals of
![]() $\mathcal A$
which never stabilizes; hence,
$\mathcal A$
which never stabilizes; hence,
![]() $\mathcal A$
is not Noetherian. This example is notable as it comes from a triangulated annulus as in [Reference Baur, King and Marsh4, §13]. The fact that such models are not nondegenerate or Noetherian indicates that they may not be the nicest dimer models on annuli from our perspective.
$\mathcal A$
is not Noetherian. This example is notable as it comes from a triangulated annulus as in [Reference Baur, King and Marsh4, §13]. The fact that such models are not nondegenerate or Noetherian indicates that they may not be the nicest dimer models on annuli from our perspective.
Example 7.15. Consider the dimer model Q on the right of Figure 15. It may be verified using the strand diagram that Q is weakly consistent, and it is not hard to see that Q is in addition nondegenerate. Boundary-finiteness of Q is immediate since all vertices are boundary.
Let
![]() $\mathcal A$
be
$\mathcal A$
be
![]() $A_Q$
or
$A_Q$
or
![]() $\widehat A_Q$
. For
$\widehat A_Q$
. For
![]() $j\in \mathbb N_{\geq 0}$
, let
$j\in \mathbb N_{\geq 0}$
, let
![]() $I_j$
be the left ideal of
$I_j$
be the left ideal of
![]() $\mathcal A$
generated by
$\mathcal A$
generated by
![]() $\{\alpha _1(\gamma _1\beta _1\gamma _2\alpha _3)^i\ :\ i\in [j]\}$
. As in Example 7.14, we may check that
$\{\alpha _1(\gamma _1\beta _1\gamma _2\alpha _3)^i\ :\ i\in [j]\}$
. As in Example 7.14, we may check that
![]() $[\alpha _1(\gamma _1\beta _1\gamma _2\alpha _3)^{j+1}]\not \in I_j$
, hence
$[\alpha _1(\gamma _1\beta _1\gamma _2\alpha _3)^{j+1}]\not \in I_j$
, hence
![]() $I_0\subsetneq I_1\subsetneq \dots $
is an increasing chain of left ideals of
$I_0\subsetneq I_1\subsetneq \dots $
is an increasing chain of left ideals of
![]() $\mathcal A$
which never stabilizes, and hence,
$\mathcal A$
which never stabilizes, and hence,
![]() $\mathcal A$
is not Noetherian. This dimer model then satisfies all assumptions of Corollary 7.9 except for Noetherianness.
$\mathcal A$
is not Noetherian. This dimer model then satisfies all assumptions of Corollary 7.9 except for Noetherianness.
Example 7.13 shows that a strongly consistent and Noetherian dimer model may fail to be boundary finite. Example 7.15 shows that a strongly consistent and boundary-finite dimer model may have a non-Noetherian (completed and noncompleted) dimer algebra. So, no conditions of Corollary 7.9 are vacuous. Further work is required to understand how the Noetherian condition interacts with weak and strong consistency, as in [Reference Beil5] on the torus. It would be of interest to obtain a condition on the strand diagram for a strongly consistent dimer model (on an annulus or in general) to be Noetherian. For now, we give examples of annulus models satisfying the conditions of Corollary 7.9.
Example 7.16. Figure 16 shows two strongly consistent dimer models on annuli satisfying Noetherianness and boundary finiteness. Consider the model Q on the right. Let
![]() $\mathcal M$
be the perfect matching consisting of the six arrows drawn vertically in Figure 16. For any vertex
$\mathcal M$
be the perfect matching consisting of the six arrows drawn vertically in Figure 16. For any vertex
![]() $w\in Q_0$
, we let
$w\in Q_0$
, we let
![]() $C_w$
be the homotopy class of paths winding once counter-clockwise around the model. It can then be checked that
$C_w$
be the homotopy class of paths winding once counter-clockwise around the model. It can then be checked that
![]() $\mathcal M(r_{C_w})=4=\mathcal M(r_{C_w^{-1}})$
for any vertex
$\mathcal M(r_{C_w})=4=\mathcal M(r_{C_w^{-1}})$
for any vertex
![]() $w\in Q_0$
. Then Lemma 7.12 shows that
$w\in Q_0$
. Then Lemma 7.12 shows that
![]() $A_Q$
and
$A_Q$
and
![]() $\widehat A_Q$
are Noetherian. The model Q is boundary-finite because any path p of length at least four is equivalent to a path which factors through a boundary vertex. We have now seen that Q is strongly consistent, Noetherian, and boundary-finite. The models of Figure 16 suggest a general construction. Note that the internal subquiver of the model on the left is an alternating affine type
$\widehat A_Q$
are Noetherian. The model Q is boundary-finite because any path p of length at least four is equivalent to a path which factors through a boundary vertex. We have now seen that Q is strongly consistent, Noetherian, and boundary-finite. The models of Figure 16 suggest a general construction. Note that the internal subquiver of the model on the left is an alternating affine type
![]() $\widetilde A_4$
quiver, and on the right, the internal subquiver is two layers of affine type
$\widetilde A_4$
quiver, and on the right, the internal subquiver is two layers of affine type
![]() $\widetilde A_4$
quivers which are connected to each other. One may obtain similar models whose internal subquiver is any number of layers of an alternating affine type
$\widetilde A_4$
quivers which are connected to each other. One may obtain similar models whose internal subquiver is any number of layers of an alternating affine type
![]() $\widetilde A_{2n}$
quiver.
$\widetilde A_{2n}$
quiver.
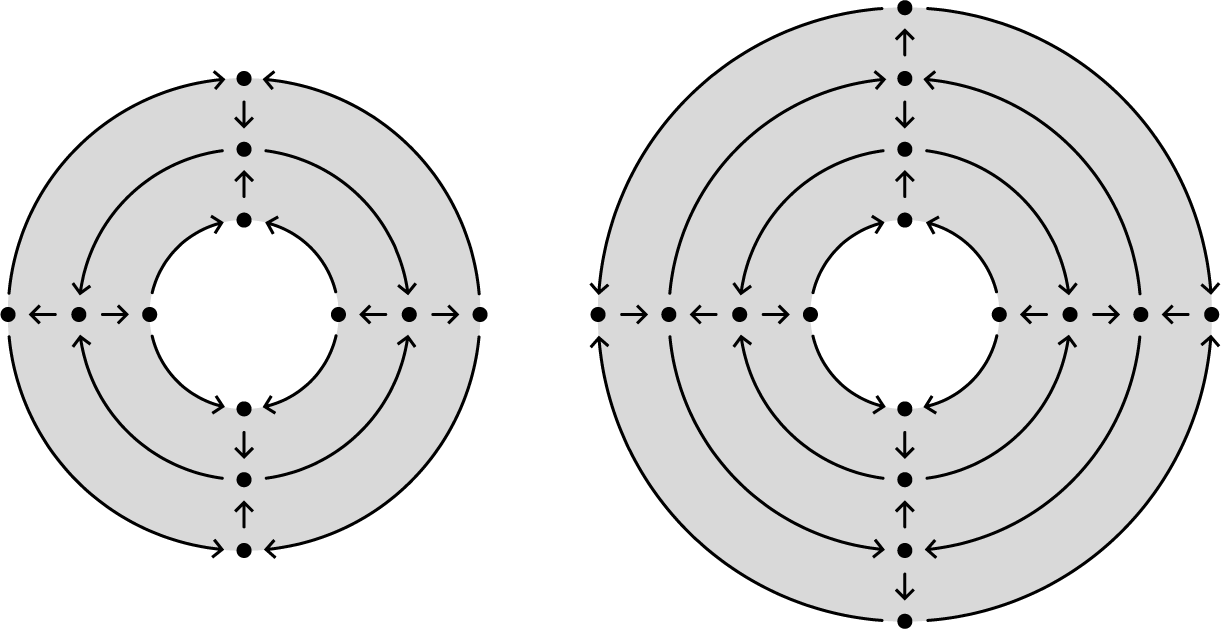
Figure 16 Two strongly consistent dimer models on annuli satisfying Noetherianness and boundary finiteness.
Example 7.17. Let Q be the dimer model of Figure 17. One may check similarly to Example 7.16 that Q is strongly consistent, Noetherian and boundary-finite. Similarly to the previous example, the internal subquiver of this dimer model consists of two layers of some orientation of an affine type
![]() $\widetilde A_{11}$
quiver, stitched together with some vertical and diagonal arrows. Again, a more general construction is indicated, and one may obtain a similar strongly consistent, Noetherian, and boundary-finite model for any number of layers of any orientation of an affine type quiver.
$\widetilde A_{11}$
quiver, stitched together with some vertical and diagonal arrows. Again, a more general construction is indicated, and one may obtain a similar strongly consistent, Noetherian, and boundary-finite model for any number of layers of any orientation of an affine type quiver.
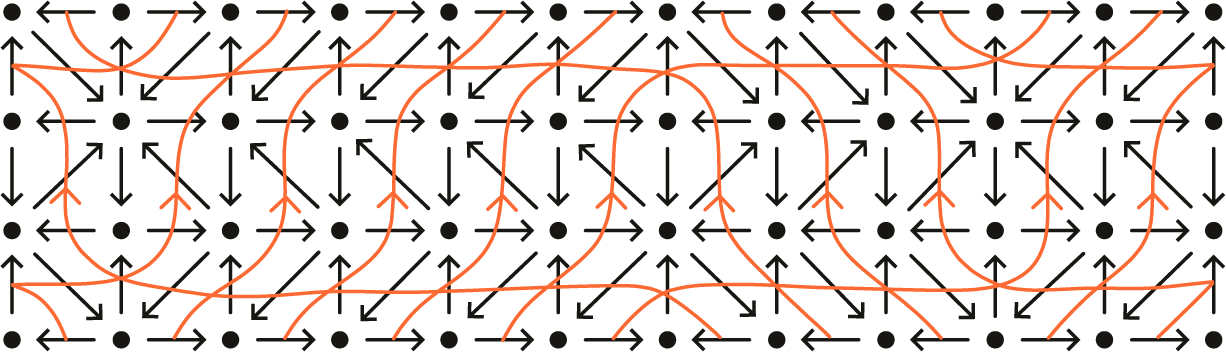
Figure 17 A strongly consistent dimer model on an annulus satisfying Noetherianness and boundary finiteness. The left and right sides should be identified. The strands going up are shown in red, while the strands going down are left out for readability.
Corollary 7.9 may be applied to the annulus models of Examples 7.16 and 7.17 to show that the Gorenstein-projective module categories over their boundary algebras categorify the cluster algebra given by their underlying quivers.
8 Extra results about equivalence classes
For this section, unless otherwise specified, we suppose that Q is a weakly consistent dimer model and
![]() $\widetilde {Q}$
is a simply connected dimer model that is not on a sphere. We use Theorem 5.2 to get some interesting results about the path equivalence classes in weakly consistent quivers. These results are not used anywhere else in the paper.
$\widetilde {Q}$
is a simply connected dimer model that is not on a sphere. We use Theorem 5.2 to get some interesting results about the path equivalence classes in weakly consistent quivers. These results are not used anywhere else in the paper.
Proposition 8.1. Let p and q be distinct elementary paths in a weakly consistent dimer model
![]() $\widetilde Q$
with the same start and end vertices. If p is to the right of q, then either p has a left-morphable arrow or q has a strictly higher c-value than p.
$\widetilde Q$
with the same start and end vertices. If p is to the right of q, then either p has a left-morphable arrow or q has a strictly higher c-value than p.
Proof. We may reduce to the case where p and q share no vertices except for the start and end vertices. Then
![]() $q^{-1}p$
defines a disk submodel
$q^{-1}p$
defines a disk submodel
![]() $Q'$
of
$Q'$
of
![]() $\widetilde Q$
in which p consists only of boundary arrows in counter-clockwise faces and q consists of boundary arrows in clockwise faces. If p has a strictly higher c-value than q in
$\widetilde Q$
in which p consists only of boundary arrows in counter-clockwise faces and q consists of boundary arrows in clockwise faces. If p has a strictly higher c-value than q in
![]() $\widetilde Q$
, then we are done. Suppose the c-value of p is less than or equal to that of q in
$\widetilde Q$
, then we are done. Suppose the c-value of p is less than or equal to that of q in
![]() $\widetilde Q$
. Then
$\widetilde Q$
. Then
![]() $[p]=[qf^m]$
for some m in
$[p]=[qf^m]$
for some m in
![]() $\widetilde Q$
. By Theorem 5.2, the same is true in
$\widetilde Q$
. By Theorem 5.2, the same is true in
![]() $Q'$
. It follows that p has a left-morphable arrow in
$Q'$
. It follows that p has a left-morphable arrow in
![]() $Q'$
, and hence in
$Q'$
, and hence in
![]() $\widetilde Q$
. This proves the desired result.
$\widetilde Q$
. This proves the desired result.
Corollary 8.2. Let
![]() $Q=\widetilde Q$
be a simply connected dimer model. Let v and w be vertices of Q. Suppose that there is a leftmost minimal path p from v to w. Then p is to the left of every minimal path and to the right of every leftmost path.
$Q=\widetilde Q$
be a simply connected dimer model. Let v and w be vertices of Q. Suppose that there is a leftmost minimal path p from v to w. Then p is to the left of every minimal path and to the right of every leftmost path.
Proof. If
![]() $p'$
is any other minimal path from v to w, Proposition 8.1 shows that p is to the left of
$p'$
is any other minimal path from v to w, Proposition 8.1 shows that p is to the left of
![]() $p'$
. If q is any other leftmost path from v to w, Proposition 8.1 shows that q is to the left of p.
$p'$
. If q is any other leftmost path from v to w, Proposition 8.1 shows that q is to the left of p.
If Q is not simply connected, we may still pass to the universal cover and apply Corollary 8.2 to gain insight into the equivalence classes of paths of Q.
Corollary 8.3. Suppose Q is a weakly consistent dimer model. If p and q are minimal homotopic leftmost paths with the same start and end vertices, then
![]() $p=q$
.
$p=q$
.
Proof. Suppose p and q are homotopic minimal leftmost paths with the same start and end vertices. Lift them to minimal leftmost paths
![]() $\tilde p$
and
$\tilde p$
and
![]() $\tilde q$
of
$\tilde q$
of
![]() $\widetilde Q$
. Since p and q are homotopic, these paths have the same start and end vertices. It suffices to show that
$\widetilde Q$
. Since p and q are homotopic, these paths have the same start and end vertices. It suffices to show that
![]() $\tilde p=\tilde q$
. Suppose this is not the case. By taking subpaths, we may reduce to the case where
$\tilde p=\tilde q$
. Suppose this is not the case. By taking subpaths, we may reduce to the case where
![]() $\tilde p$
and
$\tilde p$
and
![]() $\tilde q$
share only their start and end vertices. Say
$\tilde q$
share only their start and end vertices. Say
![]() $\tilde p$
is to the right of
$\tilde p$
is to the right of
![]() $\tilde q$
. Since both paths have the same c-value, Proposition 8.1 shows that
$\tilde q$
. Since both paths have the same c-value, Proposition 8.1 shows that
![]() $\tilde p$
has a left-morphable arrow, a contradiction.
$\tilde p$
has a left-morphable arrow, a contradiction.
Corollary 8.3 indicates that there is at most one minimal leftmost path between any two vertices of Q. In general, leftmost paths need not exist. Figure 21 gives an example of a finite weakly consistent dimer model on an annulus where a minimal path has an infinite equivalence class. Let
![]() $\alpha $
be one of the arrows of the digon of Q. Then an arbitrarily long series of left-morphs at the other arrow of the digon may be applied to
$\alpha $
be one of the arrows of the digon of Q. Then an arbitrarily long series of left-morphs at the other arrow of the digon may be applied to
![]() $\alpha $
. In other words, there is no leftmost path from the outer boundary ring to the inner boundary ring. The dimer model in the middle of Figure 15 has no 2-cycles and displays the same behavior: a minimal path from a vertex of the inner boundary to a vertex of the outer boundary may be left-morphed or right-morphed indefinitely, depending on the path.
$\alpha $
. In other words, there is no leftmost path from the outer boundary ring to the inner boundary ring. The dimer model in the middle of Figure 15 has no 2-cycles and displays the same behavior: a minimal path from a vertex of the inner boundary to a vertex of the outer boundary may be left-morphed or right-morphed indefinitely, depending on the path.
However, by assuming nondegeneracy, we guarantee the existence of leftmost and rightmost paths between any given vertices.
Theorem 8.4. Let Q be a strongly consistent dimer model. Let v and w be distinct vertices of Q and let C be a homotopy class of paths from v to w. Then there is a unique minimal leftmost path p from v to w in C.
Proof. We show the existence of a leftmost path from v to w. Uniqueness follows from Corollary 8.3. Lift v and w to vertices
![]() $\tilde v$
and
$\tilde v$
and
![]() $\tilde w$
of the universal cover model
$\tilde w$
of the universal cover model
![]() $\widetilde Q$
such that a path from
$\widetilde Q$
such that a path from
![]() $\tilde v$
to
$\tilde v$
to
![]() $\tilde w$
descends to a path of Q in homotopy class C. We consider paths on
$\tilde w$
descends to a path of Q in homotopy class C. We consider paths on
![]() $\widetilde Q$
to have the grading of their corresponding paths on Q. By path-consistency, all minimal paths from
$\widetilde Q$
to have the grading of their corresponding paths on Q. By path-consistency, all minimal paths from
![]() $\tilde v$
to
$\tilde v$
to
![]() $\tilde w$
are equivalent and hence have the same grading k. Then if
$\tilde w$
are equivalent and hence have the same grading k. Then if
![]() $\tilde q=\alpha _m\dots \alpha _1$
is a minimal path from
$\tilde q=\alpha _m\dots \alpha _1$
is a minimal path from
![]() $\tilde v$
to
$\tilde v$
to
![]() $\tilde w$
, then since the degree of each arrow is positive, we must have
$\tilde w$
, then since the degree of each arrow is positive, we must have
![]() $m\leq k$
. This shows that the length of a minimal path from
$m\leq k$
. This shows that the length of a minimal path from
![]() $\tilde v$
to
$\tilde v$
to
![]() $\tilde w$
is bounded by k. This condition guarantees that there are a finite number of minimal paths from
$\tilde w$
is bounded by k. This condition guarantees that there are a finite number of minimal paths from
![]() $\tilde v$
to
$\tilde v$
to
![]() $\tilde w$
.
$\tilde w$
.
Now consider again the minimal path
![]() $\tilde q$
from
$\tilde q$
from
![]() $\tilde v$
to
$\tilde v$
to
![]() $\tilde w$
. Let
$\tilde w$
. Let
![]() $\tilde r$
be any path from
$\tilde r$
be any path from
![]() $\tilde w$
to
$\tilde w$
to
![]() $\tilde v$
. If
$\tilde v$
. If
![]() $\tilde q$
is not leftmost, then left-morph it at some arrow
$\tilde q$
is not leftmost, then left-morph it at some arrow
![]() $\alpha _1$
to get some
$\alpha _1$
to get some
![]() $\tilde q_1$
. Then Lemma 2.20 gives that
$\tilde q_1$
. Then Lemma 2.20 gives that
![]() $\text {Wind}(\tilde r\tilde q_1,F)<\text {Wind}(\tilde r\tilde q,F)$
if F is one of the faces containing
$\text {Wind}(\tilde r\tilde q_1,F)<\text {Wind}(\tilde r\tilde q,F)$
if F is one of the faces containing
![]() $\alpha _1$
, and
$\alpha _1$
, and
![]() $\text {Wind}(\tilde r\tilde q_1,F)=\text {Wind}(\tilde r\tilde q,F)$
otherwise. Continue to left-morph to get some sequence of paths
$\text {Wind}(\tilde r\tilde q_1,F)=\text {Wind}(\tilde r\tilde q,F)$
otherwise. Continue to left-morph to get some sequence of paths
![]() $\tilde q,\tilde q_1,\tilde q_2,\dots $
. By the above inequalities, for any j, the inequality
$\tilde q,\tilde q_1,\tilde q_2,\dots $
. By the above inequalities, for any j, the inequality
![]() $\text {Wind}(\tilde r\tilde q_{j+1},F)\leq \text {Wind}(\tilde r\tilde q_j,F)$
holds for all faces F and is strict for some choice of F. Repeating this argument shows that
$\text {Wind}(\tilde r\tilde q_{j+1},F)\leq \text {Wind}(\tilde r\tilde q_j,F)$
holds for all faces F and is strict for some choice of F. Repeating this argument shows that
![]() $\tilde q_i\neq \tilde q_j$
for
$\tilde q_i\neq \tilde q_j$
for
![]() $i\neq j$
. Since there are a finite number of minimal paths from
$i\neq j$
. Since there are a finite number of minimal paths from
![]() $\tilde v$
to
$\tilde v$
to
![]() $\tilde w$
and the sequence never repeats itself, the sequence must terminate with some leftmost path
$\tilde w$
and the sequence never repeats itself, the sequence must terminate with some leftmost path
![]() $\tilde p:=\tilde q_l$
from
$\tilde p:=\tilde q_l$
from
![]() $\tilde v$
to
$\tilde v$
to
![]() $\tilde w$
. This descends to a leftmost path p from v to w in homotopy class C.
$\tilde w$
. This descends to a leftmost path p from v to w in homotopy class C.
Theorem 8.4 and Corollary 8.2 are useful tools to understand equivalence classes of paths in nondegenerate dimer models. In particular, if Q is a consistent (hence also nondegenerate) dimer model in a disk and e is the boundary idempotent of Q, the boundary algebra
![]() $eA_Qe$
may be used to obtain an additive Frobenius categorification of the ice quiver of Q [Reference Pressland48]. In a future paper, we will use these results to study boundary algebras of consistent dimer models on disks.
$eA_Qe$
may be used to obtain an additive Frobenius categorification of the ice quiver of Q [Reference Pressland48]. In a future paper, we will use these results to study boundary algebras of consistent dimer models on disks.
9 Reduction of a dimer model
There has been some interest, particularly in the disk case, in reducing a dimer model by removing digons. See [Reference Pressland48] and [Reference Broomhead11, Remark 2.9]. In particular, if a weakly consistent, Noetherian, boundary-finite dimer model Q has no 1-cycles or 2-cycles, our categorification result Corollary 7.9 shows that
![]() $\text {GP}(Q)$
categorifies the cluster algebra
$\text {GP}(Q)$
categorifies the cluster algebra
![]() $\mathscr A_Q$
given by the underlying quiver of Q. However, if Q has 1-cycles or 2-cycles, then it may not be immediately clear what cluster algebra is being categorified. Reducing a dimer model helps to avoid this issue. In [Reference Pressland48], Pressland works with consistent dimer models on a disk with more than three boundary vertices. He observes that, in this case, the removal of digons corresponds to untwisting moves in the strand diagram, and hence, their removal is straightforward. Moreover, the resulting reduced dimer models do not have any 2-cycles, and the disk version of Corollary 7.9 can be used to prove results about categorification. The situation for more general weakly consistent dimer models is more complicated, as there may be copies similar to Figure 21 contained in the dimer model whose digons may not be removed. However, such occurrences will force the dimer model to be degenerate. Then in the nondegenerate case, we may freely remove internal digons from a dimer model – that is, digons where both of its arrows are internal.
$\mathscr A_Q$
given by the underlying quiver of Q. However, if Q has 1-cycles or 2-cycles, then it may not be immediately clear what cluster algebra is being categorified. Reducing a dimer model helps to avoid this issue. In [Reference Pressland48], Pressland works with consistent dimer models on a disk with more than three boundary vertices. He observes that, in this case, the removal of digons corresponds to untwisting moves in the strand diagram, and hence, their removal is straightforward. Moreover, the resulting reduced dimer models do not have any 2-cycles, and the disk version of Corollary 7.9 can be used to prove results about categorification. The situation for more general weakly consistent dimer models is more complicated, as there may be copies similar to Figure 21 contained in the dimer model whose digons may not be removed. However, such occurrences will force the dimer model to be degenerate. Then in the nondegenerate case, we may freely remove internal digons from a dimer model – that is, digons where both of its arrows are internal.
We now consider the reduction of a dimer model by removing digons. First, we consider weakly consistent dimer models.
Proposition 9.1. Let Q be a weakly consistent dimer model with a finite number of digons. There exists a reduced dimer model
![]() $Q_{red}$
of Q satisfying the following:
$Q_{red}$
of Q satisfying the following:
-
1.
 $S(Q_{red})=S(Q)$
,
$S(Q_{red})=S(Q)$
, -
2.
 $A_{Q_{red}}\cong A_Q$
,
$A_{Q_{red}}\cong A_Q$
, -
3.
 $Q_{red}$
is weakly consistent,
$Q_{red}$
is weakly consistent, -
4. If Q is nondegenerate, then
 $Q_{red}$
is nondegenerate, and
$Q_{red}$
is nondegenerate, and -
5. Either
 $Q_{red}$
is a dimer model on a disk composed of a single digon, or every digon of
$Q_{red}$
is a dimer model on a disk composed of a single digon, or every digon of
 $Q_{red}$
is an internal face incident to only one other face.
$Q_{red}$
is an internal face incident to only one other face.
The condition (5) means that, as long as
![]() $Q_{red}$
is not composed of a single digon, every digon of
$Q_{red}$
is not composed of a single digon, every digon of
![]() $Q_{red}$
is in a configuration like that of Figure 21. See also Figure 14. In contrast, the configuration of Figure 20 is not possible in a weakly consistent dimer model.
$Q_{red}$
is in a configuration like that of Figure 21. See also Figure 14. In contrast, the configuration of Figure 20 is not possible in a weakly consistent dimer model.
Proof. Note that (3) follows from (1). Suppose that Q is not merely a digon and let
![]() $\alpha \beta $
be a digon of Q which is either a boundary face or is incident to two distinct faces. Then
$\alpha \beta $
be a digon of Q which is either a boundary face or is incident to two distinct faces. Then
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
may not both be boundary arrows. Suppose
$\beta $
may not both be boundary arrows. Suppose
![]() $\alpha \beta $
is a clockwise face; the counter-clockwise case is symmetric.
$\alpha \beta $
is a clockwise face; the counter-clockwise case is symmetric.
If
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are both internal arrows, then by assumption, the faces
$\beta $
are both internal arrows, then by assumption, the faces
![]() $F_\alpha ^{cc}$
and
$F_\alpha ^{cc}$
and
![]() $F_\beta ^{cc}$
are the distinct neighbors of the digon
$F_\beta ^{cc}$
are the distinct neighbors of the digon
![]() $\alpha \beta $
. Let
$\alpha \beta $
. Let
![]() $Q^1=(Q^1_0,Q^1_1,Q^1_2)$
be the dimer model whose underlying quiver is Q without
$Q^1=(Q^1_0,Q^1_1,Q^1_2)$
be the dimer model whose underlying quiver is Q without
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
and whose set of faces is the same as
$\beta $
and whose set of faces is the same as
![]() $Q_2$
, but with the faces
$Q_2$
, but with the faces
![]() $\{\alpha \beta ,F_\alpha ^{cc},F_\beta ^{cc}\}$
replaced with one face whose arrows are those of
$\{\alpha \beta ,F_\alpha ^{cc},F_\beta ^{cc}\}$
replaced with one face whose arrows are those of
![]() $R_\alpha ^{cc}$
and
$R_\alpha ^{cc}$
and
![]() $R_\beta ^{cc}$
. Since the dimer algebra relations of Q give
$R_\beta ^{cc}$
. Since the dimer algebra relations of Q give
![]() $[\alpha ]=[R_\beta ^{cc}]$
and
$[\alpha ]=[R_\beta ^{cc}]$
and
![]() $[\beta ]=[R_\alpha ^{cc}]$
, the dimer algebra is not changed by this operation. The surface is also unchanged by this operation. If
$[\beta ]=[R_\alpha ^{cc}]$
, the dimer algebra is not changed by this operation. The surface is also unchanged by this operation. If
![]() $\mathcal M$
is a perfect matching of Q, then
$\mathcal M$
is a perfect matching of Q, then
![]() $\mathcal M$
contains either
$\mathcal M$
contains either
![]() $\alpha $
or
$\alpha $
or
![]() $\beta $
, and the removal of this arrow from
$\beta $
, and the removal of this arrow from
![]() $\mathcal M$
gives a perfect matching of Q. Hence, if Q is nondegenerate, then
$\mathcal M$
gives a perfect matching of Q. Hence, if Q is nondegenerate, then
![]() $Q^1$
is nondegenerate. See Figure 18.
$Q^1$
is nondegenerate. See Figure 18.
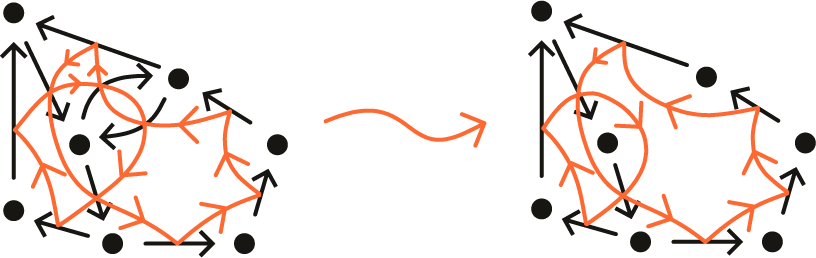
Figure 18 Removing an internal digon.
However, suppose without loss of generality that
![]() $\alpha $
is a boundary arrow and
$\alpha $
is a boundary arrow and
![]() $\beta $
is internal. Then let
$\beta $
is internal. Then let
![]() $Q^1$
be the dimer model obtained by removing the arrow
$Q^1$
be the dimer model obtained by removing the arrow
![]() $\alpha $
from
$\alpha $
from
![]() $Q_1$
and the face
$Q_1$
and the face
![]() $\alpha \beta $
from
$\alpha \beta $
from
![]() $Q_2$
. As above,
$Q_2$
. As above,
![]() $[\alpha ]=[R_\beta ^{cc}]$
in
$[\alpha ]=[R_\beta ^{cc}]$
in
![]() $A_Q$
, and hence, the dimer model is unchanged by this operation. If
$A_Q$
, and hence, the dimer model is unchanged by this operation. If
![]() $\mathcal M$
is a perfect matching of Q, then
$\mathcal M$
is a perfect matching of Q, then
![]() $\mathcal M$
contains
$\mathcal M$
contains
![]() $\alpha $
or
$\alpha $
or
![]() $\beta $
. If
$\beta $
. If
![]() $\mathcal M$
contains
$\mathcal M$
contains
![]() $\alpha $
, then removing this arrow gives a perfect matching of
$\alpha $
, then removing this arrow gives a perfect matching of
![]() $\mathcal M$
. If
$\mathcal M$
. If
![]() $\mathcal M$
contains
$\mathcal M$
contains
![]() $\beta $
, then
$\beta $
, then
![]() $\mathcal M$
is also a perfect matching of Q. Then if Q is nondegenerate, then
$\mathcal M$
is also a perfect matching of Q. Then if Q is nondegenerate, then
![]() $Q^1$
is nondegenerate. Furthermore,
$Q^1$
is nondegenerate. Furthermore,
![]() $S(Q^1)=S(Q)$
. See Figure 19.
$S(Q^1)=S(Q)$
. See Figure 19.

Figure 19 Removing a boundary digon.
Figure 20 One way that that a digon could be incident to only one other face. The strand diagram has a bad lens; hence, this configuration is not possible in a weakly consistent dimer model.
Figure 21 A reduced dimer model on an annulus with a digon which may not be removed.
In either case, we have defined a quiver
![]() $Q^1$
such that
$Q^1$
such that
![]() $S(Q^1)=S(Q)$
and
$S(Q^1)=S(Q)$
and
![]() $A_{Q^1}\cong A_Q$
. Furthermore,
$A_{Q^1}\cong A_Q$
. Furthermore,
![]() $Q^1$
has strictly less digons than Q. We may now apply this process repeatedly to remove all such digons of Q. Note that a digon cannot be removed only if it is internal and incident to only one face or it is incident to no other faces. In the latter case, such a digon constitutes the entire dimer model. Therefore, since Q has a finite number of digons, this process must terminate with some
$Q^1$
has strictly less digons than Q. We may now apply this process repeatedly to remove all such digons of Q. Note that a digon cannot be removed only if it is internal and incident to only one face or it is incident to no other faces. In the latter case, such a digon constitutes the entire dimer model. Therefore, since Q has a finite number of digons, this process must terminate with some
![]() $Q_{red}$
such that
$Q_{red}$
such that
![]() $Q_{red}$
is a dimer model on a disk composed of a single digon, or every digon of
$Q_{red}$
is a dimer model on a disk composed of a single digon, or every digon of
![]() $Q_{red}$
is internal and incident to only one other face.
$Q_{red}$
is internal and incident to only one other face.
Figure 21 shows a weakly consistent model with an internal digon which may not be removed by the process of the above theorem. Indeed, if the digon is removed, then the resulting ‘dimer model’ would have a face which is not homeomorphic to an open disk. On the level of strand diagrams, removing the digon corresponds to an untwisting move that disconnects the strand diagram. If Q has an infinite number of digons, a new problem appears. See Figure 22, which shows an infinite model with an infinite number of digons. While any finite number of digons may be removed, all of them may not be removed at once. The universal cover of the dimer model of Figure 21 displays the same behavior.
Figure 22 Shown is a dimer model on an infinite half-strip. If all digons were removed, then there would only be one infinite face making up the entire non-compact surface, which is impossible.
Remark 9.2. In [Reference Pressland47, §3], Pressland outlines a method of removing digons from general Jacobian ice quivers without changing the completed algebra. If this process is applied to the dimer model of Figure 21, the resulting ice quiver is not a dimer model.
Note that neither Figure 21 nor Figure 22 is nondegenerate. In fact, the following result shows that any strongly consistent dimer model may be reduced to a dimer model with no digons.
Corollary 9.3. Let Q be a strongly consistent dimer model. There exists a reduced dimer model
![]() $Q_{red}$
of Q satisfying the following:
$Q_{red}$
of Q satisfying the following:
-
1.
 $S(Q_{red})=S(Q)$
,
$S(Q_{red})=S(Q)$
, -
2.
 $A_{Q_{red}}\cong A_Q$
,
$A_{Q_{red}}\cong A_Q$
, -
3.
 $Q_{red}$
is strongly consistent, and
$Q_{red}$
is strongly consistent, and -
4. Either
 $Q_{red}$
is a dimer model on a disk composed of a single digon, or
$Q_{red}$
is a dimer model on a disk composed of a single digon, or
 $Q_{red}$
has no digons.
$Q_{red}$
has no digons.
Proof. Apply Proposition 9.1. If
![]() $Q_{red}$
is not a dimer model on a disk composed of a single digon, then
$Q_{red}$
is not a dimer model on a disk composed of a single digon, then
![]() $Q_{red}$
has an internal digon
$Q_{red}$
has an internal digon
![]() $\alpha \beta $
which is incident to a single other face F. Let
$\alpha \beta $
which is incident to a single other face F. Let
![]() $\gamma $
be an arrow of F which is not
$\gamma $
be an arrow of F which is not
![]() $\alpha $
or
$\alpha $
or
![]() $\beta $
. Any perfect matching
$\beta $
. Any perfect matching
![]() $\mathcal M$
must contain
$\mathcal M$
must contain
![]() $\alpha $
or
$\alpha $
or
![]() $\beta $
, since
$\beta $
, since
![]() $\alpha \beta $
is a face. Then
$\alpha \beta $
is a face. Then
![]() $\mathcal M$
cannot contain
$\mathcal M$
cannot contain
![]() $\gamma $
, since
$\gamma $
, since
![]() $\gamma $
shares a face with these arrows. We have shown that no perfect matching contains
$\gamma $
shares a face with these arrows. We have shown that no perfect matching contains
![]() $\gamma $
. Then
$\gamma $
. Then
![]() $Q_{red}$
, and by extension Q, is degenerate.
$Q_{red}$
, and by extension Q, is degenerate.
We remark that
![]() $Q_{red}$
may have 1-cycles and 2-cycles, even if it has no digons. Consider the dimer model on a torus pictured on the left of Figure 23. While the quiver Q has 2-cycles, it has no null-homotopic 2-cycles. As we see by looking at the universal cover model on the right, this means that there are no digons in Q; hence,
$Q_{red}$
may have 1-cycles and 2-cycles, even if it has no digons. Consider the dimer model on a torus pictured on the left of Figure 23. While the quiver Q has 2-cycles, it has no null-homotopic 2-cycles. As we see by looking at the universal cover model on the right, this means that there are no digons in Q; hence,
![]() $Q=Q_{red}$
is reduced.
$Q=Q_{red}$
is reduced.
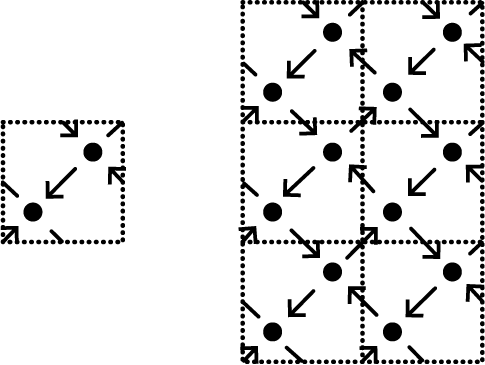
Figure 23 Shown on the left is a dimer model on a torus. Opposite dashed edges should be identified. Shown on the right is a piece of its universal cover model.
Acknowledgements
The authors thank Matthew Pressland for useful discussions and for comments on preliminary versions. The authors also thank two anonymous referees for their careful review of the manuscript.
Competing interest
The authors have no competing interests to declare.
Funding statement
The authors were supported by the NSF grant DMS-2054255.










































