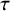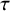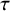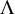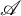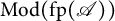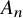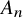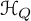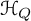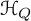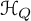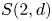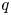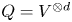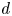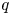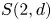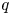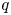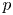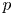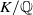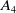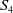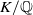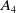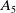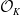Refine listing
Actions for selected content:
149 results in 16Gxx
Moduli of objects in finite length abelian categories
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mutation graph of support
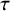 $\tau $-tilting modules over a skew-gentle algebra
$\tau $-tilting modules over a skew-gentle algebra
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 July 2025, e113
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Consistent dimer models on surfaces with boundary
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 July 2025, e114
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FISHING FOR COMPLEMENTS
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 07 July 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Homological Berglund–Hübsch–Henningson mirror symmetry for curve singularities
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 28 April 2025, pp. 385-442
- Print publication:
- May 2025
-
- Article
- Export citation
Vector fields and admissible embeddings for quiver moduli
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalised Temperley–Lieb algebras of type G(r, p, n)
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 08 April 2025, pp. 193-227
- Print publication:
- March 2025
-
- Article
- Export citation
The rigidity of filtered colimits of n-cluster tilting subcategories
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 06 February 2025, pp. 1-14
-
- Article
- Export citation
Locally finitely presented Grothendieck categories and the pure semisimplicity conjecture
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-27
-
- Article
- Export citation
On split quasi-hereditary covers and Ringel duality
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 December 2024, e105
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A smooth compactification of spaces of stability conditions: the case of the
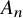 $A_{n}$-quiver
$A_{n}$-quiver
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 November 2024, e101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tachikawa's second conjecture, derived recollements, and gendo-symmetric algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 27 December 2024, pp. 2704-2737
- Print publication:
- November 2024
-
- Article
- Export citation
Resolving dualities and applications to homological invariants
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 22 October 2024, pp. 1-29
-
- Article
- Export citation
QUASI-HEREDITARY SKEW GROUP ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 24 September 2024, pp. 1-44
- Print publication:
- March 2025
-
- Article
- Export citation
DT INVARIANTS FROM VERTEX ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 20 September 2024, pp. 291-339
- Print publication:
- January 2025
-
- Article
- Export citation
Quasi-hereditary covers of Temperley–Lieb algebras and relative dominant dimension
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Skew group categories, algebras associated to Cartan matrices and folding of root lattices
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1-45
-
- Article
- Export citation
WHEN IS THE SILTING-DISCRETENESS INHERITED?
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 256 / December 2024
- Published online by Cambridge University Press:
- 01 April 2024, pp. 905-927
- Print publication:
- December 2024
-
- Article
- Export citation
Log Calabi–Yau surfaces and Jeffrey–Kirwan residues
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 04 March 2024, pp. 547-592
- Print publication:
- May 2024
-
- Article
- Export citation
Leopoldt-type theorems for non-abelian extensions of
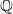 $\mathbb{Q}$
$\mathbb{Q}$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 22 January 2024, pp. 308-337
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation