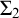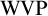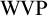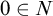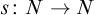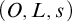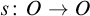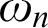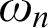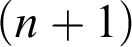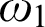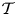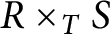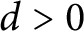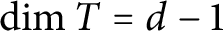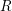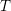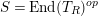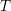Refine listing
Actions for selected content:
43 results in 18Axx
Relative cell complexes in closure spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 20 June 2025, pp. 1-9
-
- Article
- Export citation
ENRICHED CONCEPTS OF REGULAR LOGIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 April 2025, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Locally finitely presented Grothendieck categories and the pure semisimplicity conjecture
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-27
-
- Article
- Export citation
The weak Ramsey property and extreme amenability
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 11 November 2024, e96
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Flat model structures and Gorenstein objects in functor categories
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 May 2024, pp. 1-21
-
- Article
- Export citation
Functorial Fast-Growing Hierarchies
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 January 2024, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONDITIONAL FLATNESS, FIBERWISE LOCALIZATIONS, AND ADMISSIBLE REFLECTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 23 June 2023, pp. 200-220
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE WEAK VOPĚNKA PRINCIPLE FOR DEFINABLE CLASSES OF STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 June 2022, pp. 145-168
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Pirashvili-type theorem for functors on non-empty finite sets
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 01 March 2022, pp. 1-61
- Print publication:
- January 2023
-
- Article
- Export citation
A DEDEKIND-STYLE AXIOMATIZATION AND THE CORRESPONDING UNIVERSAL PROPERTY OF AN ORDINAL NUMBER SYSTEM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 26 January 2022, pp. 1396-1418
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dimensions of Ordinals: Set Theory, Homology Theory, and the First Omega Alephs
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 February 2022, pp. 526-527
- Print publication:
- December 2021
-
- Article
-
- You have access
- Export citation
ON GRAEV’S THEOREM FOR FREE PRODUCTS OF HAUSDORFF TOPOLOGICAL GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 29 March 2021, pp. 475-483
- Print publication:
- December 2021
-
- Article
- Export citation
THE YONEDA EXT AND ARBITRARY COPRODUCTS IN ABELIAN CATEGORIES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 19 March 2021, pp. 277-291
- Print publication:
- May 2022
-
- Article
- Export citation
Recollements, comma categories and morphic enhancements
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 09 March 2021, pp. 567-591
- Print publication:
- June 2022
-
- Article
- Export citation
Almost Gorenstein rings arising from fiber products
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 10 July 2020, pp. 383-400
- Print publication:
- June 2021
-
- Article
- Export citation
CATEGORICAL COMPLEXITY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 30 June 2020, e34
-
- Article
-
- You have access
- Open access
- Export citation
EXACT COMPLETION AND CONSTRUCTIVE THEORIES OF SETS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 18 June 2020, pp. 563-584
- Print publication:
- June 2020
-
- Article
-
- You have access
- Open access
- Export citation
REPETITIVE EQUIVALENCES AND TILTING THEORY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 243 / September 2021
- Published online by Cambridge University Press:
- 06 December 2019, pp. 97-136
- Print publication:
- September 2021
-
- Article
- Export citation
Décomposition de Hodge pour l’homologie stable des groupes d’automorphismes des groupes libres
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 9 / September 2019
- Published online by Cambridge University Press:
- 07 August 2019, pp. 1794-1844
- Print publication:
- September 2019
-
- Article
- Export citation
CATEGORICAL PROOF OF HOLOMORPHIC ATIYAH–BOTT FORMULA
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 20 December 2018, pp. 1739-1763
- Print publication:
- September 2020
-
- Article
- Export citation