The motivation of this article is to introduce a kind of orbit equivalence relations which can well describe structures and properties of Polish groups from the perspective of Borel reducibility. Given a Polish group G, let 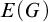 $E(G)$ be the right coset equivalence relation
$E(G)$ be the right coset equivalence relation 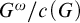 $G^\omega /c(G)$, where
$G^\omega /c(G)$, where 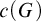 $c(G)$ is the group of all convergent sequences in G. Let G be a Polish group. (1) G is a discrete countable group containing at least two elements iff
$c(G)$ is the group of all convergent sequences in G. Let G be a Polish group. (1) G is a discrete countable group containing at least two elements iff 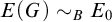 $E(G)\sim _BE_0$; (2) if G is TSI uncountable non-Archimedean, then
$E(G)\sim _BE_0$; (2) if G is TSI uncountable non-Archimedean, then 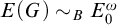 $E(G)\sim _BE_0^\omega $; (3) G is non-Archimedean iff
$E(G)\sim _BE_0^\omega $; (3) G is non-Archimedean iff 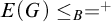 $E(G)\le _B=^+$; (4) if H is a CLI Polish group but G is not, then
$E(G)\le _B=^+$; (4) if H is a CLI Polish group but G is not, then 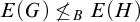 $E(G)\not \le _BE(H)$; and (5) if H is a non-Archimedean Polish group but G is not, then
$E(G)\not \le _BE(H)$; and (5) if H is a non-Archimedean Polish group but G is not, then 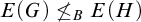 $E(G)\not \le _BE(H)$. The notion of
$E(G)\not \le _BE(H)$. The notion of 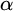 $\alpha $-l.m.-unbalanced Polish group for
$\alpha $-l.m.-unbalanced Polish group for 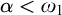 $\alpha <\omega _1$ is introduced. Let G and H be Polish groups,
$\alpha <\omega _1$ is introduced. Let G and H be Polish groups, 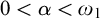 $0<\alpha <\omega _1$. If G is
$0<\alpha <\omega _1$. If G is 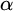 $\alpha $-l.m.-unbalanced but H is not, then
$\alpha $-l.m.-unbalanced but H is not, then 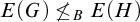 $E(G)\not \le _B E(H)$. For TSI Polish groups, the existence of Borel reduction is transformed into the existence of a well-behaved continuous mapping between topological groups. As its applications, for any Polish group G, let
$E(G)\not \le _B E(H)$. For TSI Polish groups, the existence of Borel reduction is transformed into the existence of a well-behaved continuous mapping between topological groups. As its applications, for any Polish group G, let 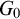 $G_0$ be the connected component of the identity element
$G_0$ be the connected component of the identity element 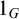 $1_G$. Let G and H be two separable TSI Lie groups. If
$1_G$. Let G and H be two separable TSI Lie groups. If 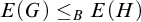 $E(G)\le _BE(H)$, then there exists a continuous locally injective map
$E(G)\le _BE(H)$, then there exists a continuous locally injective map 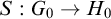 $S:G_0\to H_0$. Moreover, if
$S:G_0\to H_0$. Moreover, if 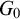 $G_0$ and
$G_0$ and 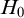 $H_0$ are abelian, S is a group homomorphism. In particular, for
$H_0$ are abelian, S is a group homomorphism. In particular, for 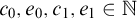 $c_0,e_0,c_1,e_1\in {\mathbb {N}}$,
$c_0,e_0,c_1,e_1\in {\mathbb {N}}$, 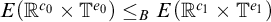 $E({\mathbb {R}}^{c_0}\times {\mathbb {T}}^{e_0})\le _BE({\mathbb {R}}^{c_1}\times {\mathbb {T}}^{e_1})$ iff
$E({\mathbb {R}}^{c_0}\times {\mathbb {T}}^{e_0})\le _BE({\mathbb {R}}^{c_1}\times {\mathbb {T}}^{e_1})$ iff 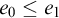 $e_0\le e_1$ and
$e_0\le e_1$ and 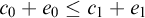 $c_0+e_0\le c_1+e_1$.
$c_0+e_0\le c_1+e_1$.
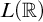 $L(\mathbb {R})$
$L(\mathbb {R})$
 $\delta $-SEPARATED SETS IN SEPARABLE METRIC SPACES AND WEAK FORMS OF CHOICE
$\delta $-SEPARATED SETS IN SEPARABLE METRIC SPACES AND WEAK FORMS OF CHOICE
 $w\diamondsuit _{\omega _1}$
$w\diamondsuit _{\omega _1}$